
Effective Evaluation of Autonomous Taxi Fleets
Philippe Mathieu and Antoine Nongaillard
Univ. Lille, CNRS, Centrale Lille, UMR 9189 - CRISTAL - Centre de Recherche en Informatique Signal et Automatique de
Lille, F-59000 Lille, France
Keywords:
Simulation, Multiagent Systems, Complex Systems, Collective Strategies, Trafic Management Systems.
Abstract:
With the advent of autonomous vehicles, self-management of taxis fleet becomes an important issue for the
automotive industry. Designing strategies for taxis turns out to be a difficult task due to a large number of
parameters and metrics involved. Performance evaluation of these strategies is also a complex problem since
effectiveness in some configurations may become inefficiency in others. After formalizing this problem we
propose several strategies based on swarm-computing techniques. Finally, we show that metric unification is
necessary and that only a multi-criterion approach illustrated by an economic analysis allows a comparison.
We conclude with a description of the simulator implemented and some examples showing the measurements
made with the proposed strategies.
1 INTRODUCTION
In recent years, research related to autonomous vehi-
cles has been on the rise for car manufacturers as well
as for academics. (Tlig et al., 2012; Cheikh and Ham-
madi, 2014; Dresner and Stone, 2008). Nowadays,
fleets of autonomous vehicles can be created and used
to solve collective tasks. One of them is the establish-
ment of taxi fleets, able to negotiate and effectively
manage customers in a geographical area.
The use of centralised optimisation techniques is
only possible if all requests from clients in a time win-
dow are known, in order to optimise the assignment
of taxis to clients according to their position. Un-
fortunately, in real life, it is not true. Without prior
knowledge on client requests, the system must handle
dynamic data, which is the main advantages of multi-
agent system approaches.
On one side, clients perceive taxis movement in
two steps: waiting to get into the taxi, which must
be carried out efficiently according to its own crite-
ria (speed, comfort. . . ) and the transportation phase
to its destination, which must also be carried out ef-
fectively (speed, price. . . ). On the other side, three
major steps structure the behaviour of a taxi. (i) The
positioning strategy, when there is no client. A rea-
sonable attitude requires taxis positioned in the vicin-
ity of future applications if they are known. The
number and position of the various customer requests
vary over time. Depending on the time of the day,
hot spots appear or disappear (arrivals of trains, ex-
its from concerts. . . ) creating varied dynamics of of-
fers and requests. (ii) The selection of a client when
there are several. Which taxi takes which customer?
This choice requires negotiation either between taxis
or with customers or even both. (iii) The transport
of the selected client. This transport requires consid-
ering static information related to the road infrastruc-
ture (in particular speed limitations, positions of traf-
fic lights) and dynamic information on this infrastruc-
ture (e.g., congestion of roads).
The fleet manager wishes of course to maximise
its profits: on the one hand reducing costs (number of
vehicles, inactive vehicles. . . ), maximising the num-
ber of people taken on, on the other hand. Conse-
quently, the number of taxis, their waiting position,
and their coordination become the primary factor (the
distribution of taxis should be based on the prediction
of applications: sometimes all at the same place, but
sometimes all equally distributed). It is necessary to
design vehicle behaviours maximising the effective-
ness of the whole fleet, from the point of view of cus-
tomers, taxis or the manager. Our objective is to iden-
tify collective strategies for the management of taxi
fleets and to know how to compare them.
This article is organised as follows. Section 2
presents the state-of-the-art related to managing ve-
hicle fleets through optimisation and simulation ap-
proaches. Section 3 describes the benefits of us-
ing multiagent systems for this kind of problem and
we describe different positioning strategies of empty
taxis as well. Section 4 presents the assessment
Mathieu, P. and Nongaillard, A.
Effective Evaluation of Autonomous Taxi Fleets.
DOI: 10.5220/0006720002970304
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 1, pages 297-304
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
297

method and the comparison of the strategies we pro-
pose. Section 5 concludes and describes the prospects
for future research.
2 LITERATURE REVIEW
Numerous works dealing with problems related to
traffic/road simulation are referenced in the literature
as (Bazzan and Klgl, 2014). These problems deal
mostly with two aspects.
Traffic regulation is one aspect in which many
works study multi-agent road simulation. Vehicle co-
ordination for effective intersection management is
carefully explored: using multiagent modelling of in-
tersection and vehicles, the overall behaviour is self-
adaptive in situations such as the appearance of pri-
ority vehicles (Dresner and Stone, 2008), or using
a two-player game modelling to characterise specific
situations (Mandiau et al., 2008), but also in a more
general framework as in (Badeig et al., 2008).
Other works focus on the design of behaviour: ei-
ther by proposing tools to support this design (Bon-
homme et al., 2014), or by proposing behaviours ded-
icated to enhance the realism of simulations: for in-
stance (Lacroix et al., 2009; Lacroix et al., 2013)
propose generation methods in order to increase be-
haviour diversity as well as the simulation realism
through a normative approach while (Bonte et al.,
2006) introduces heterogeneity in simulation through
two-wheel agents and specific behaviours in order to
study their impact on the traffic. Finally, other works
propose cooperative behaviours to improve the over-
all efficiency of a system by managing conflicts lo-
cally, guaranteeing a limited perception of agents as
well as little communication (Tlig et al., 2012).
Studies on the simulation and evaluation of a
transportation system as a whole are numerous (Man-
ley et al., 2014; Yang, 1997; Bonhomme et al., 2016;
Barcel
´
o et al., 2005). Such works often support the
design and evaluation of road behaviour. Some works
address issues related to the impact of road infrastruc-
ture modification while others deal with more spe-
cific problems such as urban-area parking (Bessghaier
et al., 2012). Recently, other studies have focused
on specific phenomena as for the vehicle-sharing
(Cheikh and Hammadi, 2014): a hybrid method based
on optimisation techniques and multi-agent systems
allows the parallel assignment of vehicles on demand,
on an environment, divided into distinct geographical
areas within which an optimal assignment is scalable.
(Billhardt et al., 2014) study the dynamic coordina-
tion of a transportation system but focus on the archi-
tecture required to achieve it and not on individual be-
haviour as we propose. They still require centralised
entity to act as a fleet operator, which we claim un-
necessary.
The problem we are interested in, the manage-
ment of taxis fleet, has already been studied under
different aspects. (Lioris et al., 2010) proposes a
discrete-event simulator supporting the design of op-
timal behaviour through learning and systematic test-
ing of many strategies (centralised and distributed).
However, these behaviours cannot adapt themselves
in front of different situations that may arise (peaks
of applications, congestion. . . ). Other studies focus
on the benefits of cooperation between taxis in the
assignment process (Maciejewski and Nagel, 2013).
This approach relies on the existence of a dispatcher
and on the amount of information shared, which
might nevertheless be reduced to a minimum if the
strategy developed becomes complex.
In contrast to approaches based on optimisation
techniques as (Cheikh and Hammadi, 2014) or (Li-
oris et al., 2010), we propose an approach based on
autonomous and adaptive agents, allowing distributed
coordination based on agents with local perception
and reasoning.
3 MULTIAGENT APPROACH
One can easily understand that in such a system, no
client should wait too long, and no taxi should remain
too inactive. Strategy evaluation contains an essen-
tial temporal dimension. This temporality can only be
measured based on real travel time as well as consid-
ering distances and congestion. Therefore, the road
infrastructure must be represented using an GIS (Ge-
ographic Information System) graph or an adjacency
matrix encoding both distances and travel times.
Based on such a representation of the road infras-
tructure, it is possible to simulate congestion, to com-
pute the shortest distance and travel time from one
point to another, and to determine the number of cus-
tomers that can be conveyed for a given period of
time, as soon as their application is regular and in-
finite. However, as soon as positioning strategies are
necessary, patterns of customer applications are irreg-
ular or, as soon as one seeks to evaluate heteroge-
neous fleets, the notion of behaviour becomes prepon-
derant. It constitutes a complex system, with many
retro-action loops. Moreover, under incomplete in-
formation, notions of perception and neighbourhood
are required: an GIS map with vehicles moving on it
become unavoidable.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
298

3.1 A Distributed Solving Required?
While it is quite clear that an GIS map and simulated
vehicles moving on it are required, such a simulation
can be implemented in two ways: centralised compu-
tation that optimises constraints and assigns taxis, or
thanks to a behavioural model in which each taxi has
its own decision model.
The perception halo restricts the volume of infor-
mation which each taxi can access, and also allows a
limited rationality. Three types of information can be
distinguished perception of infrastructure (including
roads, congestion. . . ), perception of customers (inter-
action with customers within the halo), and percep-
tion of other taxis (exchange of information between
close taxis).
A behavioural approach such as the one we pro-
pose allows the test of all these hypotheses based on
the same model: perception radius, halos shape, na-
ture of interactions as well as information exchanged.
The ideal system in which all information would be
public and immediately known to all is directly ob-
tained by considering halos of infinite radius, ac-
counting as a centralised system.
Perception of the
infrastructure
Perception of
clients
Perception of
other taxis
Figure 1: Different perception halos for a vehicle.
Numerous events only have a local impact: a
congestion to the south of Manhattan leads to very
few consequences for vehicles travelling solely to the
north. Broadcasting such information to all is useless.
Any modelling requires choosing the level of
granularity desired. Each business expert decides
what is relevant to his model, for his experiments. Of
course, the finer the granularity, the more important
the number of concepts to consider. It enriches the
model and makes it more complex, impacting its im-
plementation and its effectiveness. All models require
a compromise. For instance, is it required to specify
a behaviour to pedestrians or traffic lights? These al-
ternatives are both possible by extending our model.
However, we choose to only individualise taxis and
customers. Other vehicles will simply be represented
by a flow. Thus, each GIS road segment contains a
speed limit and its level of congestion. Similarly, cus-
tomers do not have their own behaviour, but simply a
place of appearance and a destination.
The use of individual-centred approach guaran-
tees the design of autonomous agents, and a self-
adaptive system as well that is very suitable for this
fundamentally dynamic problem. Taxis automatically
adapt to customer requests, to other taxis, to traffic
congestion. . .
3.2 Description of Strategies
First of all, the way clients are considered must be
detailled. In this study, clients are generated at spe-
cific places called client generators. Each generator
creates clients according to a predefined probability
distribution, each client is associated with a destina-
tion and a time-to-live. If no taxi picks a client up
before the term of its time-to-life, the request is can-
celled. Generators have been used to simplify mod-
elling assumption, to represent hot spots where clients
appear regularly and to facilitate stategy comparisons.
Of course, if needed, it is possible to generate clients
on any node of a given area.
The distributed management of a fleet of au-
tonomous taxis is based on three distinct tasks men-
tioned above: customer selection, customer transport
and positioning of the taxi when it is empty. The be-
haviour of a taxi should describe these three aspects
for which it is possible to adopt specific strategies. In
all these strategies, we consider that all agents (clients
and taxis) are cooperative, meaning that they all aim
at contributing to the maximization (or minimization)
of the same objective function.
3.2.1 Client Selection
The question of the customer selection will arise in
two situations: when a taxi receives several requests
for transport and when a customer applies. In the first
case, the taxi must decide which customer takes pri-
ority, whereas in the other case the question becomes
which taxi should move and transport him or her. Ob-
viously, an efficient management of the taxi fleet min-
imises unnecessary travel and thus avoids multiple
taxis to move towards the same customer.
The client selection can be managed via a
contract-net-like protocol (Smith, 1980). Indeed,
when a customer appears, he broadcasts a signal to
all taxis in the fleet (e.g., using his or her smartphone
application). Each taxi always answer to all requests
by an arrival time. Taxis decide independently of each
other to answer it or not. Indeed, each taxi has its own
policy based on various elements such as already hav-
ing a customer or not, depending on the distance with
Effective Evaluation of Autonomous Taxi Fleets
299

the client, or depending on the constraints emitted by
this client.
After receiving responses from the taxis, the client
then chooses the one that will transport him. Sim-
ilarly, each customer may have a selection process
based on its own criteria (more ecological, faster,
shortest distance. . . , lowest price). By default, a client
always chooses the taxi associated with the closest ar-
rival time. We consider that taxis will not be selected
by the client himself but by its smartphone applica-
tion, which can consider the so-called social criteria
related to the taxi fleet. The radius of the customer
call may vary in order to reach either only close vehi-
cles, or the whole fleet.
3.2.2 Taxi Positioning
The major difficulty relies mainly on the positioning
of the vehicles. Indeed, when the number of cus-
tomers is low, taxis should wait for customers. An
inactive taxi must question its positioning according
to the evolution of its knowledge (either by exchange
with others or by direct perception of its environ-
ment): Would it more likely have a client by being
placed elsewhere? All taxis must not position them-
selves and wait at the same place: some forms of co-
ordination is necessary for this purpose. The two first
strategies described next do not require any informa-
tion, their decision-making is based on their own in-
formation and the notion of fleet is nonexistent for
each individual. At the opposite, the two last strate-
gies are swarm-based since taxis share information
and use them to make their decision that can be based
either on self-interest or on social motives.
The different positioning strategies considered
are:
• random: when a taxi is empty, it selects randomly
one of the generators and goes there. If there is no
client, the vehicle waits for one.
• closest: as soon as a taxi is empty, it selects the re-
quest generator the closest to its position and goes
there. If there is no customer, the taxi join the
queue.
• probabilistic: when a taxi is empty, it selects a
generator according to the number of requests
pending and goes there. The more pending re-
quests a generator has, the more chances it has to
be selected. If there is no request, the taxi lines
up and waits. Such a strategy assumes that taxis
know the number of customers waiting on all gen-
erators.
• most-requested: when a taxi is empty, it selects
the generator associated with the largest num-
ber of pending requests, according to its knowl-
edge. Without knowledge on waiting clients, it
randomly selects one generator. When taxis inter-
sect, they can exchange information on the status
of applications in order to update their knowledge.
This strategy, based on local exchanges of infor-
mation, constitutes a swarm-based strategy.
This list of strategies does not aim at being ex-
haustive. Each of these strategies can be extended in
different versions according to the amount of infor-
mation that a taxi can recover. Indeed, the exchange
of local information can have an impact on the effec-
tiveness. The strategies described here are primarily
intended to illustrate the range of possibilities.
4 COMPARING STRATEGIES
4.1 Preconception
The comparison of behaviours in such a context raises
a large number of difficulties that must be considered
if relevant results are desired. We assume that the
evaluation of such a system relies on the aggregation
of a set C of n criteria C = {c
i
}
n
i=1
. The objective
function can be written in a very generic way:
F (c
1
, . . . , c
n
) = f (c
1
, . . . , c
n
)
The comparison of different fleet management
strategies must imperatively compare them under the
same experimental conditions, these conditions being
scripted in time. This is what we call an execution
scenario and define as a tuple S = (G, E, S, D) where
G is the GIS graph describing the road infrastructure,
E describes the traffic conditions, S = {s
i
}
u
i=1
is the
set of client generators (GIS position and appearance
rate of clients at this point) and D = {d
i
}
v
i=1
is the set
of destinations requested by customers.
All these parameters define a scenario, which
must be the same to allow comparison of strategy ef-
fectiveness. These common experimental conditions
are essential to assess the impact of simulation pa-
rameters and behaviour of taxis: such as the fleet size,
the taxis perception/interaction radius, the positioning
strategy, client selection rules. . .
The effectiveness of strategies is highly dependent
on the scenario used. Indeed, a very effective strategy
on one scenario may perform terribly on another. Fig-
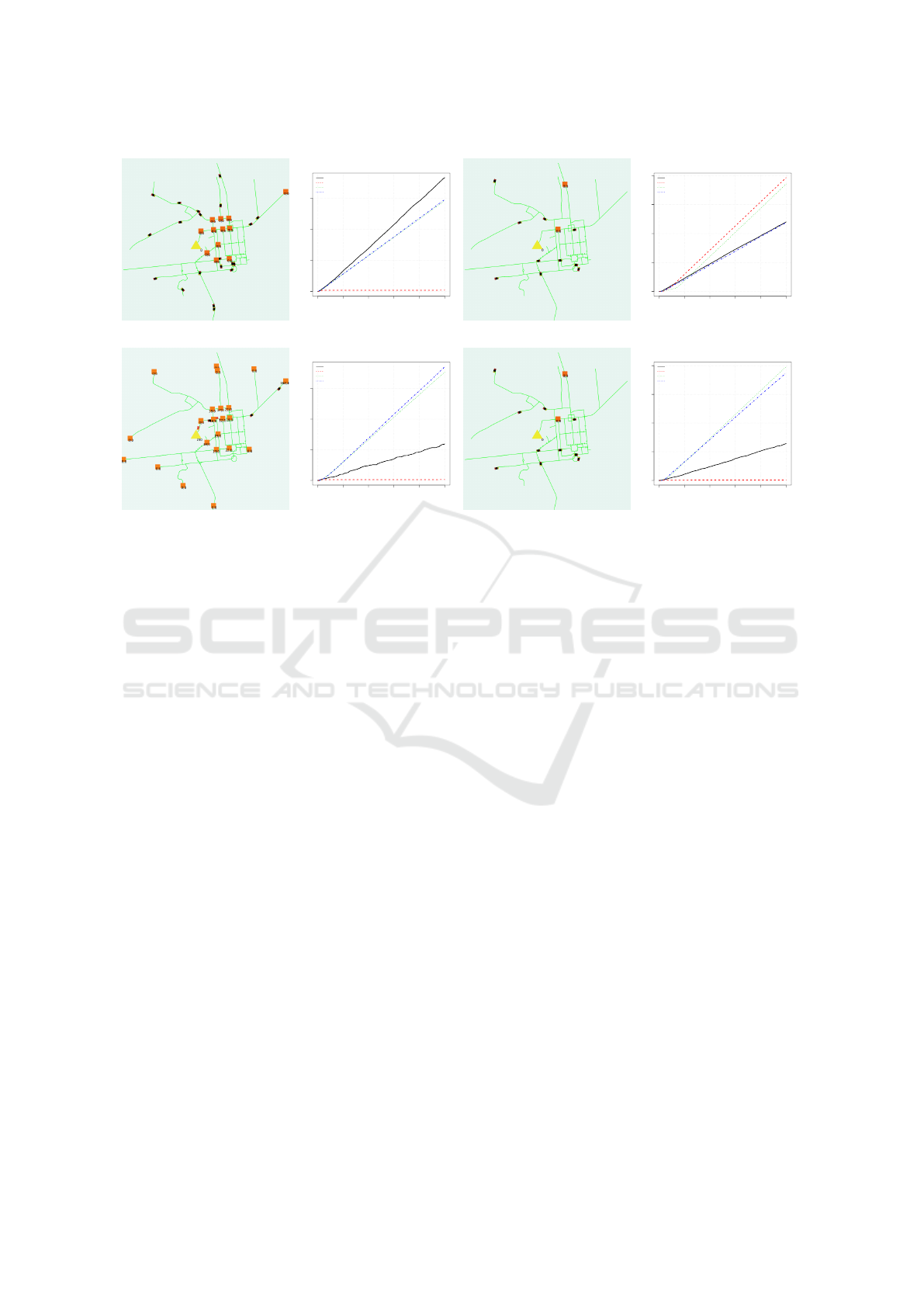
ure 2 illustrates the manipulability of results. Each
simulation was carried out on the same road infras-
tructure, on which a fleet of 10 taxis having complete
information operates. The number of customers trans-
ported is used to measure the fleet efficiency. In each
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
300
0 500 1000 1500 2000 2500
0 500 1000 1500
time
Nb of accepted clients
Random
Closest
Most requested
Probabilist
0 500 1000 1500 2000 2500
0 500 1000 1500 2000
time
Nb of accepted clients
Random
Closest
Most requested
Probabilist
(a) (b)
0 500 1000 1500 2000 2500
0 200 400 600
time
Nb of accepted clients
Random
Closest
Most requested
Probabilist
0 500 1000 1500 2000 2500
0 500 1000 1500 2000
time
Nb of accepted clients
Random
Closest
Most requested
Probabilist
(c) (d)
Figure 2: On the same road infrastructure (Richelieu town), four scenarios makes a different strategy becomes the most
effective.
of the scenarios, client generators are represented by
an orange square while the yellow triangle represents
the destination requested by customers.
According to scenario (a), a large number of
clients (2,400 clients) are waiting on the client genera-
tor the furthest from the destination, the nearest gener-
ator generates 1 client every 240 minutes and the other
10 generators have a higher generation rate (1,200
customers generated in 480 minutes per generator).
Taxis that position themselves according to a random
strategy will mostly take clients from very active gen-
erators (since they represent 10 generators out of 12):
the fleet can thus take over a maximum of applicants.
However, if taxis position themselves according to a
closest strategy, they will stop at the nearest genera-
tor, which only generates few customers and the fleet
can only achieve very limited results. According to a
positioning most-requested strategy, taxis will always
move to the farthest generator (on which a large num-
ber of clients are waiting), therefore limiting the num-
ber of taken clients. A probability strategy encourages
taxis to take clients from the most distant generator
and the 10 closer generators according to the number
of clients, leading the fleet to achieve reserved results.
According to scenario (b), a customer-generator
close to the destination is very active (2,400 cus-
tomers generated in 240 minutes), while the further
one is associated with a lower rate (480 clients in 480
minutes). Taxis following the positioning strategies
random and probabilistic will serve both generators,
reducing the total number of clients that can be ac-
cepted. Taxis acting according to a closest positioning
strategy will only take clients from the closest genera-
tor, maximising the number of clients taken. A most-
requested positioning strategy leads taxis to the near-
est generator until more pending requests appear on
the most distant one, sending taxis to the latter. Such
a strategy does not maximise the number of clients
taken.
According to scenario (c), close to the lone desti-
nation, 1 weak generator (1 client every 240 minutes)
and 10 strong generators (136 customers in 480 min-
utes), while in remote areas rely on a very strong gen-
erator (1,496 customers in 480 minutes) and 11 weak
generators (1 customer in 480 minutes). Follow-
ing the positioning strategy of closest, taxis quickly
exhaust the nearest client-generator and come to a
halt, leading to a low total number of customers ac-
cepted. The random positioning strategy makes taxis
spend time on remote generators containing only a
few clients while the most-requested strategy makes
taxis head to the generator where the largest num-
ber of requests are pending, which is also the fur-
thest, ultimately reducing the total number of cus-
tomers taken. Only the probabilistic strategy dis-
tributes taxis between close generators with numerous
waiting clients.
According to scenario (d), a strong generator is
close to the destination (1,680 customers in 240 min-
utes) while a weak generator is more distant (1,215
Effective Evaluation of Autonomous Taxi Fleets
301

customers in 480 minutes). As before, the strategies
random and probabilist distribute taxis on all gen-
erators, wasting time by taking clients from further
generators while a lot of requests are pending closer.
The nearest strategy quickly exhausts the closest gen-
erator and then immobilises the fleet. Only most-
requested strategy distributes taxis on both client-
generators, but will first exhaust the closer one, max-
imising the total number of clients transported.
These 4 scenarios allow us to show that it is pos-
sible to design a scenario specifically dedicated to
making any strategy the most effective. Moreover,
here we have chosen to look only at the total num-
ber of clients taken to assess the effectiveness of the
taxi fleet, but it is possible to do the same with other
metrics. Indeed, behavioural assessment is also very
sensitive to another aspect: the metrics chosen for the
evaluation. Indeed, even if the scenario (i.e., the ex-
perimental conditions) is the same, the evaluation of
behaviours can lead to opposite conclusions accord-
ing to the metrics chosen for the evaluation. In ad-
dition, some metrics which may seem wise at first,
turn out to be perfectly disastrous. Indeed, let us as-
sume that the efficiency of a taxi fleet is evaluated
through the waiting time of customers that should be
minimised: F = min(t
a
). It is then sufficient to match
the number of taxis n
taxi
to the number of applications
r: the waiting time t
a
tends to zero but taxis will be in-
active most of the time.
n
taxi
→ r ⇒ t
a
→ 0 but t
i
→ ∞
On the other hand, if the effectiveness of a taxi fleet
is evaluated through the inactivity time of taxis which
should be minimised: F = min(t
i
). It is then suffi-
cient to reduce the number of taxis n
taxi
to one what-
ever the request.
n
taxi
→ 1 ⇒ t
i
→ 1 but t
a
→ ∞
The lone taxi of the fleet would thus always be busy
taking customers. However, the number of accepted
clients would be very low and their waiting time ex-
tremely long.
An intuitive idea could then be to aggregate these
different aspects within the same objective function.
A solution could be to minimise the product of cus-
tomers’ waiting time and taxis’ inactivity time: F =
t
i
× t
a
. The use of a product can be interpreted as
aiming at a compromise between taxis and customers
which can sometimes have opposite interests. Unfor-
tunately, such a function is no more relevant than the
previous ones. Indeed, it is very easy to get a nil value
by playing only on size of the taxi fleet: (i) if the fleet
size tends towards infinity, the client waiting time t
a
tends towards 0 as well as the whole objective func-
tion; (ii) on the other hand, if the fleet size tends to-
wards 1, the taxis inactivity time tends towards 0 just
like the objective function.
(i) n
taxi
→ ∞ ⇒ t
a
→ 0 ⇒ F → 0
(ii) n
taxi
→ 1 ⇒ t
i
→ 0 ⇒ F → 0
Thus, finding an objective function aggregating
the different aspects of the problem is a difficult task.
It is always possible to design a scenario or manipu-
late a parameter in order to shape the value of the ob-
jective function without achieving a meaningful com-
parison. The different criteria aggregated by the ob-
jective function do not have links between them: each
represents the problem according to a specific point
of view. Moreover, these aspects have their own
value scales: their comparison often has no meaning.
Thus, in order to evaluate such a complex problem
with multiple facets, it is necessary to create a com-
mon scale of values to allow comparison of strategies.
The more the evaluation metric aggregates various as-
pects, the more difficult the manipulation.
4.2 An Economical Approach to
Compare Strategies
A lot of aspects can be considered as common val-
ues scale for the evaluation: kilometres, time, en-
ergy. . . One a unifying solution: Money. The use of
money as a unification of the other parameters is the
conventional projection of R
n
on to R with the atten-
dant problems of coverage of all the contributory fac-
tors and how to weight their combination. The taxis
are not individually economically autonomous, in the
sense that they do not try to maximize their own util-
ity, even though that may have a negative impact on
their individual welfare. The aim for a manager is
to maximise the efficiency of the whole fleet, without
considering individuals.
The effectiveness of such a system must be as-
sessed by considering the different aspects of taxi sat-
isfaction as well as customer satisfaction.
F (w
client
, w
taxi
) = f (w
client
, w
taxi
)
Customer satisfaction is based on various criteria
such as price, waiting time and travel time. Another
possible approach could be to consider a customer
satisfied as soon as he is accepted, whatever the time
he waited or the price charged. Such an assumption
clearly focuses on taxis. The objective of such a sys-
tem is to maximise the number of customers taken.
Such a study really makes sense if customers have
limited patience and stop waiting for a taxi a certain
time. They can then be considered as a perishable re-
source of the system.
The satisfaction of taxis must consider the posi-
tioning time (empty-ride) t
empty
, the travel-time t
ride
,
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
302

the flat rate per customer p
f
, the price per kilometre
when riding a client p
k
, the cost per kilometre c
k
, the
vehicle paying for itself ζ.
The empty-ride time occurs when a taxi moves
without a client, which occurs whenever he has to
reposition itself: the taxi always incurs the costs of
using the vehicle. The more a taxi moves without a
customer, the more it costs and the least profitable it
is. The purchase/rental price of the vehicle is also
considered, which must be calculated on the basis of
the vehicle price and the time needed for the vehicle
to pay for itself. Each customer accepted is charged
and an additional cost per kilometre travelled. Thus,
the profits of taxis depend directly on the number nb
of customers it takes.
The satisfaction function that a taxi aims to max-
imise can be formulated as:
w
taxi
=
(p
f
+ (p
k
− c
k
)t
charge
nb − c
k
t
vide
− ζ
In order to assess the effectiveness of the system,
it is necessary to aggregate the satisfaction of all taxis.
The choice of this aggregation function also has a lot
of serious consequences and must result from an in-
formed choice: the most common choice is the sum
∑
. However, the maximisation of a sum does not
consider the standard deviation: some drivers could
be very profitable while others would be dedicated to
making shorter journeys for example. If the direct re-
muneration of drivers depends directly on the number
of customers taken, aggregation by means of a sum
is not fair. An alternative would be to use a product
∏
, allowing a fairer distribution of the less profitable
rides between different drivers. This small example
shows the need for an informed choice for the selec-
tion of the aggregation functions involved in evaluat-
ing the effectiveness of our complex system.The eco-
nomic approach avoids manipulation thanks to the de-
sign of dedicated scenarios. The probabilist strategy
achieves great results in all scenarios whereas some
of them have been designed to make another strategy
the most effective.
Different strategies have been described in Section
3. The effectiveness of some strategies depends on the
quality of information available. Indeed, the position-
ing strategies random or closest do not required more
information than the place of the client generators.
However, other strategies like probabilistic or most-
requested perform better if the information available
for each taxi is updated in time, to know the number
of requests pending on each client generators. By in-
teracting between each other, taxis can update their
knowledge if a taxi with more recent information en-
ters within its perception radius. The larger the per-
ception radius, the more effective the fleet.When no
information is exchanged between taxis, when a first
generator is exhausted, taxis select randomly a new
one since no information is available.The taxi fleet
needs a lot more time to accept all waiting clients.
If information can be exchanged, the speed of client
acceptance will be much greater. A taxi with no infor-
mation has just to interact with one which have newer
information to make a new wiser positioning deci-
sion. The larger the interaction distance, the quicker
all clients are accepted. Depending on the size of the
halo, compared to the size of the road infrastructure
considered, also according to the number of taxis, the
benefit of exchanging information vary.
To run our experiments, the system described in
this paper has been implemented in a powerful simu-
lator. The system is able to simulate up to the whole
of the island of Manhattan (shown in Figure 3) with
a fleet of 3,000 taxis, which is globally the maximal
instance size of all traffic simulators.
Figure 3: Simulation of Manhattan Island, with several
clients sources and destinations and a fleet of 500 taxis sup-
porting customers.
5 CONCLUSION AND FUTURE
WORKS
We have presented in this paper the DCarPool model,
based on a multiagent architecture for distributed
management of autonomous taxi fleets. This centred-
individual model considers the speed limitations and
the congestion of each road, as well as customisable
variations in applications and the definition of indi-
vidual behaviour for each taxi. The system relies on
a real map (GIS environment). We have shown that
this type of problem constitutes a multi-criteria com-
plex system difficult to evaluate, especially due to its
dynamic nature. We have proposed here a list of cri-
teria to combine as well as a unified economic eval-
uation function allowing an overall evaluation of this
system. Thanks to the model we have proposed, it is
now possible in a given situation to compare different
strategies in order to obtain a multi-criteria optimum
based in particular on the satisfaction of taxis (costs
Effective Evaluation of Autonomous Taxi Fleets
303

of daily use and depreciation) and the satisfaction of
customers (fares and time spent waiting and travel-
ing). This system and the numerous possible settings
allow the flexible design of a multi-criteria objective
function relevant to any desired optimisation. Next,
the results obtained with the different decentralised
strategies must be compared with the optimal assign-
ment in order to determine the absolute effectiveness
of the proposed approch.
As electric vehicles are becoming more and more
popular, a new dimension similarly becomes essen-
tial. The notable difference between a petrol-powered
vehicle and an electric vehicle is that the latter re-
quires a downtime for its recharging. It is obviously
not desirable for all taxis to recharge at the same time.
A collective energy management policy is thus re-
quired, leading to a modification of individual strate-
gies. A taxi must be able to recharge during empty
periods or with an offset during a full period. This
obviously impacts the fleet size: it becomes more and
more important as the longer the recharging time.
REFERENCES
Badeig, F., Balbo, F., Scemama, G., and Zargayouna, M.
(2008). Agent-based coordination model for design-
ing transportation applications. In IEEE Intelligent
Transportation Systems, 2008., pages 402–407. IEEE.
Barcel
´
o, J., Codina, E., Casas, J., Ferrer, J., and Garc
´
ıa, D.
(2005). Microscopic traffic simulation: A tool for the
design, analysis and evaluation of intelligent transport
systems. Journal of Intelligent and Robotic Systems,
41(2-3):173–203.
Bazzan, A. and Klgl, F. (2014). A review on agent-based
technology for traffic and transportation. The Knowl-
edge Engineering Review, FirstView:1–29.
Bessghaier, N., Zargayouna, M., and Balbo, F. (2012). An
agent-based community to manage urban parking. Ad-
vances in Intelligent and Soft Computing, 155:17–22.
Billhardt, H., Fern
´
andez, A., Lemus, L., Lujak, M., Os-
man, N., Ossowski, S., and Sierra, C. (2014). Dy-
namic coordination in fleet management systems: To-
ward smart cyber fleets. IEEE Intelligent Systems,
29(3):70–76.
Bonhomme, A., Mathieu, P., and Picault, S. (2014). A ver-
satile description framework for modeling behaviors
in traffic simulations. In Papadopoulos, G., editor,
IEEE 26th Int. Conf. on Tools with Artificial Intelli-
gence (ICTAI’2014), pages 937–944. IEEE.
Bonhomme, A., Mathieu, P., and Picault, S. (2016). A ver-
satile multi-agent traffic simulator framework based
on real data. International Journal on Artificial Intel-
ligence Tools, 25(1):20.
Bonte, L., Mathieu, P., and Espi, S. (2006). Modlisation et
simulation des usagers des deux-roues motoriss dans
archisim. In Chevrier, V., editor, JFSMA, pages 31–
44.
Cheikh, S. B. and Hammadi, S. (2014). The alliance be-
tween optimization and multi-agent system for the
management of the dynamic carpooling. In Agent and
Multi-Agent Systems: Technologies and Applications,
pages 193–202. Springer.
Dresner, K. and Stone, P. (2008). A multiagent approach to
autonomous intersection management. J. Artif. Intell.
Res. (JAIR), 31:591–656.
Lacroix, B., Mathieu, P., and Kemeny, A. (2009). Gener-
ating various and consistent behaviors in simulations.
In Demazeau, Y. et al., editors, PAAMS, volume 55 of
Practical Advances in Intelligent and Soft Computing,
pages 110–119.
Lacroix, B., Mathieu, P., and Kemeny, A. (2013). Formaliz-
ing the construction of populations in multi-agent sim-
ulations. J. Eng. App. of AI, 26(1):211–226.
Lioris, E., Cohen, G., and de La Fortelle, A. (2010). Evalu-
ation of collective taxi systems by discrete-event sim-
ulation. In SIMUL, pages 34–39. IEEE.
Maciejewski, M. and Nagel, K. (2013). The influence of
multi-agent cooperation on the efficiency of taxi dis-
patching. In ICPPAM, pages 751–760.
Mandiau, R., Champion, A., Auberlet, J.-M., Espi, S., and
Kolski, C. (2008). Behaviour based on decision matri-
ces for a coordination between agents in a urban traffic
simulation. Appl. Intell., 28(2):121–138.
Manley, E., Cheng, T., Penn, A., and Emmonds, A. (2014).
A framework for simulating large-scale complex ur-
ban traffic dynamics through hybrid agent-based mod-
elling. Computers, Environment and Urban Systems,
pages 27–36.
Smith, R. (1980). The contract net protocol: Highlevel
communication and control in a distributed problem
solver. IEEE Trans. on Computers, C, 29:12.
Tlig, M., Buffet, O., and Simonin, O. (2012). Coopera-
tive behaviors for the self-regulation of autonomous
vehicles in space sharing conflicts. In ICTAI, pages
1126–1132. IEEE.
Yang, Q. (1997). Simulation Laboratory for Evaluating Dy-
namic Traffic Management Systems. Thse de doctorat,
Massachusetts Institute of Technology.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
304
