Approximating Viability Kernels of Non-linear Systems
Andr
´
e M. Carvalho and Jo
˜
ao S. Sequeira
Instituto Superior T
´
ecnico / Institute for Systems and Robotics, Lisbon, Portugal
Keywords:
Viability Kernel, Reachability, Non-linear Systems.
Abstract:
A typical concern in Robotics is to assess if it is possible to keep a robot inside a set of safe states, e.g., an
autonomous car that must stay on the road. That is closely tied with the problem of computing the viability
kernel of the system, i.e., the largest set of initial states for which it is guaranteed that the system has controls
that keep maintain the trajectories inside the constraint set. The approach in this paper builds on previous
work, on linear sampled-data systems. It is based on sampling the boundary of the constraint set, finding the
states inside the viability kernel using finite-horizon forward simulation. Our adaptation extends the original
algorithm, approximating the viability kernel for some non-linear systems through linearization methods. The
non-linear systems here approached are the ones described by first order differential equations with continuous
derivatives and convex with respect to the inputs. Existence and uniqueness conditions are also established
to ensure adequate results for the whole algorithm. A practical example, with a simple non-linear system, to
illustrate the proposed algorithm is also presented.
1 INTRODUCTION
This work is motivated by control problems in the
field of autonomous vehicles, namely what is the ad-
missible set of controls that keeps a vehicle on the
road. The differential inclusions provide a generali-
zation of the differential equations, commonly used to
model dynamics of vehicles that (i) has similarities to
human-like strategies to model navigation problems
and (ii) embeds uncertainties in a very intuitive way.
Viability theory(Aubin et al., 2011), models the navi-
gation of autonomous systems very similar to the way
a human driver processes information and acts. There
exists a set of trajectories that are viable - keep the
car on track, safely - instead of the usual tracking of
a specific parametrized curve in the state space. The
viability kernel is a central piece in this theory: it is
the largest set of initial states, that starting in it, there
exists at least one trajectory that is kept inside the con-
straint set.
The classical numerical method to compute the vi-
ability kernel for any type of system is based on gri-
ding the state space, in (Saint-Pierre, 1994). Howe-
ver, griding methods are known to have exponential
complexity in the number of dimensions of the sy-
stem. This method was applied in the context of au-
tonomous driving in (Liniger and Lygeros, 2017).
Our work main procedure is based in the random
supporting directions used in (Gillula et al., 2014).
The most common representation for convex sets are
polytopes and zonotopes (Girard et al., 2006). Both
objects are closed under the operations used in the
computation of reachable sets of linear systems, such
as Minkowski sums and affine-maps. Polytopes have
a major disadvantage when used in high dimensional
systems(Tiwary, 2008). Zonotopes are more appea-
ling than polytopes to compute reachable sets in these
cases (Girard, 2005).
The original forward simulation is modified into a
reachable set computation followed by testing if the
reachable and the constraint set intersect each other.
We prove that this modification yields the same, cor-
rect, result. Unlike the original work by (Gillula et al.,
2014), our adaptation can be used in non-linear sys-
tems as long as the reachable set for that system can
be computed and whether the overlapping test bet-
ween two sets can be determined. We use a method
to compute reachable sets of non-linear systems ba-
sed on (Althoff, 2010). The overlapping test is here
implemented as a simple Linear Programming opti-
mization problem, without computing explicitly the
intersection of both sets.
The paper is organized as follows. Section 2 pre-
sents background results. Section 3 describes the ori-
ginal algorithm and our adaptation to find viability
kernels of non-linear systems. Section 4 presents re-
Carvalho, A. and Sequeira, J.
Approximating Viability Kernels of Non-linear Systems.
DOI: 10.5220/0006860903330340
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 333-340
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
333

sults on a simple two-dimensional non-linear system
and section 5 presents the final remarks and future di-
rections for the work.
2 BACKGROUND
The systems considered in the paper are of the form,
(
˙x(t) = f (x(t),u(t)), for almost all t
u(t) ∈ U, x(0) = x
0
∈ X
(1)
Where, X ,U, are sets in a metric space standing, re-
spectively, for a state space and a compact control
space. Both are considered non-empty.
The conditions for existence and uniqueness of the
solutions of the differential inclusion (1) are discussed
below. Consider a set-valued map F : X Y , with
Y a set in a metric space, defined as,
∀x ∈ X , F(x) := { f (x,u)}
u∈U
=
[
u∈U
f (x, u). (2)
This is a common extension of a wide class of dif-
ferential equation models accounting for uncertainties
(see for instance (Smirnov, 2002), pp. xiv). We can
reformulate the system (1) as,
˙x(t) ∈ F(x(t)), for almost all t > 0. (3)
Continuity properties play a fundamental role in
the existence of solutions of systems in the form (1).
These are briefly reviewed below.
Definition 1. (Aubin and Cellina, 1984) F is upper
semicontinuous (USC) at ¯x ∈ X if for any open N con-
taining F( ¯x) there exists a neighborhood M of ¯x such
that F(M) ⊂ N. F is a upper semicontinous set-valued
map if it is USC for every ¯x ∈ X.
Definition 2. (Aubin and Cellina, 1984) F is lower
semicontinuous (LSC) at ¯x ∈ X if for any ¯y ∈ F( ¯x)
and any neighborhood N( ¯y), there exists a neighbor-
hood M( ¯x) of ¯x such that ∀x ∈ M( ¯x), F(x) ∩ N(¯y) 6=
/
0
F is a lower semi-continuous set-valued map if it
is LSC for every ¯x ∈ X.
The following result summarizes the continuity
properties of the dynamics map that are key to the
existence of solutions of (3).
Theorem 1. Consider (2), with X , Y , U subsets of
metric spaces. If (i) f : X × U 7→ Y is C
1
function
in both variables, (ii) for each x ∈ X , f is convex re-
lative to the second variable, u, and (iii) U is a non-
empty, compact, convex set, then ∀x ∈ X ,F(x) is a
continuous (LSC and USC) and Lipschitz set-valued
map, with non-empty, compact and convex images.
Proof: The demonstration follows by showing,
in sequence, non-emptiness, compactness, convexity,
Lipschitziness
1
and each semi-continuity.
Non-emptiness:
Since U 6=
/
0 and f (·) is a continuous function in
both variables, the set F(x) has always at least one
element, thus, it is non-empty.
Compactness:
The subset U being compact means that every
sequence, u
n
, in U has a convergent subsequence.
By definition of uniform continuity, (see for instance
(Ross, 2013)), with n a sucession index,
∀(x,u
n
)
n∈N
⊂ X × U,
lim
n→∞
(x,u
n
) = (x, ¯u) =⇒ lim
n→∞
f (x, u
n
) = f (x, ¯u).
This means that, for every convergent subse-
quence in U, we have a corresponding convergent
subsequence f (x,u
n
) ∈ F(x). Therefore, every se-
quence of elements in F(x) has at least one convergent
subsequence, the set is then sequentially compact (by
definition of compactness). Every sequentially com-
pact metric space is compact
2
, so, F(x) is compact
∀x ∈ X .
Convexity:
The convexity follows from the fact that ∀x ∈ X ,
f (x, u) is a convex, continuous function of u ∈ U and
U a convex set. The range of such function, for each
x, is a convex set.(Prop. 2.32 (Rockafellar and Wets,
1998)).
Lipschitz:
The set-valued map is globally Lipschitz at x if
there exists a positive constant L such that,
∀x
1
,x
2
∈ X , F(x
1
) ⊂ F(x
2
) + B
2
(0,L||x
1
− x
2
||),
define, d( f
1
, f
2
) := || f (x
1
,u
1
) − f (x
2
,u
2
)||,∀x
1
,x
2
∈
X , ∀u
1
,u
2
∈ U, this implies that
3
,
d( f
1
, f
2
) ≤ L||x
1
− x
2
|| ⇒
⇒ d( f
1
, f
2
)
2
≤ L
2
||x
1
− x
2
||
2
≤ L
2
(||x
1
− x
2
||
2
+ ||u
1
− u
2
||
2
) ⇒
d( f
1
, f
2
) ≤ L||(x
1
,u
1
) − (x
2
,u
2
)|| (4)
Since f is C
1
, it is a Lipschitz function,
∀x
1
,x
2
∈ X ,∀u
1
,u
2
∈ U,
|| f (x
1
,u
1
) − f (x
2
,u
2
)|| ≤ M||(x
1
,u
1
) − (x
2
,u
2
)||,
(5)
1
The property of being Lipschitz.
2
Bolzano-Weierstrass Theorem.
3
||(x,y)||
2
= x
2
1
+...++x
2
p
+y
2
1
+...+y
2
n
= ||x||
2
+||y||
2
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
334

the constant L, in (4) identifies with M in (5), so there
exists a constant such that F is Lipschitz.
Upper Semi-Continuity:
Denote
˚
B(a, r) as the open ball of center a and
radius r with some metric. To show USC, assume that
F() is not USC everywhere.
Therefore,
∃ ¯x ∈ X ,∃N ⊃ F( ¯x),∀M( ¯x),F(M(¯x)) 6⊂ N =⇒
=⇒ ∀x ∈ M(¯x),∀u ∈ U, f (x,u) 6∈ N (6)
Knowing that x is in a neighborhood of ¯x,
∀u ∈ U, ∃δ > 0,|(x,u) − (¯x,u)| < δ =⇒
=⇒ ∀ε > 0,| f (x, u) − f (¯x,u)| < ε,
that is equivalent to,
∀u ∈ U, ∀ε
u
> 0, f (x, u) ∈
˚
B( f ( ¯x, u),ε
u
) =⇒
=⇒ ∀ε
u
> 0, F(x) ⊂
[
u∈U
˚
B( f ( ¯x, u),ε
u
). (7)
To exist a neighborhood N, for F( ¯x) means that,
∃ε > 0, ∀y ∈ F( ¯x),
˚
B(y,ε) ⊂ N ⇔
⇔ ∃ε > 0,
[
u∈U
˚
B( f ( ¯x, u),ε) ⊂ N, (8)
by the transitive property of inclusions using (7) and
(8),∀x ∈ M( ¯x),F(x) ⊂ N
This contradicts the proposition in (6), therefore,
F must be USC.
Lower Semi-Continuity:
By one hand, admitting that F is not LSC everyw-
here implies,
∃ ¯x ∈ X ,∃¯y ∈ F( ¯x),∃N( ¯y), ∀M( ¯x),
∃x ∈ M( ¯x),F(x) ∩ N( ¯y) =
/
0 =⇒
∀u ∈ U, f (x, u) 6∈ N( ¯y) =⇒ 6 ∃ε > 0,| f (x, u) − ¯y| < ε.
(9)
By the other, using the definition of continuity,
∀ ¯x ∈ X ,∀x ∈ M( ¯x),∀u ∈ U,
∃ρ > 0, |(x,u) − (¯x,u)| < ρ =⇒
=⇒ ∀ε > 0,| f (x, u) − f (¯x,u)| < ε,
and, as it is valid for any u and, ¯y = f ( ¯x, u),
∀ ¯y ∈ F( ¯x),∃ε > 0,| f (x, u) − ¯y| < ε,
this contradicts (9), therefore, F is also lower semi-
continuous.

The following set operations will be of great use
throughout the paper,
Definition 3. The Minkowski Sum and Pontryagrin
Difference between two sets are defined, respectively,
as,
A ⊕ B := {a + b | ∈ A, b ∈ B},
A  B := {a | a ⊕ B ⊆ A}.
A ball is a set in some metric space M , with some
norm p, defined as,
B
p
(x,r) := {y ∈ M | ||y − x||
p
≤ r}.
2.1 Reachability and Viability
For the proper functioning of the algorithm proposed
in this work (Section 3), we have to ensure that the
reachable set can be computed and to properly define
viability kernel. Definitions of both sets are laid out in
this subsection. Afterwards we will explore the con-
ditions of existence of general finite-time reachable
sets, independently of the method of discretization or
linearization.
Definition 4. The finite time horizon, T = N
ρ
ρ, re-
achable set of the continuous non-linear system (1)
with piecewise constant input, with initial states in the
set K ⊆ X , is defined as,
Reach
T
(K ) := {x ∈ X | x = x(T ),x
0
∈ K :
∃{u
0
,..., u
N
ρ
−1
} ∈ U}
(10)
Proposition 1. Let a function f : X ×U 7→ Y be defi-
ned as in (2), and such that the conditions of Theorem
1 hold. Then, the finite-horizon reachable set, (10)
can always be computed, for any T ∈ R
+
.
Proof: From Theorem 1, F(x) is non-empty, with
compact, convex values and LSC, therefore we are in
the conditions of Theorem 1 of (Aubin and Cellina,
1984) (pp. 97). This implies the existence of at le-
ast one continuously differentiable function, x(t) for
some tight interval. Since the properties of F(x) are
verified everywhere in its domain, the local existence
of solutions becomes global. Therefore, ∀T ∈ R
+
,
there exists x(t), ∀t ∈ [0, T ].

We will also properly define the main object in the
scope of this work,
Definition 5. The finite-horizon sampled-data via-
bility kernel of K , is the set of all the initial sta-
tes in K for which there exists at least one trajec-
tory x
k
:= x(kρ), with piecewise-constant input, that
stays inside the constraint set K for the time horizon
T = ρN
ρ
.
Viab
sd
T
(K ) := {x
0
∈ K | ∀i ∈ {0,..., N
ρ
− 1},∃u
i
∈ U :
x(t) ∈ K , ∀t ∈ [0, T ]}.
Approximating Viability Kernels of Non-linear Systems
335

2.2 Discretization of Linear Systems
A linear system is described by the following diffe-
rential equation,
(
˙x(t) = Ax(t) + Bu(t) + l(t), ∀t > 0
x(t) ∈ X ,u(t) ∈ U,l(t) ∈ L,x(0) = x
0
.
(11)
With X ⊂ R
n
, U ⊂ R
d
and L ⊂ R
n
compact, convex
subsets. In the system above, l(t) is a perturbation of
the system, in our case, the linearization error. Define
the sampling time as ρ. The time horizon considered
is denoted as
¯
T , with the number of time steps being,
N
ρ
= b
¯
T /ρc. Define the integral, I
ρ
:=
R
ρ
0
e
Ar
dr. The
sampled-time discrete system becomes,
x
k+1
= A
ρ
x
k
+ B
ρ
u
k
+ I
ρ
l
k
, ∀k ∈ {0,...,N
ρ
− 1},
(12)
with, A
ρ
:= e
Aρ
, B
ρ
:= I
ρ
B.
The state of the system at some time step s, with
some initial state x
0
, is given by,
x
s
= A
s
ρ
x
0
+
s−1
∑
i=0
A
i
ρ
(B
ρ
u
s−i−1
+ I
ρ
l
s−i−1
) (13)
2.3 Linearization
The linearization of the system (1) is done using some
results in (Althoff, 2010), in the following manner,
˙x ∈ f (x
∗
,u
∗
) + A(x − x
∗
) + B(u − u
∗
) + L.
(14)
Matrices A and B are the Jacobian matrices of the
respective linearizations, in terms of state and input
variables, respectively, around the point (x
∗
,u
∗
). The
term L is the Lagrangian Remainder. Let i be the in-
dex of the i-th state variable, defining z = (x,u), the
Hessian of the i-th state variable is,
J
i
(ξ) :=
∂
2
f
i
(ξ)
∂z
2
,
where, the i-th component of the remainder, L
i
=
1
2
(z−z
∗
)
T
J
i
(ξ)(z−z
∗
), with, ξ ∈ {z
∗
+α(z−z
∗
) | α ∈
[0,1]}.
This is the continuous time, linearized system.
This system must be converted to a discrete-time ver-
sion, since that is the representation in the scope of
this work. Combining(14) with (12),





ˆx
k+1
= A
(k)
ρ
ˆx
k
+ B
(k)
ρ
u
k
+
+I
ρ
(z
∗
)( f (z
∗
) − A
(k)
x
∗
k
− B
(k)
u
∗
k
)
ˆx
k
∈ X ,u
k
∈ U, z
∗
∈ X × U,∀k ∈ N
0
(15)
The step reachable set of such linearized and dis-
cretized system (15), from the set E, around the point
z
∗
is computed as in (Girard et al., 2006),
Reach
lin
ρ
(E) := A
ρ
[E] ⊕ B
ρ
[U] (16)
+ I
ρ
( f (z
∗
) − Ax
∗
− Bu
∗
)
Usually, it is hard to compute the exact set genera-
ted by the Lagrangian remainder. For that matter, an
over-approximation is required for it (Althoff, 2010).
With the above formula (16), we can always com-
pute the reachable set if we are in the following con-
ditions:
Proposition 2. Given a function f : X × U 7→ Y de-
fined as in (2). If f is once differentiable in both va-
riables in all its domain, then, for any x
k
∈ X ,u
k
∈
U,(x
∗
,u
∗
) ∈ X × U, the step reachable set (16) can
be computed.
Proof: Since f is everywhere differentiable, the
matrices A and B (defined in (14)) always exist. It
is known that the power series defining e
tA
, conver-
ges uniformly on compact time intervals, then A
ρ
can
be computed. The integral
R
ρ
0
e
λA
dλ also converges,
so B
ρ
and I
ρ
exist and can be computed. Since dif-
ferentiability implies continuity, f (x
∗
,u
∗
) also exists.
Therefore, the step reachable set can be computed al-
ways.

2.3.1 Polytopes
A convex V -polytope, represented by a finite set of
points, {v
1
,v
2
,..., v
k
}, is the convex hull of such set
of points. P = Conv({v
1
,v
2
,..., v
k
}).
If we stack every linear inequality that defines the
polytope we have,P = {x ∈ X | Hx ≤ b}, where the
stacked matrix H and the vector b represent the inter-
section of all the half spaces (linear inequalities) that
define the polytope.
2.3.2 Zonotopes
A special class of convex polytopes are the zonoto-
pes. They will be the main type of representation for
reachable sets in this work. In (Girard, 2005) this re-
presentation is fully explained.
Definition 6. (Zonotope)
A zonotope is a set defined in an Euclidean space
R
n
, Z :=

x ∈ R
n
| x = c +
∑
p
i=1
α
i
g
i
, −1 ≤ α
i
≤ 1

,
where, c is the center of the zonotope, and, g
1
,..., g
p
are its generators, all of them are vectors in R
n
.
Denote the zonotope, Z, as the tuple, Z := (c,<
g
1
,..., g
p
>).
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
336

3 AN ALGORITHM FOR
APPROXIMATING VIABILITY
KERNELS
The main part of the algorithm overlaps with the work
done in (Gillula et al., 2014). However, our algorithm
is the result of modifying the feasibility assessment
of trajectories, which results in a faster procedure and
enabling it to be used for non-linear systems.
3.1 Basic Algorithm
The original structure of the algorithm, Algorithm 1,
is based on sampling a number of random line seg-
ments, N
r
, starting from a given point v
0
in the via-
bility kernel and ending on the intersection with the
boundary of the constraint set K . By means of bi-
secting that line segment, the algorithm extracts, up
to some tolerance, the closest point to the border of
the viability kernel, belonging to it. The under ap-
proximation is the convex hull, Conv(·), of the points
that are guaranteed to be in the viability kernel.
Algorithm 1 : (Gillula et al., 2014) Computes a polytopic
under-approximation of Viab
sd
T
(K ).
1: function POLYTOPIC-APPROX(K ,v
0
,N
r
)
2: V ← {v
0
}
3: for i from 1 to N
r
do
4: r ← SampleRay(v
0
)
5: b ← IntersectionOnBoundary(K , r)
6: v
i
← BisectionFeasibilitySearch(K ,b, K )
7: V ← V ∪{v
i
}
8: end for
9: return Conv(V )
10: end function
If F(x) is a non-empty, compact, convex set-
valued map and x taking values in a compact con-
vex set X , we assure that the output of Algorithm 1
still works for this system and it is in fact an under-
approximation of the viability kernel of the non-linear
system.
Definition 7. (Kuratowski Set Convergence (P. L. Pa-
pini, 2015))
Given a sequence of non-empty subsets, {A
n
}
∞
n=1
,
of a Banach Space X, it converges to A in the sense of
Kuratowski, with d(x,A) := inf
y∈A
||x − y||, if,
liminf
n→∞
A
n
= lim sup
n→∞
A
n
= A,
where,
limsup
n→∞
A
n
= {x ∈ X | liminf
n→∞
d(x,A
n
) = 0},
(17)
liminf
n→∞
A
n
= {x ∈ X | limsup
n→∞
d(x,A
n
) = 0}.
(18)
Theorem 2. Consider the system defined by a diffe-
rential equation such as (2). Admitting that the state
space, X , constraint set, K , and the input set, U, are
non-empty, compact convex sets, and f : X × U 7→ Y
is a C
1
function, convex in the second variable for
each fixed x. Given a number of random directi-
ons, N
r
, and an initial point v
0
∈ Viab
sd
T
(K ), and let,
S = Polytopic-Approx(K ,v
0
,N
r
), then,
S ⊆ Viab
sd
T
(K ).
Proof: Recall that, S = Conv(v
0
,v
1
,..., v
N
r
). We
want to verify that,
v
i
∈ Viab
sd
T
(K ), i ∈ {0,1, ...,N
r
} =⇒ (19)
=⇒ Conv(v
0
,v
1
,..., v
N
r
) ⊆ Viab
sd
T
(K ). (20)
A sufficient condition for this to hold is the vi-
ability kernel to be a convex set. Since we are in
the conditions of Theorem 1, we can describe the sy-
stem by a differential inclusion ˙x(t) ∈ F(x(t)), where
F(x) has the property (among others) of having non-
empty, compact, convex values and being Lipschitz.
As in (Saint-Pierre, 1994) and by the definition of fi-
nite time horizon viability kernel of the sampled data
system (Def. 5), the finite-time viability kernel for the
sampled-data system can be built recursively as
4
,
(
K
0
= K
K
n+1
= {x ∈ K
n
| K
n
∩ Reach
ρ
(x) 6=
/
0}.
Where, K
n
is the the n step viability kernel. Using a
proof from (Maidens et al., 2013),
x ∈ K
n+1
⇔ x ∈ K
n
∧ (Reach
ρ
(x) ∩ K
n
6=
/
0)
⇔ x ∈ K
n
∩ Back
ρ
(K
n
)
Notice that the set Back
ρ
(K
n
) is the set of initial
states in which there are trajectories that end in K
n
the next instant, this is the backwards reachability set.
This set coincides with the reachable set of the sy-
stem similar to (1) but with, ˙x(t) ∈ −F(x(t)), x
0
∈ K
n
,
instead(Aubin et al., 2011)(Raczynski, 2011).
If the step reachable set of the inverse dynamics is
convex, then, by construction, Viab
sd
T
(K ) = K
N
ρ
is a
convex set.
Define G(x) := −F(x). Since it was just applied
a linear map to the set-valued function, G(x) is still
non-empty, compact, convex valued, Lipschitz in X .
From (Wolenski, 1990), the step reachable set can be
computed as
5
,
Reach
ρ
(x) = lim
N→∞

I +
ρ
N
G

N
(x),
4
For upper semi-continuous set-valued maps, which is
the case here.
5
If a set-valued map G(x) is composed with itself N
many times, we denote the resulting set-valued map as
G
N
(x).
Approximating Viability Kernels of Non-linear Systems
337

notice that, ∀x ∈ K , ∀N ∈ N, the set

I +
ρ
N
G

N
(x) is
convex, because the set valued map S(x) = I +
ρ
N
G(x)
is convex (linear maps and adding 1 to every element
in every dimension of G(x)) and the composition of
convex imaged set-valued maps on convex-imaged
set-valued maps yield convex sets.
From (P. L. Papini, 2015), the limit of a sequence
of convex sets is convex, therefore, K
n
is convex
∀n ∈ N, and therefore, Viab
sd
T
(K ) is also convex. That
means that S ⊆ Viab
sd
T
(K ). 
3.2 Modified Algorithm
The procedure adapted for a more general case of
non-linear systems is how the feasibility of some
point x
0
is determined. The initial condition x
0
of the
system is feasible in some set if at least one trajectory
starting from x
0
stays inside that set. Determining if a
point is feasible in a non-linear system framework is
done with Algorithm 2.
Algorithm 2: Determines if the evolution of the system with
initial set X
0
is feasible at each iteration k in the set K
[
k
,
using reachability.
1: function FEASIBLE(N
ρ
,ρ,S,X
0
,{K
[
1
,..., K
[
N
ρ
})
2: for k from 1 to N
ρ
do
3: X
k
← Reach
S
(ρ[k − 1,k], X
k−1
)
4: if not Overlaps(X
k
,K
[
k
) then
5: return False
6: end if
7: end for
8: return True
9: end function
Proposition 3. Consider a point x
0
∈ X , if
FEASIBLE(N
ρ
,ρ, S,x
0
,{K
[
1
,..., K
[
N
ρ
}) returns True,
then x
0
∈ Viab
sd
T
(K ), with T = ρN
ρ
. Where K
[
k
is the
set obtained by applying Lemma 1 and 2 from (Gillula
et al., 2014) to the set K at the instant k.
Proof: From the algorithm returning True we
have,
∀k ∈ {1,...,N
ρ
},X
k
∩ K
[
k
6=
/
0 ⇒
∀s ∈ {0, ...,N
ρ
− 1},∃u
s
∈ U : ˆx
s+1
∈ K
[
s+1
. (21)
Using Lemma 2 from (Gillula et al., 2014) and re-
arranging the quantifiers, (21) implies that, ∀s ∈
{1,..., N
ρ
},∃{u
0
,..., u
N
ρ
−1
} : x
s
∈ K
[
. Which, by
Lemma 1 from (Gillula et al., 2014), x
0
∈ Viab
sd
T
(K ).

3.3 Computing Reachable Sets of
Non-linear Systems
Propositions 1 and 2, establish the condition in which
it is possible to compute the reachable set. The assu-
rance of these conditions is very useful if one wants to
guarantee that the algorithm terminates with a definite
answer and do not end with an ill-posed problem.
The reachable set computation using linearizati-
ons (Algorithm 3) receives as inputs the discretization
step ρ, the system’s non-linear model, S, the input
space, U, the initial condition set of the system, X
0
,
and the admissible Lagrangian remainder
¯
L.
Algorithm 3 : Computes the step reachability set of non-
linear systems (Althoff, 2010).
1: function REACH(ρ,S ,U,X
0
,L)
2: (A,B, L) ← Linearize(S ,X
0
)
3: if L 6⊆ L then
4: (X
(1)
0
,X
(2)
0
) ← Split(X
0
)
5: R
(1)
← Reach(ρ, S, U,X
(1)
0
,L)
6: R
(2)
← Reach(ρ, S, U,X
(2)
0
,L)
7: return {R
(1)
,R
(2)
}
8: else
9: R ← AX
0
⊕ BU
10: return {R}
11: end if
12: end function
In algorithm 3 we need to split a zonotope in two
sets, since the union of zonotopes is not necessarily a
zonotope, one avoids doing so, and simply add them
in a list, and checking each one.
The user must also provide the admissible Lagran-
gian remainder,
¯
L, before the splitting takes place.
The admissible bound for the remainder is used in the
erosion of the constraint set as in Lemma 1 from (Gil-
lula et al., 2014). The splitting of zonotopes is done
as in (Althoff, 2010),
3.4 Overlap between a Zonotope and a
H -polytope
In order to determine if there are trajectories that keep
the system inside the constraint set, the test for over-
lap between the reachable set and the constraint set
must be performed. Using the aforementioned defi-
nition of zonotope, one will pose this problem as a
simple feasibility program. The program will con-
sist in determining the existence of the coefficients α
i
such that the zonotope generated respects the inequa-
lity constraints derived from the facet representation
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
338

of the constraint set. The inequalities from the con-
straint set are in the form of,
Ax ≤ b. (22)
Defining the matrix where the generators of the
zonotope defining the reachable set are its columns
and the vector of the corresponding coefficients, G =

g
1
·· · g
p

, α =

α
1
·· · α
p

T
Substituting x in (22) by the definition of zo-
notope, with column-vectors, yields,A(c + Gα) ≤ b.
This is equivalent to the standard notation of ine-
qualities for optimization with α as the variable to
optimize,AGα ≤ b −Ac ⇔ A
∗
α ≤ b
∗
.
Other restrictions have to be added since each α
i
only assumes values in [−1,1], so, the optimization
problem becomes,
min
α
0
s.t. A
∗
α ≤ b
∗
,−1 ≤ α
i
≤ 1
(23)
The Overlaps(·) function, returning whether a zo-
notope Z and a polytope P intersect each other or not,
is then defined as,
Overlaps(Z,P) =

True, ∃α in (23)
False, o.w.
4 RESULTS
This section presents simulation results that point to
the correctness of the algorithm. For the sake of
simplicity, we will restrict our experiments to two-
dimensional systems. The system being tested is a
simple pendulum on a cart, with the adequate di-
mensions, where x
1
is the pendulum angle from the
upright position and x
2
its angular velocity. The sy-
stem is described by the following non-linear diffe-
rential equation.
(
˙x
1
= x
2
˙x
2
= sin x
1
− u cosx
1
(24)
Here x = (x
1
,x
2
) ∈ X ⊂ R
2
and u ∈ U = [−1,1].
The goal here is to determine the set of admissi-
ble pairs of angular position and angular velocity for
the pendulum be kept inside the constraint set, K =
[−π/6,π/6] × [−π/6, π/6], using the adapted algo-
rithm for non-linear systems. It was set ρ = 0.05, the
number of time steps, N
d
= 10, the number of sam-
pling rays was set to N
r
= 100, the bisection accuracy
ε = 0.03 and the linearization tolerance, max
x∈
¯
L
|x| =
0.03.
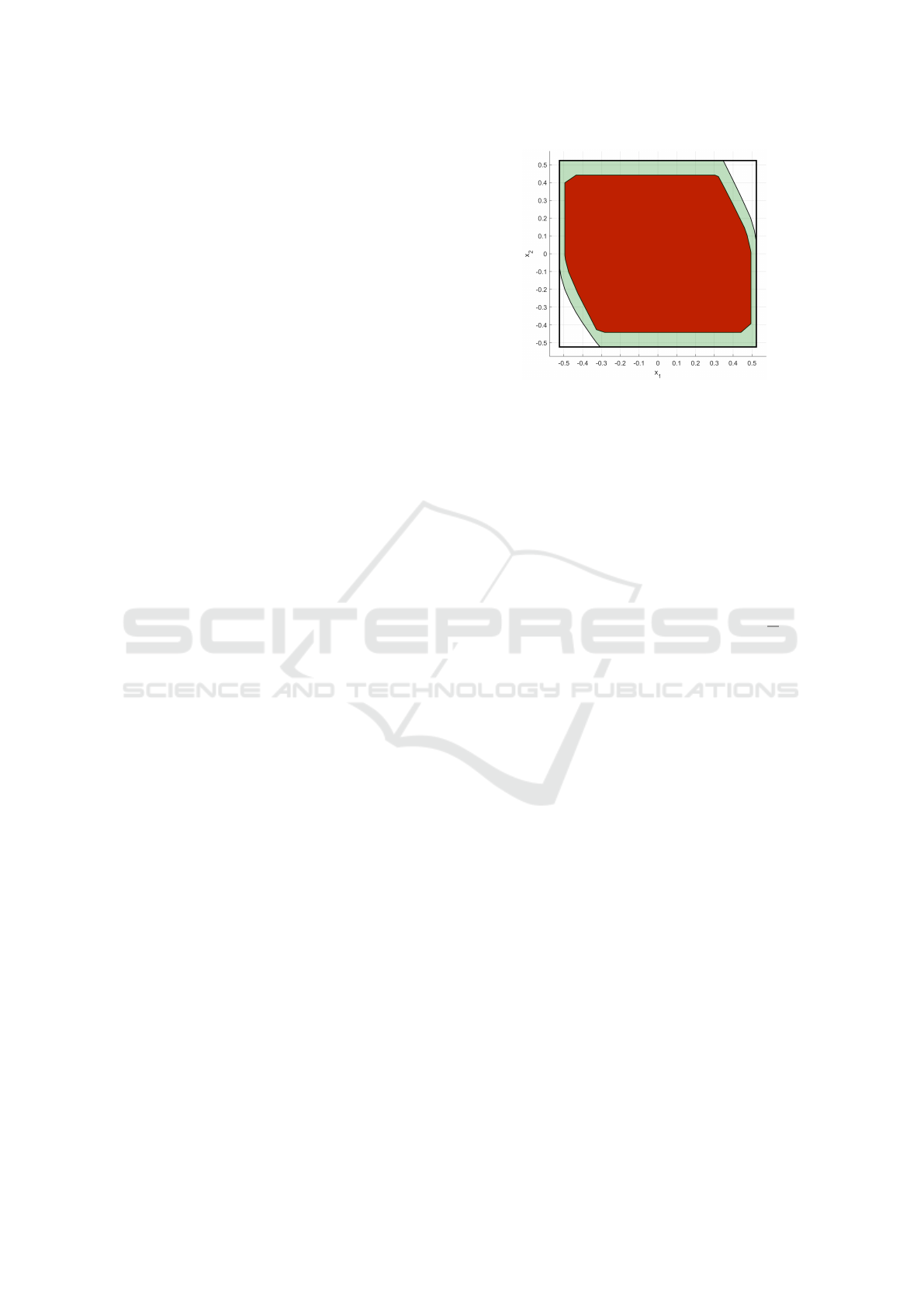
Figure 1 shows two viability kernels computed
using two different methods. The one in lighter co-
lor is computed using Saint-Pierre’s algorithm. As in
Figure 1: The outer line is the limit of the constraint set, the
light colored (green) set is the finite horizon viability kernel
with Saint-Pierre algorithm and the dark color (red) is the
kernel computed with our adaptation.
(Saint-Pierre, 1994), this algorithm can also return the
finite-time viability kernel of the system. It were used,
ρ = 0.05, the space discretization step h = 0.0033,
and the Lipschitz constant was set to L = 2, and it
stopped at the 10th iteration so as to compute the 10-
step viability kernel. The viable states computed by
our algorithm are strictly contained in the one com-
puted with the griding method. Since the accuracy of
our method is user defined by the bisection accuracy,
ε, and the acceptable Lagrangian remainder, L, our
solution can approximate the true Viab
sd
T
(K ) as close
as one would want, at the expense of more computati-
ons. Since the outer one is not constrained by having
piecewise constant inputs, it always includes the one
that is constrained.
5 CONCLUSIONS
The present work described an algorithm that adapts
Gillula’s et al. work on computing viability kernels
for non-linear, sampled systems by linearizing and
discretizing. We also prove the algorithm’s correct-
ness. The approach presented here reduces the finite
horizon viability kernel computation problem to an
iterative reachability one.
As noted in section 4, our algorithm under-
approximates the true finite horizon viability kernel.
In Figure 1 we can compare the infinite horizon viabi-
lity kernel produced by Saint-Pierre’s algorithm with
ours. A system with piece-wise constant input will
have less viable trajectories than one that can change
inputs between sampling intervals (since it is a sub-
set), so, Viab
sd
T
(K) ⊆ Viab
T
(K), where the latter set
is the finite-time viability kernel for the continuous
time system (not sampled). The results confirm this
Approximating Viability Kernels of Non-linear Systems
339

hypothesis, allowing us to confirm the correctness of
the algorithm by simulation, for this case.
For a sufficiently large linearization error tole-
rance - does not require many set splitings - the propo-
sed algorithm has a lower asymptotic complexity than
that of strategies using state space griding, as in Saint-
Pierre’s type of methods, which is O(a
n
), for some
constant a. In these cases our algorithm has a com-
plexity similar to the one proposed in (Gillula et al.,
2014), greater than O(n
2
) but smaller than O(n
3
).
There are two points to be careful when em-
ploying our algorithm. One is that methods similar
to ours only yield finite horizon viability kernels. It
is not possible to guarantee viable trajectories in in-
finite time, since for that the algorithm had to run
forever. This is not a limitation from an application
perspective. The other one is on the linearization er-
rors. If one is largely tolerant on the linearization er-
ror, our under-approximation might be too conserva-
tive or even result in the empty-set due to the erosion
process. If the tolerance is excessively strict, this may
result in an enormous amount of splittings of sets, ma-
king the algorithm much slower.
Work on how to compute tight bounds for the La-
grangian Remainder is of great importance. The per-
formance of the algorithm would be greatly improved
if clever ways of splitting and storing the splitted sets
were introduced.
Since the scope of this work is in the field of au-
tonomous vehicles, this algorithm can be directly ap-
plied for sufficiently complex models. The compu-
tation of the viability kernels will be the basis in the
synthesis of viable controls that keep the vehicle in
safe states.
ACKNOWLEDGMENT
This work was partially supported by project FCT
[UID/EEA/50009/2013].
REFERENCES
Althoff, M. (2010). Reachability Analysis and its Appli-
cation to the Safety Assessment of Autonomous Cars
(PhD Thesis). PhD thesis.
Aubin, J., Bayen, A., and Saint-Pierre, P. (2011). Viability
Theory: New Directions. Modern Birkh
`
eauser clas-
sics. Springer Berlin Heidelberg.
Aubin, J. P. and Cellina, A. (1984). Differential inclusions:
set-valued maps and viability theory. Springer-Verlag
Berlin Heidelberg.
Gillula, J. H., Kaynama, S., and Tomlin, C. J. (2014).
Sampling-based approximation of the viability ker-
nel for high-dimensional linear sampled-data systems.
Proceedings of the 17th international conference on
Hybrid systems: computation and control - HSCC 14.
Girard, A. (2005). Reachability of uncertain linear sys-
tems using zonotopes. Hybrid Systems: Computation
and Control Lecture Notes in Computer Science, page
291305.
Girard, A., Le Guernic, C., and Maler, O. (2006). Efficient
computation of reachable sets of linear time-invariant
systems with inputs. In Hespanha, J. P. and Tiwari,
A., editors, Hybrid Systems: Computation and Cont-
rol, pages 257–271, Berlin, Heidelberg. Springer Ber-
lin Heidelberg.
Liniger, A. and Lygeros, J. (2017). Real-time control for
autonomous racing based on viability theory. IEEE
Transactions on Control Systems Technology, pages
1–15.
Maidens, J. N., Kaynama, S., Mitchell, I. M., Oishi,
M. M., and Dumont, G. A. (2013). Lagrangian met-
hods for approximating the viability kernel in high-
dimensional systems. Automatica, 49(7):2017 – 2029.
P. L. Papini, S. W. (2015). Nested sequences of sets, balls,
hausdor convergence. Note di Matematica Volume 35,
Issue 2.
Raczynski, S. (2011). Uncertainty, dualism and inverse re-
achable sets. International Journal of Simulation Mo-
delling, 10(1):38–45.
Rockafellar, R. T. and Wets, R. J.-B. (1998). Variational
analysis. Springer.
Ross, K. A. (2013). Elementary Analysis: The Theory of
Calculus.
Saint-Pierre, P. (1994). Approximation of the viabi-
lity kernel. Applied Mathematics & Optimization,
29(2):187209.
Smirnov, G. V. (2002). Introduction to the theory of diffe-
rential inclusions. American Mathematical Society.
Tiwary, H. R. (2008). On the hardness of computing inter-
section, union and minkowski sum of polytopes. Dis-
crete & Computational Geometry, 40(3):469–479.
Wolenski, P. R. (1990). The exponential formula for the re-
achable set of a lipschitz differential inclusion. SIAM
Journal on Control and Optimization, 28(5):1148–
1161.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
340