Data Clustering using Homomorphic Encryption and Secure Chain

Distance Matrices

Nawal Almutairi

1,2

, Frans Coenen

and Keith Dures

Department of Computer Science, University of Liverpool, U.K.

Information Technology Department, College of Computer and Information Sciences,

King Saud University, Riyadh, Saudi Arabia

Keywords:

Privacy Preserving Data Mining, Secure Clustering, Homomorphic Encryption, Order Preserving Encryption,

Secure Chain Distance Matrices.

Abstract:

Secure data mining has emerged as an essential requirement for exchanging conﬁdential data in terms of

third party (outsourced) data analytics. An emerging form of encryption, Homomorphic Encryption, allows

a limited amount of data manipulation and, when coupled with additional information, can facilitate secure

third party data analytics. However, the resource required is substantial which leads to scalability issues.

Moreover, in many cases, data owner participation can still be signiﬁcant, thus not providing a full realisation

of the vision of third party data analytics. The focus of this paper is therefore scalable and secure third

party data clustering with only very limited data owner participation. To this end, the concept of Secure Chain

Distance Matrices is proposed. The mechanism is fully described and analysed in the context of three different

clustering algorithms. Excellent evaluation results were obtained.

1 INTRODUCTION

Data mining is a well established research ﬁeld that

has been effectively employed in many disciplines.

However, the exponential growth in data availability

has lead to the involvement of third parties for the

purpose of storing and processing data on behalf of

data owners; for example third party data mining or

collaborative data mining. The involvement of third

parties has clear security risks associated with it, such

as unauthorised data access (data leakage) and issues

concerning data privacy preservation. One current

solution is Privacy Preserving Data Mining (PPDM)

(Agrawal and Srikant, 2000; Lindell and Pinkas,

2002). The typical approach is to conceal sensitive

data attributes by applying some form of data trans-

formation to generate “sanitised” counterpartattribute

values that can be safely disclosed to (untrusted) third

parties (Chhinkaniwala and Garg, 2011). Well known

transformation techniques include value perturbation

and data anonymisation (Chhinkaniwala and Garg,

2011). Such techniques tend to operate by introduc-

ing “statistical noise” to either the entire dataset or to

selected sensitive attributes. An issue with these tech-

niques is that they cannot guarantee data conﬁdential-

ity; it might still be possible to “reverse engineer” the

original data (Vaidya et al., 2006; Berinato, 2015).

Data conﬁdentiality, and protection against leak-

age, can be assured using data encryption. However,

standard forms of encryption do not support data min-

ing activities, which typically require data manipula-

tion and record comparison. A potential solution is

the use of Homomorphic Encryption (HE) schemes

that provide malleability properties that permit lim-

ited calculation over cyphertexts without compromis-

ing security. Although HE schemes support primitive

operations that go some way to supporting data min-

ing, they do not provide an entire solution. For exam-

ple they do not support record comparison; a require-

ment with respect to many data mining algorithms.

One mechanism whereby this can be addressed is to

involve data owners so that the operations that a given

HE scheme does not support can be performed by

the data owners (Erkin et al., 2009; Liu et al., 2014).

For example, in the context of data clustering, record

similarity checking can be conducted in this manner.

However, the degree of data owner involvement can

be substantial given any kind of sophisticated data

analysis task, which in turn detracts from the vision

of third party data mining.

There has been some work that seeks to diminish

data owner participation with respect to third party

Almutairi, N., Coenen, F. and Dures, K.

Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices.

DOI: 10.5220/0006890800410050

In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 1: KDIR, pages 41-50

ISBN: 978-989-758-330-8

data clustering. Of note is the 3-D Updatable Dis-

tance Matrix (UDM) introduced in (Almutairi et al.,

2017). However, use of the UDM featured two disad-

vantages: (i) a substantial memory requirement, be-

cause the ﬁrst two dimensions of the matrix were cor-

related to the number of records in the given dataset

thus limiting the scalability and (ii) the potential for

reverse engineer given that a UDM is essentially a

(very large) set of linear equations.

Given the above, this paper proposes the idea of

the Secure Chain Distance Matrix (SCDM) which

provides for secure third party data mining us-

ing a proposed Order Preserving Encryption (OPE)

scheme, which can limit recourse to data owners dur-

ing the processing of the data (depending on the na-

ture of clustering) and features none of the mem-

ory requirement and security disadvantages associ-

ated with the UDM concept proposed in (Almutairi

et al., 2017). The novel elements of the SCDM con-

cept are ﬁrstly the chaining mechanism used, which

means that the storage requirement, compared with

UDMs, is reduced by a factor equivalent to the num-

ber of input data records (−1). Secondly, the pro-

posed Order Preserving Encryption (OPE) scheme

with which the matrix is encoded, thus allowing for

third party record comparison without the risk of po-

tential reverse engineering as in the case of UDM.

The SCDM concept is fully described and evaluated.

The evaluation is conducted in the context of three

different clustering algorithms (Nearest Neighbour,

DBSCAN and k-Means), however, the SCDM idea

clearly has wider application.

The rest of this paper is structured as follows. Sec-

tion 2 provides a review of related research. Sec-

tion 3 presents the data encryption schemes used to

provide for proposed secure clustering methods. The

proposed Secure Chain Distance Matrix (SCDM) idea

is then detailed in Section 4. The utilisation of the

SCDM concept, in the context of secure data cluster-

ing, is presented in Section 5. Section 6 then reports

on the experiments conducted to evaluate the SCDM

concept and the results obtained (in the context of se-

cure data clustering). The paper is concluded in Sec-

tion 7, with a summary of the main ﬁndings and sug-

gestion for future work.

2 PREVIOUS WORK

This section presents a review of previous work on

secure data clustering that uses HE schemes as a data

conﬁdentiality preservation method. The main chal-

lenge of HE-based privacy preserving data clustering

(and other forms of data mining), is that HE schemes

support only a limited number of operations. Sev-

eral solutions havebeen proposed to address this chal-

lenge, mostly in the context of collaborative data clus-

tering whereas the work presented in this paper is

directed at third party data clustering, which can be

broadly categorised into: (i) involving data owners

when unsupported operations are required, and (ii)

utilising the concept of “secret sharing” to delegate a

key and operations to semi-honest and non-colluding

parties that collaboratively perform operations on the

data owners’ behalf. Both have limitations in term of

communication complexity and security threats.

The main feature of the ﬁrst category is the main-

tenance of data conﬁdentiality by allowing a third

party to only manipulate cyphertexts using HE prop-

erties (no access to any secret key). In this case, in

the context of data clustering, data owner participa-

tion becomes a necessity. In some cases, the majority

of the work is done by data owners. For example,

a number of authors have proposed mechanisms for

k-means clustering using Secure Multi-Party Compu-

tation (SMPC), where data owners repeatedly cluster

their own data and only share encrypted data centroids

so that an eventual global clustering can be arrived at

(Jha et al., 2005; Mittal et al., 2014). A similar idea

is used in (Tong et al., 2018) to implement DBSCAN

where data owners independently apply DBSCAN on

their local data. The resulting boundary records and

their labels are then shared (in plaintext) with the third

party who then determines global boundary records

which are returned to the individualdata owner so that

they can update their local clusters. However, shar-

ing boundary data records in plaintext form presents

a security threat. Secure nearest neighbour clustering

is presented in (Shaneck et al., 2009) using SMPC

primitives; secure product for distance calculation

and Yao’s millionaires’ protocol for data comparison.

A signiﬁcant drawback of these proposed solutions

is that they introduce a computation/communication

overhead because of the amount of data owner partic-

ipation required.

In (Erkin et al., 2009; Liu et al., 2014; Almutairi

et al., 2017; Rahman et al., 2017) the basic idea was

for the third party to do as much of the clustering as

possible (centroid calculation, data aggregation and

so), using the properties of a selected HE scheme, and

involve data owners only when the properties of the

particular HE scheme used do not support the desired

analysis. For example, in the case of (Erkin et al.,

2009), in the context of collaborative clustering, the

adopted HE scheme does not support record similar-

ity checking, thus this is done by a randomly selected

data owner. The number of data owner participation

instances is given by n × |C| × i, where n is the num-

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

ber of records, |C| the number of centroids and i the

number of clustering iterations; thus the amount of

data owner participation is considerable. The con-

cept of “trapdoors” are used to minimise the num-

ber of data owner participation in (Liu et al., 2014).

“Static” and “dynamic” trapdoors were therefore cal-

culated by the data owners so as to convert cypher-

texts to order cyphertexts; consequently off-line com-

parison (without data owner participation) was sup-

ported. However, the main issue with this approach

was that it was very inefﬁcient, particularly when con-

sidering large datasets; in addition data owner partici-

pation could still be high (depending on the nature of

the clustering) because of the need to recalculate the

dynamic trapdoors on each iteration. An alternative is

the UDM concept presented in (Almutairi et al., 2017)

that dramatically reduces the data owner participation

overhead to |C| × i, however this also has limitations;

ﬁrstly in terms of security in that a UDM represents

a set of linear equations that might be reverse engi-

neered (although the set of linear equations is very

large), and secondly in terms of memory requirement

and communication complexity cost in that the size

of a UDM increases exponentially with the number

of records in the input dataset. The third party collab-

orative DBSCAN mechanism described in (Rahman

et al., 2017) uses HE properties to calculate the re-

quired distances. However, as noted previously, the

generated cyphers do not preserve the data ordering,

thus data owner participation was still required to de-

termine whether the distances were below or above

the DBSCAN threshold ε value.

The second category comprises more recent work

that uses “secret sharing” to eliminate data owner par-

ticipation. The basic idea is to use a scheme, as

in (Hazay et al., 2012), that mathematically splits

a secret key among multiple semi-honest and non-

colluding parties that collaboratively manipulate data

on behalf of data owners. In (Rao et al., 2015; Saman-

thula et al., 2015), the concept of secret sharing was

used to design secure computation protocols that se-

curely execute mathematical operations by third par-

ties without involving data owners in the data min-

ing process. The limitation of this approach is that

it tends to be inefﬁcient and not practical for large

datasets. In addition, the requirement for at least two

semi-honest and none-colluding parties is of concern,

and for many data owners a security risk. Moreover,

the secret key that has been generated to encrypt a

given dataset cannot be revoked by data owners, thus

a version of the data needs to be stored locally by each

individual data owners.

3 DATA ENCRYPTION

The proposed Secure Chain Distance Matrix (SCDM)

based clustering approaches utilised two encryption

schemes: (i) Liu’s HE scheme (Liu, 2013) and (ii)

a proposed Order Preserving Encryption (OPE). The

ﬁrst is used to encrypt the data to be outsourced, the

second to encrypt the CDM. Both are discussed in

further detail in the following two sub-sections, Sub-

sections 3.1 and 3.2 respectively.

3.1 Liu’s Homomorphic Encryption

Scheme

In Liu’s scheme each data attribute v is encrypted

into m sub-cyphers, C = {c

,... ,c

} where m ≥

3. Algorithm 1 shows the pseudo code for the

Encrypt(v,K(m)) where K(m) is a list of secret keys.

K(m) = [(k

),..., (k

)] and k

, s

and t

are real numbers. Given a set of sub-cyphers C =

,..., c

and the key K(m) Algorithm 2 gives the

pseudo code for the Decrypt(C,K(m)) decryption

function to return the value v.

Algorithm 1: Encrypt(v, K(m)).

1: procedure ENCRYPT(v, K(m))

2: generate m arbitrarily real random numbers

,.... .,r

3: Declare C as a real value array of m elements

4: c

= k

∗t

∗ v+ s

∗ r

+ k

∗ (r

− r

m−1

)

5: for i = 2 to m− 1 do

6: c

= k

∗t

∗ v+ s

∗ r

+ k

∗ (r

− r

i−1

)

7: c

= (k

+ s

) ∗r

8: Exit with C

Algorithm 2: Decrypt(C, K(m)).

1: procedure DECRYPT(C, K(m))

2: T =

∑

m−1

i=1

3: S = c

/(k

+ s

)

4: v = (

∑

m−1

i=1

− S∗s

)/ki)/T

5: Exit with v

The scheme has both security and homomorphic

properties. The scheme is semantically secure in that

it produces different cyphertexts for the same plain-

text on each occasion, even when the same secret key

is used. Further detail regarding the security of Liu’s

scheme is given in Section 6. In terms of its homo-

morphic properties the scheme supports: the addition

of cyphertexts ⊕ and multiplication of a cyphertext

with a real value ⊗ as shown in Equation 1. Hence

the subtraction ⊖ of cyphertexts and the division ⊘

of a cyphertexts by a real value are implemented

Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices

as given in Equation 2.

C⊕C

′

= {c

⊕ c

′

,.. .,c

⊕ c

′

} = v+v

′

r⊗C = {r⊗ c

,.. .,r ⊗ c

} = r× v

(1)

C⊖C

′

= C⊕ (−1⊗C

′

)

C⊘ r =

⊗C

(2)

3.2 Order Preserving Encryption

A Chain Distance Matrix (CDM) holds distances be-

tween every attribute value in each consecutive data

record according to whatever ordering is featured in

the data; further detail regarding the generation of

CDMs is given in Section 4. As in the case of the

UDM, the content of a CDM can be used to de-

ﬁne a set of linear equations that might allow for

re-engineering. To prevent such re-engineering the

idea is to encode the CDM, to give a Secure CDM

(SCDM), by using an Order Preserving Encryption

(OPE) scheme, a form of encryption where the order-

ing of the values is maintained so as to allow (secure)

comparison.

= [l

′

)

Cypher Space

′

= [l

′

)

′

= [l

′

)

.. .. ..

= [l

)

= [l

)

Message Space

.. .

Enc

)Enc

) Enc

)

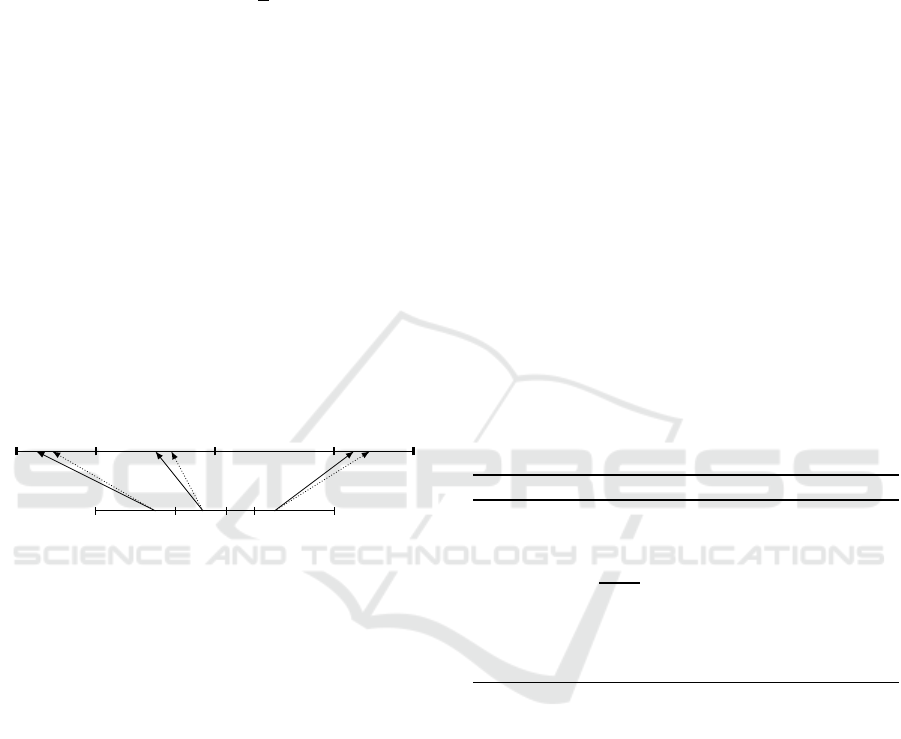
Figure 1: Message and extended cypher space splitting.

The proposed scheme is an amalgamation of two

existing OPE schemes, that of (Liu et al., 2016)

and (Liu and Wang, 2013). Using the proposed

scheme the expected message space M and the ex-

panded cypher space C is known in advance as in the

case of most OPE schemes. The expanded cypher

space should be much larger than the message space,

|C| ≫ |M|. Using the proposed scheme M = [l,r) and

C = [l

′

) where l and l

′

are the minimum bound-

ary values and r and r

′

are the maximum boundary

values (as demonstrated in Figure 1). The key fea-

ture of the proposed OPE scheme is that it obscures

any data distribution that might be included in the

generated cyphertexts using the concept of message

space splitting and non-linear cypher space expan-

sion. To generate the desired cypher space the ﬁrst

step is to randomly split the message space M into

n successive intervals M = {m

,. .. ,m

} where

= [l

) ∀(i = 1,2,. .. ,n). The process of splitting

satisﬁes the following: M = ∪

i=n

i=1

= ∪

i=n

i=1

) =

[l, r) and [l

) ∩ [l

) = φ ∀ i 6= j. Next, the cypher

space C was also split into n successive intervals C =

,. .. ,c

}. The length of the cypher space inter-

vals are determined by the density of the correspond-

ing message space interval, so that for a dense inter-

val, containing high frequency data, its corresponding

cypher space interval will result in a longer cypher in-

terval range.

Each interval has associated with it an encryption

function that maps data from the message space m

to cyphertext in the corresponding extended cypher

space c

. In context of the work presented in this

paper, the encryption function of the ith interval is

shown in Algorithm 3; the algorithm encrypts a plain-

text value x ∈ m

to an encrypted value x

′

∈ c

. Range

and Range

′

(lines 2 and 3) return the maximal and

minimal value for the message space interval m

and

the corresponding cypher space c

respectively. In

line 4 the Scale

value is calculated as a division of

the cypher space size over the corresponding message

space size. The values of the minimal cypher space,

minimal message space and the scale are used to gen-

erate a cypher x

′

(line 5). To obfuscate the occurrence

frequency of a data value a random value δ

is applied

to x

′

(lines 6 and 7). The value of δ

is sampled from

the range [0,Sens∗ Scale

) where Sens represents the

data sensitivity as proposed in (Liu and Wang, 2013);

the minimum distance between plaintext values.

Algorithm 3: Order Preserving Encryption algorithm.

1: procedure ENC

(x,Sens)

2: l

← Range(i)

3: l

′

← Range

′

(i)

4: Scale

′

−r

′

)

−r

)

5: x

′

= l

′

+ Scale

× (x− l

)

6: δ

= Random(0,Sens×Scale

)

7: x

′

= x

′

+ δ

8: Exit with x

′

4 THE SECURE CHAIN

DISTANCE MATRIX (SCDM)

Regardless of whether standard or HE encryption is

used, data encryption randomly transfers plaintexts

values in a dataset D to cyphertexts in such a way

that any ordering is not preserved. Therefore, data

comparisons cannot be directly applied to the cypher-

texts, and hence clustering algorithms cannot be di-

rectly applied. The proposed idea is to support third

party secure clustering over encrypted data using the

concept of a Secure Chain Distance Matrix (SCDM)

that holds the distance between every attribute in ev-

ery consecutive data records in D. An SCDM is a 2D

matrix whose ﬁrst dimension is n − 1 where n is the

number of records in D and whose second dimension

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

is |A| (the size of the attribute set A). An SCDM is

generated in two steps: (i) CDM calculation and (ii)

CDM encryption. Algorithm 4 gives the CDM cal-

culation process. Instead of calculating distances be-

tween attribute values in records with the correspond-

ing attribute values in every other record, as in the

case of UDMs, a CDM holds only distances between

n − 1 records. This small set of distances allows a

third party to calculate the “order” of similarity be-

tween any two data records r

and r

(where x < y) in

D as per equation 3. In the case of x = y the distance

will clearly be 0.

Algorithm 4: Chain Distance Matrix Calculation.

1: procedure CDMCALCULATION(D)

2: CDM =

0 array of n− 1 rows and |A| column

3: for i = 1 to i = n− 1 do

4: for j = 1 to j = |A| do

5: CDM

[i, j]

= D

[i, j]

− D

[i+1, j]

6: Exit with CDM

Sim(CDM, r

) =

j=|A|

∑

j=1



i=(y−1)

∑

i=x

CDM

[i, j]



(3)

Although the CDM reduces the memory require-

ment, compared to UDM, it still essentially com-

prises a set of linear equations that may support re-

engineering. Therefore, the second step is to encrypt

the matrix so that the distance ordering is preserved

to give an SCDM. To this end, the OPE described in

Sub-section 3.2 above was used. The key feature of

the encrypted CDM, the SCDM, is that a third party

now has access to the distance value ordering, not

the original distance values, between the data records.

The order of similarity is determined as per Equation

3 but with the CDM replaced by the SCDM.

5 SECURE DATA CLUSTERING

This section presents a number of examples secure

clustering algorithms that operate over HE data and

utilise the SCDM concept, two of these achieve the

ideal solution (require no data owner participation

whilst the third party processing is taking place), the

third only requires minimal data owner participation.

Whatever the case the clustering process has two

parts, data preparation (Sub-section 5.1) and the data

clustering (Sub-sections 5.2, 5.3 and 5.4), conducted

by a data owner and the third party data miner respec-

tively.

5.1 Data Preparation

The initial step in the preparation process is to trans-

late a given dataset D into a suitable format that al-

lows distance calculation and data comparison. In the

context of the work presented in this paper, casting

is used to transfer categorical values to discrete inte-

ger equivalents. The next step is to encrypt the data

attribute values to produce an encrypted dataset D

′

using Liu’s HE scheme and m = 4 (see Sub-section

3.1). The CDM is then calculated using Algorithm 4

and encoded using the proposed OPE scheme (Sub-

Section 3.2). The output from the preparation process

is the encrypted dataset D

′

and the SCDM ready to be

sent to the third party data miner.

5.2 Secure Nearest Neighbour

Clustering (SNNC)

The proposed SCDM concept was combined with

three popular clustering schemes: (i) Nearest Neigh-

bour Clustering, (ii) DBSCAN and (iii) k-Means. The

ﬁrst is discussed in this section, and the remaining two

in the followingtwo sections. The pseudo code for the

proposed SNNC approach is presented in Algorithm

5, it operates in a similar manner to the standard NNC

algorithm (Cover and Hart, 1967). The main differ-

ences are that the data and threshold values σ

′

is en-

crypted and that the similarity between data records

is determined using the SCDM. The algorithm com-

mences by adding the ﬁrst encrypted record r

′

to the

ﬁrst cluster (lines 2 and 3) and then iteratively cluster-

ing the remaining records (lines 5 to 11). As in case of

standard NNC, a record r

′

will be assigned to a clus-

ter if there exists some record r

′

whose distance from

′

is less than or equal to σ

′

(lines 5 to 8). If there is

no such record, r

′

is assigned to a new cluster (lines

10 and 11). The similarity between records r

′

and r

′

is determined using Equation 3 (and the SCDM). The

algorithm will exit with a cluster conﬁguration C.

5.3 Secure DBSCAN (SDBSCAN)

The SDBSCAN algorithm is presented in Algorithm

6. The inputs are the encrypted dataset D

′

and SCDM

previously provided by the data owner and the desired

density parameters (MinPts, ε

′

). Similar to the stan-

dard DBSCAN (Ester et al., 1996), density is deﬁned

as the minimum number of points, MinPts, within a

certain distance ε. Note that, in case of SDBSCAN

the ε value is encrypted using the OPE scheme to give

′

that allows secure comparison and hides the corre-

lation (distance) between data records when the third

party data miner executes SDBSCAN.

Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices

Algorithm 5: Secure NN clustering algorithm.

1: procedure SNNC(D

′

,SCDM,σ

′

)

2: C

= {r

′

}

3: C = {C

}

4: k = 1

5: for i = 2 to i = |D

′

| do

6: Find r

′

in some cluster inC where

Sim(SCDM,r

′

) is minimised

7: if Sim(SCDM, r

′

) ≤ σ

′

then ⊲ (Eq. 3)

8: C

= C

∪ r

′

9: else

10: k+ +

11: C

= {r

′

}

12: Exit with C

The algorithm commences by initialising the

global variables MinPts, ε

′

, SCDM and D

′

by the val-

ues received from the data owner (line 5). In line 6,

an empty set of clusters C is created and the number

of clusters so far is set to 0. For each record r

′

in D

′

that has not been previously assigned to a cluster, “un-

clustered”, the set S is determined. The set S is the ε-

neighbourhood of r

′

and comprises the set of records

in D

′

whose distance from r

′

is less than or equals to

′

. The set is determined by calling the regionQuery

procedure (line 9) where the SCDM is used to deter-

mine the overall distances between records (see Equa-

tion 3). If the number of records in S is greater than or

equals to MinPts the density requirement is satisﬁed

thus r

′

is marked as “clustered” and considered to rep-

resent a new cluster C

(lines 11 to 13). This cluster is

then expanded by considering the records in S using

the expandCluster procedure called in line 14. The

input to the expandCluster procedure is: the cluster

so far and the set S. The expandCluster procedure

is a recursive procedure. For each record in S which

has not been previously clustered we add the record

to C

and then determine the ε-neighbourhood S

for

this record (line 22). If the size of S

is greater than

or equals to MinPts we call the expandCluster pro-

cedure again and so on until all the records in D

′

are

processed at which point the algorithm will exist with

the cluster conﬁguration C.

5.4 Secure k-Means (Sk-Means)

The secure k-Means process is again very similar to

the standard k-Means algorithm (MacQueen et al.,

1967). However, the mathematical operations are re-

placed with equivalent secure operations using the

HE properties as presented in Sub-section 3.1. The

pseudo code is given in Algorithm 7. The inputs

are the encrypted dataset D

′

, the SCDM and number

of desired clusters k. The algorithm commences by:

initialising the global variables (line 5), dimensioning

Algorithm 6: Secure DBSCAN clustering algorithm.

1: global variables

2: MinPts, ε

′

, SCDM, D

′

3: end global variables

4: procedure SDBSCAN(D

′

, SCDM, MinPts, ε

′

)

5: Initialized global variables with received values

6: C =

0, k = 0

7: for i = 1 to i = |D

′

| do

8: if r

′

is Unclustered then

9: S = regionQuery(r

)

10: if |S| > MinPts then

11: mark r

′

as clustered

12: k = k+ 1

13: C

= r

′

14: C

= expandCluster(C

,S)

15: C = C ∪C

16: Exit with C

17: procedure EXPANDCLUSTER(C,S)

18: for ∀ r

′

∈ S do

19: if r

′

is Unclustered then

20: mark r

′

as clustered

21: C = C∪ r

′

22: S

= regionQuery(r

)

23: if |S

| > MinPts then

24: C = expandCluster(C,S

)

25: Exit with C

26: procedure REGIONQUERY(r

′

Index

)

27: N

= empty set

28: for ∀ r

′

∈ D do

29: distance = Sim(SCDM, r

′

Index

′

) ⊲ (Eq. 3)

30: if distance ≤ ε

′

then

31: N

.add(r

′

)

32: Exit with N

the cluster array C = {C

,. .. ,C

} and assigning

the ﬁrst k encrypted records to it (lines 6 and 7). A

centroid set Cent = {cent

,cent

,. .. ,cent

} is thus

deﬁned to hold the current centroids (lines 8 and 9).

The remaining encrypted data records are then as-

signed to a cluster according to their similarity with

respect to the cluster centroids using the populate-

Clusters procedure (called from line 10) and given at

the end of algorithm. In populateClusters the order of

similarity is calculated using the SCDM as shown in

Equation 3. A set of new centroids (Cent

′

) are then

calculated (line 11) using the HE properties of Liu’s

scheme. An iterative loop is then entered (lines 12 to

19) that repeats until stable centroids are arrived at.

The ﬁrst step of each k-Means iteration is to calcu-

late the Shift matrix S (line 13) that represents the dis-

tances between the previous iteration centroids (Cent)

and the newly calculated centroids (Cent

′

). Note that

S, is calculated using the HE properties, over the HE

data ,therefore, the next step requires recourse to the

data owner (lines 14) to decrypt matrix (S) and re-

encrypt it using OPE to give S

′

so that it can be used

to update the SCDM (line 15). The algorithm will use

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

Algorithm 7: Secure k-Means clustering algorithm.

1: global variables

2: D

′

, SCDM

3: end global variables

4: procedure SK-MEANS(D

′

, SCDM, k)

5: Initialized global variables with received values

6: C = Set of k empty clusters

7: Assign ﬁrst k records in D

′

to C (one per cluster)

8: Cent = Set of k cluster centroids

9: Assign ﬁrst K records in D

′

to Cent

10: C = PopulateClusters(k+ 1,C,Cent)

11: Cent

′

= CalculateCentroids(C)

12: while Cent 6= Cent

′

13: S = Cent ⊖Cent

′

14: S

′

= S decrypted and encrypt result using OPE

15: SCDM = SCDM +S

′

16: C = Set of k empty clusters

17: C = PopulateClusters(1,C,Cent

′

)

18: Cent = Cent

′

19: Cent

′

= CalculateCentroids(C)

20: Exit with C

21: procedure POPULATECLUSTERS(x,C,Cent)

22: id = null

23: for x = x to x = |D

′

| do

24: for y = 1 to y = |C| do

25: sim = Sim(SCDM, r

) ⊲ (Eq. 3)

26: id = cluster identiﬁer with lowest sim

value so far

27: C

= C

∪ r

∈ C)

28: Exit with C

′

to update the SCDM by concatenating the k el-

ements in S

′

to SCDM (line 15). In the follow-

ing iteration S

′

is used to update the ﬁrst k elements

in the SCDM. Using the newly calculated centroids

all records are again assigned to each cluster, using

the populateClusters procedure, in the same manner

as before; and so on until a ﬁxed conﬁguration is

reached.

6 EVALUATION

The evaluation of the proposed clustering approaches

is presented in this section. For the purpose of the

evaluation ﬁfteen datasets from the UCI data repos-

itory (Lichman, 2013) were selected in a manner so

that datasets of a variety of sizes and different num-

bers of classes could be considered (these are listed in

columns 2 and 3 of Table 1). The number of classes

in each case was used as the value for k in the case of

k-Means clustering. The proposed approaches were

implemented using the Java programming language.

The overall objective was to evaluate the proposed

algorithms in term of: (i) data owner participation,

(ii) scalability, (iii) clustering efﬁciency, (iv) cluster-

ing accuracy and (v) security.

Data owner participation was measured in terms

of the runtime required for data preparation and

SCDM generation, and the amount of data owner in-

volvement during the clustering process. Preparation

time results are presented in Table 1 where columns

4, 7 and 8 give the preparation times for: data en-

cryption, CDM calculation and CDM encryption re-

spectively. From the table, it can be seen that negli-

gible time was required for the data preparation; even

with respect to the largest dataset, Arrhythmia. For

SDBSCAN and SNNC no further data owner par-

ticipation was required, whereas in the case of Sk-

Means the participation was limited to the decryption

and re-encryption of the shift matrix, S, on each it-

eration; thus data owner participation was limited to

O(|C| × i), where |C| is the number of centroids and

i is the number of k-Means iterations, the same as in

the case of the UDM approach from (Almutairi et al.,

2017).

The chain feature in SCDM reduces the required

memory resources compared to the UDM concept in

(Almutairi et al., 2017). The number of elements in

a UDM grows exponentially with the data volume;

more formally it equals to (

n(n+1)

× |A|)) (Column

6 in Table 1 gives the number of UDM elements for

each experimental dataset). The SCDM is more com-

pact and hence requires signiﬁcant lower resource

(Column 9 in Table 1) which makes it more appro-

priate for big data. This small number of elements

means that the time required to calculate an SCDM is

less than the UDM (as shown in Columns 5 and 7 in

Table 1).

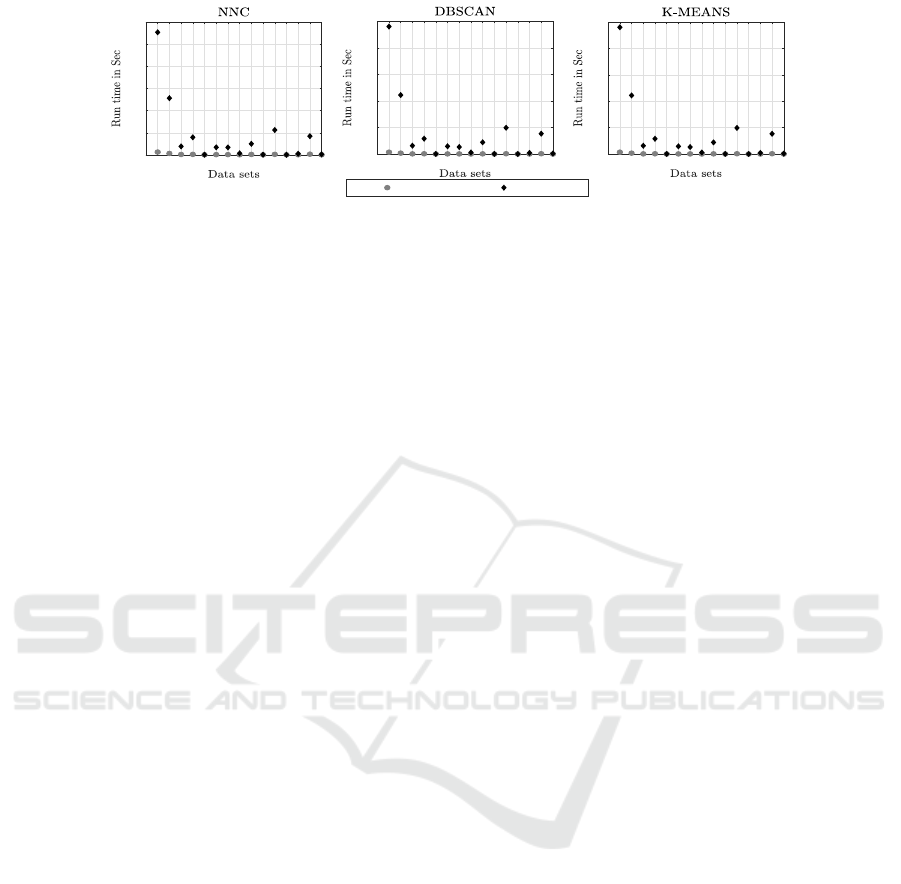
In terms of clustering efﬁciency, the runtime to

cluster the data using the proposed secure clustering

mechanisms was compared with the standard equiv-

alent processes. The runtime results are presented

in Figure 2. From the ﬁgure, it can be seen that the

overall runtimes required for the secure clustering ap-

proaches, as expected, were longer than in the case

of standard approaches, however, inspection of the

recorded results indicates that this did not present a

signiﬁcant overhead. Of course, the bigger the dataset

the larger the SCDM, and consequently the greater

the time required to interact with the SCDM to clus-

ter data.

In terms of accuracy, cluster conﬁguration “cor-

rectness” was measured by comparing the results

obtained with those obtained using standard (unen-

crypted) clustering algorithm equivalents. The pa-

rameters used (in practice selected by the data owner)

are given in columns 10 to 13 of Table 1. The accu-

racy metric used was the Silhouette Coefﬁcient (Sil.

Coef.) (Rousseeuw, 1987), a real number value be-

tween −1 and +1, the closer the value is to 1 the bet-

Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices

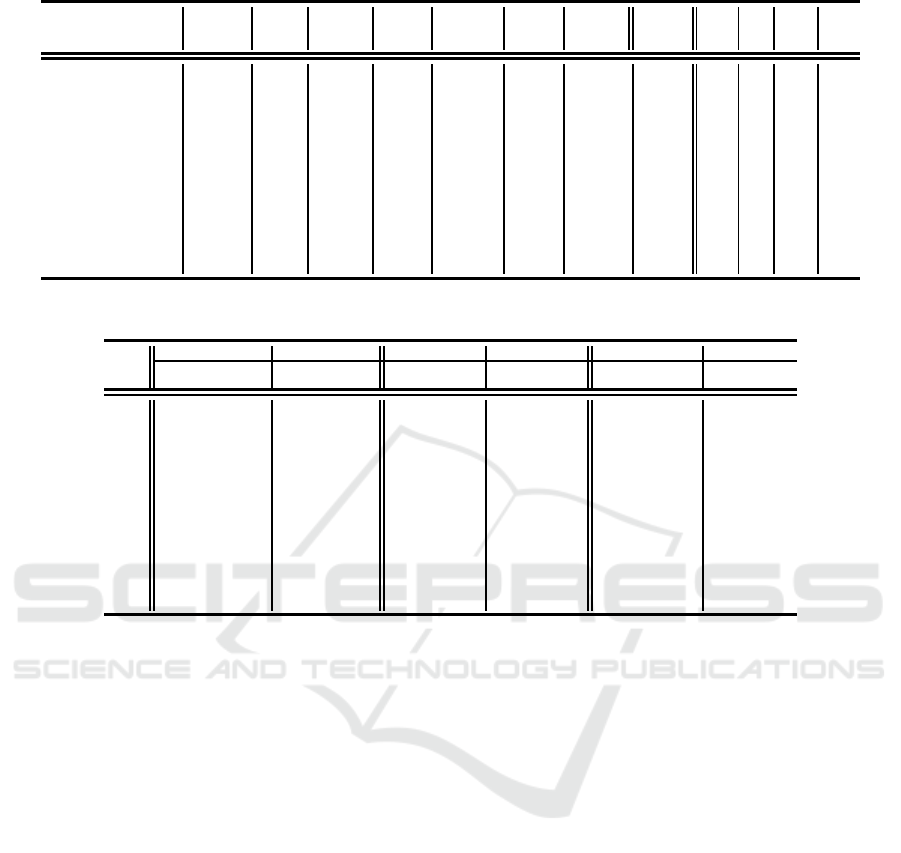
Table 1: Run times for data owner data preparation and algorithm operating statistics.

Num Data UDM UDM CDM CDM CDM σ k Min ε

No. Dataset

R × C Class Encrypt. Cal. Size Cal. Encrypt. Size Pts

Labels (MSec) (MSec) (MSec) (MSec)

1. Arrhythmia 452×279 16 11.08 218.5 28563462 3.33 136.09 125829 1 16 2 600

2. Banknote Authent.

1372×4 2 1.24 81.5 3767512 0.2 32.08 5484 5 2 2 3

3. Blood transfusion

748×4 2 0.73 28.2 1120504 0.13 20.17 2988 68 2 2 10

4. Brest Cancer

699×9 2 1.64 31.6 2201850 0.19 27.36 6282 10 2 2 5

5. Breast Tissue

106×9 6 0.36 2.1 51039 0.03 23.73 945 1 6 2 100

6. Chronic Kidney Dis.

400×24 2 1.56 20.2 1924800 0.28 37.38 9576 100 2 2 70

7. Dermatology

366×34 6 1.88 22.9 2283474 0.43 31.77 12410 18 6 2 10

8. Ecoli

336×7 8 0.98 7.8 396312 0.09 31.54 2345 1 8 3 60

9. Ind. Liver Patient

583×10 2 0.99 23.3 1702360 0.15 39.39 5820 99 2 3 40

10. Iris

150× 4 3 0.24 2.9 45300 0.04 17.87 596 1 3 5 2

11. Libras Movement

360×90 15 4.01 50.3 5848200 1.26 92.07 32310 4 15 5 5

12. Lung cancer

32×56 3 0.61 1 29568 0.05 13.34 1736 1 3 2 20

13. Parkinsons

195×22 2 1.01 6.1 420420 0.13 36 4268 73 2 3 10

14. Pima Ind. Diabetes

768×8 2 1.18 36.6 2362368 0.18 37.18 6136 100 2 5 20

15. Seeds

210×7 3 0.51 4.8 155085 0.06 26.77 1463 1 3 5 1

Table 2: Cluster conﬁguration comparison using standard and secure algorithms (differing results highlighted in bold font).

No.

Standard DBSCAN SDBSCAN Standard NNC SNNC Standard k-Means Sk-Means

Num. Sil. Num. Sil. Num. Sil. Num. Sil. Iter. Sil. Iter. Sil.

Clus. Coef Clus. Coef Clus. Coef Clus. Coef Coef Coef

1. 6 0.472 6 0.472 452 1.00 452 1 .00 10 0.536 10 0.536

7 0.922 7 0.922 21 0.895 21 0.895 16 0.407 16 0.407

27 0.971 33 0.976 34 0.999 35 0.999 12 0.595 12 0.595

4 0.678 1 0.485 108 0.903 135 0.926 3 0.515 3 0.515

3 0.628 3 0.628 105 1.00 105 1.00 18 0.984 18 0.984

19 0.970 19 0.970 243 0.999 243 0.999 8 0.723 8 0.723

16 0.853 15 0.881 32 0.919 37 0.915 15 0.744 9 0.713

1 -1 .000 1 -1 .000 2 0.353 2 0.353 23 0.628 14 0.631

7 0.789 7 0.789 100 0.997 100 0.997 13 0.569 13 0.569

10.

2 0.722 2 0.722 15 0.922 16 0.927 14 0.789 14 0.789

11.

11 0.715 11 0.715 224 0.969 224 0.969 18 0.557 18 0.557

12.

1 0.053 1 0.053 32 1.00 32 1.00 8 0.146 3 0.076

13.

5 0.829 5 0.829 11 0.953 11 0.953 7 0.406 7 0.406

14.

4 0.691 4 0.691 22 0.956 22 0.956 8 0.485 8 0.485

15.

7 0.852 7 0.852 103 0.979 103 0.979 6 0.681 6 0.681

ter the clustering. The results obtained are presented

in Table 2. From the table, it can be seen that the clus-

ter conﬁgurations produced using the proposed secure

algorithms were the same in 35 of the 45 cases (same

number of clusters). Where the conﬁgurations were

different, in one case the Sil. Coef. value was the

same, in the remaining nine cases the Sil. Coef. value

using the secure clustering was better in ﬁve of the

nine occasions. The reason for the different conﬁgu-

rations sometimes obtained was the nature of the pro-

posed OPE scheme; although ensuring that the CDM

was secure against Statistical Attacks and Cypher-

text Only Attacks by producing different cyphertext

for the same plaintext, usage of the OPE scheme did

sometimes affect the nature of the clustering because

equality is not preserved. Consequently different Sil.

Coef. values were sometimes produced in these cases,

although in most cases these differences were not sig-

niﬁcant.

The security of the proposed clustering relies on

the security of: (i) Liu’s scheme used to encrypt the

raw data and (ii) the proposed OPE scheme used to

encrypt the CDM. Liu’s scheme has been shown to

be semantically secure (Liu, 2013); given any cypher-

text C within a message m the ability of an adversary

to determine any partial information concerning the

message will be negligible in terms of the input, hence

the scheme is “probably secure”. In other words, it

will be computationally expensive to derive informa-

tion concerning the encrypted plaintext given only the

cyphertexts and the corresponding encryption public

key. This feature makes the proposed method se-

cure against Chosen-Plaintext Attack (CPA) and con-

sequently secure against Knowing Plaintext Attack

(KPA) and Cyphertext Only Attack (COA). More-

over, once the data is encrypted and outsourced to a

third party data miner, using the proposed approaches,

no decryption takes place at the third party side which

implies even more security. In terms of the pro-

posed OPE scheme, preserving the order of gener-

ated cyphertexts raises a threat of Cyphertext Only

Attacks (COAs) that use statistical features, assum-

ing that the data distribution is known. Therefore, the

adopted OPE mechanism utilises the conceptof “mes-

sage space splitting” and “non-linear cypher space ex-

pansion” to obscure the data distribution in the gener-

ated cyphertexts, thus protecting against COAs. Fur-

thermore, the encryption function has a one-to-many

mapping feature that produces different cyphertexts

for the same plaintext value even when the same keys

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

0 1 2 3 4 5 6 7 8 9 1011 1213 1415

100

150

200

250

300

0 1 2 3 4 5 6 7 8 9 1011 1213 1415

100

200

300

400

500

0 1 2 3 4 5 6 7 8 9 1011 1213 1415

100

200

300

400

500

Standard Secure

Figure 2: Comparison of run times using standard and secure clustering algorithms (NNC, DBSCAN and k-means).

are used; this makes it harder to derive any informa-

tion from inspecting the cyphertexts.

7 CONCLUSION

In this paper a secure clustering mechanisms has been

proposed using the idea of an SCDM. The usage of

the SCDM was illustrated in the context of three clus-

tering approaches: (i) Secure DBSCAN, (ii) Secure

Nearest Neighbour and (iii) Secure k-Means. The ad-

vantages offered by the SCDM are ﬁrstly that it is

compact and thus appropriate for large datasets; the

SCDM requires signiﬁcantly lower resource in terms

of memory and user interaction overhead, compared

to (say) the UDM concept presented in (Almutairi

et al., 2017). Secondly, the proposed OPE encryption

provides an adequate level of security against COA.

Thirdly, compared to other proposed secure clustering

approaches, data owner participation during the clus-

tering process is zero with respect to SDBSCAN and

SNNC, and limited with respect to Sk-Means. Eval-

uation was conducted, using ﬁfteen UCI datasets, by

comparing the operation of the secure clustering al-

gorithms with their standard counterparts. The eval-

uation demonstrated that the quality of the cluster-

ing was similar although not always identical (some-

times better). The reason for the differences was the

random parameter δ added to OPE cyphertext which

made equality comparison impossible. The runtime,

as was to be expected, was greater with respect to se-

cure clustering, but not signiﬁcantly so. For future

work, the authors intend to develop a “Super CDM”

where the represented data belongs to two or more

data owners who do not wish to share their data in an

unencrypted form.

REFERENCES

Agrawal, R. and Srikant, R. (2000). Privacy-preserving data

mining. In ACM Sigmod Record, volume 29, pages

439–450. ACM.

Almutairi, N., Coenen, F., and Dures, K. (2017). K-means

clustering using homomorphic encryption and an up-

datable distance matrix: Secure third party data clus-

tering with limited data owner interaction. In 19th

International Conference on Big Data Analytics and

Knowledge Discovery.

Berinato, S. (2015). There

Os no such thing as anonymous

data. Harvard Business Review, February.

Chhinkaniwala, H. and Garg, S. (2011). Privacy preserv-

ing data mining techniques: Challenges and issues.

In Proceedings of International Conference on Com-

puter Science & Information Technology, CSlT, page

609.

Cover, T. and Hart, P. (1967). Nearest neighbor pattern clas-

siﬁcation. IEEE transactions on information theory,

13(1):21–27.

Erkin, Z., Veugen, T., Toft, T., and Lagendijk, R. L. (2009).

Privacy-preserving user clustering in a social network.

In 2009 First IEEE International Workshop on Infor-

mation Forensics and Security (WIFS), pages 96–100.

IEEE.

Ester, M., Kriegel, H.-P., Sander, J., Xu, X., et al. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. In Kdd, volume 96,

pages 226–231.

Hazay, C., Mikkelsen, G. L., Rabin, T., and Toft, T. (2012).

Efﬁcient RSA key generation and Threshold Paillier

in the two-party setting. In CT-RSA, pages 313–331.

Springer.

Jha, S., Kruger, L., and McDaniel, P. (2005). Pri-

vacy preserving clustering. In European Symposium

on Research in Computer Security, pages 397–417.

Springer.

Lichman, M. (2013). UCI machine learning repository.

Lindell, Y. and Pinkas, B. (2002). Privacy preserving data

mining. Journal of cryptology, 15(3):177–206.

Liu, D. (2013). Homomorphic encrypton for database

querying.

Liu, D., Bertino, E., and Yi, X. (2014). Privacy of out-

sourced k-means clustering. In Proceedings of the 9th

ACM symposium on Information, computer and com-

munications security, pages 123–134. ACM.

Liu, D. and Wang, S. (2013). Nonlinear order preserving

index for encrypted database query in service cloud

environments. Concurrency and Computation: Prac-

tice and Experience, 25(13):1967–1984.

Liu, Z., Chen, X., Yang, J., Jia, C., and You, I. (2016). New

order preserving encryption model for outsourced

Data Clustering using Homomorphic Encryption and Secure Chain Distance Matrices

databases in cloud environments. Journal of Network

and Computer Applications, 59:198–207.

MacQueen, J. et al. (1967). Some methods for classiﬁcation

and analysis of multivariate observations. In Proceed-

ings of the ﬁfth Berkeley symposium on mathematical

statistics and probability, volume 1, pages 281–297.

Oakland, CA, USA.

Mittal, D., Kaur, D., and Aggarwal, A. (2014). Secure

data mining in cloud using homomorphic encryption.

In Cloud Computing in Emerging Markets (CCEM),

2014 IEEE International Conference on, pages 1–7.

IEEE.

Rahman, M. S., Basu, A., and Kiyomoto, S. (2017). To-

wards outsourced privacy-preserving multiparty DB-

SCAN. In Dependable Computing (PRDC), 2017

IEEE 22nd Paciﬁc Rim International Symposium on,

pages 225–226. IEEE.

Rao, F.-Y., Samanthula, B. K., Bertino, E., Yi, X., and Liu,

D. (2015). Privacy-preserving and outsourced multi-

user k-means clustering. In Collaboration and In-

ternet Computing (CIC), 2015 IEEE Conference on,

pages 80–89. IEEE.

Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to

the interpretation and validation of cluster analysis.

Journal of computational and applied mathematics,

20:53–65.

Samanthula, B. K., Elmehdwi, Y., and Jiang, W. (2015). K-

nearest neighbor classiﬁcation over semantically se-

cure encrypted relational data. IEEE transactions on

Knowledge and data engineering, 27(5):1261–1273.

Shaneck, M., Kim, Y., and Kumar, V. (2009). Privacy pre-

serving nearest neighbor search. In Machine Learning

in Cyber Trust, pages 247–276. Springer.

Tong, Q., Li, X., and Yuan, B. (2018). Efﬁcient distributed

clustering using boundary information. Neurocomput-

ing, 275:2355 – 2366.

Vaidya, J., Clifton, C. W., and Zhu, Y. M. (2006). Privacy

preserving data mining, volume 19. Springer Science

& Business Media.

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval