Partial Sampling Operator and Tree-structural Distance

for Multi-objective Genetic Programming

Makoto Ohki

Field of Technology, Tottori University, 4, 101 Koyama-Minami, Tottori, 680-8552, Japan

Keywords:

Genetic Programming, Multi-objective Optimization, Partial Sampling, Tree Structural Distance, NSGA-II.

Abstract:

This paper describes a technique on an optimization of tree-structure data, or genetic programming (GP), by

means of a multi-objective optimization technique. NSGA-II is applied as a frame work of the multi-objective

optimization. GP wreaks bloat of the tree structure as one of the major problem. The cause of bloat is that the

tree structure obtained by the crossover operator grows bigger and bigger but its evaluation does not improve.

To avoid the risk of bloat, a partial sampling (PS) operator is proposed instead to the crossover operator.

Repeating processes of proliferation and metastasis in PS operator, new tree structure is generated as a new

individual. Moreover, the size of the tree and a tree-structural distance (TSD) are additionally introduced into

the measure of the tree-structure data as the objective functions. And then, the optimization problem of the

tree-structure data is deﬁned as a three-objective optimization problem. TSD is also applied to the selection

of parent individuals instead to the crowding distance of the conventional NSGA-II. The effectiveness of the

proposed techniques is veriﬁed by applying to the double spiral problem.

1 INTRODUCTION

A technique of genetic programming (GP)(Koza,

1992; Koza, 1994) is an algorithm to optimize struc-

tured data based on a genetic algorithm(Goldberg,

1989; Mitchell et al., 1996). GP is applied to various

ﬁelds such as program synthesis(David and Kroening,

2017), function generations(Jamali et al., 2017) and

rule set discoveries(Ohmoto et al., 2013). Although

GP is very effective for optimizing structured data,

it has several problems such as getting into a bloat,

inadequate optimization of constant nodes, being eas-

ily captured in local optimal solution area when ap-

plied to complicated problems. The main cause of

bloat is a crossover operator which exchanges par-

tial trees of parent individuals(Nordin et al., 1995;

Angeline, 1997; Angeline, 1998; De Jong et al.,

2001), where this paper focuses on the optimization

of tree-structure data by means of GP. Several tech-

niques to reduce the bloat have been proposed by im-

proving the simple crossover operation(Koza, 1994;

De Bonet et al., 1997; M

uhlenbein and Paass, 1996;

Ito et al., 1998; Langdon, 1999; Francone et al.,

1999). Although these methods have successfully in-

hibited bloat to a certain extent, effective search has

not necessarily been performed. Moreover, there is

no theoretical basis that crossover is effective for op-

timizing the tree-structure data.

Apart from reduction of the bloat, a search method

for optimizing the graph structure has been pro-

posed(Karger, 1995). Although this method is suit-

able for searching various structural data consisting

of nodes and branches, the algorithm is complicated

and the computation cost is high.

In this paper, we exclude the crossover operator

which is the cause of bloat in GP, and propose a par-

tial sampling (PS) operator as a new operator for GP

instead. In PS operator, ﬁrst of all, a partial sample

of a partial tree structure is extracted from several in-

dividuals of a parent individual group by a prolifera-

tion. Next, the partial tree structure obtained by the

proliferation is combined with a new tree structure by

a metastasis. In this paper, two types of metastasis

are prepared for GP, one that depends on the origi-

nal upper node and the other that does not. Repeating

the proliferation and the metastasis regenerates a new

tree-structure data for the next generation.

In addition, in this paper, MOEA technique for

suppressing bloat and acquire many kinds of various

tree-structure data is applied for GP by adding the size

and the distance of the tree-structure data to the eval-

uation. One of the newly added objective functions

is the size of the tree-structure data. Furthermore, the

relative position of the target individual in the popu-

lation in terms of the tree-structural distance (TSD)

is also evaluated as an objective function. The tree-

110

Ohki, M.

Partial Sampling Operator and Tree-structural Distance for Multi-objective Genetic Programming.

DOI: 10.5220/0006894401100117

In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 110-117

ISBN: 978-989-758-327-8

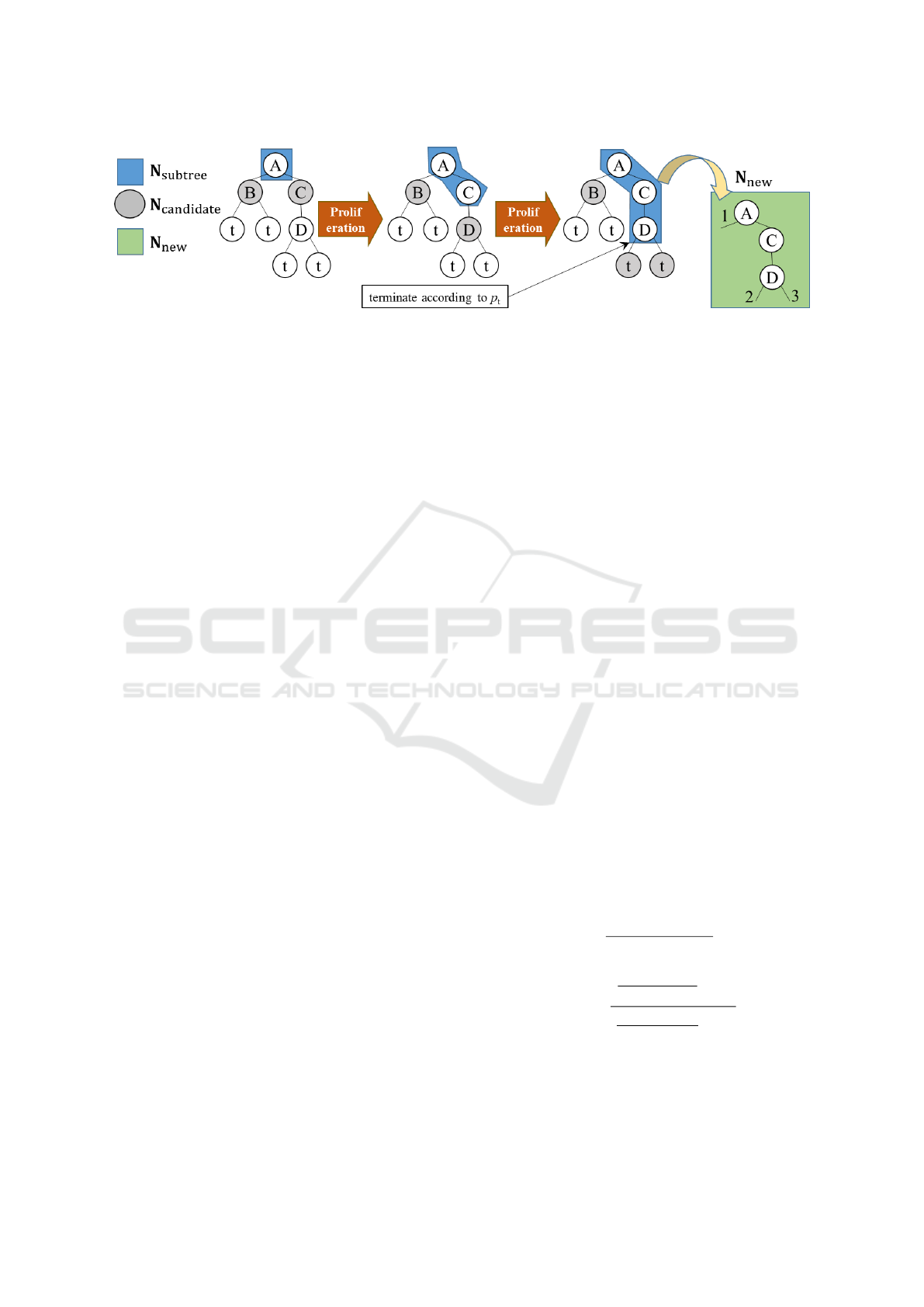
Figure 1: The initial proliferation in PS operator.

structure data optimization problem is formulated as

a three objective optimization problem by deﬁning

these three objective functions.

NSGA-II(Deb et al., 2000; Deb, 2001) is applied

to this three objective optimization problem. In the

conventional NSGA-II, a crowding distance (CD) is

applied for ranking the front set overﬂowing from the

parent group. In optimizing the tree-structure data,

we can not maintain diversity of the population by fo-

cusing only on the value of the objective function and

storing the solution near the extreme solution. In this

paper, TSD is applied, instead of CD, for ranking the

front set overﬂowing from the parent group.

In order to verify the effectiveness, the proposed

technique and the conventional techniques is applied

to a double spiral problem (De Bonet et al., 1997;

Yang and Kao, 2000). The double spiral problem is a

classiﬁcation problem containing two classes of point

sets arranged on a spiral shape to be classiﬁed with a

function. This problem is well known as one of dif-

ﬁcult problem to solve with a neural network. In this

paper, GP obtains the classifying function composed

of the ﬁnite mathematical elements.

2 PARTIAL SAMPLING

OPERATOR FOR MATING

One of the main causes of bloat is the crossover oper-

ator generally applied in the conventional GPs, used

for regenerating a new tree-structure data. This pa-

per proposes to exclude the crossover operator from

the conventional GP and to apply PS operator for re-

generation of a new tree-structure data instead of the

crossover operator. The PS operator creates a new

tree-structure data by partially sampling tree struc-

tures from a parent individual and joining them to-

gether. This procedure is called a proliferation. The

proliferation is terminated according to the probabil-

ity, p

. Partially sampled subtree structures by the

proliferation are combined together by a metastasis.

Two types of the metastasis are prepared, one that de-

pends on the original upper node and the other that

does not. We call the the former as an upper node de-

pend metastasis and the latter as a random metastasis.

In the initial proliferation, a root node, n

i,root

, of

an individual, indiv

, randomly selected from a parent

group P

is copied to a set N

subtree

as shown in Fig.1.

The initial proliferation is started from the root node,

i,root

, of the individual, indiv

. In this example, the

starting root node contains an identiﬁcation, A. Let

candidate

be a set of all lower nodes under the node

of N

subtree

, where that node is not selected as a node

of N

subtree

yet. One node is randomly selected from

candidate

and copied to N

subtree

. The proliferation ter-

minates according to the proliferation terminate prob-

ability, p

, or when N

candidate

0. When the prolif-

eration is terminated, the set N

subtree

thus obtained is

copied to N

new

, where is a set of nodes as a new tree-

structure data. The set N

subtree

is initialized to

0. Fur-

thermore, the root node of the partial tree structure

new

in the initial proliferation is randomly generated

in a low probability on the initial proliferation.

In the conventional GP with variable structure

length, small partial structures are assembled by an

regenerating operator, for example, crossover or mu-

tation, and these partial structures are combined to

generate a new tree-structure data of a large size(Poli

and Langdon, 1998; Poli et al., 2008). When the con-

ventional GP increases the average size of the tree-

structure data, the size of the partial structure also pre-

served for the next generation increases. Therefor, the

probability, p

is scheduled as follows.

AverageSize(R

)

, (1)

g+1



− p



Succeed(P

)

− p

Succeed(R

)

− p

+ p

, (2)

where p

denotes the probability, p

, at the initial gen-

eration, p

denotes the probability, p

, at the g-th gen-

eration, R

denotes a population at the g-th genera-

tion, P

⊂ R

denotes the parent group at the g-th

Partial Sampling Operator and Tree-structural Distance for Multi-objective Genetic Programming

111

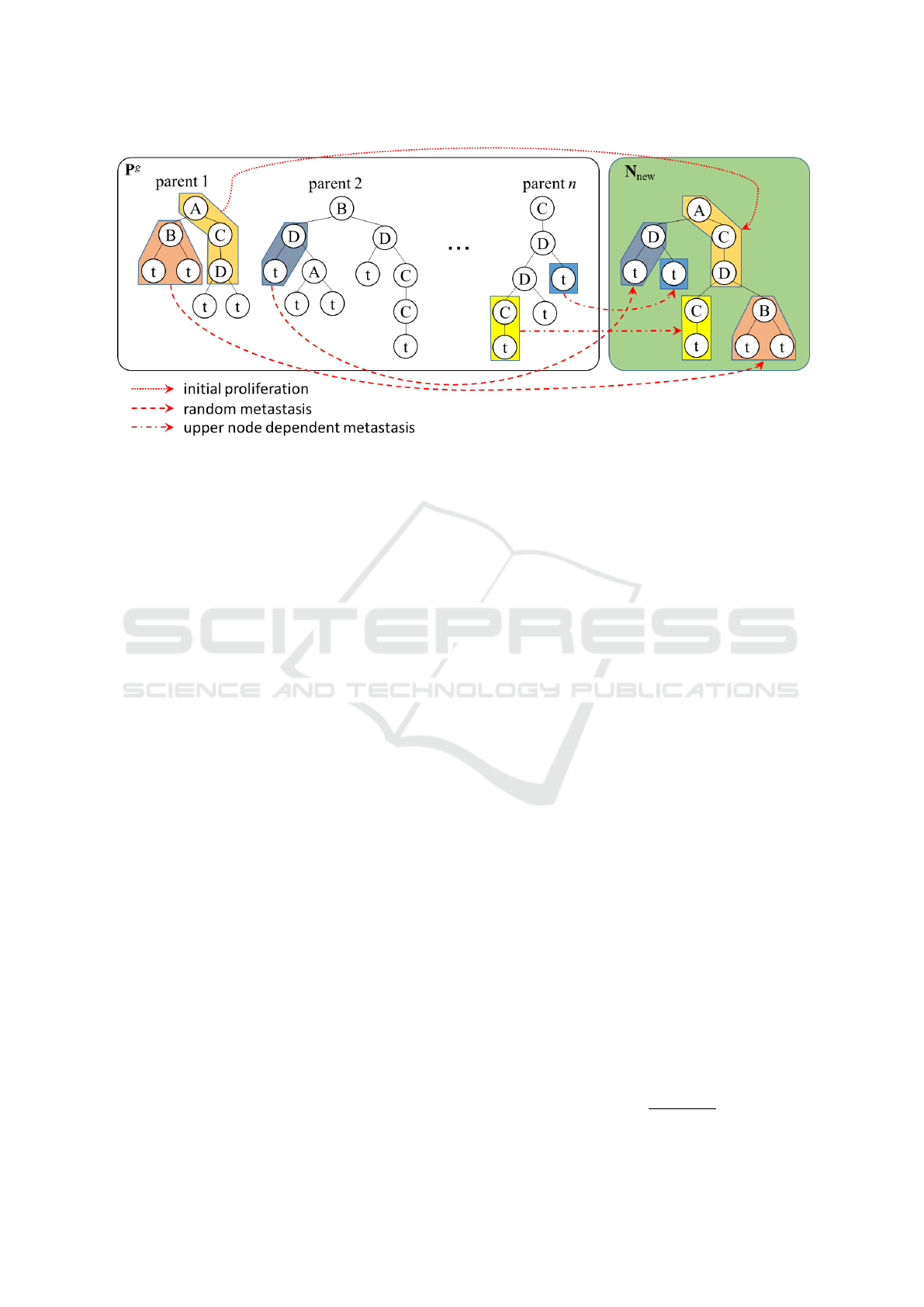
Figure 2: Outline of how a new tree structure is created by PS operator.

generation, AverageSize(·) denotes a function return-

ing the average size of the tree set, and Succeed(·)

denotes a function returning the average size of the

partial tree structure that the argument set takes over

from the previous generation. Scheduling the prob-

ability, p

, as shown above prevents the size of the

partial tree structure from explodingly increasing.

A partial tree structure is grown by applying one

of two kinds of metastasis to the partial tree struc-

ture obtained by the initial proliferation. One of two

kinds of metastasis is a random metastasis. The ran-

dom metastasis activates according to a metastasis se-

lection probability, p

met

. The other one metastasizes

depending on the upper node. The upper node de-

pend metastasis activates according to the probabil-

ity, 1 − p

met

. The partial tree structure N

new

shown

in the Fig.1 has three empty branched numbered as

1, 2 and 3. The branch 1 has the upper node A, and

the branches 2 and 3 have upper node D. Now, sup-

pose that the branch 1 is selected as a target of the

upper node depend metastasis. In the next prolifera-

tion, a node having the upper node A is selected from

the parent group, P

. On the other hand, if the ran-

dom metastasis is applied to the partial tree structure

new

, the beginning node for the next proliferation is

randomly selected from the parent group, P

A new node is selected from the parent group, P

according to the decided metastasis type. This node

is not necessarily a root node. The proliferation is

started from the selected node again.

By repeating the proliferation and the metastasis,

new tree-structure data is generated as shown in Fig.2.

However, when the metastasis applied to only one

parent individual, or when a parent individual having

the same structure as the generated tree structure, the

generated tree structure is eliminated and PS operator

is performed again. The terminal nodes are given as

a random number in a low probability, where this is

based on the conventional mutation idea.

3 MULTI-OBJECTIVE GENETIC

PROGRAMMING

Optimizing the tree-structure data based only on the

index of its own goodness brings problems that causes

bloat but also that the optimization is caught in a local

optimum region. Depending on the structure of the lo-

cal optimum region, the optimization stagnates, caus-

ing an illusion as if it were the ultimate optimal solu-

tion. To avoid the risk of such the problems, this pa-

per, therefor, proposes a technique to optimize based

on the size of the tree structure and TSD in the popu-

lation in addition to the index of the goodness of tree

structure.

In this paper, three objective functions are deﬁned

as follows to be used for the multi-objective optimiza-

tion . An objective function according to the goodness

of an individual, indiv

, is described by the following

equation.

(indiv

) = performance(root

), (3)

where root

denotes a root node of the individual,

indiv

, and performance(root

) denotes a function that

returns value of the goodness of the tree structure be-

ginning from the root node, root

An objective function according to the size of tree

structure is deﬁned by the following equation.

(indiv

) =

Size(root

)

, (4)

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

112

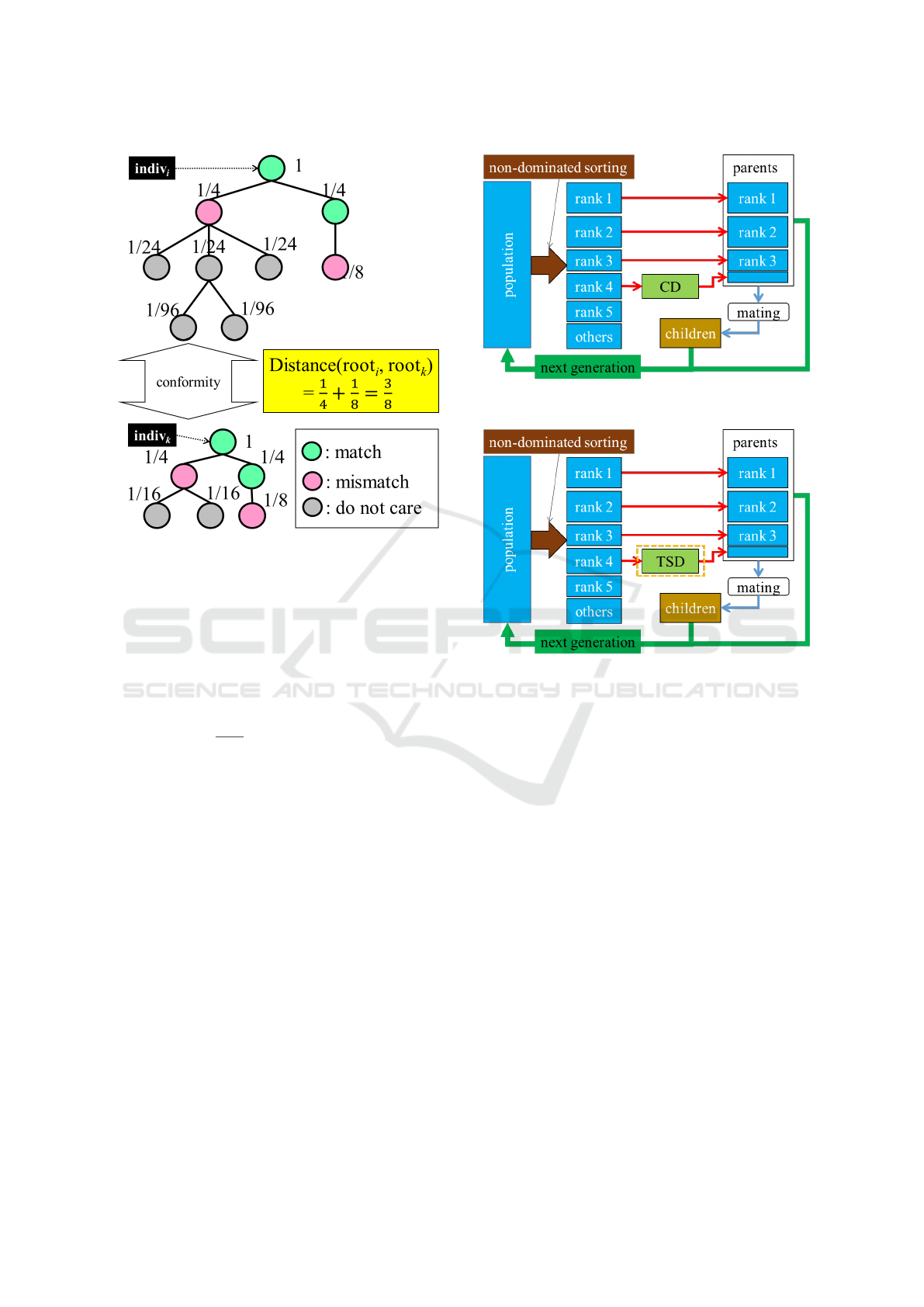
Figure 3: An example of giving weights to the tree structure

and TSD.

where Size(root

) denotes a function that returns the

number of the nodes of the tree structure beginning

from the root node, root

An objective function according to average of

TSD in the population is deﬁned by the following

equation.

(indiv

) =

pop

∑

k=1

Distance(root

,root

), (5)

where N

pop

denotes the size of the population, and

Distance(root

,root

) denotes a function that returns

TSD between indiv

and indiv

. In order to calculate

TSD, weights are given to all the nodes of the tree

structured data by means of the following steps, when

the tree structured data is initially generated. An ex-

ample of giving weights to the tree structure is shown

in Fig.3.

(Step 1) Give weight 1 to the root node.

(Step 2) Assume that W is a weight given to the cur-

rent node.

(Step 3) Equally distribute weights to the lower nodes

of the current node so that the total is W /2.

Two tree structures are compared in order from

the root node to check conformity of both nodes as

shown in Fig.3. The distance, Distance(root

,root

is initialized as zero. When different nodes are found

in the conformity comparison, the weight of that

node is added to the distance. The lower nodes

below this node are all ignored. Especially, when

Figure 4: Conventional NSGA-II with CD.

Figure 5: Modiﬁed NSGA-II with tree-structural distance.

the tree structures of both are completely different,

Distance(root

,root

) is given 1 as the maximum

value.

Now, we have deﬁned the three-objective opti-

mization problem. NSGA-II shown in Fig.4 is applied

to solve this problem. NSGA-II selects parent indi-

viduals by using non-dominated sorting and ranking

with CD. Since tree-structure data is to be optimized

in this paper, CD based only on the value of the objec-

tive function does not necessarily bring the diversity

of the tree structure. Therefore, this paper propose

to use TSD when selecting parents from the rank set

overﬂowing from the parent group. A block chart of

the modiﬁed NSGA-II with TSD is shown in Fig.5.

4 DOUBLE SPIRAL PROBLEM

A double spiral problem is applied to verify an effec-

tiveness of the proposed techniques. The double spi-

ral problem is a problem of classifying two data sets

arranged in a spiral shape, and it is known as a prob-

lem that is difﬁcult to solve even using neural net-

Partial Sampling Operator and Tree-structural Distance for Multi-objective Genetic Programming

113

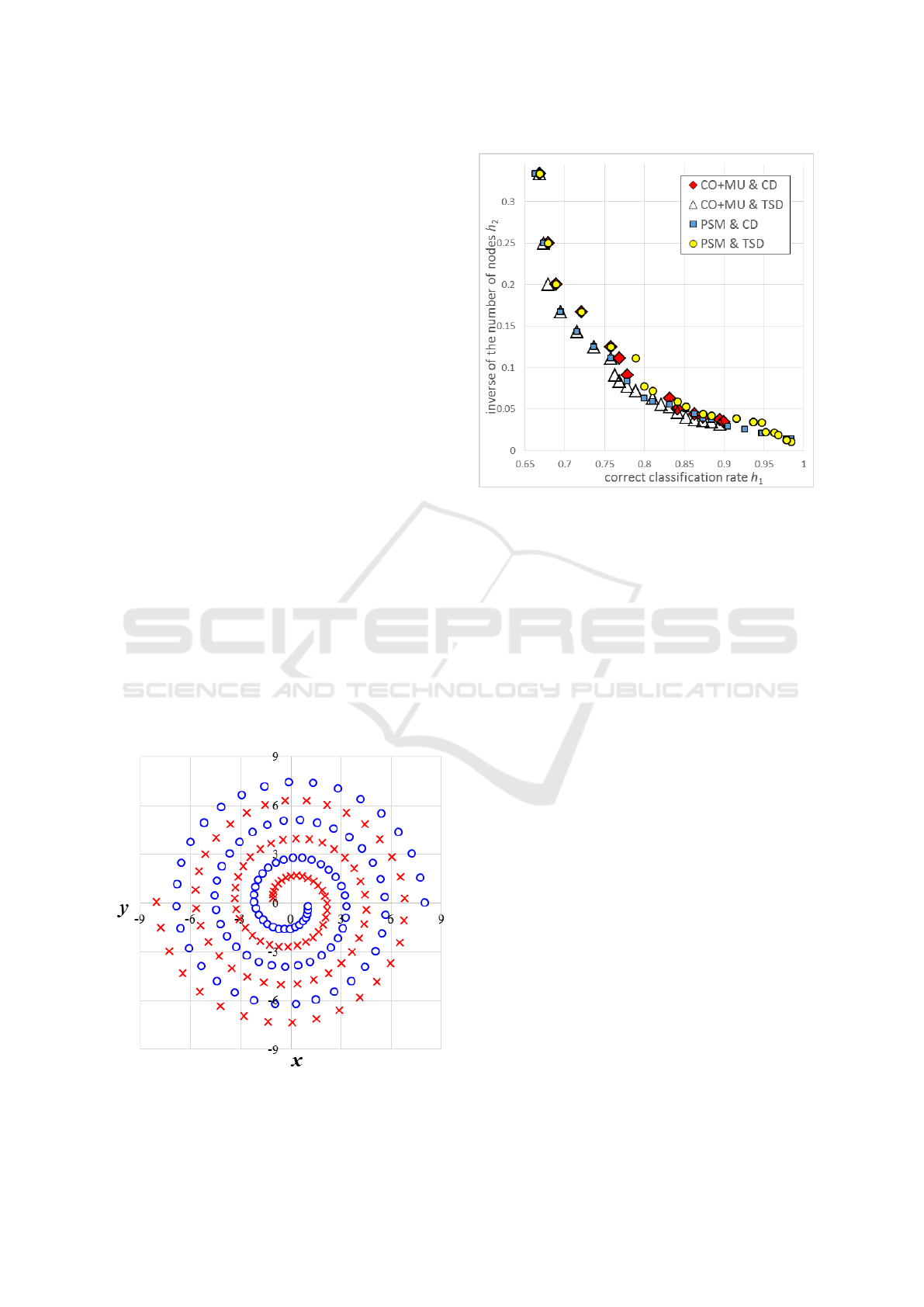
works(De Bonet et al., 1997; Yang and Kao, 2000).

These two data sets are arranged as shown in Fig.6

and are to be classiﬁed by the following function f .







f (x,y) > 0 ⇐⇒ (x,y) ∈ D

f (x,y) < 0 ⇐⇒ (x,y) ∈ D

f (x,y) = 0 ⇐⇒ FALSE,

(6)

where (x,y) denotes the coordinates of each point on

the two-dimensional plane, and D

and D

denote the

data sets expressed with the red crosses and the blue

circles shown in Fig.6 respectively. In this paper, the

case when f (x, y) = 0 is treated as classiﬁcation fail-

ure at the point (x,y).

The following nodes are prepared as ele-

ments for constituting the classifying function f .

-nonterminal nodes: {+,−,∗,÷,sin,cos,tan,iﬂtz}

-terminal nodes: {x,y,constant}

where iﬂtz denotes a function with three arguments

representing a conditional branch as follows,

iﬂtz(a,b,c) , if a < 0 then b else c,



b (a < 0),

c (otherwise).

(7)

In order to verify the effectiveness, the follow-

ing four combinations are applied to the double spi-

ral problem, combination of the conventional opera-

tors and CD (expressed as ”CO+MU & CD”), com-

bination of the conventional operators and TSD (ex-

pressed as ”CO+MU & TSD”), combination of PS

operator and CD (expressed as ”PS & CD”) and

combination of PS operator and TSD (expressed as

“PS & TSD”). The conventional operators denotes

Figure 6: Arrangement of two data sets for double spiral

problem. The red cross denotes a point in the class D

and

the blue circle denotes a point in the class D

Figure 7: Distribution on the h

-h

plane of the ﬁrst front

set in the ﬁnal generation when using each method.

the conventional crossover and the conventional mu-

tations(Koza, 1992; Koza, 1994; Ito et al., 1998;

Sawada and Kano, 2003). The size of the population,

the running generations, the number of points in the

double spiral problem are deﬁned as 100, 1,000,000

and 190 respectively. The probability, p

met

, for se-

lecting the type of the metastasis is set to 0.5, 0.25

and 0.75.

Fig.7 shows distributions on the h

− h

plane of

the ﬁrst-front set in the ﬁnal generation. As shown by

Fig.7, NSGA-II with combining PS operator and TSD

has given the best solution set, distributed in the upper

right direction, in the widest range. The solutions ob-

tained by NSGA-II with combining PS operator and

CD has relatively high diversity but their evaluations

are not so good. NSGA-II with combining the con-

ventional operators and CD has given relatively good

solutions but their diversity is low. NSGA-II with

combining the conventional operators and TSD has

given the worst solution set with the lowest diversity.

Fig.8 shows a comparison of distribution on the

-h

plane of the ﬁrst front set in the ﬁnal generation

when 3-objective and 2-objective optimizations are

executed by using the PS operator with p

met

= 0.50

and TSD for the ranking. Compared to the distribu-

tion of solutions given by 2-objective optimization,

the 3-objective optimization has acquired far better

solutions in wider range. When PS operator with

met

= 0.50 and CD are combined, the same result has

been obtained as shown in Fig.9. This shows an effec-

tiveness of multi-objective optimization of the tree-

structure data as proposed in this paper.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

114

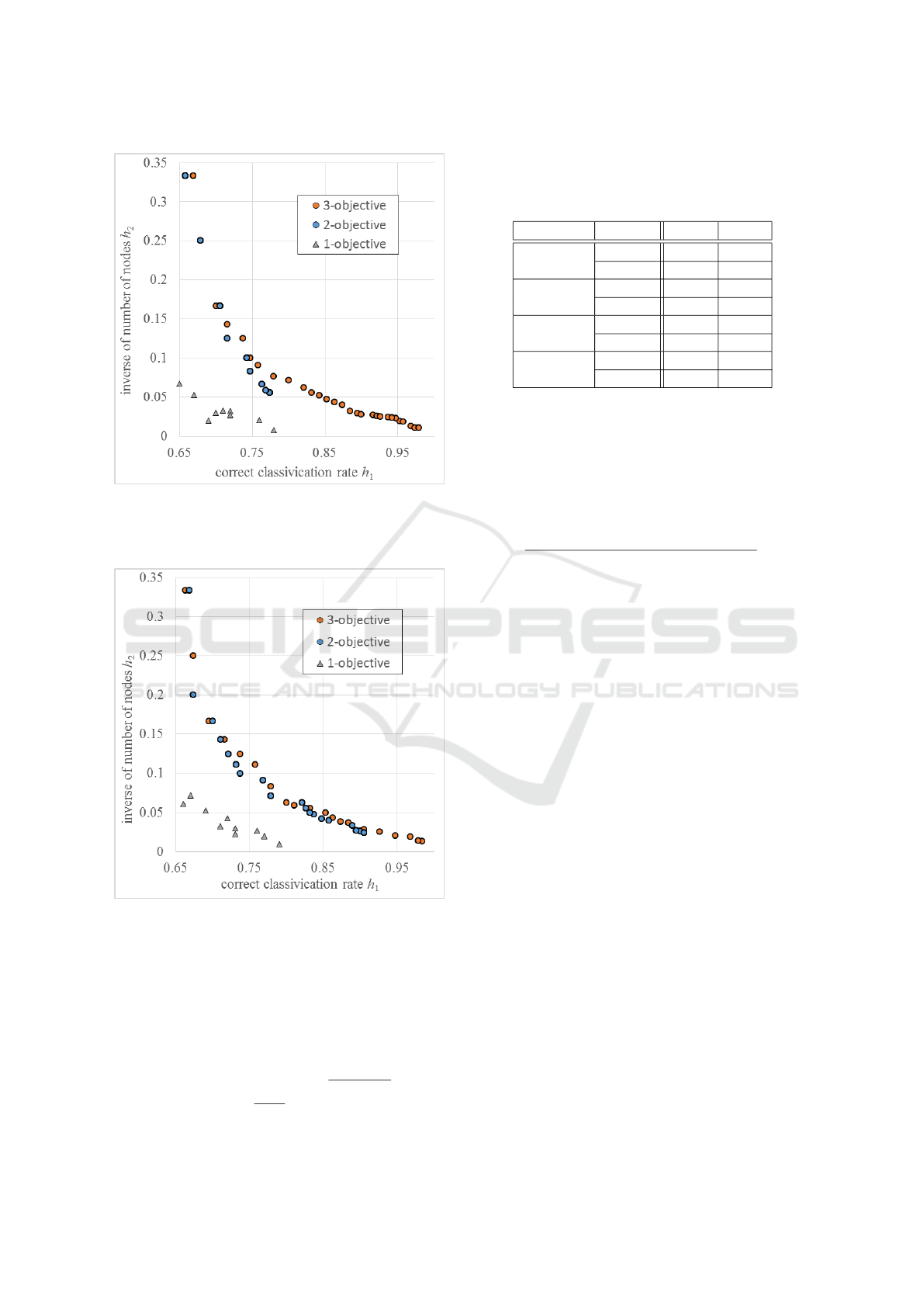
Figure 8: Comparison of distribution on the h

-h

plane of

the ﬁrst front set in the ﬁnal generation when 3-objective

and 2-objective optimizations are executed by using the PS

operator with p

met

= 0.50 and TSD for the ranking.

Figure 9: Comparison of distribution on the h

-h

plane of

the ﬁrst front set in the ﬁnal generation when 3-objective

and 2-objective optimizations are executed by using the PS

operator with p

met

= 0.50 and CD for the ranking.

Norm (Sato et al., 2006) and Maximum Spread

(MS)(Zitzler, 1999) are applied for evaluation of each

method. Norm denotes a measure of the convergence

of the population to the Pareto front P F and is deﬁned

by the following equation.

Norm(P F) =

P F

∑

j=1

∑

i=1

)

, (8)

Table 1: Values of Norm and MS as a result of three-

objective optimization given by each method. CO+MU de-

notes the conventional crossover operator and the conven-

tional mutation operators. PS denotes PS operator.

operator ranking Norm MS

CO+MU CD 0.820 1.110

TSD 0.795 1.100

PS CD 0.835 1.125

= 0.25 TSD 0.835 1.125

PS CD 0.845 1.130

= 0.50 TSD 0.865 1.140

PS CD 0.825 1.110

= 0.75 TSD 0.850 1.140

where x

denotes the j-th individual of the Pareto

front P F . The larger the Norm value, the closer the

approximate Pareto front P F. MS denotes a mea-

sure of the spread of the ﬁrst front at the ﬁnal gen-

eration(Zitzler, 1999) and is deﬁned by the following

equation.

MS(P F) =

∑

i=1



max

P F

j=1

) − min

P F

j=1

)



. (9)

The larger the MS value, the wider the spread of the

population given by the optimization.

Table 1 shows values of Norm and MS given by

each method. CO+MU denotes when the conven-

tional crossover operator and the conventional muta-

tion operators are used for the mating, PS denotes PS

operator, and p

met

= ∗. ∗ ∗ denotes when PS operator

with the metastasis selection probability, p

met

, which

is equal to ∗. ∗ ∗ is used for the mating. Fig.10 is a

graphical representation of the contents of Table 1. In

this ﬁgure, PS∗.∗∗ denotes when PS operator with the

metastasis selection probability, p

met

, which is equal

to ∗.∗∗ is used for the mating. Concerning both Norm

and MS values, the best result has been obtained by

the method using PS operator with p

met

= 0.50 and

TSD. The results using PS operator have gathered in

the upper right of the ﬁgure, whereas the results using

the conventional crossover and the conventional mu-

tation have gathered in the lower left. This shows the

superiority of PS operator. On the other hand, the ad-

vantage of TSD has not been clearly shown by this ex-

periment. TSD have optimized relatively better only

when combined with PS operator. NSGA-II even with

TSD has given the worst results when combined with

the conventional operators. The reason for this result

is considered as that TSD has a low ability to pre-

serve extreme solutions as CD does. In the case of the

multi-objective optimization of the tree structure, the

ability to retain the diversity of tree structures like the

Partial Sampling Operator and Tree-structural Distance for Multi-objective Genetic Programming

115

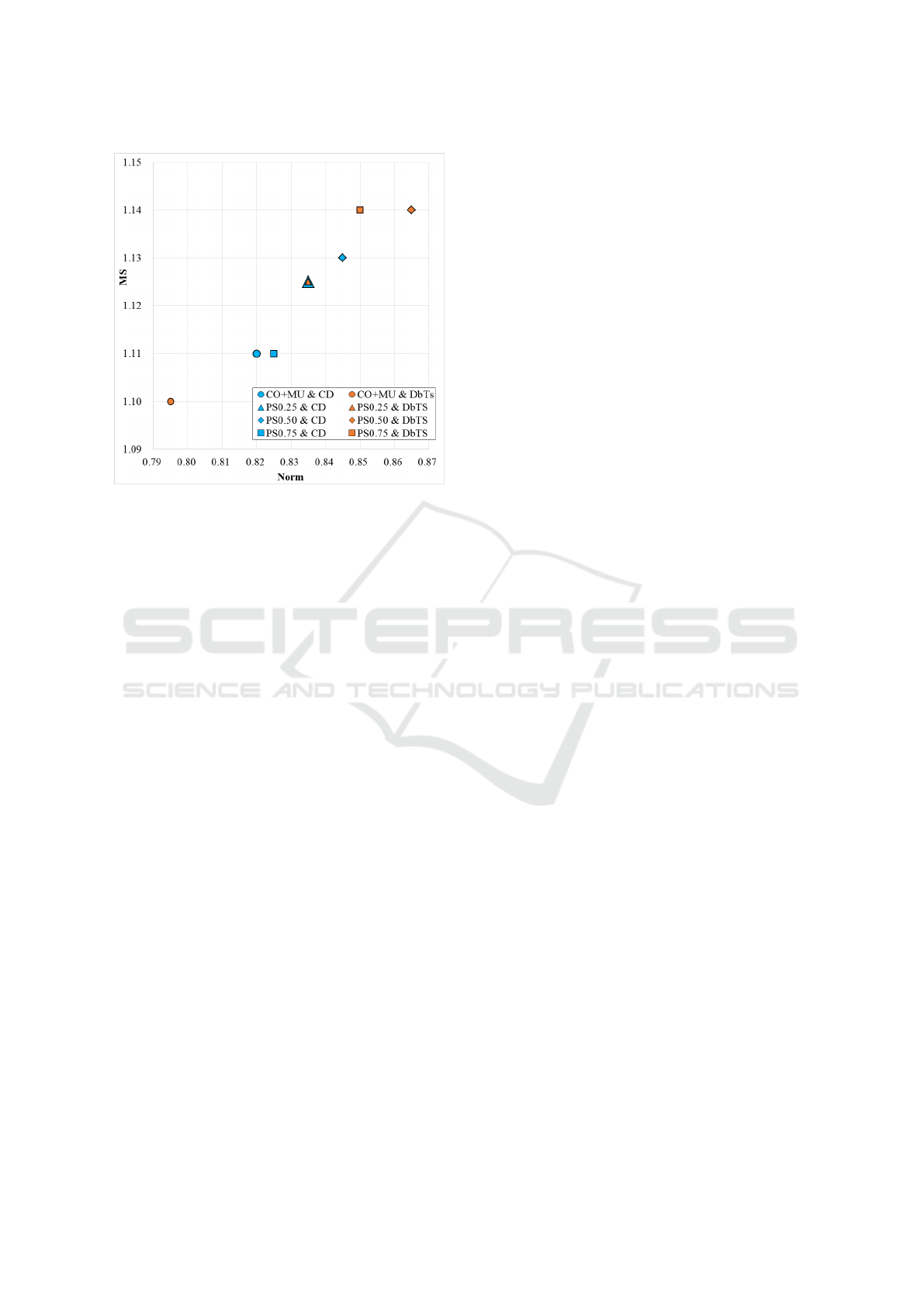
Figure 10: Comparison of results by each method on MS-

Norm plane. CO+MU denotes when the conventional

crossover operator and the conventional mutation operators

are used for the mating. PS∗. ∗ ∗ denotes when PS opera-

tor with the metastasis selection probability, p

met

, which is

equal to ∗. ∗ ∗, is used for the mating.

ranking with TSD is necessary, then an improvement

to add ability to preserve the extreme solutions like

CD should be considered.

5 CONCLUSION

In this paper, multi-objective optimization technique

have been applied to the optimization of the tree-

structure data, or GP. The size of the tree structure

and the tree structural distance (TSD) are addition-

ally introduced into the measure of the goodness of

the tree structure as the objective functions. Further-

more, the partial sampling (PS) operator is proposed

to effectively search the tree structure while avoiding

bloat. In order to verify the effectiveness of the pro-

posed techniques, they have applied to the double spi-

ral problem.

By means of the multi-objective optimization of

tree-structure data, we found that more diverse and

better tree structures are acquired. The proposed

method incorporating PS operator and TSD in NSGA-

II has given relatively good results. However, since

PS operator has low ability to numerically optimize

constant nodes of the tree structure, it has not well

worked effectively for the function optimization. In

addition, since ranking with TSD in NSGA-II has low

ability to preserve extreme solutions in the objective

function space, solutions not have been effectively se-

lected.

In the future, a technique to incorporate numeri-

cal optimization ability such as a particle swarm opti-

mization (Kenny, 1995) and the mutation to PS op-

erator and the ranking selection technique combin-

ing TSD and CD should be considered in the future.

The PS operator proposed in this paper has a mecha-

nism to terminate the proliferation, but does not have

no mechanism to forcibly exit from the PS operator.

Such the mechanism to forcibly exit from the PS op-

erator should be considered.

ACKNOWLEDGEMENTS

This research work has been supported by JSPS

KAKENHI Grant Number JP17K00339.

The author would like to thank to her families, the

late Miss Blackin’, Miss Blanc, Miss Caramel, Mr.

Civita, Miss Marron, Miss Markin’, Mr. Yukichi and

Mr. Ojarumaru, for bringing her daily healing and

good research environment.

REFERENCES

Angeline, P. J. (1997). Subtree crossover: Building block

engine or macromutation. Genetic programming,

97:9–17.

Angeline, P. J. (1998). Subtree crossover causes bloat. In

Genetic Programming 1998: Proc. 3rd Annual Con-

ference. Morgan Kaufmann.

David, C. and Kroening, D. (2017). Program synthesis:

challenges and opportunities. Phil. Trans. R. Soc. A,

375(2104):20150403.

De Bonet, J. S., Isbell Jr, C. L., and Viola, P. A. (1997).

Mimic: Finding optima by estimating probability den-

sities. In Advances in neural information processing

systems, pages 424–430.

De Jong, E. D., Watson, R. A., and Pollack, J. B. (2001).

Reducing bloat and promoting diversity using multi-

objective methods. In Proceedings of the 3rd Annual

Conference on Genetic and Evolutionary Computa-

tion, pages 11–18. Morgan Kaufmann Publishers Inc.

Deb, K. (2001). Multi-objective optimization using evolu-

tionary algorithms, volume 16. John Wiley & Sons.

Deb, K., Agrawal, S., Pratap, A., and Meyarivan, T. (2000).

A fast elitist non-dominated sorting genetic algorithm

for multi-objective optimization: Nsga-ii. In Interna-

tional Conference on Parallel Problem Solving From

Nature, pages 849–858. Springer.

Francone, F. D., Conrads, M., Banzhaf, W., and Nordin, P.

(1999). Homologous crossover in genetic program-

ming. In Proceedings of the 1st Annual Conference

on Genetic and Evolutionary Computation-Volume 2,

pages 1021–1026. Morgan Kaufmann Publishers Inc.

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

116

Goldberg, D. (1989). Genetic algorithms in optimization,

search and machine learning. Reading: Addison-

Wesley.

Ito, T., Iba, H., and Sato, S. (1998). Non-destructive depth-

dependent crossover for genetic programming. In Eu-

ropean Conference on Genetic Programming, pages

71–82. Springer.

Jamali, A., Khaleghi, E., Gholaminezhad, I., Nariman-

Zadeh, N., Gholaminia, B., and Jamal-Omidi, A.

(2017). Multi-objective genetic programming ap-

proach for robust modeling of complex manufactur-

ing processes having probabilistic uncertainty in ex-

perimental data. Journal of Intelligent Manufacturing,

28(1):149–163.

Karger, D. (1995). Random sampling in graph optimization

problems. PhD thesis, stanford university.

Kenny, J. (1995). Particle swarm optimization. In Proc.

1995 IEEE Int. Conf. Neural Networks, pages 1942–

1948.

Koza, J. R. (1992). Genetic Programming II, Automatic

Discovery of Reusable Subprograms. MIT Press,

Cambridge, MA.

Koza, J. R. (1994). Genetic programming as a means for

programming computers by natural selection. Statis-

tics and computing, 4(2):87–112.

Langdon, W. B. (1999). Size fair and homologous tree

crossovers.

Mitchell, M., Crutchﬁeld, J. P., Das, R., et al. (1996). Evolv-

ing cellular automata with genetic algorithms: A re-

view of recent work. In Proceedings of the First In-

ternational Conference on Evolutionary Computation

and Its Applications (EvCA’96), volume 8. Moscow.

uhlenbein, H. and Paass, G. (1996). From recombina-

tion of genes to the estimation of distributions i. bi-

nary parameters. In International conference on par-

allel problem solving from nature, pages 178–187.

Springer.

Nordin, P., Francone, F., and Banzhaf, W. (1995). Explic-

itly deﬁned introns and destructive crossover in ge-

netic programming. Advances in genetic program-

ming, 2:111–134.

Ohmoto, S., Takehana, Y., and Ohki, M. (2013). A con-

sideration on relationship between optimizing interval

and dealing day in optimization of stock day trading

rules. IEICE technical report, 113(2103):67–70.

Poli, R. and Langdon, W. B. (1998). On the search prop-

erties of different crossover operators in genetic pro-

gramming. Genetic Programming, pages 293–301.

Poli, R., McPhee, N. F., and Vanneschi, L. (2008). The im-

pact of population size on code growth in gp: analysis

and empirical validation. In Proceedings of the 10th

annual conference on Genetic and evolutionary com-

putation, pages 1275–1282. ACM.

Sato, M., Aguirre, H. E., and Tanaka, K. (2006). Ef-

fects of δ-similar elimination and controlled elitism

in the nsga-ii multiobjective evolutionary algorithm.

In Evolutionary Computation, 2006. CEC 2006. IEEE

Congress on, pages 1164–1171. IEEE.

Sawada, K. and Kano, H. (2003). Structured evolution strat-

egy for optimization problems using multi-objective

methods. In Proceedings of the 30th Symposium, Soc.

of Instrument and Control Eng., Mar., 2003, pages 1–

6. Society of Instrument and Control Engineering.

Yang, J.-M. and Kao, C.-Y. (2000). An evolutionary al-

gorithm to training neural networks for a two-spiral

problem. In Proceedings of the 2nd Annual Con-

ference on Genetic and Evolutionary Computation,

pages 1025–1032. Morgan Kaufmann Publishers Inc.

Zitzler, E. (1999). Evolutionary algorithms for multiobjec-

tive optimization: Methods and applications.

Partial Sampling Operator and Tree-structural Distance for Multi-objective Genetic Programming

117