Theatrical Genre Prediction using Social Network Metrics

Manisha Shukla

, Susan Gauch

and Lawrence Evalyn

Department of Computer Science and Engineering, University of Arkansas, Fayetteville, AR, U.S.A.

Department of English, University of Toronto, Toronto, ON, Canada

Keywords: Social Networks, Genre Prediction, Relationship Mining, Social Network Analysis, Network Theory.

Abstract: With the emergence of digitization, large text corpora are now available online which provide humanities

scholars an opportunity to perform literary analysis leveraging the use of computational techniques. Almost

no work has been done to study the ability of mathematical properties of network graphs to predict literary

features. In this paper, we apply network theory concepts in the field of literature to explore correlations

between the mathematical properties of the social networks of plays and the plays’ dramatic genre. Our goal

is to find metrics which can distinguish between theatrical genres without needing to consider the specific

vocabulary of the play. We generated character interaction networks of 36 Shakespeare plays and tried to

differentiate plays based on social network features captured by the character network of each play. We were

able to successfully predict the genre of Shakespeare’s plays with the help of social network metrics and hence

establish that differences of dramatic genre are successfully captured by the local and global social network

metrics of the plays. Since the technique is highly extensible, future work can be applied larger groups of

plays, including plays written by different authors, from different periods, or even in different languages.

1 INTRODUCTION

In literary studies, the three key areas of research

could be defined as philology (the study of words),

bibliography (the study of books as objects), and

criticism (the evaluation or interpretation of literary

meaning). Our paper presents a distant reading

method which may aid in the task of literary criticism,

using network graph analysis on social networks

generated from the scripts of plays.

Particularly since the advent of New Criticism,

“the basic task of literary scholarship has been close

reading of texts” (Moretti, 2011), which builds textual

interpretations from the precise study of specific

words. Computational approaches to literature offer

an alternate methodology for the work of literary

study without close reading. “Distant reading”

(Moretti, 2011) takes many forms, including

statistical topic models (Jockers and Mimno, 2013),

character profiling (Flekova and Gurevych, 2015),

character frequency analysis (Sack, 2011), and

sentiment analysis (Elsner, 2015), as mentioned in

Grayson et al. (2016). For computational methods to

produce new literary insights, they must provide

information about literary texts which is not easily

accessible by reading them and must do so for more

texts than it is feasible for a person to read. The social

networks we examine are implicit in the texts, and

thus difficult to access through simple reading, and

our technique can easily be applied to more texts than

a person may read, allowing our method to contribute

novel insights to literary analysis.

Social network analysis is well-established to

study social groups. Some scholars have applied

social network analysis to literary works for e.g. plot

analysis (Grayson et al., 2016), or for discovering

character communities (Watts, 2001), wherein nodes

represent characters, and edges represent interaction

between pairs of characters for plot analysis. Because

these graphs are handmade for a very small number

of plays, however, almost no work has been done to

study the ability of mathematical properties of

network graphs to predict literary features at scale.

We address this gap by exploring correlations

between the mathematical properties of networks and

dramatic genre. We are particularly interested to see

which measures are the most effective predictors, to

form the basis of literary analysis of the role of social

relationships in plays.

In this paper, we study the social networks of

Shakepeare’s plays to establish a correlation between

social network metrics and genre identification. We

Shukla, M., Gauch, S. and Evalyn, L.

Theatrical Genre Prediction using Social Network Metrics.

DOI: 10.5220/0006935002290236

In Proceedings of the 10th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2018) - Volume 1: KDIR, pages 229-236

ISBN: 978-989-758-330-8

229

distinguish between the three Early Modern theatrical

genres of tragedy, comedy, and history, following the

identifications provided in the first collection of

Shakespeare’s works, the First Folio. Using our

generated character networks of Shakespeare’s plays,

we found that combinations of some of the global and

local network metrics (Watts, 2001) were indeed able

to distinguish plays belonging to different genres.

This work has been used for literary analysis of the

ambiguous genre of Shakepeare’s “problem plays”

(Evalyn, et al., 2018).

2 RELATED WORK

2.1 Social Network Analysis

A social network graph is a set of vertices and edges

(called a sociogram) where vertices represent social

actors and edges represent social relations among the

vertices. However, a social network is more than just

a set of vertices and lines, as its structure contains

implicit information about the social actors and their

relationships. The graph representation of a social

network offers a systematic and mathematical method

for investigating these structures. Social network

analysis is the process of investigating social network

structures and ties through the use of network and

graph theory concepts.

As Billah and Gauch (2015, p. 4) observe, “Social

network analysis (SNA) is not a formal theory, but

rather a wide strategy for investigating social structu-

res”. These strategies borrow core concepts from

sociometry, group dynamics, and graph theory (Watts,

2001; Scott, 2000; Wasserman and Faust, 1994).

In social network analysis of human activities, the

nodes can be connected by many kinds of ties, such

as “shared values, visions, and ideas; social contacts;

kinship; conflict; financial exchanges; trade; joint

membership in organizations; and group participation

in events, among numerous other aspects of human

relationships” (Serrat, 2017). However, regardless of

the nature of the connection, “the defining feature of

social network analysis is its focus on the structure of

relationships” (Serrat, 2017). The central assumption

in SNA methodologies is that relationships between

nodes are of central importance (Serrat, 2017).

Social network analysis has been used in a wide

variety of fields, with applications as diverse as

disintegration models based on social network

analysis of terrorist organizations (Anggraini et al.,

2015), collaboration of scholars in graduate education

(Chuan-yi, et al., 2016), football team performance

based on social network analysis of relationships

between football players (Trequattrini, et al., 2015),

money laundering detection (Dreżewski, et al., 2015),

and stress disorder symptoms and correlations in U.S.

military veterans (Armour et al. 2017). In this paper

we explore the applications of social networks in

literary analysis. Specifically, we look for social

network metrics that can identify genre without

relying on the specific language of the play, which

will enable future extension to groups of plays in

different languages.

2.2 Literary Analysis with SNA

Because dramatic performances enact social

encounters, social network analysis translates

surprisingly well to fictional societies. Stiller et al.

have shown that the social networks in Shakespeare’s

plays mirror those of real human interactions,

particularly in size, clustering, and maximum degrees

of separation (Stiller, et al., 2003).

Surveying the field of literary analysis using SNA,

Moretti categorizes several types of analyses: “an

empirical, quantitative and hierarchical description of

literary characters (Jannidis et al., 2016), corpus-

based analyses exploring options for historical

periodisation of literature (Trilcke et al., 2015) and

types of aesthetic modelling of social formations in

and by literary texts (Stiller, et al., 2003; Stiller and

Hudson, 2005; Trilcke et al, 2016).” Moretti himself

uses social networks to examine the plots of three

Shakespearean tragedies, and to contrast a few

chapters of English and Chinese novels (Moretti,

2011). Work following Moretti has focused on

historical periodization, as in Algee-Hewitt’s

examination of 3,439 plays looking only at the Gini

Coefficient of each play’s eigenvector centrality to

track ensemble casts from 1500 to 1920 (Algee-

Hewitt, 2017).

Our project focuses on a novel application, the

classification of literary genre. When scaled up to a

corpus covering a wider historical time span, our

approach to genre could also provide insight on the

historic periodization of literature.

Moretti also identifies that, in the application of

SNA to literature, “methods for the automated

extraction of network data (named entity recognition,

co-reference resolution) and their evaluation are of

particular importance,” (Moretti, 2011), which we

accomplish in this paper.

2.3 Gephi Toolkit

Gephi is an open source software for graph and

network analysis, which allows for fast visualization

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

230

and manipulation of large networks. As a generalist

tool, “it provides easy and broad access to network

data and allows for spatializing, filtering, navigating,

manipulating and clustering” (Bastian, Heymann and

Jacomy, 2009). Gephi also calculates a wide range of

mathematical features for each graph, which we use

as the basis for our mathematical analysis (as

discussed in more detail in 3.3).

3 OUR DESIGN

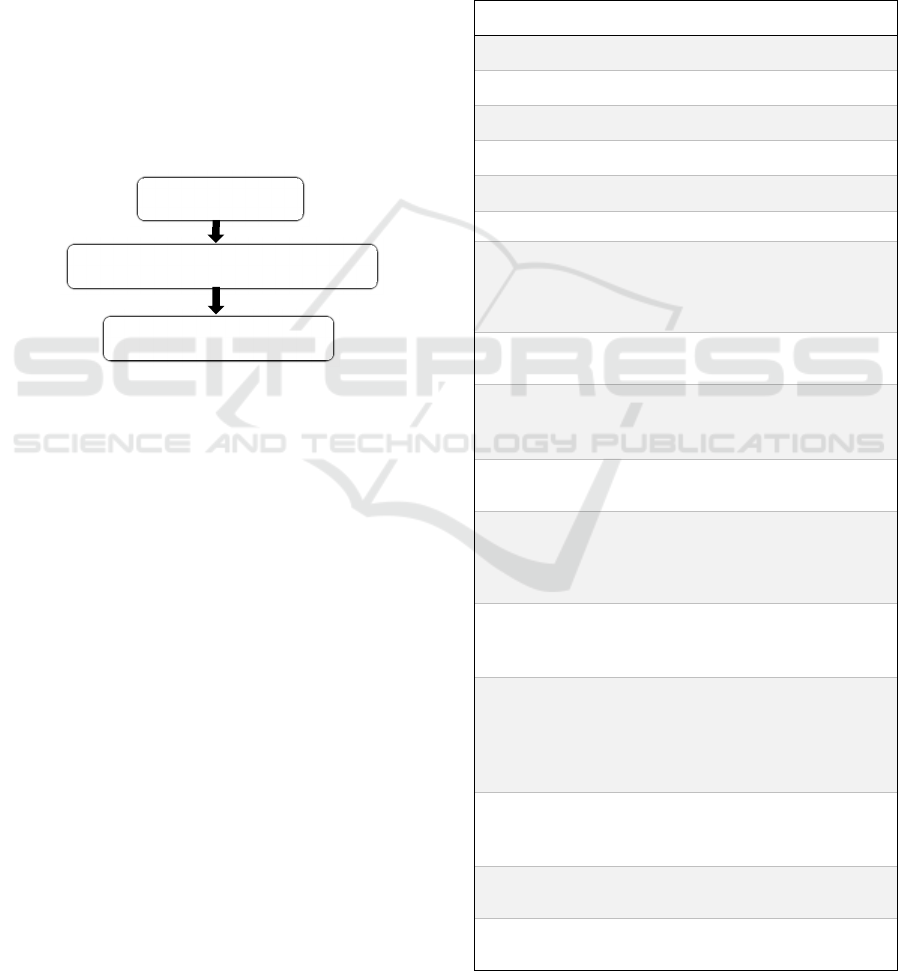
Our system for identifying genre consists of three

building blocks: the Play Parser, the Social Network

Generator and the Genre Predictor. Figure 1 shows

the main components of the system architecture,

which are discussed in more detail in the following

subsections.

Figure 1: Block diagram of our system.

3.1 Play Parser

The main purpose of this component is to

automatically parse TEI encoded XML format play to

extract basic information such as the total number of

characters, the name and role of each character, and

the total number of acts and scenes in a play. For each

scene, we used our parsed information to determine

which characters were present in the scene (using

stage directions to

account for entrances and exits

during a scene), and how many lines and words were

spoken by each character. We also extracted some

“Play Features” (shown in Table 1) which were

incorporated into our analysis.

3.2 Social Network Metric Calculator

This component creates each play’s social network

graph using the information generated by the play

parser described in 3.1 and then calculates its network

features. We used the Gephi API to generate graph

files. Each file maps characters as node and

communication between characters as an edge. Each

character stores as an attribute total number of lines

and words spoken by that character in the play. After

this mapping, each edge is weighted with the sum of

total number of words

spoken by the two characters

in their shared scenes. Once the basic structure is

ready, using inbuilt functions of Gephi

API we

calculate 16

metrics of graph and node features.

These are the “Networks Features” of our extracted

features, as shown in Table 1.

Table 1: All Extracted Features from Shakespeare’s plays.

Here g represents a play graph, c a character node in a

graph, and e an edge in graph.

Play Features

1. tot_characters = total number of characters in g

2. tot_edges = total number of edges in g

3. tot_lines = total number of lines spoken by c in g

4. tot_words = total number of words spoken by c in g

Network Features

5. Degree = set of adjacent nodes of c in the graph

6. Criticality = A k-critical graph is a critical graph

with chromatic number k; a graph G with chromatic

number k is k-vertex-critical if each of its vertices is a

critical element.

7. Eigenvector = A measure of c’s importance in a

network based on c’s connections.

8. Eccentricity = The eccentricity of a node c in a

connected graph is the maximum graph distance

between it and any other node.

9. Closeness Centrality = The average distance from a

given node c to all other nodes in the network.

10. Harmonic Centrality = In a (not necessarily

connected) graph, the harmonic centrality reverses the

sum and reciprocal operations in the definition of

closeness centrality.

11. Betweeness Centrality = Node Betweenness

Centrality measures how often a node appears on

shortest paths between nodes in the network.

12. Clustering Coefficient = The clustering coefficient,

when applied to a single node, is a measure of how

complete the neighborhood of a node is. When applied

to an entire network, it is the average clustering

coefficient over all nodes in the network.

13. Density = Measures how close the network is to

complete. A complete graph has all possible edges and

density equal to 1.

14. Diameter = The maximal distance between all pairs

of nodes.

15. Path Length = The average graph-distance between

all pairs of nodes.

Social Network Metric Calculator

Genre Predictor

Pla

Parse

Theatrical Genre Prediction using Social Network Metrics

231

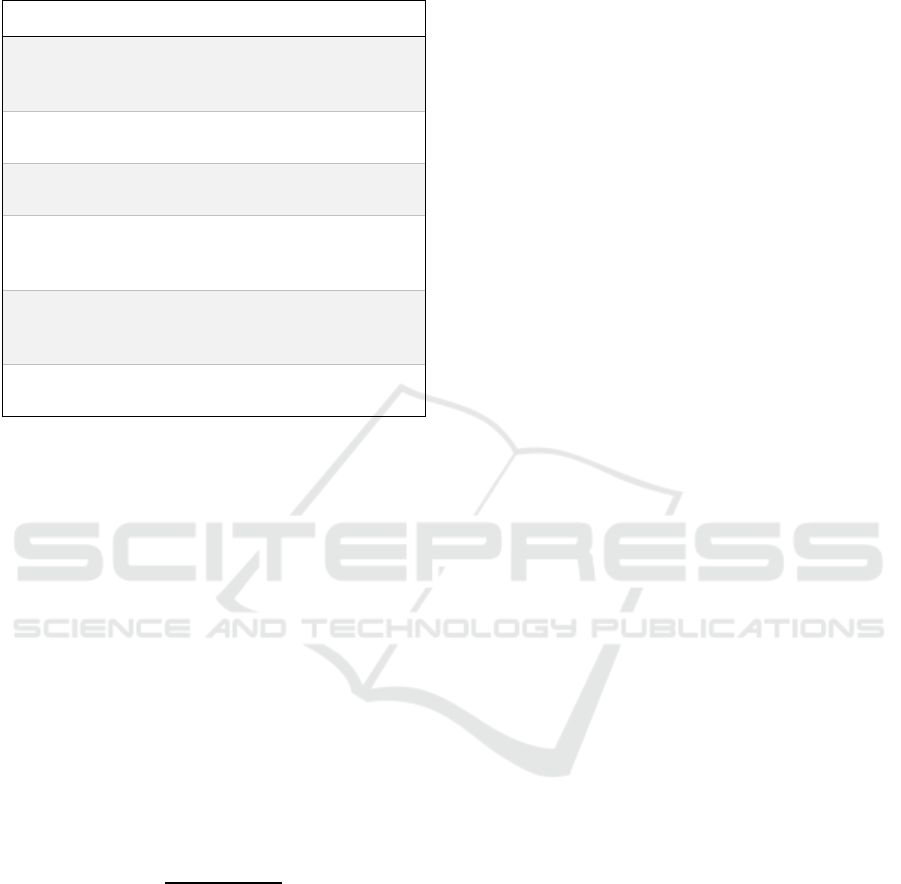
Table 1: All Extracted Features from Shakespeare’s plays.

Here g represents a play graph, c a character node in a

graph, and e an edge in graph (cont.).

Network Features

16. Connected Components: A connected component is

a maximal set of nodes such that each pair of nodes is

connected by a path.

17. Modularity = Measures how well a network

decomposes into modular communities.

18. Weighted Degree = for node c, the sum of the

weights of its edges.

19. Average Degree = for graph g, the sum of the

degrees of all the nodes in the graph divided by the

total number of nodes in the graph.

20. Average Weighted Degree = For graph g, the sum

of the weighted degrees of all the nodes in the graph

divided by the total number of nodes in the graph.

21. Radius = The radius of a graph is the minimum

graph eccentricity of any node in the graph.

3.2.1 Extracted Features

As extracted features, we chose to use most simple

and easily quantifiable metrics, such as the total

number of characters in the play (see Table 1). As our

results in 4.3.1 and 4.3.3 demonstrate, despite their

simplicity as features, the number of edges and the

number of words spoken in a play can play a crucial

role in identifying the genre.

3.2.2 Network Features

We compute the network features of the graph using

the Gephi library. For features that describe an

individual node, such as degree or eigenvector, we

calculated the network centralized value using the

following network level centralization index

(Newman, 2010):

=

∑

[

∗





]





∑

[

∗





]



(1)

Where,

= maximum value for all the nodes in the graph and

= value of current node.

Denominator is the maximum of the summation over

all the possible networks. This method normalizes

across the graphs, allowing us to use node metrics as

graph metrics for evaluation purposes.

3.3 Genre Predictor

The genre predictor is a support vector machine binary

classifier. Support Vector Machines (SVMs) are a

popular machine learning method for classification,

regression, and other learning tasks. Since our

classification problem had more than two classes, we

combined SVM with One vs One (OvO) classification.

This works as follows: choose a pair of classes from a

set of n classes, which in our case is three (comedy,

history and tragedy) and develop a binary classifier for

each pair. Create all possible combinations of pairs of

classes from n and then for each pair develop a binary

SVM. The final class is assigned to each unseen play

based on the class chosen by maximum number of

binary SVM classifiers. By using OvO, our SVM is

much less sensitive to the problems of unbalanced

datasets, which is particularly helpful given the

different sizes of each of our three classes and our small

overall sample size (Chang and Lin, 2011).

4 EXPERIMENTS

4.1 Dataset

Our dataset is comprised of 36 plays by Shakespeare,

in TEI encoded XML files. XML format was chosen

as it was much easier to fetch required information

from the plays along with maintaining accuracy in the

extraction. The dataset is that of the WordHoard

Shakespeare, downloaded from the website

showcases.exist-db.org. It consists of comedies (All’s

Well That Ends Well, As You Like It, A Midsummer

Night’s Dream, Love’s Labour’s Lost, Measure for

Measure, Much Ado About Nothing, The Comedy of

Errors, The Merchant of Venice, The Merry Wives of

Windsor, The Taming of the Shrew, The Tempest,

The Winter’s Tale, Twelfth Night or What You Will,

Two Gentlemen of Verona), histories (The First Part

of King Henry the Fourth¸ The First Part of King

Henry the Sixth, The Life and Death of King John,

The Life of King Henry the Eighth, The Life of King

Henry the Fifth, The Second Part of King Henry the

Fourth¸ The Second Part of King Henry the Sixth¸

The Third Part of King Henry the Sixth¸ The Tragedy

of King Richard the Second, The Tragedy of King

Richard the Third) and tragedies (Antony and

Cleopatra, Coriolanus, Cymbeline, Hamlet Prince of

Denmark, Julius Caesar, King Lear, Macbeth¸

Othello the Moor of Venice, Romeo and Juliet,

Timon of Athens, Titus Andronicus, Troilus and

Cressida).We split the dataset into five subsets,

evenly balancing each genre in each subset. These

were then used to perform five-fold cross validation.

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

232

4.2 Experimental Setup

Our generated network graphs are then used to test our

central question: whether the social network of

characters in a play can be used as a proxy for features

of the play’s narrative content. Can we use social

network metrics to distinguish between the dramatic

genres of tragedy, comedy, and history? We used 21

different mathematical features as mentioned in Table

1 to test our hypothesis. We first tested how well

individual features were able to distinguish between

different genres. Our second test considered of all

combinations of pairs of extracted and network

features, and the third test used combinations of three,

four and five feature sets to see if adding on more

features would increase accuracy of classifier’s genre

prediction. Section 4.3 discusses the result of each test.

4.3 Results

The following table shows the calculated average

value for each network metric per genre.

Table 2: Average feature value for each genre.

Features Comedy History Tragedy

Characters 23.14 44 38.333

Edges 132 233 217.75

Words 22426.42 27238.2 27050.58

Lines 2586.5 3070.2 3215

Criticality 0.03 0.022 0.020

Eigenvector 0.34 0.59 0.52

Eccentricity 8.63 19.11 13.01

Closeness 9.28 27.42 24.95

Harmonic 0.19 0.31 0.29

Betweenness 0.01 0.010 0.011

Clustering

Coefficient

0.84 0.82 0.83

Graph Density 0.52 0.25 0.34

Diameter 2.85 4.3 3.08

Path Length 1.516 2.02 1.71

Connected

Components

1.07 1.7 1.5

Degree 0.37 0.46 0.52

Modularity 0.14 0.25 0.16

Weighted Degree 1306.85 1022.02 1457.85

Average Degree 11.31 10.39 11.38

Average Weighted

Degree

11353.31 7349.09 9136.53

Radius 1.78 1.3 1.33

4.3.1 Single Feature Accuracy

Our first test attempted to identify genre using only

single feature at a time. However, no single feature

was independently sufficient to identify the genre. Of

the features tested, path length provided the greatest

accuracy (66.43%) for genre identification. Even

though this metric does not achieve 100%, it is much

better than random, which would be 33.3%.

Table 3: Genre prediction accuracy using a single feature.

Feature Accuracy

Path Length 66.43

Graph Density 61.07

Diameter 58.57

Characters 55.71

Eigenvector 55.71

Eccentricity 55.71

Harmonic 55.71

Average Weighted Degree 55.71

Lines 55.36

Degree 55.36

Closeness 52.50

Connected Components 50.35

Modularity 50.00

Words 47.50

Edges 47.14

Radius 47.14

Weighted Degree 44.28

Criticality 41.43

Clustering Coefficient 38.93

Average Degree 33.21

Betweenness 27.85

4.3.2 Pair of Features Accuracy

However, when features were used in pairs, the

network graphs achieved greater accuracy in

identifying the genre of Shakespeare plays. Table 4

shows the pairs of metrics which were able to identify

genre with accuracy higher than the maximum

individual feature accuracy for genre prediction.

Theatrical Genre Prediction using Social Network Metrics

233

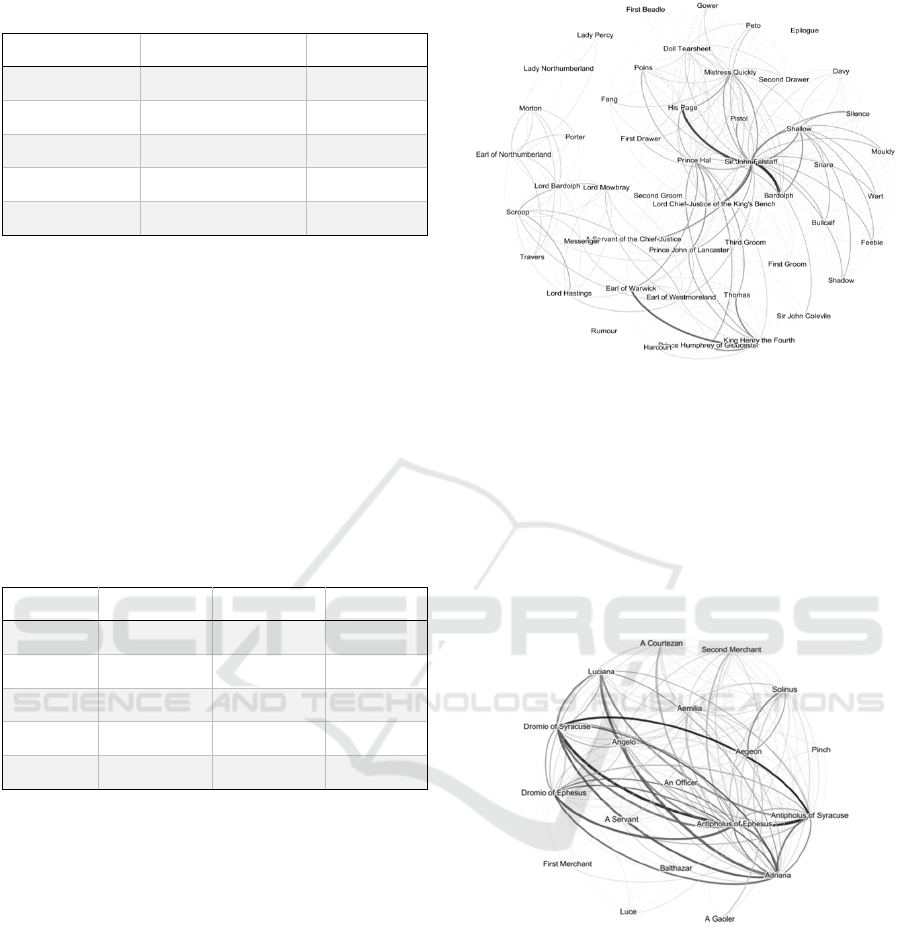
Table 4: Pairs which provided above 70% accuracy.

Feature 1 Feature 2 Accuracy

Harmonic Diameter 72.50

Harmonic Path Length 72.50

Graph Density Diameter 72.50

Graph Density Path Length 72.50

Lines Path Length 72.14

4.3.3 Multiple Features Accuracy

If we combine three features, the network graphs

again achieve 10% higher accuracy in genre

identification. Table 5 shows the triads which were

able to identify genre with more than 80% accuracy.

Adding additional features continued to increase

accuracy. The highest observed accuracy was

88.93%, using five metrics that are a combination of

play characteristics (Words and Lines) and SNA

features (Closeness, Graph Density, and Average

Weighted Degree).

Table 5: Triples which provided above 80% accuracy.

Feature 1 Feature 2 Feature 3 Accuracy

Words Characters Lines 83.57

Words Lines Eigenvector 83.21

Words Lines Closeness 81.07

Lines Eigenvector Path Length 80.71

Lines Harmonic Path Length 80.71

4.3.4 Discussion

The relevance of path length and graph density in

distinguishing genres is visually obvious when

individual comedy and history networks are

compared.

Our networks reveal that histories feature highly

dispersed networks, with large numbers of very minor

characters, such as “First,” “Second,” and “Third”

members of groups like soldiers and ambassadors

(Figure 2). Characters in histories form social

subgroups, joined through chains of acquaintance.

Comedies, in contrast, feature networks with far

fewer characters, in which nearly everybody speaks

to nearly everybody else at some point (Figure 3).

These basic findings offer novel support for literary

research on Early Modern histories and comedies

(Evalyn, Gauch and Shukla, 2018).

Figure 2: Network graph of The Second Part of King Henry

The Fourth, a history.

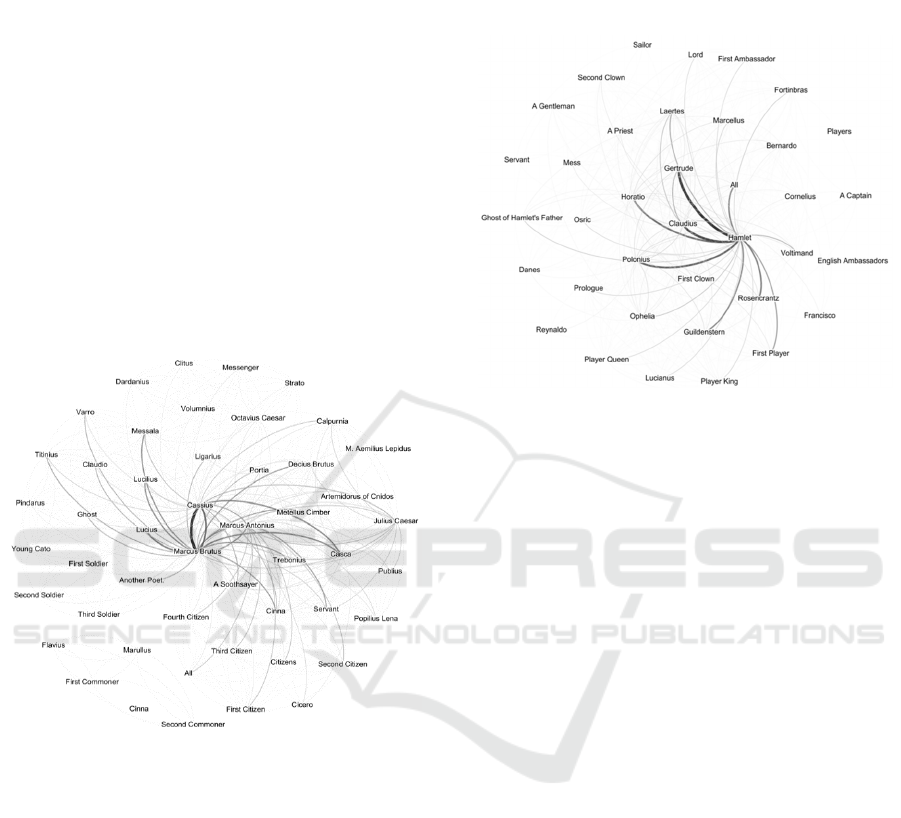
Tragedies are more difficult to distinguish. It is of

interest to literary scholars to discover that tragedies

appear not to have a formula for their social

relationships. They feature networks somewhere

between history and comedy in their density and

show more variety overall (Figures 4 and 5).

Therefore, more complex metrics are needed in

combination to accurately identify all three genres.

Figure 3: Network graph of The Comedy of Errors, a

comedy.

A comparison of Table 4 and Table 5 shows that

the sets of three factors which provide higher

accuracy do not necessarily always include the

features which were able to provide better accuracy

as pairs. Many of the pairs, for example, include

graph density or path length as one of the two

identifying features, but none of the triples include

graph density as a feature for maximizing the

accuracy, and the triples instead include the number

of words and lines as the most commonly useful

feature.

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

234

Each metric thus seems to capture a specific kind

of information about the play which are more relevant

in combination with different other metrics.

Closeness, for example, is only able to provide 52.5%

accuracy alone, but reaches 88.9% when combined

with lines, words, graph density and average

weighted degree. Similarly, the harmonic centrality

only provides 55.7% accuracy alone, but when

considered alongside pairs of other features, the

combination is more informative.

Specifically, it seems that classification is most

successful when metrics of the play’s size (words,

characters, lines) are combined with metrics of the

interconnectedness of its social network (density,

path length, harmonic or closeness centrality,

eigenvector). The non-SNA features of play size are

insufficient to identify genre alone but provide useful

context for SNA metrics for classification.

Figure 4: Network graph of Julius Caesar, a tragedy.

5 CONCLUSIONS

In this paper, we successfully classify plays based on

their genre without using the actual words of the

plays. Our networks of the well-studied works of

Shakespeare can provide a baseline against which to

contextualize similar studies of other plays. The

network graphs themselves provide a new insight into

the plays, revealing the hidden shape of social

relationships between characters. The application of

mathematical graph analysis to these networks

provides a dramatically faster and more scalable way

to determine important information about them, in

this case their genre.

To apply these findings to literary research, we

have explored in more detail the genre attributions of

Shakespeare’s romances and problem plays (Evalyn,

Gauch and Shukla, 2018). We have also made the

network graphs and selected mathematical features

available online at text.csce.uark.edu/SNAPlays.html.

Figure 5: Network graph of Hamlet, a tragedy.

6 FUTURE WORK

Since the parser is highly extensible and can be used

with any plays encoded in TEI, future work applying

these methods to literary analysis does not need to be

restricted to plays that are similar to Shakespeare’s

but could be used to compare plays over a long period

of time. Future work doesn’t even need to be

restricted to plays written in English; one future

application in development, for example, will study

eighteenth century plays written in English, French,

and German. As we develop our website, we will add

functionality for others to upload their own TEI

encoded plays and download the resulting Gephi file,

enabling broad applicability of our methods to new

literary research problems.

Future refinements to the social network

generator could make edges between nodes

directional, to better capture imbalanced relationships

between characters; this level of detail was not

necessary to distinguish between Shakespeare’s

plays, but might be important for different

identification tasks. Natural Language Processing

(NLP) could also be integrated into the parser to more

accurately identify the targets of speech, to capture

instances where characters are on stage but cannot

hear what is being said or are not being spoken to.

These kinds of improvements would reduce “false

positives” in the creation of edges between nodes,

perhaps enabling better analysis of larger or more

complicated groups of literary plays.

Theatrical Genre Prediction using Social Network Metrics

235

REFERENCES

Algee-Hewitt, M. (2017). Distributed Character:

Quantitative Models of the English Stage, 1500-1920.

In Digital Humanities 2017: Book of Abstracts.

Montreal: McGill University and Université de

Montréal, pp. 119–21.

Anggraini, D., Madenda, S., Wibowo, E. P. and

Boumedjout, L. (2015). Network Disintegration in

Criminal Network. In 11th International Conference on

Signal-Image Technology & Internet-Based Systems

(SITIS), Bangkok, pp. 192-199.

Armour, C., Fried, E. I., Deserno, M. K., Tsai, J. and

Pietrzak, R. H. (2017). A network analysis of DSM-5

posttraumatic stress disorder symptoms and correlates

in U.S. military veterans. In Journal of Anxiety

Disorders, Volume 45, 2017, Pages 49-59.

Bastian, M., Heymann, S. and Jacomy, M. (2009). Gephi:

An Open Source Software for Exploring and

Manipulating Networks. In International AAAI

Conference on Web and Social Media, North America.

Billah, S. M. and Gauch. S. (2015). Social network analysis

for predicting emerging researchers. In 7th IC3K,

Lisbon.

Chang, C. C. and Lin, C. J. (2011). LIBSVM: A library for

support vector machines. ACM Trans. In Intell. Syst.

Technol. 2, 3, Article 27, 27 pages.

Chuan-yi, W., Xiao-hong, L. and Yi, C. (2016). An

empirical study on the collaboration of scholars in

graduate education: based on the social network

analysis. In ICIIP '16. ACM, New York, NY, USA,

Article 36, 7 pages.

Dreżewski, R., Sepielak, J. and Filipkowski, W. (2015).

The application of social network analysis algorithms

in a system supporting money laundering detection. In

Information Sciences, Volume 295, 2015, Pages 18-32,

ISSN 0020-0255.

Elsner, M. (2015). Abstract Representations of Plot

Struture. LiLT (Linguistic Issues in Language

Technology), 12(5).

Evalyn, L., Gauch S. and Shukla, M. (2018). Analyzing

Social Networks of XML Plays: Exploring

Shakespeare’s Genres. https://dh2018.adho.org/en/

analyzing-social-networks-of-xml-plays-exploring-

shakespeares-genres/.

Fischer, F., Göbel, M., Kampkaspar, D. and Trilcke, P.

(2015). Digital Network Analysis of Dramatic Texts. In

Digital Humanities 2015 Conference Abstracts.

University of Western Sydney.

Flekova and Gurevych, I. (2015). Personality Profiling of

Fictional Characters using Sense-Level Links between

Lexical Resources. In Proc. Conference on Empirical

Methods in Natural Language Processing, pages 1805–

1816.

Grayson, S., Wade, K., Meaney, G., Rothwell, J., Mulvany

M. and Greene, D. (2016). Discovering structure in

social networks of 19th century fiction. In Proceedings

of the 8th ACM Conference on Web Science. ACM, New

York, NY, USA, 325-326.

Jannidis, F., Reger, I., Krug, M., Weimer, L.,

Macharowsky, L. and Puppe, F. (2016). Comparison of

Methods for the Identification of Main Characters in

German Novels. In Digital Humanities Conference

Abstracts, Jagiellonian University & Pedagogical

University, Kraków, pp. 578–82.

Jockers, M. L. and Mimno, D. (2013). Significant themes

in 19th-century literature. In Poetics, 41(6):750–769.

Moretti, F. (2011). Network Theory, Plot Analysis. New

Left Review, 68:80–102.

Newman, M. E. J. (2010). Networks: An Introduction.

Oxford, UK: Oxford University Press.

Sack, G. (2011). Simulating plot: Towards a generative

model of narrative structure. In 2011 AAAI Fall

Symposium Series.

Scott, J. (2000). “Social Network Analysis: A Handbook”,

ed., Sage Publications, London.

Serrat, O. (2017). Social network analysis. In Knowledge

solutions (pp. 39-43). Springer, Singapore.

Stiller, J. and Hudson, M. (2005). Weak Links and Scene

Cliques within the Small World of Shakespeare. In

Journal of Cultural and Evolutionary Psychology 3, pp.

57–73.

Stiller, J., Nettle, D. and Dunbar, R. I. M. (2003). The Small

World of Shakespeare's Plays. In Human Nature, 14(4):

397–408.

Trequattrini, R., Lombardi, R. and Battista, M. (2015).

Network analysis and football team performance: a first

application. In Team Performance Management: An

International Journal, Vol. 21 Issue: 1/2, pp.85-110.

Trilcke, P., Fischer, F., Göbel, M. and Kampkaspar, D.

(2015). In 200 Years of Literary Network Data.

Trilcke, P., Fischer, F., Göbel, M., Kampkaspar, D. and

Kittel, C. (2016). Theatre Plays as 'Small Worlds'

Network Data on the History and Typology of German

Drama, 1730–1930. In Digital Humanities 2016

Conference Abstracts. Jagiellonian University &

Pedagogical University, Kraków, pp. 385–87.

Wasserman, S. and Faust, K. (1994). “Social Network

Analysis: Methods and Applications”, Cambridge

University Press.

Watts, D. (2001). “Small Worlds: The Dynamics of

Networks between Order and Randomness”, Princeton

University Press.

KDIR 2018 - 10th International Conference on Knowledge Discovery and Information Retrieval

236