
A Study of the Implementation Effectiveness of the CDIO Education
Model
Jing Wang
1
, Xumei Yuan
1
1
YanShan University, Qinhuangdao, P.R., China
Keywords: CDIO education model; CEM; Implementation effectiveness; empirical study.
Abstract: The CDIO education model is the latest achievement in the reform of international engineering education in
recent years. China introduced the model and initiated pilot implementation in late 2005. After more than
ten years of investigation and practical experience, the higher education institutions that participated have
developed and consolidated their own training characteristics. Through the analysis of the evaluation
standards for engineering personnel as well as elements of the CDIO curriculum, this paper employed the
catastrophe evaluation method to constructs the evaluation index system, and to assess the effectiveness of
the CDIO engineering education model at the university.
1 INTRODUCTION
The conceive-design-implement-operate (CDIO)
engineering education model was initiated by a
multinational research team comprising members
from the Massachusetts Institute of Technology
(MIT) and several Swedish universities. It focuses
on providing students with a realistic engineering
setting that embodies the entire life cycle of a
product, from conceptual design to operational
implementation and even maintenance. This allows
students to study engineering in a proactive and
hands-on way, through courses that are organically
connected, thereby enabling them to develop into
engineers capable of solving practical engineering
problems in today’s complex environment[1-2]. In
late 2005, Shantou University was the first Chinese
institution that introduced this model to
pilotimplementation in five departments of its
College of Engineering. In April 2008, a study
group, established by Department of Higher
Education of China’s Ministry of Education,
dedicated to develop the research and practice
related to the CDIO engineering education model[3].
These two steps pronounce the construction of
CDIO, which highlight the best of talent cultivation
in engineering colleges.
Although researchers consistently have
investigating the theory of CDIO, the deployment of
this model is not scaled and the implementation is
beyond the college capacities. The investigation of
working principle of CDIO is the foundation of
application, which exploits the best of both by
defining engineering education strategies. The focus
on the study of CDIO principles in recent years has
called for corresponding support research in this
field. Effectiveness evaluation is one such field ,
with technical approaches exploring the potential of
CDIO for engineering education. Thus, in this study,
graduates of the mechanical departments of YS
University were selected as participants. The
Catastrophe Evaluation Method (CEM) was adopted
to comprehensively evaluate and verify the
effectiveness of the CDIO engineering education
model through empirical research. The paper is
arranged as follows. Section 2 introduces the basic
principle of catastrophe evaluation method. Section
3 presents a general overview of system for indicator
evaluation. Methodology of data collection as well
as the sample preprocessing approach is depicted in
section 4. Section 5 provides a modeling based on
the theory of CEM to examine the CDIO application
and the testing outcome is given. Section 6 shows
the discussion, conclusion and future steps to be
taken.

2 CATASTROPHE EVALUATION
METHOD
2.1 Fundamental Concept
Learning is a highly complex psychological activity.
The evaluation of students’ learning effectiveness is
inevitably provisional and largely depending on the
subjective experience as well as the specific
evaluation criteria. CEM(Catastrophe theory
evaluation method) is a comprehensive evaluation
method developed on the basis of catastrophe
theory. Traditional evaluation process considers
merely the relative importance of evaluation indices
without assigning weights to other parts.CEM can
effectively avoid errors in artificially determining
weights on quantitative evaluation. Therefore, the
evaluation results reduce subjectivity without
limiting overall robustness and are calculated in a
simple and convenient way[4-7]. This study adopted
CEM to assess each student’s achievement of the
expected learning.
CEM is an evaluation method considering the
purpose of an evaluation system, which constructs
the evaluation index system and breaks down its
contradictions in a multi-level manner consistent
with the mechanism of the system itself. The overall
indicator is gradually broken down into sub-
indicators, and the target units are presented as an
inverted tree. By determining the grade of the
underlying evaluation index,and the state variable is
normalized using the catastrophe fuzzy subordinate
function. Hereafter, the decision-making outcome is
evaluated[8-10].
2.2 Evaluation Method
The common catastrophe models contain the fold,
cusp, swallowtail, and butterfly catastrophe systems.
We employ the swallowtail and butterfly catastrophe
systems in this paper. Swallowtail catastrophe is
utilized for the condition of three control variables
while butterfly catastrophe for four. A potential
function f(x) can be used to express the state
variable x for each system[11-12].
The swallowtail catastrophe potential function is:
(1)
The butterfly catastrophe potential function is:
(2)
The coefficients a, b, c, and d indicate the control
variables of x.
The swallowtail catastrophe equilibrium surface
could be obtained by a first derivative of f(x), Again,
f^'(x) =0,thus:
The swallowtail catastrophe equilibrium surface
was:
(3)
The butterfly catastrophe equilibrium surface
was:
(4)
The singular point set of the equilibrium surface
could be obtained by a second derivative of f(x),
Again
, eliminating the state variable x
through simultaneous equations f^'(x) =0 and f^'' (x)
=0. Thus, a bifurcation equation of the catastrophe
system is obtained.
The swallowtail catastrophe bifurcation equation
was:
(5)
The butterfly catastrophe bifurcation equation
was:
(6)
The bifurcation equation showed that when the
control variables satisfy this equation, a mutation
occurs in the system and the effect of each control
variable upon the mutation would be obtained[13-
14].
A normalization equation was used to convert
the different qualitative states of the control
variables in the system into the same state and
calculate different x values for each control variable
of the same target. Normalization equation is the
basic computing formula that using catastrophe
theory to comprehensive analysis and evaluation
system, It carries out quantized recursive operation
for system, Therefore, the total catastrophe
subordinate function, of the system characterized is
obtained by the state characteristics of the system.
Thus:

The swallowtail catastrophe normalization
equation was:
(7)
The butterfly catastrophe normalization equation
was:
(8)
According to the fuzzy decision theory, the
complementary and non-complementary principles
should be adopted during evaluation, which depend
on the relationship between variables. The
complementary principle is utilized when there is a
certain relationship between the variables in the
system where the state variable x takes the average
value of the catastrophe level of each
variable
. In contrast, the non-complementary principle
is for all the variables irreplaceable where the state
variable x takes the minimum value of the
catastrophe level of each variable
.
As such, the minimax criterion was applied.
3. CONSTRUCTING THE
EVALUATION INDICATOR
SYSTEM
The aim of the CDIO engineering education model
is to nurture students in a modern, team-based
environment, enabling them to become engineers
who are proficient in applying CDIO in the context
of complex and value-added engineering products,
processes, and systems. The evaluation of
implementation effectiveness was determined by all
the relevant stakeholders in students’ learning. In
this study, we invite graduates, the direct recipients
of education, to be participants. Thereby, their
achievements of the expected learning are assessed
in relation to the CDIO engineering education model
by examining their personal development and
professional abilities[15-18]. The main influencing
factors determining the ability to achieve the
expected effectiveness were confirmed by applying
the evaluation standards for engineering personnel
as well as elements of the CDIO curriculum. The
main factors were broken down, one by one, into a
number of indicators to build a hierarchical structure
for the evaluation indicator system.
Based on the CDIO outline and on the relevant
requirements of educational evaluation, the authors
of this study divided the evaluation criteria into 4
two-level indexes from the four dimensions of
"subject knowledge" "personal skills and attitudes"
"non-technical skills""career competence and
development " , then16 three-level evaluation
indicators again.To ensure their validity, experts
were consulted to assess the indicators in terms of
substance and scope. In the first round, seven
domestic experts who promoted the CDIO
engineering education model were employed to
evaluate the 16 indicators. After repeated
consultation and deliberation, they finalized 14
evaluation indicators, which were included in the
first draft of the questionnaire design, as shown
below:

Figure1: Evaluation index system of the CDIO Education Model.
In the second round, 14 domestic experts with
experience of implementing the CDIO engineering
education model were invited to test the validity of
the questionnaire and measure its representativeness
using the content validity ratio.
Table1:Test of the content validity ratio.
Notes:
• V-A: Very Appropriate, A=10 points
• M-A: More Appropriate, B=8 points
• A: Appropriate,C= 6points
• N-A: Not Very Appropriate, D=4 points
• I: Inappropriate,F=0 points
The content validity of the indicators shown
above ranged between 8.0 and 8.5, which
demonstrates high content validity; the indicators
selected for evaluating the effectiveness of the CDIO
engineering education model, therefore, were
appropriate. The state variable x represented the
expected level of achievement when implementing
the CDIO model. The evaluation range of the 14
indicators included five levels: very satisfied,
satisfied, average, dissatisfied and very dissatisfied;
whose respective values were 5, 4, 3, 2, and 1.
According to CEM, the overall evaluation
indicator (A) is at the top of the evaluation system
for the achievement of expected learning in the
CDIO engineering education model. The middle
layer presents a butterfly catastrophe, with indicators
(B1), (B2), (B3), and (B4) corresponding to the
control variables
,
,
,
; of the
catastrophe system. The catastrophe systems
displayed from left to right are as follows:
swallowtail, butterfly, swallowtail, and butterfly.
Evaluation indicators 1, 2 and 3 are related to
“subject knowledge” and correspond to the control
variables
,
,
of the catastrophe system.
Evaluation indicators 4, 5, 6 and 7 are related to
“personal skills and attitudes” and correspond to the
control variables
,
,
,
of the
catastrophe system. Evaluation indicators 8, 9 and
10 are related to “non-technical skills” and
correspond to the control variables
,
,
of the catastrophe system. Evaluation indicators
11, 12, 13 and 14 are related to “career competence
and development” and correspond to the control
variables
,
,
,
of the catastrophe
system. As the study evaluated the achievement of
the expected effectiveness of the CDIO model, the
complementary principle applied to each catastrophe
model.
4. DATA SOURCES AND SAMPLE
DESCRIPTIONS
The participants in this study graduated from YS
University between 2011 and 2017. During their
studies, they were taught using a “project-based”

model based on the concept of CDIO. For the
survey, a total of 328 questionnaires were sent out,
of which 250 were returned, and valid
questionnaires 248.The data is composed as follows:
Table2: Questionnaire statistics.
4.1 Data Reliability Test
This study adopted the Cronbach’s α reliability
coefficient for evaluation, using this formula[19]:
α
(9)
where n is the total number of items in the scale,
is the intra-item variance of the score of the ith item,
and
is the variance of the total score of all the
items. The survey data into the formula (9), by
calculation, this questionnaire’s Cronbach’s
α=0.726, the “Subject knowledge” Cronbach’s
α=0.257, the “Personal skills and attitudes”
Cronbach’ s α=0.951, the “Non-technical skills”
Cronbach’s α=0.454, the “Career competence and
development” Cronbach’s α=0.342. The internal
consistencies of the four dimensions of the
questionnaire and the questionnaire as a whole were
above 0.70, so meet the requirements of exploratory
research.
4.2 Normalized Transformation
To obtain a better distribution of research data, a
normalized transformation was performed on the
original data by subtracting the minimum value from
the original data of each variable and dividing by the
range (the difference between the maximum and
minimum value of each variable), using this
formula[20-21]:
(10)
where i is the number of indicators , i=1,2,……,
and j is the number of units, j=1,2,…….
In this paper, the normalization transformation is
used to normalize the index system step by step.
Because of the complexity of the calculation
process, this paper only takes the evaluation data of
the 2011 graduates as an example to show the
deducing process of the implementation
effectiveness CDIO education model evaluation.
First, the original values of each indicator at the
lowest level were processed using equation(10), the
results are shown as table3:
Table3: The data of the 2011 graduates' evaluation of
normalization transformation.
After processing, the values were between 0 and
1. Next, the values were converted using formulas 2-
7 and 2-8:
:
According to the principle of complementarity:
According to the same method, the evaluation
data of the 2012-2017 graduates can also be
calculated,as shown in table 4:

Table4:Evaluation index value and result.
5. EVALUATION RESULTS
VERIFY AND ANALYSIS
5.1 The Evaluation Result of Principal
Component Analysis
CEM is used to evaluate the implementation
effectiveness of the CDIO education model, whether
this method is reliable or practical? Therefore, this
paper uses the evaluation index system as shown in
figure 1 and the evaluation data collected, using the
method of principal components analysis(PCA) to
verify this example. If the evaluation results of the
two methods are consistent, then there is a reason to
believe that the evaluation result of CME is true and
effective, so it can avoids the chance of consistency
of the evaluation results. PCA is a common method
in multivariate statistical analysis, the calculation
procedure is as follows:
First, suppose there are m evaluation objects and
n evaluation indexes, and the scores of each
principal component are calculated):
(11)
isthe value of the kth principal component
about item the valuated object,
isthe normalized
value of the ith evaluating index about item the
valuated object,
is the load value of the k th
principal component about item I th of evaluation,
λ
is the characteristic value of the kth principal
component.
Second the proportion of the variance
contribution of each principal component is the
weight, the score of composite principal component
of each evaluated object was calculated.
(12)
is the comprehensive score of the tth evaluated
object,
is the weight of the score about the kth
principal component, s is the number of principal
components extracted( the number of principal
components extracted is determined by the
accumulated variance contribution rate of over
85%)[22-23].According to the above steps,
evaluation of the implementation effect of education
mode of CDIO project of 2011-2017 graduates, The
results are shown in table5.
Table5:Evaluation result of PCA.
5.2 Consistency Check of Two
Evaluation Results
The consistency of the evaluation results of the
mutation evaluation method and the principal
component analysis method was tested by the
Kendall cofactor test. The results are shown in
table6.
Table6: Test result of Kendall.

It can be seen that the coefficients of Kendall's
collaborative test for the evaluation results of the 7th
graduates are all between 0-1, and the probability p
all the 0.00. The evaluation results of the two
methods are verified by the Kendall’s, so the
evaluation results of the two methods are statistically
signify cant consistent.
The core of the CEM is to establish a recursive
algorithm for the multi-objective and multi-level
comprehensive evaluation problem by using the
normalized formula deduce the bifurcation equation
of the catastrophe theory. Its main advantage is that
it avoids the concept of direct use of "weights"
which are difficult to be determined and they are
subjective. At the same time, because the normalized
formula reflects the mechanism of the evaluation
index to a certain extent, the catastrophe evaluation
model can consider the importance of each
evaluation index reasonably and quantitatively.
5.3 Evaluation Results Analysis
The learning process of the traditional teaching
mode has been arranged by the predecessors
according to the optimal structure, and the students
only need to absorb and understand quickly. But the
CDIO engineering education mode with "project"
for the driver, around the "project" is completed, will
be this major should master the fragmentation of
knowledge and ability construction, it and the
emphasis of the traditional teaching mode has great
differences.
As the learning experience, knowledge base,
reading exposure, cognitive level, academic skills,
and practical abilities of each student are different,
inconsistent effectiveness was achieved in the
implementation of the CDIO engineering education
model. The model emphasizes student-centered
learning, requiring students to abandon the
traditional model of passive reception and to
embrace active participation in the learning process.
The results showed that the overall evaluation of the
students’ achievement in relation to “subject
knowledge” was high. Through implementing the
CDIO model, students better understood or
remembered abstract theories and concepts, and
were able to apply their theoretical knowledge in
practical engineering situations. They also formed
new cognitive frameworks relating to professional
learning in order to help strengthen their grasp of
fundamental knowledge.
The evaluation of “personal skills and attitudes”
focused on a comparison with traditional teaching
methods, and addressed the limitations of the
students’ knowledge of engineering technology and
methods in the context of multi-level, multi-area,
and large-scale complex systems. The
implementation of the CDIO education model made
students realize that there are unpredictable
challenges in learning and enhanced their individual
capabilities and attitudes by repeatedly strengthening
their skills of engineering reasoning, systematic
thinking and critical thinking, practical hands-on
training, and solving complex engineering problems.
According to the graduates’ feedback, the CDIO
model achieved relatively good levels of
effectiveness here.
The development of “non-technical skills”
among students mainly depended on the “projects”
offered during the implementation of the CDIO
model. A “project” is a broad concept and an
important factor worthy of further study. The
specific content of a project can effectively stimulate
enthusiasm for learning. During projects, factors
such as team composition and the nature of the
collaborative atmosphere among team members
directly influenced the frequency and intensity of
communication during the learning process, thereby
directly affecting the students’ development of non-
technical skills. The graduates rated this area as
average. This result will encourage schools to focus
more on the selection of project content, team
composition, and evaluation methods in order to
achieve higher teaching effectiveness when the
CDIO education model is implemented in the future.
“Career competence and development” focused
on the training of the ideal qualities necessary for
engineers. Limited teaching hours in institutions are
a huge constraint on the facilitation of career
development. The CDIO education model guides
students to form product-oriented values that enable
them to recognize the professional abilities of
engineers in visual thinking, effective
communication, social responsibility, and
accountability during their autonomous practice of
the CDIO model. This ensures that the students
demonstrate greater creativity in their future
engineering careers. The graduates rated this area as
relatively good.
Based on the standards of classroom teaching
effectiveness and on the characteristics of the CDIO
education model, the overall evaluation was
classified using five levels: excellent ( Result ≥
0.90 ) , good ( 0.80 ≤ Result < 0.90 ) , average
( 0.70≤ Result< 0.80) , pass( 0.60≤ Result<
0.70) and fail(Result<0.60).So it can be seen
that the evaluation of the graduates is good,
indicating that the graduates have a higher
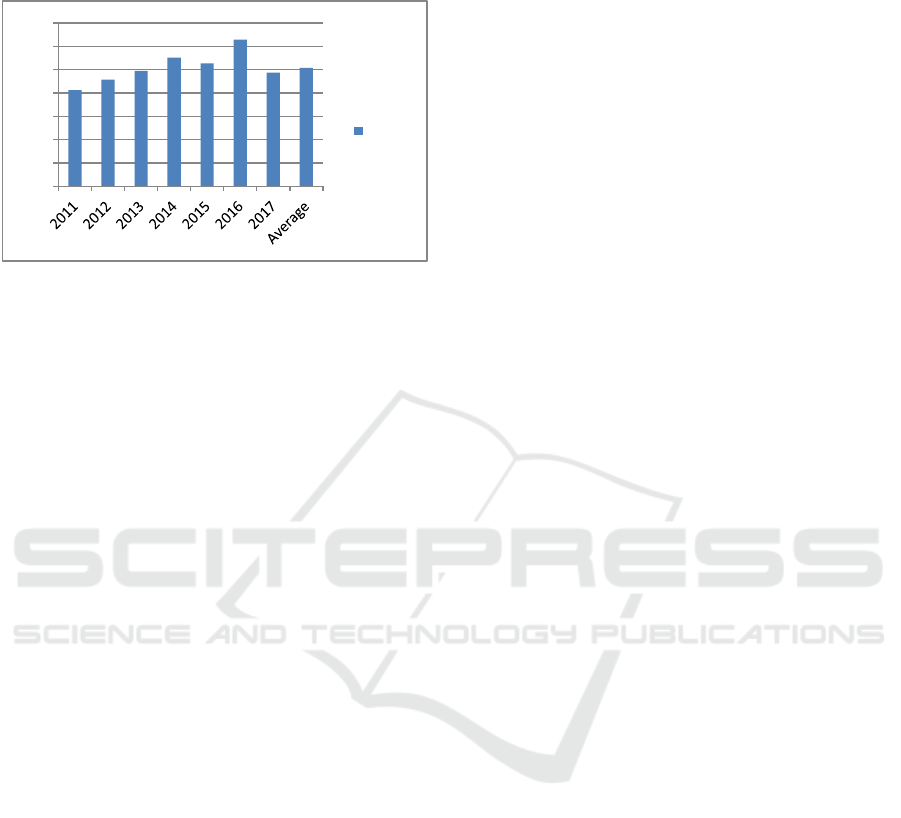
recognition of the effect of the CDIO teaching
model.
Figure2: 2011-2017 Bar graph of evaluation results.
Students can learn in the same major, and the
group will not have the extreme ability difference.
Compared with the results of the seven graduates,
we can see that the overall trend of scores is getting
higher and higher. As for the reasons for the low
score of the 2017 graduates, the author once again
communicated with the graduates and learned that
the number of students in this class is more than that
of the previous grade. As a local university with
traditional engineering advantages, YS university is
limited by practical difficulties such as shortage of
resources for running schools.
Evaluation feedback from graduates has always
been an effective means for higher education
institutions to strengthen their relationships with
corporations and society, to obtain external
information, to reform personnel training models,
and to improve the quality of the teaching they offer.
By comparing the evaluation feedback of students
who graduated in different years, we found that
students who graduated earlier reflected more on
their experiences and achievements under the CDIO
model after their graduation. This shows that the
CDIO education model has indeed established a
solid professional foundation among students,
allowing them to accumulate qualities and abilities
that offer them more opportunities to perform well
as engineers in their working lives.
There is no fixed standard for the
implementation of the CDIO education model.
Higher education institutions adopt their own
appropriate methods of implementing the model to
ensure that students continuously accumulate and
practice innovation and teamwork, to ensure that
they develop practical and analytical abilities, and to
ensure that, during their participation, they gradually
build up a scientist’s pragmatic sense of judgment.
The evaluation results from several cohorts of YS
University graduates show that the CDIO model
achieved results that were good or excellent. The
students’ awareness of, and satisfaction with, the
CDIO engineering education philosophy were also
high. In future, higher institutions should continue to
review and improve the implementation of the CDIO
education model and strive to achieve better
expected results, ultimately promoting the model.
REFERENCES
1. Crawley, E.F., Malmqvist, J., Östlund, S., & Brodeur,
D.R.2012. Rethinking Engineering Education: The
CDIO Approach. M. (Gu, P., Shen, M., & Lu X. Trans).
Higher Education Press(Beijing,China 2012), 1-2.
2. Fan, Y., Zhang, X., Xie, X.2015.Design and
Development of a Course in Professionalism and
Ethics for CDIO Curriculum in China. J. Sci Eng
Ethics(No.21, 2015), 1381-1389.
3. Gu, P.,Bao N., etc. 2012.CDIO in China(Part I).
J.Research in Higher Education of Engineering,(Mar.
2012), 24-40.
4. Meng, H., Wang, Y. 2008. The comprehensive
Evaluation of Knowledge Innovation System of
Research University Based on CEM. J. Operations
Research and Management Science, (Vol17.3, 2008),
80-87.
5. Shi, Y.,Liu, Y., He, J. 2003. Further Study on Some
Questions of Catastrophe Evaluation Method. J.
Engineering Journal of Wuhan University, (Vol36.4,
2003),132-136.
6. E. Michael Staman., Research in Higher
Education:Catastrophe theory in higher education
research. M.Vol16(1), 41-53(1982)
7. Liu, C., Li, J. 2011. Application of Catastrophe
Progression Method Simulation in Gas Hazard
Assessment of Coal mine. J. Computer Engineering
and Applications, (Vol 47.6, 2011), 231-234.
8. Matthijs Koopmans,Dimitrios Stamovlasis.2016.
Complex Dynamical Systems in Education:
Concept,Methods and Applications.M. Springer
International Publishing, (Switzerland, 2016), 141-
175.
9. Qin, G. 2015. Research on the Evaluation of
Comprehensively Innovative Capacity in the Industrial
Transfer Demonstration Area of the Cities along the
Yangtze River Based on the Series Catastrophe
Theory. J. Science and Technology Management
Research, (Vol 16, 2015), 83-86.
10. Du,X. 1994. The application of Catastrophe Theory in
the economic field. M. University of Electronic
Science and Technology Press. (1994), 24-31.
11. Li, Y., Wu, J., The Catastrophe Series Approach to
Acquisition Performance of Listed Companies. J.
Journal of Guizhou College of Finance and
Economics .(Vol 4, 2014), 20-23.
0,8
0,81
0,82
0,83
0,84
0,85
0,86
0,87
Result

12. Su R. 2006. The Value of Mutation Theory in
Education Research Methodology. J. Journal of
Fujian Medical University (Social Science
Edition),(Vol.7.2, 2006), 38-41.
13. Chen, Y. 2016. Zhang, S., et. al., Comprehensive
assessment and hierarchical management of the
sustainable utilization of urban water resources based
on catastrophe theory. J.Journal of the Taiwan
Institute of Chemical Engineer. (Vol 60, 2016), 430-
437.
14. Shi, Y. 1997. Application of Catastrophe Evaluation
Method in Management Benefit Evaluation of Water
System. J.Water Conservancy Economy, (Vol 5, 1997),
52-55.
15. Gu, X. 2009. Connecting Abstrace Theories with
Concrete Engineering Skills in the CDIO Learning
Cycle.J. Research in Higher Education of Engineering,
(Vol 1, 2009), 11-23.
16. Edward F. Crawley. 2008. The CDIO Syllabus: A
Statement of Goals for Undergraduate Engineering
Education.(Online).http://cdio.org/cdio-syllabus-
rept/index.html.
17. Johan Malmqvist. 2006. Kristina Edström., Svante
Gunnarsson., Sören Östlund.,The Application of
CDIO Standards in The Evaluation of Swedish
Engineering Degree Programmes. M. World
Transaction on Engineering and Technology
Education .(Vol.5.2, 2006), 361-364.
18. Zheng, W. 2010. CDIO-Based Research and Practice
of Innovative Engineering and Technical Talent
Training Mode. D. Dalian University of Technology,
(2010)
19. What does Cronbach’s alpha mean? UCLA -
Available at: (Online )
http://www.ats.ucla.edu/stat/spss/faq/alpha.html.
(2014)
20. Jeffrey Penney. 2017. A self-referece problem in test
score normalization. J. Economics of Education
Review,(Vol 61.1, 2017)79-84.
21. Cheng, M., Zhang, L. 1996. Application of the
catastrophe evaluation method in the evaluation of
administering national tax education. J. Forecasting,
(Vol 4, 1996), 63-65.
22. Kuroda M., Mori Y., Lizuka M., et. al., Acceleration
of the Alternating Least Squares Algorithm for
Principal Components Analysis.J. Computational
Statistics and Data Analysis,(Vol 55.1, 2011), 143-153.
23. Liang.,X., Yang F., etc. 2011. Study on the multilayer
financial center system in China based on evaluation
of urban financial competitiveness.J. Systems
Engineering-Theory & Practice,(Vol.31.10, 2011),
1847-1857.
