Zero-sum Distinguishers for Round-reduced GIMLI Permutation

Jiahao Cai

1,2,3

, Zihao Wei

1,2,3

, Yingjie Zhang

1,2,3

, Siwei Sun

1,2,3

and Lei Hu

1,2,3

State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, China

Data Assurance and Communication Security Research Center,

Chinese Academy of Sciences, China

School of Cyber Security, University of Chinese Academy of Sciences, China

Keywords:

GIMLI, Integral, Division Property, Zero-sum, Degree evaluation, MILP.

Abstract:

GIMLI is a 384-bit permutation proposed by Bernstein et al. at CHES 2017. It is designed with the goal of

achieving both high security and high performance across a wide range of hardware and software platforms.

Since GIMLI can be used as a building block for many cryptographic schemes, it is important to understand

its concrete security. To the best of our knowledge, third party cryptanalysis of GIMLI is limited. In this

paper, we identify some zero-sum distinguishers for 14-round GIMLI with the inside-out technique, which are

one-round longer than the integral distinguishers presented by the designers. Although we obtain improved

cryptanalysis results, these zero-sum distinguishers are far from threatening the full version of GIMLI.

1 INTRODUCTION

Permutations with large state sizes and desired cryp-

tographic properties facilitate the construction of

many cryptographic schemes, including high-security

(tweakable) block ciphers, stream ciphers, message

authentication codes, hash functions, etc. For ex-

ample, the winner of the SHA-3 competition, Kec-

cak hash function, uses a permutation operating on

a 1600-bit state known as the Keccak- f permuta-

tion (Bertoni et al., 2013). Also, we have message

authentication code (Chaskey (Mouha et al., 2014)),

and stream cipher (Salsa20 (Bernstein, 2008)) built on

ARX permutations. However, existing designs suffer

from the problem of showing signiﬁcant performance

variation when implemented in different platforms,

severely limiting their range of applications. There-

fore, a single primitive that performs well (not neces-

sarily the best) on all common platforms will beneﬁt

the designers and implementors a lot.

With this goal in mind, Bernstein et al. pre-

sented the GIMLI design at CHES 2017 (Bernstein

et al., 2017). What distinguishes GIMLI from pre-

vious designs is that its performance strikes the bal-

ance across a wide spectrum of platforms by skill-

fully avoiding those platform-speciﬁc hazards lead-

ing to poor performance for many primitives simulta-

neously. Therefore, cryptographic schemes designed

based on GIMLI are expected to be efﬁcient when

implemented on 64-bit Intel/AMD server CPUs, 32-

bit ARM smartphone CPUs, 32-bit ARM microcon-

trollers, 8-bit AVR microcontrollers, FPGAs, and

ASICs with or without side-channel protections. We

refer the reader to http://gimli.cr.yp.to for sample im-

plementations and detailed benchmarks.

Given these merits of GIMLI, it has the potential

to be employed in many future designs. Therefore,

it is essential to have a thorough understanding of its

security. Besides the initial cryptanalysis provided by

the designers (Bernstein et al., 2017), we are aware of

only one third party cryptanalysis (Hamburg, 2017).

However, the claimed results of (Hamburg, 2017)

is largely irrelevant to the original design, since the

“attack” is against an artiﬁcial and ad-hoc mode (see

http://gimli.cr.yp.to/statement.html for the statement

from the GIMLI team). In this paper, we provide an-

other third party cryptanalysis concerning Zero-Sum

Distinguishers by using MILP, which has been used

to automate many cryptanalytic techniques (Mouha

et al., 2012; Sun et al., 2014; Xiang et al., 2016;

Sasaki and Todo, 2017; Cui et al., 2016; Shi et al.,

2018; Fu et al., 2016). We identify a set of zero-sum

distinguishers for 14-round GIMLI. To the best of

our knowledge, these are the best distinguishers for

GIMLI so far.

Organization. In Section 2, we give a brief de-

scription of the GIMLI permutation. We show how

Cai, J., Wei, Z., Zhang, Y., Sun, S. and Hu, L.

Zero-sum Distinguishers for Round-reduced GIMLI Permutation.

DOI: 10.5220/0007249000380043

In Proceedings of the 5th International Conference on Information Systems Security and Privacy (ICISSP 2019), pages 38-43

ISBN: 978-989-758-359-9

 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

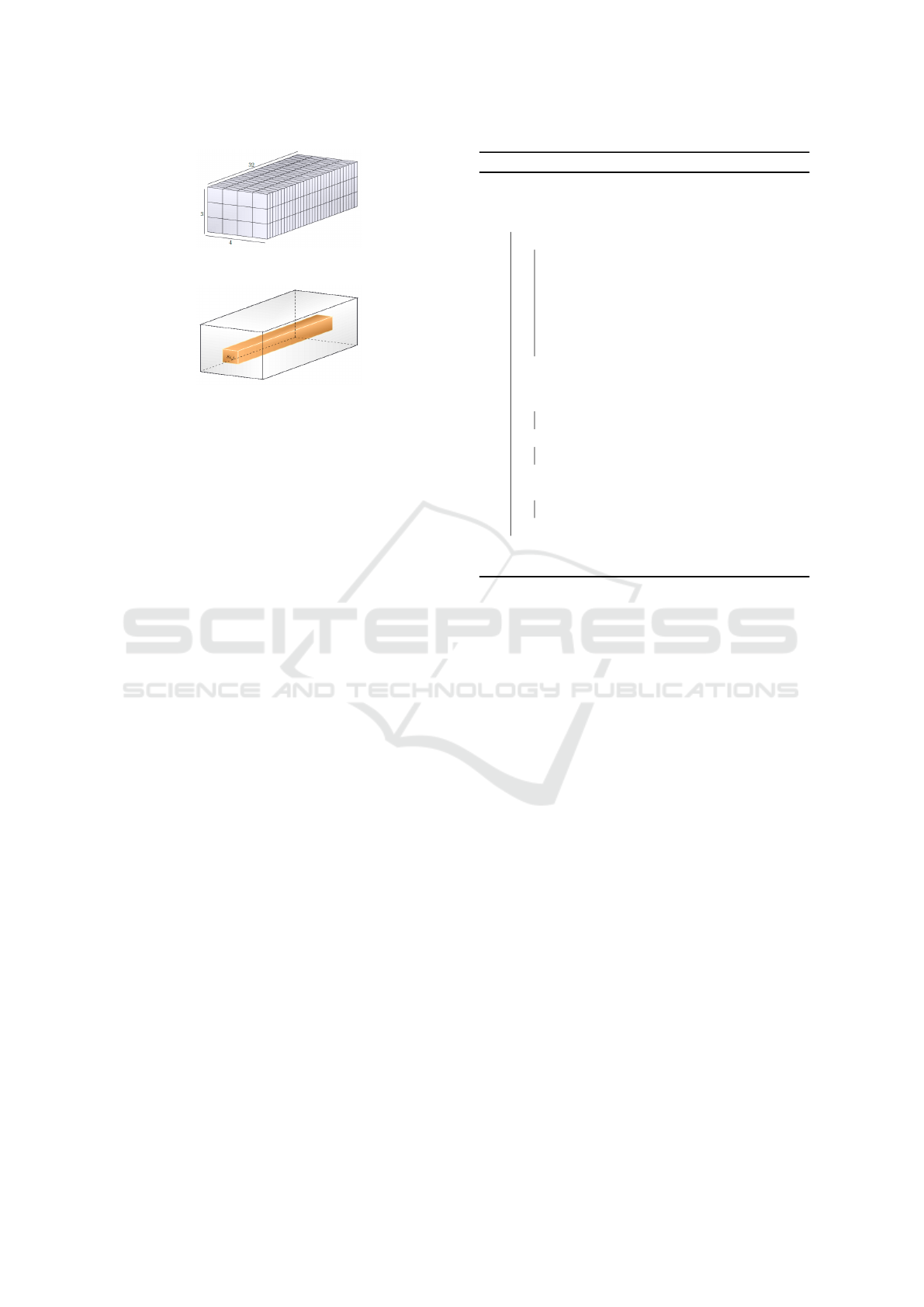
Fig 1: The state of GIMLI.

Fig 2: The 32-bit word s

i, j

in row i and column j.

to evaluate the algebraic degree of a boolean function

with division property in Section 3, which is the main

cryptanalytic tool employed in this work. The inside-

out technique for ﬁnding zero-sums is introduced in

Section 4. In Section 5, we identify many zero-sum

distinguishers of 14-round GIMLI with the methods

presented in Section 3 and Section 4. We conclude in

Section 6 and give some discussion of future work.

2 DESCRIPTION OF THE GIMLI

PERMUTATION

GIMLI is a 384-bit permutation. There are 24 rounds

in GIMLI, numbered 24,23, . . . , 1. The input 384-bit

data is arranged into a 3 × 4 matrix of 32-bit words as

shown in Fig. 1. Let s

i, j

∈ W denote the 32-bit word

in row i and column j for 0 ≤ i < 3 and 0 ≤ j < 4,

where W is the set of all 32-bit words (see Fig. 2).

The 384-bit state is then manipulated according to Al-

gorithm 2 to produce the output. The inverse of the

GIMLI permutation can be derived from Algorithm 1

and we put it into Appendix 6.

3 ALGEBRAIC DEGREE

EVALUATION WITH DIVISION

PROPERTY

The Division property, introduced by Todo at EU-

ROCRYPT 2015 (Todo, 2015), is a generalization

of the integral property, and its bit-based version

was applied in the cryptanalysis of SIMON at FSE

2016 (Todo and Morii, 2016).

Let F

denote the ﬁnite ﬁeld of two elements, and

Z represent the set of integers. The Hamming weight

wt(v) of a vector v ∈ F

is deﬁned as the number of

Algorithm 1: The GIMLI permutation.

Input: s = (s

i, j

) ∈ W

3×4

Output: GIMLI(s) = (s

i, j

) ∈ W

3×4

1 for r from 24 downto 1 inclusive do

2 for j ∈ {0, · · · , 3} do

3 x ← s

0, j

≪ 24

4 y ← s

1, j

≪ 9

5 z ← s

2, j

6 s

2, j

← x ⊕ (z  1) ⊕ ((y ∧ z)  2)

7 s

1, j

← y ⊕ x ⊕ ((x ∨ z)  1)

8 s

0, j

← z ⊕ y ⊕ ((x ∧ y)  3)

9 end

11 if r mod 4 = 0 then

12 s

0,0

0,1

0,2

0,3

← s

0,1

0,0

0,3

0,2

13 else if r mod 4 = 2 then

14 s

0,0

0,1

0,2

0,3

← s

0,2

0,3

0,0

0,1

15 end

16 if r mod 4 = 0 then

17 s

0,0

= s

0,0

⊕ 0x9e377900 ⊕ r

18 end

19 end

20 return (s

i, j

)

nonzero entries in v. For vectors k = (k

,··· , k

n−1

)

and u = (u

,··· , u

n−1

) in {0, 1}

⊆ Z, we say u <

k if u

≥ k

for any i ∈ {0, ··· , n − 1}.

Let f : F

→ F

be an n-variable boolean function

whose Algebraic Normal Form (ANF) is

f (x) =

v∈F

· x

where v = (v

,··· , v

n−1

), x

∏

n−1

i=0

, and we

call a

∈ F

the ANF coefﬁcient of f . The algebraic

degree of f is deﬁned as deg( f ) = max{wt(v) : a

0}. A vectorial boolean function G = (g

,··· , g

m−1

) :

→ F

is a sequence of m boolean functions g

→ F

with 0 ≤ i < m, and the algebraic degree

deg(G) of G is deﬁned as max{deg(g

) : 0 ≤ i < m}.

Deﬁnition 1 (Bit-based Division Property (Todo and

Morii, 2016)). Let X be a multiset whose elements

belong to F

. When the multiset X has the division

property D

, where K denotes a subset of {0, 1}

⊆

, it satisﬁes the following condition

x∈X

(x) =

(

unknown if there are k ∈ K, s.t. u < k

0 otherwise

where u = (u

,··· , u

n−1

) ∈ {0, 1}

⊆ Z

, x =

,··· , x

n−1

) ∈ F

, and π

(x) =

∏

n−1

i=0

If a multiset X has division property D

, after the

application of a vectorial boolean function F : F

→

Zero-sum Distinguishers for Round-reduced GIMLI Permutation

, the division property of the output multiset Y be-

comes D

. We say D

propagates to D

, which is

denoted by D

−→ D

, or K

−→ K

Deﬁnition 2 (Division Trail (Xiang et al., 2016)). Let

F be the round function of an iterated block cipher.

Assume that the input multi-set to the block cipher has

initial division property D

with K

= {k}. This ini-

tial division property propagates through the round

function which forms a chain

−→ D

−→ ·· ·

For any vector k

∗

∈ K

(i ≥ 1), there must exist a

vector k

∗

i−1

in K

i−1

such that k

∗

i−1

can propagate to

∗

according to the rules of division property prop-

agation. Furthermore, for (k

,··· , k

) ∈ K

× · ·· × K

, if k

i−1

can propagate to k

for all

i ∈ {1,2,··· , r}, we call (k

,··· , k

) an r-round

division trail.

Given k and k

, whether there is a division trail

k → k

for F can be determined by the resolution of

a Mixed-Integer Linear Programming (MILP) model

encoding the propagation rules of the division proper-

ties (Xiang et al., 2016). We refer the reader to (Xi-

ang et al., 2016) for more information on MILP-aided

analysis of division properties.

Besides its natural application in ﬁnding integral

distinguishers, it turns out that the division property

can be a very generic tool for probing the structure of

boolean functions whose explicit ANFs are not avail-

able due to resource limitation. In particular, the prop-

agation of division properties can be used to evaluate

the degree of a boolean function (Todo et al., 2017).

Lemma 1 (Todo, Isobe, Hao, and Meier (Todo et al.,

2017)). Let f : F

→ F

be a boolean function whose

ANF coefﬁcients are denoted by a

(v ∈ F

), and k ∈

. Then a

= 0 for all v < k if there is no division

trail such that k

−→ 1.

Lemma 1 leads to the following two propositions

for evaluating the degrees of (vectorial) boolean func-

tions.

Proposition 1. Let f : F

→ F

be a boolean function.

Then the degree of f is upper bounded by d + 1 where

d = max

k∈F

{wt(k) : k

−→ 1 is a division trail}.

Proposition 2. Let F : F

→ F

be a vectorial

boolean function. Then the degree of F is upper

bounded by d + 1 where d = max

k∈F

{wt(k) : k

−→

is a division trail for some j ∈ {0, ·· · , n − 1}} and

is the jth unit vector.

G H

F(x)

Fig 3: F = H ◦ G.

4 THE INSIDE-OUT TECHNIQUE

FOR FINDING ZERO-SUM

DISTINGUISHERS

The so-called zero-sum distinguisher was proposed

by Aumasson and Meier in (Aumasson and Meier,

2009), which can be regarded as a generalization

of the integral property (a.k.a. saturation prop-

erty) (Daemen et al., 1997; Knudsen and Wagner,

2002).

Deﬁnition 3 (Zero-Sum Distinguisher (Aumasson

and Meier, 2009; Boura and Canteaut, 2010)). Let

F : F

→ F

be a permutation. A zero-sum is a set

X ⊆ F

of inputs such that

x∈X

x ≡ 0 and

x∈X

F(x) ≡ 0 .

Since it is expected that a randomly chosen permuta-

tion does not have many zero-sums, the existence of

many such sets of inputs can be seen as a distinguish-

ing property of F.

The zero-sum distinguishers are intimately related

to the integral distinguishers whose existence has a

close connection with the degree of the underlying

boolean functions.

Let I be a subset of {0,··· , n−1} with cardinality

|I |, and δ(I ) be the subspace spanned by {e

: i ∈ I }.

For a vector a ∈ F

, δ

(I ) is deﬁned to be the set

{x + a : x ∈ δ(I )}. That is, δ

(I ) is the set of all

vectors whose values indexed by I traverse all pos-

sible values while the values at other positions are

ﬁxed to constants according to a. It is easy to check

that for any a ∈ F

, and any I whose cardinality is

strictly greater than 1, ⊕

x∈δ

(I )

x ≡ 0. Moreover, if

deg(F) < n, and |I | > deg(F), then for any a ∈ F

x∈δ

(I )

F(x) ≡ 0.

Therefore, many zero-sums δ

(I ) for F with

deg(F) < n can be identiﬁed. Since F is a permu-

tation, we can construct zero-sums from the mid-

dle (the inside-out technique (Aumasson and Meier,

2009; Boura and Canteaut, 2010)) by exploiting the

knowledge of the degrees of both the forward and

backward directions of F as depicted in Fig. 3.

Firstly, F is decomposed into H ◦ G, where G and

H are n-bit permutations. Assuming that deg(G

−1

) <

n and deg(H) < n, then for any a ∈ F

and I with

ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy

0 1

. . .

(I)

5 rounds

5 6

. . .

9 rounds

Fig 4: Apply the inside-out technique to 14-round GIMLI.

|I | = max{deg(G

−1

),deg(H)} + 1, δ

(I ) is a zero-

sum for both G

−1

and H. Consequently, we have

x∈G

−1

(δ

(I ))

x ≡ 0

and

x∈G

−1

(δ

(I ))

F(x) =

x∈G

−1

(δ

(I ))

H ◦ G(x)

y∈δ

(I )

H(y)

= 0

which indicates that G

−1

(δ

(I )) is a zero-sum for F.

5 ZERO-SUM DISTINGUISHERS

FOR ROUND-REDUCED GIMLI

To apply the inside-out technique, We split the 14-

round GIMLI into the ﬁrst 5 rounds (denoted by G)

and the last 9 rounds (denoted by H) as depicted in

Fig. 4. Then the degrees of G

−1

and H are evaluated

with the method introduced in Sect. 3. Therefore, we

need to set up MILP models encoding the propagation

of division properties for round-reduced GIMLI and

its inverse. According to the speciﬁcation of GIMLI

presented in Algorithm 1 (also see Appendix 6 for

its inverse), the MILP models can be constructed by

properly assembling the MILP models for the follow-

ing three operations.

Modeling S-box. We treat the non-linear operation

) = (y ∧ z,x ∨ z, x ∧ y) in GIMLI as a 3 × 3 S-

box, and use the method presented in (Boura and Can-

teaut, 2016) to retrieve its propagation rules (see Ta-

ble 1) of the division property. Using the convex hull

computation approach (Sun et al., 2014), the propa-

gation rule shown in Table 1 can be transformed into

the following linear inequalities











x + z − 2x

− 3y

− 2z

+ 2 ≥ 0

− x +y

+ z

≥ 0

− z + x

+ y

≥ 0

− y + x

+ z

≥ 0

x + y + z − x

− y

− z

≥ 0

where all variables involved are binaries.

Table 1: Propagation rule of (x

) = (y ∧ z, x ∨z, x ∧ y).

Input Output

(0,0, 0) (0,0, 0)

(0,0, 1) (0,1, 0) (1, 0, 0)

(0,1, 0) (0,0, 1) (1, 0, 0)

(0,1, 1) (1,0, 0)

(1,0, 0) (0,0, 1) (0, 1, 0)

(1,0, 1) (0,1, 0) (1, 0, 1)

(1,1, 0) (0,0, 1)

(1,1, 1) (1,0, 1)

Modeling COPY. Let a

COPY

−−−→ (b

,··· , b

m−1

) be a

division trail of COPY. Then a = b

+ · ·· + b

m−1

where all variables involved are binaries.

Modeling XOR. Let (a

,··· , a

m−1

)

XOR

−−−→ b be a di-

vision trail of XOR. Then a

+ ··· + a

m−1

= b, where

all variables involved are binaries.

After assembling the above constraints for all op-

erations involved in the underlying permutation, we

can check whether d is an upper bound of the degree

of the permutation as follows. We impose additional

constraints dictating that

n−1

∑

i=0

≥ d and

n−1

∑

i=0

= 1, (1)

where u

’s and v

’s are the variables representing the

input and output division properties, respectively (n =

384 for GIMLI). If the resulting model is infeasible,

then the algebraic degree of the underlying permuta-

tion is upper bounded by d due to Proposition 2.

Firstly, we evaluate the degree of H. Note that the

degree evaluation of H has already been done by the

design team. However, we still perform this process

to verify our implementation against the results pro-

vided by the designers. The upper bounds of the de-

grees for round reduced versions of H (up to 9 rounds)

are summarized in Table 2, which match the results

provided in (Bernstein et al., 2017).

We then evaluate the degrees of round-reduced

−1

, and the results are listed in Table 3. Note that

the bounds we get are not necessarily tight. In our

experiment, we observed that when we set the d in

equation (1) to be a very small value, the resolution

time of the MILP model can be very long. Therefore,

we prefer to choose a d which may be much larger

than the degree of the analyzed permutation.

According to the above results and the discus-

sion of Sect. 4, We can conclude that G

−1

(δ

(I ))

with |I | > 350 is a zero-sum of 14-round GIMLI for

any a ∈ F

. Finally, we note that all models are

solved by the Gurobi optimizer (Gurobi Optimization,

2013) and all experiments are performed on a com-

Zero-sum Distinguishers for Round-reduced GIMLI Permutation

Table 2: The upper bounds of the degrees of round-reduced GIMLI.

# Rounds 1 2 3 4 5 6 7 8 9

Bounds 2 4 8 16 29 52 95 163 266

Table 3: The upper bounds of the degrees of round-reduced G

−1

# rounds 1 2 3 4 5

Bounds 32 63 141 170 350

puter running Ubuntu 16.04 TLS system with Intel(R)

Core(TM) i5-4590 CPU @ 3.30GHz.

6 CONCLUSION AND

DISCUSSION

In this work, by analyzing the degrees of round-

reduced versions of the GIMLI permutation and its

inverse, we obtained a set of 14-round zero-sum dis-

tinguishers, which achieves one-round improvement

compared with the results offered by the designers.

More speciﬁcally, the 14-round zero-sum distinguish-

ers are constructed with the knowledge of the alge-

braic degree of the vectorial boolean function repre-

senting the output of 9-round GIMLI permutation and

the upper bound of the degree of the inverse of 5-

round GIMLI permutation, where the evaluation of the

algebraic degrees is performed by solving MILP mod-

els encoding the propagation of the division proper-

ties. Note that we are only able to get the upper bound

of the algebraic degrees under our current computa-

tional resources. Therefore, it is interesting to investi-

gate whether tighter bounds can be obtained. We ex-

pect that a more accurate degree evaluation may help

to extend the zero-sum distinguisher one more round.

ACKNOWLEDGEMENTS

The authors thank the anonymous reviewers for many

helpful comments. The work is supported by the Chi-

nese Major Program of National Cryptography De-

velopment Foundation (Grant No. MMJJ20180102),

the National Natural Science Foundation of China

(61732021, 61802400, 61772519, 61802399), the

Youth Innovation Promotion Association of Chinese

Academy of Sciences, and the Institute of Informa-

tion Engineering, CAS (Grant No. Y7Z0251103).

REFERENCES

Aumasson, J.-P. and Meier, W. (2009). Zero-sum distin-

guishers for reduced Keccak-f and for the core func-

tions of Luffa and Hamsi. Available at http://131002.

net/data/papers/AM09.pdf.

Bernstein, D. J. (2008). The salsa20 family of stream

ciphers. In New Stream Cipher Designs - The

eSTREAM Finalists, pages 84–97. https://cr.yp.to/

snufﬂe/salsafamily-20071225.pdf.

Bernstein, D. J., K

olbl, S., Lucks, S., Massolino, P. M. C.,

Mendel, F., Nawaz, K., Schneider, T., Schwabe, P.,

Standaert, F., Todo, Y., and Viguier, B. (2017). Gimli

: A cross-platform permutation. In Cryptographic

Hardware and Embedded Systems - CHES 2017 - 19th

International Conference, Taipei, Taiwan, September

25-28, 2017, Proceedings, pages 299–320.

Bertoni, G., Daemen, J., Peeters, M., and Assche, G. V.

(2013). Keccak. In Advances in Cryptology - EU-

ROCRYPT 2013, 32nd Annual International Confer-

ence on the Theory and Applications of Cryptographic

Techniques, Athens, Greece, May 26-30, 2013. Pro-

ceedings, pages 313–314. https://keccak.team/ﬁles/

Keccak-reference-3.0.pdf.

Boura, C. and Canteaut, A. (2010). A zero-sum property

for the Keccak-f permutation with 18 rounds. In IEEE

International Symposium on Information Theory, ISIT

2010, June 13-18, 2010, Austin, Texas, USA, Proceed-

ings, pages 2488–2492.

Boura, C. and Canteaut, A. (2016). Another view of the di-

vision property. In Advances in Cryptology - CRYPTO

2016 - 36th Annual International Cryptology Confer-

ence, Santa Barbara, CA, USA, August 14-18, 2016,

Proceedings, Part I, pages 654–682.

Cui, T., Jia, K., Fu, K., Chen, S., and Wang, M. (2016). New

automatic search tool for impossible differentials and

zero-correlation linear approximations. IACR Cryp-

tology ePrint Archive, 2016:689.

Daemen, J., Knudsen, L. R., and Rijmen, V. (1997). The

block cipher square. In Fast Software Encryption, 4th

International Workshop, FSE 1997, Haifa, Israel, Jan-

uary 20-22, 1997, Proceedings, pages 149–165.

Fu, K., Wang, M., Guo, Y., Sun, S., and Hu, L. (2016).

Milp-based automatic search algorithms for differen-

tial and linear trails for speck. In Fast Software En-

cryption - 23rd International Conference, FSE 2016,

Bochum, Germany, March 20-23, 2016, Revised Se-

lected Papers, pages 268–288.

ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy

Gurobi Optimization (2013). Gurobi optimizer reference

manual. http://www.gurobi.com.

Hamburg, M. (2017). Cryptanalysis of 22

rounds of

Gimli. Cryptology ePrint Archive, Report 2017/743.

https://eprint.iacr.org/2017/743.

Knudsen, L. R. and Wagner, D. A. (2002). Integral crypt-

analysis. In Fast Software Encryption, 9th Interna-

tional Workshop, FSE 2002, Leuven, Belgium, Febru-

ary 4-6, 2002, Revised Papers, pages 112–127.

Mouha, N., Mennink, B., Herrewege, A. V., Watanabe, D.,

Preneel, B., and Verbauwhede, I. (2014). Chaskey:

An efﬁcient MAC algorithm for 32-bit microcon-

trollers. In Selected Areas in Cryptography - SAC

2014 - 21st International Conference, Montreal, QC,

Canada, August 14-15, 2014, Revised Selected Pa-

pers, pages 306–323.

Mouha, N., Wang, Q., Gu, D., and Preneel, B. (2012). Dif-

ferential and linear cryptanalysis using mixed-integer

linear programming. In Information Security and

Cryptology –ISC 2012, pages 57–76. Springer.

Sasaki, Y. and Todo, Y. (2017). New impossible differen-

tial search tool from design and cryptanalysis aspects

- revealing structural properties of several ciphers.

In Advances in Cryptology - EUROCRYPT 2017 -

36th Annual International Conference on the Theory

and Applications of Cryptographic Techniques, Paris,

France, April 30 - May 4, 2017, Proceedings, Part III,

pages 185–215.

Shi, D., Sun, S., Derbez, P., Todo, Y., Sun, B., and Hu, L.

(2018). Programming the demirci-selc¸uk meet-in-the-

middle attack with constraints. In Advances in Cryp-

tology - ASIACRYPT 2018 - 24th International Con-

ference on the Theory and Application of Cryptology

and Information Security, Brisbane, QLD, Australia,

December 2-6, 2018, Proceedings, Part II, pages 3–

34.

Sun, S., Hu, L., Wang, P., Qiao, K., Ma, X., and Song, L.

(2014). Automatic security evaluation and (related-

key) differential characteristic search: Application to

simon, present, lblock, DES(L) and other bit-oriented

block ciphers. In Advances in Cryptology - ASI-

ACRYPT 2014 - 20th International Conference on the

Theory and Application of Cryptology and Informa-

tion Security, Kaoshiung, Taiwan, R.O.C., December

7-11, 2014. Proceedings, Part I, pages 158–178.

Todo, Y. (2015). Structural evaluation by generalized in-

tegral property. In Advances in Cryptology - EU-

ROCRYPT 2015 - 34th Annual International Confer-

ence on the Theory and Applications of Cryptographic

Techniques, Soﬁa, Bulgaria, April 26-30, 2015, Pro-

ceedings, Part I, pages 287–314.

Todo, Y., Isobe, T., Hao, Y., and Meier, W. (2017). Cube

attacks on non-blackbox polynomials based on divi-

sion property. In Advances in Cryptology - CRYPTO

2017 - 37th Annual International Cryptology Confer-

ence, Santa Barbara, CA, USA, August 20-24, 2017,

Proceedings, Part III, pages 250–279.

Todo, Y. and Morii, M. (2016). Bit-based division prop-

erty and application to SIMON family. In Fast

Software Encryption - 23rd International Conference,

FSE 2016, Bochum, Germany, March 20-23, 2016,

Revised Selected Papers, pages 357–377.

Xiang, Z., Zhang, W., Bao, Z., and Lin, D. (2016). Apply-

ing MILP method to searching integral distinguishers

based on division property for 6 lightweight block ci-

phers. In Advances in Cryptology - ASIACRYPT 2016

- 22nd International Conference on the Theory and

Application of Cryptology and Information Security,

Hanoi, Vietnam, December 4-8, 2016, Proceedings,

Part I, pages 648–678.

APPENDIX

Algorithm 2: The reversed GIMLI permutation

Input: s = (s

i, j

) ∈ W

3×4

Output: GIMLI

−1

(s) = ( ˜s

i, j

) ∈ W

3×4

1 for r from 24 downto 1 inclusive do

2 if r mod 4 = 0 then

3 s

0,0

= s

0,0

⊕ 0x9e377900 ⊕ r

4 end

5 if r mod 4 = 0 then

6 s

0,0

0,1

0,2

0,3

← s

0,1

0,0

0,3

0,2

7 else if r mod 4 = 2 then

8 s

0,0

0,1

0,2

0,3

← s

0,2

0,3

0,0

0,1

9 end

11 for j ∈ {0, · · · , 3} do

12 ˜s

0, j,0

← s

2, j,0

13 ˜s

1, j,0

← s

1, j,0

⊕ ˜s

0, j,0

14 ˜s

2, j,0

← s

0, j,0

⊕ ˜s

1, j,0

15 ˜s

0, j,1

← s

2, j,1

⊕ ˜s

2, j,0

16 ˜s

1, j,1

← s

1, j,1

⊕ ˜s

0, j,1

⊕ (˜s

2, j,0

∨ ˜s

0, j,0

)

17 ˜s

2, j,1

← s

0, j,1

⊕ ˜s

1, j,1

18 ˜s

0, j,2

← s

2, j,2

⊕ ˜s

2, j,1

⊕ (˜s

1, j,0

∧ ˜s

2, j,0

)

19 ˜s

1, j,2

← s

1, j,2

⊕ ˜s

0, j,2

⊕ (˜s

2, j,1

∨ ˜s

0, j,1

)

20 ˜s

2, j,2

← s

0, j,2

⊕ ˜s

1, j,2

22 for k ∈ {3,··· , 31} do

23 ˜s

0, j,k

← s

2, j,k

⊕ ˜s

2, j,k−1

⊕ (˜s

1, j,k−2

∧

˜s

2, j,k−2

)

24 ˜s

1, j,k

←

1, j,k

⊕ ˜s

0, j,k

⊕ (˜s

2, j,k−1

∨ ˜s

0, j,k−1

)

25 ˜s

2, j,k

←

0, j,k

⊕ ˜s

1, j,k

⊕ (˜s

0, j,k−3

∧ ˜s

1, j,k−3

)

26 end

28 ˜s

0, j

← ˜s

0, j

≪ −24

29 ˜s

1, j

← ˜s

1, j

≪ −9

30 end

31 end

32 return (˜s

i, j

)

Zero-sum Distinguishers for Round-reduced GIMLI Permutation