Bragg Grating Solitons in a Dual-core System with Separated Bragg
Grating and Cubic-quintic Nonlinearity
Nadia Anam
1
, Tanvir Ahmed
2
and Javid Atai
1
1
School of Electrical and Information Engineering, The University of Sydney, NSW 2006, Australia
2
Department of Electrical and Electronic Engineering, Rajshahi University of Engineering and Technology,
Rajshahi 6204, Bangladesh
Keywords:
Bragg Solitons, Fiber Bragg Grating, Dual-core System.
Abstract:
We analyze the stability of solitons in a semilinear dual-core system where one core is linear with a Bragg
grating and the other core is uniform and has cubic-quintic nonlinearity. It is found that there exist three
spectral gaps in the model’s linear spectrum. The quiescent soliton solutions are found by means of numerical
techniques. It is found that the soliton solutions exist only in both the upper and lower bandgaps. Two distinct
and disjoint families of solitons (i.e. Type 1 and Type 2 solitons) are found in the upper and lower bandgaps
that are separated by a border. Stability of solitons are analyzed numerically. The stability analysis shows that
stable Type 1 solitons may only exist in a part of the upper bandgap. Type 2 solitons in both upper and lower
gaps are found to be unstable.
1 INTRODUCTION
Fiber Bragg Gratings (FBGs) have found use in nu-
merous applications such as filtering, dispersion com-
pensation, and sensing (Kashyap, 1999; Krug et al.,
1995; Loh et al., 1996; Litchinitser et al., 1997; Cao
et al., 2012). As a result of the variation of re-
fractive index, the FBGs possess a distinctive fea-
ture, namely the existence of a bandgap in their lin-
ear spectrum within which linear waves do not prop-
agate (Kashyap, 1999). Additionally, the coupling
between transmitted and reflected waves in an FBG
gives rise to an effective dispersion that can be 10
6
times stronger than the chromatic dispersion of sil-
ica (de Sterke and Sipe, 1994; Eggleton et al., 1997).
At sufficiently high intensities, Bragg grating solitons
can be generated in FBGs through a balance between
the effective dispersion of the FBG and the nonlinear-
ity of the medium (de Sterke and Sipe, 1994).
The generation and observation of Bragg grat-
ing (BG) solitons have been of great interest mainly
because of their potential applications in generation
of slow light and development of novel optical de-
lay lines and memory elements. Consequently, BG
solitons have been studied extensively both theoret-
ically (Aceves and Wabnitz, 1989; Christodoulides
and Joseph, 1989; Malomed and Tasgal, 1994;
Barashenkov et al., 1998; De Rossi et al., 1998; Neill
and Atai, 2006) and experimentally (Eggleton et al.,
1996; de Sterke et al., 1997; Eggleton et al., 1999)
in Kerr nonlinear media. To date, BG solitons prop-
agating at 23% of speed of light in the medium have
been reported (Mok et al., 2006). Theoretical studies
haveshown that BG solitons may exist in other optical
structures and nonlinearities such as dual-core fibers
(Atai and Malomed, 2000; Atai and Malomed, 2001b;
Mak et al., 1998; Atai and Baratali, 2012), photonic
crystal waveguides (Monat et al., 2010; Neill and
Atai, 2007; Atai et al., 2006), waveguide arrays (Man-
delik et al., 2004; Tan et al., 2009; Dong et al., 2011),
and cubic-quintic nonlinear medium (Atai and Mal-
omed, 2001a; Dasanayaka and Atai, 2010).
Nonlinear couplers with non-identical cores (par-
ticularly semi-linear ones) possess better switching
characteristics than the standard dual-core fibers (Atai
and Chen, 1992; Atai and Chen, 1993; Bertolotti
et al., 1995). The presence of Bragg grating in one
or both cores in such dual-core fibers will poten-
tially lead to novel switching and slow light devices.
Therefore, in this paper, we study the stability of
zero-velocity solitons in a semilinear dual-core sys-
tem where one core is linear with a Bragg grating
written on it and the other one is uniform and has
cubic-quintic nonlinearity.
24
Anam, N., Ahmed, T. and Atai, J.
Bragg Grating Solitons in a Dual-core System with Separated Bragg Grating and Cubic-quintic Nonlinearity.
DOI: 10.5220/0007251300240028
In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2019), pages 24-28
ISBN: 978-989-758-364-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 THE MODEL AND ITS LINEAR
SPECTRUM
We consider the propagation of light in a dual-core
fiber where one core is linear and has a Bragg grating
and the other one is a uniform fiber with cubic-quintic
nonlinearity. The mathematical model for such a sys-
tem can be expressed as follows:
iu
t
+ iu
x
+

|v|
2
+
1
2
|u|
2

u−q

1
4
|u|
4
+
3
2
|u|
2
|v|
2
+
3
4
|v|
4

u+ φ = 0,
iv
t
−iv
x
+

|u|
2
+
1
2
|v|
2

v−q

1
4
|v|
4
+
3
2
|v|
2
|u|
2
+
3
4
|u|
4

v+ ψ = 0,
iφ
t
+ icφ
x
+ u + λψ = 0,
iψ
t
−icψ
x
+ v+ λφ = 0.
(1)
Here, u and v are the forward-propagating and
backward-propagating waves in the nonlinear core
and their counterparts in the linear core are repre-
sented by φ and ψ, respectively. q is the parameter
that controls the strength of the quintic nonlinearity.
The coupling coefficient between the forward- and
backward-propagating waves induced by Bragg grat-
ings in the linear core is denoted by λ and c is the
group velocity for this core. The linear coupling co-
efficient between the two cores and the group velocity
in the nonlinear core are set equal to 1.
In order to determine the spectral regions where
solitons may exist, it is essential to analyze the lin-
ear spectrum of the model. Substituting u, v,φ,ψ ∼
exp(ikx −iωt) into the linearized version of Eqs. (1)
results in the following dispersion relation:
ω
4
−

1+ c
2

k
2
+

2+ λ
2

ω
2
+

ck
2
−1

2
+ λ
2
k
2
= 0.
(2)
The dispersion relation (2) is identical to that of Ref.
(Atai and Malomed, 2001b). For c = 0, Eq. (2) gives
rise to three disjoint gaps (Atai and Malomed, 2001b).
When λ >
1
√
2
, the gaps are given by



























λ < ω <
r
1+
λ
2
4
+
λ
2
;
−
r
1+
λ
2
4
−
λ
2
!
< ω <
r
1+
λ
2
4
−
λ
2
;
−
r
1+
λ
2
4
+
λ
2
!
< ω < −λ,
and for λ <
1
√
2
, the gaps are as follows:

























r
1+
λ
2
4
−
λ
2
!
< ω <
r
1+
λ
2
4
+
λ
2
;
−λ < ω < λ;
−
r
1+
λ
2
4
+
λ
2
!
< ω < −
r
1+
λ
2
4
−
λ
2
!
.
For λ =
1
√
2
, the three gaps combine into a single gap
defined by −
√
2 < ω <
√
2. Examples of dispersion
diagrams for different values of λ are shown in Fig. 1.
In the case of c 6= 0, the characteristics of the dis-
persion diagrams change significantly. More specifi-
cally, the upper and lower gaps of the dispersion dia-
gram overlap with one branch of the continuous spec-
trum. This means that only the central gap remains a
genuine one (Atai and Malomed, 2001b).
0
5
10
15
k
−4
−2
0
2
4
ω
λ = 0.3
λ = 1.5
Figure 1: Linear spectrum for Eqs. (1) at c = 0 for different
values of λ.
3 SOLITON SOLUTIONS AND
THEIR STABILITY
To obtain stationary zero velocity soli-
ton solutions for the system, we first
substitute {u(x,t),v(x,t),ϕ(x,t),ψ(x,t)}=
{U(x),V(x), Φ(x),Ψ(x)}e
(−iωt)
into Eqs. (1).
Upon simplification and invoking the symmetry
conditions from quiescent solitons i.e. U = −V
∗
and Φ = −Ψ
∗
, we arrive at the following system of
ordinary differential equations:
ωU + iU
x
+
3
2
|U|
2
U −
5
2
q|U|
4
U + Φ = 0,
ωΦ+ icΦ
x
+U −λΦ
∗
= 0.
(3)
Bragg Grating Solitons in a Dual-core System with Separated Bragg Grating and Cubic-quintic Nonlinearity
25

-80 -40 0 40 80
x
t
0
2000
(a)
-80 -40 0 40 80
x
t
0
2000
(b)
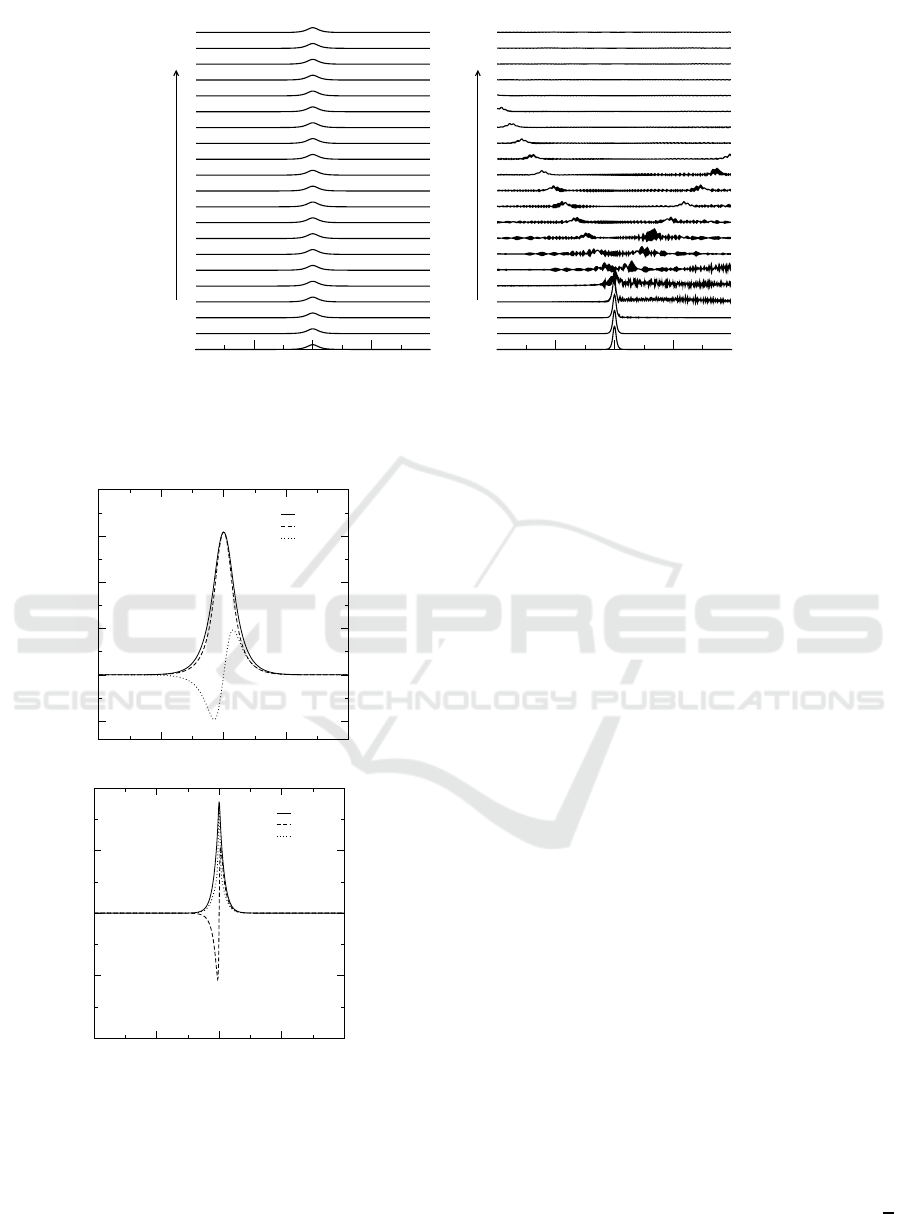
Figure 3: Examples of propagation of Type 1 zero-velocity solitons. (a) a stable soliton in the upper gap for λ = 1, c = 0,
ω = 1.6 and q = 0.13 and (b) an unstable soliton in the lower gap for λ = 1, c = 0, ω = −1.41 and q = 0.16 . Only the u
components are shown here.
-10
-5
0
5
10
x
(a)
-0.5
0
0.5
1
1.5
2
|u|
Re (u)
Im (u)
-20 -10 0 10 20
x
(b)
-2
-1
0
1
2
|u|
Re (u)
Im (u)
Figure 2: Soliton solutions at c = 0 for (a) Type 1 soliton in
the upper gap at λ = 1.2, ω = 1.56, q = 0.12 and (b) Type
2 soliton in the lower gap at λ = 1.2, ω = −1.5, q = 0.5.
Eqs. (3) can be solved numerically using the re-
laxation algorithm to obtain soliton solutions. The re-
sults of the numerical analysis show that soliton solu-
tions exist only in the upper gap and the lower gap.
Moreover, in each gap (i.e. upper and lower gap),
there exist two different and disjoint families of soli-
tons (henceforth referred to as Type 1 and Type 2).
The Type 1 and Type 2 families differ in their phase
structure and amplitude. In particular, Type 2 solitons
are characterized by a sharp nonsingular peak. Fig.
2 displays examples of Type 1 and Type 2 solitons in
the upper and lower bandgaps.
In order to determine the stability of the quiescent
BG solitons, we have conducted a numerical stabil-
ity analysis by solving Eqs. (1) using symmetrized
split-step method (Agrawal, 2013). The results sug-
gest that for a given λ, stable Type 1 solitons exist
only in a certain region of the upper band gap. Addi-
tionally, Type 2 solitons are unstable in both the upper
and lower gaps. Figs. 3 and 4 show examples of the
propagationof Type 1 and Type 2 solitons in the upper
and lower gaps. A noteworthy feature of these figures
is that Type 2 solitons are highly unstable and decay
into radiation very quickly. The results of the stability
analysis for λ = 1 are presented in Fig. 5.
4 CONCLUSIONS
We study the existence and stability of the Bragg grat-
ing solitons in a dual-core system where one core is
linear and is equipped with a Bragg grating and the
other one is uniform with cubic-quintic nonlinearity.
for c = 0, the linear spectrum of the system has three
distinct gaps which merge into one gap when the cou-
pling coefficient between the core is equal to 1/
√
2.
In the case of c 6= 0, the upper and lower gaps overlap
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
26

-80 -40 0 40 80
x
t
0
100
(a)(a)
-80 -40 0 40 80
x
t
0
100
(b)
Figure 4: Examples of propagation of Type 2 zero-velocity solitons. (a) an unstable solution in the upper gap for λ = 1, c = 0,
ω = 1.21 and q = 0.63 and (b) an unstable solution in the lower gap for λ = 1, c = 0, ω = −1.47 and q = 0.38 . Only the u
components are shown here.
1.02
1.2
1.4
1.61
0 0.1 0.2 0.3 0.4
0.5 0.6
0.7 0.8 0.9 1
q
-1.61
-1.4
-1.2
-1.02
No Soliton Solutions
ω
Stable Type 1
Unstable Type 1
Unstable Type 2
Unstable Type 1
Unstable Type 2
Figure 5: Stability diagram for c = 0 and λ = 1 in the (q, ω)
plane. The dashed curves are the borders separating the
Type 1 and Type 2 families of solitons.
with one branch of the continuous spectrum. There-
fore, only the central gap will be a genuine bandgap.
The soliton solutions for the systems are found using
the relaxation algorithm. It is found that there are no
soliton solutions in the central bandgap. On the other
hand, there exist two different and disjoint families of
solitons, namely Type 1 and Type 2, in the upper and
lower bandgaps.
Stability of the solitons are investigated by means
of numerical techniques. It is found that the Type 2
solitons in both upper and lower bandgaps are unsta-
ble and decay into radiation. The results also suggest
that stable Type 1 solitons may only exist in a certain
region within the upper bandgap.
REFERENCES
Aceves, A. B. and Wabnitz, S. (1989). Self-induced trans-
parency solitons in nonlinear refractive periodic me-
dia. Phys. Lett. A, 141:37–42.
Agrawal, G. P. (2013). Nonlinear Fiber Optics. Academic
Press, San Diego, 5th edition.
Atai, J. and Baratali, B. H. (2012). Gap solitons in dual-core
bragg gratings with dispersive reflectivity. J. Opt.,
14:065202.
Atai, J. and Chen, Y. (1992). Nonlinear couplers composed
of different nonlinear cores. J. Appl. Phys., 72:24–27.
Atai, J. and Chen, Y. (1993). Nonlinear mismatches be-
tween two cores of saturable nonlinear couplers. IEEE
J. Quant. Elec., 29:242–249.
Atai, J. and Malomed, B. A. (2000). Bragg-grating soli-
tons in a semilinear dual-core system. Phys. Rev. E,
62:8713–8718.
Atai, J. and Malomed, B. A. (2001a). Families of bragg-
grating solitons in a cubic-quintic medium. Phys. Lett.
A, 284(6):247 – 252.
Atai, J. and Malomed, B. A. (2001b). Solitary waves in
systems with separated bragg grating and nonlinearity.
Phys. Rev. E, 64:066617.
Atai, J., Malomed, B. A., and Merhasin, I. M. (2006). Sta-
bility and collisions of gapsolitons in a model of a hol-
low optical fiber. Optics Communications, 265(1):342
– 348.
Barashenkov, I. V., Pelinovsky, D. E., and Zemlyanaya,
E. V. (1998). Vibrations and oscillatory instabilities
of gap solitons. Phys. Rev. Lett., 80:5117–5120.
Bragg Grating Solitons in a Dual-core System with Separated Bragg Grating and Cubic-quintic Nonlinearity
27

Bertolotti, M., Monaco, M., and Sibilia, C. (1995). Role of
the asymmetry in a third-order nonlinear directional
coupler. Opt. Comm., 116:405–410.
Cao, H., Atai, J., Shu, X., and Chen, G. (2012). Di-
rect design of high channel-count fiber bragg grat-
ing filters with low index modulation. Opt. Express,
20(11):12095–12110.
Christodoulides, D. N. and Joseph, R. I. (1989). Slow bragg
solitons in nonlinear periodic structures. Phys. Rev.
Lett., 62:1746–1749.
Dasanayaka, S. and Atai, J. (2010). Stability of Bragg grat-
ing solitons in a cubic-quintic nonlinear medium with
dispersive reflectivity. Phys. Lett. A, 375(2):225 – 229.
De Rossi, A., Conti, C., and Trillo, S. (1998). Stability,
multistability, and wobbling of optical gap solitons.
Phys. Rev. Lett., 81:85–88.
de Sterke, C. M., Eggleton, B. J., and Krug, P. A. (1997).
High-intensity pulse propagation in uniform gratings
and grating superstructures. IEEE J. Lightwave Tech-
nol., 15:1494–1502.
de Sterke, C. M. and Sipe, J. E. (1994). Gap solitons. Prog.
Optics, 33:203–260.
Dong, R., R¨uter, C. E., Kip, D., Cuevas, J., Kevrekidis,
P. G., Song, D., and Xu, J. (2011). Dark-bright gap
solitons in coupled-mode one-dimensional saturable
waveguide arrays. Phys. Rev. A, 83:063816.
Eggleton, B. J., de Sterke, C. M., and Slusher, R. E. (1997).
Nonlinear pulse propagation in Bragg gratings. J. Opt.
Soc. Am. B, 14:2980–2993.
Eggleton, B. J., de Sterke, C. M., and Slusher, R. E. (1999).
Bragg solitons in the nonlinear schr¨odinger limit: ex-
periment and theory. J. Opt. Soc. Am. B, 16:587–599.
Eggleton, B. J., Slusher, R. E., Krug, P. A., and Sipe, J. E.
(1996). Bragg grating solitons. Phys. Rev. Lett.,
76:1627–1630.
Kashyap, R. (1999). Fiber bragg gratings. Academic Press,
San Diego; London.
Krug, P. A., Stephens, T., Yoffe, G., Ouellette, F., Hill, P.,
and Dhosi, G. (1995). Dispersion compensation over
270 km at 10 gbit/s using an offset-core chirped fibre
bragg grating. Electron. Lett., 31:1091.
Litchinitser, N. M., Eggleton, B. J., and Patterson, D. B.
(1997). Fiber bragg gratings for dispersion compen-
sation in transmission: theoretical model and design
criteria for nearly ideal pulse recompression. IEEE J.
Lightwave Technol., 15:1303–1313.
Loh, W. H., Laming, R. I., Robinson, N., Cavaciuti, A.,
Vaninetti, F., Anderson, C. J., Zervas, M. N., and Cole,
M. J. (1996). Dispersion compensation over distances
in excess of 500 km for 10-gb/s systems using chirped
fiber gratings. IEEE Photon. Technol. Lett., 24:944–
946.
Mak, W. C. K., Malomed, B. A., and Chu, P. L. (1998).
Solitary waves in coupled nonlinear waveguides with
Bragg gratings. J. Opt. Soc. Am. B, 15:1685–1692.
Malomed, B. A. and Tasgal, R. S. (1994). Vibration modes
of a gap soliton in a nonlinear optical medium. Phys.
Rev. E, 49:5787–5796.
Mandelik, D., Morandotti, R., Aitchison, J. S., and Silber-
berg, Y. (2004). Gap solitons in waveguide arrays.
Phys. Rev. Lett., 92:093904.
Mok, J. T., de Sterke, C. M., Littler, I. C. M., and Eggle-
ton, B. J. (2006). Dispersionless slow light using gap
solitons. Nature Phys., 2:775–780.
Monat, C., de Sterke, M., and Eggleton, B. J. (2010). Slow
light enhanced nonlinear optics in periodic structures.
J. Opt., 12:104003.
Neill, D. R. and Atai, J. (2006). Collision dynamics of gap
solitons in kerr media. Phys. Lett. A, 353:416–421.
Neill, D. R. and Atai, J. (2007). Gap solitons in a hollow
optical fiber in the normal dispersion regime. Phys.
Lett. A, 367:73–82.
Tan, Y., Chen, F., Beliˇcev, P. P., Stepi´c, M., Maluckov, A.,
R¨uter, C. E., and Kip, D. (2009). Gap solitons in de-
focusing lithium niobate binary waveguide arrays fab-
ricated by proton implantation and selective light illu-
mination. Appl. Phys. B, 95:531–535.
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
28