The Growing N-Gram Algorithm:

A Novel Approach to String Clustering

Corrado Grappiolo

, Eline Verwielen

and Nils Noorman

ESI (TNO), Eindhoven, The Netherlands

Unafﬁliated, Valkenswaard, The Netherlands

Philips Healthcare, Best, The Netherlands

Keywords:

String Clustering, N-Grams, Operational Usage Modelling, System Veriﬁcation Testing.

Abstract:

Connected high-tech systems allow the gathering of operational data at unprecedented volumes. A direct

beneﬁt of this is the possibility to extract usage models, that is, a generic representations of how such systems

are used in their ﬁeld of application. Usage models are extremely important, as they can help in understanding

the discrepancies between how a system was designed to be used and how it is used in practice. We interpret

usage modelling as an unsupervised learning task and present a novel algorithm, hereafter called Growing N-

Grams (GNG), which relies on n-grams — arguably the most popular modelling technique for natural language

processing — to cluster and model, in a two-step rationale, a dataset of strings. We empirically compare its

performance against some other common techniques for string processing and clustering. The gathered results

suggest that the GNG algorithm is a viable approach to usage modelling.

1 INTRODUCTION

Connected high-tech systems allow the gathering of

operational data at unprecedented volumes, usually

in the form of log ﬁles. These, although historically

mainly used for software debugging purposes, bring

new opportunities to understanding how end-users are

actually using a system, opposed to how they were

designed to be used, for instance during system de-

sign. To be able to extract relevant log information

and aggregate it into usage models can therefore be

extremely beneﬁcial. Usage models can help to iden-

tify particular types of behaviour, leading to insights

which can serve as a basis for product improvements.

System veriﬁcation can certainly beneﬁt from us-

age models. During system veriﬁcation, it is evalu-

ated whether the system complies to regulations, re-

quirements and speciﬁcations. System reliability ver-

iﬁcation is part of this process. The goal of reliability

veriﬁcation is to drive a system with realistic clini-

cal scenarios in conditions which were not expected

beforehand, taking care that the system is not load-

and stress-tested. To evaluate the reliability of a sys-

tem, its response has to be monitored at test time. If

the response is not as expected, then the system has

made a failure which may impact the operator or the

patient. Reliability ﬁgures are usually expressed as

Figure 1: Philips Image Guided Therapy’s Azurion

interventional x-ray system https://www.philips.com.eg/

healthcare/solutions/interventional-devices-and-therapies.

mean time between failures, ranging from a few hun-

dreds to thousands of hours. Ideally, the system is

put under “average” use during reliability veriﬁcation.

However, it is difﬁcult to determine what exactly the

average use exactly is.

Our ultimate goal is the design of a computational

framework for system (reliability) veriﬁcation testing

capable of distinguishing “average” usage (and other

types of usage). Ideally, the framework would lever-

age usage models to identify, from a given dataset,

logs depicting normal behaviour, and then to re-

execute them. Additionally, such framework should

Grappiolo, C., Verwielen, E. and Noorman, N.

The Growing N-Gram Algorithm: A Novel Approach to String Clustering.

DOI: 10.5220/0007259200520063

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 52-63

ISBN: 978-989-758-351-3

Table 1: Example of an x-ray sequence.

Step Action Symbol

1 table movement start 1

2 x-ray arm movement start 2

3 table movement stop 3

4 x-ray arm movement stop 4

5 table movement start 1

6 table movement stop 3

7 table movement start 1

8 table movement stop 3

9 user-interface 5

10 user-interface 5

11 user-interface 5

12 x-ray acquisition start 6

13 table movement start 1

14 x-ray arm movement start 2

15 table movement stop 3

16 x-ray arm movement stop 4

17 x-ray acquisition stop 7

be able to continuously maintain up-to-date represen-

tations of different behaviour types. We focus our

attention on operational data of Philips Healthcare’s

Image Guided Therapy interventional systems (IGT)

— see Figure 1 — which make the task of modelling

normal behaviour far from being trivial: the ﬂexibil-

ity of this system, the medical staff’s variety in ed-

ucational background, their familiarity with manoeu-

vring the system and the different pathologies of the

patients, result in an almost inﬁnite amount of differ-

ent usage types. Our interest, more speciﬁcally, is on

the sequence of high-level actions performed by the

users on the x-ray system during a medical procedure,

rather than its low-level details, such as motor/sensor

readings. Table 1 depicts an example of such x-ray

sequences.

Since we hold no a-priori knowledge on how

many usage behaviours exist we interpret usage mod-

elling as an unsupervised learning task. Assuming the

successful partitioning of a given dataset into clusters,

so that the similarity of behaviours represented by the

string belonging to the same cluster is maximised,

whilst the similarity of behaviours across clusters is

minimised, the subsequent task would correspond to

the extraction of a usage model for each cluster. Nat-

ural Language Processing (NLP) techniques are par-

ticularly useful. More speciﬁcally, we aim at extract-

ing a n-gram model for each retrieved cluster. The

main key-feature of n-grams is that they can lead to

the creation of probabilistic graphs which can then be

used for classiﬁcation purposes (Jurafsky and Martin,

2014). In our approach, each node of a n-gram graph

corresponds to a log action, whilst the edges connect-

ing nodes correspond to the conditional probability of

an action occurring given a ﬁnite sequence of previ-

ous actions.

Three main research questions arise: (1) how well

do existing techniques used for string/text/document

clustering perform on our data? (2) How can we com-

pare the outcome of different clustering algorithms

corresponding to a different number of clusters? (3)

Is it possible to provide an alternative clustering ap-

proach?

To answer the ﬁrst research question we consid-

ered k-means and complete-link hierarchical cluster-

ing — two of the most common clustering algorithms

— in presence of raw text-data and string similar-

ity measures or given a data transformation technique

which converts the raw data into a vectorised form.

The second research question is answered by lever-

aging on our modelling approach, which essentially

aims to create probabilistic graphs for each cluster, to

retrieve probability-based metrics — entropy in our

case — to compare partitions obtained by using dif-

ferent algorithms and data transformation techniques.

Concerning the third research question, we propose a

novel algorithm, hereafter called Growing N-Grams

(GNG). GNG creates new or updates existing n-gram

models in a two-step rationale. First, given an in-

put string to cluster, the algorithm relies on the exist-

ing models’ symbols to identify the candidate models

which share most commonalities with the string. If

none are found, a new n-gram model based on that

string is created. Otherwise, the algorithm calculates,

for each candidate model, the chain probability of that

string; the string is then assigned to the model which

returned the highest probability, with the consequence

that the winner model’s n-grams and probabilities are

updated to encompass the input string. To the authors’

best knowledge, there has never been an attempt to

perform string clustering directly by means of n-gram

classiﬁcation.

We conducted an empirical evaluation of string

clustering based on a dataset describing sub-

sequences of the Bolus chase procedure, a technique

in peripheral arteriography, performed on Philips

Healthcare’s IGT interventional systems

. Once the

set of n-gram models is built, the evaluation procedure

consists of calculating the entropy score of the chain

probabilities calculated by each n-gram model for a

given validation set of strings. The rationale is the

following: an optimal clustering partition would lead

to n-gram models which do not “overlap”, meaning

that given an input string all but one model will return

a very low chain probability, hence low entropy. On

the other hand, the worst clustering partition would

The dataset, algorithms and additional content can

be found using the following link: https://github.com/

bracciolo22/Growing-n-Grams.

The Growing N-Gram Algorithm: A Novel Approach to String Clustering

lead to n-gram models with some degree of overlap,

meaning that all models will return similar probabil-

ity values, thus resulting in a high entropy score. By

n-gram overlap we intend the existence of sub-graphs

of nodes, edges and related probabilities, which are

the same among different n-gram models, or at least

very close to each other.

The gathered results suggest that: (1) GNG can

outperform all other algorithms given appropriate hy-

perparameter setting; (2) there might be a relation-

ship between the statistical properties of the dataset

at hand and the hyperparameters leading to the op-

timal performance of GNG; (3) complete-link clus-

tering with a simple string similarity measure such

as the Levenshtein distance can lead to good results;

(4) string vectorisation does not offer straightforward

computational beneﬁts. The investigation allows us

to conclude that not only is GNG a novel, viable ap-

proach to string clustering, but its algorithmic struc-

ture is also suitable for our goal to create a framework

for system (reliability) veriﬁcation testing, given that

it can continuously create new models and update ex-

isting ones, hence maintaining up-to-date representa-

tions of system usage, without the need to perform

data pre-processing or pairwise distance matrix cal-

culations.

The remainder of this document is organised as

follows: Section 2 presents an overview of string clus-

tering approaches existing in the literature. Section 3

formalises the problem at hand and the performance

measure used for our empirical evaluation. Section 4

introduces the Growing N-Gram algorithm. Section 5

presents the experimental protocol adopted and the

details regarding the algorithms considered. Section 6

describes and discusses the obtained results. Sec-

tion 7 outlines some possible future work directions.

Section 8 concludes the research.

2 RELATED WORK

One of the most popular approaches to text and doc-

ument clustering focuses on converting the text data

into a vectorised form, so that a similarity measure

— mostly cosine similarity — can be computed and

hence used by the most generic clustering algorithms,

such as k-means (Bishop et al., 1995; Duda and

Hart, 1973) and its numerous variants, or hierarchi-

cal clustering (Anderberg, 1973), in its agglomera-

tive variation (Zhao et al., 2005; Jain and Dubes,

1988). Another term used to describe document vec-

torisation is bag-of-words (BOW). The idea is to

leverage the statistical information of words popu-

lating a document to represent data in a vectorised

Figure 2: Clustering algorithms and data processing ap-

proaches considered in our study.

form, most often retrieved by a combination of tech-

niques called Term Frequency and Inverse Document

Frequency (tf-idf), (Raghavan and Birchard, 1979;

Salton, 1989)). In essence, BOW abstracts docu-

ments as sets of words and ignores order dependen-

cies. Hornik et al. (Buchta et al., 2012) utilise BOW

and cosine similarity with spherical k-means (Dhillon

and Modha, 2001); Steinbach et al. (Steinbach et al.,

2000), instead, propose a new variant of k-means,

called bisecting k-means, to cluster vectorised doc-

uments, and compare their results against agglomer-

ative hierarchical clustering. Mahdavi and Abolhas-

sani (Mahdavi and Abolhassani, 2009) propose an-

other ﬂavour of k-means — named harmony k-means

— with the same data transformation techniques. Fi-

nally, Cutting et al. (Cutting et al., 2017) combine

both k-means and hierarchical clustering in an algo-

rithm called Scatter/Gather, although the underlying

data processing part is very similar to the other previ-

ous work. Other related work are those of Balaban-

taray et al. (Balabantaray et al., 2015) on k-medoids

and, most relevantly, of Zhao and Karypis (Zhao et al.,

2005), which provide an extensive research on hier-

archical clustering, both agglomerative and divisive,

even by proposing a novel constrained version of it,

on vectorised documents. Our work shares with all

these the idea of using BOW with tf-idf for data vec-

torisation followed by k-means and hierarchical clus-

tering. We differ from them on the nature of the data

— strings rather than documents — and also on the

fact that we are truly unaware of how many clusters

exist, making the setting of k much more difﬁcult.

For a broader overview of text clustering applications

please refer to (Aggarwal and Zhai, 2012) and (An-

drews and Fox, 2007) among other.

The recent raise in popularity and performance of

neural-based computing — e.g. deep learning — has

also contributed to NLP and therefore document clus-

tering. Within this ﬁeld, the vectorisation of docu-

ments and words is usually referred to as word em-

beddings (Dai et al., 2015). The key concept corre-

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

sponds to train a neural network to predict a word

given a contextual neighbourhood of text, and sub-

sequently utilises only part of the trained network

to convert an input text into a vector of real values.

The context of a given word is mainly obtained by

two similar techniques: skip-gram (Dai et al., 2015)

and continuous-bag-of-words (Mikolov et al., 2013a),

which both rely on a window of text around the given

word, with the difference that skip-gram takes into ac-

count the order of words. Word embedding led to

a vast plethora of work, see for instance Mikolov et

al. (Mikolov et al., 2013b), Lau and Baldwin (Lau and

Baldwin, 2016), Bengio et al. (Bengio et al., 2003),

Kiros et al (Kiros et al., 2015), Kim (Kim, 2014),

Zhang et al. (Zhang et al., 2015), Xu et al. (Xu et al.,

2015), or Tai et al. (Tai et al., 2015), to name few.

Intuitively, neural computing for word embedding is

extremely popular and should not be ignored, that is

why we considered it in our empirical evaluation. On

the other hand, understanding the most consolidated

approach or even network ﬂavour is not a trivial task

at all. We arbitrarily decided to rely on the work of

Le and Mikolov (Le and Mikolov, 2014) — primar-

ily for its popularity and practical ease of use of their

algorithm — as an alternative approach to document

vectorisation in combination with k-means and hier-

archical clustering for benchmarking purposes.

As previously said, the data in our possession

shares similarities also with sequences of strings with

a predeﬁned vocabulary. With this respect, there ex-

ist a vast plethora of string similarity measures which

do not require any data transformation phase. Among

these, the most widely known are arguably the Leven-

shtein or edit distance (Levenshtein, 1966) and vari-

ants (Pettersson et al., 2013; Ackroyd, 1980; Marzal

and Vidal, 1993; Yujian and Bo, 2007), and the Jaro

distance (Jaro, 1989). These metrics have been used,

for instance, by Rajalingam and Ranjini (Rajalingam

and Ranjini, 2011) in combination with agglomera-

tive hierarchical clustering, albeit they pre-processed

their text data by binary encoding; by Lu and Fu (Lu

and Fu, 1978) in combination with k-nearest neigh-

bour for sentence-to-sentence clustering; by da Cruz

Nassif and Hruschka (da Cruz Nassif and Hruschka,

2013) in combination with partitional k-means, k-

medoids and agglomerative clustering for partitioning

ﬁlenames — hence strings of characters — in a foren-

sic context. Another important relevant work is done

by Wurzenberger et al. (Wurzenberger et al., 2017),

who investigated several metrics for clustering log

lines, though in a semi-supervised setting. Similarly

to these work, we will embark the task of clustering

our usage data by means of Levenshtein, normalised

Levenshtein, and Jaro metrics.

N-grams (Chen and Goodman, 1999; Jurafsky and

Martin, 2014; Kneser and Ney, 1995; Brown et al.,

1992) — i.e. sequences of n symbols — are exten-

sively used in NLP, especially when combined with

the Markov property (Markov, 1971), since they lead

to the construction of probabilistic graphs. These al-

low for e.g. character and word prediction (Lesher

and Rinkus, 2002; Lesher et al., 1998) and lan-

guage modelling (Bungum and Gamb

ack, 2012; Si-

ivola and Pellom, 2005). In accordance with these

works, in fact, our ultimate goal is to model each

cluster of operational data, depicting different usage

behaviours, into a n-gram model. Attempts to lever-

age n-grams for text clustering have also been done.

Ismail and Rahman (Ismail and Rahman, 2014) use

the chain probability computed on tri-grams to calcu-

late the similarity score of word pairs, and then decide

whether to cluster them together based on a thresh-

olding rationale. Ke

selj et al. (Ke

selj et al., 2003),

instead, rely solely on the most frequent n-grams to

calculate the similarity between document author pro-

ﬁles; similar strategy is adopted by Miao et al. (Miao

et al., 2005), where they use most frequent n-grams as

distances to be used by k-means for document clus-

tering. Although our approach shares the use of chain

probabilities and thresholding to determine whether

a string should belong to a model, the n-grams are

used in their entirety rather than just their most fre-

quent terms, they are incrementally built through the

assignment of new strings to related clusters, and ﬁ-

nally no other clustering algorithm such as k-means is

used.

3 PROBLEM STATEMENT

This section formally introduces the problem at hand,

the strategy to solve it, and the performance measure

used to evaluate the solutions found. In order not to

overcrowd the manuscript, only the most important

concepts are presented. Finally, in order to maintain

the mathematical notions as simple and as clear as

possible, sub- and super-script indices will be omit-

ted when not necessary.

Let D be a dataset composed of |D| = d strings

, i = 1 .. . d. Each string w is composed of a vari-

able number of characters or symbols x belonging to

a vocabulary V . V is retrieved from D. D can con-

tain more than one occurrence of a string w, and each

string can contain more than one occurrence of the

same symbol. The goal is to partition D into k clus-

ters C

, i = 1, . . . k and to build, for each cluster C

, a

n-gram G

solely based on the strings belonging to C

All n-gram models share the same value for n, that is

The Growing N-Gram Algorithm: A Novel Approach to String Clustering

the history of past events to be taken into account. No

information is known, a priori, about k. We will refer

to the set of n-gram models M = {G

, G

, . . . G

}

as an ensemble of models. Given a string w composed

of a sequence of m symbols w = x

, x

, . . . x

and

an n-gram model G, the chain probability of w given

G and n is calculated as follows:

P(w | G) = P(x

, x

, . . . x

| G) ≈

≈

∏

i=1

P(x

| x

i−1

, . . . x

i−n+1

, G)

(1)

therefore, the assignment of w to a n-gram model G is

obtained as follows:

win

= argmax

(P(w | G), ∀ G ∈ M) (2)

and, consequently, the corresponding cluster C

win

also retrieved. As we will show in Section 5, different

algorithms — or even the repeated execution of the

same algorithm — might lead to a different number

of clusters. In order to evaluate how well the parti-

tioning task is performed, given an input string w, we

calculate the entropy of the ensemble’s chain proba-

bilities:

H (w) = −

∑

i=1

P(w| G

) log P(w | G

) (3)

The rationale is the following: a good partition

would lead to an ensemble which, for a given w,

would return very low chain probability values for

all-but-one model G — i.e. the model obtained from

Equation 2 — which instead would return a very high

probability. Such a set of probabilities would lead

to an extremely low entropy. On the other hand, a

bad partitioning would lead to an ensemble in which

all models return chain probability values which are

close to each other, hence a high entropy score.

Given a set of ensembles M = {M

. . . M

}

resulting from a clustering-modelling task of m dif-

ferent algorithms, and a validation set W composed

of |W | = l strings, the best ensemble is deﬁned as

follows:

∗

= argmin

∑

i = 1

)

, ∀ M ∈ M (4)

that is, it is the ensemble which returns the lowest av-

erage entropy score (and lowest standard deviation)

calculated over the whole validation set.

4 THE GROWING N-GRAM

ALGORITHM

The GNG algorithm is presented as pseudo-code in

the next column of this page. The algorithm takes as

Algorithm 1: The Growing N-Gram Algorithm.

1 GNG(D , τ

, τ

, δ

, τ

min

, τ

max

)

2 M =

3 while |D| > 0 do

4 shu f f le(D)

5 for each w ∈ D do

6 s = set(w)

7 M

, M

8 for each m ∈ M do

9 if s \ m > τ

then

10 M

← M

∪ {m}

11 end if

12 if s \ m ≤ τ

then

13 M

← M

∪ {m}

14 end if

15 end for

16 if M

≡ M then

17 m = new n gram(w)

18 M ← M ∪ {m}

19 pop(w, D)

20 else if |M

| > 0 then

21 m = argmax(P(w|G), ∀ G ∈ M

)

22 update(m, w)

23 pop(w, D)

24 else

25 do nothing

26 end if

27 end for each

28 τ

← max(τ

− δ

, τ

min

)

29 τ

← max(τ

+ δ

, τ

max

)

30 end while

31 return M

input: (1) a dataset D of strings to be partitioned into

clusters, (2) two thresholds, namely τ

and τ

, which

regulate the creation of new models or the update of

existing ones, (3) two parameters δ

and δ

, which

modify the values of their respective τs so that the

whole dataset is processed, (4) two parameters τ

min

and τ

max

, which are used to bound the values of τ

and τ

respectively.

GNG assigns each string w ∈ D to one and only

one model m ∈ M , see lines 17 and 22. The pop

function call in lines 19 and 23 simply means that w,

once assigned to a model m, is removed from D. For

simplicity, the algorithm does not explicitly state how

to maintain the cluster composition of each model.

For each w, the algorithm ﬁrst extracts the set s of

its unique symbols (line 6), then evaluates it with the

symbols of each m ∈ M. The evaluation is done via

set difference and this is compared against the two

thresholds τ

and τ

(lines 9 and 12 respectively). Two

subsets of M, M

and M

, are used to keep track of

which model satisﬁes which threshold condition —

lines 10 and 13 respectively. Please note that M

and

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

Table 2: Dataset Details

Feature Train Test Validation Total

Size 5301 663 662 6626

Unique Strings 1673 281 310 2019

String Intersection with Training Set 113 131

Alphabet Size 88 57 61 91

Alphabet Intersection with Training Set 56 59

Avg. String Length 7.18 7.93 7.82 7.32

Std. Dev. String Length 13.28 26.92 12.11 15.11

Median string Length 4 4 4 4

Min. String Length 2 2 2 2

Max. String Length 345 617 148 617

do not partition M, meaning that it is possible that

some model in M might belong neither to M

nor to

during a GNG iteration.

In essence, M

corresponds to the set of models

in M which are too far from w, whilst M

are the set

of models in M which are close enough to w. If all

existing models are too far from w (line 16), then a

new n-gram model based on w is created (line 17) and

added to the ensemble (line 18). Alternatively, and in

case there are some models which are close enough to

w (line 20), the model in M

which returns the highest

chain probability calculated in accordance with Equa-

tion (2) is retrieved and updated with w (lines 21 and

22). In case no creation or update is performed, the

string remains unassigned (line 25) and the algorithm

continues by processing the next string. The update

of an n-gram model simply corresponds to updating

the n-gram counts of that model given w. The con-

sequence of this is that the calculation of the model’s

chain probabilities will also become up-to-date (Ju-

rafsky and Martin, 2014; Kneser and Ney, 1995).

At the end of one dataset processing loop, some

strings might still be unassigned. This is because the

constraints based on τ

and τ

might be too strict. The

algorithm then relaxes such constraints in lines 28 and

29. τ

is decreased, whilst τ

is increased. Both are

bounded by their respective τ

min

and τ

max

. D is guar-

anteed to be fully partitioned into clusters/models if,

eventually, τ

= 0 or τ

= τ

5 EXPERIMENTAL PROTOCOL

In order to evaluate the viability of our GNG algo-

rithm we conducted an empirical investigation based

on sub-sequences of the Bolus chase procedure, a

technique in peripheral arteriography, performed on

IGT systems. For optimal handling, we represented

the log data as tokenised strings based on a vocabulary

V of actions extracted from the dataset. An example

of log tokenisation is depicted in Table 1. We gath-

ered and tokenised 6626 x-ray sequences leading to a

vocabulary of 91 symbols. It is important to remark

that each string w can only terminate with one out of

four possible symbols representing the end of an x-ray

exposure type. The statistical details of our dataset

are reported in Table 2. As it can be observed, the

dataset contains a lot of repeated sequences — only

30% of instances are unique, which indeed gives us a

hint that there must exist some usage patterns, though

the string overlap between train and test/validation set

is minor (40.21% and 46.62%). On the other hand, all

sets share most of the symbols.

Given the ﬁrst research question introduced in

Section 1, and the related work presented in Section 2,

we decided to compare our GNG algorithm with sev-

eral others, based on the following:

• Data Representation: we considered both the case

in which each w ∈ D is vectorised or not;

• String Vectorisation: we considered two tech-

niques: (1) tf-idf and (2) Gensim’s implementa-

tion of the doc2vec algorithm (Rehurek and Sojka,

2010). The similarity score of vectorised strings is

calculated via cosine distance;

• Non-vectorised Data: in order to calculate the

similarity of two strings we considered: (1) the

Levenshtein distance, (2) the normalised Leven-

shtein distance, and (3) the Jaro distance;

• Clustering Algorithms: we considered k-means

and complete-link hierarchical clustering;

• Determining the Number of Clusters gor k-means:

we run k-means for k = 2, . . . k

max

and rely on

the silhouette coefﬁcient in order to retrieve the

best k-value.

• Determining the Number of Clusters for

Complete-link: we rely on the elbow rule

calculated on the percentage of variance un-

explained for k = 2, . . . k

max

. The elbow is

retrieved by performing a two-segment curve ﬁt-

ting task; the value k is the one which minimises

The Growing N-Gram Algorithm: A Novel Approach to String Clustering

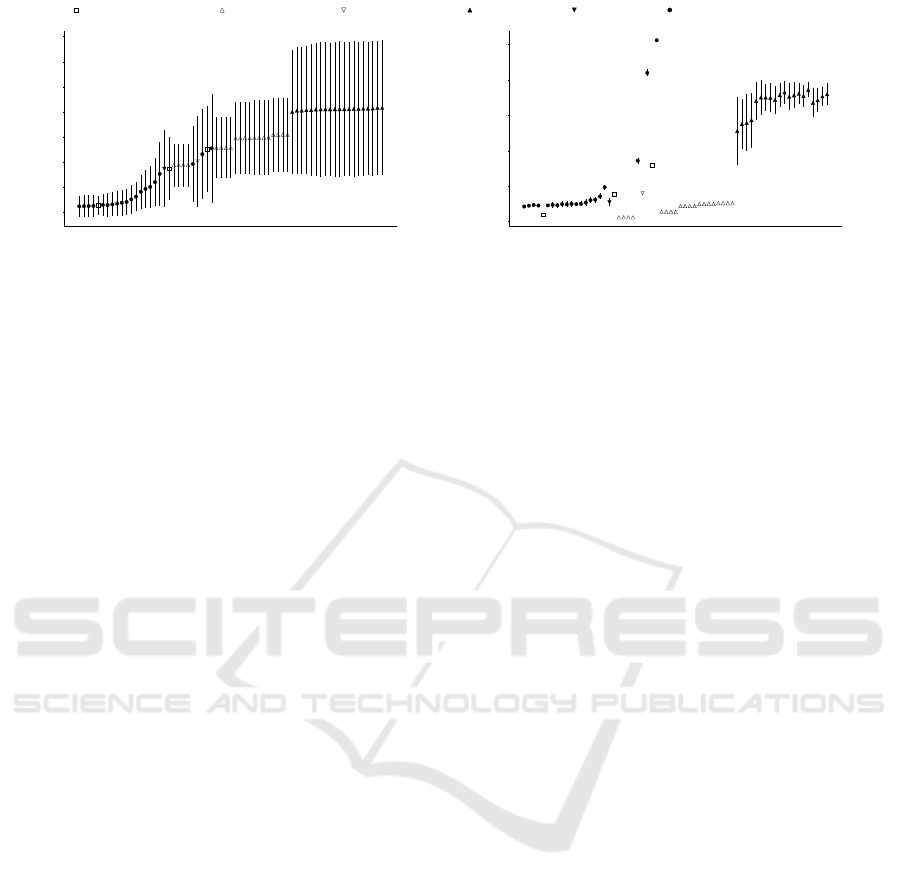
1 5 10 15 20 25 30 35 40 45 50 55 60 65

Algorithm Ran k

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

Entropy

Complete-link with string similarity Comp lete -link with doc2vec Complete-link with tf-idf

(a) Algorithm performance

1 5 10 15 20 25 30 35 40 45 50 55 60 65

Algorithm Ra nked per Entropy

100

150

200

250

Number of Clusters/Models

k-Means with doc2vec k-Means with tf-idf

Growing N-Gram

(b) Number of clusters/models per algorithm

Figure 3: Overview of the clustering algorithms considered in our investigation. Fig. (3a): average and standard deviation

entropy scores per algorithm; Fig. (3b): average number and standard deviation of clusters/models per ranked algorithm.

the mean square error between the percentage

of variance unexplained curve and the ﬁtted

segments.

• N-Gram Modelling: we rely on Kneser-Ney

smoothing (Kneser and Ney, 1995). This is also

implemented for GNG.

We decided to rely on generic forms of k-

means and complete-link in order to have a broad

overview of the performance that these algorithms

could achieve. Similarly, Gensim’s doc2vec was cho-

sen due to its popularity in the neural computing-

based NLP community. A summary of the ap-

proaches and algorithms considered can be observed

in Figure2. Moreover:

• we partition D into train-test-validation sets —

80%, 10% and 10% of D respectively. The sets

are deﬁned a priori and are the same for all algo-

rithms and their repetitions. The train set is used

by all algorithms to perform the clustering task. k-

means relies on the test set to identify the value for

k via silhouette score. The validation set is used

to identify the best algorithm/ensemble in accor-

dance with Equation (4);

• all k-means and GNG instantiations are repeated

30 times. The same is done for complete-link in

combination with doc2vec, whilst for the other

complete-link settings, given their deterministic

characteristics, only one repetition is performed;

• doc2vec is implemented with: train epoch 100,

vector size vs ∈ {2, 4, 6, 8, 10}, window size

ws ∈ {2, 5, 10, 20}, α = 0.025 for a total of

20 possible settings;

• for both k-means and complete-link, k

max

= 200;

• for GNG, we investigated τ

∈ {1, . . . 20},

= − 1, δ

= 1, δ

= 0.5, τ

min

= τ

max

= 1;

• n = 2 for all n-gram models.

In total, therefore, we considered 20 settings for

GNG, 21 settings for k-means (20 for doc2vec), 24

settings for complete-link (20 for doc2vec), resulting

in 65 algorithmic settings.

6 RESULTS AND DISCUSSION

Figure 3a depicts the average and standard deviation

entropy scores of the 65 algorithmic settings. The al-

gorithms are ranked by average entropy score increas-

ing. Once again, the lower the entropy score, the bet-

ter the classiﬁcation task, hence the clustering task.

Furthermore, Figure 3b depicts the average and stan-

dard deviation number of clusters/models returned by

each algorithm ordered in accordance with the rank of

Figure 3a.

17 out of the ﬁrst 18 best ranked algorithms are in-

stances of GNG. The τ

values range from τ

= 20,

which achieves the best average entropy score of

0.1109 (Std. Dev.=0.2077), to τ

= 4 (18

), with

average score 0.7587 (Std. Dev. = 0.6311). Inter-

estingly, τ

= 20 resembles the average plus stan-

dard deviation string length for both train and vali-

dation set (20.46 respectively 19.93), whilst τ

= 4

corresponds to the median string length for both train

and validation set — see Table 2. A Welch’s t-test

with α = 0.01 under the null hypothesis that GNG

with τ

= 20 has the same average performance as

the other algorithms lead to a p-value which make us

reject such hypothesis from the fourth ranked algo-

rithm — i.e. GNG with τ

= 18 onward (the p-value

for such comparison is 0.00001675, t = − 4.3048,

d f = 39718). An example of a mid-to-large model

obtained via GNG with τ

= 20 can be seen in Fig-

ure 5.

Complete-link resulted in the second best per-

forming algorithm. Strikingly, when complete-link is

combined with the Levenshtein distance, its perfor-

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

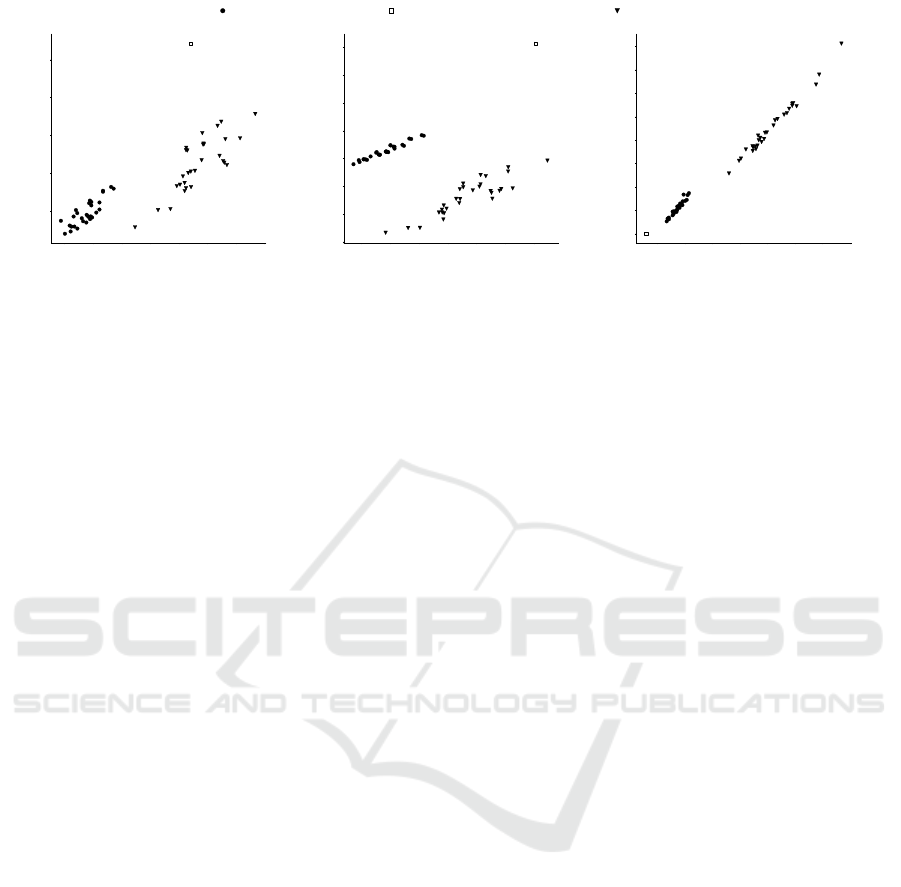
14 16 18 20 22 24 26 28

Node Avg.

Node Std. Dev.

GNG τ

= 20

(a) Number of Nodes

60 70 80 90 100 110 120

Edge Avg.

100

125

150

175

200

225

Edge Std. Dev.

Complete Link with Levenshtein

(b) Number of Edges

3 4 5 6 7 8 9 10

Edge Overlap Avg.

Edge Overlap Std. Dev.

k-Means with tf-idf

Figure 4: Distribution details of n-gram model sizes and overlap for each of the three algorithm’s best performance: Fig.( 4a)

number of nodes, Fig. 4b number of edges, Fig. 4c edge overlap across models over 30 algorithmic iterations.

mance corresponds to the ﬁfth best result, with an av-

erage entropy score of 0.13 (Std. Dev. = 0.1905).

Another remarkable ﬁnding is that complete-link,

when coupled with doc2vec, resulted in average (and

Std. Dev.) entropy scores which were solely de-

pendent on the vector size parameter. In other

words, given e.g. vs = 2, complete-link for all

ws ∈ {2, 5, 10, 20} scored an average entropy of

0.9349 (Std. Dev. = 0.4289). This is observed for all

vs ∈ {2, 4, 6, 18, 10}. The independence on ws for

complete-link given vs is also observed in terms of av-

erage number of clusters retrieved, see Figure 3b. It is

hard to ﬁnd a plausible explanation of such behaviour.

Although one might expect results along these lines

for large ws values given the string length statistics

of our dataset, it is not clear why the same is also

achieved for ws = {2, 5} as well. Further inves-

tigations aimed at shedding light on such results are

encouraged, even beyond the case study considered

here.

Another key-ﬁnding is the poor performance that

k-means achieves when coupled with doc2vec. The

20 settings correspond to the 20 worst ranked perfor-

mances and, unlike what was observed for complete-

link, it is not possible to ﬁnd correlations between vs,

ws and the entropy scores. Moreover, the recorded

standard deviations are the biggest across all algo-

rithms considered. An explanation could be that

doc2vec essentially adopts a bag-of-word vectorisa-

tion approach, hence ignores the order of symbols in

strings, which is in fact a fundamental property of our

data. This is also partly observed by the performance

of both k-means and complete-link combined with

tf-idf (ranked 19

and 26

respectively). Another

possible explanation could be that doc2vec might re-

quire many more training epochs in order to provide

reliable embeddings: the rank of complete-link with

doc2vec is in fact ordered by vs increasing, which also

corresponds to a higher number of neurons in the em-

bedding models, therefore more weights to be trained.

Along these lines, one might argue that doc2vec re-

quires much bigger datasets.

To conclude, by looking at Figure 3b, we can ob-

serve that there is no correlation between the number

of clusters and classiﬁcation performance. This sup-

ports our claim that the average entropy score is a vi-

able measure for the evaluation of clusters of strings

when these can be generalised by probabilistic mod-

els.

We now centre our attention on analysing why

GNG with τ

= 20 has led to the best entropy

scores, as opposed complete-link with Levenshtein

distance and k-means setting with tf-idf, i.e. the two

best alternative benchmark algorithms. The perfor-

mance details can be found in Table 3. Figure 4a

depicts the average and standard deviation of nodes

of the resulting ensembles across each of the 30 it-

erated runs; Figure 4b depicts the same type of in-

formation, albeit about the number of edges compos-

ing the n-gram models, and ﬁnally Figure 4c depicts

the average and standard deviation number of edges

which are shared across models of the same ensem-

ble. Again, n-gram models can be considered as prob-

abilistic graphs, where the nodes corresponds to uni-

grams/unique symbols of the n-gram, and the edges

correspond to the probability of observing a symbol

given a previous one, since in our investigation we

consider n = 2.

By observing Figures 4a and 4b, we can see

that GNG leads to ensembles composed of generally

smaller models than complete-link and k-means, both

in terms of nodes and edges composing them. The

standard deviation values of the nodes is also smaller

than the other two algorithms, and although this is not

seen for edges, the range of GNG’s standard deviation

is much smaller than the other two algorithms. This

The Growing N-Gram Algorithm: A Novel Approach to String Clustering

Table 3: Algorithm Performance - Selected Details.

Rank Algorithm Parameters Avg. Entropy (Std. Dev.) Avg. Num. Clusters (Std. Dev.)

1 GNG τ

= 20 0.1109 (0.2077) 21.3 (2.33)

5 Complete-link Levenshtein 0.13 (0.1905) 10 (0)

19 k-means tf-idf 0.8603 (0.767) 27.3 (5.53)

also means that GNG is more robust against the ran-

domisation of the dataset, which also sets the initial

conditions of the algorithm. The high standard devi-

ation in edge distribution suggests that GNG gener-

ates ensembles where some models have many edges

and some others less. Such behaviour, although much

stronger in magnitude, is also observed for complete-

link, as opposed to the k-means setting.

By looking at Figure 4c, moreover, we can see

how little edge overlap is obtained by complete-link

and GNG, as opposed to k-means, which also sup-

ports our assumption that low model overlap leads to

low entropy scores. Strikingly, complete-link results

in ensembles with a lower edge overlap than GNG,

yet its entropy score is signiﬁcantly worse. A plau-

sible explanation could be that complete-link, being

based on Levenshtein distance, calculates string sim-

ilarities solely based symbols (hence graph nodes), as

opposed to GNG, which instead takes into account

both nodes (for new model creation) and edges (for

model update).

This might make complete-link more focused on

the symbols in strings rather than sequences of sym-

bols, possibly leading to a higher degree of over-

ﬁtting: during validation, complete-link would face

more sequences with out-of-vocabulary symbols than

GNG, hence leading to low probabilities across dif-

ferent models, hence similar chain probability values,

hence higher entropy scores than GNG. GNG with

slightly higher edge overlap, on the other hand, is

able to generate models which leave room for slightly

different sequences, hence more generic ones, which

would lead to lower entropy scores during validation.

7 FUTURE WORK

The results presented in the previous Section suggest

that our GNG algorithm is a viable approach to string

clustering and modelling. However, in order to better

understand how generic and robust our algorithm is,

a vast amount of research is still required. We here

outline what we consider being the most salient topics

of investigation.

First and foremost, GNG should be tested against

different dataset types. An immediate investigation

would correspond clustering full medical procedures

rather then their sub-sequences. GNG should also be

tested in the presence of a smaller/larger vocabulary,

and possibly even towards pure text data, rather than

sequences of symbols.

A thorough investigation on GNG’s hyperparam-

eters is due, as well as considering other settings for

the benchmark algorithms considered. We believe

that understanding the role of τ

and therefore its δ

and τ

max

has higher importance than the studies about

. For instance, during preliminary investigations of

our algorithms, we understood that if τ

is initially

set to 1 and τ

max

> 1, the algorithm tends to grow

a handful of huge models encompassing most of the

strings in D and few others composed of one string

only. That is why we decided, for this investigation,

to begin with τ

= − 1, δ

= 0.5 — i.e. no up-

date actions for the ﬁrst three iterations but just cre-

ations. To some extent, the behaviour we obtained by

GNG would somewhat correspond to ﬁrst spawning

far away centroids, and subsequently scatter new/up-

date existing ones. Should this be the real key strength

of GNG then this could mean that τ

could be auto-

matically toggled (i.e. set to values greater than zero)

once a certain portion of D has been assigned to mod-

els. Moreover, as it was highlighted in Section 6, τ

appears to be related to the string length statistics of

the dataset at hand. Should this be also observed in

the presence of other datasets, then it could be pos-

sible to make GNG hyperparameter-free. Another

way to investigate whether GNG can indeed become

hyperparameter-free is the application of it in super-

vised learning scenarios. By adding constraints on the

returned ensemble size, GNG could autonomously set

its τ

, τ

to perform optimal clustering and modelling.

Finally, further investigations on the effect that the

size of n-grams history has on the performance of

GNG (and other algorithms) is due. Another strategy

would even correspond into making GNG, or even

each model independently, to become able to chose

their own n value.

As explained in Section 1, our ultimate goal is the

creation of a computational framework which helps

identifying “average” usage for system (reliability)

veriﬁcation. The idea is to leverage usage models

to identify (i.e. classify), from a given dataset, logs

depicting normal behaviour, and then to re-execute

them. This requires a high level of self-adaptation

by the algorithm in charge of maintaining the usage

models. We claim that GNG implements a computa-

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

tional approach which is much more prone to self-

adaptation than those relying on pairwise distance

matrices of string vectorisation since, unlike the lat-

ter two, it does not require any form of data pre-

processing. Nevertheless, in order to achieve full

GNG’s self-adaptation, future work could focus on:

(1) understanding whether and how to re-initialise

GNG’s hyperparameters each time new strings are

to be processed; (2) re-design the algorithm to ac-

cept data-streams rather than batches; (3) allowing

the possibility to discard old models which have not

been updated in long time; (4) allowing the possibil-

ity to merge models which perhaps started far away

but after several update actions now manifest an ex-

cessively high degree of overlap; (5) allow the exis-

tence of unassigned strings (i.e. line 25 in the pseudo-

code) rather than coercively assign them to potentially

wrong models. Ultimately, we envision GNG as an

algorithm which, given a (stream) dataset, automat-

ically sets its hyperparameters — even n, or differ-

ent ns for different models — performs its cluster-

ing/modelling computation repeatedly until its inter-

nal entropy converges, is capable of merging/split-

ting/discarding models, and ﬁnally is also capable of

maintaining a genealogy of models, so that it can even

backtrack its decisions and possibly highlight how

system usage evolved through time.

The performance target of our investigation fo-

cussed on minimising average entropy scores, given

a set of algorithms and hyperparameters. While

this gives insights on the computational efﬁciency of

our GNG algorithm, it does not provide insights on

whether the retrieved models are semantically correct.

In order to leverage the model for the identiﬁcation of

“average” system usage, we necessarily need to verify

whether or not the models make sense from the view-

point of domain experts. However, models such as

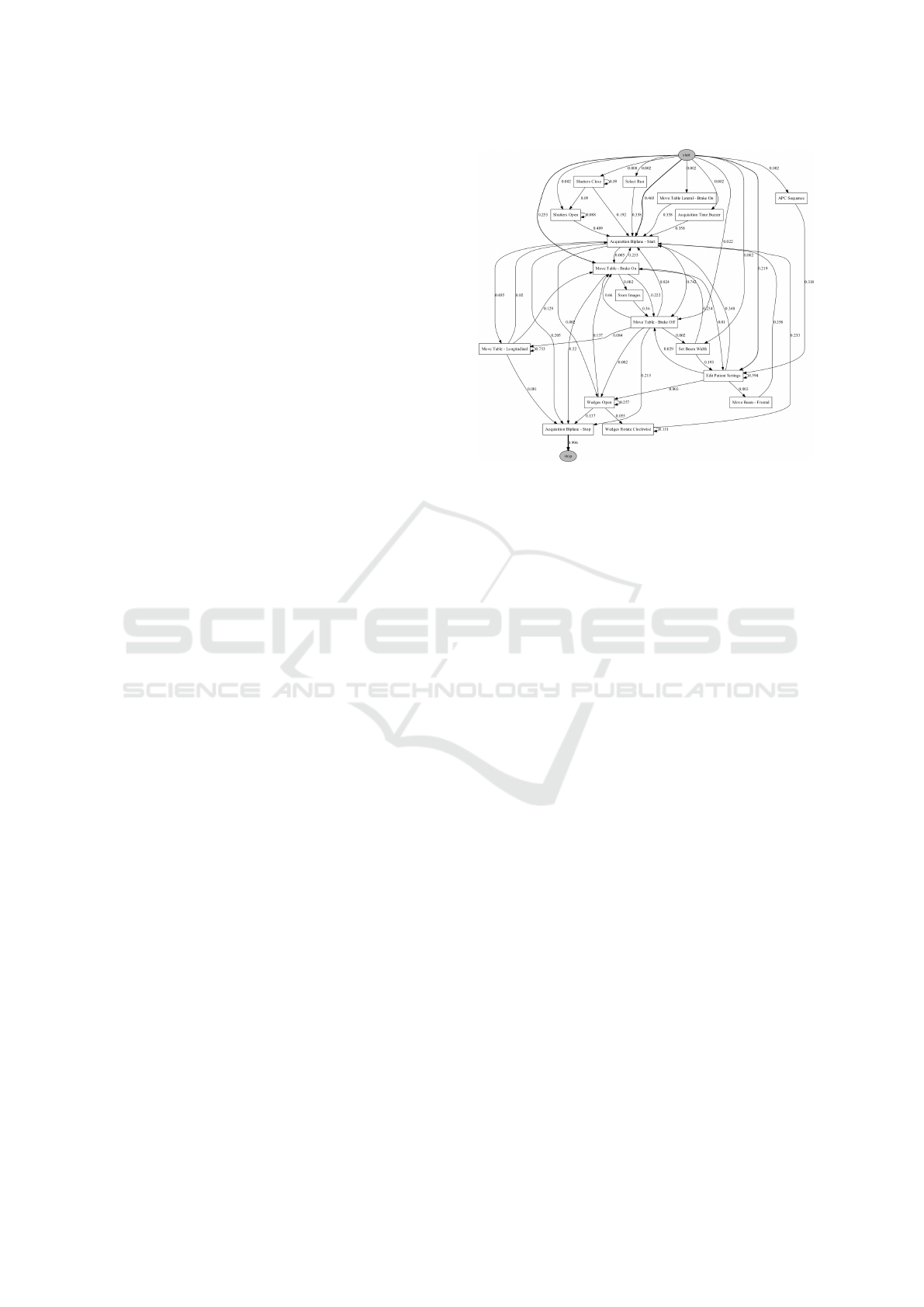
the one shown in Figure 5, let alone bigger ones, are

not easy to grasp by domain experts, as we witnessed

during early stages of our research. An alternative

approach, given the probabilistic nature of our mod-

els, is to traverse them based on such probabilities

and record traces of visited nodes. The traces, which

we would call synthetic bolus chase procedures, could

then be evaluated by domain experts. The trace eval-

uation would semantically validate the goodness of

the usage models, albeit in an indirected and par-

tial way. To pursue this investigation we launched a

crowd-sourced experiment in which experts from dif-

ferent domains (e.g. engineering, clinical, research)

are asked to observe traces — which might either be

synthetic or real ones extracted directly from raw data

— and to judge whether they would occur during clin-

ical practice of Bolus Chase, much like a Turing test

Figure 5: An example of a n-gram model obtained via GNG

with τ

= 20. It is composed of 20 nodes and 56 edges

and represents a cluster of 160 strings, 55 of which unique.

The values along the edges correspond to the conditional

probabilities. The values do not sum up to one because of

Kneser-Ney smoothing.

for artiﬁcial intelligence. The experiment is expected

to run until Spring 2019.

8 CONCLUSIONS

Connected high-tech systems allow the gathering of

operational data at unprecedented volumes. A direct

beneﬁt of this is the possibility to leverage data to

draw usage models, in order to shorten the gap be-

tween how a system is designed to operate and how

it is actually used. Usage models are beneﬁcial for

system reliability veriﬁcation, part of system veriﬁca-

tion testing, in which knowledge of “normal” system

behaviour is required. Our ultimate goal is the design

of a computational framework which helps identify-

ing “average” usage for system veriﬁcation. We in-

terpreted the task of modelling usage behaviours as

string clustering/modelling task. We relied on n-gram

modelling for the representation of usage models —

one n-gram model per retrieved cluster — and con-

sidered three algorithmic approaches to string clus-

tering. The ﬁrst two are based on the most commonly

used k-means and complete-link and rely on either

the transformation of the string data into vectorised

forms, or the use of pairwise string-based similar-

ity measures. We proposed a third approach and its

related algorithm, called Growing N-Grams, which

builds new or updates existing n-gram models based

on string-model similarities and chain probabilities

The Growing N-Gram Algorithm: A Novel Approach to String Clustering

computed given the models, hence by avoiding any

form of data pre-processing. We conducted an em-

pirical evaluation of our approach based on a dataset

representing sub-sequences of the Bolus chase pro-

cedure, a technique in peripheral arteriography, per-

formed on Philips Healthcare’s Image Guided Ther-

apy interventional systems. The gathered results sug-

gest that Growing N-Grams can return cluster com-

positions with lower entropy scores of classiﬁcation,

which indicate the algorithm’s ability to retrieve dif-

ferent usage behaviours.

Growing N-Grams appears to be more prone to

self-adaptation than other algorithms considered in

our study, which also implies it could be better ﬁt for

our ultimate goal. We also highlighted a plethora of

future work which would ultimately lead to the deﬁ-

nition of a fully adaptive algorithm.

ACKNOWLEDGEMENTS

The research is carried out as part of the ITEA3 14035

REFLEXION project under the responsibility of the

Embedded Systems Innovation by TNO (ESI) with

Royal Philips as carrying industrial partner. The RE-

FLEXION research is supported by the Netherlands

Organisation for Applied Scientiﬁc Research TNO

and Netherlands Ministry of Economic Affairs.

REFERENCES

Ackroyd, M. (1980). Isolated word recognition using the

weighted levenshtein distance. IEEE Transactions on

Acoustics, Speech, and Signal Processing, 28(2):243–

244.

Aggarwal, C. C. and Zhai, C. (2012). A survey of text clus-

tering algorithms. In Mining text data, pages 77–128.

Springer.

Anderberg, M. R. (1973). Cluster analysis for applica-

tions. Technical report, Ofﬁce of the Assistant for

Study Support Kirtland AFB N MEX.

Andrews, N. O. and Fox, E. A. (2007). Recent develop-

ments in document clustering.

Balabantaray, R. C., Sarma, C., and Jha, M. (2015). Docu-

ment clustering using k-means and k-medoids. arXiv

preprint arXiv:1502.07938.

Bengio, Y., Ducharme, R., Vincent, P., and Jauvin, C.

(2003). A neural probabilistic language model. Jour-

nal of machine learning research, 3(Feb):1137–1155.

Bishop, C., Bishop, C. M., et al. (1995). Neural networks

for pattern recognition. Oxford university press.

Brown, P. F., Desouza, P. V., Mercer, R. L., Pietra, V.

J. D., and Lai, J. C. (1992). Class-based n-gram mod-

els of natural language. Computational linguistics,

18(4):467–479.

Buchta, C., Kober, M., Feinerer, I., and Hornik, K. (2012).

Spherical k-means clustering. Journal of Statistical

Software, 50(10):1–22.

Bungum, L. and Gamb

ack, B. (2012). Efﬁcient ngram lan-

guage modeling for billion word webcorpora. In Pro-

ceedings of the 8th International Conference on Lan-

guage Resources and Evaluation, pages 6–12.

Chen, S. F. and Goodman, J. (1999). An empirical study of

smoothing techniques for language modeling. Com-

puter Speech & Language, 13(4):359–394.

Cutting, D. R., Karger, D. R., Pedersen, J. O., and Tukey,

J. W. (2017). Scatter/gather: A cluster-based approach

to browsing large document collections. In ACM SI-

GIR Forum, volume 51, pages 148–159. ACM.

da Cruz Nassif, L. F. and Hruschka, E. R. (2013). Docu-

ment clustering for forensic analysis: an approach for

improving computer inspection. IEEE transactions on

information forensics and security, 8(1):46–54.

Dai, A. M., Olah, C., and Le, Q. V. (2015). Document

embedding with paragraph vectors. arXiv preprint

arXiv:1507.07998.

Dhillon, I. S. and Modha, D. S. (2001). Concept decom-

positions for large sparse text data using clustering.

Machine learning, 42(1-2):143–175.

Duda, R. O. and Hart, P. E. (1973). Pattern classiﬁcation

and scene analysis. A Wiley-Interscience Publication,

New York: Wiley, 1973.

Ismail, S. and Rahman, M. S. (2014). Bangla word clus-

tering based on n-gram language model. In Electri-

cal Engineering and Information & Communication

Technology (ICEEICT), 2014 International Confer-

ence on, pages 1–5. IEEE.

Jain, A. K. and Dubes, R. C. (1988). Algorithms for Clus-

tering Data. Prentice-Hall, Inc., Upper Saddle River,

NJ, USA.

Jaro, M. A. (1989). Advances in record-linkage methodol-

ogy as applied to matching the 1985 census of tampa,

ﬂorida. Journal of the American Statistical Associa-

tion, 84(406):414–420.

Jurafsky, D. and Martin, J. H. (2014). Speech and language

processing, volume 3. Pearson London.

selj, V., Peng, F., Cercone, N., and Thomas, C. (2003).

N-gram-based author proﬁles for authorship attribu-

tion. In Proceedings of the conference paciﬁc asso-

ciation for computational linguistics, PACLING, vol-

ume 3, pages 255–264.

Kim, Y. (2014). Convolutional neural networks for sentence

classiﬁcation. arXiv preprint arXiv:1408.5882.

Kiros, R., Zhu, Y., Salakhutdinov, R. R., Zemel, R., Ur-

tasun, R., Torralba, A., and Fidler, S. (2015). Skip-

thought vectors. In Advances in neural information

processing systems, pages 3294–3302.

Kneser, R. and Ney, H. (1995). Improved backing-off for

m-gram language modeling. In icassp, volume 1, page

181e4.

Lau, J. H. and Baldwin, T. (2016). An empirical evalua-

tion of doc2vec with practical insights into document

embedding generation. CoRR, abs/1607.05368.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

Le, Q. and Mikolov, T. (2014). Distributed representations

of sentences and documents. In International Confer-

ence on Machine Learning, pages 1188–1196.

Lesher, G. and Rinkus, G. (2002). Leveraging word pre-

diction to improve character prediction in a scanning

conﬁguration. In Proceedings of the RESNA 2002 An-

nual Conference, pages 90–92.

Lesher, G. W., Moulton, B. J., and Higginbotham, D. J.

(1998). Optimal character arrangements for ambigu-

ous keyboards. IEEE Transactions on Rehabilitation

Engineering, 6(4):415–423.

Levenshtein, V. I. (1966). Binary codes capable of cor-

recting deletions, insertions, and reversals. In Soviet

physics doklady, volume 10, pages 707–710.

Lu, S.-Y. and Fu, K. S. (1978). A sentence-to-sentence

clustering procedure for pattern analysis. IEEE Trans-

actions on Systems, Man, and Cybernetics, 8(5):381–

389.

Mahdavi, M. and Abolhassani, H. (2009). Harmony k-

means algorithm for document clustering. Data Min-

ing and Knowledge Discovery, 18(3):370–391.

Markov, A. (1971). Extension of the limit theorems of prob-

ability theory to a sum of variables connected in a

chain.

Marzal, A. and Vidal, E. (1993). Computation of normal-

ized edit distance and applications. IEEE transac-

tions on pattern analysis and machine intelligence,

15(9):926–932.

Miao, Y., Ke

selj, V., and Milios, E. (2005). Document clus-

tering using character n-grams: a comparative eval-

uation with term-based and word-based clustering.

In Proceedings of the 14th ACM international con-

ference on Information and knowledge management,

pages 357–358. ACM.

Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a).

Efﬁcient estimation of word representations in vector

space. arXiv preprint arXiv:1301.3781.

Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and

Dean, J. (2013b). Distributed representations of words

and phrases and their compositionality. In Advances in

neural information processing systems, pages 3111–

3119.

Pettersson, E., Megyesi, B., and Nivre, J. (2013). Nor-

malisation of historical text using context-sensitive

weighted levenshtein distance and compound split-

ting. In Proceedings of the 19th Nordic Conference of

Computational Linguistics (NODALIDA 2013); May

22-24; 2013; Oslo University; Norway. NEALT Pro-

ceedings Series 16, number 085, pages 163–179.

Link

oping University Electronic Press.

Raghavan, V. V. and Birchard, K. (1979). A clustering strat-

egy based on a formalism of the reproductive process

in natural systems. In ACM SIGIR Forum, volume 14,

pages 10–22. ACM.

Rajalingam, N. and Ranjini, K. (2011). Hierarchical clus-

tering algorithm-a comparative study. International

Journal of Computer Applications, 19(3):42–46.

Rehurek, R. and Sojka, P. (2010). Software framework for

topic modelling with large corpora. In In Proceedings

of the LREC 2010 Workshop on New Challenges for

NLP Frameworks. Citeseer.

Salton, G. (1989). Automatic text processing: The transfor-

mation, analysis, and retrieval of. Reading: Addison-

Wesley.

Siivola, V. and Pellom, B. L. (2005). Growing an n-gram

language model. In Ninth European Conference on

Speech Communication and Technology.

Steinbach, M., Karypis, G., Kumar, V., et al. (2000). A com-

parison of document clustering techniques. In KDD

workshop on text mining, volume 400, pages 525–526.

Boston.

Tai, K. S., Socher, R., and Manning, C. D. (2015). Im-

proved semantic representations from tree-structured

long short-term memory networks. arXiv preprint

arXiv:1503.00075.

Wurzenberger, M., Skopik, F., Landauer, M., Greitbauer, P.,

Fiedler, R., and Kastner, W. (2017). Incremental clus-

tering for semi-supervised anomaly detection applied

on log data. In Proceedings of the 12th International

Conference on Availability, Reliability and Security,

Article, number 31.

Xu, J., Wang, P., Tian, G., Xu, B., Zhao, J., Wang, F., and

Hao, H. (2015). Short text clustering via convolutional

neural networks. In VS@ HLT-NAACL, pages 62–69.

Yujian, L. and Bo, L. (2007). A normalized levenshtein dis-

tance metric. IEEE transactions on pattern analysis

and machine intelligence, 29(6):1091–1095.

Zhang, X., Zhao, J., and LeCun, Y. (2015). Character-

level convolutional networks for text classiﬁcation. In

Advances in neural information processing systems,

pages 649–657.

Zhao, Y., Karypis, G., and Fayyad, U. (2005). Hierarchi-

cal clustering algorithms for document datasets. Data

mining and knowledge discovery, 10(2):141–168.

The Growing N-Gram Algorithm: A Novel Approach to String Clustering