Acceleration of Backpropagation Training

with Selective Momentum Term

Diego Santiago de Meneses Carvalho

and Areolino de Almeida Neto

Department of Computing, IFMA, Sao Luis, Brazil

Department of Informatics, UFMA, Sao Luis, Brazil

Keywords:

Artiﬁcial Neural Networks, Momentum Term, Correlation Coefﬁcient, BP with Selective Momentum.

Abstract:

In many cases it is very hard to get an Artiﬁcial Neural Network (ANN) suitable for learning the solution, i.e., it

cannot acquire the desired knowledge or needs an enormous number of training iterations. In order to improve

the learning of ANN type Multi-Layer Perceptron (MLP), this work describes a new methodology for selecting

weights, which will have the momentum term added to variation calculus of their values during each training

iteration via Backpropagation (BP) algorithm. For that, the Pearson or Spearman correlation coefﬁcients are

used. Even very popular, the usage of BP algorithm has some drawbacks, among them the high convergence

time is highlighted. A well-known technique used to reduce this disadvantage is the momentum term, which

tries to accelerate the ANN learning keeping its stability, but when it is applied in all weights, as commonly

used, with inadequate parameters, the result can be easily a failure in the training or at least an insigniﬁcant

reduction of the ANN training time. The use of the Selective Momentum Term (SMT) can reduce the training

time and, therefore, be also used for improving the training of deep neural networks.

1 INTRODUCTION

For decades studies are performed based on example

of intelligence. These studies, known as Artiﬁcial In-

telligence (AI), yielded some techniques that, within

its limitations, can mimic part of human intelligence.

One of the relevant features of AI techniques is the

capacity of learning, so, the capacity of acquiring new

knowledge and changing the behavior as new knowl-

edge is obtained.

Among these techniques we can mention the Arti-

ﬁcial Neural Networks (ANNs), which have a similar

structure of human neural networks, i.e. many inter-

connections among processing units and these inter-

connections, after a training process, are able to accu-

mulate knowledge and ”learn” a desired behavior.

However, in many cases it is very hard to get an

ANN suitable for learning the solution, i.e., it cannot

acquire the desired knowledge or needs an enormous

number of training iterations.

This study aims to develop an innovation to train-

ing ANNs by introducing the momentum term in the

updating calculus of some weights, in order to accel-

erate the decrease of the mean square error and thus

reducing the learning time. That means, it is intended

to cause ANN type of multilayer perceptron (MLP)

trained with the Backpropagation (BP) algorithm to

reach the mean square error values in fewer iterations

keeping the quality of learning and without signiﬁcant

computational load.

According to (Goodfellow et al., 2016), due to

the ease of training, autoencoders have been used as

building blocks to form a deep neural network, where

each level is associated with an autoencoder that can

be formed separately. The selective momentum term

can be applied to each block formed by MLP.

The next section shows the theoretical basis of the

development of this work, once it describes the learn-

ing of ANN chosen emphasizing the advantages and

disadvantages of BP algorithm. Section 3 shows some

related works. In section 4 the methodology proposed

is presented, as well as the experiments performed

and the results obtained. Concluding the article, the

last section shows relevant conclusions.

2 BACKPROPAGATION

TRAINING

The MLP, a very popular type of ANN, is used for

many different problems. However there are some

Carvalho, D. and Neto, A.

Acceleration of Backpropagation Training with Selective Momentum Term.

DOI: 10.5220/0007272004430450

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 443-450

ISBN: 978-989-758-350-6

443

parameters to be set up by estimate: the amount

of hidden layers, the number of neurons, the acti-

vation function, the usage of bias, initial values of

weights, the learning rate and the usage of momentum

term. The choice of these parameters has no rule and

ANN designer uses some heuristics or even a random

choice currently.

The learning process or training is an iterative pro-

cess of weights modiﬁcation until the output of ANN

is close to the desired value for the given input data.

This process is usually performed by an algorithm,

which has rules for the weights adjustment.

The most used algorithm for training MLP net-

works is called Backpropagation (BP). This algorithm

implements a supervised learning and its main pur-

pose is to minimize the mean square error of the

ANN’s output. The BP algorithm applies the gradi-

ent descent method.

Each BP interaction works in two phases: forward

and backward. In the ﬁrst phase, there is no change

in the value of weights, just the propagation of input

signals towards output layer for the purpose of cal-

culating the error of the network. In the backward

phase, the network output error is used to adjust the

weights. The output error travels backward, layer by

layer, from the output layer until the ﬁrst hidden layer.

The error of each layer is used to adjust the weights

before this layer. The variation of each weight is per-

formed using the following equation:

∆W

i j

= η.e

. f

.out

(1)

In equation 1, ∆W

i j

is the change in the weight be-

tween the neuron i in the output layer and neuron j in

the hidden layer, η is the learning rate, e

corresponds

to the output error of the neuron i; f’

is the derivative

of the neuron i activation function with respect to its

net input, and ﬁnally, out

represents the output value

of neuron j in the hidden layer.

As BP algorithm provides changes in the weights,

a proper initialization of these parameters must be

done, because the success of the training is strongly

dependent on the initial values of the weights. They

are generally set randomly. If these values are not

suitable for the problem at hand, the learning pro-

cess can get stuck in a local minimum and then can

no longer reduce the ANNs output error, except if a

higher learning rate is used or another initialization

is performed, which will not necessarily guarantee a

successful training.

In practice, to get a proper level of output error,

many attempts are executed, because different weight

initializations, learning rates, amount of hidden neu-

rons, ANN topologies (layers with bias or not), activa-

tion functions in neurons and so on must be tried until

one ﬁnds a suitable set up for these items. So, one

problem faced in training via BP concerns the lack

an appropriate methodology for setting some param-

eters and other elements. Among them, the learning

rate is deﬁned by the designer and is extremely im-

portant for ANNs learning, because it determines the

step size of each iteration, which implies to get stuck

in a local minimum or continue searching a suitable

minimum or even the global one of the ANNs output

error. Besides, high value of learning rate accelerates

the learning, but can cause instability in the learning.

As BP algorithm has a simple implementation,

low computational complexity and fast response,

many researchers try to overcome the major drawback

of MLP network, the high convergence time, consid-

ering the sum of time wasted with all attempts un-

til a suitable ANN is found. Therefore this research

presents a technique to surpass this disadvantage.

Some techniques have been developed toward im-

proving the convergence of learning. The momentum

term is one of these techniques, which can accelerate

the networks learning convergence while maintaining

its stability. Equation 2 shows this technique:

∆W

i j

= η.e

. f

.out

+ α.∆W

i j

(n − 1) (2)

In the above equation, ∆W

i j

is the change in the

weight between the neuron i in the output layer and

neuron j in the hidden layer, η is the learning rate, e

corresponds to the output error of the neuron i; f’

the derivative of the neuron i activation function with

respect to its net input, and ﬁnally, out

represents the

output value of neuron j in the hidden layer, α is the

momentum term constant and n is the current iteration

of algorithm execution.

The weights updating becomes a balance between

the current step and the previous calculated ones. This

is implemented by applying a constant α (0 < α ≤

1), called momentum constant, on the last iteration of

change in the weight vector. In this way, the next

change of weight will be roughly in the same direc-

tion of the previous one and, depending on the situ-

ation, this small acceleration can be enough to over-

come any existing local minimum.

3 RELATED WORKS

In (Xiu-Juan and Cheng-Guo, 2009), the authors im-

proved the convergence of BP algorithm increasing

the error signal by increasing the momentum constant

and self-adaptive learning rate. Thus they can avoid

updates toward regions where the error is growing,

ensuring greater accuracy and stability.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

444

In (Shi et al., 2012), the used momentum term var-

ied between 0 and 1. When the ANN output error is

dropping normally, the momentum terms value is 0,

indicating the weights updating will be based on the

normal gradient descent. When a local minimum is

reached, its value is 1, indicating the weights updat-

ing will be based on its last value update.

The work (You and Li, 2014) modiﬁes the tradi-

tional BP in two aspects: insertion of an additional

momentum term and use of self-adaptive learning

rate. The difference between the traditional momen-

tum term and the additional one is the last one does

not consider the gradient only, but also the effects of a

possible updating of weights. The self-adaptive learn-

ing rate is based on the error, as in previous works.

Finally, work (Shao and Zheng, 2009) proposes a

new BP algorithm with a variable momentum coefﬁ-

cient, which is dynamically adjusted based on the er-

rors gradient and on the latest weights update. When

the angle between them is less than 90

◦

, the momen-

tum coefﬁcient is a positive value between 0 and 10

and when the angle is more than 90

◦

, the momentum

coefﬁcient is 0.

4 BP WITH SELECTIVE

MOMENTUM TERM

Due to the difﬁculties in the training process using

original BP, several techniques have been developed

in order to improve the learning. One technique very

interesting is called momentum term, which consists

of adding a term to the calculation of the variation of

the weights, as shown in equation 2. However, the

current research shows the way this technique is cur-

rently applied cannot be the most suitable for some

problems. Based on this information, in this section

a variation on original momentum term is presented,

as well how this variation can be used to accelerate

the training. This proposal uses a correlation coefﬁ-

cient as a rule for selecting which weights should be

updated using the momentum term.

4.1 Correlation

According to (Larson and Farber, 2003), a correlation

is a relationship between two variables, where data

may be represented by ordered pairs (x, y), with x be-

ing the independent variable (or explanatory) and y

the dependent variable (or response).

One way to analyze the correlation between two

variables is through the linear correlation coefﬁcient.

This coefﬁcient is limited in the range [-1, 1], and a

value close to 1 indicates a strong positive correlation

between the variables, a value close to -1 indicates a

strong negative correlation and values close to 0 indi-

cate the absence of a linear relationship between the

variables. Remember that the coefﬁcient does not im-

ply causality.

4.1.1 Pearson Correlation Coefﬁcient

The Pearson correlation coefﬁcient is also called

product-moment correlation coefﬁcient, because it

multiplies the scores (product) of two variables and

after calculates the average (time) of the product of a

group of n observations. Equation 3 summarizes this

process:

r =

∑

xy − (

∑

x)(

∑

− (

∑

− (

∑

(3)

In above equation, r corresponds to the Pearson

coefﬁcient, n is the number of observations, x is the

independent variable and y is the dependent variable.

The Pearson correlation coefﬁcient is a paramet-

ric measure that performs three assumptions: the ﬁrst

one is the relationship between variables is linear; the

second one is the variables should be measured in in-

tervals and the last one is the variables should have

a normal joint bivariate distribution, which means for

each given x, the variable y is normally distributed.

According (Lira, 2004), among the factors that af-

fect the intensity of the correlation coefﬁcient, one

can list the sample size, the outliers, the restriction

on the amplitude of one or both variables and mea-

surement errors.

4.1.2 Spearman Correlation Coefﬁcient

The Spearman correlation coefﬁcient (ρ), or Spear-

man’s rank (intervals deﬁned in the sample database)

correlation coefﬁcient, is a non-parametric correla-

tion measure unlike the Pearson correlation coefﬁ-

cient does, because it does not make any assumptions.

Equation 4 below shows the calculation process.

ρ = 1 −

∑

− n)

(4)

In the above equation, n is the number of pairs (x

) and d

is the difference between the rank of x

and

rank of y

The Spearman correlation coefﬁcient is more ap-

propriate than the Pearson correlation coefﬁcient in

the following cases:

• The data does not form a well-behaved data set,

with some data quite distant from the others;

• There is a nonlinear relationship;

• The amount of samples is small.

Acceleration of Backpropagation Training with Selective Momentum Term

445

In this work, equations 3 and 4 use the value of

each weight as the independent variable (x), the net-

work error value as the dependent variable (y) and the

size of the iteration interval as the number of observa-

tions (n).

4.2 Description of Developed

Methodology

Currently, most designers, who use the momentum

term, concern to choose the appropriate value for α

constant and apply it to correct all weights. However,

(Haykin, 1994) shows that learning must be acceler-

ated in weights that maintains the same algebraic sig-

nal for several consecutive training iterations. On the

other hand, weights, which often change the algebraic

sign for a certain period of consecutive iterations, in-

dicate the global minimum is near, so the acceleration

applied could destabilize the algorithm around that

point.

Based on the paragraph above, this work suggests

a way to identify the weights that should be adjusted

using the momentum term during the training. For

such identiﬁcation the correlation coefﬁcients men-

tioned above are used. The procedure is described

below:

1. A ﬁxed number of iterations (n) for correlation

calculation is deﬁned by the ANNs designer;

2. During ANNs training, after each n steps of itera-

tion, the correlation coefﬁcient (Pearson or Spear-

man) between each weight and the error is calcu-

lated;

3. Correlation coefﬁcients close to 1 or -1 indicate a

strong linear correlation between the weight and

the ANNs error and possibly a path in a steep de-

scent. So, the weights with those correlation coef-

ﬁcient values are selected for the addition of mo-

mentum term with maximum constant (α = 1) for

the next n iterations.

For the ﬁrst n iterations the momentum term is not

applied because there is not sufﬁcient data to calculate

the correlation coefﬁcient.

Note that the Spearman correlation coefﬁcient is

less sensitive to outliers than Pearson coefﬁcient. For

that reason, in this work, the momentum term was ap-

plied to weights whose Spearman coefﬁcient in mag-

nitude is equal to 1 and Pearson coefﬁcient in magni-

tude is greater than 0.95.

5 RESULTS

The following subsections show how the test environ-

ment was assembled and the obtained results.

5.1 Test Environment

The ﬁrst stage of tests compared the traditional BP,

BP with momentum term in all weights and BP with

selective momentum term (momentum term in some

weights). The second step identiﬁes the correlation

coefﬁcient (Pearson or Spearman) which had the best

result. In this step it was also performed a ran-

dom weight selection for adjustment using momentum

term in order to verify if selecting proper weights is

the key for the improvement or not.

In both steps it was deﬁned previously the num-

ber of neurons of the hidden layer, the learning rate,

the value of the mean square error of the network

output and the size of iterations range for correla-

tion coefﬁcients calculation. It is important to men-

tion that for each approach the networks were trained

with the same architecture (MLP with the same ini-

tial values for the weights, only one hidden layer and

the same number of neurons in the hidden layer), the

same computer (i3 core processor, 4Gb of RAM and

Windows 10 operating system) and the same software

(MATLAB, v. R2015a). The results presented are the

number of iterations, the time in seconds and the suc-

cess rate of each approach.

In order to evaluate all approaches, tests were per-

formed with several quantities of neurons in the hid-

den layer, starting with seven units and going up to

105, adding seven neurons each time.

For each number of neurons in the hidden layer,

each step was performed 20 times, each one with dif-

ferent initial values of the weights. So, a total of 300

(20 initializations x 15 settings) different runs were

carried out per stage.

As the focus of this research is to improve the

training of MLP type ANN, an already solved prob-

lem of classiﬁcation was chosen to validate the pro-

posal: breast cancer detection. The Wisconsin Breast

Cancer was used, which is available at the UCI repos-

itory and contains 699 associated events with nine at-

tributes. The ANNs used in this study had to classify

events as benign or malignant processing the nine at-

tributes.

Analizing the data set, one can verify there are

empty values in some attributes of 16 events, there-

fore they were discarded and not used in this research.

From the remaining data, 477 events were used for

training and 205 for generalization tests.

About the ANNs structure, all ANNs had nine

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

446

neurons in the input layer (one neuron for each value

from event), the output layer had just one neuron, rep-

resenting benign or malignant event. The characteris-

tics of the hidden layer have already been deﬁned in

the previous section.

In order to determine the value of the learning

rate and the mean square error used in the tests,

some ANNs were trained using only the traditional

BP. From these tests, the best values for the learn-

ing rate and the mean square error were 0.0001 and

0.0145, respectively. These values indicate a success

rate around 98%, which corresponds to the percent-

age of times that the network could indicate correctly

a benign or malignant event, after training.

Concerning the size of the interval for correlation

coefﬁcient calculation, many tests were performed in

order to deﬁne empirically the adequate amount of it-

erations. For instance, using just 10 iterations, good

results for the training iterations reduction were ob-

tained, but it wasted time as much as the traditional

BP. With 50 iterations, all local minima could not be

avoided and some tests were unsuccessful for the de-

sired knowledge. The amount of 20 iterations showed

more suitable results for all criteria, that means, good

reduction in the number of iterations, not much time

for running and successful knowledge were achieved.

Therefore, the following results were performed using

this size of iterations.

It is worth noting that only ﬁve tests using BP

with momentum term and α = 1 (momentum term con-

stant) reached the desired error, thus those cases were

deleted from the next two tables.

5.2 Results

After the ﬁrst stage, some results were generated,

which are presented in Table 1, showing the average

number of iterations on the 20 trainings.

According to Table 1, using the methodology pro-

posed in this paper, the case with the largest number

of iterations was using seven neurons in the hidden

layer only, i.e. 1,523 iterations for achieving the de-

sired error. On the other hand, Table 1 shows the least

iterations were obtained with 105 neurons in the hid-

den layer, when just 195 iterations was necessary to

reach this error. Also according to the same table,

with 35 neurons in the hidden layer, there was a great

reduction in the number of iterations: from 5,814 us-

ing the traditional BP to just 363 iterations with the

proposed methodology. At the same time, for com-

parison purpose, using BP with momentum term and

α = 0.5, the number of iterations dropped to 2,988.

From the values on Table 1, Figure 1 was gener-

ated, which shows a graph of the percentage of re-

duction in the number of iterations provided by the

proposed method when compared to other methods

tested, for each amount of neurons in the hidden layer.

The graph demonstrates the best performance of BP

with Selective Momentum Term, because when com-

pared to other approaches, in all cases there was a re-

duction in the number of training iterations.

Yet in Figure 1, the average reduction provided

by this research was 92% compared to traditional BP

and 62% compared to BP with momentum term and

α = 0.9. The reduction compared to BP with max-

imum momentum term cannot be calculated, due to

the existence of training that were trapped in a local

minimum and therefore no results were obtained with

that approach. However, one can highlight that the

BP with selective momentum term was able to avoid

all existing local minima, because it was successful in

all training.

Still comparing the criteria of speed, Table 2

shows the average time in seconds of performed train-

ing. In this table, the case of the lowest average time

with the methodology proposed in this paper occurred

when the hidden layer had 14 neurons, in this case

the desired error was reached in just 2.36 s. With the

same number of neurons in the hidden layer, using

the BP with momentum term and α = 0.1, the aver-

age time was 22.79 s. In percentage, one can notice

the proposed method could reduce 79% of the time of

traditional BP and was result slightly better than the

BP with momentum term and α = 0.9.

Table 3 was also produced in the ﬁrst stage. It

shows the results of generalization tests for each ap-

proach, where the average hit rate, calculated over 20

trainings (20 different weight initializations), is pre-

sented. It is noticed that the variation in hit rates is

very small, except for BP with maximum momentum

term, due to the trainings were trapped in a local min-

imum. It is worth mentioning that the results for BP

with Selective Momentum Term of the ﬁrst stage were

achieved using the Pearson correlation coefﬁcient.

After the second stage, Tables 4 and 5 were gener-

ated. All data were obtained taking into consideration

the same characteristics of ANNs used to produce the

tables 1 and 2. But now, the comparison is related

to use of correlation coefﬁcients, not the methods of

training.

According to Table 4, the highest amount of iter-

ations using this proposal occurred when there were

seven neurons in the hidden layer and when the Pear-

son correlation coefﬁcient was used, in this case 4,524

iterations were necessary to achieve the desired error.

The lowest number of iterations was obtained with 98

neurons in the hidden layer using Spearman correla-

tion coefﬁcient, when just 201 iterations were neces-

Acceleration of Backpropagation Training with Selective Momentum Term

447

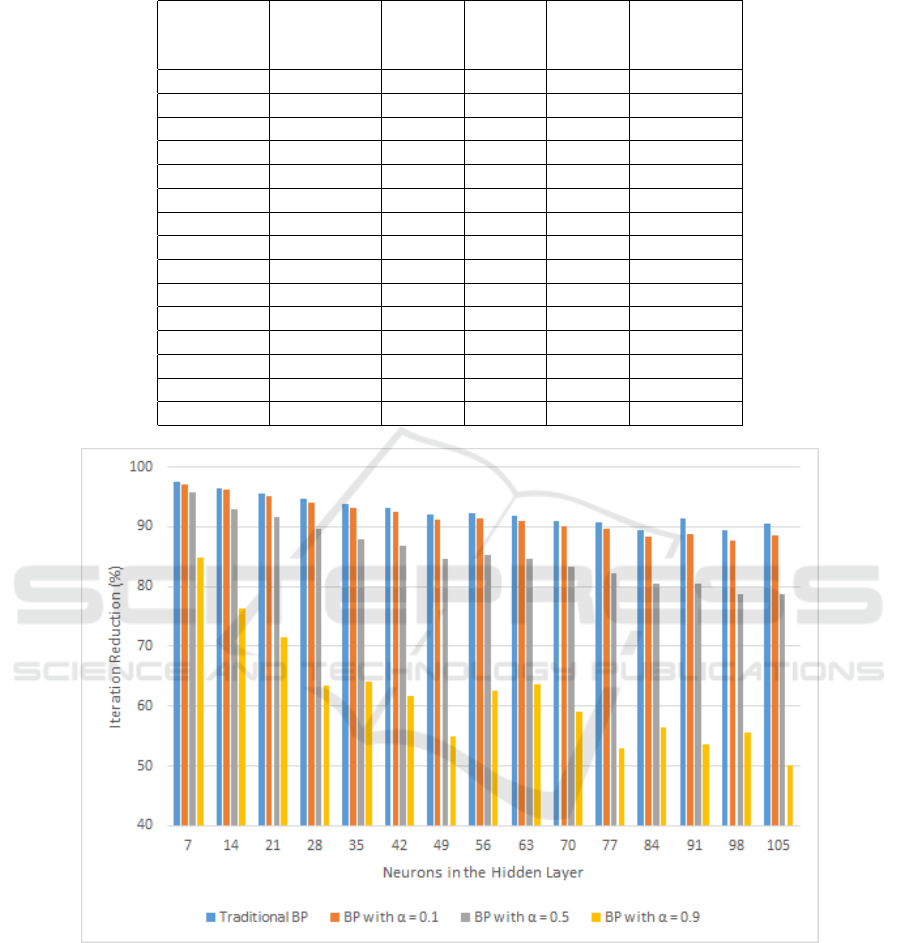
Table 1: Average number of iterations.

Neurons in Traditional BP BP BP BP

the Hidden BP with with with Selective

Layer α = 0.1 α = 0.5 α = 0.9 Momentum

7 60281 51741 36063 10038 1523

14 16944 15241 8365 2468 585

21 10544 9611 5585 1656 473

28 7516 6772 3879 1091 399

35 5814 5229 2988 1013 363

42 4681 4214 2427 836 320

49 3797 3419 1964 670 302

56 3392 3054 1766 697 261

63 3036 2738 1616 686 250

70 2673 2409 1430 587 240

77 2424 2183 1279 480 226

84 2188 1965 1169 527 229

91 2474 1908 1097 465 215

98 2026 1757 1003 483 214

105 2039 1706 918 390 195

Figure 1: Percentage reduction in the number of iterations.

sary to get the same error.

On the average, the best results were for the Spear-

man and Pearson’s correlation coefﬁcient with 408

and 589 iterations, respectively. And as expected, the

use of random selection of weights required a higher

number of iterations than the correlation coefﬁcients,

681 iterations on average.

Table 5 shows the average time for each number

of neurons in the hidden layer. The best results were

obtained with random selection of weights, because

it requires less time for processing the calculation,

followed by Pearson correlation coefﬁcient. On gen-

eralization tests also does not occur big differences

among the coefﬁcients, so the presentation of a new

table can be suppressed. In average, the Pearson cor-

relation coefﬁcient obtained a hit rate of 98.17, the

Spearman correlation coefﬁcient 98.15 and with ran-

dom selection of weights were obtained 98.02.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

448

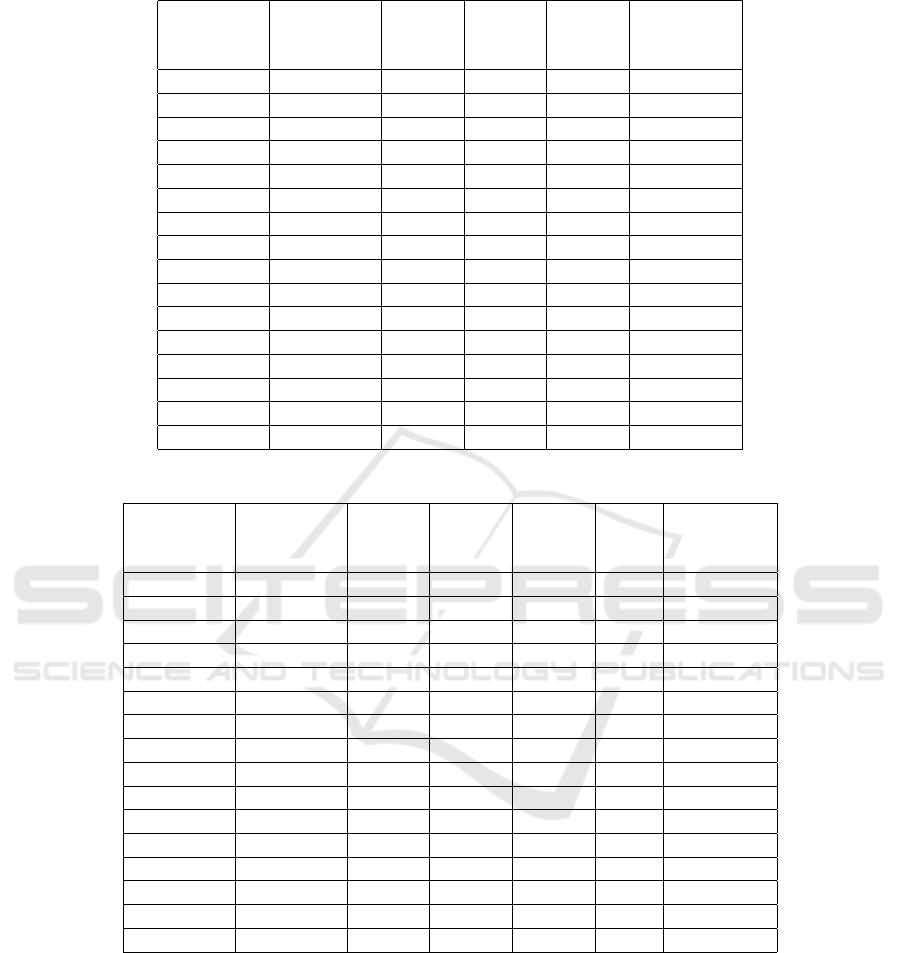
Table 2: Average time.

Neurons in Traditional BP BP BP BP

the Hidden BP with with with Selective

Layer α = 0.1 α = 0.5 α = 0.9 Momentum

7 88.27 83.47 77.93 17.89 6.28

14 21.95 22.79 12.63 3.72 2.36

21 20.73 22.53 12.71 3.79 3.09

28 18.80 20.25 11.47 3.38 3.41

35 16.06 17.24 9.81 3.40 3.63

42 14.94 16.32 9.19 3.22 3.66

49 12.30 13.00 7.66 2.65 3.54

56 12.42 13.68 7.64 3.15 3.48

63 16.78 18.46 10.81 4.65 4.85

70 16.32 17.54 10.35 4.36 5.14

77 15.88 17.19 10.15 3.81 5.32

84 14.83 16.14 9.58 4.44 5.65

91 18.21 16.91 9.72 4.18 5.65

98 13.81 13.42 7.89 3.83 4.83

105 14.41 14.35 7.69 3.27 4.72

Average 21.04 21.55 14.34 4.64 4.36

Table 3: Hit rate.

Neurons in Traditional BP BP BP BP BP

the Hidden BP with with with with Selective

Layer α = 0.1 α = 0.5 α = 0.9 α = 1 Momentum

7 98.04 98.07 98.04 98.41 63.60 97.73

14 98.31 98.29 98.31 98.14 79.12 98.09

21 98.46 98.43 98.41 98.19 84.63 98.24

28 98.36 98.39 98.41 98.39 85.34 98.31

35 98.58 98.58 98.60 98.48 82.63 98.21

42 98.48 98.46 98.46 98.46 87.34 98.26

49 98.46 98.46 98.46 98.41 83.24 98.26

56 98.24 98.24 98.19 98.34 77.26 97.92

63 98.34 98.34 98.34 98.31 83.97 97.97

70 98.43 98.43 98.58 98.51 81.48 98.07

77 98.36 98.36 98.39 98.51 82.85 98.02

84 98.53 98.58 98.43 98.43 85.82 98.21

91 98.46 98.43 98.51 98.43 88.26 98.19

98 98.31 98.36 98.41 98.43 87.56 98.26

105 98.48 98.53 98.53 98.34 81.26 98.02

Average 98.39 98.40 98.40 98.39 82.29 98.12

6 CONCLUSIONS

This paper presented an innovative methodology to

use the momentum term in Backpropagation (BP) al-

gorithm, which was able to accelerate signiﬁcantly

the training and to avoid local minima more effec-

tively. The proposed methodology was called Back-

propagation with Selective Momentum Term.

The new methodology has been subjected to a

load of comparative tests with traditional BP and BP

with momentum term in all weights. In order to per-

form the tests, a well-known classiﬁcation problem

(breast cancer detection) was chosen and has solved.

The test results showed a greater reduction in the

number of iterations in all cases, when compared to

training with traditional BP. The amount of iterations

reduction (50.06% to 97.70%) was obtained consider-

ing the same mean square error that was achieved by

Acceleration of Backpropagation Training with Selective Momentum Term

449

Table 4: Average number of iterations.

Neurons in the Aleatory Pearson Spearman

Hidden Layer

7 4117 4524 1772

14 1156 622 657

21 899 496 490

28 590 407 416

35 521 355 378

42 436 310 303

49 379 292 278

56 340 262 254

63 332 252 245

70 283 238 235

77 256 230 264

84 229 212 214

91 240 213 203

98 212 211 201

105 221 206 205

Average 681 589 408

Table 5: Average time.

Neurons in the Aleatory Pearson Spearman

Hidden Layer

7 3.42 9.58 5.12

14 1.45 2.37 3.49

21 1.47 2.69 3.79

28 1.18 2.81 4.10

35 1.39 3.07 4.84

42 1.22 3.08 4.31

49 1.21 3.32 4.53

56 1.27 3.47 5.00

63 3.19 8.38 11.8

70 2.94 8.59 12.5

77 2.92 8.95 15.31

84 2.88 9.14 13.40

91 3.15 9.67 13.68

98 3.95 12.42 18.53

105 1.42 4.81 6.89

Average 2.20 6.15 8.48

the other approaches.

But fewer iterations do not mean faster, so a com-

parison involving execution time of tested approaches

was performed and many times the proposed method-

ology got the best results, i.e., even with an additional

computational load (correlation coefﬁcients calcula-

tion), the time to process the program was shorter than

one processed by other approaches. In some cases, se-

lecting weights randomly for receiving the momentum

term could be faster, because that procedure is simpler

than correlation calculation.

Besides, even using the maximum value (α =

1) for the momentum term constant, the proposed

methodology was able to avoid the local minima in all

tests, what was not possible for traditional BP and BP

with momentum term in all weights. Based on these

results, one can say that BP with Selective Momen-

tum Term is a very interesting option for the improve-

ment of BP algorithm and therefore use it in other

techniques, like stacked auto-encoded deep learning,

which has many hidden layers, each one can utilize

BP algorithm for the weights connected to them.

ACKNOWLEDGEMENTS

The authors acknowledge FAPEMA, CAPES, UFMA

and IFMA for technical and ﬁnancial support to this

research. Special acknowledgements to PPGCC and

MecaNet.

REFERENCES

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. MIT Press. http://www.deeplearningbook.

org.

Haykin, S. (1994). Neural networks: a comprehensive foun-

dation. Prentice Hall PTR.

Larson, R. and Farber, B. (2003). Elementary statistics.

Prentice Hall.

Lira, S. A. (2004). Correlation analysis: theoretical and

construction approach (in portuguese). curitiba, 2004.

196p. Master’s thesis, Center of Exact Sciences and

Technology, UFPR.

Shao, H. and Zheng, G. (2009). A new bp algorithm with

adaptive momentum for fnns training. In Intelligent

Systems, 2009. GCIS’09. WRI Global Congress on,

volume 4, pages 16–20. IEEE.

Shi, L., Hou, W., Shi, J., and Liu, H. (2012). The intelli-

gent bit design of aviation integrated computer system

based on improved bp neural network. In Prognostics

and System Health Management (PHM), 2012 IEEE

Conference on, pages 1–6. IEEE.

Xiu-Juan, F. and Cheng-Guo, L. (2009). The research in

yarn quality prediction model based on an improved

bp algorithm. In Computer Science and Information

Engineering, 2009 WRI World Congress on, volume 2,

pages 167–172. IEEE.

You, M. and Li, Y. (2014). Automatic classiﬁcation of the

diabetes retina image based on improved bp neural

network. In Control Conference (CCC), 2014 33rd

Chinese, pages 5021–5025. IEEE.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

450