
Scheduling on Dedicated Machines with Energy Consumption Limit
Istv
´
an M
´
odos
1,2
, Kiryl Kalodkin
1,2
, P
ˇ
remysl
ˇ
S
˚
ucha
1
and Zden
ˇ
ek Hanz
´
alek
1
1
Czech Institute of Informatics, Robotics, and Cybernetics, Czech Technical University in Prague, Czech Republic
2
Department of Control Engineering, Czech Technical University in Prague, Czech Republic
Keywords:
Scheduling, Dedicated Machines, Energy Consumption Limits.
Abstract:
This work studies a problem of scheduling non-preemptive independent jobs on dedicated machines while con-
sidering an energy consumption limit. The problem is motivated by energy-demanding production processes,
such as glass tempering and steel hardening, in which a material is heated to high temperature in furnaces. The
production companies have contracts with electric utilities that specify a maximum energy consumption limit.
If the heating in the furnaces is not planned carefully, the energy spikes overshoot the energy consumption
limit, and the companies must pay large penalty fees. In this paper, we propose two exact methods that find
schedules with the minimum makespan such that the energy limit is satisfied. The first proposed method is a
Constraint Programming model and the second one finds the optimal solution by iteratively re-solving a Mixed
Integer Linear Programming model with a decreasing scheduling horizon. The iterative algorithm exploits the
fact that the start times do not need to be modeled explicitly, which leads to an efficient method for solving
instances with a higher number of shorter jobs. The experimental results show that our methods outperform
an adapted approach from the literature for a related problem.
1 INTRODUCTION
The motivation for this work comes from produc-
tion processes in which batches of material are heated
in furnaces to high temperature, e.g., glass temper-
ing and steel hardening. Heating of the material is
energy-demanding and causes spikes in the energy
consumption profile if multiple furnaces are heating
the material at the same time. These consumption
spikes pose a problem since the production companies
have contracts with an electric utility, which specify a
maximum energy consumption limit in every 15 min-
utes metering interval. Failing to comply with the
energy consumption limit leads to substantial penalty
fees which are directly proportional to the consumed
energy over the contracted limit.
Usually, the production companies are schedul-
ing their production either manually or using special-
ized software. However, only classical scheduling
criteria and constraints such as due dates, makespan,
changeover times, etc., are considered. Consequently,
the resulting production schedules may violate the
contracted energy consumption limit. This work pro-
poses two exact scheduling methods for dedicated
machines that take into account these energy limits
alongside traditional scheduling aspects.
1.1 Related Work
A similar problem of satisfying a maximum power de-
mand was studied by (Bruzzone et al., 2012; Fang
et al., 2013). Their models try to comply with the
maximum power demand at every time instant. This
problem can be seen as a special case of our problem
in which the length of the metering interval is 1.
Another related problem to the energy consump-
tion limit is electrical load tracking (Nolde and
Morari, 2010; Ha
¨
ıt and Artigues, 2011; Ha
¨
ıt and
Artigues, 2011; Hadera et al., 2015; Gajic et al.,
2017), where the objective is to minimize the abso-
lute difference between the actual and contracted en-
ergy consumption over all metering intervals. In the
load tracking problem, both over-consumption and
under-consumption of the energy are penalized and
the authors usually consider minimization of the en-
ergy consumption deviation. Thus, the violation of
the contracted energy consumption is a soft constraint
in the electrical load tracking problem.
The energy consumption limits were considered in
the domain of lot sizing (Masmoudi et al., 2017; Rap-
ine et al., 2018). In contrast to scheduling, the goal of
the lot sizing problem is to determine the quantity of
the produced products by the machines in each period
so that the demand is satisfied.
Módos, I., Kalodkin, K., Š˚ucha, P. and Hanzálek, Z.
Scheduling on Dedicated Machines with Energy Consumption Limit.
DOI: 10.5220/0007307200530062
In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 53-62
ISBN: 978-989-758-352-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
53

The most similar problem to ours is the robust
scheduling problem presented in (M
´
odos et al., 2017).
The authors proposed algorithms for designing robust
schedules guaranteeing that the energy consumption
limits are not violated even if some jobs are delayed
due to unexpected circumstances. However, the au-
thors consider only a single machine, thus their prob-
lem is a special case of the parallel machine schedul-
ing problem. Although there is no machine alloca-
tion in the parallel scheduling problem with energy
consumption limits, the schedules on the machines in-
fluence each other through the energy limit, thus the
problem cannot be solved independently on each ma-
chine.
1.2 Contribution
In this paper, we propose two exact methods for the
problem of scheduling non-preemptive independent
jobs on dedicated machines so that the makespan is
minimized. The resulting schedules must also sat-
isfy the energy consumption limit in every metering
interval. The first method is a Constraint Program-
ming (CP) model and the second one is a Mixed In-
teger Linear Programming (MILP) based iterative al-
gorithm which exploits the fact, that the start times
of the jobs do not need to be modeled explicitly. As
shown in the experiments, both of the methods out-
perform an adapted MILP model from (Ha
¨
ıt and Ar-
tigues, 2011; Ha
¨
ıt and Artigues, 2011) w.r.t. the to-
tal number of solved instances to optimality. More-
over, we believe that our novel ideas for modeling the
overlap of the jobs with the metering intervals can
be used to increase the performance of the models
for scheduling with real-time energy prices (Merkert
et al., 2015; Zhao et al., 2018), where the cost of en-
ergy may change every hour.
2 PROBLEM STATEMENT
Let J = {J
1
, J
2
, . . . , J
n
} be a set of jobs and let
M = {M
1
, M
2
, . . . , M
m
} be a set of machines. For
each job J
j
∈ J we define its processing time p
j
∈ N
>0
and dedicated machine µ
j
∈ M , on which the job has
to be processed without preemption. The set of jobs
that have to be processed on machine M
k
is denoted as
J
k
. Moreover, for each job J
j
we also define its power
consumption P
j
∈ R
>0
that represents the power con-
sumption of machine µ
j
when processing job J
j
, i.e.,
it is the constant rate at which the energy is consumed
at every time instant. Therefore, the total consumed
energy by each job J
j
is p
j
· P
j
.
Let s
j
∈ N
≥0
denotes a start time of job J
j
∈ J .
The jobs have to be scheduled within scheduling hori-
zon H ∈ N
>0
, i.e., the jobs must complete at most at
time H. The scheduling horizon is divided into a set
of metering intervals I = {I
1
, I
2
, . . . , I
H
D
} with equal
length of D ∈ N
>0
(it is assumed that H is a multiple
of D). For all metering intervals, we define the same
energy limit E
max
representing the upper bound on the
total energy consumption of the jobs in each metering
interval
1
. We say that vector of start times s = (s
j
)
J
j
∈J
does not violate the energy limit in metering interval
I
i
if and only if
∑
J
j
∈J
Overlap( j, s
j
, i) · P
j
≤ E
max
, (1)
where Overlap( j, s
j
, i) represents the overlap length
of job J
j
with metering interval I
i
if starting at time
s
j
. Start times s are feasible if the jobs on each ma-
chine are not overlapping and the energy limit is not
violated in any metering interval. An example of a
feasible schedule of 30 jobs on four machines can be
seen in Fig. 1.
The goal of our scheduling problem is to find
feasible start times such that makespan C
max
, i.e.,
the maximum completion time of all jobs, is mini-
mized. We denote this problem in Graham’s notation
as m|E
max
|C
max
.
The problem m|E
max
|C
max
is N P -hard since we
can reduce 3-partition problem to the decision vari-
ant 1|p
j
= 1, E
max
|− of our scheduling problem. In
the 3-partition problem, we are given bound B and
multiset A = {a
1
, a
2
, . . . , a
3·q
} of integers such that
B
4
< a
j
<
B
2
and
∑
a
j
∈A
a
j
= q · B. In this problem we
ask the question whether there exist sets A
1
, . . . , A
q
such that (i) ∪
q
i=1
A
i
= A, (ii) A
i
1
∩A
i
2
=
/
0 for all i
1
6= i
2
and (iii)
∑
a
j
∈A
i
a
j
= B for all i. The reduction maps
each integer a
j
to a unit length job with power con-
sumption P
j
= a
j
. The energy limit is set to B, length
of each metering intervals to 3 and the number of me-
tering intervals is q.
3 SOLUTION APPROACHES
In this section, we propose two exact approaches to
the problem stated in Section 2: (i) a CP model (see
Section 3.1) and (ii) a MILP-based iterative algorithm
(see Section 3.2), which exploits the fact that the start
1
Usually, the energy consumption limit is contracted for
a longer time period such as a month. Therefore, the energy
limit is constant within the scheduling horizon. However,
our solution methods can be easily generalized to the case
where the energy limit varies, but due to the above men-
tioned reason and simplicity of the methods we consider
only one energy limit.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
54
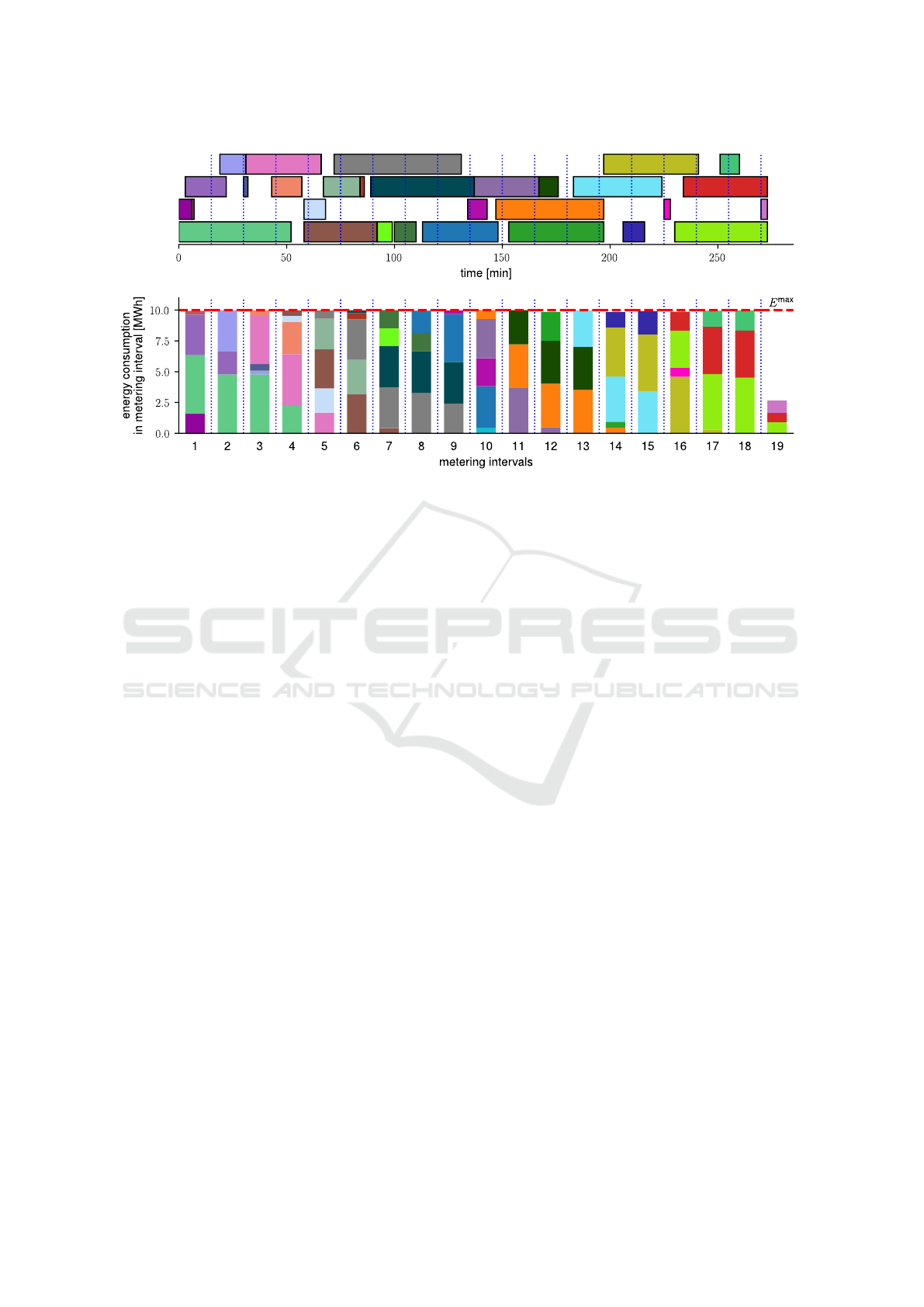
Figure 1: An example of a feasible schedule of 30 jobs on four machines. The figure below the schedule illustrates the energy
consumption of the jobs in each 15 minutes metering interval, i.e., the height of each colored box equals Overlap( j, s
j
, i) · P
j
.
The same color in both figures represents the same job. The energy consumption limit is denoted by the dashed horizontal red
line.
times of the jobs do not need to be modeled explicitly
(the start times from the model are obtained using an
algorithm described in Section 3.2.2).
3.1 CP Model
The first proposed solution approach is a CP model
which will be described using IBM CP Optimizer for-
malism (Laborie et al., 2018). CP uses a notion of
interval variables representing a time interval, whose
start time, completion time and length has to be de-
cided by a solver. Our model has one interval vari-
able x
j
for each job J
j
∈ J that denotes the time in-
terval in which the job is scheduled. The idea be-
hind the model is to use CP function Overlap, which
computes the length of the overlap between a job’s
interval variable and a metering interval given by its
start and end. The overlaps in a metering interval are
multiplied by the corresponding power consumption,
added together and constrained to be at most E
max
.
Note that the cumulative functions cannot be used
for modeling the energy consumption since the height
of an elementary cumulative function is a constant
whereas our problem would require the height to be
a function of the overlap length with a metering inter-
val.
The complete model follows
min max
J
j
∈J
EndOf(x
j
) (2)
EndOf(x
j
) ≤ H, ∀J
j
∈ J (3)
LengthOf(x
j
) = p
j
, ∀J
j
∈ J (4)
NoOverlap({x
j
: J
j
∈ J
k
}), ∀M
k
∈ M (5)
∑
J
j
∈J
Overlap(x
j
, (i − 1) · D, i · D) · P
j
≤ E
max
,
∀I
i
∈ I
(6)
The objective (2) minimizes the maximum com-
pletion time of all the jobs. Constraint (3) guaran-
tees that the completion time of every job is bounded
by the scheduling horizon H. The following con-
straint (4) sets the length of an interval variable x
j
corresponding to some job J
j
to be p
j
. Global con-
straint NoOverlap in (5) ensures that the jobs on each
dedicated machine are not overlapping. Finally, the
energy limit in every metering interval is enforced by
constraint (6).
3.2 MILP-based Iterative Algorithm
In this section, we present a MILP formulation that
does not explicitly model the start times of the jobs;
we call it an implicit model. However, the implicit
model can optimize the makespan only in the last me-
tering interval of the scheduling horizon, thus it may
found suboptimal solutions to the scheduling prob-
lem presented in Section 2. This issue is mitigated by
Scheduling on Dedicated Machines with Energy Consumption Limit
55

wrapping the implicit model in a loop that iteratively
tightens the scheduling horizon until an optimal solu-
tion to the original problem is found.
First, we introduce the implicit MILP model, see
Section 3.2.1. The following Section 3.2.2 shows how
the start times could be reconstructed from a feasible
solution to the implicit MILP model. The last Sec-
tion 3.2.3 wraps the implicit MILP model into an it-
erative algorithm.
3.2.1 Implicit MILP Model
As noted above, the implicit model is solved itera-
tively with a decreasing horizon. Let us denote by
I
i
max
the last metering interval, which is considered
in the model. To avoid notational clutter, the set of
metering intervals in this subsection is redefined to
I = {I
1
, I
2
, . . . , I
i
max
}.
Similarly as the CP model, an overlap of the jobs
with metering intervals needs to be formulated. How-
ever, MILP does not contain any constructs such as
Overlap, thus we must model the overlap using linear
expressions ourselves. We observed that for “shorter”
jobs the overlap constraints can be modeled much
simpler than for “longer” jobs, thus we split the set
of jobs into non-spannable and spannable jobs, i.e.,
the set of spannable jobs is
J
span
= {J
j
∈ J : p
j
≥ D + 1}, (7)
while the set of non-spannable jobs is J \ J
span
.
For modeling purposes, we also need to determine
the maximum number of consecutive metering inter-
vals in which job J
j
can have non-zero overlap for any
feasible start times s; this number will be denoted as
Ω
j
.
Observation 1. The maximum number of consecu-
tive metering intervals that can have non-zero overlap
with job J
j
for any feasible start times s is
Ω
j
=
l
p
j
D
m
+ 1. (8)
Proof. See Appendix 5.1.
The implicit MILP model uses the following vari-
ables: (i) d
j,i
∈ N
≥0
denoting the length of the
overlap between job J
j
and metering interval I
i
, (ii)
x
s
j,i
∈ {0, 1} indicating whether spannable job J
j
starts
in metering interval I
i
, (iii) x
+
j,i
∈ {0, 1} expressing
whether job J
j
has non-zero overlap in metering in-
terval I
i
, and (iv) Z ∈ N
≥0
representing the objective
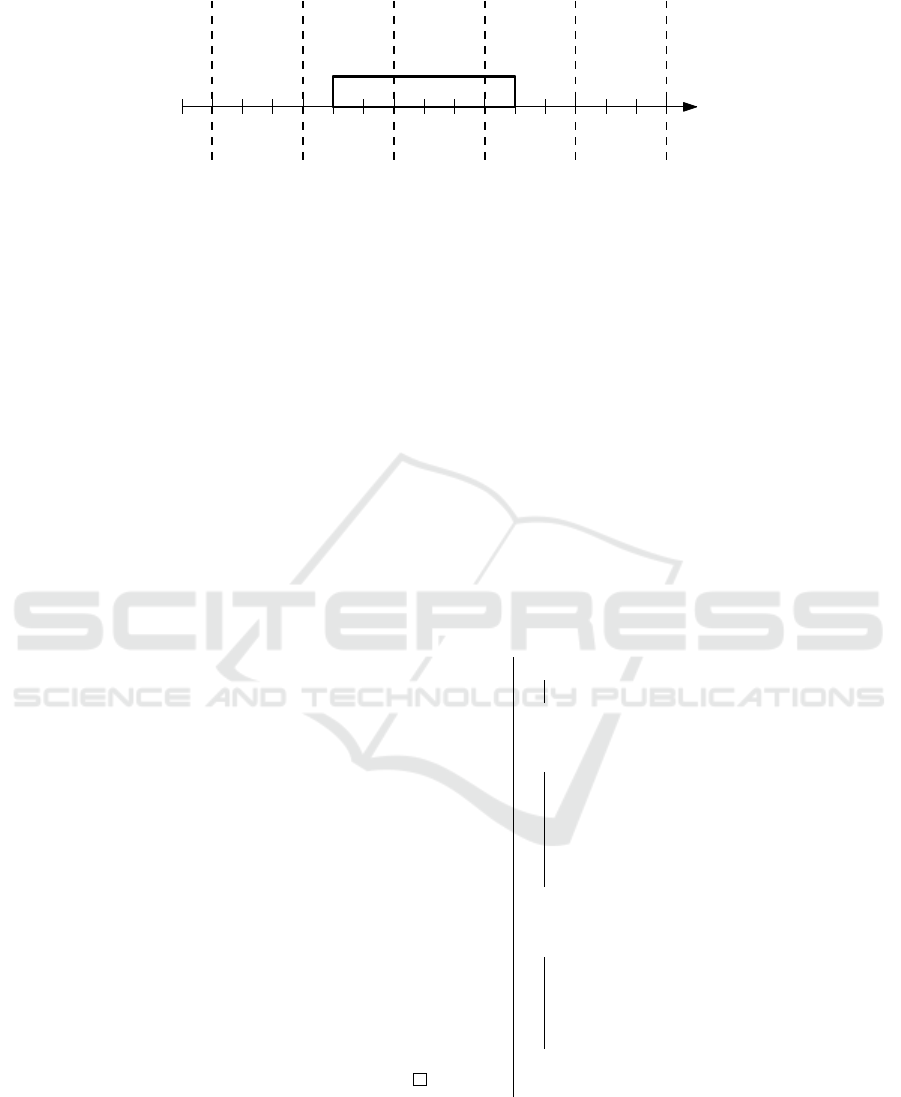
value. Fig. 2 shows an example illustrating the vari-
ables used in the implicit MILP model.
The complete model follows
min Z (9)
Z ≥
∑
J
j
∈J
k
d
j,i
max
, ∀M
k
∈ M (10)
∑
J
j
∈J
k
d
j,i
≤ D, ∀I
i
∈ I , ∀M
k
∈ M (11)
∑
J
j
∈J
d
j,i
· P
j
≤ E
max
, ∀I
i
∈ I (12)
∑
I
i
∈I
d
j,i
= p
j
, ∀J
j
∈ J (13)
SOS
2
(d
j,1
, . . . , d
j,i
max
), ∀J
j
∈ J \ J
span
(14)
∑
I
i
∈I
x
s
j,i
= 1, ∀J
j
∈ J
span
(15)
d
j,i
≤ D ·
i
∑
i
0
=max(1,i−Ω
j
+1)
x
s
j,i
0
, ∀J
j
∈ J
span
, ∀I
i
∈ I
(16)
D · (x
+
j,i−1
+ x
+
j,i+1
− 1) ≤ d
j,i
,
∀J
j
∈ J
span
, ∀I
i
∈ I \ {I
1
, I
i
max
}
(17)
d
j,i
≤ min(D, p
j
) · x
+
j,i
, ∀J
j
∈ J , ∀I
i
∈ I (18)
x
+
j
1
,i
+ x
+
j
1
,i+1
+ x
+
j
2
,i
+ x
+
j
2
,i+1
≤ 3,
∀M
k
∈ M , ∀I
i
∈ I \ {I
i
max
},
∀J
j
1
, J
j
2
∈ J
k
: J
j
1
6= J
j
2
, p
j
1
≥ 2, p
j
2
≥ 2,
p
j
1
+ p
j
2
≤ 2 · D
(19)
In the following paragraphs, the model will be ex-
plained in detail.
The objective of the model is to minimize the
maximum total overlap in I
i
max
over all machines,
see Eq. (10). A simple observation is that no idle
time between two consecutive jobs on the same ma-
chine is necessary in I
i
max
, since the subsequent job
is fully contained in I
i
max
and shifting it to the com-
pletion time of the preceding job has no effect on the
consumed energy in I
i
max
. Therefore, minimization of
the maximum total overlap in I
i
max
also minimizes the
makespan in I
i
max
.
The following constraint (11) ensures, that the to-
tal overlap in every metering interval is at most the
length of the metering intervals. Constraint (12) mod-
els the energy limit and constraint (13) restricts the
sum of the overlaps of one job to be its processing
time.
Next, the continuity of the jobs over metering in-
tervals is modeled, i.e., only adjacent metering inter-
vals can have non-zero overlap with a job. The non-
preemption of the jobs is then ensured by the start
times reconstruction procedure, see Section 3.2.2. As
noted before, for non-spannable jobs this constraint
can be modeled easier than for the spannable jobs,
thus the explanation is split into two parts. We start
by handling the non-spannable jobs first.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
56
I
i
I
i−1
I
i+1
J
j
I
i−2
I
i+2
time
x
+
j;i−2
= 0
x
s
j;i−2
= 0
d
j;i−2
= 0
x
+
j;i−1
= 1
x
s
j;i−1
= 1
d
j;i−1
= 2
x
+
j;i
= 1
x
s
j;i
= 0
d
j;i
= 3
x
+
j;i+1
= 1
x
s
j;i+1
= 0
d
j;i+1
= 1
x
+
j;i+2
= 0
x
s
j;i+2
= 0
d
j;i+2
= 0
Figure 2: An example illustrating the values of variables for job J
j
that are used in the implicit MILP model. The length of
the metering intervals is 3.
Due to Observation 1, the non-spannable jobs can
overlap at most two consecutive metering intervals.
This can be exploited by modeling the continuity of
the jobs using special-ordered set (Gurobi, 2018) con-
straint of type 2 (SOS
2
). SOS
2
receives a list of or-
dered variables (can be continuous, binary or integer)
and the constraint ensures that at most two consec-
utive variables in this list can have non-zero value.
The continuity of every non-spannable job is then
achieved by passing the ordered list of overlap vari-
ables to SOS
2
constraint, see constraint (14).
The spannable jobs may overlap more than two
consecutive intervals, thus SOS
2
constraint cannot
be used. The continuity is modeled using four con-
straints (15)-(18). The first constraint (15) requires
that the job starts in some metering interval. The sec-
ond constraint (16) ensures that at most Ω
j
consecu-
tive intervals have non-zero overlap with job J
j
. The
third constraint (17) enforces that if job J
j
has non-
zero overlap with metering intervals I
i−1
, I
i+1
, then
the job spans the whole metering interval I
i
. The last
constraint (18) pushes variable x
+
j,i
to be 1 if job J
j
has
non-zero overlap with metering interval I
i
.
Finally, the last constraint (19) of the model en-
sures that two jobs J
j
1
, J
j
2
on the same machine are
not overlapping on a boundary of two consecutive
metering intervals. Notice that due to the following
lemma this constraint has to be included only for a
pair of jobs with p
j
1
+ p
j
2
≤ 2 · D.
Lemma 1. Let J
j
1
, J
j
2
∈ J be two jobs such
that j
1
6= j
2
, µ
j
1
= µ
j
2
, p
j
1
≥ 2, p
j
2
≥ 2 and
p
j
1
+ p
j
2
≥ 2 · D + 1. Let d = (d
j,i
)
J
j
∈J ,I
i
∈I
be
values for some feasible solution to the MILP model
from Section 3.2. Then Eq. (19) holds for J
j
1
, J
j
2
in
any metering interval I
i
∈ I \ {I
i
max
}.
Proof. See Appendix 5.1.
3.2.2 Reconstruction of the Start Times
As was noted above, the model does not include vari-
ables that represent the start times explicitly. How-
ever, a simple algorithm exists that reconstructs start
times s from the values of feasible overlap variables d.
The full pseudocode of the reconstruction algorithm is
listed in Algorithm 1.
The algorithm first assigns the start times to the
jobs that lies on a boundary of at least two metering
intervals. For these jobs, the start time is unambigu-
ous since it equals i
s
· D − d
j,i
s
, where I
i
s
is the first
metering interval in which the job has non-zero over-
lap.
Afterwards, the start times of the rest of the jobs,
i.e., having non-zero overlap in only one metering in-
terval, are assigned. Since the order of such jobs in
a particular metering interval is not important, their
start times are assigned in arbitrary order. The jobs are
assigned at the earliest start time in the corresponding
metering interval. After each assignment, the earliest
start time is increased by the processing time of the
assigned job.
Function ReconstructStartTimes(d):
foreach I
i
∈ I do
earliestStartTimes[i] ← (i −1) · D
end
foreach {J
j
∈ J : |{I
i
∈ I : d
j,i
> 0}| ≥ 2}
do
i
s
← argmin
i=1,...,i
max
d
j,i
> 0
i
c
← argmax
i=1,...,i
max
d
j,i
> 0
s
j
← i
s
· D − d
j,i
s
earliestStartTimes[i
c
] ←
earliestStartTimes[i
c
] + d
j,i
c
end
foreach {J
j
∈ J : |{I
i
∈ I : d
j,i
> 0}| = 1}
do
I
i
s
← I
i
∈ I : d
j,i
> 0
s
j
← earliestStartTimes[i
s
]
earliestStartTimes[i
s
] ←
earliestStartTimes[i
s
] + p
j
end
return s
Algorithm 1: Reconstruction of start times s from overlap
variables d.
3.2.3 Iterative Algorithm
Since the implicit MILP model only optimizes the
makespan in I
i
max
, the optimal solution found by the
Scheduling on Dedicated Machines with Energy Consumption Limit
57

implicit model might be suboptimal for the original
problem stated in Section 2. The idea of the itera-
tive algorithm is to progressively decrease i
max
and
re-solve the implicit model until an optimal solution
to the original problem is found. The full pseudocode
of the iterative algorithm is listed in Algorithm 2.
The algorithm starts by checking the feasibil-
ity of the given problem instance by trying to find
any feasible solution within the whole scheduling
horizon H. If the instance is infeasible, function
SolveImplicitMILP returns an empty set instead of
a vector of start times. If the solution is feasible, the
algorithm starts iterating until the optimal solution is
found.
To determine the optimality of a feasible solution,
the algorithm tests its objective value Z. A non-zero
objective value means that the found solution is opti-
mal to the original problem since makespan is greater
than (i
max
− 1) · D. On the other hand, if the objec-
tive is zero, a shorter solution ending in the previ-
ous metering interval might exist to the original prob-
lem. Therefore, i
max
is decreased by one, the implicit
model is re-solved with the smaller horizon, and the
tests on the objective value are repeated.
Notice that in every iteration the previously found
start times are passed to SolveImplicitMILP, which
are used as an initial solution (by transformation to
the overlap variables) to reduce the running time of
the implicit model.
Function IterativeImplicitMILP():
i
max
←
H
D
s, Z ← SolveImplicitMILP(i
max
,
/
0)
if s =
/
0 then
/* The original problem is
infeasible. */
return
/
0
end
while Z = 0 do
i
max
← i
max
− 1
s, Z ← SolveImplicitMILP(i
max
, s)
end
/* Found optimal solution to the
original problem. */
return s
Algorithm 2: MILP-based iterative algorithm.
4 EXPERIMENTS
In the experiments, we compare the presented ap-
proaches from Section 3 w.r.t. finding the optimal so-
lutions to a given set of generated instances and prov-
ing their optimality. Although in practice it is often
necessary to find high-quality solutions in short time,
proving that a solution is also optimal is valuable in-
formation. The aim of the experiments is to deter-
mine, how two different parameters affect the solv-
ing time: (i) number of spannable jobs in an instance
and (ii) the energy limit tightness w.r.t. the power con-
sumption of the jobs. In addition to the proposed ex-
periments we also compare the solution approaches
w.r.t. the quality of the found solutions (which can be
sub-optimal).
For the comparison with the existing literature, we
include in the experiments a MILP model that was
adapted from a similar problem (Ha
¨
ıt and Artigues,
2011). The model is described in Appendix 5.2, and
we will refer to this model as Disjunctive MILP.
All experiments were executed on 2x Intel(R)
Xeon(R) Silver 4110 CPU @ 2.10GHz with 188GB
of RAM (16 cores in total). For solving the MILP
and CP models, we used Gurobi 8 and IBM CP Opti-
mizer 12.8, respectively. The multi-threading settings
for each solver was set to default, i.e., the solvers can
use all the available cores for computation.
The source codes of the methods
and the generated instances are publicly
available at https://github.com/CTU-IIG/
EnergyLimitsScheduling and https://github.com/
CTU-IIG/EnergyLimitsSchedulingDatasets, respec-
tively.
4.1 Instances
The instances for the experiments were generated as
follows. The energy limit and the length of the me-
tering intervals were fixed to 1000 and 15, respec-
tively. To explore how the solving time is affected
by the number of spannable jobs in an instance, we
use parameter α
α =
|J
span
|
|J |
. (20)
The processing time of each spannable job is sam-
pled from discrete uniform distribution U{D +1, 60}
while the processing time of the non-spannable jobs is
sampled from discrete uniform distribution U{1, D}.
Another evaluated parameter in the experiments is
β that controls the tightness of the energy limit. Given
fixed β, the power consumption of each job is then
sampled from continuous uniform distribution
U
β ·
E
max
m · D
, 2 ·
E
max
m · D
. (21)
To ensure that no job can violate the energy limit
by itself, the power consumption is clamped, i.e., if
min(D, p
j
)·P
j
> E
max
for some job J
j
, its power con-
sumption is modified to
E
max
min(D,p
j
)
.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
58
To distribute the jobs between the machines, each
job is assigned to a random machine with uniform dis-
tribution. Finally, the length of the scheduling horizon
is set to the sum of all jobs’ processing times in an
instance. The analysis of the results shows that this
horizon is large enough to guarantee the existence of
a feasible solution.
For each n ∈ {10, 20, 30}, m ∈ {2, 4},
α ∈ {0.1, 0.25, 0.5, 0.75, 0.9} and
β ∈ {0.8, 1.0, 1.2, 1.4, 1.6} we randomly gener-
ated 10 instances using the scheme described above.
Therefore, the generated dataset has 1500 instances
in total.
4.2 Results
The results section is divided into two parts. The first
part analyzes the ability of the proposed approaches to
prove the solutions’ optimality based on the examined
parameters n, m, α, β. The second part compares the
solution approaches w.r.t. the quality of the found so-
lutions. In the subsequent text, the following abbrevi-
ations of the solution approaches are used: (i) CP: CP
model (see Section 3.1), (ii) MILP-IMP: MILP-based
iterative algorithm (see Section 3.2) and (iii) MILP-
DIS: Disjunctive MILP model (see Appendix 5.2).
4.2.1 Finding Optimal Solutions and Proving
Their Optimality
The results are shown in Tables 1 to 3; each of the
tables provides a different view of the same results.
Each row of the table shows the number of optimally
solved instances by each approach. For example,
in Table 2 the row denoted as α = 0.25 shows the re-
sults for instances with n ∈ {10, 20, 30}, m ∈ {2, 4},
α = 0.25 and β ∈ {0.8, 1.0, 1.2, 1.4, 1.6}. To highlight
the best method in each row, the best values are shown
in bold. The time-limit given to each method for each
instance was 300s.
Table 1 shows, how the methods scale with the
increasing size of the instances. Except of the small-
est instances with n = 10, m = 2, MILP-IMP model
either outperforms or is at least as good as the other
approaches. For example, 53.2% of the instances with
n = 30, m = 4 were solved optimally by MILP-IMP,
whereas the CP approach solved 34.4% and MILP-
DIS only 14.4% of the instances.
The next Table 2 compares the approaches ac-
cording to the increasing spannable ratio α. We see
that the performance of the implicit MILP model de-
creases with increasing α. The implicit MILP model
outperforms the CP approach when the number of
shorter jobs is higher or the same; on the other hand,
CP is better for the higher spannable ratio. With
Table 1: Number of proved optimal solutions out of 250
with varying n,m.
n m CP MILP-IMP MILP-DIS
10 2 247 207 234
10 4 250 250 250
20 2 14 46 16
20 4 127 177 144
30 2 3 11 0
30 4 86 133 36
Table 2: Number of proved optimal solutions out of 300
with varying α.
α CP MILP-IMP MILP-DIS
0.1 154 239 187
0.25 165 207 157
0.5 151 163 134
0.75 134 128 113
0.9 123 87 89
exception of α = 0.9, MILP-DIS is outperformed
by MILP-IMP. The efficiency of MILP-IMP for the
smaller spannable ratio can be explained by break-
ing of symmetries, i.e, the solver does not have to
sequence the non-spannable jobs that are wholly pro-
cessed within one metering interval.
The following Table 3 illustrates, how the tight-
ness of the energy limit β affects the performance. We
see that MILP-IMP outperforms other approaches.
From the results we may infer that the tighter limit
leads to harder instances, which corresponds with the
intuition since our scheduling problem without the en-
ergy limit is trivially solvable (any left-shifted sched-
ule is optimal).
Table 3: Number of proved optimal solutions out of 300
with varying β.
β CP MILP-IMP MILP-DIS
0.8 185 198 150
1.0 159 181 148
1.2 144 162 136
1.4 125 152 127
1.6 114 131 119
4.2.2 Comparison of the Quality of the Found
Solutions
In addition to the previous results, we also examined
the total makespan achieved by each method within
the time limit for varying n, m, see Table 4. Instances,
for which at least one method did not find any so-
lution, are not included (there are 5 such instances,
in all cases a solution was not found by MILP-DIS
Scheduling on Dedicated Machines with Energy Consumption Limit
59

Table 4: Total makespan with varying n, m.
n m CP MILP-IMP MILP-DIS
10 2 46419 46451 46425
10 4 26028 26028 26028
20 2 94673 95736 97456
20 4 49206 49284 49394
30 2 133389 136744 140814
30 4 69938 70250 71033
method). The table reveals that CP outperforms all
the other approaches, which is not surprising since
IBM CP Optimizer is primarily designed to find good
solutions. With the exception of the instances with
n = 10, m = 2, MILP-IMP has smaller or the same
total makespan as MILP-DIS.
5 CONCLUSION
Managing the production is becoming increasingly
complex without computer-aided systems. On the
other hand, traditional scheduling constraints and ob-
jectives are not enough to design realistic produc-
tion schedules. In this work, we explored a schedul-
ing problem with a practical production constraint of
satisfying the contracted energy consumption limits.
This problem emerges in energy-demanding produc-
tion processes, such as glass tempering or steel hard-
ening, in which a material is heated in furnaces to
high temperature. The heating in the furnaces has to
be planned carefully; otherwise, the resulting energy
spikes lead to a violation of the energy limits.
We propose two exact algorithms for the studied
scheduling problem with dedicated machines: (i) a
Constraint Programming model and (ii) a Mixed In-
teger Linear Programming based iterative algorithm.
The iterative algorithm exploits the fact that the start
times do not need to be modeled explicitly, which al-
lows us to efficiently solve instances having a higher
number of shorter jobs. To compare the algorithms
with the approaches from literature, we adapted an ex-
isting Mixed Integer Linear Programming model for
a similar problem (Ha
¨
ıt and Artigues, 2011; Ha
¨
ıt and
Artigues, 2011). To summarize the experimental re-
sults on a dataset consisting of instances with 10 to
30 jobs, our best method proves the optimality for
54.9% instances, whereas the Mixed Integer Linear
Programming model inspired by the existing litera-
ture proves the optimality for 45.3% instances.
In the future, our aim is to extend our iterative al-
gorithm to the job shop scheduling problem with en-
ergy consumption limit, where the research challenge
is handling of the precedences between the operations
of the same job.
ACKNOWLEDGEMENTS
The work in this paper was supported by the Technol-
ogy Agency of the Czech Republic under the Centre
for Applied Cybernetics TE01020197.
REFERENCES
Bruzzone, A., Anghinolfi, D., Paolucci, M., and Tonelli,
F. (2012). Energy-aware scheduling for improving
manufacturing process sustainability: A mathematical
model for flexible flow shops. CIRP Annals - Manu-
facturing Technology, 61(1):459–462.
Fang, K., Uhan, N. A., Zhao, F., and Sutherland, J. W.
(2013). Flow shop scheduling with peak power con-
sumption constraints. Annals of Operations Research,
206(1):115–145.
Gajic, D., Hadera, H., Onofri, L., Harjunkoski, I., and Gen-
naro, S. D. (2017). Implementation of an integrated
production and electricity optimization system in melt
shop. Journal of Cleaner Production, 155:39 – 46.
Sustainable Development of Energy, Water and Envi-
ronmental Systems.
Gurobi (2018). Constraints. http://www.gurobi.
com/documentation/8.0/refman/constraints.html. Ac-
cessed September 18, 2018.
Hadera, H., Harjunkoski, I., Sand, G., Grossmann, I. E.,
and Engell, S. (2015). Optimization of steel pro-
duction scheduling with complex time-sensitive elec-
tricity cost. Computers & Chemical Engineering,
76:117–136.
Ha
¨
ıt, A. and Artigues, C. (2011). A hybrid CP/MILP
method for scheduling with energy costs. European
Journal of Industrial Engineering, 5(4):471–489.
Ha
¨
ıt, A. and Artigues, C. (2011). On electrical load tracking
scheduling for a steel plant. Computers & Chemical
Engineering, 35(12):3044–3047.
Laborie, P., Rogerie, J., Shaw, P., and Vil
´
ım, P. (2018).
IBM ILOG CP optimizer for scheduling. Constraints,
23(2):210–250.
Masmoudi, O., Yalaoui, A., Ouazene, Y., and Chehade, H.
(2017). Lot-sizing in a multi-stage flow line produc-
tion system with energy consideration. International
Journal of Production Research, 55(6):1640–1663.
Merkert, L., Harjunkoski, I., Isaksson, A., S
¨
aynevirta, S.,
Saarela, A., and Sand, G. (2015). Scheduling and en-
ergy – industrial challenges and opportunities. Com-
puters & Chemical Engineering, 72(0):183 – 198.
M
´
odos, I.,
ˇ
S
˚
ucha, P., and Hanz
´
alek, Z. (2017). Algo-
rithms for robust production scheduling with energy
consumption limits. Computers & Industrial Engi-
neering, 112:391 – 408.
Nolde, K. and Morari, M. (2010). Electrical load tracking
scheduling of a steel plant. Computers & Chemical
Engineering, 34(11):1899–1903.
Rapine, C., Goisque, G., and Akbalik, A. (2018). Energy-
aware lot sizing problem: Complexity analysis and ex-
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
60

act algorithms. International Journal of Production
Economics, 203:254 – 263.
Zhao, S., Grossmann, I. E., and Tang, L. (2018). Integrated
scheduling of rolling sector in steel production with
consideration of energy consumption under time-of-
use electricity prices. Computers & Chemical Engi-
neering, 111:55 – 65.
APPENDIX
5.1 Proofs
Observation 1. The maximum number of consecu-
tive metering intervals that can have non-zero overlap
with job J
j
for any feasible start times s is
Ω
j
=
l
p
j
D
m
+ 1. (8)
Proof. Let I
i
s
be the metering interval, where the job
starts and let I
i
c
be the metering interval, where the
job completes; thus d
j,i
s
∈ N
>0
, d
j,i
c
∈ N
>0
. Consider
the following two cases
1. I
i
s
= I
i
c
: This implies that the job has non-zero
overlap with only one metering interval in s. Since
Ω
j
≥ 1, the lemma holds.
2. I
i
s
< I
i
c
: Since the job is processed without pre-
emption, the job completely fills up each metering
interval between I
i
s
, I
i
c
, i.e., the overlap length of
the job with each metering interval between I
i
s
, I
i
c
is D. The number of such metering intervals is
q = i
c
− i
s
. The processing time can be then writ-
ten as
p
j
= q · D + d
j,i
s
+ d
j,i
c
. (22)
To finish our proof, we need to show that
Ω
j
≥ q + 2, (23)
i.e., the number of metering intervals with non-
zero overlap in s is at most Ω
j
.
Notice that from the definition of the ceiling func-
tion it holds that
Ω
j
=
l
p
j
D
m
+ 1 =
p
j
D
+ ε
| {z }
∈N
>0
+1 (24)
where ε ∈ [0, 1). Therefore,
Ω
j
=
p
j
D
+ ε + 1
= q +
d
j,i
s
D
+
d
j,i
c
D
+ ε
| {z }
∈N
>0
+1
≥ q + 2.
The last inequality follows from
q ∈ N
≥0
, Ω
j
∈ N
>0
, d
j,i
s
∈ N
>0
, d
j,i
c
∈ N
>0
.
Lemma 1. Let J
j
1
, J
j
2
∈ J be two jobs such
that j
1
6= j
2
, µ
j
1
= µ
j
2
, p
j
1
≥ 2, p
j
2
≥ 2 and
p
j
1
+ p
j
2
≥ 2 · D + 1. Let d = (d
j,i
)
J
j
∈J ,I
i
∈I
be
values for some feasible solution to the MILP model
from Section 3.2. Then Eq. (19) holds for J
j
1
, J
j
2
in
any metering interval I
i
∈ I \ {I
i
max
}.
Proof. By contradiction. Assume that I
i
∈ I \ {I
i
max
}
is a metering interval such that Eq. (19) is violated,
i.e., d
j
1
,i
≥ 1, d
j
1
,i+1
≥ 1, d
j
2
,i
≥ 1, d
j
2
,i+1
≥ 1. Since
Eq. (11) holds, we know that
d
j
1
,i
+ d
j
2
,i
≤ D (25)
d
j
1
,i+1
+ d
j
2
,i+1
≤ D , (26)
thus
d
j
1
,i
+ d
j
1
,i+1
+ d
j
2
,i
+ d
j
2
,i+1
≤ 2 · D. (27)
For J
j
∈ {J
j
1
, J
j
2
}, one of the following two cases
are possible
1. d
j,i
+ d
j,i+1
= p
j
2. d
j,i
+ d
j,i+1
< p
j
. This means that the job has
non-zero overlap with either I
i−1
or I
i+2
. Due
to Eq. (17), either d
j,i
or d
j,i+1
is pushed to
be at least D, i.e., either d
j,i
≥ D, d
j,i+1
≥ 1 or
d
j,i
≥ 1, d
j,i+1
≥ D.
The proof is now split according to combinations
of those cases
• Case 1 holds for J
j
1
and Case 1 holds for J
j
2
: By
substitution we get
p
j
1
+ p
j
2
≤ 2 · D, (28)
which is a contradiction with our initial assump-
tion p
j
1
+ p
j
2
≥ 2 · D + 1.
• Case 2 holds for J
j
1
and Case 2 holds for J
j
2
: By
substitution we get
D + 1 + D + 1 ≤ 2 · D , (29)
which is an obvious contradiction.
• Case 1 holds for J
j
1
and Case 2 holds for J
j
2
:
W.l.o.g., assume that d
j
1
,i
≥ D. Since d
j
2
,i
≥ 1,
we get d
j
1
,i
+ d
j
2
,i
≥ D + 1, which is a contradic-
tion with d
j
1
,i
+ d
j
2
,i
≤ D.
• Case 2 holds for J
j
1
and Case 1 holds for J
j
2
:
Proof is analogous to the previous one.
Scheduling on Dedicated Machines with Energy Consumption Limit
61

5.2 Disjunctive MILP Model
The disjunctive MILP model uses the formulation for
computing the jobs’ overlaps with the metering inter-
vals that was presented in (Ha
¨
ıt and Artigues, 2011;
Ha
¨
ıt and Artigues, 2011). We adapted the model pro-
posed in (Ha
¨
ıt and Artigues, 2011; Ha
¨
ıt and Artigues,
2011) to the parallel machine scheduling with energy
consumption limits and makespan as an objective.
The complete model follows
min C
max
(30)
C
max
≥ s
j
+ p
j
, ∀J
j
∈ J (31)
s
j
+ p
j
≤ s
j
0
+ M · (1 − x
j, j
0
),
∀M
k
∈ M , ∀J
j
, J
j
0
∈ J
k
: j < j
0
(32)
s
j
0
+ p
j
0
≤ s
j
+ M · x
j, j
0
,
∀M
k
∈ M , ∀J
j
, J
j
0
∈ J
k
: j < j
0
(33)
s
j
≥ i · D · (1 − z
s
j,i
), ∀J
j
∈ J , ∀I
i
∈ I \ {I
H
D
} (34)
s
j
≤ i · D − 1 + M · (1 − z
s
j,i
),
∀J
j
∈ J , ∀I
i
∈ I \ {I
H
D
}
(35)
z
s
j,i+1
≥ z
s
j,i
, ∀J
j
∈ J , ∀I
i
∈ I \ {I
H
D
} (36)
z
s
j,
H
D
= 1, ∀J
j
∈ J (37)
s
j
+ p
j
≥ (i − 1)· D · (1 − z
c
j,i
) + 1,
∀J
j
∈ J , ∀I
i
∈ I
(38)
s
j
+ p
j
≤ (i − 1)· D + M · (1 − z
c
j,i
),
∀J
j
∈ J , ∀I
i
∈ I
(39)
z
c
j,i+1
≥ z
c
j,i
, ∀J
j
∈ J , ∀I
i
∈ I \ {I
H
D
} (40)
d
j,i
≤ D · (z
s
j,i
− z
c
j,i
), ∀J
j
∈ J , ∀I
i
∈ I (41)
∑
I
i
∈I
d
j,i
= p
j
, ∀J
j
∈ J (42)
d
j,i
≥ D · (z
s
j,i−1
− z
c
j,i+1
),
∀J
j
∈ J , ∀I
i
∈ I \ {I
1
, I
H
D
}
(43)
d
j,i
≥ i · D · (1 − z
s
j,i−1
) − s
j
− D · z
c
j,i+1
,
∀J
j
∈ J , ∀I
i
∈ I \ {I
1
, I
H
D
}
(44)
d
j,i
≥ s
j
+ p
j
− i · D + D · z
s
j,i−1
− M · (1 − z
c
j,i+1
),
∀J
j
∈ J , ∀I
i
∈ I \ {I
1
, I
H
D
}
(45)
d
j,1
≥ D · z
s
j,1
− s
j
− D · z
c
j,2
, ∀J
j
∈ J (46)
d
j,
H
D
≥ s
j
+ p
j
− H + D · z
s
j,
H
D
−1
, ∀J
j
∈ J (47)
∑
J
j
∈J
d
j,i
· P
j
≤ E
max
, ∀I
i
∈ I (48)
The disjunctive MILP model uses the following
variables: (i) C
max
∈ N is the makespan of the sched-
ule, (ii) s
j
∈ N
≥0
denotes the start time of job J
j
, (iii)
x
j, j
0
∈ {0, 1} represents whether job J
j
is scheduled
before job J
j
0
, (iv) d
j,i
∈ N
≥0
expresses the length of
the overlap between job J
j
and metering interval I
i
, (v)
z
s
j,i
∈ {0, 1} denotes whether s
j
∈ [0, i ·D −1], and (vi)
z
c
j,i
∈ {0, 1} denotes whether s
j
+ p
j
∈ [0, (i − 1) · D].
The objective (30) minimizes the makespan,
which is the maximum of the completion times of the
jobs, see constraint (31). The non-overlapping of the
jobs is ensured by constraints (32) and (33). Con-
straints (34)-(47) models the overlaps of the jobs with
the metering intervals; see (Ha
¨
ıt and Artigues, 2011)
for details. The last constraint (48) enforces the en-
ergy limit.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
62
