Quantum Bit Error Rate Analysis of the Polarization based BB84
Protocol in the Presence of Channel Errors
Ágoston Schranz and Eszter Udvary
Department of Broadband Infocommunications and Electromagnetic Theory,
Budapest University of Technology and Economics,
Keywords:
Quantum Key Distribution (QKD), BB84, Polarization Switching, Polarization Rotation, Quantum Bit Error
Rate (QBER).
Abstract:
In the BB84 quantum key distribution (QKD) protocol, the communicating parties do a quantum bit error rate
(QBER) test to determine whether there is an eavesdropper trying to gain information about the secret key.
However, the QBER is not only influenced by the eavesdropper’s strategies, but also by the imperfections of the
physical devices and the channel through which the quantum states propagate. We developed a simple channel
model with error parameters describing the channel and the potential polarization switching in the transmitter,
to see how those effects influence the QBER in a polarization-qubit BB84 implementation. Certain well-defined
probabilistic channel models are compared to see which is responsible for the highest error probability.
1 INTRODUCTION
The first quantum key distribution protocol, commonly
referred to as BB84, was published in 1984 by Char-
les Bennett and Gilles Brassard (Bennett and Bras-
sard, 1984). During the key exchange, the transmitter
(Alice) sends a qubit randomly prepared in one of two
conjugate bases, and the receiver (Bob) chooses one of
the bases also randomly, to measure the quantum state.
Afterwards, the two parties disclose their basis choi-
ces on a public channel, keeping only those measured
values where they chose the same and discarding ever-
ything else. A random subsequence of the raw key is
then compared to calculate the quantum bit error rate.
This part of the protocol makes it possible to detect
eavesdropping, and the key distribution is aborted if
the QBER exceeds a predefined threshold value.
The original BB84 paper already introduced an
eavesdropper (Eve) performing the so called intercept-
and-resend (I-R) strategy, measuring Alice’s qubits
randomly and sending the measured state towards Bob.
If Eve performs it for every qubit, she gains an average
information of 0.5 bits per key bit, but this attack intro-
duces an average QBER of 0.25, even if the transmitter
and the channel are both ideal. Performing it for a
smaller portion of qubits reduces the QBER, but also
decreases the average information gained about the
key bits. This is due to the no-cloning theorem, which
states, that no arbitrary unknown quantum state can be
perfectly copied by the same device (Wootters and Zu-
rek, 1982). We must note, that there exist more refined
attacks than the I-R, resulting in lower QBERs, most
notably the phase-covariant cloning machine with a
QBER of 0.14644 (Bruß et al., 2000). In this paper, we
deal with the most common implementation of qubits
in BB84, that of linearly polarized single photons.
However, physical channels are not perfect in terms
of quantum state transmission, which may introduce
errors in the probabilistic measurements at the recei-
ving end. Such imperfections might originate even
from the transmitter. As an example, vertical-cavity
surface-emitting lasers (VCSELs) are known to exhi-
bit a phenomenon called polarization switching (PS),
which causes the output light that is originally pola-
rized along one of two orthogonal directions (polari-
zation eigemodes) to rapidly switch to the orthogonal
polarization (San Miguel et al., 1995; Martín-Regalado
et al., 1997). If Bob chose the same basis as Alice,
such a switch would introduce a certain quantum bit
error assuming that the channel is free from any further
imperfections, and there is no eavesdropper present.
Polarization switching is depending on the laser’s cur-
rent, and with careful considerations, it can be elimina-
ted for any specific device, or as shown in our previous
work, even utilized for polarization modulation in the
BB84 protocol (Schranz and Udvary, 2018). Regard-
Schranz, Á. and Udvary, E.
Quantum Bit Error Rate Analysis of the Polarization based BB84 Protocol in the Presence of Channel Errors.
DOI: 10.5220/0007384101810189
In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2019), pages 181-189
ISBN: 978-989-758-364-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
181

less, in this paper, we maintain the possibility of a
PS at the transmitter, always happening between two
orthogonal states.
The more important issue is that of qubit errors
resulting from the fact that the channel (be it an op-
tical fiber or free-space) can alter the quantum states
in such a way that even measurements in the correct
basis will yield erroneous results. These can be small
disturbances which may only present themselves with
very low probability, but nevertheless, their effects are
best not to be neglected.
Furthermore, in this paper we are not dealing with
the fact that due to a number of reasons (absorption,
coupling losses, the non-unit quantum efficiency of
single photon detectors, the Poissonian photon statis-
tics of semiconductor lasers used as a substitute for
true single photon sources, etc.), some of the states
sent by Alice will not be detected by Bob. We also
assume that all such losses are polarization indepen-
dent, affecting every quantum state ( |0i , |1i , |+i and
|−i representing linear polarizations with angles 0° ,
90° , +45° and −45° , respectively) in the same way.
If the QBER is calculated using only those time bins
when both Alice and Bob used the same basis and
Bob did receive a photon, then excluding the effects of
losses does not reduce the generality of the error rate
analysis.
In Section 2, we define the parameters necessary
for our analysis and set up a polarization rotation error
model for the channel. In Section 3, we derive the
QBER rates for all possible combinations of errors
caused by eavesdropping, polarization switches and
polarization rotation. Section 4 deals with obtaining
the error parameters of several channel models defined
by their polarization angle distribution. Finally, in
Section 5 we show how this analysis might be useful,
when one wants to determine the amount of QBER
originating from eavesdropping. QBER is also referred
to as erroneous measurement probability throughout
the paper.
2 GENERAL DEFINITIONS AND
CHANNEL MODELLING
We introduce the polarization switching rate (PSR) pa-
rameter r as the average ratio of qubits for which a PS
happens in Alice’s transmitter, and channel error rates
e
1
and e
2
for channel sections 1 and 2, respectively.
The latter are defined as the probability that measuring
polarization in the correct basis yields an erroneous
result. For simplicity, we assume that all errors in all
channel sections are independent of the input state and
the basis it was sent in (every polarization state is af-
fected likewise), and that PSR is also basis and state
independent.
Two simple conclusions regarding an
eavesdropping-free system arise from our defi-
nitions.
1. Given a transmitter with PSR r and an error-free
channel, the probability of correct and bad measu-
rement results in the correct basis is C
0,r
= 1 −r
and E
0,r
= r, respectively.
2. Given a PS-free transmitter and a channel with an
error rate e , the probability of correct and bad mea-
surement results in the correct basis is C
e,0
= 1 −e
and E
e,0
= e , respectively. This results directly
from our definition of e.
The total error rate calculations are always con-
cerning the raw keys, not taking into account the dis-
carded results due to basis choice differences. This
ultimately does not change the calculations, because
polarization switches and channel errors are indepen-
dent from (and uncorrelated with) Bob’s basis choices.
EA
r
B
CH
1
: e
1
CH
2
: e
2
CH: e
Figure 1: Diagram of the channel model in the presence and
in the absence of eavesdropping. A: Alice, E: Eve, B: Bob.
The presence of Eve cuts the channel CH into two sections,
CH
1
and CH
2
. The respective PSR and error parameters are
denoted above every element.
2.1 The Channel Error Model
In the previous sections we described the channel only
by its general error probability parameter e , but we did
not specify the origin and nature of those errors. This
leads to problems in cases where eavesdropping and
channel errors are both present, because our definition
of e didn’t include how it influences measurements
when the transmitting and receiving bases are diffe-
rent. Before calculating these general error rates, we
need to have more information about how the channel
introduces errors. Our basic assumption is, that this is
done by rotating the polarization by an angle ϑ.
Malus’ law states that if a polarizer is irradiated
by linearly polarized light angled at ϑ relative to the
polarizing axis, a proportion of cos
2
(ϑ) of the light is
transmitted, while a proportion of sin
2
(ϑ) will be bloc-
ked or reflected. This can be translated to the single
photon level as the following: if a linearly polarized
photon is sent and measured in the same basis, but
its polarization angle is rotated along the way by an
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
182

angle ϑ , the probability of measuring the state to be
orthogonal to the original state is equal to sin
2
(ϑ).
2.1.1 Fixed Angle Polarization Rotation
First assume a channel, that introduces a systematic
error by rotating the polarization of all incoming states
by a fixed value of α . Although fixed polarization ro-
tations or those following a discrete probability distri-
bution might be unphysical, analyzing their properties
provides a good understanding for practical cases with
continuous rotation angle distributions.
For every qubit sent, the rotation angle, therefore
the measurement error probability is constant, meaning
that e can be calculated by Malus’ law as
e = sin
2
(α). (1)
2.1.2 Random Polarization Rotation
In a practical case, the error probability depends on
the rotation angle θ , which itself is a random variable
characterized by a probability density function (PDF)
p
θ
(ϑ) . The error probability sin
2
(θ) is a function of
the angle, becoming a random variable itself. Thus
we need to average the errors of all possible rotations
weighed by the PDF of the rotation angle itself. This
way e can be calculated as the expectation value of the
error probability, E[sin
2
(θ)].
3 ERROR RATES FOR ALL
COMBINATIONS OF ERROR
SOURCES
In Section 2. we have defined two parameters e and r
as error rates for situations without eavesdropping, if
either only the channel, or only the transmitter may be
responsible for faulty measurements. In this section,
we include the possibility of an eavesdropper Eve, split-
ting the channel into two sections. We assume Eve to
use the simple intercept-and-resend attack for every
single qubit, to maximize the amount of information
gained. During the following subsections, all possible
combinations of error sources are taken into account
and analyzed individually, with a small channel mo-
del depicting the actual parameters. The resulting
correct and erroneous measurement probabilities at
Bob’s side are calculated as well, following the no-
tation of C
e,r
/ E
e,r
if there is no eavesdropping, and
C
e
1
,e
2
,r
/ E
e
1
,e
2
,r
to denote the presence of Eve.
3.1 Polarization Switching and Channel
Errors in the Absence of
Eavesdropping
A
r
B
CH: e
We have seen the error rates if only either polarization
switching or channel polarization rotation is present.
However, combining both error sources, the situation
gets more complicated. In this case, polarization swit-
ches and channel errors may counteract each other,
leading to correct measurements. This can be under-
stood easily: a polarization switch would introduce a
certain measurement error, but a polarization rotation
makes it possible that Eve measures the original state.
Measurement errors happen in two cases: when po-
larization does not switch but the channel introduces
an error, or when the polarization switches and the
channel does not introduce an error, leading to a total
error rate of
E
e,r
= (1−r)e + (1−e)r = e + r −2re. (2)
Conversely, correct measurements happen when
either none of the two problems arise, or the two effects
cancel each other out.
C
e,r
= (1−r)(1 −e) +re (3)
= 1−e −r + 2re = 1 −E
e,r
(4)
It is easy to see that these equations are symmetric
with respect to e and r . An interesting consequence
of the error cancelling is that the correct measurement
rate C
e,r
is near one if both parameters are very low or
both parameters are very high, obtaining the maximum
value if e = r = 0 or e = r = 1 ( C
0,0
= C
1,1
= 1 ). In
turn, almost all measurements are faulty if one of the
parameters is very high with the other being very low,
reaching zero if e = 1,r = 0 or e = 0,r = 1 . Plotting
E
e,r
and C
e,r
as a function of the parameters yields
saddle-like surfaces (Fig. 2).
3.2 Eavesdropping, Polarization
Switching and Channel Errors
Introducing eavesdropping to the analysis requires
some easily justifiable restraints. Therefore, the basis
choices of Eve and Bob are taken to be independent
from each other. Moreover, for every qubit, we sup-
pose that Bob chooses the correct basis (otherwise the
results are later discarded, not presenting themselves
in the error calculations).
Quantum Bit Error Rate Analysis of the Polarization based BB84 Protocol in the Presence of Channel Errors
183

0
0.2
0.4
0.6
0
0.8
1
0.5
1
0.5
1
0
0
0.2
0.4
0.6
0.8
1
Figure 2: Erroneous measurement probability in the correct
basis as a function of PSR r and channel error parameter e ,
in the absence of eavesdropping.
EA
r
B
CH
1
: e
1
CH
2
: e
2
First, we analyze events that happen before Eve’s
measurement, letting e
2
= 0 . Table 1 represents the
probabilities by which the eavesdropper would obtain
correct or wrong measurement results choosing the
correct or wrong bases. Since Eve is the first to mea-
sure the qubits, if she chooses the correct basis, these
values are the same as Bob’s in Section 3.1, replacing e
with e
1
. Also, if Eve chose correctly, Bob will always
measure the same result as Eve. On the other hand, if
Eve chose the wrong basis, our parameter definition
for e is not enough to correctly describe the probabi-
lities of measured values; a more detailed knowledge
about the channel would be necessary. This lack of
knowledge is represented by p . However, the state Eve
resends and Bob receives will certainly be one of the
wrong basis states, and his outcome would be com-
pletely random (0.5). This happens regardless of the
value of p , and the nature of the first channel section;
Eve’s measurement erases the previous polarization
rotation, therefore p is irrelevant.
Table 1: Eve’s measurement probabilities, when both po-
larization switches and the first channel section may cause
errors.
Eve’s meas. res.
Eve’s basis choice
Correct Wrong
Correct e
1
r + (1 −e
1
)(1−r) 0.5+ p
Wrong e
1
(1−r) + (1 −e
1
)r 0.5 − p
Now set r = e
1
= 0 and analyze the section bet-
ween Eve and Bob. Table 2 lists Eve’s measurement
probabilities for this case. Since there is no error be-
tween Alice and the eavesdropper, if Eve chose the
correct basis, Bob would only see errors caused by the
second channel section. The correct and wrong measu-
rement probabilities are thus, by definition, 1−e
2
and
e
2
. On the other hand, if Eve uses the wrong basis and
sends Bob a state that is rotated by 45 degrees with
respect to his basis states, it is impossible to give a
general description of what will happen, based only
on our definition of e
2
, which only accounts for the
error probability when the sent state was in the final
measurement basis. The exact nature of the channel is
necessary for a complete analysis.
Table 2: Eve’s measurement probabilities, when the only
source of error is the second channel section.
Eve’s meas. res.
Eve’s basis choice
Correct Wrong
Correct 1 0.5
Wrong 0 0.5
We can introduce the following assumption to re-
duce the complexity of the problem. Let’s restrict
the possible polarization rotations performed by the
channel to those, which can be described by a probabi-
lity density function symmetric around zero, an even
function f
even
θ
(ϑ) . This restriction will be maintained
for the rest of the calculations for simplicity.
Assume a simple case when Alice sends a bit 1 in
the rectilinear basis, |1i , which is randomly rotated
in CH
1
by either an angle +ϑ or −ϑ . Eve measures
the state in the diagonal basis. For an undisturbed
|1i state, her measurement results could be 0 or 1,
both with p
1
= p
0
= cos
2

π
4

=
1
2
. If the state was
rotated by +ϑ , the probabilities would change to p
0
=
cos
2

π
4
−ϑ

and p
1
= cos
2

π
4
+ ϑ

. On average, the
total error probability in this case is
p
|1i
error
=
1
2
h
p
|1i
error
|
(θ=+ϑ)
+ p
|1i
error
|
(θ=−ϑ)
i
(5)
=
1
2
h
cos
2

π
4
−ϑ

+ cos
2

π
4
+ ϑ
i
. (6)
Since we know that
cos
2

π
4
+ ϑ

=
1
2
−
sin(2ϑ)
2
, (7)
this probability reduces to
p
|1i
error
=
1
2

1
2
−
sin(2ϑ)
2
+
1
2
−
sin(−2ϑ)
2

(8)
=
1
2

1
2
−
sin(2ϑ)
2
+
1
2
+
sin(2ϑ)
2

=
1
2
(9)
The same end result applies for every other origi-
nal state |0i , |+i and |−i . For the latter two, ϑ should
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
184

|−i: 1
|+i: 0
|0i: 0
|1i: 1
Figure 3: Bit mapping in the BB84 protocol. Polarization
states |0i and |+i represent zeros, |1i and |−i represent ones
in their respective bases.
be replaced by −ϑ , owing to the bit-to-state mapping
of BB84 (Fig. 3). All original states are equiproba-
ble, and all of them have an error probability of
1
2
,
therefore the total error probability in case when Eve
measures in the wrong basis is
1
2
, regardless of the
second channel section’s errors.
This conclusion can be extended to any case, where
the rotation angle θ is a zero-mean random variable
with an even PDF f
even
θ
(ϑ) . At this point, we can turn
the weighted sum in Eq. 5 into an expectation value
calculation (10).
p
|1i
error
=
Z
∞
−∞
cos
2

π
4
+ ϑ

· f
even
θ
(ϑ)dϑ (10)
=
Z
∞
−∞

1
2
+
sin(2ϑ)
2

· f
even
θ
(ϑ)dϑ (11)
=
1
2
(12)
Usint the linearity of the integral, the first part
of the sum in (11) evaluates to 1/2 since the area
under the curve of any PDF is unit. The second part is
an integral of an odd function with symmetric limits,
which – further assuming that it exists – yields zero.
The most general case is when all three errors may
happen during a single qubit’s transmission. Summa-
rizing the individual analysis of the errors happening
before and after the eavesdropper, we can calculate the
QBER. If Eve choose the wrong basis, Bob would me-
asure any value with probability 0.5, regardless of any
errors happening due to the second channel section. If
Eve choose, however, the correct basis, correct measu-
rement at Bob’s can occur in the following situations:
• Eve measured the correct value and the second
section caused no error at the receiver. This hap-
pens with a probability of [e
1
r + (1 −e
1
)(1 −
r)](1 −e
2
).
• Eve measured the incorrect value, but the se-
cond section’s rotation caused Bob to measure
the original value, ultimately. The probability is
[e
1
(1−r) + (1 −e
1
)r]e
2
.
This can be read as the following: if an even num-
ber of errors "happen" during the transmission, they
will cancel each other’s effects and lead to a correct
measurement value, while an odd number of errors
lead to an erroneous value.
Averaging all situations, we can arrive at the fol-
lowing general formulae for the correct and wrong
measurement probabilities, the latter representing the
QBER.
C
e
1
,e
2
,r
=0.75−
e
1
+ e
2
+ r
2
(13)
+ (e
1
r + e
2
r + e
1
e
2
) −2 ·e
1
e
2
r
E
e
1
,e
2
,r
=0.25+
e
1
+ e
2
+ r
2
(14)
−(e
1
r + e
2
r + e
1
e
2
) + 2 ·e
1
e
2
r
3.3 Summary
The formulae (concluded for the QBER in Table 3) are
consistent with each other, meaning that it could be ea-
sily shown that all specific results (when one or more
error sources are not present) can be obtained if we
insert zeros in the most general equations for the error
parameters not present in the individual cases. Also,
switching any two parameter values would mean no
difference, since all formulae are symmetric with re-
spect to all of e
1
, e
2
and r . Note that these results only
apply for the instance of simple intercept-and-resend
attacks, and it would take a different approach to de-
rive similar formulae for other types of eavesdropping
strategies using the same error parameter definitions.
4 CHANNELS WITH
WELL-DEFINED PROBABILITY
DISTRIBUTIONS FOR
POLARIZATION ROTATION
In the previous sections we developed a framework
for error calculations, mostly independent from the
channel’s exact probability distribution for the polari-
zation angle rotation θ , represented by the probability
density function f
θ
(ϑ) . The only restriction limited
the generality of this framework for distributions with
zero-mean symmetric distributions. In this section,
we discuss several channel models with well defined
error mechanisms, with an emphasis on the calculation
of the e parameter, defined as the expectation value
of sin
2
(θ) , being a function of the distribution para-
meters. We use the notation σ
2
( σ ) for the variance
(standard deviation) of the probability distribution, and
in Sec. 4.4 reparametrize the distributions with σ for
the simplicity of comparison.
Quantum Bit Error Rate Analysis of the Polarization based BB84 Protocol in the Presence of Channel Errors
185

Table 3: Conclusive table of erroneous measurement probabilities for all combinative cases of eavesdropping, polarization
switching and channel errors.
e
1
/e
2
/r Without eavesdropping With eavesdropping
0/0/0 0 0.25
e
1
/0/0
e
0.25+ 0.5 ·e
1
0/e
2
/0 0.25+ 0.5 ·e
2
e
1
/e
2
/0 0.25+ 0.5 ·(e
1
+ e
2
) −e
1
e
2
0/0/r r 0.25+ 0.5 ·r
e
1
/0/r
e + r −2 ·er
0.25+ 0.5 ·(e
1
+ r) −e
1
r
0/e
2
/r 0.25+ 0.5 ·(e
2
+ r) −e
2
r
e
1
/e
2
/r 0.25+ 0.5 ·(e
1
+ e
2
+ r) −(e
1
r + e
2
r + e
1
e
2
) + 2 ·e
1
e
2
r
4.1 Symmetric Two-point Rotation
Angle Distribution
A discrete two-point distribution T (a, b, q) is a gene-
ralization of the Bernoulli distribution, where the two
obtainable values are a and b , with probabilities q and
1 −q , respectively. Symmetry is achieved when the
two outcomes are equiprobable ( q = 0.5 ). Assuming a
channel with θ ∼ T (−α, α,0.5) , rotating the polariza-
tion angle of the incoming states randomly by either
+α or −α , the PDF can be written in terms of the Dirac
delta function δ(ϑ):
f
tp
θ
(ϑ) = 0.5[δ(ϑ + α) + δ(ϑ −α)], (15)
Since sin
2
(·) is an even function, this channel’s
error parameter is equivalent to that of a fixed angle
polarization rotating channel with an angle +α or −α ,
confirmed by the calculations as well:
e
tp
= E[sin
2
(θ)] =
Z
∞
−∞
f
tp
θ
(ϑ) ·sin
2
(ϑ)dϑ (16)
= 0.5
Z
∞
−∞
sin
2
(ϑ) ·δ(ϑ + α)dϑ
(17)
+ 0.5
Z
∞
−∞
sin
2
(ϑ) ·δ(ϑ −α)dϑ
= 0.5

sin
2
(α) + sin
2
(−α)

(18)
= sin
2
(α). (19)
The error parameter of the symmetric two-point
distribution is periodic with a period of π , oscilla-
ting around 0.5 , between minima with value 0 at
points α = π/2 + kπ,k ∈ Z and maxima with value 1
at points α = kπ,k ∈ Z . The periodicity is a property
specific only to this specific distribution in the set of
all zero-mean symmetric distributions. Since all conti-
nuous distributions in the set will spread increasingly
as the variance grows, their error parameters will tend
to 0.5 as σ → ∞.
4.2 Uniform Rotation Angle
Distribution
Now assume a channel that rotates the polarization
angle of each qubit by a random angle θ following
a continuous uniform distribution U(−α, α) within
limits −α and α . This distribution is parametrized
by a mean value of zero and standard deviation of
σ = α/
√
3 . The PDF of the rotation angle is then
given by
f
uni
θ
(ϑ) =
(
1
2α
, if ϑ ∈ [−α;α]
0, otherwise.
(20)
The expectation value of the error probability can
be analytically calculated, resulting in
e
uni
= E[sin
2
(θ)] (21)
=
Z
∞
−∞
f
uni
θ
(ϑ) ·sin
2
(ϑ)dϑ (22)
=
1
2α
Z
α
−α
sin
2
(ϑ)dϑ (23)
=
1
2α
Z
α
−α
1 −cos(2ϑ)
2
dϑ (24)
=
1
2
−
sin(α)cos(α)
2α
. (25)
Note that e
uni
is undefined for the limiting case of
α = 0 , but lim
α→0
e
uni
= 0 , agreeing with the expec-
tations that a degenerate distribution (a certain event)
with zero mean and variance causes no measurement
errors. As expected, for increasing variance (the case
of large α ), e
uni
approaches 0.5 , oscillating around this
value.
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
186

4.3 Normal Rotation Angle Distribution
For our third model, we chose an example of higher
practical value: a normal distribution with mean zero
and variance σ
2
, denoted by N (0,σ
2
) . This has been
reported to be the approximate distribution for the
angle of polarization rotation caused by turbulence du-
ring free-space propagation, as a result of the central-
limit theorem (Zhang et al., 2014; Zhang et al., 2016;
Zhang et al., 2018). The approximation can be applied
when the turbulence strength is low enough, so that the
magnitude of the depolarized field component is small
compared to the magnitude of the original, linearly po-
larized electric field ( M =


E
y


/
|
E
0
|
). In this situation,
the rotation angle can be approximated by the ratio of
depolarized field components ( θ ≈ M ) (Strohbehn and
Clifford, 1967).
The PDF of this distribution has the form of
f
norm
θ
(ϑ) =
1
√
2πσ
2
e
−
ϑ
2
2σ
2
. (26)
The calculation of the expectation value can be
done analytically once again, resulting in
e
norm
= E[sin
2
(θ)] (27)
=
Z
∞
−∞
f
norm
θ
(ϑ) ·sin
2
(ϑ)dϑ (28)
=
1
√
2πσ
2
Z
∞
−∞
sin
2
(ϑ) ·e
−
ϑ
2
2σ
2
dϑ (29)
=
1
2
(1−e
−2σ
2
) (30)
The error parameter of the normal distribution is
thus a monotonically increasing function of σ , obtai-
ning a value of 0 for σ = 0 and approaching 0.5 as
σ → +∞ , but its value never exceeds 0.5 , as opposed
to the uniform distribution’s e
uni
.
4.4 Comparison of Different Models
To obtain a more appropriate comparison between
them, we parametrized the three previously mentio-
ned distributions to have the same mean and variance
(0 and σ
2
): a two-point distribution T (−σ, σ, 0.5) , a
uniform distribution U(−
√
3σ,
√
3σ) and a normal
distribution N (0,σ
2
) . The parameter of the uniform
distribution is reparametrized as
e
uni
=
1
2
−
sin(
√
3σ)cos(
√
3σ)
2
√
3σ
. (31)
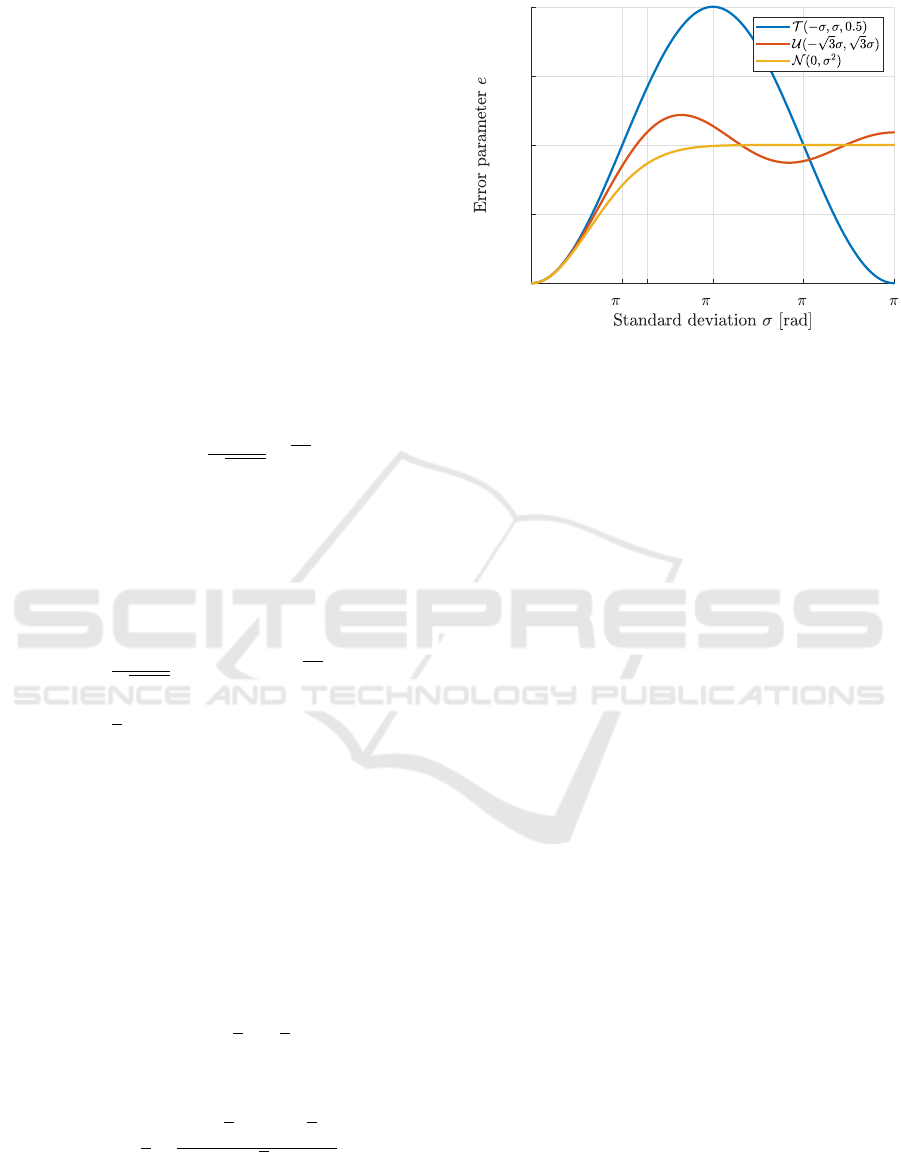
In Fig. 4, we can see the error parameters of
all three distributions as the function of standard de-
viation σ . The three curves are distinctly different
0
/4
1
/2 3 /4
0
0.25
0.5
0.75
1
Figure 4: Error parameter e as a function of standard devia-
tion σ in case of a two-point, a uniform and a normal rotation
angle distribution.
when shown for a wide range of standard deviation,
σ ∈ [0, π] , However, zooming in on the section with
the most physical significance, when σ is small, would
reveal that the e values are very similar across all these
distributions. Quantitatively, for a given standard de-
viation σ < σ
A,B
0
– except for σ = 0 , where e is identi-
cally zero) –, the two-point distribution has a higher
error parameter than both the uniform and the normal,
while the uniform distribution has a higher e compared
to the normal. Given two distributions A and B, the
limit deviation σ
A,B
0
is the highest standard deviation,
for which
e
B
(σ) ≤ e
A
(σ),∀σ : 0 < σ ≤ σ
A,B
0
. (32)
The respective approximate limit deviations for the
three distributions are the following: σ
tp,uni
0
≈ 2.409 ,
σ
tp,norm
0
≈ 2.356 , σ
uni,norm
0
≈ 1.816 . All these values
represent high standard deviations with respect to po-
larization rotation, far from the small-angle approxi-
mation for which the theoretical normal distribution
caused by turbulence was derived. We examined the
differences for 0 < σ < 0.2 rad , which is still a wider
range than for which the approximations hold, and
found that they are almost negligible (Fig. 5). The
absolute (defined as e
tp
−e
norm
and e
uni
−e
norm
) and
relative differences (normalized by e
norm
in both cases)
for small σ are monotonically increasing with growing
standard deviation. For σ = 0.2 , the higher absolute
difference is ∼ 1.028·10
−3
, while the higher relative
difference is ∼2.67 ·10
−2
.
Quantum Bit Error Rate Analysis of the Polarization based BB84 Protocol in the Presence of Channel Errors
187

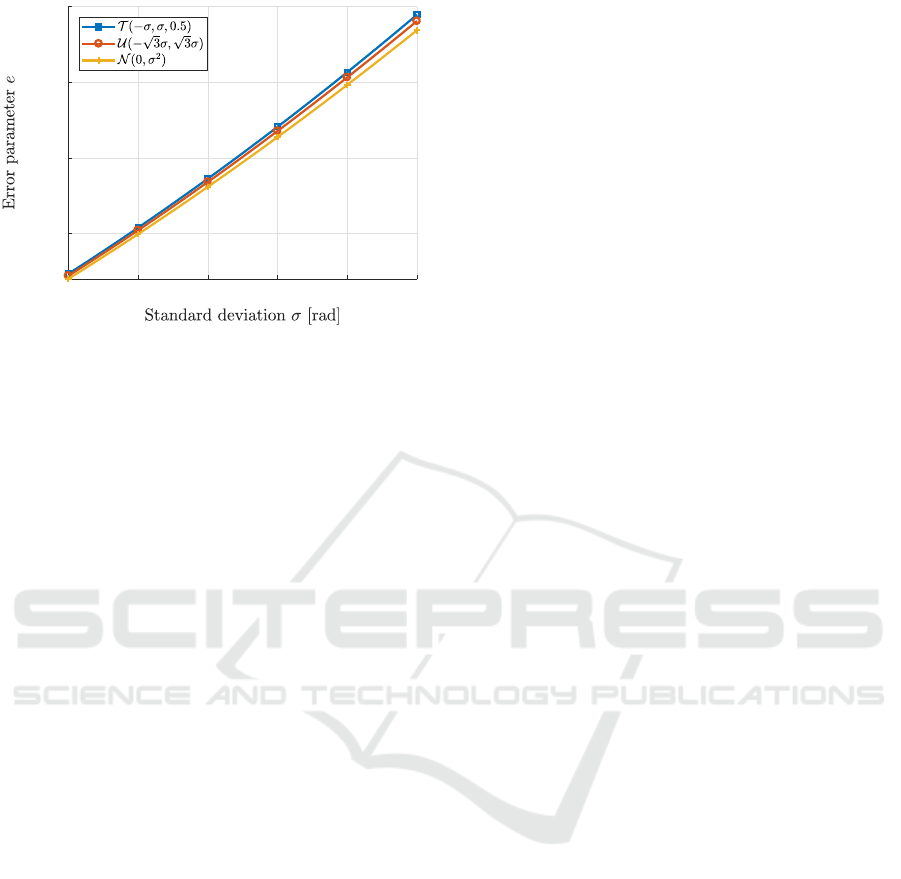
0.15 0.16 0.17 0.18 0.19 0.2
0.025
0.03
0.035
0.04
Figure 5: Close-up of the error parameter e as a function of
standard deviation σ for the three different distributions for
small values of σ.
5 PRACTICAL APPLICATIONS
IN QKD SYSTEMS
The framework and the results derived in previous
sections can be used in practical QKD systems to ana-
lyze what portion of the QBER is a result of channel
errors and/or polarization switching in the transmitter,
and what is the portion that cannot be described by
these factors, presumably originating from eavesdrop-
ping.
The QKD transmitter is assumed to be inaccessible
by Eve, and we can observe its behaviour to almost
full extent, therefore we presume to possess accurate
information about its polarization switching rate, the r
parameter. In a perfect channel, the measured QBER
ratio E
0,0,r
can be easily corrected by subtracting 0.5·r ,
to see what percentage of the errors originate from
other sources, mostly eavesdropping.
The advantage of the framework is that there is no
need to have an accurate description of the channel
in terms of the probability distribution of polarization
angle rotation. After obtaining a measurement about
the standard deviation the channel’s polarization angle
rotation and calculating the worst-case error parameter
(which looks to be that of the two-point distribution,
but it needs to be proven), we can correct our measu-
red QBER. The corrected value will tell us a rough
number of how much information the potential ea-
vesdropper has gained, making it easier to find the
optimal rejection threshold value. Not that since error
variance measurements describe the whole channel,
there remains the question of how the error parameters
of the two channel sections relate to that of the full,
eavesdropping-free channel, a problem that depends
on Eve’s exact location, presumed to be unknown by
Alice and Bob.
In a practical situation, where protection against
eavesdropping is the main goal, it is safer to choose
the model with the highest possible error parameter
to derive the final rejection threshold of QBER, above
which the presence of an eavesdropper is presumed.
The damages resulting from aborting the process even
in the absence of eavesdropping due to an overestima-
tion of error would be very rare if σ is small, because
of the low differences between the error parameters of
the analyzed distributions. Additionally, a false abor-
tion is still better than to underestimate the error, and
let an eavesdropped process continue, allowing Eve to
gain significant information about the key.
6 CONCLUSION
We have seen that by introducing a simple model we
can describe the effects of device and channel imper-
fections on the QBER of the polarization-qubit based
BB84 QKD protocol. This can help determine the
two communicating parties the approximate portion
of QBER originating from eavesdropping, thus the
information possibly gained by the unauthorized ea-
vesdropper. QBER formulae have been derived for
all possible combinations of errors described in the
model, assuming that Eve uses a simple intercept-and-
resend attack strategy. Different channel models were
analyzed and their respective error parameters were
calculated and compared, with a high emphasis on the
case of small polarization angle rotations.
Further examination of the possible PDFs descri-
bing the channel’s polarization angle rotation is ne-
cessary, to prove whether the two-point distribution is
indeed the one with the highest error parameter for a
given standard deviation, in the case of small deviati-
ons.
ACKNOWLEDGEMENTS
This research was supported by the National Rese-
arch Development and Innovation Office of Hungary
within the Quantum Technology National Excellence
Program (Project No. 2017-1.2.1-NKP-2017-00001).
REFERENCES
Bennett, C. H. and Brassard, G. (1984). Quantum cryp-
tography: Public key distribution and coin tossing.
In Proceedings of IEEE International Conference on
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
188

Computers, Systems and Signal Processing, volume
175, page 8. IEEE.
Bruß, D., Cinchetti, M., D’Ariano, G. M., and Macchiavello,
C. (2000). Phase-covariant quantum cloning. Physical
Review A, 62(1):012302.
Martín-Regalado, J., Prati, F., San Miguel, M., and Abraham,
N. (1997). Polarization properties of vertical-cavity
surface-emitting lasers. IEEE Journal of Quantum
Electronics, 33(5):765–783.
San Miguel, M., Feng, Q., and Moloney, J. V. (1995). Light-
polarization dynamics in surface-emitting semiconduc-
tor lasers. Physical Review A, 52(2):1728.
Schranz, Á. and Udvary, E. (2018). Transmitter design pro-
posal for the BB84 quantum key distribution protocol
using polarization modulated vertical cavity surface-
emitting lasers. In Proceedings of the 6th International
Conference on Photonics, Optics and Laser Techno-
logy, pages 252–258.
Strohbehn, J. and Clifford, S. (1967). Polarization and angle-
of-arrival fluctuations for a plane wave propagated
through a turbulent medium. IEEE Transactions on
Antennas and Propagation, 15(3):416–421.
Wootters, W. K. and Zurek, W. H. (1982). A single quantum
cannot be cloned. Nature, 299(5886):802–803.
Zhang, J., Ding, S., Zhai, H., and Dang, A. (2014). Theo-
retical and experimental studies of polarization fluctu-
ations over atmospheric turbulent channels for wire-
less optical communication systems. Optics express,
22(26):32482–32488.
Zhang, J., Li, R., and Dang, A. (2016). Experimental studies
on characteristics of polarization parameters over at-
mospheric turbulence. In ECOC 2016; 42nd European
Conference on Optical Communication; Proceedings
of, pages 1–3. VDE.
Zhang, J., Li, Z., and Dang, A. (2018). Performance of
wireless optical communication systems under pola-
rization effects over atmospheric turbulence. Optics
Communications, 416:207–213.
Quantum Bit Error Rate Analysis of the Polarization based BB84 Protocol in the Presence of Channel Errors
189