Using Synchronizing Heuristics to Construct Homing Sequences

Berk Çiri¸sci

, M. Yu¸sa Emek

, Ege Sorguç

, Kamer Kaya

and Husnu Yenigun

Computer Science and Engineering, Sabanci University, Istanbul, Turkey

Computer Engineering, Middle East Technical University, Ankara, Turkey

Keywords:

Finite State Machines, Homing Sequences, Synchronizing Sequences.

Abstract:

Computing a shortest synchronizing sequence of an automaton is an NP-Hard problem. There are well-known

heuristics to ﬁnd short synchronizing sequences. Finding a shortest homing sequence is also an NP-Hard prob-

lem. Unlike existing heuristics to ﬁnd synchronizing sequences, homing heuristics are not widely studied. In

this paper, we discover a relation between synchronizing and homing sequences by creating an automaton

called homing automaton. By applying synchronizing heuristics on this automaton we get short homing se-

quences. Furthermore, we adapt some of the synchronizing heuristics to construct homing sequences.

1 INTRODUCTION

In model based testing (Broy et al., 2005) and in par-

ticular, for ﬁnite state machine based testing (Lee and

Yannakakis, 1996), test sequences are designed to be

applied at a designated state. For the test sequence

to be applied, the implementation under test must be

brought to this particular state, which is accomplished

by using a ﬁnal state recognition sequence, such as a

synchronizing sequence or a homing sequence (Ko-

havi, 1978; Lee and Yannakakis, 1996).

A synchronizing sequence is an input sequence

such that when this input sequence is applied, the sys-

tem moves to a particular state, regardless of the ini-

tial state of the system. On the other hand, a hom-

ing sequence is an input sequence such that when this

sequence is applied to the system, the response ob-

served from the system makes it possible to identify

the ﬁnal state reached. Note that, using homing se-

quences requires one to observe the reaction of the

system under test to the sequence applied. However

when a synchronizing sequence is used, no such ob-

servation is required. Therefore, one may prefer to

use a synchronizing sequence for ﬁnal state identiﬁ-

cation. Unfortunately, a synchronizing sequence may

not exist for a ﬁnite state machine, whereas a homing

sequence always exists for a minimal, deterministic,

and completely speciﬁed FSMs (Kohavi, 1978; Broy

et al., 2005; Lee and Yannakakis, 1996).

Whether one uses a synchronizing sequence or a

homing sequence, it is obviously preferable to use

a sequence as short as possible. Unfortunately, the

problem of ﬁnding a shortest synchronizing sequence

and ﬁnding a shortest homing sequence is known to

be NP–hard (Eppstein, 1990; Broy et al., 2005).

There exist heuristic algorithms, known as syn-

chronizing heuristics, for constructing short syn-

chronizing sequences. Among such heuristics are

Greedy (Eppstein, 1990), Cycle (Trahtman, 2004),

SynchroP (Roman, 2009), SynchroPL(Roman, 2009),

FastSynchro (Kudlacik et al., 2012), and forward

and backward synchronization heuristics (Roman and

Szykula, 2015).

Although synchronizing heuristics are widely

studied in the literature, to the best of our knowledge,

there does not exist many (if not any) heuristic algo-

rithm to construct short homing sequences, apart from

a variant of the algorithm given as Fast–HS in Sec-

tion 5 (see e.g. (Broy et al., 2005)), which originally

appeared in (Ginsburg, 1958; Moore, 1956).

In this paper, we suggest several homing heuristics

to construct short homing sequences. We ﬁrst deﬁne

an automaton called a homing automaton (see e.g.

Figure 3) of a given ﬁnite state machine (see e.g. Fig-

ure 2). We show that a synchronizing sequence of the

homing automaton is a homing sequence of the given

ﬁnite state machine (for example, aa is a homing se-

quence for the ﬁnite state machine in Figure 2 and it

is also a synchronizing sequence for the automaton in

Figure 3.

This allows us to use the existing synchronizing

heuristics as heuristic algorithms to construct short

homing sequences for the given ﬁnite state machine.

We then show how the existing synchronizing heuris-

362

Çiri¸sci, B., Emek, M., Sorguç, E., Kaya, K. and Yenigun, H.

Using Synchronizing Heuristics to Construct Homing Sequences.

DOI: 10.5220/0007403503620369

In Proceedings of the 7th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2019), pages 362-369

ISBN: 978-989-758-358-2

tics can be modiﬁed to work directly on the given

ﬁnite state machine to construct homing sequences.

We present an experimental study to assess the per-

formance of these approaches as well.

In (Güniçen et al., 2014), a similar relation was

studied between distinguishing sequences of a ﬁnite

state machine and the synchronizing sequences of an

automaton derived from the given ﬁnite state ma-

chines. Our work has been inspired from (Güniçen

et al., 2014). However, we deﬁne the automaton from

the given ﬁnite state machine differently compared

to (Güniçen et al., 2014), so that the synchronizing

sequences of the automaton corresponds to the hom-

ing sequences (not to the distingushing sequences) of

the given ﬁnite state machine. In addition, we suggest

modiﬁcations of the existing synchronizing heuristics

that allows us to use these heuristics directly on the

ﬁnite state machine.

A similar work also appeared in (Kushik and

Yevtushenko, 2015). However, (Kushik and Yev-

tushenko, 2015) considers nondeterministic ﬁnite

state machines, whereas in our work we consider de-

terministic ﬁnite state machines. When the approach

is considered as restricted to the deterministic case,

it becomes possible to use efﬁcient synchronizing

heuristics developed for deterministic automata for

computing homing sequences.

The rest of the paper is organized as follows. Sec-

tion 2 introduces the notation and gives the back-

ground. Section 3 shows how we form the relation

between the synchronizing sequences and the homing

sequences. We introduce two synchronizing heuris-

tics existing in the literature that one can use to derive

homing sequences in Section 4. We then show in Sec-

tion 5 how the synchronizing heuristics introduced in

Section 4 can be modiﬁed to be applied on the ﬁnite

state machines directly. The experimental study that

we have performed together with concluding remarks

are given in Section 6.

2 PRELIMINARIES

A Deterministic Finite Automaton (DFA) (or simply

an automaton) is a triple A = (S,X,δ) where S is a

ﬁnite set of states, X is a ﬁnite set of alphabet (or

input) symbols, and δ : S ×X → S is a transition func-

tion. When δ is a total (resp. partial) function, A is

called complete (resp. partial). In this work we only

consider complete DFAs unless stated otherwise.

A Deterministic Finite State Machine (FSM) is

a tuple M = (S,X,Y,δ,λ) where S is a ﬁnite set of

states, X is a ﬁnite set of alphabet (or input) symbols,

Y is a ﬁnite set of output symbols, δ : S × X → S is

Figure 1: An automaton A

b/1

b/0

a/0

b/1

a/1

a/0

Figure 2: An FSM M

a transition function, and λ : S × X → Y is an output

function. In this work, we always consider complete

FSMs, which means the functions δ and λ are total

functions.

An automaton and an FSM can be visualized as a

graph, where the states correspond to the nodes and

the transitions correspond to the edges of the graph.

For an automaton the edges of the graph are labeled

by input symbols, whereas for an FSM the edges are

labeled by an input and an output symbol. In Figure 1

and Figure 2, an example automaton and an example

FSM are given.

An input sequence ¯x ∈ X



is a concatenation of

zero or more input symbols. More formally, an input

sequence ¯x is a sequence of input symbols x

...x

for some k ≥ 0 where x

,...,x

∈ Σ. As can be

seen from the deﬁnition, an input sequence may have

no symbols; in this case it is called the empty se-

quence and denoted by ε.

For both automata and FSMs, the transition func-

tion δ is extended to input sequences as follows.

For a state s ∈ S, an input sequence ¯x ∈ X



and an

input symbol x ∈ X, we let

δ(s,ε) = s,

δ(s,x ¯x) =

δ(δ(s,x), ¯x). Similarly, the output function of FSMs

is extended to input sequences as follows:

λ(s,ε) = ε,

λ(s,x ¯x) = λ(s,x)

λ(δ(s,x), ¯x). By abusing the notation

we will continue using the symbols δ and λ for

δ and

Using Synchronizing Heuristics to Construct Homing Sequences

363

λ, respectively.

Finally for both automata and FSMs, the transition

function δ is extended to a set of states as follows. For

a set of states S

⊆ S and an input sequence ¯x ∈ X



δ(S

, ¯x) = {δ(s, ¯x) | s ∈ S

An FSM M = (S,X,Y,δ,λ) is said to be minimal

if for any two different states s

∈ S, there exists an

input sequence ¯x ∈ Σ



such that λ(s

, ¯x) 6= λ(s

, ¯x).

Deﬁnition 1. For an FSM M = (S, X,Y,δ,λ), a

Homing Sequence (HS) of M is an input sequence

H ∈ X



such that for all states s

∈ S, λ(s

H) =

λ(s

H) =⇒ δ(s

H) = δ(s

H).

Intuitively, an HS

H is an input sequence such that

for all states output sequence to

H uniquely identiﬁes

the ﬁnal state. In other words, if the current state of

an FSM is not known, then a homing sequence can

be applied to the FSM and the output sequence pro-

duced by the FSM will tell us the ﬁnal state reached.

A homing sequence is also called a homing word in

the literature.

For FSM M

given in Figure 2 aa is an HS. If M is

minimal, then there certainly exists an HS for M (Ko-

havi, 1978). If M is not minimal, there may also be

an HS for M. Furthermore, when M is not minimal, it

is always possible to ﬁnd an equivalent minimal FSM

such that M

is minimal (Kohavi, 1978).

Deﬁnition 2. For an automaton A = (S,X,δ), a Syn-

chronizing Sequence (SS) of A is an input sequence

R ∈ X



such that |δ(S,

R)| = 1.

A synchronizing sequence is also called a reset se-

quence in the literature. An automaton does not nec-

essarily have an SS. It is known that the existence of

an SS for an automaton can be checked in polynomial

time (Eppstein, 1990).

For a set of states C ⊆ S we use the notation C

{{s

}|s

∈ C} to denote the set of multisets with

cardinality 2 with elements from C, i.e C

is the set

of all subsets of C with cardinality 2, where repetition

is allowed. An element {s

} ∈ C

is called a pair.

Furthermore it is called a singleton pair (or an s–pair)

if s

= s

, otherwise it is called a different pair (or a d–

pair). The set of s–pairs and d–pairs in C

is denoted

by C

and C

respectively. A sequence (word) w is

said to be a merging sequence for a pair {s

} ∈ S

if δ({s

},w) is a singleton. Note that for an s–pair,

every sequence (including ε) is a merging sequence.

3 THE RELATION BETWEEN

HOMING SEQUENCES AND

SYNCHRONIZING SEQUENCES

In this section, we will derive an automaton A

from

a given FSM M. We call A

the the homing automa-

ton of M. The construction of A

from M is similar

to the construction of product automaton (as exists in

the literature) from a given automaton to analyse the

existence of and to ﬁnd synchronizing sequences.

Deﬁnition 3. Let M = (S, X ,Y,δ,λ) be an FSM. The

homing automaton (HA) A

of M is an automaton

= (S

,X,δ

) which is constructed as follows:

- The set S

consists of all 2-element subsets

of S and an extra state q



. Formally we have

= {{s

} | s

∈ S ∧ s

6= s

} ∪ {q



- The transition function δ

is deﬁned as follows:

• For an input symbol x ∈ X, δ



,x) = q



• For q = {s

} ∈ S

and an input symbol x ∈ X,

– If δ(s

,x) = δ(s

,x)), then δ

(q,x) = q



– If λ(s

,x) 6= λ(s

,x)), then δ

(q,x) = q



– Otherwise, δ

(q,x) = {δ(s

,x),δ(s

,x)}.

As an example, the HA for FSM M

given in Fig-

ure 2 is depicted in Figure 3.

Lemma 1. Let M = (S,X,Y, δ, λ) be an FSM, A

,X,δ

) be the HA of M. For an input sequence

¯x ∈ X



, (λ(s

, ¯x) 6= λ(s

, ¯x))∨(δ(s

, ¯x) = δ(s

, ¯x)) ⇐⇒

({s

}, ¯x) = q



Proof. Let ¯x = ¯x

x ¯x

where ¯x

, ¯x

∈ X



and x ∈

X such that (δ(s

, ¯x

) 6= δ(s

, ¯x

)) ∧ (λ(s

, ¯x

) =

λ(s

, ¯x

)). So the new state according to δ

= {δ(s

, ¯x

),δ(s

, ¯x

)}. If λ(s

, ¯x

x) 6= λ(s

, ¯x

x) then

,x) = q



and δ



, ¯x

) = q



. If λ(s

, ¯x

x) =

λ(s

, ¯x

x) but δ(s

, ¯x

x) = δ(s

, ¯x

x) then δ

,x) = q



and δ



, ¯x

) = q



For the reverse direction, again writing ¯x = ¯x

x ¯x

where ¯x

, ¯x

∈ X



and x ∈ X such that δ

({s

}, ¯x

) =

} for some states s

and δ

({s

}, ¯x

x) = q



This means that λ(s

, ¯x

) = λ(s

, ¯x

) and δ(s

, ¯x

) 6=

δ(s

, ¯x

) but after consuming input x, λ(s

, ¯x

x) 6=

λ(s

, ¯x

x) where x is the ﬁrst input which forces FSM

to produce different outputs. Or δ(s

, ¯x

x) = δ(s

, ¯x

x),

in this case x is the merging input. This proves that

(λ(s

, ¯x) 6= λ(s

, ¯x)) ∨ (δ(s

, ¯x) = δ(s

, ¯x)).

We can now give the following theorem that states

the relation between HSs of M and SSs of A

Theorem 1. Let M = (S,X,Y,δ,λ) be an FSM and

= (S

,X,δ

) be the HA of M. An input sequence

¯x ∈ X



is an HS for M iff ¯x is an SS for A

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

364

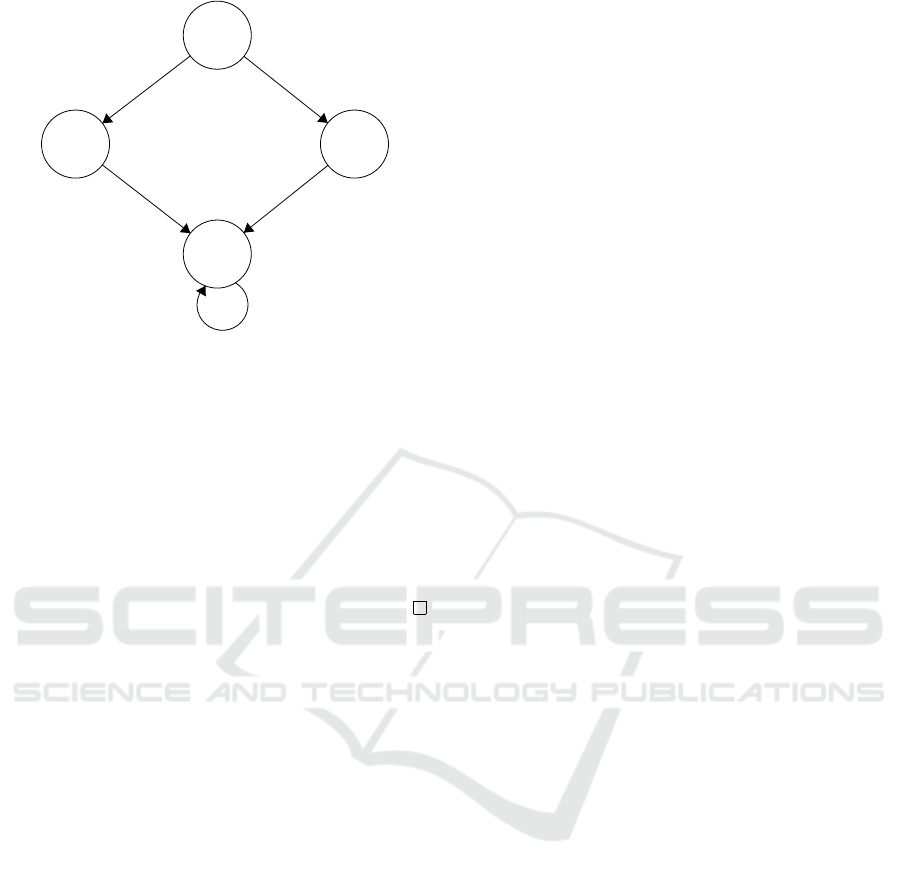
{0,1}

{0,2} {1,2}



a,b

Figure 3: A

of M

in Figure 2.

Proof. If ¯x is an HS of M, for any two states s

and s

in M, λ(s

, ¯x) 6= λ(s

, ¯x) or δ(s

, ¯x) = δ(s

, ¯x). Lemma

1 states that δ

({s

}, ¯x) = q



for any {s

} ∈ S

For q



, δ



, ¯x) = q



. Hence ¯x is an SS for A

If ¯x is an SS for A

, ﬁrst note that δ



, ¯x) = q



For any state of A

of the form {s

}, we must also

have δ

({s

}, ¯x) = q



. From the other direction of

Lemma 1, we have for any pair of states λ(s

, ¯x) 6=

λ(s

, ¯x) or δ(s

, ¯x) = δ(s

, ¯x).

For example, consider the Homing Automaton A

given in Figure 3 of the FSM M

given in Figure 2.

One can see that aa is an HS for M

and it is also an

SS for A

4 SYNCHRONIZING

HEURISTICS FOR HOMING

AUTOMATON

Although ﬁnding a shortest SS is known to be an NP-

Hard problem, ﬁnding a short SS by applying heuris-

tics is studied widely. As shown in Theorem 1, ﬁnd-

ing an HS for an FSM M is equivalent to ﬁnding an SS

for its corresponding homing automaton A

. Based

on Theorem 1, we can apply widely known SS heuris-

tics to A

in order to ﬁnd a possibly short HS for FSM

M. Please recall that an SS may not exist for an au-

tomaton in general. However, for a homing automa-

ton of a minimal FSM, an SS will always exist due to

Theorem 1.

Among such SS heuristics, Greedy is one of the

fastest and the earliest that appeared in the litera-

ture (Eppstein, 1990). Other than Greedy heuristic,

SynchroP is one of the best known heuristics in terms

of ﬁnding short SSs (Roman, 2005). Although, Syn-

chroP is good in terms of length, it is slow compared

to Greedy since it performs a deeper analysis on the

automaton.

Both Greedy and SynchroP heuristics have two

phases. Phase 1 is common in these heuristics. The

purpose of Phase 1 is to compute a shortest merging

word τ

{i, j}

for each {s

} ∈ S

. This computation

is performed by using a backward breadth ﬁrst search

(see e.g. Figure 4 in (Cirisci et al., 2018)), rooted at

s-pairs {s

} ∈ S

, where these s-pair nodes are the

nodes at level 0 of the BFS forest. A d-pair {s

} ap-

pears at level k of the BFS forest if |τ

{i, j}

| = k. When

the automaton has a synchronizing sequence, each d-

pair should have a merging word since it is a nec-

essary condition for synchronizing automata (Epp-

stein, 1990). Phase 1 requires Ω(n

) time since each

} ∈ S

is considered exactly once.

Even though Phase 2 of Greedy and Phase 2 of

SynchroP (e.g. see Figure 5 and Figure 6 in (Cirisci

et al., 2018)) are different, they are quite similar. For

both algorithms, Phase 2 keeps track of a set of ac-

tive states C and iteratively reduces the cardinality of

C. In each iteration, a d-pair {s

} ∈ C

in the ac-

tive states is selected to be merged. After selecting

}, the current (active) state set C is updated by

applying τ

{i, j}

, i.e. C is updated as δ(C, τ

{i, j}

). Ap-

plying τ

{i, j}

will deﬁnitely merge {s

}, and it may

merge some more states in C as well. This process

will iterate until all states are merged so that C be-

comes singleton.

Phase 2 of Greedy and Phase 2 of SynchroP only

differ in the way they select the d-pair {s

} ∈ C

to be used in an iteration. While Greedy simply con-

siders a d-pair {s

} ∈ C

having a shortest merg-

ing word τ

{i, j}

, SynchroP selects a d-pair {s

} ∈ C

such that ϕ(δ(C,τ

{i, j}

)) is minimized, where ϕ(S

) for

a set of states S

⊆ S is deﬁned as:

ϕ(S

) =

∑

∈S

|τ

{i, j}

ϕ(S

) is a heuristic indication of how hard is to

bring set S

to a singleton. The intuition here is that,

the larger the cost ϕ(S

) is, the longer a synchroniz-

ing sequence would be required to bring S

to a sin-

gleton set. For an automaton with p input symbols

and n states, the common ﬁrst phase of Greedy and

SynchroP needs O(pn

) time (Eppstein, 1990). The

second phase of Greedy can be implemented to run

in O(n

) time (Eppstein, 1990), whereas the second

phase of SynchroP runs in O(n

) time (Roman, 2005).

Therefore, the overall time complexity for Greedy is

O(pn

+ n

) and for SynchroP it is O(pn

+ n

As suggested by Theorem 1, in order to construct

a homing sequence for an FSM M, one can ﬁrst con-

Using Synchronizing Heuristics to Construct Homing Sequences

365

struct the homing automaton A

of M, and then use

Greedy or SynchroP heuristics to ﬁnd a synchronizing

sequence for A

, which will be a homing sequence

for M. Constructing the homing automaton A

M = (S,X,Y, δ, λ) would require O(pn

) time where

p = |X| and n = |S|. Note that the number of states of

is 1 +n(n−1)/2, and A

still has p input symbols

(see Deﬁnition 3). Therefore, applying Greedy to A

requires O(pn

+ n

) time, and applying SynchroP to

requires O(pn

+ n

). These complexities would

allow one to use synchronizing heuristics on homing

automaton only for FSMs with small number of states

in practice.

In the next section, we consider adapt-

ing/modifying the synchronizing heuristics to

construct a homing sequence directly from the FSM,

without constructing a homing automaton.

5 ADAPTING SYNCHRONIZING

HEURISTICS FOR HOMING

SEQUENCE CONSTRUCTION

The high computational complexity of applying syn-

chronizing heuristics on homing automata results

from the fact that, the homing automata already have

the number of states squared compared to the number

of states of the corresponding FSM. In this section,

we present heuristic algorithms that work directly on

the FSM.

Inspired by the synchronizing heuristics that are

given in Section 4, we implemented three differ-

ent homing heuristics, Fast–HS, Greedy–HS and

SynchroP–HS, for constructing a homing sequence of

an FSM. These homing heuristics consist of two sepa-

rate phases, as in the case of synchronizing heuristics.

Phase 1 is common in all these heuristics and

given as Algorithm 4. In Phase 1, a shortest homing

word τ

{i, j}

for each {s

} ∈ S

is computed by using

a breadth ﬁrst search. Generation of the BFS forest is

very similar to what is done in synchronizing heuris-

tics, except that a d-pair {s

} that gives different

outputs for its states, i.e. when λ(s

,x) 6= λ(s

,x) for

an input symbol x ∈ Σ, is located at level 1 of the for-

est by setting τ

{i, j}

= x.

Similar to the synchronizing heuristics, Phase 2

of homing heuristics iteratively builds a homing se-

quence. In each iteration, again a pair {s

} is

picked (how this pair is picked depends on the heuris-

tic used), and the corresponding homing word τ

{i, j}

appended to the homing sequence Γ accumulated so

far. However, instead of tracking the set of states yet

to be merged, the set D of state pairs yet to be homed

Algorithm 1: Phase 1 of Homing Heuristics.

Input : An FSM M = (S,Σ,O,δ,λ)

Output : A homing word for all {s

} ∈ S

1: Q ← an empty queue  Q: BFS frontier

2: P ←

0  P: nodes of BFS forest constructed

3: for {s

} ∈ S

4: push {s

} onto Q

5: insert {s

} into P

6: set τ

{i,i}

← ε

7: end for

8: for ({s

} ∈ S

) ∧ ({s

} 6∈ P) do

9: for x ∈ Σ do

10: if λ(s

,x) 6= λ(s

,x) then

11: push {s

} onto Q

12: insert {s

} into P

13: set τ

{i, j}

← x

14: end if

15: end for

16: end for

17: while P 6= S

18: {s

} ← pop next item from Q

19: for x ∈ Σ do

20: for {s

} ∈ δ

−1

({s

},x) do

21: if {s

} 6∈ P then

22: τ

{k,l}

← xτ

{i, j}

23: push {s

} onto Q

24: P ← P ∪ {{s

}}

25: end if

26: end for

27: end for

28: end while

are tracked. Initially, S is set to S

, i.e. all d–pairs.

When the set of d–pairs yet to be merged becomes

the empty set, the iterations stop.

Phase 2 of Fast–HS (Algorithm 2) does not per-

form a search in the set of d–pairs but it randomly

selects a d–pair from the current d–pair set to home.

Unlike Fast–HS, in Phase 2 of Greedy–HS (Algo-

rithm 3) the d-pair to be selected is searched among

all d–pairs yet to be homed in D, and the d-pair that

has a shortest homing word is selected.

Phase 2 of SynchroP–HS (Algorithm 4) performs

a deeper analysis. Similar to synhronizing heuristic

SynchroP, the homing heuristic SynchroP–HS iterates

through the all the d–pairs in D and determines the d–

pair to be homed according to the Φ cost given below,

where D is a set of d–pairs and τ

{i, j}

is the homing

word for the d–pair {s

Φ(D) =

∑

}∈D

|τ

{i, j}

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

366

Algorithm 2: Phase 2 of Fast–HS.

Input : An FSM M = (S,Σ,O,δ,λ),τ

{i, j}

for

all {s

} ∈ S

Output : Homing sequence Γ for M

1: D ← S

 D: current set of d–pairs

2: Γ ← ε  HS to be constructed, initially empty

3: while D 6=

0 do  There are pairs to be homed

4: Let {s

} be a random pair from D

5: Γ ← Γτ

{i, j}

6: D

←

7: for {s

} ∈ D do

8: if δ(s

,τ

}

) 6= δ(s

,τ

}

) and

λ(s

,τ

}

) = λ(s

,τ

}

) then

9: insert δ({s

},τ

{i, j}

) into D

10: end if

11: end for

12: D ← D

13: end while

Algorithm 3: Phase 2 of Greedy–HS.

Input : An FSM M = (S,Σ,O,δ,λ),τ

{i, j}

for

all {i, j} ∈ S

Output : Homing sequence Γ for M

1: D ← S

 D: current set of d–pairs

2: Γ ← ε  HS to be constructed, initially empty

3: while D 6=

0 do  There are pairs to be homed

4: {s

} ← argmin

}∈D

|τ

{k,l}

5: Γ ← Γτ

{i, j}

6: D

←

7: for {s

} ∈ D do

8: if δ(s

,τ

{i, j}

) 6= δ(s

,τ

{i, j}

) and

λ(s

,τ

{i, j}

) = λ(s

,τ

{i, j}

) then

9: insert δ({s

},τ

{i, j}

) into D

10: end if

11: end for

12: D ← D

13: end while

6 EXPERIMENTS AND

CONCLUSION

In this section, we explain the experimental study

we have conducted to assess the performance of the

heuristics suggested in this paper. Similar to the other

works in the literature, we used randomly generated

FSMs in our experiments, where for each state s

∈ S

and for each input symbol x ∈ X, the next state δ(s

,x)

is randomly set to a state s

∈ S, and the output λ(s

,x)

is randomly set to an output symbol y ∈ Y .

We experimented with FSMs with number of

Algorithm 4: Phase 2 of SynchroP–HS.

Input : An FSM M = (S,Σ,O,δ,λ),τ

{i, j}

for

all {i, j} ∈ S

Output : Homing sequence Γ for M

1: D ← S

 D: current set of d–pairs

2: Γ ← ε  HS to be constructed, initially empty

3: while D 6=

0 do  There are pairs to be homed

4: for {s

} ∈ D do

5: D

{i, j}

←

6: for {s

} ∈ D do

7: if δ(s

,τ

{i, j}

) 6= δ(s

,τ

{i, j}

) and

λ(s

,τ

{i, j}

) = λ(s

,τ

{i, j}

) then

8: insert δ({s

},τ

{i, j}

) into D

{i, j}

9: end if

10: end for

11: end for

12: {s

} ← argmin

}∈D

Φ(D

{k,l}

)

13: D ← D

{i, j}

14: end while

states n ∈ {32,64}, the number of input symbols

p ∈ {2,4,8}, and the number of output symbols q ∈

{2,4,8}. For each combination of n, p,q values, we

generated 100 random FSMs. Hence a total of 1800

FSMs are used in the experiments. All algorithms are

implemented in C++ and the times elapsed are mea-

sured in terms of microseconds.

We implemented 2 synchronizing heuristics

which ﬁnd synchronizing sequences (corresponding

to a homing sequence on the FSM) on homing au-

tomata. These are Greedy and SynchroP heuristics

given in Section 4. After creating the HA A

ex-

plained in Section 3, we applied the implemented syn-

chronizing heuristics on the A

. The time required

for constructing the homing automaton can be seen

in the column HA Time in Table 1. Compared to the

rest of the algorithm, the time required for the con-

struction of A

is negligible. Greedy and SynchroP

share the ﬁrst phase. The column P1 Time in Table 1

gives the time for this common phase 1. As known

from the literature, Phase 1 time dominates Phase 2

time for Greedy, whereas the Phase 2 time dominates

Phase 1 time for SynchroP. Hence, the running time

for Greedy is faster compared to SynchroP. Also as

expected, SynchroP constructs sequences with shorter

lengths compared to Greedy.

We have also implemented a brute–force exponen-

tial time algorithm to construct the shortest homing

sequences. For small states sizes like 32 and 64, it is

possible to compute the shortest homing sequences.

The columns under the Shortest in Table 1 give the

time required to compute and length of the shortest

homing sequences. The experiments show that, at

Using Synchronizing Heuristics to Construct Homing Sequences

367

Table 1: Experiments for using synchronizing heuristics on homing automata.

States Inputs Outputs

Shortest SS based

Length Time HA Time P1 Time

Greedy SynchroP

Length P2 time Length P2 time

32 2 2 6.1 2410 46 11480 7.59 10 6.69 1925547

32 2 4 4.02 320 27 7372 4.79 5 4.32 1134028

32 2 8 3.04 96 16 5493 3.54 3 3.21 465578

32 4 2 5.2 10253 54 10298 7.15 7 6.21 2341436

32 4 4 3.7 580 53 10158 4.69 5 4.07 1306012

32 4 8 3 154 33 7649 3.56 3 3.05 516154

32 8 2 5 41776 127 16875 7.07 7 5.62 2922721

32 8 4 3.19 1590 80 11880 4.67 4 3.92 1328281

32 8 8 2.97 394 69 11249 3.56 3 3.1 561097

64 2 2 7.65 24051 185 240952 9.46 24 8.45 559041289

64 2 4 4.93 2281 161 203926 5.81 22 5.13 359077761

64 2 8 3.73 695 123 202362 4.28 21 3.98 145568201

64 4 2 6.95 278938 447 365706 9.18 24 7.75 795062568

64 4 4 4.25 10815 298 280419 5.69 16 5 428513432

64 4 8 3.12 1052 237 367358 4.24 12 3.81 154977902

64 8 2 6.24 6746717 806 525592 9.04 23 7.33 1000322128

64 8 4 4 19652 628 400603 5.65 16 4.9 456867018

64 8 8 3 1222 459 411719 4.24 13 3.78 154973825

Table 2: Experiments with homing heuristics on FSMs.

States Inputs Outputs

HS based

P1 Time

Fast–HS Greedy–HS SynchroP–HS

Length P2 time Length P2 time Length P2 time

32 2 2 81 7.69 181 7.71 149 7.22 3019

32 2 4 52 4.8 120 4.8 104 4.65 2127

32 2 8 33 3.58 86 3.57 55 3.41 1594

32 4 2 56 7.2 117 7.14 85 6.76 1850

32 4 4 49 4.7 126 4.7 88 4.59 2272

32 4 8 16 3.59 89 3.59 56 3.49 1784

32 8 2 66 7.1 132 7.09 99 6.7 2167

32 8 4 28 4.7 98 4.7 67 4.54 1823

32 8 8 18 3.58 95 3.58 63 3.52 2004

64 2 2 278 9.53 313 9.66 302 9.14 25852

64 2 4 278 5.68 282 5.84 253 5.64 27990

64 2 8 231 4.27 231 4.27 194 4.24 26139

64 4 2 424 9.24 385 9.24 351 8.59 30794

64 4 4 292 5.69 270 5.73 243 5.57 26754

64 4 8 222 4.29 217 4.29 193 4.27 25266

64 8 2 474 9.15 356 9.14 320 8.72 27811

64 8 4 328 5.69 298 5.69 260 5.54 27936

64 8 8 164 4.29 217 4.29 182 4.24 24772

Table 3: Experiments on larger state sizes.

States Inputs Outputs

Fast HS Greedy HS

Length P2 Time Length P2 Time

2048 2 2 19.46 14816 19.57 18509

4096 2 2 21.62 52520 21.47 63327

8192 2 2 23.79 168106 23.76 224572

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

368

least for the small state sizes used in these experi-

ments, the heuristics ﬁnd homing sequences which

are not too long compared to the shortest possible.

On the other hand, the time used by these heuris-

tics indicate that the methods based on using syn-

chronizing heuristics on homing automata will not

scale well. As noted before, the main reason is the

fact homing automata requires squaring the number

of states in the computation.

In order to enhance the time performance, we have

adapted the approach used in synchronizing heuristics

to compute homing sequences directly on FSMs. We

implemented 3 homing heuristics introduced in Sec-

tion 5, namely Fast–HS, Greedy–HS, and SyncrhoP–

HS. We experimented with these heuristics using the

same set of randomly generated FSMs.

Note that the three homing heuristics share their

ﬁrst phase given as Algorithm 4. In all experiments

we measured the time for the Phase 1 of these heuris-

tics (given in P1 Time in Table 2) and the time to home

all d–pairs, which is Phase 2 of heuristics (given in

columns P2 time in Table 2), separately. The time

performance of homing heuristics in Table 2 are much

better compared to the time performance of the syn-

chronizing heuristics given in Table 1. Note that, the

time it takes for these heuristics is much faster (es-

pecially for Greedy–HS and Fast–HS) compared to

the time needed to ﬁnd the shortest homing sequence

given in Table 1. As expected, however, the perfor-

mance on the length of the homing sequences de-

grades slightly, when we use the homing heuristics.

Note that Fast–HS picks the d–pair to be used ran-

domly, whereas Greedy–HS selects the d–pair with

the shortest homing word. Therefore, one would ex-

pect Fast–HS to have faster Phase 2 time compared to

Greedy–HS. Although this doesn’t seem to be the case

for the results given in Table 2, one can see that as the

state size increases (especially when the number of

inputs is small), the speed of Fast–HS becomes ap-

parent. Table 3 shows the experiment that reveals the

difference between speeds of Fast–HS and Greedy–

HS. We also see that as state size grows the gap be-

tween the Phase 1 and Phase 2 time increases such

that Phase 1 of Greedy–HS and Fast–HS is up to 10

times slower than the Phase 2 of these heuristics.

In this work, we have used an idea taken from

(Güniçen et al., 2014) which allows us to use synchro-

nizing heuristics for computing homing sequences.

Similar to the results obtained in (Güniçen et al.,

2014), this work shows how the existing synchroniz-

ing heuristics can be used to compute short homing

sequences. As a future work, the same idea can be

adapted to compute Unique Input Output (UIO) se-

quences as well. Since this problem is known to be

hard (Lee and Yannakakis, 1996), there are heuris-

tics to compute short UIO sequences. From a given

FSM, one can construct an automaton such that a syn-

chronizing sequence (for a subset of states) on this au-

tomaton corresponds to a UIO sequence of the orig-

inal FSM. This would similarly allow us to use ex-

isting synchronizing heuristics to compute UIO se-

quences.

REFERENCES

Broy, M., Jonsson, B., Katoen, J., Leucker, M., and

Pretschner, A., editors (2005). Model-Based Testing

of Reactive Systems, Advanced Lectures, volume 3472

of Lecture Notes in Computer Science. Springer.

Cirisci, B., Kahraman, M. K., Yildirimoglu, C. U., Kaya,

K., and Yenigün, H. (2018). Using structure of au-

tomata for faster synchronizing heuristics. In Proc. of

MODELSWARD’18, pages 544–551.

Eppstein, D. (1990). Reset sequences for monotonic au-

tomata. SIAM J. Comput., 19(3):500–510.

Ginsburg, S. (1958). On the length of the smallest uniform

experiment which distinguishes the terminal states of

a machine. J. ACM, 5(3):266–280.

Güniçen, C.,

Inan, K., Türker, U. C., and Yenigün, H.

(2014). The relation between preset distinguishing

sequences and synchronizing sequences. Formal As-

pects of Computing, 26(6):1153–1167.

Kohavi, Z. (1978). Switching and Finite Automata Theory.

McGraw–Hill, New York.

Kudlacik, R., Roman, A., and Wagner, H. (2012). Effective

synchronizing algorithms. Expert Systems with Appli-

cations, 39(14):11746–11757.

Kushik, N. and Yevtushenko, N. (2015). Describing hom-

ing and distinguishing sequences for nondeterminis-

tic ﬁnite state machines via synchronizing automata.

In Drewes, F., editor, Implementation and Application

of Automata, pages 188–198, Cham. Springer Interna-

tional Publishing.

Lee, D. and Yannakakis, M. (1996). Principles and methods

of testing ﬁnite state machines-a survey. Proceedings

of the IEEE, 84(8):1090–1123.

Moore, M. E. (1956). Gedanken-experiments on sequential

machines. Automata studies, pages 129–153.

Roman, A. (2005). New algorithms for ﬁnding short re-

set sequences in synchronizing automata. In IEC

(Prague), pages 13–17.

Roman, A. (2009). Synchronizing ﬁnite automata with

short reset words. Applied Mathematics and Compu-

tation, 209(1):125–136.

Roman, A. and Szykula, M. (2015). Forward and backward

synchronizing algorithms. Expert Systems with Appli-

cations, 42(24):9512–9527.

Trahtman, A. N. (2004). Some results of implemented al-

gorithms of synchronization. In 10th Journees Mon-

toises d’Inform.

Using Synchronizing Heuristics to Construct Homing Sequences

369