A PSO based Approach to Assign Segments

for Reducing Excavated Soil in Shield Tunneling

Koya Ihara

, Shohei Kato

1,2

, Takehiko Nakaya

, Tomoaki Ogi

and Hiroichi Masuda

Dept. of Computer Science and Engineering, Graduate School of Engineering, Nagoya Institute of Technology,

Gokiso-cho, Showa-ku, Nagoya 466-8555, Japan

Frontier Research Institute for Information Science, Nagoya Institute of Technology,

Gokiso-cho, Showa-ku, Nagoya 466-8555, Japan

Shimizu Corporation, 2-16-1 Kyobashi, Chuo-ku, Tokyo 104-8370, Japan

Keywords:

Constrained Combinatorial Optimization, Genetic Algorithm, Particle Swarm Optimization, Shield Tunneling.

Abstract:

It is expected that artiﬁcial intelligence reduces labor and improves productivity of the shield tunneling, which

is one of tunnel construction methods. In a planning process of the shield tunneling, segments of a tunnel are

assigned along to a predetermined curve called the planning line. Conventionally, skilled engineers manually

assign the segments to minimize gaps between each segment and the planning line. Nevertheless, we have only

to reduce each gap less than a tolerance, and there is a demand to reduce the amount of soil excavated along

to the segments. Handling the reducing gaps as constraints and reducing the amount of excavated soil as an

objective, this paper addresses the segment assignment as a constrained combinatorial optimization problem.

These constraints are severe, and the problem has an extremely narrow feasible region. For this problem, we

proposed the ε constrained integer categorical particle swarm optimization (εICPSO), adapting a constraint

handling method called the ε constrained method to the integer categorical particle swarm optimization. The

effectiveness of the εICPSO to the segment assignment is shown by the two-dimensional simulator experiment

using real construction data. The experimental results show that the proposed method has a potential to reduce

the amount of excavated soil as compared to the conventional method (skilled engineer) while keeping the all

gaps between segments and the planning line falling within the tolerance. The εICPSO statistically performed

the best in all the test problems.

1 INTRODUCTION

In the construction industry of all over the world,

manpower shortage is serious problem. Windapo, A.

O. reported that a skilled labor shortage is preponde-

rant and it contributes to a decrease in productivity

and product quality in the South African construction

industry (Windapo, 2016).

The Japanese construction industry also has pro-

blems: manpower shortage, ageing workers, and de-

crease in international competitiveness. Since No-

vember 2015, the Japanese Ministry of Land, Infra-

structure, Transport and Tourism (MLIT) has been

promoted the i-Construction (Suzuki, 2016), an ef-

fort aiming to optimize and upgrade the whole pro-

cess from investigation and design, construction and

inspection, up to maintenance. Its major concepts are

utilization of information and communication techno-

logy and introducing innovative technology such as

artiﬁcial intelligence (AI) by cooperation between in-

dustries, governments, and academia. Our research

aims to develop a practical construction support sy-

stem according to the i-Construction.

The shield tunneling (Maidl et al., 2013; Japan

Society of Civil Engineers, 2007) is a tunnel con-

struction method used around the globe. It is neces-

sary to construct tunnels under sever conditions such

as urban areas. In the civil engineering and mechani-

cal engineering domains, the shield tunneling techni-

ques have been studied intensively (Koyama, 2003).

There are also a few studies (Suwansawat and Ein-

stein, 2006; Hasanipanah et al., 2016) about shield

tunneling in artiﬁcial intelligence domain. However

no studies have focused planning processes of shield

tunneling. In the planning process, segments of the

tunnel are assigned along to the predetermined plan-

ning line, where the tunnel is expected to be con-

structed. Conventionally, skilled engineers manually

assign the segments to minimize gaps between each

segment and the planning line. Nevertheless, we have

only to reduce each gap less than a tolerance, and

there is a demand to reduce the amount of soil ex-

cavated along to the segments.

It is assume that automation and optimization of

328

Ihara, K., Kato, S., Nakaya, T., Ogi, T. and Masuda, H.

A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling.

DOI: 10.5220/0007407803280336

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 328-336

ISBN: 978-989-758-350-6

the segment assignment contribute to eliminate a skil-

led labor shortage and to improve productivity. This

paper addresses the segment assignment as a constrai-

ned combinatorial optimization problem. This pro-

blem has severe constraints, and its feasible region

is extremely narrow as compared with its large se-

arch space. For optimization problems having severe

constraints, Takahama and Sakai proposed the ε con-

strained method (Takahama and Sakai, 2005). The

ε constrained method is a method that adds the abi-

lity of constraint handling to the algorithms which

was originally designed for unconstrained optimiza-

tion problems. Although this method has been adap-

ted to several continuous optimizations (Takahama

and Sakai, 2010; Bonyadi et al., 2013; Yang et al.,

2014), there is no report of adapting it to discrete op-

timizations. Adapting the ε constrained method to

the Integer Categorical Particle Swarm Optimization

(ICPSO) (Strasser et al., 2016), we propose ε con-

strained ICPSO (εICPSO) for constrained combina-

torial optimization. We attempt to verify the effecti-

veness of the εICPSO to segment assignment through

the two-dimensional simulation experiment using real

construction data.

2 RELATED WORK

There are studies of adapting the ε constrained met-

hod to metaheuristics algorithms, e.g., particle swarm

optimization (PSO) (Kennedy, 2011), differential

evolution (DE) (Storn and Price, 1997), multiob-

jective evolutionary algorithm based on decomposi-

tion (MOEA/D) (Zhang and Li, 2007), and so on. Ta-

kahama and Sakai proposed an ε constrained differen-

tial evolution (εDE) (Takahama and Sakai, 2006), and

its extended version using an archive (Takahama and

Sakai, 2010). Takahama and Sakai proposed an ε con-

strained particle swarm optimizer (εPSO) (Takahama

and Sakai, 2005). Bonyadi, Li, and Michalewicz pro-

posed the hybrid method of εPSO and an other con-

straint handling method (Bonyadi et al., 2013). Yang,

Cai, and Fan introduced the ε constrained method into

MOEA/D in order to extend it for constrained multi-

objective optimization problems (Yang et al., 2014).

All of these methods are applicable to only continu-

ous optimization problems. Few researches have re-

ported on discrete constrained optimization methods

adapting the ε constrained method.

3 SEGMENT ASSIGNMENT

In this section, we explain the segment assignment

and its formulation as constrained combinatorial opti-

mization problem.

3.1 Shield Tunneling

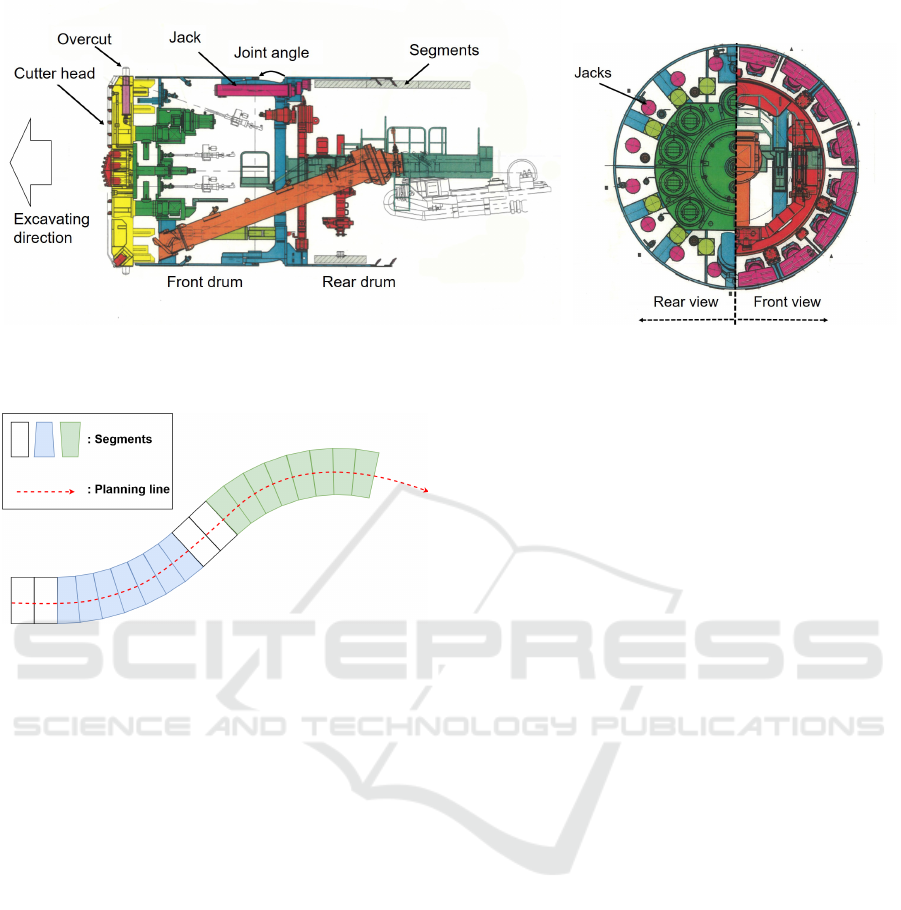
The shield tunneling is a tunnel construction met-

hod using excavation machines called shield machi-

nes shown in Figure 1. The front surface of the shield

machine has cutters, called the cutter head, to exca-

vate grounds. The over cut, which is the external cut-

ter equipped outside of the front surface, is controlled

so that the machine body can pass without contacting

to ground wall. A shield machines is divided to a front

drum and a rear drum. The angle between the front

drum and the rear drum, called joint angle, is control-

led for the shield machine to go around curves. Seg-

ments are assembled at the rear of the shield machine.

The shield machine is propelled by the reaction force

given from its jack pushing the located segment.

3.2 Segment Assignment Problem

In planning process, multiple types of segments are

provided for each construction and they are assig-

ned along to the planning line consisting of straight

lines and curves so that the gaps between each seg-

ment and the planning line fall within a tolerance as

shown in Figure 2. Conventionally, skilled engineers

manually assign segments in order to minimize gaps

without considering construction costs. However, be-

cause this assignment roughly determine the excava-

tion route of shield machine, it is assumed that optimi-

zation of this assignment reduce shield construction

costs. Thus we focus on the segments assignment pro-

blems for reducing the amount of excavated soil.

There are following two demands in the segment

assignment. (1) To make the gaps between each seg-

ment and the planning line fall within the tolerance.

(2) To reduce the amount of soil excavated according

to the segments by the shield machine. In this paper,

the former is treated as an inequality constraint, and

the latter is treated as an objective function. We de-

ﬁne segment assignment as the following constrained

combinatorial optimization problem.

minimize f (x

x),

subject to (g

x) − g

) ≤ 0, (1)

∈ {1, ··· , k}, (i = 0, ··· , n)

where x

∈ {1, ·· · ,k} corresponds to the type of

the segment assigned to i-th position, and k is the

number of types. A decision variable vector x

x =

A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling

329

(a) Side View (b) Rear and Front View

Figure 1: An Example of Construction Diagrams of A Shield Machine.

Figure 2: An Example of Segment Assignment.

, x

, · · ·x

) expresses the assigned segments. The

objective function f (x

x) is the amount of soil excava-

ted along to segments x

x by the shield machine; g

as the gap between the i-th segment and the planning

line; and g

is the gap tolerance.

This problem has n-dimensional decision variable

vector, and n is generally over several hundreds. The

problem has an extremely large search space. Howe-

ver, it is required to earn a solution in a short time,

because the segment assignment plan is should be re-

created when the practical construction deviates from

the plan. Population-based metaheuristics, such as

swarm intelligence (SI), is often used for optimiza-

tion problems in the real-world because of its ease

of parallelization and efﬁciency of its multi-point se-

arch (Hassanien and Emary, 2018; Soares et al., 2016;

Zhang et al., 2014; Glover and Kochenberger, 2006).

Although there are many discrete optimization algo-

rithms based on SI, they often only consider inte-

ger problems (Kennedy and Eberhart, 1995; Pampara

et al., 2005). The segment assignment has variables

whose values are not numerical but categorical and

unordered. The PSO is one of the most widely used

algorithm belonging to SI. Integer Categorical PSO

(ICPSO), presented in (Strasser et al., 2016), outper-

formed other discrete versions of PSO in unordered

discrete optimization. In addition, the gap tolerance

is commonly about 50 mm, whereas the diameter

of segments is around 10 m. The segment assignment

has n severe constraints. For handling the severe con-

straints, the ε constrained method is proposed by (Ta-

kahama and Sakai, 2005). Thus, we adapt the ε con-

strained method to ICPSO for constrained combina-

torial optimization.

4 PROPOSED METHOD

This section describes the considering constrained

combinatorial optimization problems, ε constrained

method, and εICPSO.

4.1 Problem Domain

In the proposed method, we consider the following

constrained optimization problem.

minimize f (x

x),

subject to g

x) ≤ 0, ( j = 1, ··· , q)

x) = 0, ( j = 1, ··· , r)

∈ {l

, · · · , u

}, (i = 1, ··· , n)

where x

x = (x

, · · · , x

) is an n-dimensional decision

variable vector; f (x

x) is a objective function; g

x) ≤ 0

are q inequality constraints; and h

x) = 0 are r equa-

lity constraints. f (x

x), g

x), and h

x) are real-valued

functions. The integer values l

, and u

are the lower

and upper bounds of x

respectively. The search space

is deﬁned by the lower and upper bounds; the feasible

region is deﬁned by the inequality and equality con-

straints.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

330

4.2 ε Constrained Method

The ε constrained method (Takahama and Sakai,

2005) adds the ability of constraint handling to the

algorithms originally designed for unconstrained op-

timization problems. This method introduces ε level

comparison, which is a comparison operator conside-

ring both the constraints and objective values for ran-

king candidate solutions. In this method, constraint

violation ϕ(x

x) is deﬁned as a measure of how much

constraints a solution violates. The constraint viola-

tion can be given by the maximum of all constraints

of all constraints or the sum of all constraints.

ϕ(x

x) = max{max

{0, g

x)}, max

x)|},

ϕ(x

x) =

∑

max{0, g

x)}

∑

x)|

, (2)

where p is a positive number. In this paper, constrain

violation is given by (2), the sum of all constraints.

The ε level comparison (<

,≤

) is deﬁned as an

order relation on the set of ( f (x

x), ϕ(x

x)). If f

( f

) and

(ϕ

) are the objective values and the constraint vi-

olation of solution point x

) respectively, then the

comparison operators <

and ≤

are deﬁned by the

following:

( f

, ϕ

) <

( f

, ϕ

) ⇔











< f

, (ϕ

, ϕ

≤ ε)

< f

, (ϕ

= ϕ

)

< ϕ

, otherwise

( f

, ϕ

) ≤

( f

, ϕ

) ⇔











≤ f

, (ϕ

, ϕ

≤ ε)

≤ f

, (ϕ

= ϕ

)

< ϕ

, otherwise

This deﬁnition means that the ε level comparison

compares two solutions by constraint violation value

ﬁrst. If both solutions have violation value under a

small threshold ε the two solutions are then compa-

red by the objective function value only.

4.3 εICPSO

The εICPSO is a constrained combinatorial optimiza-

tion algorithm based on ICPSO with candidate soluti-

ons ranked by the ε level comparison. The ICPSO is

a novel PSO algorithm that has been shown to surpass

other discrete PSO algorithms (Strasser et al., 2016).

In the PSO, particles search for the best position of the

search space. Particles have a position and a velocity,

and the position correspond to a candidate solution.

Original PSO assumes continuous state variables. In

the ICPSO, the representation of the particle’s posi-

tion is altered so that each attribute in a particle is a

distribution over its possible values rather than a va-

lue itself similarly to Estimation of Distribution Al-

gorithms (EDAs) (Larra

naga and Lozano, 2002). A

particle is evaluated by sampling a candidate solution

from these distributions and then calculating its ﬁt-

ness. In this subsection, the εICPSO is described in

more detail.

In the εICPSO, a particle p’s position X

is repre-

sented as

= [D

p,1

, D

p,2

, · · · , D

p,n

where each D

p,i

is the probability distribution for va-

riable X

. In other words, each component of the po-

sition vector is a set of probabilities

p,i

= [d

p,i

, d

p,i

, · · · , d

p,i

where d

p,i

denotes the probability that variable X

ta-

kes on value j for particle p. A particle p’s velocity

is a vector of n vector φ, which control the parti-

cle’s probability distributions.

= [φ

p,1

, φ

p,2

, · · · , φ

p,n

p,1

= [ψ

p,i

, ψ

p,i

, · · · , ψ

p,n

where ψ

p,i

corresponds to velocity of particle p for

variable i in state j. The velocity and position update

equations are applied directly to the values in the dis-

tribution.

=ωV

+U(0, ϕ

) ⊗ (pBest − X

)

+U(0, ϕ

) ⊗ (gBest − X

where each operator is performed component-wise

over each variable in the vector; and U(0, ϕ

) and

U(0, ϕ

) are uniformly distributed random numbers

between 0 and ϕ

and 0 and ϕ

respectively. The vec-

tor pBest is the best position in the search space this

particle has ever reached; the gBest is the best po-

sition in the search space any particle in the swarm

has ever reached. The particle moves in the search

space by adding the updated velocity to the particle’s

position vector at the current iteration. The particle’s

behavior is controlled with adjusting the parameter ω,

, and ϕ

known as inertia, the cognitive component

and the social component.

After the velocity and position update, any value

outside [0,1] is mapped to the nearest boundary in or-

der to maintain a valid probability. In addition, the

distribution is then normalized to ensure that its va-

lues sum to 1.

To evaluate a particle p, its distributions are

sampled to create a candidate solution S

p,1

, s

p,2

, · · · , s

p,n

] where s

p, j

denotes the state of va-

riable X

. The samples are evaluated by the ﬁtness

A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling

331

function, and then the distributions are evaluated by

their own sample’s ﬁtness value.

When a sample produced by a particle exceed the

global or local best in ε level comparison, the best

values are updated using both the distribution from

the particle position P

and the sample itself S

. For-

mally, for all states j ∈ Vals(X

) the global best’s pro-

bability is updated as

gB,i











ε × d

p,i

( j ̸= s

p,i

)

p,i

∑

k∈Vals(X

)

∧k̸= j

(1 − ε) × d

p,i

( j = s

p,i

)

where ε, the scaling factor, is a user-controlled para-

meter that determines the magnitude of the shift in the

distribution restricted to [0, 1), and d

gB,i

is the global

best position’s probability that variable X

takes value

j. This update increases the probability of the distri-

bution producing samples similar to the best sample,

while maintaining a valid probability distribution. In

other words, it ensures that the best position’s pro-

bability of producing a variable identical to the best

sample’s greater than 1−εwhich can be shown as fol-

lows:

gB,i

= d

p,i

∑

j∈S

,k)

(1 − ε) × d

p,i

= ε × d

p,i

+ (1 − ε) × d

p,i

∑

j∈S

,k)

(1 − ε) × d

p,i

= ε × d

p,i

+ (1 − ε),

where S

, k) = { j| j ∈ Vals(X

) ∧ j ̸= k} and k =

p,i

. The scaling factor should be controlled accor-

ding to the dimension of the decision variable, since a

large dimension increases the difference between the

best sample and a sample expected to be produced by

the updated distribution. The local best is updated in

exactly the same way. At the end of the algorithm, the

global best sample is returned as the solution.

5 EXPERIMENT

We attempt to verify the effectiveness of εICPSO

to segment assignment through the two-dimensional

simulation experiment using real construction data

with comparison with the ε constrained genetic algo-

rithm (εDGA) (Ihara et al., 2018). Candidate solu-

tions (assigned segments) are evaluated by the two-

dimensional simulator we developed. Solutions are

encoded to particles and integer chromosome and

they are evolved by the εICPSO and εDGA.

Figure 3: Model of Shield Machines in the Two-

dimensional Simulator.

5.1 Two-dimensional Simulator for

Segment Assignment

In the two-dimensional simulator, we consider the

shield machines as shown in Figure 3. The simulator

evaluates segments by the area of the region a shield

machine passed along to the segments assuming that

the amount of excavated soils is in proportion to the

area. The area of the region through which the front

of the shield machine passes is determined by the pro-

duct of the width of the shield machine and the total

length of the planning line. Thus, We deﬁne the area

of the excavated ﬁeld excluding this ﬁeld as the ﬁtness

because this ﬁeld does not depend on segment assig-

nment. This ﬁtness is equivalent to the amount of the

soil excavated by the overcut.

5.2 Conventional Method

In the construction site, segments are manually as-

signed by skilled engineers. However it is difﬁcult

to compare with real skilled engineers’ assignment,

because engineers take a lot of time to assign seg-

ments in each problem. Since skilled engineers as-

ring the amount of excavated soil, their methods are

approximately equivalent to the greedy method where

segments are assigned to minimize gaps. Thus we

compare the proposed methods to the greedy method

instead of skilled engineers.

5.3 εDGA

For the segment assignment problem, Ihara et al. pro-

posed the εDGA (Ihara et al., 2018), which is a com-

bination of the ε constraint method and discrete ge-

netic algorithm. The εDGA is basically based on

standard genetic algorithms, but in the algorithm, in-

dividuals are ranked by the ε level comparison with

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

332

(a) pl01

(b) pl02

(d) segments

(e) shield machine

Figure 4: Dimensions [mm] of the planning lines, the segments, and the shield machine used in the experiments.

the ε level controlled in each generation. In particu-

lar, the parents are selected by selection methods ba-

sed on comparison of individuals such as tournament

selection (Miller et al., 1995) and ranking selection

(Goldberg and Deb, 1991) using the ε level compari-

son instead of general comparison. Elite individuals

are also selected by ε level comparison to carry over

to the next generation according to elitism. The ﬂow

of the method is shown as follows:

1. Initialization: initial population is generated by

randomness or heuristics with population size of

2. Determining terminate or not: If the termination

conditions satisfy, this algorithm terminates. In

this paper, the algorithm ends in the T th generati-

ons.

3. Controlling the ε level: the feasible region is tem-

porarily expanded by controlling the ε level. It is

desirable that ε level decrease as generations go

by.

4. Parents selection: individuals are ranked by ε le-

vel comparison, and selected by selection met-

hods only based on ranking solutions to insert into

a mating pool.

5. Crossover: crossover operators are applied to pa-

rents picked from the mating pool in order.

6. Mutation: when offspring are produced, each off-

spring has chance of mutation.

7. Replacement: N

elite individuals are selected to

carry out to the next generation instead of N

worst offspring selected by the ε level compari-

son.

8. Return to step 2.

5.4 Initialization

In the constrained optimization problem, it is desira-

ble search starts from in or near its feasible region,

especially when the feasible region is narrow. A feasi-

ble solution can be found easily by the greedy method

in the segment assignment as noted above. This ex-

periment uses the feasible solution discovered by the

greedy method for initializations. The εICPSO rand-

omly initialized velocity and position vectors, then as-

suming that the feasible solution is earned by sam-

pling a particle p’s position, the p’s local best and the

global best are updated. In the εDGA initial individu-

als are created by the applying the uniform mutation

to the feasible solution.

5.5 Experimental Setup

The algorithms tackle the constrained combinatorial

optimization problem deﬁned in (1). Planning lines

are deﬁned by the given series of curvature radius R

and length L. Figure 4a, 4b, and 4c show the planning

lines used in the experiment

pl01

pl02

, and

pl03

The segments are deﬁned as shown in Figure 4d, and

we use the segment sets

sg01

and

sg02

, which in-

clude segments whose type number is from one to

three, and from one to ﬁve, respectively. The gap to-

lerance g

is set to 50 mm in each problem.

We conduct 50 trials of evolutions where ﬁtness

evaluations are limited up to 500,000 times with both

the εICPSO and εDGA. The εICPSO uses a swarm of

size 100, and the swarm is evolved for 5, 000 itera-

tions, owing to the recommendation of (Engelbrecht,

2014), which demonstrated that a large swarm may,

counterintuitively, have difﬁculty exploring the search

space. The cognitive component ϕ

and social com-

ponent ϕ

are set to 1.49618, and the inertia ω is

0.729, which has been found to encourage convergent

A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling

333

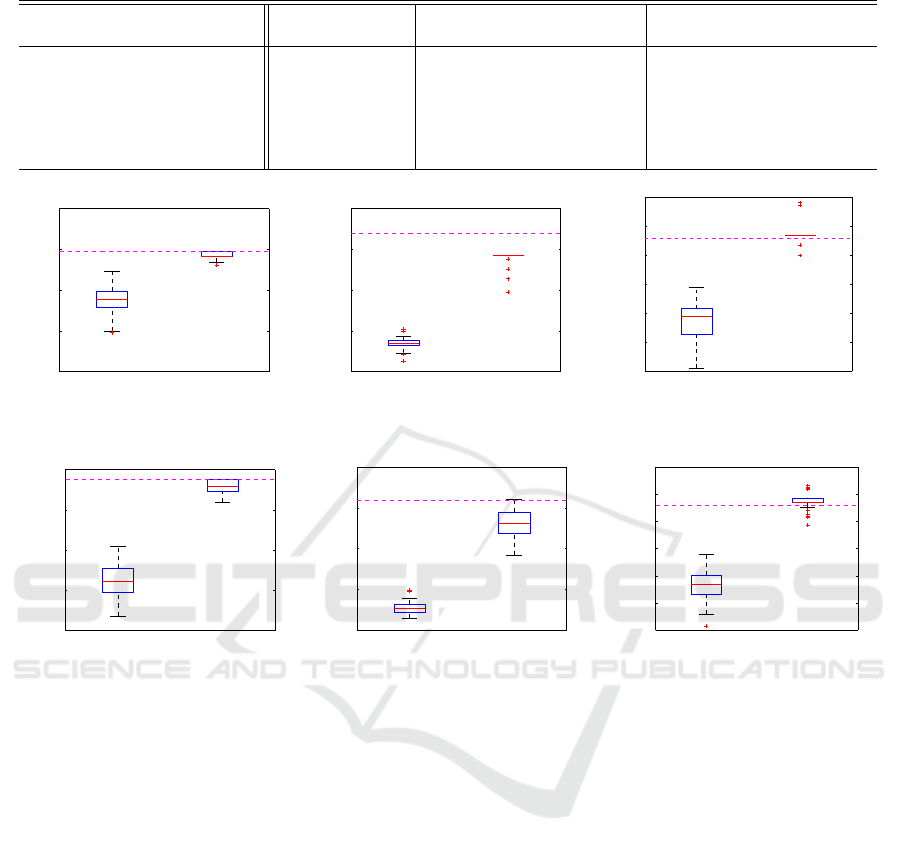
Table 1: Experimental Result [m

]50trials.

Problem Skilled engineer εICPSO εDGA

Segment set Planning line (greedy method) average best worst average best worst

sg01

(k = 3)

pl01

(n=267) 107.48 106.87 106.47 107.23 107.42 107.30 107.47

pl02

(n=210) 102.54 102.26 102.22 102.30 102.47 102.39 102.48

pl03

(n=325) 105.33 105.18 105.10 105.24 105.33 105.30 105.39

sg02

(k = 5)

pl01

(n=267) 107.35 106.84 106.67 107.01 107.32 107.24 107.35

pl02

(n=210) 102.52 102.25 102.22 102.29 102.46 102.38 102.52

pl03

(n=325) 105.08 104.93 104.85 104.99 105.08 105.04 105.11

106

106.5

107

107.5

108

Method

Fitness

Epsilon ICPSO Epsilon DGA

(a)

sg01

pl01

102.2

102.3

102.4

102.5

102.6

Method

Fitness

Epsilon ICPSO Epsilon DGA

(b)

sg01

pl02

105.1

105.15

105.2

105.25

105.3

105.35

105.4

Method

Fitness

Epsilon ICPSO Epsilon DGA

(c)

sg01

pl03

106.6

106.8

107

107.2

107.4

Method

Fitness

Epsilon ICPSO Epsilon DGA

(d)

sg02

pl01

102.2

102.3

102.4

102.5

102.6

Method

Fitness

Epsilon ICPSO Epsilon DGA

(e)

sg02

pl02

104.85

104.9

104.95

105

105.05

105.1

105.15

Method

Fitness

Epsilon ICPSO Epsilon DGA

(f)

sg02

pl03

Figure 5: Box plots of ﬁtness scores of the εDGA and εICPSO for each problem with 50 trials, with horizontal dashed lines

representing the conventional method’s evaluations.

trajectories (Eberhart and Shi, 2000). In the

pl01

and

pl02

problems, the scaling factor ε = 5.0 × 10

−4

, and

in the

pl03

problems, ε = 1.0 × 10

−4

, due to large

dimensions of the problems. In the εDGA, populati-

ons are evolved for 500 generations, with a population

of size 1, 000. Uniform crossover (Syswerda, 1989)

is applied 95% of the time offspring are produced,

and each offspring does uniform mutation (Goldberg,

1989) where each gene has a 5% chance of change to

random value. Through the evolutions, ε level is set

to 0.

5.6 Experimental Results

The experimental results show that the proposed met-

hod have a potential to ﬁnd the segment assignment

reducing the amount of excavated soil as compared

to the conventional method (skilled engineer) while

keeping the all gaps between segments and the plan-

ning line falling within the tolerance. Table 1 shows

the experimental results on the problems (Figure 4).

In the table, ”average”, “best”, and “worst” are the

average value, the best value, and the worst value of

50 trials on the each problem respectively. Bold va-

lues indicate algorithms that statistically signiﬁcantly

outperformed all other methods (paired Student t-

Test, α = 0.01). Figure 5 illustrates the performance

of the εICPSO and εDGA. Their ﬁtness scores are

shown as box plots, where the boxes represent the

25th to 75th percentiles, the lines within the boxes

represent the median, and the lines outside the boxes

represent the minimum and maximum values. The

conventional method’s scores are represented by the

horizontal dashed lines.

It is clear that the εICPSO has clear advantage

over the εDGA. In all the problems, the εICPSO sta-

tistically performs the best. In particular, the worst

scores of εICPSO exceed the εDGA’s best and the

skilled engineer’s score. In complex problems, with

large n or k, the difference in the performance is espe-

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

334

cially remarkable. Although the εDGA has potential

to ﬁnd the solution superior to the skilled engineer in

terms of the best score, the its score averagely almost

equivalent and at worst inferior in the

pl03

problems.

6 CONCLUSION

We addressed the segment assignment in shield tun-

neling as a constrained combinatorial optimization

problem. This paper proposed the εICPSO and de-

monstrated its effectiveness to segment assignment

problems. The experimental results showed its poten-

tial to reduce construction costs as compared with the

conventional method. In all the test problems, the pro-

posed method outperformed all the comparative met-

hods. In the future, we will make more experiments

using three-dimensional simulator for more accurate

evaluation of the proposed method.

REFERENCES

Bonyadi, M., Li, X., and Michalewicz, Z. (2013). A hy-

brid particle swarm with velocity mutation for con-

straint optimization problems. In Proceedings of the

15th annual conference on Genetic and evolutionary

computation, pages 1–8. ACM.

Eberhart, R. C. and Shi, Y. (2000). Comparing inertia weig-

hts and constriction factors in particle swarm optimi-

zation. In

Evolutionary Computation, 2000. Procee-

dings of the 2000 Congress on, volume 1, pages 84–

88. IEEE.

Engelbrecht, A. P. (2014). Fitness function evaluations: A

fair stopping condition? In Swarm Intelligence (SIS),

2014 IEEE Symposium on , pages 1–8. IEEE.

Glover, F. W. and Kochenberger, G. A. (2006). Handbook

of metaheuristics, volume 57. Springer Science & Bu-

siness Media.

Goldberg, D. (1989). Genetic algorithms in search, optimi-

zation and machine learning. Addison-Wesley, Rea-

ding, MA.

Goldberg, D. E. and Deb, K. (1991). A comparative analysis

of selection schemes used in genetic algorithms. In

Foundations of genetic algorithms, volume 1, pages

69–93. Elsevier.

Hasanipanah, M., Noorian-Bidgoli, M., Armaghani, D. J.,

and Khamesi, H. (2016). Feasibility of pso-ann model

for predicting surface settlement caused by tunneling.

Engineering with Computers, 32(4):705–715.

Hassanien, A. E. and Emary, E. (2018). Swarm intelligence:

principles, advances, and applications . CRC Press.

Ihara, K., Kato, S., Nakaya, T., and Ogi, T. (2018). Con-

strained GA based segment assignment in shield tun-

neling to minimize the amount of excavated soil. In

2018 IEEE 7th Global Conference on Consumer Elec-

tronics (GCCE), pages 229–230. IEEE.

Japan Society of Civil Engineers (2007). Standard speci-

ﬁcations for tunneling-2006: shield tunnels. Tunnel

Engineering Committee.

Kennedy, J. (2011). Particle swarm optimization. In Ency-

clopedia of machine learning, pages 760–766. Sprin-

ger.

Kennedy, J. and Eberhart, R. (1995). Particle swarm optimi-

zation. In IEEE International Conference on Neural

Networks, pages 1942–1948. IEEE.

Koyama, Y. (2003). Present status and technology of shield

tunneling method in japan. Tunnelling and Under-

ground Space Technology, 18(2-3):145–159.

Larra

naga, P. and Lozano, J. A. (2002). Estimation of distri-

bution algorithms: A new tool for evolutionary com-

putation, volume 2. Springer Science & Business Me-

dia.

Maidl, B., Herrenknecht, M., Maidl, U., and Wehrmeyer, G.

(2013). Mechanised shield tunnelling. John Wiley &

Sons.

Miller, B. L., Goldberg, D. E., et al. (1995). Genetic algo-

rithms, tournament selection, and the effects of noise.

Complex systems, 9(3):193–212.

Pampara, G., Franken, N., and Engelbrecht, A. P. (2005).

Combining particle swarm optimisation with angle

modulation to solve binary problems. In Evolutionary

Computation, 2005. The 2005 IEEE Congress on, vo-

lume 1, pages 89–96. IEEE.

Soares, J., Ghazvini, M. A. F., Silva, M., and Vale,

Z. (2016). Multi-dimensional signaling method for

population-based metaheuristics: Solving the large-

scale scheduling problem in smart grids. Swarm and

Evolutionary Computation, 29:13–32.

Storn, R. and Price, K. (1997). Differential evolution–a

simple and efﬁcient heuristic for global optimization

over continuous spaces. Journal of global optimiza-

tion, 11(4):341–359.

Strasser, S., Goodman, R., Sheppard, J., and Butcher, S.

(2016). A new discrete particle swarm optimization

algorithm. In Proceedings of the Genetic and Evo-

lutionary Computation Conference (GECCO), pages

53–60. ACM.

Suwansawat, S. and Einstein, H. H. (2006). Artiﬁcial neural

networks for predicting the maximum surface settle-

ment caused by epb shield tunneling. Tunnelling and

underground space technology, 21(2):133–150.

Suzuki, A. (2016). 2016 annual report of NILIM: Pro-

ductivity improvement in infrastrucure development

process using i-construction. http://www.nilim.go.jp/

english/annual/annual2016/ar2016e.html. Accessed:

2018-10-23.

Syswerda, G. (1989). Uniform crossover in genetic al-

gorithms. In Proceedings of the third international

conference on Genetic algorithms, pages 2–9. Morgan

Kaufmann Publishers.

Takahama, T. and Sakai, S. (2005). Constrained optimiza-

tion by ε constrained particle swarm optimizer with

ε-level control. In Soft computing as transdisciplinary

science and technology, pages 1019–1029. Springer.

Takahama, T. and Sakai, S. (2006). Constrained optimi-

zation by the ε constrained differential evolution with

A PSO based Approach to Assign Segments for Reducing Excavated Soil in Shield Tunneling

335

gradient-based mutation and feasible elites. In Evo-

lutionary Computation, 2006. CEC 2006. IEEE Con-

gress on, pages 1–8. IEEE.

Takahama, T. and Sakai, S. (2010). Constrained optimiza-

tion by the ε constrained differential evolution with an

archive and gradient-based mutation. In Evolutionary

Computation (CEC), 2010 IEEE Congress on, pages

1–9. IEEE.

Windapo, A. O. (2016). Skilled labour supply in the south

african construction industry: The nexus between cer-

tiﬁcation, quality of work output and shortages. SA

Journal of Human Resource Management, 14(1):1–8.

Yang, Z., Cai, X., and Fan, Z. (2014). Epsilon constrai-

ned method for constrained multiobjective optimiza-

tion problems: some preliminary results. In Procee-

dings of the Companion Publication of the 2014 An-

nual Conference on Genetic and Evolutionary Com-

putation, pages 1181–1186. ACM.

Zhang, Q. and Li, H. (2007). MOEA/D: A multiob-

jective evolutionary algorithm based on decomposi-

tion. IEEE Transactions on evolutionary computation,

11(6):712–731.

Zhang, Z., Long, K., Wang, J., and Dressler, F. (2014).

On swarm intelligence inspired self-organized net-

working: its bionic mechanisms, designing principles

and optimization approaches. IEEE Communications

Surveys & Tutorials, 16(1):513–537.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

336