A Novel Approach for Development of Neural Network based Electrical

Machine Models for HEV System-level Design Optimization

Christian Gletter

, Andre Mayer

, Josef Kallo

, Thomas Winsel

and Oliver Nelles

Daimler AG, Stuttgart, Germany

Faculty of Engineering, Computer Sciences and Psychology, Ulm University, Germany

Department of Mechanical Engineering, Kempten University of Applied Sciences, Germany

Department of Mechanical Engineering, University of Siegen, Germany

Keywords:

Neural Networks, Scalable Component Model, Electrical Machine, Hybrid Electric Vehicles, System-level

Design, Multilayer Perceptron.

Abstract:

To ﬁnd the optimal system-level design of hybrid electric vehicles (HEVs), component models are used in

simulations to evaluate a large number of different designs within a high dimensional design space. As the

electrical machine (EM) represents a key component of the HEV powertrain in terms of energy consumption,

models require scalability and sufﬁcient accuracy with manageable computational effort. This paper presents

a novel approach for the development of scalable EM models based on Neural Networks (NN). The models

are trained with data derived by a Finite Element Analysis (FEA) based scaling procedure and capable to rep-

resent the characteristics of a wide range of EM designs without the incorporation of further details. Once a

model is trained, it can be directly used in system-level design optimization. The practicality of the model is

proven within an exemplary simulation study and its goodness of ﬁt to the training data is validated by a sta-

tistical analysis. This approach can help to reduce the computational effort of EM efﬁciency maps calculation,

since only a small number of time-consuming FEA based scaling simulations must be performed prior to the

optimization.

1 INTRODUCTION

Since the system-level design of HEVs considers dif-

ferent topologies, technologies and component sizes

as well as control strategies, the optimization of such

systems becomes a challenging task. Therefore, re-

search has been done on optimal control strategies

(Wirasingha and Emadi, 2011), component sizing

(Gao and Porandla, 2005) and topology optimization

(Hofman et al., 2012). Within the latest publications,

optimization-based frameworks are being developed

to consider two or more system levels within the op-

timization problem (Silvas et al., 2016). Thus, the

number of design variables and therefore the number

of evaluations for HEV designs increases. Since sim-

ulation models are used for the evaluation of different

HEV designs, appropriate component models, e.g.,

the electrical machine as a key component of HEV

powertrain, must be scalable with corresponding de-

sign variables while satisfying accuracy and compu-

tational effort requirements.

In system-level design optimization the axial and

radial dimensions and/or the number of turns per coil

are often used for sizing the EM. Therefore, so called

scaling laws are suitable to describe the functional re-

lationship between a change in the design variable

and its effect on the EM characteristics within spe-

ciﬁc limitations (e.g., same basic construction). In

(Buecherl et al., 2010) analytical models based on

equivalent circuits of different types of EMs are de-

veloped. The axial and radial scaling is expressed

by scalar factors, which are applied within scaling

laws to represent the inﬂuence on the equivalent cir-

cuit’s elements such as resistances (losses) and induc-

tances and thus the EM characteristics. Analytical

scaling laws are also applied in the method presented

in (Stipetic and Goss, 2016), where a saturated ﬂux-

linkage model and loss model are used to determine

the characteristics of a reference electrical machine.

Here, the winding is considered as additional design

variable and incorporated by a speciﬁc scaling factor.

Another approach is the use of existing efﬁciency

maps as baseline models and applying scaling meth-

ods to adapt the characteristics of the component

Gletter, C., Mayer, A., Kallo, J., Winsel, T. and Nelles, O.

A Novel Approach for Development of Neural Network based Electrical Machine Models for HEV System-level Design Optimization.

DOI: 10.5220/0007570300170024

In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 17-24

ISBN: 978-989-758-374-2

within an appropriate design range. The baseline

efﬁciency maps are obtained by measurement data

or highly accurate but time-consuming modeling ap-

proaches such as Finite Element Analysis (FEA). In

(Zhou et al., 2015), a database which represents basic

EM characteristics over a wide design range, is ob-

tained by FEA. The baseline design is then scaled by

means of dimensional quantities and the number of

turns per coil to generate new EM designs. A simi-

lar approach is presented in (Domingues et al., 2016),

where a database represents EMs separated by the cat-

egories constant power speed range (CPSR) and outer

radius. The efﬁciency maps of new machine designs

are then calculated by applying a linear axial scaling

law to speciﬁc electrical machine losses.

(Vaillant, 2016) proposes an interesting scaling

method based on data representing combined efﬁ-

ciency maps of EM and power electronics (PE) and

thus the EM system. The baseline designs are catego-

rized into classes of EM systems with different axial

dimensions and therefore different power levels. In

order to calculate new efﬁciency maps, a regression

function is ﬁtted to a data set consisting of one nor-

malized speed-torque combination for each baseline

map within one class. Repeating this step for each

speed-torque combination allows one to scale the ef-

ﬁciency maps by varying the power of the EM system.

In order to allow the development of data based

efﬁciency models without explicit consideration of

scaling laws and presorting different machine designs

into speciﬁc classes, a powerful nonlinear regression

method is required. Since speciﬁc types of Neu-

ral Networks are known as universal approximators

(Hornik et al., 1989) and thus are capable of mod-

eling complex nonlinear system behavior, this paper

presents a novel approach for the development of scal-

able efﬁciency models based on NNs for the use in

system-level design optimization.

2 NEURAL NETWORKS

The idea of NN is originally motivated by the repli-

cation of powerful structure of biological neural net-

works for tasks such as information processing, learn-

ing and adaptation (Nelles, 2001). Thus, NNs are well

suited to learn and adapt system behavior from data of

the process within the system i.e the functional rela-

tionship between the input and output variables.

2.1 Multilayer Perceptron

The exemplary network structure of a multilayer per-

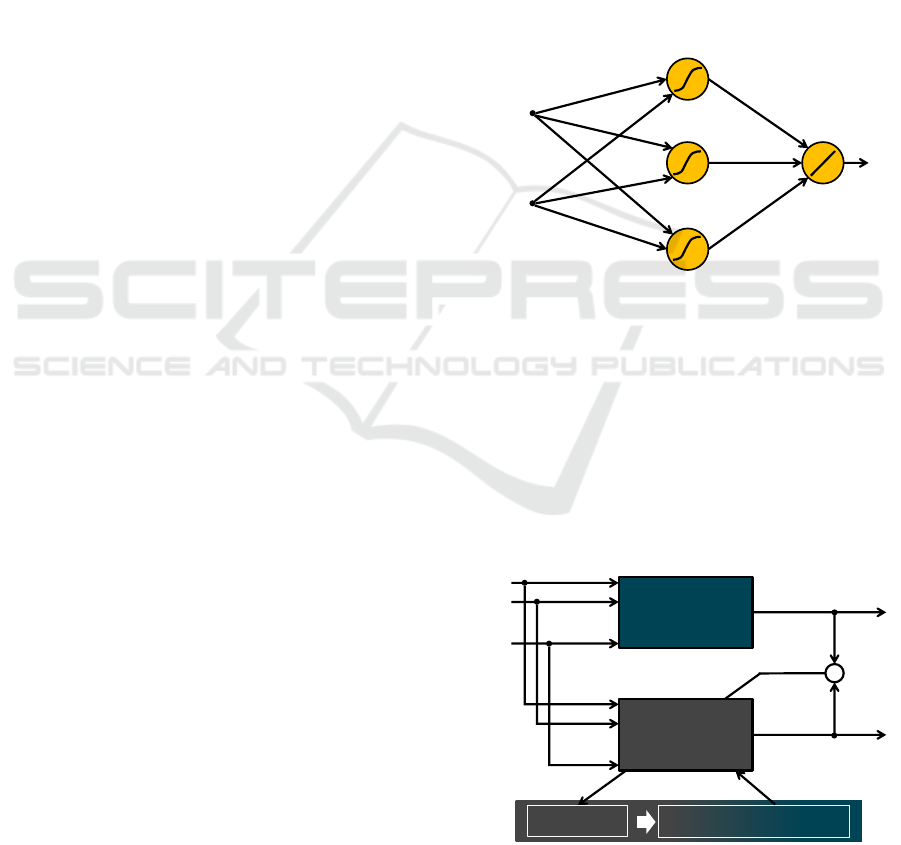
ceptron (MLP) is shown in Figure 1 since this type of

NN is used in this work. It consists of one input layer,

one hidden layer and one output layer, and therefore

represents a three layer network. The mathematical

expression for this single output network is given by

ˆy = b

(2)

∑

i=1

(2)

(1)

∑

j=1

(1)

i, j

, (1)

where N

denotes the total number of neurons i within

the hidden layer and N

the number of inputs u

. The

weights and biases, which are optimized by a train-

ing algorithm, are denoted by w and b, respectively.

The superscripts (1) and (2) refer to the correspond-

ing layer (hidden and output layer).

⋮

Input

Layer

Hidden

Layer

Output

Layer

𝑦

𝑢

𝑃

Figure 1: Structure of a three layer perceptron.

The nonlinear nature of the MLP arises through

one-dimensional so-called activation functions σ. A

common choice of activation function is the hyper-

bolic tangent (tanh), which is also used in this work.

2.2 Training of Multilayer Perceptrons

In general, the adaption of a model in order to repre-

sent a process behavior is known as system identiﬁca-

tion (Nelles, 2001).













Process /

Simulation





Model













 



Evaluation

Strategy: 















Figure 2: Schematic of system identiﬁcation process, mod-

iﬁed (Nelles, 2001).

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

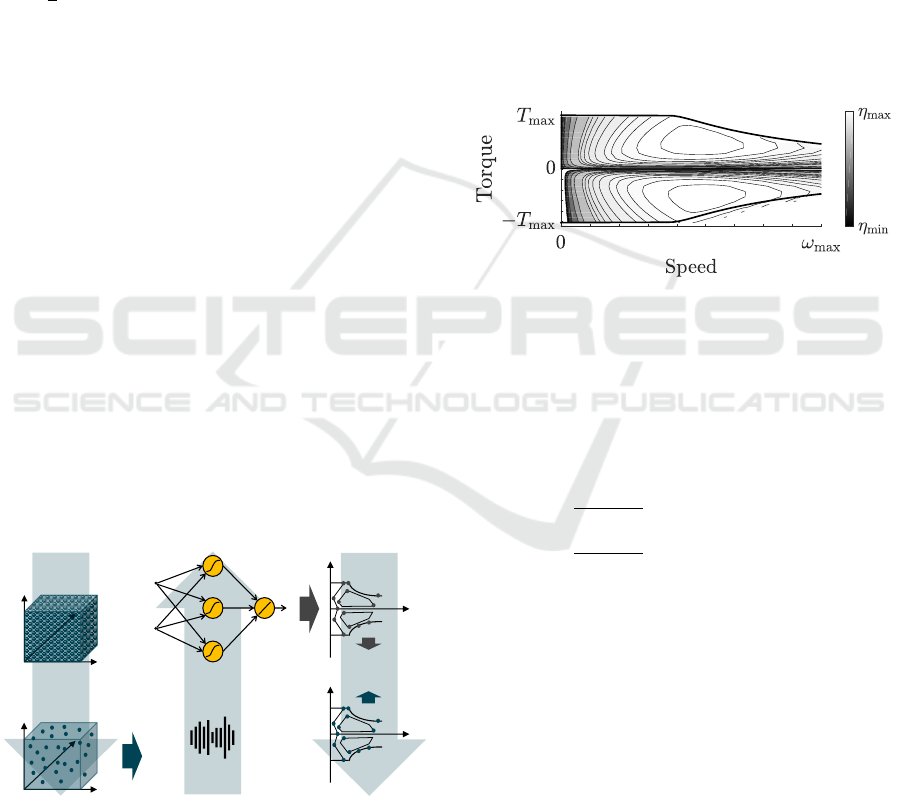
Figure 2 illustrates the system identiﬁcation

schematically. An optimization procedure varies the

biases and the weights of the MLP in both layers,

while the model is fed with the same inputs as the pro-

cess. The optimization goal is to minimize the model

error e given by the difference of the process output

y and the model output ˆy. The block diagram in the

ﬁgure suggests an online optimization procedure. In

this work, the training for the MLP is carried out of-

ﬂine and thus is based on a data set consisting of pre-

viously gathered data points within the design space,

i.e different combinations of values of the input vari-

ables u = [u

, u

, . . . , u

]

, and its corresponding out-

put values y. The values y for each input combination

u may be drawn either from measurements of the real

process or from complex simulation models. In the

literature, different algorithms have been used for the

training of MLPs, where the most common one is the

backpropagation algorithm. Since this paper focuses

on a novel approach for the application of MLPs in the

development of scalable efﬁciency models of electri-

cal machines, the well-known training algorithms will

not be discussed in detail. However, for further details

on backpropagation algorithm the reader may refer to

(Rumelhart et al., 1986).

3 METHODICAL APPROACH

Based on the theoretical background of Multilayer

Perceptrons and model training, the methodical ap-

proach for the development MLP-based scalable EM

models (SEMMs) is explained within this section. An

overview of the approach is shown schematically in

Figure 3.

Database Modeling Validation

Design

Experiments

FEA

Models

Design

Space

MLP´s

Model

Error

MLP

Training

Data

Figure 3: Schematic of the methodical approach for devel-

opment of MLP-based scalable EM models.

Starting from the left top, a wide range of different

electrical machines are described within the design

space. The term design describes a speciﬁc electri-

cal machine characterized by its corresponding design

variables. In order to reduce the computational effort,

a design of experiments (DoE) approach is applied,

which leads to the corresponding training data for the

MLP training illustrated in the middle of the ﬁgure.

Subsequent to the training procedure, the accuracy

of the MLP-based scalable EM model is assessed by

comparison with highly accurate FEA based models.

In the following, the elements of the methodical ap-

proach will be described in detail.

3.1 Efﬁciency Maps of Electrical

Machines

In HEV system-level design optimization, electrical

machines are usually modeled as efﬁciency maps of

the form η

, ω

), as it is plotted in Figure 4.

Figure 4: Example of an EM efﬁciency map.

In this diagram, the torque limitations are repre-

sented by the bold lines for motoring T

EM,max

and gen-

erating −T

EM,max

. The efﬁciencies are given by the

isolines within the maximum torque curves and cal-

culated as the ratio of the mechanical power output

EM,mech

and the electrical power input P

EM,el











EM,mech

EM,el

for P

EM,mech

> 0 (mot.)

EM,el

EM,mech

for P

EM,mech

< 0 (gen.)

(2)

As it can be seen from the formulation above, the

calculation of the efﬁciency maps differs for motor-

ing and generating. In this work, P

EM,el

describes the

power either drawn from or supplied to the battery of

the HEV. The approximation of the efﬁciency behav-

ior can become a challenging task especially in areas

close to the origin axes, since the efﬁciency is not de-

ﬁned within this regions. Thus, a pragmatic approach

is to carry out ﬁrst the approximation of the electri-

cal power map P

EM,el

, ω

) and then second the

calculation of η

by the deﬁnition given in (2).

3.2 Database and Design Space

The models in this approach consider all losses within

the electrical and mechanical path, e.g., the EM’s iron

A Novel Approach for Development of Neural Network based Electrical Machine Models for HEV System-level Design Optimization

losses, copper losses and friction losses, as well as

losses caused by power electronics (PE) and thus rep-

resent the whole EM system.

3.2.1 FEA Model Database

In order to allow the consideration of possible EM

system designs over a wide design range with suit-

able accuracy, the training data is based on highly ac-

curate simulation models. In this work, an analyti-

cal scaling procedure is applied to a set of FEA mod-

els, where each FEA model represents an EM with a

speciﬁc active diameter d

. The analytical scaling

along the design dimensions length l

and number

of turns per coil TC

allows one to consider EMs

spread over the whole design space within the train-

ing data. In this work, only permanent magnet syn-

chronous motors (PMSM) are considered. Further-

more, the technology of these machines is identical in

terms of e.g., magnet layout, winding diagram etc to

represent an unbiased data set. The design space to be

covered by the MLP-based SEMM is deﬁned by the

continuous geometrical EM parameters active diame-

ter and length as well as the discrete number of turns

per coil. Each design within the database refers to an

efﬁciency optimized EM system including the elec-

trical machine and its corresponding PE and is char-

acterized by its speciﬁc efﬁciency map (see (2)) and

its maximum torque curves. Due to the deﬁnition of

continuous design variables, the theoretical number of

possible EM designs is inﬁnite.

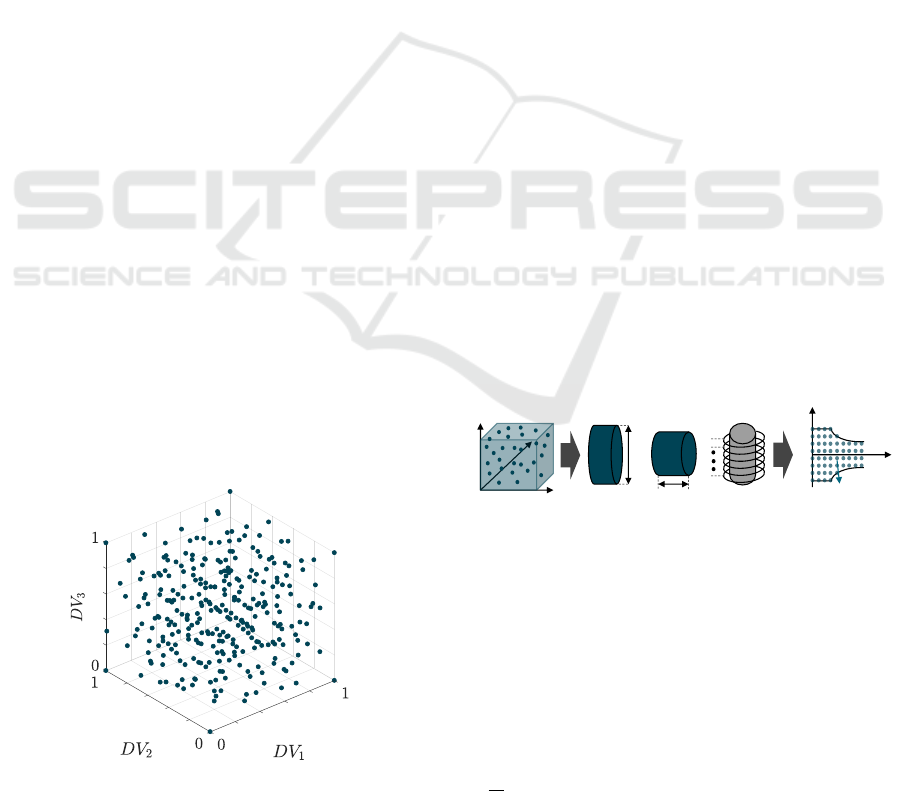
3.2.2 Design of Experiments

Since the efﬁciency maps of each machine design are

based on a large number of torque and speed combi-

nations, the computational effort of the training pro-

cess increases with the number of considered machine

designs.

Figure 5: Illustration of a Sobol design with three design

variables and 300 electrical machine designs.

Furthermore, the more designs are considered, the

more time-consuming simulations are required for

the generation of the training data. Due to the high

computational effort of the FEA simulations based

data generation and in order to realize a practica-

ble methodology for the development of scalable EM

models, a DoE approach is applied to reduce the num-

ber of considered designs while maintaining a sufﬁ-

cient amount of data for the MLP training. Therefore,

a Sobol distributed spaceﬁlling design (cf. (Sant-

ner et al., 2003)) is used for the choice of a suitable

amount of informative training data within the design

space. For clarity, Figure 5 illustrates a Sobol de-

sign with three design variables (DV

) deﬁned on the

normalized interval [0, 1]. Within this work, the vari-

ables d

, l

and TC

span a 3 dimensional design

space over speciﬁc variable ranges.

3.3 Scalable Electrical Machine Model

The characteristics of single EM design are deﬁned by

their efﬁciency maps and the maximum torque curves

and therefore, the two separated models ˆy

Con

and ˆy

Lim

are used for the approximation of the electrical power

consumption map and the torque limitations respec-

tively. The scalability of the models is given by the

consideration of different EM designs an the interpo-

lation capability of the MLP.

3.3.1 Training Data

The training data is based on 300 EM designs deﬁned

by the design parameters d

, l

and TC

where

each design refers to a torque-speed-grid with several

thousand sample points.

EM Designs Design Parameters Sampling Points

𝑇

𝜔

𝑙

𝑑

𝑇𝐶

𝑃

EM,el

(𝑇, 𝜔)

Figure 6: Schematic of the training data composition.

Figure 6 illustrates schematically the generation

and composition of the training data for the training

process. The target y

Con

for the training process of

ˆy

Con

is deﬁned by the electrical power P

EM,el

of the

EM systems at each sample point of the torque-speed-

grids. Thus, the input training data of a single ma-

chine design is represented by the matrix

Con,i







EM,i

. . . d

EM,i

. . . l

EM,i

. . . TC

EM,i

EM,i,1

EM,i,2

. . . T

EM,i,N

EM,i,1

EM,i,2

. . . ω

EM,i,N







, (3)

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

where N

denotes the number of torque-speed-

combinations of a single EM. Thus, the entire training

data set for M machine designs is given by:

Con

= [U

Con,1

Con,2

. . . U

Con,M

] (4)

According to the schematic in Figure 6 and in analogy

to the formulations of (3) and (4) the target data of a

single machine design is given by the vector

Con,i

= [P

EM,el,i,1

EM,el,i,2

. . . P

EM,el,i,N

], (5)

and the entire target data is represented by:

Con

= [y

Con,1

, y

Con,2

, . . . , y

Con,M

] (6)

Furthermore, the respective vectors of speed val-

ues ω

EM,i

= [ω

EM,i,1

EM,i,2

. . . ω

EM,i,N

] and the

corresponding vectors of maximum torque values

EM,max,i

= [T

EM,max,i,1

EM,max,i,2

. . . T

EM,max,i,N

]

with N

elements are used for the training of the scal-

able torque limitation model ˆy

Lim

= [U

Lim,1

Lim,2

. . . U

Lim,M

] (7)

Lim

= [T

EM,max,1

EM,max,2

. . . T

EM,max,M

] (8)

In analogy to 3, the ﬁrst three rows of the matrices

lim,i

in 7 are the corresponding values of the design

variables of the i-th machine design.

3.3.2 Training Process

In this work, a nonlinear optimization of the weights

and biases is carried out by the Levenberg-Marquard

algorithm (Marquardt, 1963) to minimize the sum

squared errors of the two models. The used optimiza-

tion technique speeds up the training convergence

compared to the standard gradient descend backprop-

agation algorithm (Hagan and Menhaj, 1994). Fur-

thermore, the training convergence depends on a suit-

able initialization of weights and biases. Thus, a

widely accepted approach based on statistical analysis

for controlled activation weight initialization (Drago

and Ridella, 1992) is applied within this paper. The

attributes of the utilized MLPs are shown in Table 1:

Table 1: Attributes of the utilized models.

Model Structure σ Objective

ˆy

Con

5-80-1 tanh SSE

ˆy

Lim

4-12-12-1 tanh SSE

Both models use hyperbolic tangent (tanh) as ac-

tivation function and are trained by the minimization

of the sum-squared-error

SSE

∑

m=1

(y(m) − ˆy(m))

, (9)

where N

denotes the length of the respective training

data set. The model structure is given by a structure

code, where the ﬁrst number refers to the number of

inputs, the last number refers to the number of out-

puts and the remaining numbers refer to the respec-

tive number of hidden layer neurons. The structure

of the MLPs in this work is found by iteratively in-

creasing the number of hidden layer neurons until the

model accuracy requirements are met (bias-variance

tradeoff, see (Winsel, 2002)). In case the potential

of accuracy improvement is exhausted prior the re-

quirements are met, an additional hidden layer is used

and the procedure is repeated. Thus, the consumption

model ˆy

Con

was found as a three layer network with 5

inputs, one hidden layer with 80 neurons and 1 output.

For an accurate approximation of the constant torque

characteristics, 2 hidden layers have shown a better

performance and thus are used in this work within the

limitation model ˆy

Lim

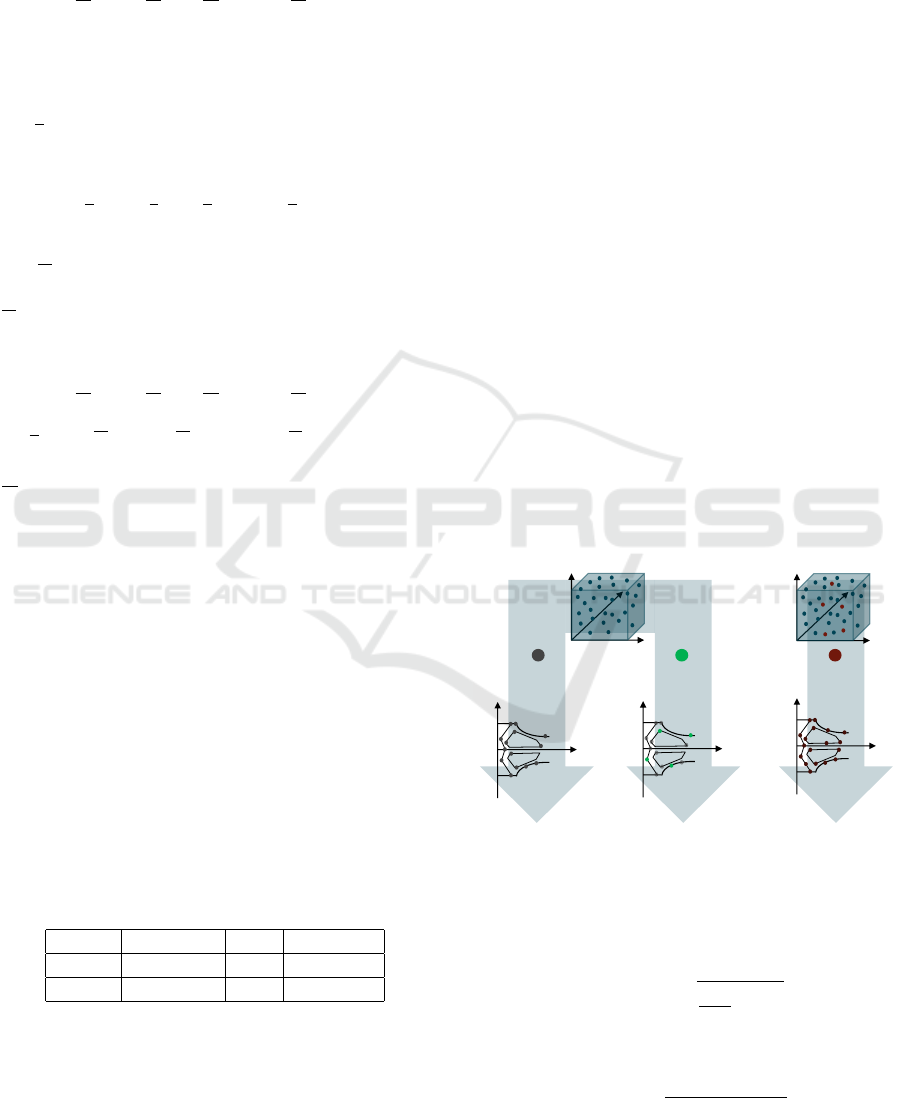
3.4 Model Validation

The validation of the models is split into two steps

and illustrated schematically in Figure 7. The ﬁrst

step is carried out during the training process by di-

viding the data set into a training set and a validation

set consisting of speed-torque combinations and the

corresponding electrical power values.

Model Training

DoE Data Set

Extended Data Set

1st Step Validation 2nd Step Validation

Validation

Data

Training

Data

Validation

Data

Figure 7: Schematic illustration of the model validation.

Thus, an amount of 20 % of the data points is used

to validate the model performance within the electri-

cal power maps of each EM existent in the training

data by applying the statistics RMSE

val

given by

RMSE

val

SSE

val

, (10)

and coefﬁcient of determination R

val

= 1 −

SSE

val

∑

m=1

(y(m) − ¯y)

, (11)

A Novel Approach for Development of Neural Network based Electrical Machine Models for HEV System-level Design Optimization

as a measure of the goodness of the model ﬁt (Magee,

1990), where ¯y denotes the mean of the output values.

These statistics are also used within the second step

of model validation. Therefore, an additional data

set consisting of EM designs not included within the

training data is used for the validation of the interpo-

lation behavior of the scalable models. In this con-

text, the goodness of interpolation behavior is deﬁned

by the extent of overﬁtting or underﬁtting within the

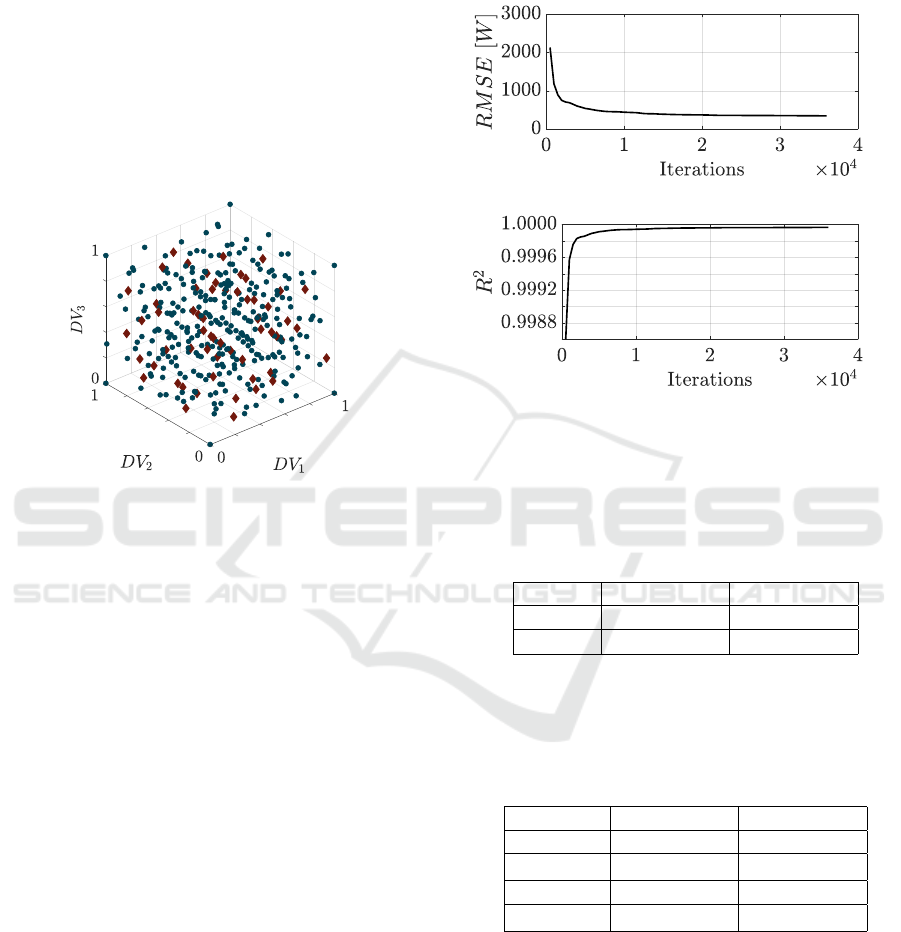
model. Figure 8 shows the distribution of 60 EM de-

signs as they are used for the second step of model

validation.

Figure 8: Distribution of additional EM designs for model

validation.

The EM designs for the validation (red diamonds)

are given by an extension of the original Sobol distri-

bution and the data is generated by following the data

generation procedure described in Section 3.2 for the

additional designs.

4 RESULTS

In this section, the introduced methodology is applied

on the deﬁned FEA simulation based training data set

and veriﬁed by an exemplary analysis of the training

convergence and the resulting model error of the con-

sumption model ˆy

Con

. With respect to the application

ﬁeld in HEV system-level design, a simulation study

is carried out to prove the model performance within

a practical context.

4.1 Model Analysis

The veriﬁcation of the model performance is carried

out during the model training and shown in Figure

9. In diagram a), the minimization progress of the

RMSE is plotted against the number of iterations.

Considering R

on its deﬁned co-domain [0, 1], val-

ues close to 1 represent a good model ﬁt if the train-

ing data is not affected with measurement uncertainty.

Since the progress of R

converges to 1, the trained

model achieves the required performance.

(a) RMSE

(b) Coefﬁcient of determination R

Figure 9: Training convergence and model veriﬁcation.

The success of the training is summarized for the

consumption model ˆy

Con

and the limitation model

ˆy

Lim

by the resulting statistics given in Table 2:

Table 2: Resulting tranining statistics.

Statistic ˆy

Con

ˆy

Lim

RMSE 344 W 2.85 Nm

0.999963479 0.999593949

Furthermore, the validation conﬁrms the goodness

of the model ﬁt with similar statistics as achieved dur-

ing the veriﬁcation process. These measures are given

for both models and two validation steps in Table 3

Table 3: Resulting validation statistics.

Statistic ˆy

Con

ˆy

Lim

RMSE

val,1

345 W 2.85 Nm

val,1

0.999963305 0.999597185

RMSE

val,2

324 W 2.87 Nm

val,2

0.999967438 0.999569435

Due to the application ﬁeld in HEV system-level

design, the scalable EM models require rather high

values of R

than in other modeling tasks since small

deviations in electrical power maps can lead to signi-

ﬁcant differences within the evaluation of energy con-

sumption. For example an model error of 10 W does

not signiﬁcantly affect the evaluation of energy con-

sumption at high loads e.g., 100 kW, but does in areas

of small loads as it is present in typical driving cycles.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

4.2 Simulation Study

In order to prove the practicality of the developed

MLP-based scalable EM models, an exemplary sim-

ulation study is carried out. Thereby, the operat-

ing points of the EM in electric drive mode for spe-

ciﬁc HEV topologies are used for the evaluation of

the electrical energy consumption. These operating

points are drawn from a hybrid vehicle simulation

model and refer to the Worldwide Harmonized Light

Vehicles Test Procedure (WLTP). Figure 10 illustrates

the operating points plotted into the efﬁciency maps

of an exemplary FEA based model a) and the corre-

sponding MLP model b) for a speciﬁc EM design.

(a) FEA based Model

(b) MLP Model

Figure 10: Efﬁciency maps with WLPT operating points.

The qualitative comparison of the map character-

istics shows notably deviations in areas close to zero

torque and close to the torque limitation curves. This

behavior was observed for a wide range within the

considered design space. In order to quantitatively

asses the deviations signiﬁcance in means of energy

consumption evaluation, 5 EM designs (including de-

signs not represented within the training data) are var-

ied within 3 different HEV topologies and thus are

evaluated at different operating points.

Table 4: Relative deviations of energy consumption.

Variations Top 1 Top 2 Top 3

0.131 % 0.691 % 0.867 %

0.387 % 1.048 % 0.143 %

2.662 % 2.202 % 1.480 %

0.404 % 1.004 % 0.226 %

1.153 % 0.553 % 0.169 %

The relative deviations of the MLP models elec-

trical energy consumptions are given in Table 4. The

investigated electrical machine EM

is conspicuous

because of a rather high relative deviation compared

to the remaining values. In this case, EM

is charac-

terized by a high maximum torque and thus oversized

with respect to the WLTP operating points. Keeping

this fact in mind, signiﬁcant deviation can be over-

come by an adequate setting of the design variable

limits. Since the deviations of the remaining EM de-

signs mostly show values smaller than 1 %, the scal-

able EM models possesses sufﬁcient accuracy and

saving potential in terms of computation time if more

than 1800 simulations are carried out (see Fig. 11).

Figure 11: Break even point of simulation numbers.

The diagram shown above can be adapted to ar-

bitrary data generation procedures to assess the efﬁ-

ciency of the proposed modelling approach.

5 CONCLUSIONS

The main focus of this research is a methodical ap-

proach using the strength of Neural Networks in non-

linear function approximation for the development of

scalable EM models. This work is motivated by typ-

ical requirements in HEV system-level design opti-

mization in terms of component modeling, namely

scalability and the achievement of sufﬁcient accuracy

with practicable computational effort.

The MLP-based scalable EM models developed

in this paper are capable to represent the characteris-

tics of each EM design within the given design space.

Thus, once the model is trained, it can be directly im-

plemented and used within typical HEV system-level

design simulation studies, e.g., component sizing, by

varying the speciﬁed design variables. Since only a

small number of FEA simulations and analytical scal-

ing procedures must be performed uniquely, the intro-

duced approach beneﬁts from high saving potential in

terms of computational effort. The MLP model’s per-

formance is validated by a statistical analysis and its

practicality is proven within an application example.

Future work will include research on different opti-

mization targets, e.g., single losses of the EM system,

and network structures to further increase the model

performance.

A Novel Approach for Development of Neural Network based Electrical Machine Models for HEV System-level Design Optimization

REFERENCES

Buecherl, D., Bertram, C., Thanheiser, A., and Herzog,

H.-G. (2010). Scalability as a degree of freedom in

electric drive train simulation. In 2010 IEEE Vehicle

Power and Propulsion Conference. IEEE.

Domingues, G., Reinap, A., and Alakula, M. (2016). De-

sign and cost optimization of electriﬁed automotive

powertrain. In 2016 International Conference on

Electrical Systems for Aircraft, Railway, Ship Propul-

sion and Road Vehicles & International Transporta-

tion Electriﬁcation Conference (ESARS-ITEC). IEEE.

Drago, G. and Ridella, S. (1992). Statistically controlled ac-

tivation weight initialization (SCAWI). IEEE Trans-

actions on Neural Networks, 3(4):627–631.

Gao, W. and Porandla, S. (2005). Design optimization of

a parallel hybrid electric powertrain. In 2005 IEEE

Vehicle Power and Propulsion Conference. IEEE.

Hagan, M. and Menhaj, M. (1994). Training feedforward

networks with the marquardt algorithm. IEEE Trans-

actions on Neural Networks, 5(6):989–993.

Hofman, T., Ebbesen, S., and Guzzella, L. (2012). Topol-

ogy optimization for hybrid electric vehicles with au-

tomated transmissions. IEEE Transactions on Vehicu-

lar Technology, 61(6):2442–2451.

Hornik, K., Stinchcombe, M., and White, H. (1989). Multi-

layer feedforward networks are universal approxima-

tors. Neural Networks, 2(5):359–366.

Magee, L. (1990). R2measures based on wald and like-

lihood ratio joint signiﬁcance tests. The American

Statistician, 44(3):250–253.

Marquardt, D. W. (1963). An algorithm for least-squares

estimation of nonlinear parameters. Journal of

the Society for Industrial and Applied Mathematics,

11(2):431–441.

Nelles, O. (2001). Nonlinear System Identiﬁcation.

Springer Berlin Heidelberg.

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986).

Learning representations by back-propagating errors.

Nature, 323(6088):533–536.

Santner, T. J., Williams, B. J., and Notz, W. I. (2003).

The Design and Analysis of Computer Experiments.

Springer New York.

Silvas, E., Hofman, T., Murgovski, N., Etman, P., and Stein-

buch, M. (2016). Review of optimization strategies for

system-level design in hybrid electric vehicles. IEEE

Transactions on Vehicular Technology, pages 1–1.

Stipetic, S. and Goss, J. (2016). Calculation of efﬁciency

maps using scalable saturated ﬂux-linkage and loss

model of a synchronous motor. In 2016 XXII Inter-

national Conference on Electrical Machines (ICEM).

IEEE.

Vaillant, M. (2016). Design Space Exploration zur

multikriteriellen Optimierung elektrischer Sport-

wagenantriebsstr

ange: Variation von Topologie

und Komponenteneigenschaften zur Steigerung von

Fahrleistungen und Tank-to-Wheel Wirkungsgrad.

PhD thesis, KIT Karlsruhe.

Winsel, T. (2002). Stabile neuronale Prozessmodelle - au-

tomatisierte Generierung echtzeitfhiger Modelle zur

Nachbildung des dynamischen Verhaltens von Ver-

brennungsmotoren. VDI-Verlag, Dsseldorf.

Wirasingha, S. G. and Emadi, A. (2011). Classiﬁcation and

review of control strategies for plug-in hybrid electric

vehicles. IEEE Transactions on Vehicular Technology,

60(1):111–122.

Zhou, K., Ivanco, A., Filipi, Z., and Hofmann, H. (2015).

Finite-element-based computationally efﬁcient scal-

able electric machine model suitable for electriﬁed

powertrain simulation and optimization. IEEE Trans-

actions on Industry Applications, 51(6):4435–4445.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems