How Complex is to Solve a Hard Problem with Accepting Splicing

Systems

Victor Mitrana

1,3 a

, Andrei P

aun

2 b

and Mihaela P

aun

3 c

Department of Information Systems, Polytechnic University of Madrid, Crta. de Valencia km. 7 - 28031 Madrid, Spain

Faculty of Mathematics and Computer Science, University of Bucharest, Str. Academiei 14, 010014 Bucharest, Romania

National Institute for Research and Development of Biological Sciences, Independentei Bd. 296, Bucharest, Romania

Keywords:

Splicing, Accepting Splicing System, Computational Complexity, Descriptional Complexity, 3-colorability

Problem.

Abstract:

We deﬁne a variant of accepting splicing system that can be used as a problem solver. A condition for halting

the computation on a given input as well as a condition for making a decision as soon as the computation has

stopped is considered. An algorithm based on this accepting splicing system that solves a well-known NP-

complete problem, namely the 3-colorability problem is presented. We discuss an efﬁcient solution in terms

of running time and additional resources (axioms, supplementary symbols, number of splicing rules. More

precisely, for a given graph with n vertices and m edges, our solution runs in O(nm) time, and needs O(mn

)

other resources. Two variants of this algorithm of a reduced time complexity at an exponential increase of the

other resources are ﬁnally discussed.

1 INTRODUCTION

One of the basic phenomenon in genetic engineer-

ing is that by which genetic material is recombined.

This phenomenon, called splicing, allows to geneti-

cally modify a biological entity for different purposes

like: more resistant plants, organisms better adapted

to weather changes, production of hormones, etc. The

chemicals involved in the recombination of DNA se-

quences are two types of enzymes: restriction en-

zymes which cut the DNA at speciﬁc sites (called

recognition sites) yielding two fragments with the so-

called “sticky ends”, and ligase which rejoin frag-

ments with sticky ends. A computational model based

on an operation abstracted from the splicing operation

described above has been deﬁned in (Head, 1987).

The model viewed as a language generating device

is called splicing system. Roughly speaking, the

two DNA molecules are represented by strings while

the restriction enzymes are represented by quadruples

of strings, called splicing rules, indicating the sites

where the two strings are to be cut. The compatibility

for rejoining is deﬁned by the fact that two fragments

https://orcid.org/0000-0002-1457-8933

https://orcid.org/0000-0002-1644-8198

https://orcid.org/0000-0002-3342-9140

can be rejoined if they were obtained by applying the

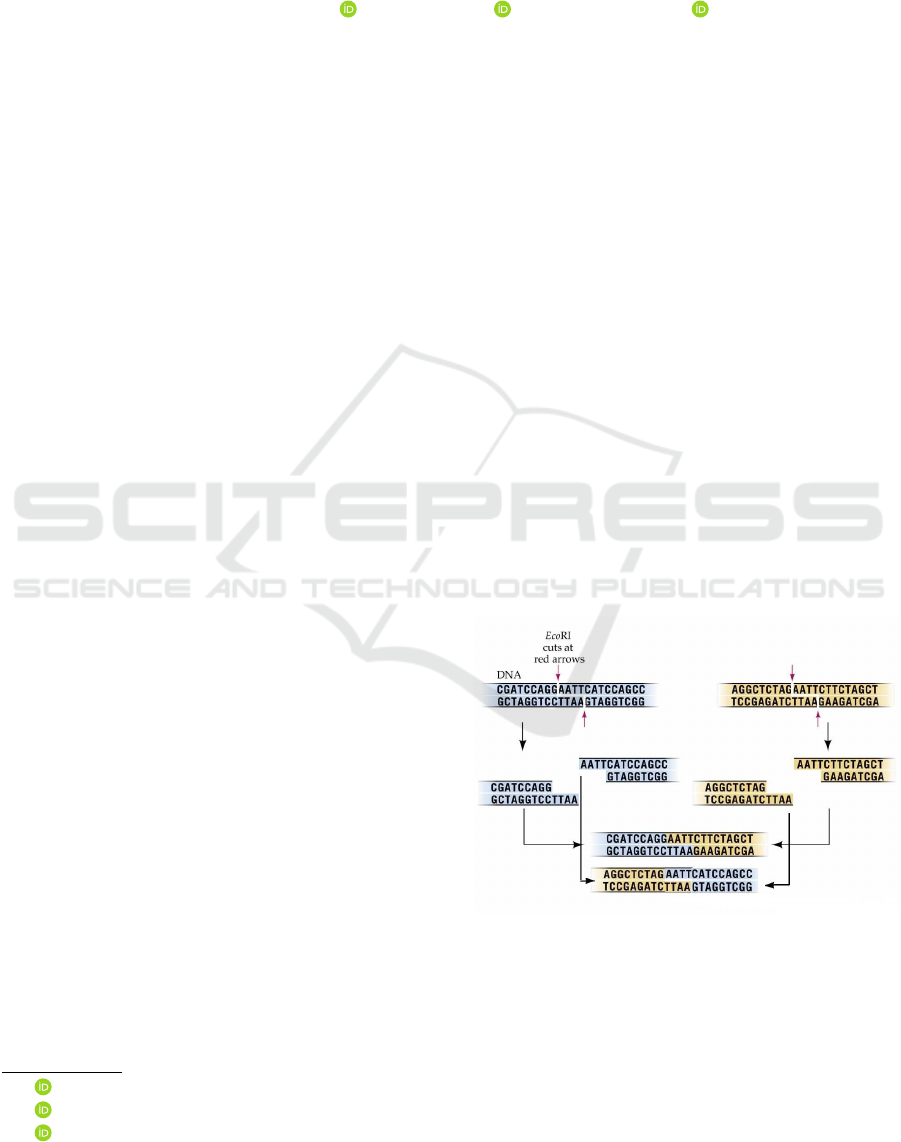
same splicing rule. The splicing operation is illus-

trated in Figure 1.

Figure 1: Splicing operation.

Most research in the area of splicing systems

has been focused on deﬁning different types of such

systems and investigating their computational power

from a language generating point of view. For several

years, it was an open problem whether or not splic-

ing systems are more powerful than ﬁnite automata,

from a computational power point of view. The prob-

lem was ﬁrst solved in (Culik and Harju, 1991), and

Mitrana, V., P

aun, A. and P

aun, M.

How Complex is to Solve a Hard Problem with Accepting Splicing Systems.

DOI: 10.5220/0007715900270035

In Proceedings of the 4th International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2019), pages 27-35

ISBN: 978-989-758-366-7

later on, a constructive proof was proposed in (Pixton,

1996). In these papers it was proved that splicing sys-

tems are strictly weaker that ﬁnite automata. In order

to increase the computational power of these systems,

many variants have been deﬁned and investigated; we

mention here just a few of them: distributed splicing

systems (Csuhaj-Varj

u et al. 1996)), extended splic-

ing systems (P

aun et al. 1996), splicing systems with

multisets (Denninghoff and Gatterdam, 1989), splic-

ing systems with permitting and forbidding contexts

(Freund et al. 1999), splicing systems with a regular

set of rules (P

aun, 1996), programmed and evolving

splicing systems (P

aun et al. 1997). Under certain

circumstances, splicing systems are shown to be able

to simulate Turing machines, see (P

aun et al. 1998).

This result suggests the possibility to consider splic-

ing systems as theoretical models of programmable

universal DNA computers based on the splicing op-

eration. Two comprehensive surveys can be found in

(Head et al. 1997) and (P

aun et al. 1998).

Splicing systems working with circular strings are

inspired by a recombinant behavior of circular DNA

in plasamids. Two variants of circular splicing sys-

tems have been introduced in (Siromoney et al. 1992)

and (Pixton, 1995)

Networks with nodes hosting splicing processors

(NSP) have been considered in (Manea et al. 2007).

The NSP model resembles some features of another

distributed computing system, namely test tube dis-

tributed splicing systems introduced in (Csuhaj-Varj

et al. 1996)) and further investigated in (P

aun, 1998).

A characterization of the complexity class NP as

the class of languages accepted by restricted NSPs

in polynomial time was proposed. Furthermore, a

similar characterization was proposed for the class

PSPACE as the class of languages accepted by re-

stricted NSPs with at most polynomial length of the

strings used in the derivation. In (Manea et al. 2006)

it was proved that NSPs (unrestricted, this time) of

constant size accept all recursively enumerable lan-

guages, and can solve all problems in NP in polyno-

mial time; also an universality result for NSPs was

proposed. In both cases the number of nodes needed

was 7. In (Loos et al. 2009) it is shown that compu-

tational completeness can be achieved by NSPs of 2

nodes. In the same paper a more involved construc-

tion, showing that NSPs of size 3 can simulate the

computations of a non-deterministic Turing machine

in parallel, is presented.

A new protocol of cooperation in networks of

splicing processors, namely the polarization, has been

introduced in (Bordihn et al. 2017) and further in-

vestigated in (Bordihn et al. 2018). The polariza-

tion protocol requires that each node has a polariza-

tion deﬁned as a value in the set {+,0,−} (posi-

tive, neutral, negative) and the data have assigned a

value in the same set which is computed by a valu-

ation mapping. Now the communication is based on

the compatibility between the polarization of nodes

and the value of data. A quantitative generalization

of these networks, called networks of splicing pro-

cessors with evaluation sets have been introduced in

omez-Canaval et al. 2016). In a network of splic-

ing processors with evaluation sets, unlike in all the

aforementioned cases, the valuation mapping returns

the exact value computed for data. The new model re-

ﬁnes the communication protocol based on polariza-

tion discussed above, in which each polarization may

be viewed as one of the intervals of integers (−∞, 0),

{0}, and (0,∞), to a more complex polarization based

on more intervals. The new model tries to resemble

the biological concept of the concentration gradient

in a solution. Now, the strategy of communication

between two nodes follows the compatibility between

their accepting values with respect to some predeﬁned

evaluation sets and the values of the data computed

by a valuation mapping. More precisely, the values

of data have to be in the set of accepting values with

respect to some evaluation set of symbols. This new

communication protocol might be interpreted as the

movement of molecules or particles along a concen-

tration gradient between two areas.

Other fundamental algorithmic problems regard-

ing splicing systems, namely recognition and synthe-

sis are considered in a series of papers starting with

(Bonizzoni and Mauri, 2005). Recognition problem

refers to the design of an algorithm able to decide

whether or not a given regular language is a splicing

language, while the synthesis problem refers to the

possibility of effectively constructing a splicing sys-

tem that generates a given regular language.

A surprising application of splicing systems which

are used an automatic music composer is proposed in

(De Felice et al. 2017). This approach might be seen

as a possible bio-inspired strategy for automatic mu-

sic composition. The model in the aforementioned

work is tailored on 4-voice chorale-like music. Along

these lines, a new approach for both recognition and

automatic composition of styles for musical collec-

tives is designed in (De Prisco et al. 2017). Infor-

mally speaking, such a system exploits a machine

learning recognizer, based on one-class support vec-

tor machines and neural networks for style recogni-

tion, and a splicing composer, for music composition

(in the style of the whole collective).

Starting from some ideas considered in (Loos et

al. 2006), a novel look at splicing systems is pro-

posed in (Mitrana et al. 2010), namely these systems

COMPLEXIS 2019 - 4th International Conference on Complexity, Future Information Systems and Risk

are considered as accepting devices. More precisely,

one deﬁnes the concept of accepting splicing system.

The rough idea is to consider that an accepting splic-

ing system receives as input a string which enters, to-

gether with a given ﬁnite set of axioms, into an it-

erated splicing process until a string from a speciﬁc

ﬁnite sets of strings is produced. When such a string

is produced, the computational process halts. In this

paper, we consider the case when a decision can be

made as soon as the computation halts. To this aim,

we consider a two ﬁnite sets of strings, a set of halting

strings such that when a halting string is produced the

computation halts, and a set of accepting strings. For

making a decision, it sufﬁces to check whether or not

at least one accepting string has been obtained.

The paper is organized as follows. In the next sec-

tion we present the basic deﬁnitions and the main con-

cept, that of an accepting splicing system viewed as a

problem solver. We deﬁne one computational com-

plexity measure , similar to the time complexity in

most models, which measures the number of splicing

steps necessary for a computation to halt. Then we

deﬁne a few descriptional complexity measures like:

the number of axioms, the number of supplementary

symbols, the number of rules, the length of the longest

splicing rule, and the number of halting or accepting

strings. In the third section, we consider a very well-

known NP-complete problem, that of 3-colorability,

and propose an algorithm based on accepting splicing

systems (an AccSS-algorithm) to solve this problem.

We give both informal explanations as well as formal

deﬁnitions on the way our algorithm works. After-

wards, we evaluate the computational and descrip-

tional complexity of our algorithm. Thus, we prove

that given a graph with n vertices and m edges, there is

an AccSS-algorithm that decides the 3-colorability for

this graph in O(nm) time and O(mn

) other resources

(axioms, symbols, splicing rules). Finally, we discuss

two variants of this algorithm that need a reduced time

complexity, but this is achieved at an exponential in-

crease of the other resources.

2 MAIN CONCEPT

We start by summarizing the notions used throughout

the paper. For all undeﬁned notions the reader may

consult (Rozenberg and Salomaa, 1997). An alphabet

is a ﬁnite and nonempty set of symbols. The cardinal-

ity of a ﬁnite set A is written card(A). Any ﬁnite se-

quence of symbols from an alphabet V is called string

over V . The set of all strings over V is denoted by V

∗

and the empty string is denoted by λ. The length of

a string x is denoted by |x| while al ph(x) denotes the

minimal alphabet W such that x ∈ W

∗

A splicing rule over V is 4-tuple [(u

);(u

)],

with u

∈ V

∗

. For a splicing rule r =

[(u

);(u

)] and a pair of strings x, y ∈ V

∗

, we

write

(x,y) = {y

| x = x

,y = y

}

∪{x

| x = x

,y = y

}

for some x

∈ V

∗

. The analogy with the

situation depicted in Figure 1 is immediate: the

two strings represent the two double stranded DNA

molecules, while the restriction enzyme is repre-

sented by the splicing rule. This deﬁnition is extended

to a set of splicing rules R and a set of strings A by

(A) =

[

r∈R

[

∈A

When the set of splicing rules is clear, we omit the

subscript.

Note that this deﬁnition assumes that arbitrarily

many copies of all strings in A are available for splic-

ing. This is a natural assumption from the biological

point of view because every such string, encoding a

DNA molecule, can be duplicated sufﬁciently many

times by the PCR procedure, a well deﬁned technique

for amplifying the genetic material (Rabinov, 1996).

We now recall the deﬁnition and terminology for

accepting splicing systems, following (Mitrana et al.

2010). It is worth noting that the deﬁnition presented

here differs from those in (Mitrana et al. 2010) and

(Arroyo et al. 2013) because we use here accepting

splicing systems as decision problem solvers. To this

aim, we need a condition for halting the computation

and a condition for making the decision. Furthermore,

we need that all systems halt on every input An ac-

cepting splicing system (AccSS for short) is a 8-tuple

Γ = (V,U,<,>, A, R, H, F),

where V is the input alphabet, U is the working al-

phabet, V ⊂ U, <,> are two symbols in U \V called

endmarkers, A ⊆ U

∗

is the set of initial strings (ax-

ioms), while R is a set of splicing rules over U. Fur-

thermore, H and F are ﬁnite sets of strings over U;

the elements of H are called halting strings and those

of F are called accepting strings.

Let Γ = (V,U, <, >, A,R,H,F) be an AccSS and a

string w ∈ V

∗

; we deﬁne the following iterated splic-

ing

(A,w) = σ

(A ∪ {w}),

i+1

(A,w) = σ

(τ

(A,w) ∪ A),i ≥ 1.

Again, the subscript R may be omitted when it is self-

understood. Note that if no splicing rule is applicable

to a string different than an axiom at some step, it

How Complex is to Solve a Hard Problem with Accepting Splicing Systems

disappears from the set of all available strings in the

next splicing step. A computation of Γ on w is the

sequence of sets (τ

(A,w))

i≥0

. Such a computation is

ﬁnite (we say that Γ halts on w ∈ V

∗

) if there exists

k ≥ 0 such that τ

(A,w)∩ H 6=

0. An input string w is

accepted by Γ if Γ halts on w as above and τ

(A,w) ∩

F 6=

0; otherwise, w is rejected. A string W is decided

by Γ if Γ halts on w. A set of strings L is decided by Γ

if Γ accepts all strings in L and rejects all strings that

do not belong to L. As we want to consider AccSS as

problem solvers, we assume that every AccSS in what

follows halts on every input string.

We now deﬁne the following computational com-

plexity measure for an AccSS Γ = (V,U,<,>,A,R,F)

that halts on every input:

Time

(w) = min{k | τ

(A,w) ∩ H 6=

0},

Time

(n) = max{Time

(w) | |w| = n}.

It is worth noting that a similar measure with a differ-

ent deﬁnition was introduced in (Loos and Ogihara,

2007) for generating splicing systems.

We also deﬁne the following descriptional complexity

measures for an AccSS Γ = (V,U, <,>,A,R,F) that

halts on every input:

Ax(Γ) = card(A),

Symb(Γ) = card(U \V),

NSplice(Γ) = card(R),

LSplice(Γ) = max{|u

| |

[(u

);(u

)] ∈ R},

Final(Γ) = max(card(H),card(F)).

We mention here another work considering some

descriptional complexity measures for generating

splicing systems, namely (Loos et al. 2008). In this

paper, the measures are the total length of the rules

and the size of the initial language. These measures

are related to the size of the minimal ﬁnite automata

accepting the same language.

We discuss below the potential of AccSS to solve

complex decidability problems. We now formally de-

ﬁne what an AccSS-algorithm is. A decidability prob-

lem P is said to be solved in time O(t(n)) by AccSSs

if there exists a family G of AccSSs, which can be

constructed by an effective procedure, such that for

each instance x of size O(n) of the problem P , en-

coded by a string w, one can effectively construct an

AccSS Γ(x) ∈ G such that the computation of Γ(x )

on w halts in time O(t(n)) with at least an accepting

string obtained during the computation if and only if

the x is a true instance. This effective construction is

called an O(t(n)) time AccSS-algorithm for the con-

sidered problem.

3 AN AccSS -ALGORITHM FOR

THE 3-COLORABILITY

PROBLEM

Given a connected undirected graph without loops,

the 3-colorability problem is to decide whether or not

is it possible to color each vertex by using three colors

(say, red, blue, and green) such that no two adjacent

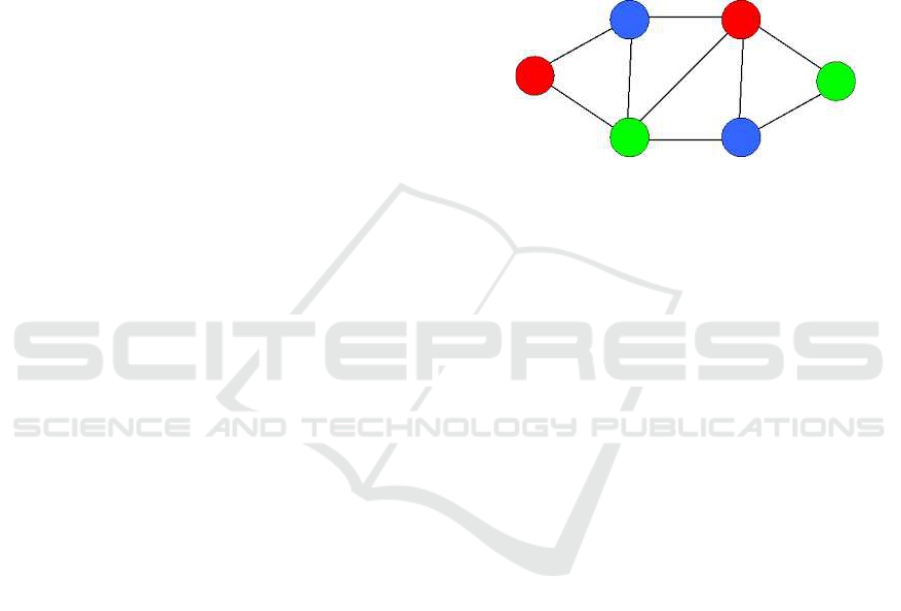
vertices are of the same color. For instance, the graph

in Figure 2 is correctly colored.

Figure 2: Graph correctly colored with three colors.

The problem is known to be NP-complete (Garey

and Johnson, 1979). Let Y = (B, Q) be a graph with

set of vertices B = {1,2,...,n} and set of edges Q =

,..., e

}, where each e

is given in the form

= {k

}, for some 1 ≤ k

6= k

≤ n.

We now present an AccSS-algorithm for the 3-

colorability problem and analyze its computational

and descriptional complexity.

3.1 AccSS-algorithm

The input string is < a

...e

>. The algorithm

has two main phases. In the ﬁrst phase all strings en-

coding graph colorings, namely strings of the form

< x

...x

...e

where x ∈ {r,b,g} are produced in parallel by splic-

ing. The meaning of this encoding is that the node i

is colored by red, blue, green if r

, respectively.

In the second phase, the graph colorings obtained in

the ﬁrst phase are to be checked for correctness, that

is they are correct colorings. All the strings encoding

correct colorings will lead simultaneously to accept-

ing strings. If the graph cannot be correctly colored,

the computation will halt with no accepting string ob-

tained.

A complete formal solution is presented in the

next two sections. The general idea is that used by

most of the DNA-based algorithms: a ﬁrst phase is

dedicated to the generation of solution space, and a

second phase which searches the correct solutions by

ﬁltering the whole solution space. The parameters of

Γ are to be constructed dynamically as follows. We

give the splicing rules for each phase, hence the set

COMPLEXIS 2019 - 4th International Conference on Complexity, Future Information Systems and Risk

of splicing rules R of Γ is the set containing all these

rules. Similarly, the set of axioms A contains all the

axioms presented for each phase. The working alpha-

bet U is formed by all symbols that appear in the ax-

ioms and splicing rules listed for each phase.

3.1.1 First Phase

The ﬁrst phase can be accomplished with the fol-

lowing splicing rules and axioms distributed in three

groups, each of them having subgroups:

1. [(<,a);(< C

,#)], and < C

# is an axiom.

2.1. [(†,C

a);(X

)],† ∈ {<} ∪ {b

i−1

}

and X

is an axiom,1 ≤ i ≤ n.

2.2. [(X

a,†

);(X

†

i+1

,#)],†

∈ {a, e

†

∈ {b

},and X

†

i+1

# is an axiom,

1 ≤ i ≤ n − 1.

2.3. [(X

a,e

);(X

†,#)],† ∈ {b

and X

†# is an axiom.

2.4. [(<,Y

);(#,Y

)],and #Y

is an axiom,1 ≤ i ≤ n.

3.1. [(<,Y

);(X

,†C

a)],† ∈ {b

3.2. [(†

i−1

);(X

i−1

,†

a)],†

∈ {b

i−2

†

∈ {b

i−1

},3 ≤ i ≤ n.

3.3. [(†

);(X

,†

)],†

∈ {b

n−1

†

∈ {b

We explain how an arbitrary string

< x

...x

...e

>, with x ∈ {r,b,g}, is

produced from the input string w =< a

...e

by using the splicing rules listed above. The ﬁrst

splicing rule that can be applied is the rule in

the group 1 which can be applied to the pair of

strings formed by the input string and the axiom

< C

#. This splicing step yields two new strings

< C

...e

> and < #. The string < # cannot

be involved in further splicing steps, hence it will

disappear in the next splicing step. Therefore, we

can say that the role of the ﬁrst splicing step is to

introduce the symbol C

before the ﬁrst occurrence

of a in the input string. The rough idea of the next

splicing steps is that symbols C

, 1 ≤ i ≤ n, scan

the input string from left to right following the next

procedure: each C

scans the symbol a next to it, re-

places this occurrence of a by a symbol in {b

moves to the right of this symbol, and changes itself

into either C

i+1

, if i < n or it is removed, if i = n.

Inductively, this happens as follows. Assume that the

current string is < x

...x

i−1

n−i+1

...e

with x ∈ {r, b,g}, and i < n. A rule in the subgroup

2.1 is applied to the current string and the axiom

. Two strings are obtained < x

...x

i−1

and

n−i+1

...e

>. Now, a rule in the subgroup

2.2 is applied to X

n−i+1

...e

> and to

one of the axioms X

†C

i+1

#, where † ∈ {b

Thus three new words are obtained simultaneously:

i+1

n−i

...e

>, X

i+1

n−i

...e

and X

i+1

n−i

...e

>. In the same splicing

step, a rule in subgroup 2.4 is applied to an axiom #Y

and to < x

...x

i−1

. As a result of this splicing the

string < x

...x

i−1

is obtained. Now the process

of coloring the node i ends by applying a splicing rule

in the subgroup 3.2 to each of the three strings afore-

mentioned and to one of the strings < x

...x

i−1

All the strings < x

...x

i+1

n−i

...e

> are

now produced.

It is worth mentioning that the rules in subgroups

2.3 and 3.3 replace the rules in 2.2 and 3.2, respec-

tively, when i = n in the above discussion. Now the

whole process described above is iterated until all

strings < x

...x

...e

>, with x ∈ {r, b,g} are

produced.

A short discussion is necessary here. First, it is

easy to note that all the other strings that are by-

products of the splicing rules applied in the process

discussed above will not be involved in further splic-

ing steps because they cannot be cut by any splicing

rule. Second, when applying a rule in the third group

the two strings that are joined do not necessarily come

from the same string cut with rules in the subgroup

2.1, but this fact does not introduce any illegal string,

that is all the strings obtained after applying rules in

the third group are still valid partial colorings of the

graph. Note that by partial coloring we mean that ev-

ery node of the graph is either colored with exactly

one color or it is not colored yet.

3.1.2 Second Phase

The second phase starts when the ﬁrst

phase is ﬁnished, that is when all strings

< x

...x

...e

>, with x ∈ {r, b, g} are

produced. Informally, the second phase checks

whether every such string as above is a correct

coloring. This means that for each e

= {k

6= x

holds. This is to be done by checking this

condition for e

, e

, ..., e

For a better understanding of this checking pro-

cess we need some preparatives. For every symbol

encoding the edge {k

} we write e

, and

if one of the two nodes k

is colored blue, green,

and red, respectively, while the other node is not col-

ored yet. Now the checking process is to be accom-

plished as follows. The preﬁx < x

...x

of each of

the strings < x

...x

...e

>, with x ∈ {r,b,g}

will be scanned by every symbol e

, 1 ≤ k ≤ m, from

right to left such that:

(i) If e

meets b

or b

to its left, then e

is replaced

How Complex is to Solve a Hard Problem with Accepting Splicing Systems

by e

(ii) If e

meets g

or g

to its left, then e

is replaced

(iii) If e

meets r

or r

to its left, then e

is replaced

(iv) If e

meets a symbol in {g

} to its

left, then e

is deleted.

(v) If

meets a symbol in {b

} to its

left, then

is deleted.

(vi) If

meets a symbol in {g

} to its

left, then

is deleted.

(vii) In all the other cases, e

, and

are replaced

by a new symbol Q, which will continue to scan

the rest of the string until either the left endmarker

or another occurrence of Q is met.

(viii) If a symbol x

was scanned by all symbols e

, 1 ≤

k ≤ m, then it is deleted.

We give now the formal deﬁnitions of splicing

rules, distributed in groups and subgroups, and those

of axioms.

1. [(♣,x

);(♦

i, j

,♥

i, j

)] and ♦

i, j

♥

i, j

is an axiom,

♣ ∈ {<, Q} ∪



i−1

, if i > 1

0, if i = 1

∈ {e

},1 ≤ j ≤ m,1 ≤ i ≤ n.

2.1. [(♣,♥

i, j

);(#,♥

i, j

)] and #♥

i, j

is an axiom,

♣ ∈ {<, Q} ∪



i−1

, if i > 1

0, if i = 1

1 ≤ j ≤ m,1 ≤ i ≤ n.

2.2. [(♦

i, j

i+1

);(♦

i, j

,#)],

and ♦

i, j

# is an axiom,x ∈ {b, g,r},

∈ {e

} and

• if i /∈ { j

, j

}, then Y

= Z

• if i ∈ { j

, j

}, and Z

= e

, then







, if x = b,

, if x = g,

, if x = r,

• if i ∈ { j

, j

}, then Y

= λ provided that

x ∈ {g,r} and Z

= e

x ∈ {b, r} and Z

x ∈ {b, g} and Z

•Y

= Q, in all the other cases,

1 ≤ j ≤ m,1 ≤ i ≤ n.

3. [(♣,♥

i, j

);(♦

i, j

P)],Z

∈ {Q, e

,λ},

♣ ∈ {<, Q} ∪



i−1

, if i > 1

0, if i = 1

P 6= #, 1 ≤ j ≤ m,1 ≤ i ≤ n.

In order to clarify the roles of these splicing rules

we show how they are used for fulﬁlling the con-

ditions (i)-(vi) and partly (vii) deﬁned above. Let

< αx

β, for some strings α,β, be an arbitrary string

available at this splicing step. We take the axiom

♦

i, j

♥

i, j

and apply a rule in group 1 to this pair of

strings. The two new strings are: α♥

i, j

and ♦

i, j

β.

Now, in the same splicing step, α♥

i, j

is transformed

into α♥

i, j

by using a rule in subgroup 2.1, while

♦

i, j

β is spliced by a rule in subgroup 2.2. As one

can easily see, all the conditions (i)-(vi) are consid-

ered in the deﬁnition of rules in subgroup 2.2. More-

over, the condition for introducing the new symbol Q

is also considered. The meaning for introducing Q is

that the coloring encoded by the string < αx

β is

illegal for the edge e

For the second part of condition (vii) and condi-

tion (viii) we give only some informal explanations

without formally deﬁning the rules, which can be eas-

ily deﬁned by the reader. The condition (viii) assumes

that a symbol x

reached the right endmarker >. This

symbol can be easily deleted now by using one splic-

ing rule that cuts the string just before x

> and re-

places this segment by > only. As soon as a sym-

bol Q has still to scan symbols from right to left, this

can be easily done in three simple splicing steps using

rules similar to those in subgroups 2.1 (ﬁrst splicing

step), 2.2 and 2.4 (second splicing step), and 3.2 (third

splicing step).

When no splicing rule can be applied anymore,

only strings of the form < Q

>, for some 1 ≤ s ≤ m

and possibly one string more, namely <>, have been

produced. By the aforementioned explanations, we

conclude that each string obtained in the ﬁrst phase,

which does not encode a legal coloring, will eventu-

ally lead, at the end of the second phase, to a string

< Q

>, for some 1 ≤ s ≤ m. On the other hand,

each string obtained in the ﬁrst phase, which does en-

code a legal coloring, will eventually lead, at the end

of the second phase, to <>. It is clear that, if <>

is obtained, it is produced before any of the strings

< Q

>. Now, it sufﬁces to reduce, by splicing, all

the strings < Q

> to just one, namely < Q > and con-

sider the set of of halting strings H = {<>,< Q >}

and F = {<>}, and the construction of the AccSS-

algorithm is complete.

3.1.3 Evaluating Time Complexity

We ﬁrst evaluate the time complexity of the AccSS

constructed in the Section 3. Insertion of C

takes one

step, each coloring of a node takes 3 steps, hence the

ﬁrst phase takes a total number of 3n + 1 steps. Note

that each splicing step may be formed by a number of

individual splicings that are done in parallel. Again

we make use of the assumption that the each string

appears in a sufﬁcient number of copies such that if

COMPLEXIS 2019 - 4th International Conference on Complexity, Future Information Systems and Risk

a splicing rule is applicable to a certain string, it can

effectively be used.

The second phase requires, in the worst case, that

the preﬁx < x

...x

to be scanned by every symbol

, 1 ≤ i ≤ m. Each such symbol can scan the preﬁx

in 3n splicing steps. As there are m such symbols,

the total number of steps is 3nm. Furthermore, the

number of steps necessary to delete the symbols x

as required by the condition (viii) is n. Finally, the

number of steps to reduce < Q

> to < Q > is at most

We now conclude that the time complexity of our

algorithm is O(nm)

3.1.4 Evaluating Descriptional Complexity

We now evaluate the descriptional complexity mea-

sures deﬁned in Section 2. In the ﬁrst phase we have

the followings:

• The set of axioms used in the ﬁrst phase is

= {C

#,X

#} ∪

| 1 ≤ i ≤ n} ∪ {X

†C

i+1

# |

† ∈ {b

},1 ≤ i ≤ n − 1} ∪

{#Y

| 1 ≤ i ≤ n}.

Therefore, the number of axioms is 5n + 1.

• We use the following set of symbols:

= {<,>,#} ∪ {C

| 1 ≤ i ≤ n} ∪

| 1 ≤ i ≤ n}.

Therefore, the number of new symbols is 8n + 3.

• The number of splicing rules in each subgroup is

given in Table 1. Consequently, there are 16n − 5

Table 1: The number of splicing rules.

Subgroup Number of splicing rules

1 1

2.1 3n

2.2 3(n − 1)

2.3 3

2.4 n

3.1 3

3.2 9(n − 2)

3.3 9

splicing rules.

• The maximal length of a splicing rule is 8.

For the second phase an exact evaluation of all

measures is rather cumbersome, but we can evaluate

the order of these measures.

• The number of axioms used is at most 14n.

• The number of symbols used is 6nm + 4m + 2.

• The number of splicing rules is at most 5mn(n +

1) + 12mn + n + m

• The maximal length of a splicing rule is 8.

Finally, Final(Γ) = 2.

We conclude that

Ax(Γ) = O(n),

Symb(Γ) = O(mn),

NSplice(Γ) = O(mn

LSplice(Γ) = 8,

Final(Γ) = 2.

3.2 Two Variants

It is worth noting that the algorithm presented above

can be accelerated to O(n) time at an exponential cost

of rules and axioms (O(5

n)), and a linear cost of the

length of splicing rules. It can also be accelerated to

O(n) time at the same cost of rules, axioms and num-

ber of symbols but a constant length of the splicing

rules. We brieﬂy discuss these variants in the sequel.

The second phase can be changed as follows. In-

stead of scanning the preﬁx from right to left with

each symbol e

, we can do this scanning process with

the whole segment e

...e

. The splicing rules for

doing this are:

[(♣,x

...Z

);(#,Y

...Y

)],

where ♣ =



<, if i = 1

i−1

, if i > 1,

...Y

is an an axiom,

∈ {Q, e

}, and

• if i /∈ { j

, j

}, then Y

= Z

• if i ∈ { j

, j

}, and Z

= e

, then







, if x = b,

, if x = g,

, if x = r,

• if i ∈ { j

, j

}, then Y

= λ provided that

x ∈ {g,r} and Z

= e

x ∈ {b, r} and Z

x ∈ {b, g} and Z

•Y

= Q, in all the other cases,

1 ≤ j ≤ m,1 ≤ i ≤ n.

As one can easily see, at every splicing step the

segment Z

...Z

is updated with respect to the

value of x

and moves to the left. Therefore, after

n splicing steps either a segment consisting of some

occurrences of Q reaches the left endmarker, or the

string is <>.

As far as the descriptional complexity of this vari-

ant, we note that the number of splicing rules as well

How Complex is to Solve a Hard Problem with Accepting Splicing Systems

as that of axioms is O(5

n). Furthermore, the maxi-

mal length of a splicing rule is 2m + 4.

Another variant could consider symbols for en-

coding the segments, hence the number of symbols

explodes exponentially but the maximal length of a

splicing rule remains constant.

As a consequence of the constructions and com-

plexity evaluations above, we can conclude

Theorem 1. Let G be a graph with n vertices and m

edges, without loops.

1. There is an AccSS-algorithm that decides the 3-

colorability for G in O(nm) time and O(mn

)

other resources (axioms, symbols, splicing rules).

2. There is an AccSS-algorithm that decides the 3-

colorability for G in O(n) time, O(5

n) axioms

and splicing rules, and O(m) maximal length of

the splicing rules.

3. There is an AccSS-algorithm that decides the 3-

colorability for G in O(n) time, O(5

n) axioms,

symbols, and splicing rules, and a constant maxi-

mal length of splicing rules.

We also want to stress that the technique used in

the construction of the above AccSS-algorithm can

be employed for constructing similar algorithms for

other intractable problems.

4 CONCLUSIONS AND FURTHER

WORK

A new variant of accepting splicing system that can be

used as a problem solver was introduced. This model

may be used as a problem solver because the condi-

tion for halting the computation on a given input is

accompanied by a condition for making a decision as

soon as the computation has stopped. An algorithm

based on this accepting splicing system that solves

a well-known NP-complete problem, namely the 3-

colorability problem is presented. The time efﬁciency

of this solution is analyzed together with some de-

scriptional complexity measures for axioms, supple-

mentary symbols, number of splicing rules. More pre-

cisely, for a given graph with n vertices and m edges,

our solution runs in O(nm) time, and needs O(mn

)

other resources. Two variants of this algorithm of a

reduced time complexity at an exponential increase

of the other resources are also discussed.

We discuss here a few possible ways, that ap-

pear attractive to us, of continuing the work started

here. From a theoretical point of view, a complete in-

vestigation of the computational power of this model

seems to be of interest. This investigation could con-

tribute to a more complete picture of the study started

in (Mitrana et al. 2010). From a more practical

point of view, would like to consider possible soft-

ware implementations of this model that could be

similar to those reported in the literature for other

bio-inspired models. Along these lines, software sim-

ulators for this model using massively parallel plat-

forms for multi-core desktop computers, clusters of

computers and cloud resources similarly to the ap-

proached proposed in (G

omez-Canaval et al. 2015)

and (G

omez-Canaval et al. 2015) might lead to rel-

evant results. In (G

omez-Canaval et al. 2015), it

is shown that massively distributed platforms for big

data scenarios makes them potential candidates for

the development of ultra-scalable simulators able to

simulate different variants of bio-inspired models. In

particular, computing platforms by developing an en-

gine that uses Apache Giraph on top of the Hadoop

platform might be useful. The results of some experi-

ments with such simulators suggest that they might be

amenable to minimize the growth of processing data,

hence to be adapted for models like that discussed

here.

ACKNOWLEDGEMENTS

Work supported by a grant of the Romanian Na-

tional Authority for Scientiﬁc Research and Innova-

tion, project number POC P-37-257.

REFERENCES

Arroyo, F., Castellanos, J., Dassow, J., Mitrana, V., and

anchez-Couso, J.R. (2013). Accepting splicing sys-

tems with permitting and forbidding words. Acta Inf.

50 pp.1–14.

Bonizzoni, P. and Mauri, G. (2005). Regular splicing lan-

guages and subclasses. Theoret. Comput. Sci. 340 pp.

349–363.

Bordihn, H., Mitrana, V., P

aun, A., P

aun, M. (2017). Net-

works of polarized splicing processors. In Theory and

Practice of Natural Computing, TPNC 2017, LNCS

10687, Springer, Berlin, Heidelberg, pp. 165–177.

Bordihn, H., Mitrana, V., Negru, M.C., P

aun, A., P

aun, M.

(2018). Small networks of polarized splicing proces-

sors are universal. Natural Computing, 17 pp. 799–

809.

Csuhaj-Varj

u, E., Kari, L. and P

aun, Gh. (1996). Test tube

distributed systems based on splicing. Computers and

AI 15 pp. 211–232.

Culik, K, and Harju, T. (1991). Splicing semigroups of

dominoes and DNA. Discrete Appl. Math. 31 pp. 261-

277.

Denninghoff, K.L. and Gatterdam, R.W. (1989). On the un-

decidability of splicing systems. Intern. J. Computer

Math. 27 pp. 133–145.

COMPLEXIS 2019 - 4th International Conference on Complexity, Future Information Systems and Risk

De Felice, C., De Prisco, R., Malandrino, D., Zaccagnino,

G., Zaccagnino, R., and Zizza, R. (2017). Splicing

music composition. Inf. Sci. 385 pp. 196–212.

Freund, R., Kari, L., and P

aun, Gh. (1999). DNA com-

puting based on splicing. The existence of universal

computers. Theory of Computing Syst. 32 pp. 69–112.

Garey, M., and Johnson, D. (1979). Computers and

Intractability: A Guide to the Theory of NP-

Completeness. W. H. Freeman & Co. New York.

omez-Canaval, S., Mitrana, V., S

anchez-Couso, J.S.

(2016). Networks of splicing processors with evalu-

ation sets as optimization problems solvers. Informa-

tion Sciencs 369, 457–466.

omez-Canaval, S., Ortega, A., Orgaz, P. (2015). Dis-

tributed simulation of NEPs based on-demand cloud

elastic computation. In Advances in Computational

Intelligence, LNCS 9094, Springer, Berlin, Heidel-

berg, pp. 40–54.

omez-Canaval, S., Ordozgoiti, B., Mozo, A. (2015).

NPEPE: Massive natural computing engine for opti-

mally solving NP-complete problems in Big Data sce-

narios. In Communications in Computer and Infor-

mation Science 539, Springer, Berlin, Heidelberg, pp.

207–217.

Head, T. (1987). Formal language theory and DNA: an anal-

ysis of the generative capacity of speciﬁc recombinant

behaviours. Bull. Math. Biology 49 pp. 737–759.

Head, T., P

aun, Gh., and Pixton, D. (1997). Language

theory and molecular genetics. Chapter 7, vol. 2, in

(Rozenberg and Salomaa, 1997).

Loos, R., Malcher, A., and Wotschke, D. (2008). De-

scriptional complexity of splicing systems. Intern. J.

Found. Comp. Sci. 19 pp. 813–826.

Loos, R. and Ogihara, M. (2007). Complexity theory for

splicing systems. Theor. Comput. Sci. 386 pp. 132–

150.

Loos, R., Martin-Vide, C., and Mitrana, V. (2006). Solv-

ing SAT and HPP with accepting splicing systems.

In Proc. 9th Parallel Problem Solving from Nature

(PPSN IX), LNCS 4193, Springer-Verlag, Berlin, pp.

771-777.

Loos, R., Manea, F., Mitrana, V. (2009). On small, reduced,

and fast universal accepting networks of splicing pro-

cessors. Theoretical Computer Science 410, pp. 406–

416.

Manea, F., Mart

ın-Vide, C., Mitrana, V. (2006). All NP-

problems can be solved in polynomial time by ac-

cepting networks of splicing processors of constant

size. In: DNA Computing. LNCS, vol. 4287, Springer,

Berlin, Heidelberg, pp. 47–57.

Manea, F., Mart

ın-Vide, C., Mitrana, V. (2007). Accepting

networks of splicing processors: Complexity results.

Theoretical Computer Science 371, pp. 72–82.

Mitrana, V., Petre, I., and Rogojin, V. (2010) Accepting

splicing systems. Theor. Comput. Sci. 411 pp. 2414–

2422.

aun, Gh. (1996). Regular extended H systems are compu-

tationally universal. J. Automata, Languages, Combi-

natorics, 1 pp. 27–36.

aun, G. (1998). Distributed architectures in DNA com-

puting based on splicing: Limiting the size of com-

ponents. In Unconventional Models of Computation,

Springer, Berlin, Heidelberg, pp 323–335.

aun, Gh., Rozenberg, G., and Salomaa, A. (1996). Com-

puting by splicing. Theoret. Comput. Sci. 168 pp. 321-

336.

Paun, Gh., Rozenberg, G., and Salomaa, A. (1997). Com-

puting by splicing. Programmed and evolving splicing

systems. IEEE Intern. Conf. on Evolutionary Comput-

ing, Indianapolis, pp. 273–277.

Paun, Gh., Rozenberg, G., and Salomaa, A. (1998). DNA

Computing - New Computing Paradigms, Springer-

Verlag, Berlin.

Pixton, D. (1996). Regularity of Splicing Languages. Dis-

crete Appl. Math., 69 pp. 101-124.

Pixton, D. (1995). Linear and circular splicing systems. In

First International Symposium on Intelligence in Neu-

ral and Biological Systems. INBS’95, IEEE Herndon,

VA, USA, pp. 181–188.

De Prisco, R., Malandrino, D., Zaccagnino, G., Zaccagnino,

R., and Zizza, R. (2017). Splicing-inspired recog-

nition and composition of musical collectives styles.

In Theory and Practice of Natural Computing - 6th

International Conference, TPNC 2017, LNCS 10687,

Springer-Verlag, Berlin, pp. 219–231.

Rabinow, P. (1996). Making PCR: A Story of Biotechnology.

University of Chicago Press.

Rozenberg, G, and Salomaa, A. (eds.) (1997). Handbook of

Formal Languages, vol. I-III, Springer-Verlag, Berlin.

Siromoney, R., Suhramanian, K.G., and Rajkumar Dare, V.

(1992) Circular DNA and splicing systems. In In-

ternational Conference on Parallel Image Analysis,

ICPIA 1992, LNCS 654, Springer-Verlag, Berlin, pp.

260–273.

How Complex is to Solve a Hard Problem with Accepting Splicing Systems