MATE-BOOSTER: Design of an e-Learning Course to Boost

Mathematical Competence

Alice Barana

, Marina Marchisio

and Raffaella Miori

Department of Mathematics, University of Turin, Via Carlo Alberto 10, 10123 Torino, Italy

IIS “Eugenio Bona” di Biella, Via Antonio Gramsci 22, 13900 Biella, Italy

Keywords: Automatic Formative Assessment, Basic Mathematical Competence, Constructivist Learning Environment,

Learning Design, Problem Solving, Virtual Learning Environment.

Abstract: In the transition from lower to upper secondary education, Italian students are expected to have achieved a

level of competence which allows them to use knowledge and abilities to model and to understand scientific

and technical disciplines. Gaps or misunderstandings in basic knowledge can hinder the effort of students

who attend technical high schools, where the core subjects are based on Mathematics. This paper deals with

the design of a project conceived to strengthen mathematical competences of students attending the first year

of a technical upper secondary school through an online course named “MATE-BOOSTER”. The online

activities on the web-based platform have been developed using didactic methodologies founded on

constructivist assumptions, as problem posing and problem solving, collaborative learning, learning by doing,

automatic and adaptive formative assessment. In this work the process of design of MATE-BOOSTER is

shown, the methodologies chosen are discussed, and the online activities are analysed from a constructivist

perspective.

1 INTRODUCTION

Italian students completing lower secondary

education – which in Italy ends at 8th grade – are

supposed to have developed a positive attitude

towards Mathematics and to understand how

mathematical tools can be useful in many situations

to operate in the real world (MIUR, 2012). INVALSI

is the national institute in charge of verifying that the

learning outcomes are achieved: it administers

surveys and standardized tests in order to guarantee

the quality of Italian instruction and to make it

possible to be compared at international level. The

results of INVALSI surveys highlight how, at all

stages, but at the end of 8

grade of instruction in

particular, there are still difficulties in the deep

understanding of basic mathematical concepts, in the

ability of applying knowledge to solve problems in

real contexts and, above all, in the process of

argumentation, which shows the difficulty in

formalizing the intuitive knowledge (INVALSI,

2017). These gaps increase in importance when

https://orcid.org/0000-0001-9947-5580

https://orcid.org/0000-0003-1007-5404

students enrol to upper secondary school and they

have to approach scientific and technical subjects,

whose understanding relies upon their basic

mathematical competence. This problem is

particularly evident in technical upper secondary

schools, where specialized disciplines are studied at

an advanced theoretical level, though students’

average mathematical competence is lower than in

Lyceums, as the national surveys show (INVALSI,

2017). The ability to use mathematical thinking to

solve problems related to the real experience or to

other disciplines – in other words, mathematical

competence (MIUR, 2010; Pellerey, 2004) – thus

acquires relevance in the delicate period of transition

that young people go through when they enrol to

upper secondary school, when school successes and

failures are deeply interlaced with the shaping of their

characters (Debnam et al., 2014; Mariani, 2006)

The Head Teacher of the Technical Upper

Secondary School “Eugenio Bona” of Biella, together

with her team of Mathematics teachers, designed a

project aimed to strengthen the basic mathematical

280

Barana, A., Marchisio, M. and Miori, R.

MATE-BOOSTER: Design of an e-Learning Course to Boost Mathematical Competence.

DOI: 10.5220/0007721702800291

In Proceedings of the 11th International Conference on Computer Supported Education (CSEDU 2019), pages 280-291

ISBN: 978-989-758-367-4

competences of first year students with the support of

an e-learning platform and digital materials. The

project, called “MATE-BOOSTER”, has been

implemented in collaboration with the department of

Mathematics of the University of Turin, which has a

long experience in the development of virtual

environments for learning Mathematics, especially to

prevent school failure (Barana et al., 2017b; Barana

and Marchisio, 2015) and to support students in the

transition from lower to upper secondary school

(Barana et al., 2016). The project started in September

2018 and it is currently developing.

This paper focuses on the design of the project;

the methodologies chosen in relation to the students’

needs are deeply discussed and the process which led

to the realization of innovative digital materials is

shown and exemplified.

2 STATE OF THE ART

2.1 Web based Constructivist Learning

Environments

The choice of the methodologies for developing the

learning materials has been made on constructivist

assumptions, according to which knowledge is

situated, being a product of the activity, context and

culture in which it has been developed and used

(Brown et al., 1989). Learning is seen as a lifelong

active process of knowledge building mediated by

experiences and relations with the environment and

the community (von Glasersfeld, 1989); thus

constructivist learning environments should provide

authentic activities and real world problems which

can engage students. In Mathematics education this

theme has been investigated by many researchers, as

Schoenfeld who suggests that Mathematical thinking

should be a tool to interpret quantitative phenomena

of the outside world and it should be developed at

school through meaningful modellization activities

(Schoenfeld, 1992).

One of the main implications of the constructivist

idea of the learner creating his or her own knowledge

is the shift from a teacher-centred to a student-centred

approach. If students become the protagonists, the

teachers need to leave the stage and move aside,

changing their role from leaders to mentors, and their

task from knowledge transmission to the creation of a

suitable environment for learning (Cornelius-White,

2007).

The community where the learner is integrated in

is a core element as well. The sharing of opinions

opens the mind and favours the process of knowledge

building. Thus a constructivist learning environment

should facilitate collaboration and activities should

require discussion and interaction among peers (Lave,

1991).

Moreover, activities should be rooted in

assessment with a formative value in order to inform

both teachers and students about progresses (Scriven,

1966). Assessment and metacognition are deeply

interlaced: frequent and well-structured feedback

helps learners understand where they are going and

how they are going, giving information not only about

how the task has been performed (task level), but also

about the process that should have been mastered

(process level), and enabling self-regulation and self-

monitoring of actions (self-regulation level) (Hattie

and Timperley, 2007).

Strategies as formative assessment, collaborative

learning and relevant problem solving are also

indicated by several researches as useful enablers of

learners’ engagement, which is related to high

learning achievements (Ng et al., 2018). Improving

engagement is particularly important in students with

challenging backgrounds, learning difficulties or low

scholastic performances; in these contexts,

interventions that only focus on the reinforcement of

basic knowledge are often little effective, if they don’t

rely on approaches which promote interest,

motivation and self-efficacy (Haberman, 2010).

Technology can support the creation of

constructivist digital environments, as it can provide

computer mediated communication, computer

supported collaborative work, case based learning

environments, computer supported cognitive tools

(Jonassen et al., 1995), as well as instruments for self

and peer assessment (Kearns, 2012) and for automatic

evaluation (Barana et al., 2015).

The analysis of the implementation of web based

constructivist learning environments has involved

many authors in literature in the last twenty years and

several models have been designed to engage students

of different school levels, in e-learning or blended

modality, in learning several disciplines (Alonso et

al., 2005; Czerkawski and Lyman, 2016; Lefoe, 1998;

Sangsawang, 2015). Their results mainly deal with

the relations between strategies, media and tool used

and processes activated. Constructivist instructional

designers generally accept as a valid and well-

established framework for building learning

environments the seven learning goals devised by

Cunningham, Duffy and Knuth in 1993 and

illustrated by Honebein (1996); they are:

1. to provide experience with the knowledge

construction process;

MATE-BOOSTER: Design of an e-Learning Course to Boost Mathematical Competence

281

2. to provide experience in and appreciation of

multiple perspectives;

3. to embed learning in realistic and relevant

contexts;

4. to encourage ownership and voice in the

learning process;

5. to embed learning in social experience;

6. to encourage the use of multiple modes of

representation; and

7. to encourage self-awareness in the knowledge

construction process.

2.1 Automatic Formative Assessment

In a virtual learning environment, formative

assessment can be easily automatized in order to

provide students immediate and personalized

feedback. There are several Automatic Assessment

Systems (AAS) that allow the creation of questions

for STEM (Science, Technology, Engineering and

Mathematics); those which are based on a Computer

Algebra System (CAS) support the creation of

automatically graded open Mathematical answers,

such as formulas and equations, but also sets, vectors

and graphs, which are accepted for their meaning, not

only for their form.

These tools can be usefully adopted to enhance

learning, master problem solving strategies,

improving metacognition, facilitate adaptive teaching

strategies and support teachers’ work (Barana et al.,

in press).

Using Moebius AAS (Moebius Assessment,

2018), the Department of Mathematics of the

University of Turin has designed a model for the

formative automatic assessment for Mathematics,

based on the following principles (Barana et al.,

2018):

1. availability of the assignments to the students,

who can work at their own pace;

2. algorithm-based questions and answers, so that

at every attempt the students are expected to

repeat solving processes on different values;

3. open-ended answers, going beyond the

multiple-choice modality;

4. immediate feedback, returned to the students at

a moment that is useful to identify and correct

mistakes;

5. contextualization of problems in the real world,

to make tasks relevant to students;

6. interactive feedback, which appears when

students give the wrong answer to a problem. It

has the form of a step-by step guided resolution

which interactively shows a possible process

for solving the task.

The last one consists of a step-by-step approach

to problem solving with automatic assessment, but it

is conceptualized in terms of feedback, highlighting

the formative function that the sub-questions fulfil for

a student who failed the main task. The interactive

nature of this feedback and its immediacy prevent

students from not processing it, a risk well-known in

literature which causes formative feedback to lose all

of its powerful effects (Sadler, 1989). Moreover,

students are rewarded with partial grading, which

improves motivation.

This model relies on other models of online

assessment and feedback developed in literature, such

as Nicol and MacfarlaneDick’s principles for the

development of self-regulated learning (Nicol and

MacfarlaneDick, 2006) and Hattie’s model of

feedback to enhance learning (Hattie and Timperley,

2007).

3 METHODOLOGY

The MATE-BOOSTER project was conceived with

the aim of strengthening basic mathematical

competence of first-year students of a technical upper

secondary school, acting with methodologies and

tools able to activate students’ motivation and

engagement, in order to prevent failures in scientific,

technological and economic subjects which are at the

core of their curriculum. The main feature of the

project involves the creation of a web-based course in

a virtual learning environment where students can

revise the contents in a self-paced way or under their

teachers’ guide, both in the classroom and at home.

Materials have been created according to didactic

methodologies which are in line with the theories of

constructivism and formative assessment outlined in

the previous paragraph.

The project involves 202 students of nine classes

with their seven teachers of Mathematics, plus one

teacher in charge of coordinating the works from

inside the school.

MATE-BOOSTER has been developed following

a model of learning design of “ASSURE” (Heinich et

al., 1999), which includes the following steps:

1. Analyse the learners;

2. State objectives;

3. Select methods, media and materials;

4. Utilize media and materials;

5. Require learner participation;

6. Evaluate and revise.

The whole design process has been conducted by

researchers from the Department of Mathematics of

the University of Turin in close collaboration with the

CSEDU 2019 - 11th International Conference on Computer Supported Education

282

teachers of Mathematics of the nine classes involved.

In fact, it has been considered essential that teachers

share the instructional strategies, approve the didactic

materials and are consulted at each step of the design;

otherwise they couldn’t present the project to their

students in a convincing way that make them take part

in the online activities.

4 DESIGN OF THE COURSE

4.1 Analysis of the Learners

The analysis of the learning needs, preceding the

development of the course, was carried out with two

different aims:

 to examine students’ competence in

Mathematics, and the gaps in their knowledge;

 to inquire about students’ motivations to the

study in general and to the study of

Mathematics in particular.

Two different tools have thus been chosen for

these objectives: an entry test to assess the initial

competence and a questionnaire to understand their

motivations.

The entry test was composed of 20 multiple

choice questions to be answered in 45 minutes. For

each correct answer students got 5 points, 0 for

incorrect or ungiven answers. It has been

administered online with an automatic assessment

system. All students took the test on the same day (8

October 2018); some settings were added to the test

to prevent students from cheating: the questions and

the choice of the answers were shuffled, there were

some random numeric parameters, there was only one

attempt available with an automatically set time limit,

so that the test automatically quitted after 45 minutes.

Few days before the date of the test, students were

given the log in data to access the platform where the

test would take place; there, they could find a sample

test with the instructions to navigate through the

questions.

Questions were distributed among the core topics

studied in the lower secondary school, in proportion

to the time generally dedicated to each one. Each

question referred to one of the main content areas of

the curriculum (numbers, space and shapes, functions

and relations, data and predictions), moreover there

were two questions about simple logic reasonings.

More details are shown in Table 1.

Questions were built in order to verify the

comprehension of particular concepts or processes,

not just to check the memorization of rules or

formulas.

Table 1: Content areas and topics of the questions.

Content

area

Number of

questions

Topics

Number 8 Rational numbers,

number estimation,

fractions, percentages,

powers

Space and

shapes

4 Perimeter and area of

plane figures.

Functions

and

relations

4 Symbolic computations,

equations, proportions.

Data and

predictions

2 Tabular and graphic

representation of

frequencies.

Logic

reasonings

2 Simple logic reasonings

involving order

relations and set theory.

The results of the test have been statistically

treated using the difficulty index, which corresponds

to the ratio between the number of correct answers

and the sample size, and the discrimination index,

which is the difference between the difficulty indexes

of the best performing group and the worst

performing one, where the two groups are equal sized

and cover the whole sample (Ebel, 1954). The test

reliability has been assessed through the Cronbach

Alpha.

Results of the entry tests were not particularly

good, with an average score of 41/100, meaning that

the level of difficulty was quite high, at least for the

students of this school. Nobody scored more than 80

out of 100, while the lowest registered score was

5/100. If aggregated by classes, the average score

varied significantly, from a minimum of 34/100 to a

maximum of 54/100; the belonging to a specific class

explains the 18.5% of the variance of test results

(square eta = 0.185, p<0.0001). It can be noticed that

the best performers attend a curriculum which is more

rooted in Mathematics than the worst performers.

Results aggregated by content areas show the same

trend as INVALSI tests: space and shapes turned out

to be the most difficult area, with an average index of

difficulty of 0.27; it was followed by logic reasonings

(0.36), whilst data and predictions was the easiest one

(0.60). Results for numbers and relations hung around

0.40.

The difficulty of questions ranged from 0.22 to

0.87; only 4 out of 20 questions can be considered

“easy”, reaching more than 50% of correct answers.

The majority of questions can be considered coherent

with the general test, since the discrimination index is

greater than 0.25 for the 75% of the questions.

Questions with a low discrimination index have been

qualitatively analysed: they include frequent

MATE-BOOSTER: Design of an e-Learning Course to Boost Mathematical Competence

283

misunderstandings among the incorrect options or

high-level reasonings that caused also the most

skilled students to make mistakes (Tristan Lopez,

1998). The test Cronbach Alpha was 0.65; it was

negatively influenced by these questions which

hindered the students. Our claim is that this test is

quite efficient for grade 9 students, but in general

students who enrol to a technical secondary school

like this one have low-level competence in

Mathematics, that the test highlighted.

The questionnaire was composed of 33 statements

where students were asked to state their level of

agreement with Likert scale from 1 to 4 (completely

disagree – completely agree) or from 1 to 5

(insufficient – excellent). It was administered online

on the same platform where the entry test took place.

The questionnaire is inspired by the student

questionnaire of 2012 PISA survey, when

Mathematics was the main focus (OECD, 2013). It

was aimed to measure attitudes and behaviours

towards school and Mathematics, in particular

intrinsic motivation (shown by students that study

mathematics because they like it), instrumental

motivation (shown by students that study

Mathematics because it will be useful for their

future), perseverance, openness to problem solving,

perceived control over success in Mathematics, ethic

and respect of school roles, mathematical activities

outside school. Moreover, it was asked if students

have an internet connection and a device

(tablet/computer) at their home. It emerged that

students’ intrinsic motivation is not so high (the

average is 2.6 in a scale from 1 to 4), although it varies

widely (standard deviation: 0.9), while instrumental

motivation is higher (the average is 3.1 in a scale from

1 to 4, standard deviation: 0.5). All students have the

possibility to use a computer with internet connection

for large part of their time at home. Deeper analysis

on the answers to the questionnaire will be carried out

later in the project; the information gained will be

used to better interpret the outcomes.

4.2 Statement of the Objectives

In the light of the results of the entry test and of the

questionnaire, during a focus group researchers and

teachers listed the learning outcomes of the course.

The choice of the topic that the course should cover

was made considering the contents needed to

understand the scientific courses of the first years

(Mathematics, Computer Science, Economy,

Science, Physics). They are the following:

 fractions (operating with rational numbers);

 proportions (calculating the unknow term of a

proportion, to solve problems involving direct

and inverse proportionality in real contexts);

 percentages (calculating percentages in real

contexts);

 powers (knowing the meaning of

exponentiation and applying the properties of

powers);

 mathematical formulas and functions (working

with symbols and formulas and with their

graphical representations);

 equations (reading and building equations,

solving linear equations in one unknown);

 plane geometrical shapes (knowing and

calculating measures of angles, triangles and

squares);

 statistics and probability (managing data,

descriptive statistics indexes and graphical

representations, calculating elementary

probabilities in real contexts);

 mathematical language (understanding and

using different registers of representation:

verbal, symbolic, graphical, geometrical,

numerical);

 logics (managing simple logic reasonings using

Boolean operators).

4.3 Selection of Methods, Media and

Materials

The choice to create an online course which students

can use at home in a self-paced modality has been

validated by their availability of technological

devices to access the material, expressed in the

questionnaire. Moreover, in all the classrooms of the

school there is an Interactive White Board (IWB) that

teachers can use to show students the platform and to

complete the activities together; the school has three

computer labs and several tablets that allow students

to work with the course activities even at school. As

a Virtual Learning Environment, an integrated

Moodle platform has been adopted, managed by the

ICT services of the Department of Computer Science

of the University of Turin, in collaboration with the

Department of Mathematics, the same platform where

the entry test and the questionnaire have been

delivered. MATE-BOOSTER has been inserted on an

instance of the Moodle platform that the University

of Turin commonly adopts for e-learning and that

often hosts school teachers and students for

educational projects (Barana et al., 2017a, 2017c;

Barana and Marchisio, 2016a; Giraudo et al., 2014;

Marchisio et al., 2017). It is integrated with an

Advanced Computing Environment (Maple) for the

CSEDU 2019 - 11th International Conference on Computer Supported Education

284

creation of interactive materials, and with Moebius

Assessment for automatically graded assignments.

The didactic methodologies for the development

of the contents have been selected on the base of the

constructivist framework and of the evidence gained

during previous experiences of e-learning courses

(Barana and Marchisio, 2016b). They are the

following:

 Problem posing and problem solving:

assuming the social-constructive insight of

problem solving, problems are considered as

learning environments where mathematical

knowledge is created in a collaborative

discussion starting from a problem. The top-

down order traditionally used to study

Mathematics is inverted: from the analysis of a

real-world situation, paths to the solutions are

drawn, in a constructive approach toward the

discipline. Afterward, the solving steps are

synthetized and generalized, introducing the

typical rigor of Mathematics. Learning

technologies are used both for online

cooperation and as a mean of representation of

the solving process: freed from the burden of

calculations, students can focus on the solving

strategy, find relationships and better

understand the solutions (Brancaccio et al.,

2015).

 Collaborative learning: in a Virtual Learning

Environment, collaboration can be fostered

through activities for synchronous or

asynchronous discussion; it enhances students’

comprehension of problems and of

Mathematical concepts. Moreover, positive

collaborations affect the quality of the

environment and they are reflected on students’

motivation. Collaborative virtual learning

environments force the shift of the teachers’

role, who let students create their own learning

– but carefully monitoring it (Barana and

Marchisio, 2017).

 Learning by doing: interactivity enhances

students’ engagement and contributes to

increase their motivation. Feedback that

students get from activities help them control

their learning and move forward (Gossen et al.,

2018).

 Automatic formative assessment: implemented

with an AAS specialized for STEM, it allows

students to practice at their own pace and to

obtain immediate feedback to acknowledge

their own level of preparation. Questions and

assignments can be enhanced by varying them

in a random controlled form, inserting parts

expressed in a special programming language.

This allows a great variety of assessment

modalities which strengthen reasoning until it

is mastered: students can obtain different data

or graphics at every new attempt, the system

can adaptively suggest guided resolutions,

feedback and questions can automatically be

proposed on the base of previous answers

(Barana et al., 2018).

The process of creation of the materials took place

in a “Management course”, where school teachers

could access and follow the work, propose ideas and

suggestions, get in touch with the researchers.

The structure given to the course is modular,

according to the general guidelines for the creation of

e-learning course (Rogerson-Revell, 2007), each

module corresponding to a different topic, to the

purpose of addressing students through the course

topics and to show at a glance the whole content.

Figure 1 shows the course homepage with the 11

modules in a grid format, chosen for its graphical

impact on the learner.

All the modules have a fixed structure, composed

of submodules containing:

1. materials with theoretical explanation of the

fundamental concepts in the form of e-book,

that students can read online or download in

pdf. Explanations begin with problems and are

correlated with examples, graphics and images;

2. interactive materials for the exploration of the

concepts illustrated in the e-book, which help

students to put theory into practice, to visualize

Figure 1: Homepage of the course with the modules in grid

format.

MATE-BOOSTER: Design of an e-Learning Course to Boost Mathematical Competence

285

and analyse different representations of the

same mathematical structures when parameters

change;

3. automatically graded assignments to check the

understanding of the concepts presented and of

the related abilities.

At the end of every module there are:

4. one or more real-world problems which require

the use of the contents of that unit to be solved;

5. a final test, automatically graded, to verify the

achievement of the learning objectives

expected for the module.

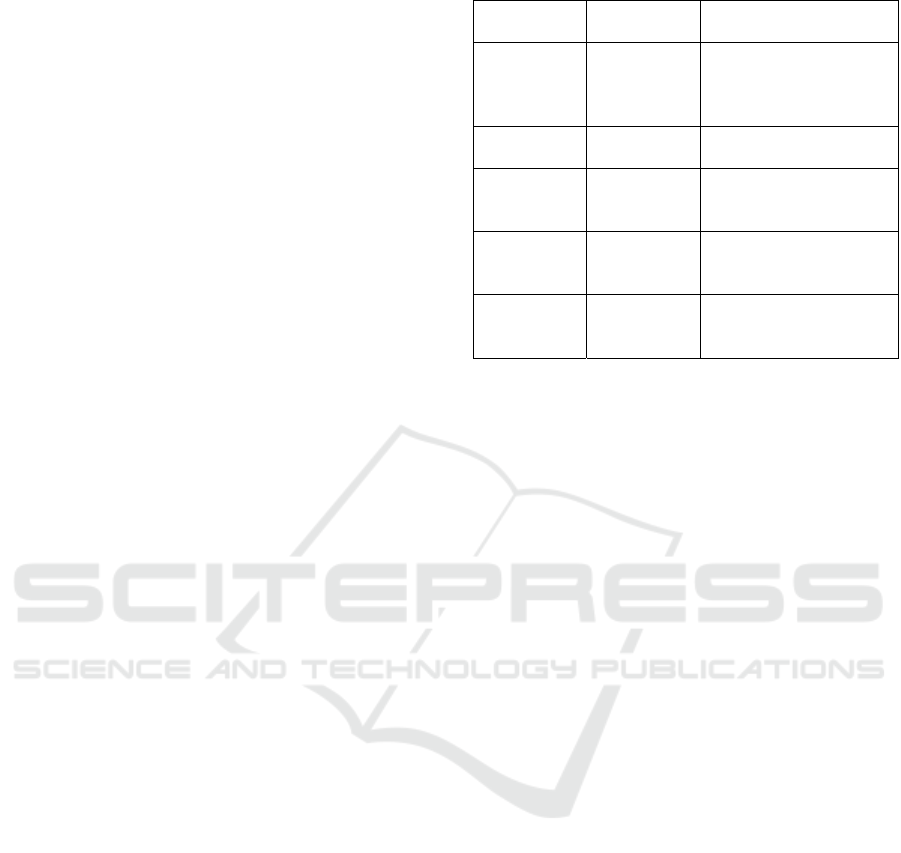
Figure 2 shows an example of course module.

Taking into account the methodologies chosen

and the needs of the students, their frequent

misunderstandings emerged both in the entry test and

from teachers’ experience, the didactic materials have

been created to populate the modules. As an example,

in the entry tests one of the most difficult questions

was about the properties of powers, in which students

had to choose the only wrong answer between 4

equalities (difficulty index: 0.34). A set of questions

were developed, focused on the most frequent

mistakes in the applications of the properties of

powers, on the scheme of the question shown in

Figure 3. Initially, students are asked to decide

whether an equality involving properties of powers

was correct or incorrect. They can earn half the score

if they answer correctly; after that, they are asked to

fill two subsequent sections which refer to the general

rule to apply, through which they can earn up to the

remaining half of the score. The last two sections can

have a double function: justifying the choice, if the

student had answered correctly to the first part, or

showing a reasoning process, if the student had given

the wrong answer (or guessed by chance) to the first

step. Once they finish the test, students can try it again

and find questions with a similar structure but

different examples of applications of the same and

other power properties. This is an example of

question with interactive feedback: after the first

Figure 2: Structure of a module.

Figure 3: Example of a question with interactive feedback.

section the student receives a first feedback in a form

of green tick or a red cross depending on whether he

answered correctly or not; the following sections are a

feedback about how he was supposed to develop his

reasoning in order to reach the solution. The feedback

is interactive, because the student has to complete step

by step the sub-questions, following the proposed

reasoning.

Figure 4 shows an example of problem solving

question developed with the automatic assessment,

related to the module about mathematical formulas and

functions. A real-world problem is given and students

can explore different solving strategies: a numerical

solution through an interactive table; a symbolic

solution through an open-ended response area which

offers the possibility to enter formulas through a

symbolic equation editor, and a graphic solution, made

possible through the graph of the function entered by

the students generated by the system. Students can

compare the different mathematical representations of

the real world situation and deepen their understanding

of the involved concepts, namely functions and their

zeros. When they try the question again, students will

find different values that allow them to repeat the

process and to acquire awareness of the meanings

laying behind abstract mathematical objects.

Within the online course there are also a forum of

discussion for students, a progress bar, through which

learners can visualize their learning steps, and a link to

the gradebook, where all the assignments results are

recorded.

CSEDU 2019 - 11th International Conference on Computer Supported Education

286

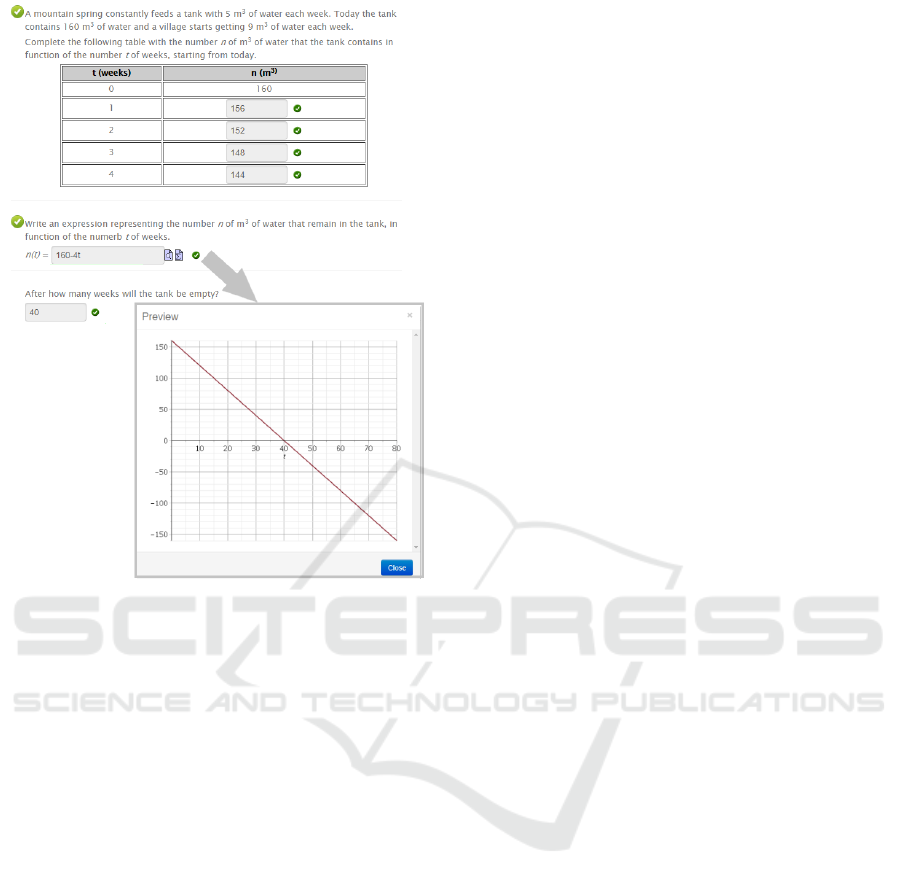
Figure 4. An example of real world problem with automatic

assessment.

4.4 Utilization of the Materials

Once the course was completed, it has been

duplicated in 9 single courses, one for each class, so

that teachers can easily control the progress of their

own students and give them personalized support and

advise.

Courses were opened to the students at the end of

October 2018, and they are currently ongoing; they

will be active until Spring 2019, even though students

will be able to access the contents successively to the

estimate end of the project.

Students received an e-mail at their institutional

e-mail address with the indications to log in the

platform and to access the materials. Interactive

instructions about how to use the automatic

assessment were provided to the students directly

through the platform. The teachers were also asked to

repeat the instructions to the classes at school and to

show through the IWB how to use the materials. The

learning materials can thus be used by students who

need to revise basic skills at their own pace, but it is

also suitable to class activities of different kind when

teachers need to introduce new topics based on

previous knowledge or assign differentiated activities

to different group of students.

4.5 Requirement of Learner

Participation

Aware that little motivated students won’t be too keen

on autonomously doing online mathematical

activities in their spare time, some expedients have

been taken in order to assure their frequency to the

course.

The main one is the certification: students who

initially have low grades will be required to present,

by the month of April, the certificate of completion of

the course. The certificate can be automatically

downloaded from the platform, at the condition that

all the activities will figure as completed. So, they are

forced to use the materials.

If the certification acts as “external” motivational

lever, the learning methodologies chosen to develop

the materials contribute to the development of

intrinsic motivation. The real contexts, the immediate

feedback, adaptivity and interactivity make all the

materials engaging and useful to get prepared, so that

students who try the activities can acknowledge their

usefulness and go on with the modules. The

interactive feedback provided through automatic

assessment help them understand solving strategies

and processes, contributing to the development of

self-regulation. Through a progress bar they can be

made aware of their position in the learning path and

be motivated to complete it.

In addition, all teachers have been asked to

present the course to their classes, to invite them to do

the activities as homework and to recall the problems

during lessons. In fact, students need to see the course

as linked to their study and not as an external and

additional duty; the more they are convinced of the

usefulness of the online course for their learning, the

more easily they will participate. The collaboration

with the teachers could also have the positive effect

to renew their teaching practices, introducing the use

of the didactic methodologies and technologies

adopted in the online course. As a consequence, not

only the online course, but the whole school

experience with Mathematics could be more

engaging for the students, who can be facilitated in

the development of interest for Mathematics.

4.6 Evaluation and Revision

In April 2019, when the time limit for the course

completion will come, an evaluation of the course

will be performed in several modalities.

The achievement of the learning outcomes will be

assessed through a final test, similar to the entry one,

for all the students. The appreciation of the course

MATE-BOOSTER: Design of an e-Learning Course to Boost Mathematical Competence

287

will be evaluated via a questionnaire, which

investigates the appreciation and perceived

usefulness of the online activities to get a better

understanding of the contents. Teachers will be

interviewed to express their point of view about

students’ performances.

Data collected through the two tests, the two

questionnaires, platform usage and students’ scores

and teachers’ interviews will be cross-checked in

order to understand key strengths and limits of

MATE-BOOSTER for future implementations of the

project.

5 FIRST RESULTS AND

DISCUSSION

The project is at a too early stage to get results from

students. Nevertheless, the appreciation from the

teachers involved is very high, since they perceive the

online course as a valid support for their didactic, for

reducing failures and motivating students.

The design of the course, made according to

constructivist directions, actually respects the seven

goals for building constructivist learning

environments theorized by Cunningham, Duffy and

Knuth.

1. Real-world problems offer students a learning

environment in which to create mathematical

knowledge starting from a specific case;

exploration activities let students build and

associate meanings to mathematical concepts;

adaptive questions with step-by-step guided

solutions help them manage a complex

resolution following their own ideas. Thus,

students get to experience the very

knowledge construction process.

2. Interactive exploration materials show

Mathematics from different points of view; the

resolution of the problems is often discussed

offering more than one solving process; peer

discussions ask students to come to terms with

different opinions and ways of understanding.

These features can provide learners with

experience in and appreciation of multiple

perspectives.

3. Not only all the problems, but also great part of

the automatically graded questions and of the

interactive materials are contextualized in real-

world situations, interesting and challeging for

students. In this way learning is embedded in

realistic and relevant contexts.

4. When opening the online course, students can

choose their own path between the offered

topics and materials. They are at the center of

their own learning. All the activities do not

flow automatically in front of students’ eyes:

they have to autonomously get into each one

and browse pages and questions with a click,

thus enhancing their commitment. In this way

ownership and voice in the learning process

can be encouraged.

5. Students’ work, their problems and successes

are not isolated: they can share them with other

learners through the forum. Moreover, MATE-

BOOSTER is inserted in a blended context,

where students actually meet every morning at

school and teachers are adviced to discuss the

activities during the lessons, to the purpose of

embedding learning in social experience.

6. Exploring activities often present the same

concept with different registers (in words,

symbolic, graphic, tabular, and so on) and try

to simplify its understanding via a shift of

automatically graded assignments and in the

problems, in order to encourage students to

the use of multiple modes of representation.

7. Immediate feedback facilitates students’

acknowledgement of their preparation;

moreover, the tracking of activities and the

progress bar offer them a visual insight of the

learning path that they have undertaken.

Automatically graded open answers and

interactive feedback ask students to explain

processes, not only to give results. Hence, the

course activities pursue the goal to encourage

self-awareness in the knowledge

construction process.

Thus MATE-BOOSTER can be a suitable

learning environment where students can reinforce

their knowledge with a constructivist approach.

In the design of the course a special attention has

been dedicated to feedback, considered a core

element for promoting success. MATE-BOOSTER

feedback works at three levels: at task level, when it

informs students whether the task has been performed

correctly or knowledge has been achieved; at process

level, when it explains how the task should be

performed; and at self-regulation level, when it helps

learners monitor their own learning. Table 2 shows

the MATE-BOOSTER features and activities which

provide the three kinds of feedback.

CSEDU 2019 - 11th International Conference on Computer Supported Education

288

6 CONCLUSIONS

In summary, MATE-BOOSTER has been conceived

with the aim of supporting students in the transition

from lower to upper secondary school by strengthening

basic mathematical competences. The project has been

managed using a design method of ASSURE kind

(Analyse the learners; State objectives; Select

methods, media and materials; Utilize media and

materials; Require learner participation; Evaluate and

revise). The core action of the project involves the

implementation of an online course that students can

use at their own pace as a support to their study. The

design of the virtual learning environment has been

carried out according to constructivist assumptions,

and under the seven goals for building constructivist

learning environments theorized by Cunningham,

Duffy and Knuth (to provide experience with the

knowledge construction process; to provide experience

in and appreciation of multiple perspectives; to embed

learning in realistic and relevant contexts; to encourage

ownership and voice in the learning process; to embed

learning in social experience; to encourage the use of

multiple modes of representation; and to encourage

self-awareness in the knowledge construction process).

The learning methodologies used are problem posing

and problem solving, collaborative learning, learning

by doing and automatic formative assessment.

In the course design, the collaboration of the

researchers with the school teachers of Mathematics is

a key strategy to maximize learners’ participation,

since the presentation of the course is filtered by the

teachers’ voice.

The course is currently open to students and the

results, in terms of teachers’ and students’ satisfaction

and competence achieved, will be analysed as soon as

they will be available and used for perfecting the

course and proposing it again.

Table 2: Analysis of the feedback provided by MATE-

BOOSTER.

Level of

feedback

MATE-BOOSTER features

Task level

Immediate feedback from automatic

grading; interactions with peers and

teachers

Process level

Interactive feedback; resolutions of

the problem; interaction with peers

and teachers

Self-regulation

level

Automatic assessment, tracking of

activity completion, progress bar,

gradebook, certification.

Since in Italy schools and teachers need to offer

paths for the revision to students who get low marks,

including individualized courses and further

assessment, similar courses could have a double

effect on the optimization of scholastic resources:

firstly, they could reduce failures at their root, as they

are often due to gaps in the basic knowledge that

cause difficulties in learning new things; secondl,

they can be used as part of the paths of content

revision, because the topics included within the

course are those which are required in advanced for

understanding the first year course, and they are

usually object of the revision courses. Thus, schools

using online courses as MATE-BOOSTER could

save human resources in delivering revision courses

and collocate them elsewhere, such as in projects for

the innovation of methodologies and curricula. This

procedure could be even promoted by the Ministry of

Education, maybe proposing a format that schools

can customize. The project could be extended to other

core disciplines, such as Italian and Foreign

Languages, with the collaboration of experts in these

disciplines.

REFERENCES

Alonso, F., Lopez, G., Manrique, D., Vines, J.M., 2005. An

instructional model for web-based e-learning education

with a blended learning process approach. British

Journal of Educational Technology 36(2), pp. 217–235.

Barana, A., Bogino, A., Fioravera, M., Marchisio, M.,

Rabellino, S., 2017a. Open Platform of self-paced

MOOCs for the continual improvement of Academic

Guidance and Knowledge Strengthening in Tertiary

Education. Journal of e-Learning and Knowledge

Society 13(3), pp. 109-119. https://doi.org/10.20368/

1971-8829/1383

Barana, A., Conte, A., Fioravera, M., Marchisio, M.,

Rabellino, S., 2018. A Model of Formative Automatic

Assessment and Interactive Feedback for STEM. In:

Proceedings of 2018 IEEE 42nd Annual Computer

Software and Applications Conference (COMPSAC),

pp. 1016–1025. https://doi.org/10.1109/COMPSAC.

2018.00178

Barana, A., Fioravera, M., Marchisio, M., Rabellino, S.,

2017b. Adaptive Teaching Supported by ICTs to

Reduce the School Failure in the Project “Scuola Dei

Compiti.” In: Proceedings of 2017 IEEE 41st Annual

Computer Software and Applications Conference

(COMPSAC), pp. 432–437. https://doi.org/10.1109/

COMPSAC.2017.44

Barana, A., Marchisio, M., 2017. Sviluppare competenze di

problem solving e di collaborative working

nell’alternanza scuola-lavoro attraverso il Digital Mate

Training. In: Atti di Didamatica 2017, pp. 1–10.

MATE-BOOSTER: Design of an e-Learning Course to Boost Mathematical Competence

289

Barana, A., Marchisio, M., 2016a. Dall’esperienza di

Digital Mate Training all’attività di Alternanza Scuola

Lavoro. Mondo Digitale 15(64), pp. 63-82.

Barana, A., Marchisio, M., 2016b. Ten Good Reasons to

Adopt an Automated Formative Assessment Model for

Learning and Teaching Mathematics and Scientific

Disciplines. Procedia - Social and Behavioral Sciences

228, pp. 608–613. https://doi.org/10.1016/j.sbspro.

2016.07.093

Barana, A., Marchisio, M., 2015. “Testi digitali interattivi”

per il recupero nella matematica nel progetto per la

riduzione della dispersione scolastica “Scuola dei

Compiti.” Form@re 15(1), pp. 129–142.

https://doi.org/10.13128/formare-15430

Barana, A., Marchisio, M., Bogino, A., Operti, L.,

Fioravera, M., Rabellino, S., Floris, F., 2017c. Self-

Paced Approach in Synergistic Model for Supporting

and Testing Students. In: Proceedings of 2017 IEEE

41st Annual Computer Software and Applications

Conference (COMPSAC), pp. 407–412.

https://doi.org/10.1109/COMPSAC.2017.211

Barana, A., Marchisio, M., Pardini, C., 2016. COSAM:

Corso Online per lo Sviluppo di Abilità Matematiche

per facilitare il passaggio tra la scuola secondaria di

primo e di secondo grado. In: Design the Future!

Extended abstract della Multiconferenza

EMEMITALIA2016. Genova University Press, pp. 436–

447.

Barana, A., Marchisio, M., Rabellino, S., 2015. Automated

Assessment in Mathematics, in: Proceedings of 2015

IEEE 39th Annual Computer Software and

Applications Conference (COMPSAC), IEEE,

Taichung, Taiwan, pp. 670–671. https://doi.org/10.

1109/COMPSAC.2015.105

Barana, A., Marchisio, M., Sacchet, M., in press.

Advantages of the Use of Formative Automatic

Assessment for Learning Mathematics. In: Proceedings

of 2018 TEA Conference.

Brancaccio, A., Marchisio, M., Palumbo, C., Pardini, C.,

Patrucco, A., Zich, R., 2015. Problem Posing and

Solving: Strategic Italian Key Action to Enhance

Teaching and Learning Mathematics and Informatics in

the High School. In: Proceedings of 2015 IEEE 39th

Annual Computer Software and Applications

Conference (COMPSAC), IEEE, Taichung, Taiwan,

pp. 845–850. https://doi.org/10.1109/COMPSAC.

2015.126

Brown, J. S., Collins, A., Duguid, P., 1989. Situated

Cognition and the Culture of Learning. Educational

Researcher 18(1), pp. 32–42.

Cornelius-White, J., 2007. Learner-Centered Teacher-

Student Relationships Are Effective: A Meta-Analysis.

Review of Educational Research 77, pp. 113–143.

https://doi.org/10.3102/003465430298563

Czerkawski, B.C., Lyman, E.W., 2016. An Instructional

Design Framework for Fostering Student Engagement

in Online Learning Environments. TechTrends 60, pp.

532–539. https://doi.org/10.1007/s11528-016-0110-z

Debnam, K. J., Lindstrom Johnson, S., Waasdorp, T.E.,

Bradshaw, C.P., 2014. Equity, connection, and

engagement in the school context to promote positive

youth development. Journal of Research on

Adolescence 24(3), pp. 447–459.

Ebel, R. L., 1954. Procedures for the Analysis of Classroom

Tests. Educational and Psychological Measurement

14(2), pp. 352-364.

Giraudo, M. T., Marchisio, M., Pardini, C., 2014. Tutoring

con le nuove tecnologie per ridurre l’insuccesso

scolastico e favorire l’apprendimento della matematica

nella scuola secondaria. Mondo Digitale 13(51), pp.

834-843.

Gossen, F., Kuhn, D., Margaria, T., Lamprecht, A.-L.,

2018. Computational Thinking: Learning by Doing

with the Cinco Adventure Game Tool. In: Proceedings

of 2018 IEEE 42nd Annual Computer Software and

Applications Conference (COMPSAC), pp. 990–999.

Haberman, M., 2010. The Pedagogy of Poverty versus

Good Teaching. Phi Delta Kappan 92(2), 81–87.

https://doi.org/10.1177/003172171009200223

Hattie, J., Timperley, H., 2007. The Power of Feedback.

Review of Educational Research 77(1), 81–112.

https://doi.org/10.3102/003465430298487

Heinich, R., Molenda, M., Russel, J. D., Smaldino, S. E.,

1999. Instructional Media and Technologies for

Learning, 6th ed. Prince Hall, Upper Saddle River, NJ.

Honebein, P. C., 1996. Seven Goals for the Design of

Constructivist Learning Environments. In:

Constructivist Learning Environments. Educational

Technology Publications, New York, pp. 11–24.

INVALSI, 2017. Rilevazioni nazionali degli apprendimenti

2016-17 - Rapporto dei risultati.

Jonassen, D., Davidson, M., Collins, M., Campbell, J.,

Haag, B. B., 1995. Constructivism and computer

mediated communication in distance education.

American Journal of Distance Education 9(2), pp. 7–

26. https://doi.org/10.1080/08923649509526885

Kearns, L. R., 2012. Student Assessment in Online

Learning: Challenges and Effective Practices.

MERLOT Journal of Online Learning and Teaching,

8(3), pp. 198-208.

Lave, J., 1991. Situating learning in communities of

practice., in: Resnick, L.B., Levine, J.M., Teasley, S.D.

(Eds.), Perspectives on Socially Shared Cognition.

American Psychological Association, Washington, pp.

63–82. https://doi.org/10.1037/10096-003

Lefoe, G., 1998. Creating Constructivist Learning

Environments on the Web: The Challenge in Higher

Education.

Marchisio, M., Rabellino, S., Spinello, E., Torbidone, G.,

2017. Advanced e-learning for IT-Army officers

through Virtual Learning Eenvironments. Journal of e-

Learning and Knowledge Society 13(3), pp. 59–70.

https://doi.org/10.20368/1971-8829/1382

Mariani, A. M., 2006. La scuola può fare molto ma non può

fare tutto. Sei, Torino.

MIUR, 2012. Indicazioni Nazionali per il curricolo della

scuola dell’infanzia e del primo ciclo d’istruzione.

MIUR, 2010. Istituti Tecnici: Linee guida per il passaggio

al nuovo ordinamento.

CSEDU 2019 - 11th International Conference on Computer Supported Education

290

Moebius Assessment (2018) [online]. Available at:

https://www.digitaled.com/products/assessment/.

[Accessed 2 Jan. 2019]

Ng, C., Bartlett, B., Elliott, S.N., 2018. Empowering

engagement: creating learning opportunities for

students from challenging backgrounds. Springer

Science+Business Media, New York, NY.

Nicol, D. J., MacfarlaneDick, D., 2006. Formative

assessment and selfregulated learning: a model and

seven principles of good feedback practice. Studies in

Higher Education 31(2), pp. 199–218.

OECD, 2013. PISA 2012 results: Ready to learn. OECD,

Paris.

Pellerey, M., 2004. Le competenze individuali e il portfolio.

La Nuova Italia Scientifica, Roma.

Rogerson-Revell, P., 2007. Directions in e-learning tools

and technologies and their relevance to online distance

language education. Open Learning 22(1), pp. 57–74.

Sadler, D. R., 1989. Formative assessment and the design

of instructional systems. Instructional Science 18(2),

pp. 119–144.

Sangsawang, T., 2015. Instructional Design Framework for

Educational Media. Procedia - Social and Behavioral

Sciences 176, pp. 65–80.

Schoenfeld, A., 1992. Learning to think mathematically:

Problem solving, metacognition, and sense making in

mathematics, in: Handbook of Research on

Mathematics Teaching and Learning. Macmillian, New

York, pp. 334–370.

Scriven, M., 1966. The methodology of evaluation. Social

Science Education Consortium. Lafayette, Ind: Purdue

University.

Tristan Lopez, A., 1998. The Item Discrimination Index:

Does it Work? Rasch Measurement Transactions 12(1),

626.

von Glasersfeld, E., 1989. Constructivism in Education. In:

Husen, T., Postlethwaite, T.N. (Eds.), The International

Encyclopedia of Education. Pergamon Press,

Oxford/New York, pp. 162–163.

MATE-BOOSTER: Design of an e-Learning Course to Boost Mathematical Competence

291