
A MapReduce based Approach for Circle Detection
Mateus Menezes Azevedo Coelho, Dylan Nakandakari Sugimoto, Gabriel Adriano de Melo,
Vitor Venceslau Curtis and Juliana de Melo Bezerra
Computer Science Department, ITA, S
˜
ao Jos
´
e dos Campos, Brazil
Keywords:
MapReduce, Parallel Processing, Distributed Processing, Circle Detection, Hough Transform.
Abstract:
Circle detection algorithms applied on images are used in different contexts and areas, such as bacteria iden-
tification in Medicine and ball identification in a humanoid robot soccer competition. Specialization and
processing time are critical issues in existing algorithms and implementations so that good detection results
to different situations usually impact the execution time. Aiming to deal with trade-off of specialization and
performance, this paper proposes a parallel algorithm for circle detection using Hough Transform and MapRe-
duce paradigm. We also compared its performance relative to its serial implementation and the one provided
by the OpenCV library. The proposed approach is useful for maintaining an accessible time execution while
increasing results’ quality, moreover it is general in terms of usability, which aid the identification of circles
for different circumstances and inconstant environment.
1 INTRODUCTION
Circle detection on images can be applied in various
scientific fields, including Engineering and Medicine.
One example is the identification of a ball contour by
a robot during a humanoid robot soccer league (Ki-
tano et al., 1997). The robot should be able to detect
the ball (which is a circle in 2D space) and then act ac-
cordingly in the game. Another example is counting
the number of bacteria colonies that arise on a petri
dish, whose concentration is proportional to this num-
ber.
Distinct approaches can be used to solve a cir-
cle identification problem. For instance, SURF
(Speeded-Up Robust Features) algorithm (Bay et al.,
2008) uses pattern recognition to detect circles. This
kind of algorithm requires the extraction of features
that may not be always available. An example is coin
counting, where we need to identify the head and the
tail side of a coin. Other drawback is that such algo-
rithms can require some artificial intelligence prepro-
cessing in order to identify key points.
Hough Transform (Duda and Hart, 1972) based
methods are used for identifying different geomet-
ric shapes in an image, such as lines, circles or el-
lipses. There are even libraries that implement and
optimize such algorithms, as the image processing li-
brary OpenCV (Bradski, 2000).
The Hough Transform algorithm (Duda and Hart,
1972) has two main phases. The first phase is to iden-
tify the boundary points in a certain image. The sec-
ond phase is the one that takes more processing time
for circle detection, if in a generalized implementa-
tion, since every pixel in an image can be a circle cen-
ter, and every diameter that is smaller than the image’s
width and height is possible.
This algorithm, when implemented without sim-
plifications and executed in a generic way (such as
no radius limitation), has a long computing time and
large cost of memory space, which can affect algo-
rithm usage in real problems. A way to solve this
issue is to make parallel the Hough Transform al-
gorithm, so that the computing time and the mem-
ory space problems can be amortized. A parallel ap-
proach requires splitting the image and merging the
results, always considering performance, result gen-
eralization, and result quality.
To deal with parallelism, MapReduce is a promis-
ing solution. MapReduce is a programming model
and an associated implementation for processing a
large amount of data (Dean and Ghemawat, 2004).
Using this concept to implement a parallel version of
a certain algorithm, two main functions are needed
to develop the algorithm: Map and Reduce. A Map
function processes an initial set of key/value pairs that
is used to generate a set of intermediate key/value
pairs. A Reduce function merges all intermediate
values associated with the same intermediate key.
454
Coelho, M., Sugimoto, D., Melo, G., Curtis, V. and Bezerra, J.
A MapReduce based Approach for Circle Detection.
DOI: 10.5220/0007827604540459
In Proceedings of the 14th International Conference on Software Technologies (ICSOFT 2019), pages 454-459
ISBN: 978-989-758-379-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

MapReduce allows a “split to conquer” vision of an
algorithm, which can have its performance improved
by parallel processing.
Sere et al. (2016) discussed a way of implement-
ing Hough Transform with the MapReduce concept
in order to develop a line detection application. They
also indicated the possibility to apply the same idea
to other shapes. We extend the previous work to con-
sider circle detection. In this paper, we then propose
a parallel approach to circle detection problem, based
on MapReduce model. The proposal is compared in
terms of result quality and execution time with serial-
ized implementations.
2 CIRCLE DETECTION WITH
HOUGH TRANSFORM AND
MAPREDUCE
Our work is based on the Generalized Hough Trans-
form algorithm (Duda and Hart, 1972), which is de-
scribed with its simplifications in this section. The
same algorithm is implemented on serialized ap-
proach as well as parallel approach. The parallel
algorithm, based on MapReduce paradigm, uses the
Apache Spark framework (Zaharia et al., 2016) tech-
nology to support parallel execution.
2.1 Serialized Hough Transform for
Circle Detection
The algorithm responsible for the serial execution of
the Hough Transform in circles is detailed on the list-
ing 1. The algorithm receives the input file and then it
stores the image in a matrix. The image is filtered
in order to avoid boundary detection errors, in this
case, using a Gaussian Filter. For boundary detec-
tion, the Canny Edge Detection (Canny, 1986) is ap-
plied. Later, the algorithm considers that the circles
that can be correctly detected have its radius between
5 pixels and half of the minimum value of the image
dimensions. Such approximation is made to avoid de-
tection errors, for example simple points being con-
sidered circles.
Then, we initialize the candidate’s data structure
that is used for saving the number of boundary points
at a certain distance from a point. For each pixel that
was detected as boundary by Canny Edge, we sum
one to each other pixel that is a circle candidate for
the first pixel at a given radius, in other words, whose
distance to it is between the circle’s radius detection
range. Then we return the circles after a selection over
the candidates. This selection is based on the num-
ber of boundary pixels at a certain distance from the
given circle center and done by the function FilterCir-
clesFromcandidates. This function simply search for
the locally maximum points in the accumulated data
structure that are greater than a threshold defined by
its radius.
Algorithm 1: Serial Circle Detection.
1: function SERIALHOUGHCIRCLES(img):
2: input = applyGaussianFilter(img)
3: input = cannyEdge(input)
4:
5: length = int(min(rows/2,col/2))
6: radius = [range(5,length)]
7: cands = InitCandidates()
8:
9: for r in radius do:
10: for pixel in input do:
11: if pixel is boundary then:
12: for angle in range(0,360) do:
13: centerCand = get Center(pixel,r, angle)
14: if centerCand in image then:
15: cands[r][centerCand]+ = 1
16: return FilterCirclesFromCandidates (cand)
2.2 Parallel Hough Transform for
Circle Detection
The algorithm responsible for the parallel execution
of the Hough Transform for circles is described in list-
ing 2. It is the result of an adaptation of the algorithm
1 to the MapReduce paradigm, following directives of
the Spark’s resilient distributed dataset.
The algorithm behaves essentially in the same
way. It receives the image as a parameter and filters it
before applying the Canny Edge detection. Then, the
spark context variable, which is responsible for coor-
dinating the parallel execution, is initialized, as well
as the candidates, which are an accumulator variable.
The image is split into windows with maximum
dimensions as 50x50. This was a reasonable choice
for the division of work so that the overhead for split-
ting and synchronizing the workers is not greater than
time for computing the Hough Transform in the win-
dow. Using the spark context variable, the function
upCand is executed for each image window. This
function is the same as the algorithm 1 as it just update
the candidates in the given window sequentially. For
each pixel that was detected as boundary by Canny
Edge of each window, this function sums one to each
other pixel that is a circle candidate whose distance to
it is between the circle’s radius detection range. This
process of summing one for each pixel is done by the
A MapReduce based Approach for Circle Detection
455

3DAccumulator as there are 3 degrees of freedom in
which every possible circle is evaluated: its x and y
coordinates center position and its radius r. After the
end of the execution, the upCand function’s results
are updated. Then, the candidates are filtered such
that the circle identification is correct.
Algorithm 2: Parallel Circle Detection.
1: function PARALLELHOUGHCIRCLES(img):
2: input = applyGaussianFilter(img)
3: input = cannyEdge(input)
4: sc = getSparkContext()
5:
6: cands = sc.accumulator(3DAccumulator)
7:
8: windows = splitImage(input)
9:
10: sc.parallelize(windows). f oreach(upCand)
11: return FilterCirclesFromCandidates (cand)
3 EVALUATION
We compared results of four implementations for cir-
cle detection. Two algorithms are those described
in the previous section, known as ’Serial Circle De-
tection’ (Algorithm 1) and ’Parallel Circle Detection’
(Algorithm 2). The two other implementations were
based on the OpenCV Hough Transform circle de-
tection function (Bradski, 2000). We worked with a
OpenCV execution using delimited radius, here called
as ’Simplified OpenCV Circle Detection’. We also
worked with a OpenCV execution with no maximum
radius, here called ’General OpenCV Circle Detec-
tion’.
The evaluation criteria include: processing time,
detection results, and algorithm generalization. Pro-
cessing time is an important criterion for algorithms
to characterize performance. Detection results is the
evaluation of the implementation itself, considering
circles correctly detected and circles not detected. Al-
gorithm generalization criterion is related to how the
same algorithm can be used in different situations, in
other words, it is the flexibility that it has in relation
to its parameters. A more general algorithm is ex-
pected to work well in more tests cases than a more
specialized one, in our case, this means to detect the
desired circles even with the presence of shadows and
differences in illumination.
These criteria are considered in the execution of
the algorithms over the same images, with images re-
lated to different applications. These images where
randomly selected from the images search results that
included circular objects such as tennis balls, ge-
ographical features such as roundabouts, maps and
trees and finally microscopical images of bacteria.
For each implementation, the Hough Transform
processing time was measured. We do not measure
only the circle identification, but also all processing
functions executed over the image to assist the iden-
tification. For example, to use the OpenCV Hough
Transform implementation for circles and obtain an
acceptable response, it is important to process previ-
ously the image with a Gaussian blur (Hsiao et al.,
2007).
Table 1 shows the results of the execution of the
four implementations for circle detection. The used
machine was a computer with two Intel(R) Xeon(R)
CPU E5-2670 v3 @ 2.30GHz, totaling 48 threads and
128 GB of RAM. The Serial (Algorithm 1) and Par-
allel (Algorithm 1) algorithms were implemented in
Python language, being the Parallel adapted to inte-
grate with the Spark technologies, which is the inter-
face with the cluster. The program’s mean execution
time was calculated using at least 3 executions for the
more time consuming implementation and 5 for the
OpenCV implementations.
Table 1: Processing time of Hough Transform implementa-
tions for circle detection.
Implementation Mean Processing Time (sec)
Simplified OpenCV 0.013
General OpenCV 0.015
Serial (Algorithm 1) 924
Parallel (Algorithm 2) 44.2
The algorithms 1 and 2 had a worse performance
compared to the OpenCV implementation, the main
reason for that being the fact that OpenCV was im-
plemented in C using highly optimized operations
while our implementation was made in Python3 and
executed using its interpreter. Therefore, there is a
multiplicative constant that maps between the times
from the compiled code execution to its interpreta-
tion, which is a order of magnitude higher. Also, the
ratio between our serial and parallel implementations
is limited by the number of cores in which the parallel
version was run. One of the benefits of the parallel al-
gorithm is that its performance can be easily improved
by using a better cluster.
Regarding the detection results, we use as exam-
ple a bacteria cologne photo. The algorithms must
then attempt to identify such colognes as circles. The
red dots in the images were the centers of the detected
circles while its circumference is shown in green.
Serial (Algorithm 1) and Parallel (Algorithm 2)
are essentially the same, the only difference is the ap-
plication of a parallel execution strategy. So, as ex-
ICSOFT 2019 - 14th International Conference on Software Technologies
456
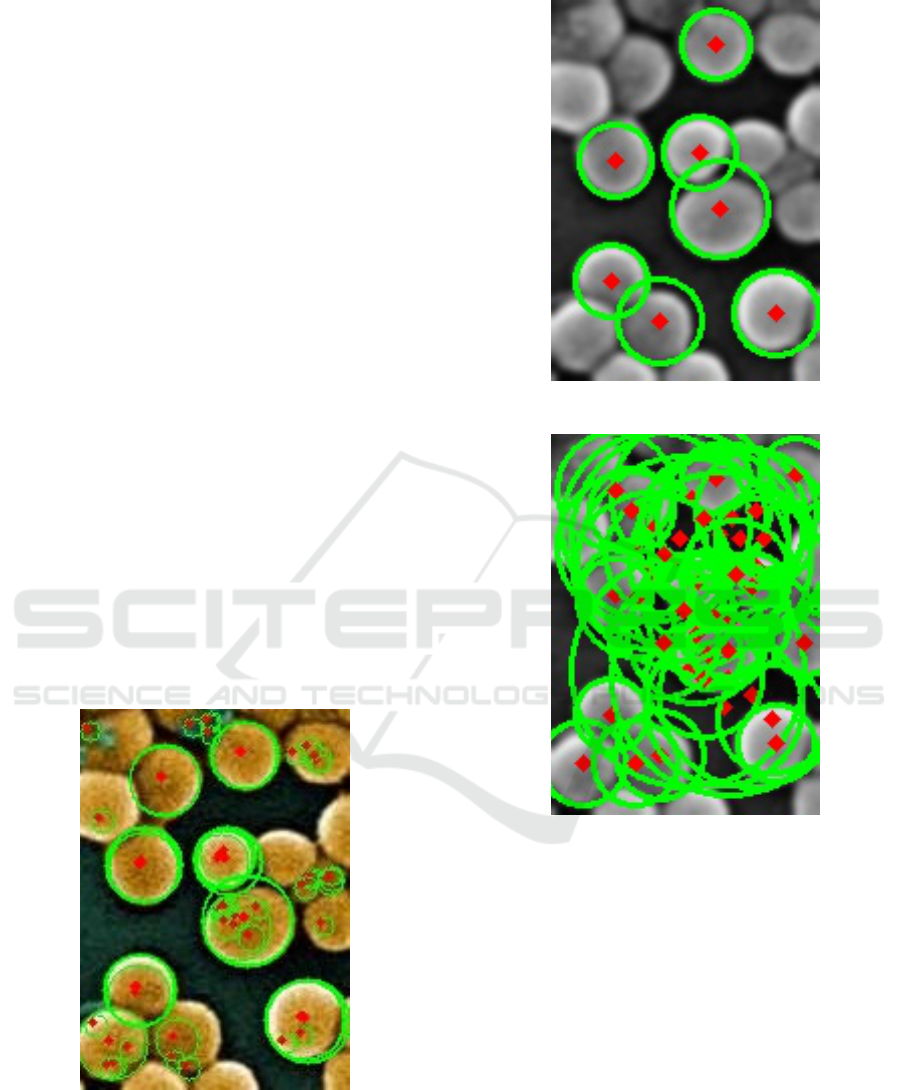
pected, the detection results are the same, as show in
Figure 1. It is important to note that not all bacteria
were found to have a circular shape that could be de-
tected by the algorithm and that some inner features
had a deeply round shape that was detected by the al-
gorithm. Nevertheless, the algorithm was able to find
important circles that would help to characterize the
image.
The result for the execution of the ’Simplified
OpenCV’ is presented in Figure 2. The OpenCV
implementation requires the input image to be in
grayscale as it can work only with one color chan-
nel. We observed that with a specialized parameter
range, such as the radius that ranged between 15 to 40
pixels and the threshold parameter, the algorithm was
able to select only the circles in which it had the most
confidence. In this way the smaller features were fil-
tered out but other important circles were also left out
of the final results. Our implementation has the ad-
vantage that it doesn’t need the user to manually se-
lect the range as it is able to automatically sweep the
entire range of possible radius, selecting the larggest
acumullation points.
The result for the execution of the ’General
OpenCV’ is presented in Figure 3. We noted that this
detection result wasn’t good as it identified a exces-
sive number of circles that shouldn’t be marked, ren-
dering the analysis less useful. This image was also
loaded as grayscale because it is the only input format
the OpenCV implementation accepts.
Figure 1: Detection Result of Serial (Algoritm 1) and Par-
allel (Algorithm 2).
The last evaluation criterion was the algorithm
generalization. The implementation provided by
OpenCV has a low generalization power, since to
achieve a good result, some parameters have to be
Figure 2: Detection Result of Simplified OpenCV.
Figure 3: Detection Result of General OpenCV.
changed accordingly, such as the circle’s radius limits
and the parameter related to the internal Canny Edge
detector, which mean that assuming a certain range
for the radius is usually needed for adequate results.
Accordingly to the OpenCV documentation, there is
the parameter d which is the ratio between the image
resolution and the accumulator resolution, the param1
which is the higher threshold of the two threshold that
are passed to the internal canny edge detector as the
lower one is twice smaller, and the param2 is the ac-
cumulator threshold for the centers of the circles at the
detection stage so that the smaller it is, the more false
circles may be detected (Team, 2014). Some parame-
ter’s configuration may require more processing time
as the accumulation space would be bigger or more
densely populated. This process of choosing the right
parameter may be time consuming and it is this point
A MapReduce based Approach for Circle Detection
457

that our algorithm excels.
This issue is not a problem to Serial (Algorithm 1)
neither to the proposed Parallel (Algorithm 2), which
do not need to receive guessed parameters and its de-
tection performance does not change abruptly. For
instance, specifying an small radius range of 10 pix-
els has a better performance than specifying the range
from zero to half the image’s width. Also, the parame-
ters associated with the OpenCV implementation may
vary from image to image, depending on the scale and
the illumination presented in the image.
When there is an obstructed circle, the OpenCV
implementation has a higher chance of considering it
a circle, depending on the tolerance of its parameters,
which mostly increase wrong identification cases. But
both the Serial and the proposed Parallel implementa-
tions (Algorithm 1 and Algorithm 2, respectively) are
robust enough to identify the obstructed circles with-
out affecting the result quality.
4 CONCLUSIONS
In a context of circle identification, where the envi-
ronment variables, such as light, changes quickly, it
is very important to have an algorithm implementa-
tion that allows result stability and quality without a
dynamic change on the received parameters. This im-
plementation is the objective of this paper, which was
motivated by the need to balance circle identification
performance with the achievement of appropriated re-
sults independent of contexts.
In this context, we proposed a parallel algorithm
for circle identification. We applied Hough Trans-
form as the foundation for our algorithm and added
parallelism using the MapReduce paradigm. For exe-
cution purposes, we used Spark framework, which is
a framework to support distributed computing.
We compared the proposed parallel algorithm
with analogous implementations, also using Hough
Transform. We investigated the serial version of
our proposal. We also explored the OpenCV Hough
Transform Algorithm in two ways: in a simplified
way (with predefined parameters) and in a general
way (without predefined parameters).
We found that the main advantage of our proposal
as well as its serialized version is the algorithm gen-
eralization. Such implementations can than be used
to detect different objects as a circle in distinct con-
texts without the need to set specialized configura-
tions. Regarding the detection results, the OpenCV
achieved good results when properly configured. The
OpenCV in a general way was unable to identify cir-
cles correctly, since it ended up with many false pos-
itives. To avoid it, some parameters, such as circle
radius limits, should be defined, even when the ade-
quate values for them are mutable, like when the cam-
era gets closer to the object, the circle radius limits
should change, or when the environment gets lighter,
a different filter parameter should be applied. As ex-
pected, our parallel algorithm gave the same detection
results that its serialized version. However, some re-
sults were not small formations not consistent with
the expected circles, so we need to investigate how to
improve the algorithm in this way.
Regarding performance, OpenCV implementation
has a very good performance, mainly when the pa-
rameters are specified correctly. But, since this im-
plementation relies deeply on the correct choice of
these parameters, when the context changes a little
the performance may decay significantly. The serial
algorithm has the largest processing time of the eval-
uated algorithms, while having a generalized perfor-
mance as good as our parallel implementation. Nev-
ertheless, this serial algorithm can take up to a day of
processing time for high resolution images. Although
the performance of the proposed parallel algorithm
was not impressive, such parallel approach requires
further evaluations, since it relies on cluster architec-
ture and processing power. The interesting result is
that the performance of parallel algorithm is not neg-
atively impacted by context changes.
More experiments and comparisons should be
studied. As future work, we intend to investigate other
parallelism framework different from Spark, other
programming languages, as well as other execution
platform in order to improve performance of our par-
allel algorithm. We will also test different blurring fil-
ters and edge detectors, aiming to reduce the errors in
the circles identification. We argue that, with an opti-
mized implementation, our proposal can adequately
support circle detection in real distributed systems’
problems.
REFERENCES
Bay, H., Ess, A., Tuytelaars, T., and Van Gool, L. (2008).
Speeded-up robust features (surf). Comput. Vis. Image
Underst., 110(3):346–359.
Bradski, G. (2000). The OpenCV Library. Dr. Dobb’s Jour-
nal of Software Tools.
Canny, J. (1986). A computational approach to edge de-
tection. IEEE Trans. Pattern Anal. Mach. Intell.,
8(6):679–698.
Dean, J. and Ghemawat, S. (2004). Mapreduce: Simplified
data processing on large clusters. In Proceedings of
the 6th Conference on Symposium on Operating Sys-
tems Design & Implementation - Volume 6, OSDI’04,
ICSOFT 2019 - 14th International Conference on Software Technologies
458

pages 10–10, Berkeley, CA, USA. USENIX Associa-
tion.
Duda, R. O. and Hart, P. E. (1972). Use of the hough trans-
formation to detect lines and curves in pictures. Com-
mun. ACM, 15(1):11–15.
Hsiao, P.-Y., Chou, S.-S., and Huang, F.-C. (2007). Generic
2-d gaussian smoothing filter for noisy image process-
ing. TENCON 2007 - 2007 IEEE Region 10 Confer-
ence, pages 1–4.
Kitano, H., Asada, M., Kuniyoshi, Y., Noda, I., and Osawa,
E. (1997). Robocup: The robot world cup initiative. In
Proceedings of the First International Conference on
Autonomous Agents, AGENTS ’97, pages 340–347,
New York, NY, USA. ACM.
Team, O. D. (2014). Feature detection. In OpenCV API
Reference.
Zaharia, M., Xin, R. S., Wendell, P., Das, T., Armbrust,
M., Dave, A., Meng, X., Rosen, J., Venkataraman, S.,
Franklin, M. J., Ghodsi, A., Gonzalez, J., Shenker, S.,
and Stoica, I. (2016). Apache spark: A unified engine
for big data processing. Commun. ACM, 59(11):56–
65.
A MapReduce based Approach for Circle Detection
459
