
Numerical Simulation of Internal Wave Attractors in Horizontally
Elongated Domains with Sloping Boundaries
Ilias Sibgatullin
1,2,3
, Xu Xiulin
3
, Evgeny Ermanuyk
4
, Daniil Ryazanov
1,3
and Kirill Vatutin
1,3
1
Ivannikov Institute for System Programming, Russian Academy of Sciences, Moscow, Russia
2
Shirshov Institute of Oceanology, Russian Academy of Sciences, Moscow, Russia
3
Moscow Lomonosov State University, Moscow, Russia
4
Lavrentyev Institute of Hydrodynamics, Russian Academy of Sciences, Novosibirsk, Russia
Keywords:
Internal Waves, Inertial Waves, Mixing, Wave Turbulence.
Abstract:
Global tides create continuous input of mechanical energy to the ocean, and produce inertia-gravity waves
which change the processes of vertical mixing, affect background stratification, create mean and zonal cur-
rents. Internal and inertial wave attractors may arise in natural ocean and coastal topography, and due to
energy accumulation they produce turbulence or increase turbulence intensity even for moderate values of the
input energy. Previous studies of internal wave attractors at a laboratory scale were concerned mostly with
basins of comparable vertical and horizontal dimensions, while in ocean we typically deal with horizontally
elongated geometries and low ratios between the tidal and buoyancy frequencies. In this work we describe
laminar and turbulent regimes of internal wave attractors in domains with large aspect ratio subject to forcing
at low non-dimensional frequency.
1 INTRODUCTION
A large amount of energy is constantly injected into
interior of the Ocean due to interaction of barotropic
tides with the bottom topography. As a result the
inertia-gravity waves radiate from generation sites,
producing significant effects on the vertical mixing
and stratification (Morozov, 1995; Dauxois et al.,
2018). In addition, inertia-gravity wave motion
resulting from tides can produce mean and zonal
flows (Winters, 2015; Manders and Maas, 2004; Har-
lander and Maas, 2007). Inertia and gravity waves
possess a very peculiar dispersion relation, which for
certain frequency defines only the direction of wave
propagation with respect to gravity or angular veloc-
ity vector. It was shown theoretically, experimentally
and numerically, that in closed basins with sloping
boundaries there may exist an attracting geometrical
structure in physical space, a wave attractor. The the-
ory of wave attractors in ideal fluids is well elabo-
rated now, and in (Maas et al., 1997) one can see a
diagram illustrating a rich variety of internal wave-
ray patterns in a closed domain as function of two pa-
rameters, governing the geometry of the domain and
the wave-ray slopes. While this diagram is very use-
ful to identify the domains of parameters correspond-
ing to strong energy focusing in ideal fluid, it is not
fully relevant to real fluids, with effects due to vis-
cosity and wave turbulence included. Previous works
(Brouzet et al., 2016b; Brouzet et al., 2016a; Brouzet
et al., 2017) considered trapezoidal geometry of the
fluid domain, with comparable vertical and horizontal
dimensions. Transition to nonlinear wave turbulence
was studied in details, and scaling laws were investi-
gated for such a geometric setup.
In the present paper we show some numerical
results for internal wave attractors in a horizontally
elongated domain at low ratio between forcing and
buoyancy frequency, which is closer to typical situa-
tions in oceanology applications.
2 MATHEMATICAL MODEL
The subject of this study is the internal wave dynam-
ics in a closed domain with one border inclined with
respect to the vertical. Such a geometry can naturally
occur near ridges, coastal areas, continental slopes
and so on. We perform Direct Numerical Simulations
366
Sibgatullin, I., Xiulin, X., Ermanuyk, E., Ryazanov, D. and Vatutin, K.
Numerical Simulation of Internal Wave Attractors in Horizontally Elongated Domains with Sloping Boundaries.
DOI: 10.5220/0007909203660370
In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 366-370
ISBN: 978-989-758-371-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
within the framework of a mathematical model con-
sisting of Navier – Stokes equations coupled to trans-
port and diffusion of salt and continuity equations,
and the boundary conditions given below:
∂~v
∂t
+ (~v,∇)~v = −∇
˜p
ρ
m
+ ν∆~v + ρ
s
~g; (1)
∂ρ
s
∂t
+ (~v,∇)ρ
s
= λ
s
∆ρ
s
, div(~v) = 0, (2)
where ~v – velocity; ρ = ρ
m
+ ρ
s
– density; ρ
m
– min-
imal density; ρ
s
– salt density; ˜p - pressure ρ
m
; ν –
kinematic viscosity; λ
s
– coefficient of salt diffusion.
We consider a continuously stratified initial state
with constant buoyancy frequency
N(z) =
s
−
g
ρ(z)
dρ(z)
dz
We prescribe the no-slip condition at all rigid
boundaries except for one boundary where we apply
a specific harmonic forcing. In the case of rotating
fluid, different types of such forcing are introduced in
(Sibgatullin et al., 2017), which describes for the first
time the laminar and weakly turbulent inertial wave
regimes in an annular frustum. In the case of strati-
fied fluid, the boundary conditions and external forc-
ing closely mimicking the experimental ones are de-
scribed in (Brouzet et al., 2016b).
Figure 1: Internal wave attractors for two geometries, hav-
ing opposite slopes of the right boundary with respect to the
gravity direction. Vertical component of velocity is shown
with color. The energy flows in opposite directions in left
and right configurations, otherwise the dynamics is similar.
Figure 1 presents the sketch of the generic geomer-
ical setup used in analytical, numerical and experi-
mental studies of the wave attractors. The fluid is
confined inside a trapezoidal prism, with two bases
of the trapeze perpendicular to gravity, the left wall
being vertical and the right wall tilted by a certain
angle α. The first attempts to model wave attractors
assumed two-dimensionality of the flow (Grisouard
et al., 2008). This assumption allowed a fully rel-
evant qualitative simulation of wave attractors, with
relatively poor quantitative agreement between nu-
merical and experimental results. Later, the first fully
3D DNS greatly improved the quantitative agreement
between experiments and simulations both in linear
and non-linear regimes, and showed the significance
of the dissipation at the lateral walls of the fluid do-
main (Brouzet et al., 2016b; Brouzet et al., 2016a;
Beckebanze et al., 2018). Interestingly, numerical
simulations of wave attractors generated by a span-
wise localized wave maker in the otherwise two-
dimensional setup demonstarted a strong qualitative
trend toward two-dimensionality of wave motion, but
with specific non-uniform energy distribution in span-
wise direction and significant effects due to the lateral
walls (Pillet et al., 2018).
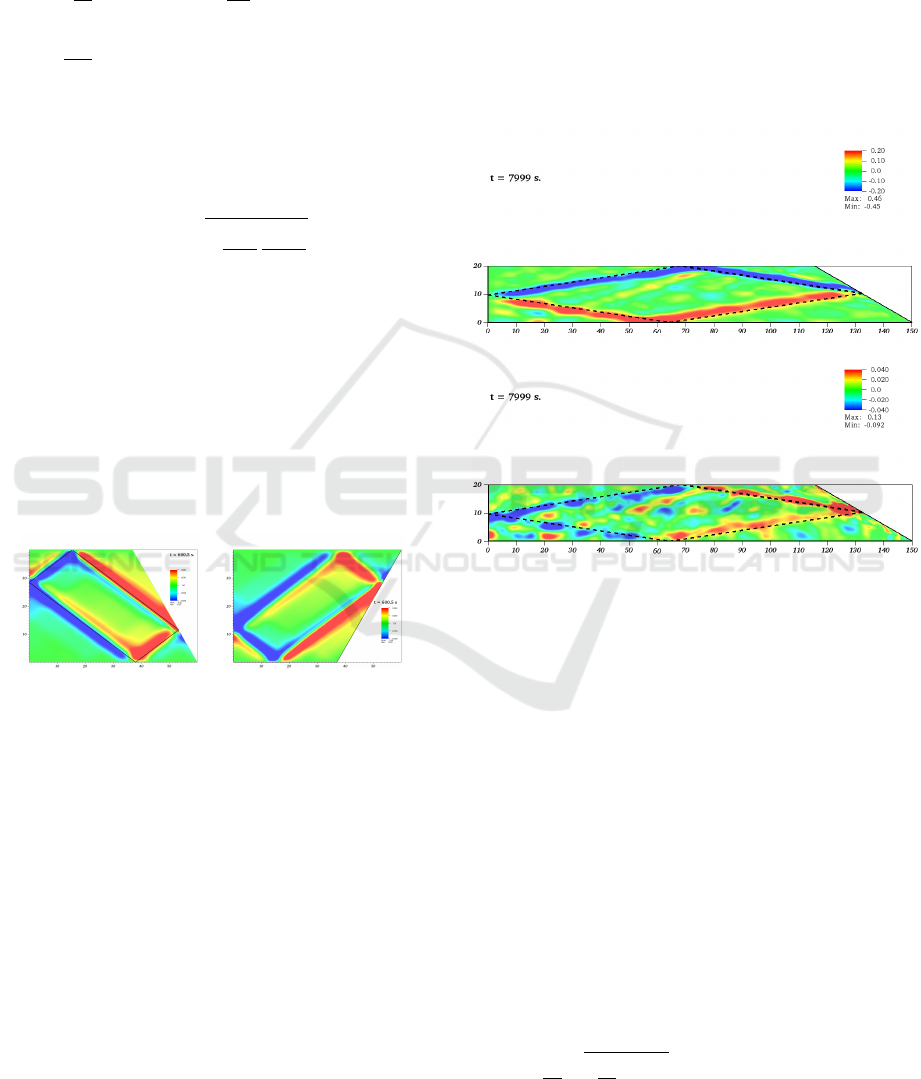
Figure 2: α = 60
◦
, a=0.02 cm, horizontal and vertical com-
ponents of velocity.
Substituting the solution in form of monochromatic
travelling waves into linearised Euler equations de-
scribing the motion of a uniformly stratified ideal
fluid, one can obtain the following dispersion relation:
ω
2
0
= N
2
sin
2
(θ), (3)
where ω
0
– wave frequency. It can be seen that the
dispersion relation admits the propagation of waves
in form of oblique wave beams, but does not contain
any length scale. In many practical problems a qual-
itative description of wave patterns can be obtained
by neglecting the width of wave beams and consid-
ering the propagation of wave rays. The problem of
wave-ray billiard in the geometric setup presented in
Figure 1 can be re-scaled by introducing two quan-
tities d and τ, d being the parameter responsible for
the slope (with the limiting values −1 and +1 cor-
responding to triangular and rectangular geometry),
and τ =
2H
L
r
N
ω
0
2
− 1 being the parameter respon-
sible for the forcing frequency. In ideal fluid, a di-
Numerical Simulation of Internal Wave Attractors in Horizontally Elongated Domains with Sloping Boundaries
367
agram of Lyapunov exponents of internal wave rays
(Maas et al., 1997) characterises the wave regimes,
and show the domains of strong convergence toward
attractors. However, in real world viscosity and wave
turbulence come into play, adding a rich variety of
linear and non-linear regimes.
In numerical simulations of linear regimes one
needs to resolve the boundary layers at rigid bound-
aries, and the structure of the attractor beams, which
appear in form of oblique viscous shear layers. In
simulations of strongly nonlinear regimes, one needs
to resolve the small-scale patterns resulting from a
cascade of wave-wave interactions. In a density-
stratified fluid the numerical simulations are com-
plicated by necessity to resolve the diffusion of the
stratifying agent, and at high values of the Prandtl-
Schmidt number the small-scale structures appear,
which greatly complicate the interaction of the waves
beams of the attractors with the walls (Sibgatullin and
Kalugin, 2016). In direct numerical simulations de-
scribed in the present paper we use the spectral ele-
ment method, which proves to be highly efficient for
this type of problems (Brouzet et al., 2016b; Brouzet
et al., 2016a; Beckebanze et al., 2018).
Figure 3: α = 60
◦
, a=0.05 cm, horizontal and vertical com-
ponents of velocity.
3 NUMERICAL RESULTS
Many previous studies on dynamics of internal wave
attractors used the trapezoidal geometry depicted in
Figure 1 (Mass et al., 1997; Scolan et al., 2013;
Brouzet et al., 2016b; Brouzet et al., 2016a; Becke-
banze et al., 2018; Brouzet et al., 2017; Dauxois et al.,
2017), where the largest base of the trapezium varied
between 30 to 150 cm and the fluid depth was about
2/3 of the largest base. The angle of the slope with the
gravity was typically about 30
◦
. The external forcing
was realized by moving vertical boundary of the fluid
volume or by oscillating the tank filled with the den-
sity stratified water.
Significant change of aspect (depth-to-length) ra-
tio of the geometrical setup may introduce new dy-
namical effects in the behaviour of the system at lam-
inar and turbulent regimes. Of particular interest is the
horizontally elongated geometry, which is relevant to
typical applications in oceanography.
In the following, the tidal forcing is simulated in
a highly simplified way by imposing small-amplitude
oscillations of the largest base of the trapezium L in
the following form:
ξ = asin(2πx/L)sin(ω
0
t)
We take the length of the domain L = 150 cm and
the depth is H = 20 cm. The value of the buoyancy
frequency is N = 1 rad/s. The kinematic viscosity of
the fluid is taken to be ν = 0.002 cm
2
/s, five times
smaller than the viscosity of water. The global Stokes
number, which can be introduced as St = H
2
N/ν
is 2 · 10
5
. In the present paper we are mostly con-
cerned with the qualitative effects observed in hori-
zontally elongated domains. Therefore we perform
two-dimensional simulations.
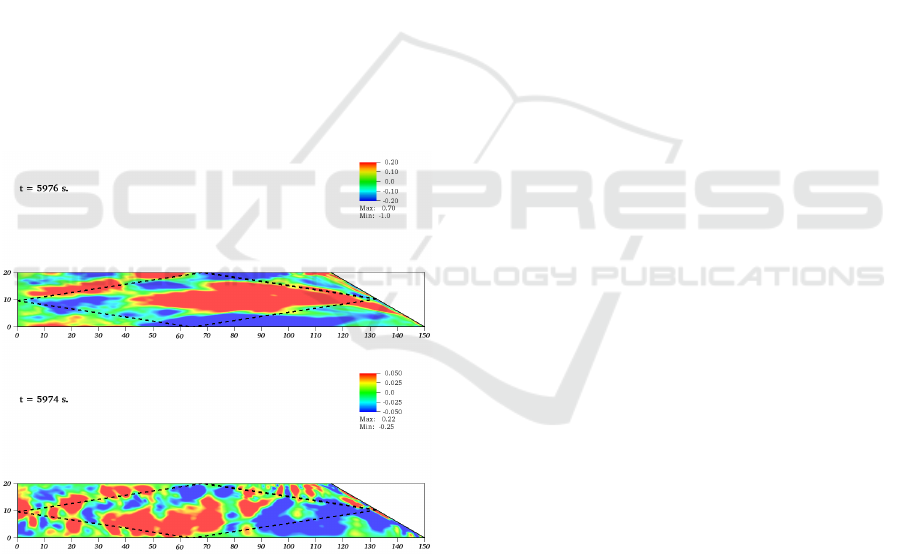
Figure 2 shows the horizontal and vertical com-
ponents of velocity field at small forcing amplitude
a = 0.02 cm. The narrow wave beams are localized
in the vicinity of the theoretical sceleton of the at-
tractor given by solution of the wave-ray billiard and
marked with a black dashed line. One can identify
the presence of nonlinear effects, in particular, wave
beams at double frequency 2ω
0
emitted at the points
of reflection of the primary wave beam. Note that the
possibility of super-harmonic effects is an important
feature of the horizontally elongated setup. In pre-
vious studies of wave turbulence in internal wave at-
tractors (Scolan et al., 2013; Brouzet et al., 2016b;
Brouzet et al., 2016a) the typical non-dimensional
forcing frequency was ω
0
/N > 0.5. Therefore the
super-harmonics could exist only in form of evanes-
cent waves. The present study considers a more real-
istic case where the super-harmonic waves are prop-
agative.
Figure 3 shows the horizontal and vertical compo-
nents of the velocity field for the forcing amplitude
a = 0.05 cm (i.e. only 2.5 times larger than in the
case shown in Figure 2). Note that the forcing am-
plitude remains very small compared to the size of
the fluid domain: a/L is about 3 · 10
−4
. The wave
pattern now is completely different: we can see at
the same time the small-scale structures located in
ONM-CozD 2019 - Special Session on Observations and Numerical Modeling of the Coastal Ocean Zone Dynamics
368

the upper right corner, and the large-scale structures
in the bulk of the domain. This observation sug-
gests the existence of the inverse cascade resulting
from the complex turbulent wave motion. This qual-
itative consideration is to be confirmed by a careful
Fourier-Hilbert analysis being performed at present
time. Importantly, the observed snapshot bears no re-
semblance to a classic pattern of internal wave attrac-
tor. Therefore, at high energy input into the system
the fact that a particular geometry admits the exis-
tence of wave attractors may be completely hidden by
wave turbulence although the concentration of energy
at the attractor is at the origin of the observed energy
cascade. This is particularly important for interpreta-
tion of oceanographic measurements which typically
deal rather with the large-scale patterns seen Figure 3
than with the narrow-beam patterns presented in Fig-
ure 2. Establishing the link between the two patterns
may significantly enrich our understanding of the un-
derlying nonlinear dynamics. Broad numerical calcu-
lations are now under way, focused at the analysis of
the spectra of the wave motions in space and time and
other characteristics of wave turbulence in different
areas of horizontally elongated fluid domains.
4 CONCLUSIONS
This communication describes the peculiarities of in-
ternal wave turbulence in horizontally elongated con-
fined fluid domains with one sloping wall. The wave
attractors in such a geometry typically have a lower
amplitude threshold corresponding to onset of wave
turbulence as compared to conventional setups where
length and depth of the fluid domain are comparable.
The most important result of this study consists in
revealing the inverse cascade. We consider the time-
evolution of the internal wave regime from the state
of rest toward formation of the attractor and transition
to a fully developed wave turbulence via a cascade of
wave-wave interactions. In the regime of wave turbu-
lence we observe the small scale structures to merge
and form larger structures. This result may explain
in particular why internal wave attractors are hard to
detect in natural conditions: we see here that they ini-
tially act as a source of wave turbulence, but after-
wards they are hidden behind the large scale turbu-
lence arising due to development of the inverse cas-
cade.
ACKNOWLEDGEMENTS
This research was supported by the Russian
Ministry of Education and Science (Agreement
14.616.21.0075, Project ID RFMEFI61617X0075).
The computations are performed using the equipment
of the shared research facilities of HPC computing re-
sources at Lomonosov Moscow State University.
REFERENCES
Beckebanze, F., Brouzet, C., Sibgatullin, I. N., and Maas,
L. R. M. (2018). Damping of quasi-two-dimensional
internal wave attractors by rigid-wall friction. Journal
of Fluid Mechanics, 841:614–635.
Brouzet, C., Ermanyuk, E., Joubaud, S., Sibgatullin, I., and
Dauxois, T. (2016a). Energy cascade in internal-wave
attractors. EPL (Europhysics Letters), 113(4):44001.
Brouzet, C., Sibgatullin, I., Scolan, H., Ermanyuk, E., and
Dauxois, T. (2016b). Internal wave attractors exam-
ined using laboratory experiments and 3d numerical
simulations. Journal of Fluid Mechanics, 793:109–
131.
Brouzet, C., Sibgatullin, I. N., Ermanyuk, E. V., Joubaud,
S., and Dauxois, T. (2017). Scale effects in internal
wave attractors. Phys. Rev. Fluids, 2:114803.
Dauxois, T., Brouzet, C., Ermanyuk, E., Joubaud, S.,
Tourneau, D. L., and Sibgatullin, I. (2017). Energy
cascade in internal wave attractors. Procedia IUTAM,
20:120 – 127. 24th International Congress of Theo-
retical and Applied Mechanics.
Dauxois, T., Ermanyuk, E., Brouzet, C., Joubaud, S., and
Sibgatullin, I. (2018). Abyssal Mixing in the Labora-
tory, pages 221–237. Springer International Publish-
ing, Cham.
Grisouard, N., Staquet, C., and Pairaud, I. (2008). Numeri-
cal simulation of a two-dimensional internal wave at-
tractor. Journal of Fluid Mechanics, 614:1.
Harlander, U. and Maas, L. R. M. (2007). Internal boundary
layers in a well-mixed equatorial atmosphere/ocean.
Dynamics of Atmospheres and Oceans, 44:1–28.
Maas, L. R. M., Benielli, D., Sommeria, J., and Lam, F.-
P. A. (1997). Observation of an internal wave attractor
in a confined, stably stratified fluid. Nature, 388:557–
561.
Manders, A. M. M. and Maas, L. R. M. (2004). On the
three-dimensional structure of the inertial wave field
in a rectangular basin with one sloping boundary.
Fluid Dynamics Research, 35(1):1.
Mass, L., Benielli, D., Sommeria, J., and Lam, F.-P. A.
(1997). Observation of an internal wave attrac-
tor in a confined, stably stratified fluid. Nature,
388(6642):557.
Morozov, E. G. (1995). Semidiurnal internal wave global
field. Deep Sea Research Part I: Oceanographic Re-
search Papers, 42(1):135 – 148.
Pillet, G., Ermanyuk, E. V., Maas, L. R. M., Sibgatullin,
I. N., and Dauxois, T. (2018). Internal wave attractors
Numerical Simulation of Internal Wave Attractors in Horizontally Elongated Domains with Sloping Boundaries
369

in three-dimensional geometries: trapping by oblique
reflection. Journal of Fluid Mechanics, 845:203–225.
Scolan, H., Ermanyuk, E., and Dauxois, T. (2013). Non-
linear fate of internal wave attractors. Physical review
letters, 110(23):234501.
Sibgatullin, I., Ermanyuk, E., Maas, L., Xu, X., and
Dauxois, T. (2017). Direct numerical simulation of
three-dimensional inertial wave attractors. In 2017
Ivannikov ISPRAS Open Conference (ISPRAS), pages
137–143.
Sibgatullin, I. and Kalugin, M. (2016). High-resolution
simulation of internal waves attractors and impact
of interaction of high amplitude internal waves with
walls on dynamics of waves attractors. ECCOMAS
Congress 2016 - Proceedings of the 7th European
Congress on Computational Methods in Applied Sci-
ences and Engineering, 4:7130–7137.
Winters, K. B. (2015). Tidally-forced flow in a rotating,
stratified, shoaling basin. Ocean Modelling, 90:72–
81.
ONM-CozD 2019 - Special Session on Observations and Numerical Modeling of the Coastal Ocean Zone Dynamics
370
