Noise-induced Signal Corruption in Nonlinear Fourier-based Optical
Transmission System in the Presence of Discrete Eigenvalues
Maryna L. Pankratova
a
, Anastasiia Vasylchenkova and Jaroslaw E. Prilepsky
b
Aston Institute of Photonic Technologies, Aston University, Aston Triangle, B4 7ET, Birmingham, U.K.
Keywords:
Optical Communications, Nonlinear Fourier Transform, Noise, Soliton, Correlation Properties.
Abstract:
We present the numerical analysis of the correlation properties of the amplifier spontaneous emission (ASE)
noise transformed into the nonlinear Fourier (NF) domain, addressing the noise-induced corruptions in the
communication systems employing the nonlinear Fourier transform (NFT) based signal processing. In our
current work we deal with the orthogonal frequency division multiplexing (OFDM) modulation of a contin-
uous NF spectrum and account for the presence of discrete (soliton) eigenvalues. This approach is aimed at
extending our previous studies that referred to the modulation of continuous NF spectrum only. The effec-
tive noise covariance functions are obtained from numerical simulations for a range of propagation distances,
values of discrete eigenvalue, and different effective signal power levels. We report the existence of the corre-
lations between the continuous and discrete parts of the NF spectrum.
1 INTRODUCTION
The rise of interest to the nonlinear frequency division
multiplexing technique (NFDM), the optical trans-
mission method based on the NFT signal processing
and the modulation of effective modes inside the NF
domain, can be explained by effective absence of the
nonlinear cross-talk between the different multiplexed
signal components provided by this method (Turit-
syn et al., 2017; Yousefi and Kschischang, 2014; Le
et al., 2017). In turn, the latter is believed to the
major source of the capacity degradation in modern
optical transmission lines (Essiambre et al., 2010).
For the NFDM, the data transmission takes place in-
side the NF domain, where the residual weak non-
linear cross-talk occurs only because of the deviation
of the true optical channel from the idealised math-
ematical model. At the same time, the invevitable
presence of the optical noise in the channel, occur-
ing due to the amplification, can significantly hamper
the quality and reach of the NFT-based transmission,
affecting both continous and discrete parts of the NF
(Civelli et al., 2017; Garcia-Gomez and Aref, 2019).
Therefore, the study of the noise-induced signal cor-
ruption occurring inside the NF domain constitutes an
important direction in the research related to improve-
a
https://orcid.org/0000-0002-5974-6160
b
https://orcid.org/0000-0002-3035-4112
ment of the NFT-based optical transmission system’s
throughput.
The NFT-based optical transmission involves
three basic steps (Turitsyn et al., 2017): (i) mapping
the signal from the NF spectral domain to the space-
time domain using the inverse NFT, INFT; (ii) the
signal propagation inside the NFT domain that ac-
tually boils down to the phase rotation of individual
NF spectral components obeying the linear disper-
sion law; (iii) the NFT signal processing at the re-
ceiver and compensation of the accumulated phase ro-
tation. However, as noted before, in practice, the real
fibre differs from the idealised mathematical model
attributed to the NFT operations. The main mas-
ter model governing the light propagation in a ide-
alised lossless single mode fibre is the lossless non-
linear Schr
¨
odinger equation (NLSE). The NLSE for
the envelope electric field function q(z,t) in presence
of ASE noise can be written down as
iq
z
− q
tt
− 2|q|
2
q = η(z,t), (1)
where z and t are the normalised distance along the
fibre and the normalised retarded time in the frame
co-moving with the envelope, respectively (Agrawal,
2012). The presence of ASE is taken into account via
the η(z,t) term in the right hand side of the equation,
modelled as the distributed additive white Gaussian
noise (AWGN) with zero mean and normalised power
258
Pankratova, M., Vasylchenkova, A. and Pr ilepsky, J.
Noise-induced Signal Corruption in Nonlinear Fourier-based Optical Transmission System in the Presence of Discrete Eigenvalues.
DOI: 10.5220/0007921002580264
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 258-264
ISBN: 978-989-758-378-0
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

spectral density D:
E[η(z,t)η
∗
(z
0
,t
0
)] = 2Dδ(t −t
0
)δ(z − z
0
),
where E[. ..] stands for expectation value. Eq. (1) as-
sumes ideal distributed Raman amplification with full
compensation of the fibre loss. However, this modes
can also serve as a good leading approximation for the
path-averaged description of the light propagation in
the presence of lumped amplification (Le et al., 2015;
Kamalian et al., 2017).
The NLSE, Eq. (1), with the zero right hand side
is integrable, meaning that the explicit forms of the
forward and inverse NFT operation attributed to such
an equation are known (Zakharov and Shabat, 1972).
The forward NFT of a given localised (having a fi-
nite norm) signal can be calculated by considering the
Zakharov-Shabat problem for two auxiliary functions
v
1
(t,ζ) and v
2
(t,ζ):
∂v
1
(t,ζ)
∂t
= q(t)v
2
− iζv
1
,
∂v
2
(t,ζ)
∂t
= − ¯q(t)v
1
+ iζv
2
,
(2)
In Eq. (2) the input pulse shape q(t) (we drop the de-
pendence on z) acts as an effective potential and the
overbar here and below means the complex conjugate.
The spectral parameter ζ entering Eq. (2) is a gen-
erally complex quantity, ζ = ξ + iρ, playing the role
of the nonlinear analogue of conventional frequency.
The “potential” q(t) decays as t → ±∞. To define the
NF spectral data, one fixes two linearly-independent
left Jost solutions of Eq. (2), φ(t,ζ) = [φ
1
,φ
2
]
T
with
the initial condition at the left infinity, and two right
Jost functions, ψ(t, ζ) = [φ
1
,φ
2
]
T
, fixed by the condi-
tion at the right infinity:
φ(ζ,t) ∼

1
0

e
−iζt
, t → −∞, (3a)
ψ(ζ,t) ∼

0
1

e
iζt
, t → ∞. (3b)
The right and left Jost functions are linearly depen-
dent and relate through the Jost scattering coefficients
a(ζ) and b(ζ); these two complex quantities consti-
tute the essecne of the NFT signal decomposition. In
the explicitly form, these scattering coefficients for
the real spectral parameter ζ = ξ can be obtained as
a(ζ) = lim
t→∞
φ
1
(t,ζ)e
iζt
, b(ζ) = lim
t→∞
φ
2
(t,ζ)e
−iζt
.
(4)
This definition is typically used in the numerical com-
putation of the NFT spectrum (Vasylchenkova et al.,
2019). For the right reflection coefficient, r(ξ), which
gives us the continuous part of the NF spectrum, we
have the following expression:
r(ζ) = b(ζ)/a(ζ). (5)
The unperturbed z-evolution of the Jost coefficients
a(ζ), b(ζ), and right reflection coefficient is given by
∂a
∂z
= 0,
∂b
∂z
= 2i ζ
2
b(ζ), (6a)
∂r
∂z
= 2i ζ
2
r(ζ). (6b)
In addition, the NF decomposition of a given potential
can include discrete spectrum component: the com-
plex eigenvalues and the associated complex ampli-
tudes. The former are defined as the zeros of the
first Jost coefficient a(ζ
k
) = 0, ℑ[ζ
k
] > 0, while the
latter are the residues of the right coefficient r(ξ) at
the given eigenvalue (Vasylchenkova et al., 2019):
C
k
= b(ζ
k
)/a
0
(ζ
k
). Their unperturbed dynamics are
also trivial and follows from Eqs. (6):
∂ζ
k
∂z
= 0, (7a)
∂C
k
∂z
= 2i ζ
2
k
C
k
.. (7b)
In the presence of the deviation from the noise-
less NLSE, the dynamics of NF spectrum quantities,
Eqs. (6), (7), changes. Applying the perturbation the-
ory to the to the evolution of nonlinear spectral data
(Derevyanko et al., 2016; Kaup, 1976; Kaup and
Newell, 1978), the perturbed z-evolution of the re-
flection coefficient change in the leading order with
respect to the perturbation is given by the following
equations (cf. Eqs. (6)-(7)):
∂r
∂z
− 2iξ
2
r = −
1
a
2
I[φ, φ], (8a)
∂ζ
k
∂z
= −C
k
I[ψ, ψ]



ζ
k
(8b)
where I[u, v] is the projection of the noisy perturbation
η(t,z) on the corresponding unperturbed squared Jost
functions:
I[u, v; ζ] =
∞
Z
−∞
dt

η(t,z) u
2
(ζ,t, z)v
2
(ζ,t, z)
+
¯
η(t,z) u
1
(ζ,t, z)v
1
(ζ,t, z)

. (9)
These equations describe the effective coupling be-
tween the NF modes arising due to the deviations
from the pure NLSE, see also (Kazakopoulos and
Moustakas, 2016)
Within the NFT-based transmission concept, we
can use both continuous and discrete spectra as data
carriers (Le et al., 2017). In this work we we gen-
erate a pulse in a frequency domain, then apply the
INFT to find the respective wave-shape in the time do-
main. After that we add the solitonic nonlinear spec-
tral component corresponding to the eigenvalue ζ
sol
Noise-induced Signal Corruption in Nonlinear Fourier-based Optical Transmission System in the Presence of Discrete Eigenvalues
259

using the Darboux transform (Aref et al., 2018). The
overall signal modulation and wave-from generation
method is identical to that from (Le et al., 2017). Af-
ter the modulation and synthesis stage the signal is
launched into the optical fibre. At the receiver, lo-
cated at the distance z = L, one performs the forward
NFT operation to recover the spectral profile r (ξ, L),
and removes the accumulated phase rotation:
r(ξ, L) = e
4iξ
2
L
(ξ − ζ
sol
)
(ξ −
¯
ζ
sol
)
r(ξ, z = 0). (10)
For the detailed scheme of the nonlinear inverse syn-
thesis NFT transmission method see (Derevyanko
et al., 2016) and for the details of the Darboux trans-
form computation see (Aref, 2016; Aref et al., 2018).
The general flowchart referring to the NFT-based
transmission is given in Fig. 1.
The presence of ASE in the optical fibre translates
into the effective noise inside the NF domain which
can be presented as an effective additive terms N(·) in
the compensated NF spectrum:
e
−4iξ
2
L
r(ξ, L) = r(ξ,0) + N(ξ,r(ξ,0)),
ζ
sol
(L) = ζ
sol
(z = 0) + N
sol
(ζ
sol
,r(ξ,0)).
(11)
This effective noise terms in the NF do-
main, N(ξ,r(ξ,0)) and N
sol
(ζ
sol
,r(ξ,0)), are input-
dependent. The nosie N describing the action on
the discrete spectrum is not circularly polarised even
in the absence of the solitary eigenvalues. The
latter means that when identifying this noise we
need to consider not only the covariance func-
tion E[N(ξ)
¯
N(ξ
0
)], but also the pseudocovariance
E[N(ξ)N(ξ
0
)]. In (Derevyanko et al., 2016) the an-
alytical expressions for both covariance and pseudo-
covariance of the NF domain noise were obtained, un-
der assumption of ideal distributed amplification, high
signal-to-noise ratio and sufficiently long distances.
The resulting expressions have the form:
E[N(ξ)N
∗
(ξ
0
)] = 2DLπ δ(ξ − ξ
0
)E
1
(ξ), (12)
E[N(ξ)N(ξ
0
)] = 2DLπ δ(ξ − ξ
0
)E
2
(ξ), (13)
where each E
i
(ξ) also depends on the effective power
inside the NF domain since the noise is input-
dependent. The explicit expressions for E
1
and E
2
in the absence od the discrete spectrum were approxi-
mately derived in the Gaussian approximation as fol-
lows (Derevyanko et al., 2016):
E
1
(ξ) = 1 + |r(ξ,0)|
2
+ |r(ξ, 0)|
4
, (14)
E
2
(ξ) = r(ξ,0)
2
. (15)
Note that a more accurate theory for the discrete
NF spectra perturbations resulted in the non-Gaussian
statistics (Derevyanko et al., 2003; Shevchenko et al.,
2015), so expressions (14), (15) are approximate and
refer to the leading order properties. In addition to
these two characteristics of the continuous NF spectra
considered in the absence of discrete eigenvalues in
our previous studies (Pankratova et al., 2018; Pankra-
tova et al., 2018), in this work we also address the fol-
lowing quantity referring to the correlations between
the continuous and discrete NF spectra parts:
E[N(ξ)N
sol
] = 2DL E
sol
(ξ,ζ
sol
). (16)
The linear limits of the covariance and pseudocovari-
ance, Eqs. (14), (15), correspond to the correlators of
the linear system defined in the conventional Fourier
domain with the appropriate replacement of the fre-
quency variable ξ, because in this limit the NFT con-
verges to the conventional Fourier transform. The
latter occurs when one deals with the small effective
power corresponding to the profile r(ξ), i.e. when the
magnitude of the carriers’ coefficients c
k
in Eq. (17)
tends to zero. Note also that, generally, the pseudo-
density E
2
(ξ) is a complex-valued function.
In this work we use the sinc-based spectral wave-
form of subcarriers defined on the continuous nonlin-
ear spectrum part, corresponding to the NFT imple-
mentation of OFDM modulation (Le et al., 2014; Le
et al., 2015; Kazakopoulos and Moustakas, 2016; Le
et al., 2017; Aref et al., 2018). The nonlinear spec-
trum has the following form:
r(ξ, z = 0) =
N
ch
/2
∑
k=−N
ch
/2
c
k
sinc(2ξ − k), (17)
where c
k
are the information-bearing complex coeffi-
cients that are randomly taken from a QPSK modu-
lation constellation; N
ch
is the number of subcarriers,
and sinc(x) = sin(πx)/(πx).
In the current study, we numerically examine the
properties of effective nonlinear noise arising inside
the NF domain due to the progenitor ASE η, Eq. (1),
affecting the signal evolution in the space-time do-
main. We note that the noise properties inside the
NF domain have attracted a considerable attention
recently due to the studies referring to the capac-
ity estimates for the NFT-based optical transmission
methods (Derevyanko et al., 2016; Shevchenko et al.,
2015; Shevchenko et al., 2018; Tavakkolnia and Sa-
fari, 2017; Tavakkolnia et al., 2018), and also in view
of the serious noise effect on the NFT-based transmis-
sion properties (Civelli et al., 2017).
Recently, we showed in (Pankratova et al., 2018;
Pankratova et al., 2018) that the correlation properties
of NFT noise depend on the signal power and prop-
agation distance in a non-trivial way, deviating from
the simplified theory presented in (Derevyanko et al.,
OPTICS 2019 - 10th International Conference on Optical Communication Systems
260

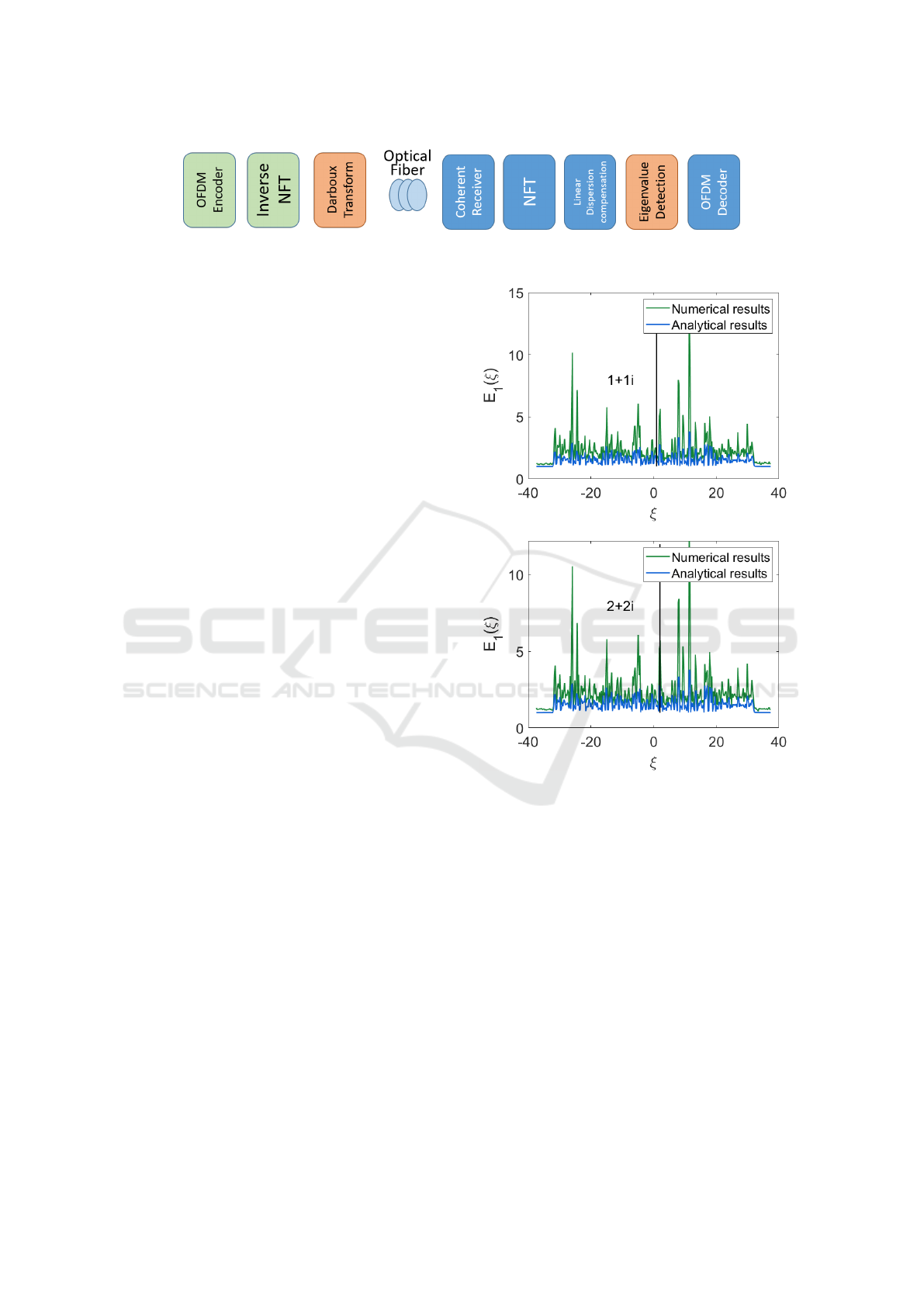
Figure 1: Basic elements of the communication system based on the nonlinear inverse synthesis with both continuous and
discrete spectra present.
2016). In this paper we intend to consider the im-
pact of discrete spectra on the correlation properties
of the effective noise inside the NF domain and com-
pare those with the case where the discrete eigenval-
ues are absent.
2 SIMULATIONS AND RESULTS
We consider the transmission of the optical signal
down the single-mode fibre with standard parame-
ters (Derevyanko et al., 2016; Aref et al., 2018)
for the range of fiber lengths (up to 1500 km) and
N
ch
=128 subcarriers. To investigate the properties
of the effective noise inside the NF domain, we use
the parameter S = |c
k
|
2
as a measure effective sig-
nal power. In the QPSK modulation scheme involv-
ing only the phases of coefficients all symbols have
the same power for the same absolute value of c
k
.
In Figs. 2 and 3, we present the results for the ab-
solute values of the nonlinear power spectral density
|E
1
(ξ)| (12) and an absolute value of the pseudoden-
sity |E
2
(ξ)| (16), both versus the nonlinear frequency
ξ, extracted from the numerical simulations for a par-
ticular realisation of randomly-modulated coefficients
c
k
from (17), compared with the analytical expres-
sions, Eqs. (11)-(16). In both figures the panes (a)-(d)
represent the spectral density and pseudodencsity in
the presence of a specific eigenvalue chosen from the
set λ
1−4
=[1 + i, 2 + i, 1 + 2i, 2 + 2i].
Then we perform a comparison of the numeri-
cally obtained covariance density E
1
(ξ), Fig. 2, and
pseudo-density E
2
(ξ), Fig. 3, with the analytical ex-
pressions using the propagation distance 500 km. The
black vertical line is marking the position of eigen-
value. We confirm that, as it was pointed out in
(Pankratova et al., 2018; Pankratova et al., 2018), the
theory tends to underestimate the true density of the
NFT noise intensity. In the case considered here, i.e.
when we have non-zero discrete spectrum, this obser-
vation can be explained by the fact that the analyti-
cal expression was derived for the continuous spectra
only and in the assumption of large propagation dis-
tances and high SNR. In addition, it was shown in our
previous works that covariance and pseudocavariance
depend on the propagation distance, the fact which is
Figure 2: Power spectral density |E
1
(ξ)|, Eq. (12) on the
nonlinear frequency ξ, for a range of eigenvalue values from
top to bottom λ
1,4
and for L = 500 km. The effective power
in the continuous NF spectrum is S = 0.405.
not actually taken into account in the theory. Also,
the numerical error emerging in the computation of
NFT at the transmitter and receiver can result in the
additional effective numerical noise.
In Fig. 4 we present the measure of the correla-
tion between the continuous and discrete NF spectra,
Eq. (16). It can be seen from the graph that there
is a maximum related to the real part of the respec-
tive eigenvalue (marked by a straight vertical line) on
each dependence. However, we also noticed the ap-
pearance of some additional maxima at other values
of spectral parameter ξ that require further studies.
In Fig. 5 we present the deviation of our nu-
merical results from ones obtained analytically in
Noise-induced Signal Corruption in Nonlinear Fourier-based Optical Transmission System in the Presence of Discrete Eigenvalues
261

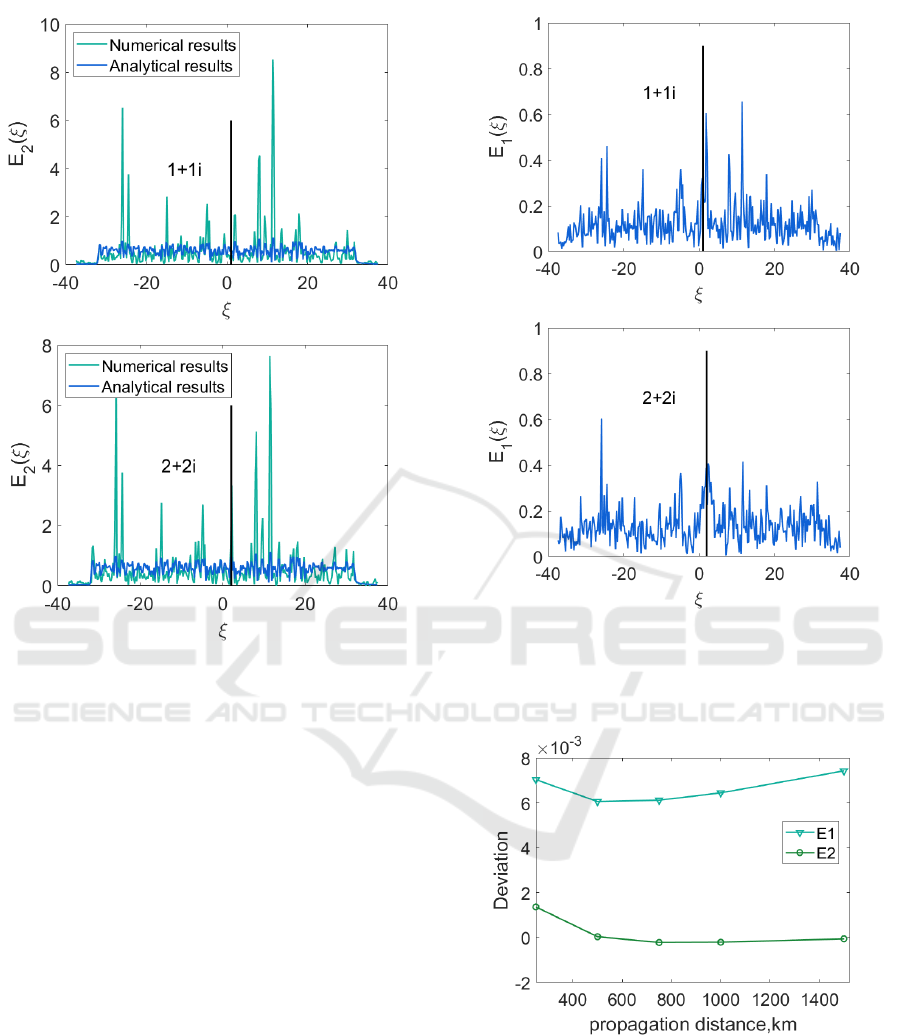
Figure 3: Power spectral pseudodensity |E
2
(ξ)|, Eq. (16) on
the nonlinear frequency ξ, for a range of eigenvalue values
from top to bottom λ
1,4
and for L = 500 km. The effective
power in the continuous NF spectrum is S = 0.405.
(Derevyanko et al., 2016) as a function of distance
for one value of signal power defined inside the NF
domain, S = 0.45. We present the relative deviation
between our numerical calculation and analytical re-
sults in dependence on the propagation distance:
deviation =
Z
|E
numerical
1,2
(ξ) − E
analytical
1,2
(ξ)|dξ.
It can be seen from that figure that the deviation is
increasing with distance, since the theory is not tak-
ing into account the noise dependence on propagation
distance. Also, additional simulations confirmed the
observation from our previous works that the devia-
tion is increasing with the growth of signal power.
3 CONCLUSIONS
In this work, the properties of the effective noise
emerging in the NFT domain due to presence of pro-
genitor ASE noise in the optical domain were investi-
gated. In our study we took into account the presence
Figure 4: Correlation of continuous and discrete spectra
dependence on the nonlinear frequency ξ, for a range of
eigenvalue values from top to bottom λ
1,4
and for L = 500
km. The effective power in the continuous NF spectrum is
S = 0.405.
Figure 5: Deviation of our numerical results for covariance
E
1
(ξ) and pseudocovariance E
2
(ξ) from theory proposed
in (Derevyanko et al., 2016) as a function of propagation
distance for S = 0.405.
of both continuous and discrete NF spectra parts. It
is shown that the presence of eigenvalue affect con-
tinuous spectra in a non-trivial way: in addition to the
peak referring to the real part of the eigenvalue we
observed the appearance of some additional peaks at
OPTICS 2019 - 10th International Conference on Optical Communication Systems
262

other values of parameter ξ. Our results have indi-
cated that the channel defined inside the NF domain
is a complicated nonlinear channel with the mem-
ory depending on the propagation distance, power,
and on the presence of eigenvalues. Our findings can
be used further to optimise the performance of NFT-
based transmission systems with modulation of con-
tinuous and discrete spectra.
ACKNOWLEDGEMENTS
MLP: This project was supported by the Horizon
2020 programme under the MSCA-IF-EF-ST No
751561. JEP acknowledges the support of Lev-
erhulme Project RPG-2018-063. JEP is thank-
ful to Erasmus+ mobility programme. The au-
thors acknowledge helpful comments of Dr S. A.
Derevyanko.
REFERENCES
Agrawal, G. P. (2012). Fiber-optic communication systems,
volume 222. John Wiley & Sons.
Aref, V. (2016). Control and detection of discrete spectral
amplitudes in nonlinear fourier transform. Arxiv.org.
Aref, V., Le, S., and Buelow, H. (2018). Modulation over
nonlinear fourier spectrum: Continuous and discrete
spectrum. Journal Lightwave Technologies, 36:1289.
Civelli, S., Forestieri, E., and Secondini, M. (2017). Why
noise and dispersion may seriously hamper nonlin-
ear frequency-division multiplexing. IEEE Photonics
Technology Letters, 29(16):1332–1335.
Derevyanko, S. A., Prilepsky, J. E., and Turitsyn, S. K.
(2016). Capacity estimates for optical transmission
based on the nonlinear fourier transform. Nature Com-
mun, 7(12710):307.
Derevyanko, S. A., Turitsyn, S., and Yakushev, D. (2003).
Non-gaussian statistics of an optical soliton in the
presence of amplified spontaneous emission. Optics
letters, 28(21):2097–2099.
Essiambre, R.-J., Kramer, G., Winzer, P. J., Foschini, G. J.,
and Goebel, B. (2010). Capacity limits of optical
fiber networks. Journal of Lightwave Technology,
28(4):662–701.
Garcia-Gomez, F. J. and Aref, V. (2019). Statistics of the
nonlinear discrete spectrum of a noisy pulse. arXiv
preprint arXiv:1901.11419.
Kamalian, M., Prilepsky, J. E., Le, S. T., and Turitsyn, S. K.
(2017). On the design of nft-based communication
systems with lumped amplification. Journal of Light-
wave Technology, 35(24):5464–5472.
Kaup, D. (1976). A perturbation expansion for the
zakharov–shabat inverse scattering transform. SIAM
Journal on Applied Mathematics, 31(1):121–133.
Kaup, D. J. and Newell, A. C. (1978). Solitons as particles,
oscillators, and in slowly changing media: a singular
perturbation theory. Proceedings of the Royal Society
of London. A. Mathematical and Physical Sciences,
361(1707):413–446.
Kazakopoulos, P. and Moustakas, A. L. (2016). On the soli-
ton spectral efficiency in non-linear optical fibers. In
2016 IEEE International Symposium on Information
Theory (ISIT), pages 610–614. IEEE.
Le, S., Aref, V., and Buelow, H. (2017). Nonlinear signal
multiplexing for communication beyond the kerr non-
linearity limit. Nature Photonics, 11:570.
Le, S. T., Prilepsky, J. E., and Turitsyn, S. K. (2014).
Nonlinear inverse synthesis for high spectral effi-
ciency transmission in optical fibers. Optics Express,
22:26270.
Le, S. T., Prilepsky, J. E., and Turitsyn, S. K. (2015).
Nonlinear inverse synthesis technique for optical
links with lumped amplification. Optics express,
23(7):8317–8328.
Pankratova, M., Vasylchenkova, A., Prilepsky, J. E., and
Derevyanko, S. A. (2018). Properties of the effective
noise in the nonlinear fourier transform-based trans-
mission. In Frontiers in Optics, pages JW3A–83. Op-
tical Society of America.
Pankratova, M. L., Vasylchenkova, A., Prilepsky, J., and
Derevyanko, S. A. (2018). Study of noise-induced
signal corruption for nonlinear fourier-based optical
transmission. In 2018 IEEE British and Irish Confer-
ence on Optics and Photonics (BICOP), pages 1–3.
Shevchenko, N. A., Derevyanko, S. A., Prilepsky, J. E.,
Alvarado, A., Bayvel, P., and Turitsyn, S. K. (2018).
Capacity lower bounds of the noncentral chi-channel
with applications to soliton amplitude modulation.
IEEE Transactions on Communications, 66(7):2978–
2993.
Shevchenko, N. A., Prilepsky, J. E., Derevyanko, S. A., Al-
varado, A., Bayvel, P., and Turitsyn, S. K. (2015). A
lower bound on the per soliton capacity of the nonlin-
ear optical fibre channel. In 2015 IEEE Information
Theory Workshop-Fall (ITW), pages 104–108. IEEE.
Tavakkolnia, I., Alvarado, A., and Safari, M. (2018). Ca-
pacity estimates of single soliton communication. In
2018 European Conference on Optical Communica-
tion (ECOC), pages 1–3. IEEE.
Tavakkolnia, I. and Safari, M. (2017). Capacity analysis
of signaling on the continuous spectrum of nonlin-
ear optical fibers. Journal of Lightwave Technology,
35(11):2086–2097.
Turitsyn, S. K., Prilepsky, J. E., Le, S. T., Wahls, S., Frumin,
L. L., Kamalian, M., and Derevyanko, S. A. (2017).
Nonlinear fourier transform for optical data process-
ing and transmission: advances and perspectives. Op-
tica, 4:307.
Vasylchenkova, A., Prilepsky, J., Shepelsky, D., and Chat-
topadhyay, A. (2019). Direct nonlinear fourier trans-
form algorithms for the computation of solitonic spec-
tra in focusing nonlinear schr
¨
odinger equation. Com-
munications in Nonlinear Science and Numerical Sim-
ulation, 68:347–371.
Noise-induced Signal Corruption in Nonlinear Fourier-based Optical Transmission System in the Presence of Discrete Eigenvalues
263

Yousefi, M. and Kschischang, F. (2014). Information trans-
mission using the nonlinear fourier transform, part i–
iii. IEEE Trans. Inf. Theory, 60:4312.
Zakharov, V. E. and Shabat, A. B. (1972). Exact theory
of 2-dimensional self-focusing and one-dimensional
self-modulation of waves in nonlinear media. Soviet
Physics-JETP, 34:62.
OPTICS 2019 - 10th International Conference on Optical Communication Systems
264