Formalizing the Safety Functions to Assure the Software Quality
of NPP Safety Important Systems
Elena Ph. Jharko
a
V.A. Trapeznikov Institute of Control Sciences of Russian Academy of Science, 65 Profsoyuznaya, Moscow 117997, Russia
Keywords: Nuclear Power Plant, Quality Assurance, Safety Functions, Software, Validation, Verification.
Abstract: One of the most critical tasks in the software complexes quality assurance is the procedure of forming
requirements to a developed or modified system and subsequent their verification. The essential errors are
making in the first life cycle stages – these are errors in determining requirements, selecting the architecture,
high-level design. Faults of safety critically important software may considerably damage the equipment or
properties, as well to lead to an essential detriment of the environment and human victims. Increasing
requirements to the software quality of NPP (nuclear power plant) safety important systems at all stages of
the life cycle is concerned with increasing the software complexity and functionality and has led the necessity
of developing approaches to justify both the system itself safety and software involved in the systems make-
up. In the paper, an approach is considered, based on the “safety functions”, meeting which in the sequel is
verifying. This approach is used under the soft- and hardware complexes software assurance of upper level
systems of automated process control systems and may be applied for the fault tolerance analysis, information-
and cyber- security of soft- and hardware complexes.
1 INTRODUCTION
Information technologies lay a crucial role in
installation, operation, and engineering maintenance
of critically important infrastructures that have high
requirements for the reliability and safety. Bugs
(faults) or emergencies in systems of high operation
risk plants, relating to critically important
infrastructures, may:
 Lead to destroying or severe damages of highly
expensive equipment;
 Considerably harm the environment;
 Lead to threats for the health and life of people.
Developing the automation of critical
infrastructure plants with high operation risk,
involving ones in the nuclear power engineering, is
characterized by the tendency of developing
automated process control systems (APCS)
implementing considerably more complicated
algorithms of control and data analysis with applying
compound soft- and hardware complexes (SHWC)
(Barmakov, 2006; Byvaikov et al., 2006; Kogan et al.,
2014; Mengazetdinov et al., 2014; Poletykin et al.,
a
https://orcid.org/0000-0002-8895-4786
2017). Developing SHWC, their verification, and
validation, and, in the course of the time,
modernization is to correspond and meet an adopted
safety level.
As requirements to critical infrastructure plants
increase, the software complexity and software
importance in providing whole system functions are
sharply enlarging. Software (SW) plays the
increasingly important role in revealing and
monitoring critical factors, as well as in safety critical
functions (Hill and Tilley, 2010; Rankin and Jiang,
2011; Eoma et al., 2013; Cheng et al., 2014; Maeran
et al., 2018). Broad expansion of soft- and hardware
systems for high operation risk plants has led to the
necessity of developing methods to justify such
systems safety.
Under justifying the safety, in existing approaches
(Leveson et al., 1991; Bozzano et al., 2003; Jharko,
2003; Akerlund at al., 2006) applying quality and
safety models plays the central role. At the same time,
the system approach to determining these models is
as usual a rarity. Providing the APCS software quality
at all stages of its life cycle is based on the qualitative
and quantitative analysis that, by the regulatory
Jharko, E.
Formalizing the Safety Functions to Assure the Software Quality of NPP Safety Important Systems.
DOI: 10.5220/0007922506370644
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 637-644
ISBN: 978-989-758-380-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
637

documentation, is to be implemented at all stages.
The qualitative and quantitative software quality
analysis is to account two constituent parts of soft-
and hardware complexes: hardware and software
(Smith et al., 2000).
SHWC SW is an integral system component
influencing safety as a whole, but meanwhile, there
are absent universal and commonly adopted methods
of proving the SW safety. Due to this, an approach is
spread being a sophisticated application of methods
and tools of increasing the system safety level at all
system life cycle stages, meanwhile developing new
verification techniques is a vital problem.
Selecting and determining safety functions relate
to the validation stage implementing the
formalization utility of the safety proof problem and
directly influence the quality of the subsequent
SHWC verification.
2 SOFTWARE QUALITY AND
FEATURES OF DETERMINING
SAFETY FUNCTIONS
The software provides a considerable impact in
functions implemented by systems important for
safety. The software can support additional functions
introduced by the design of a developed or already
performed system. For NPP (nuclear power plant)
safety important systems the software safety life cycle
is intimately concerned with the safety life cycle of
the system itself. Specifying requirements to software
is a part of specifying requirements to the system.
Required software quality is hard to achieve, since
obtaining the required SW quality is concerned with
the process the development, methods and the process
control. The SW quality is achieving due to applying
the development methodology and applying
verification and validation methods within the SW
development life cycle of NPP safety important
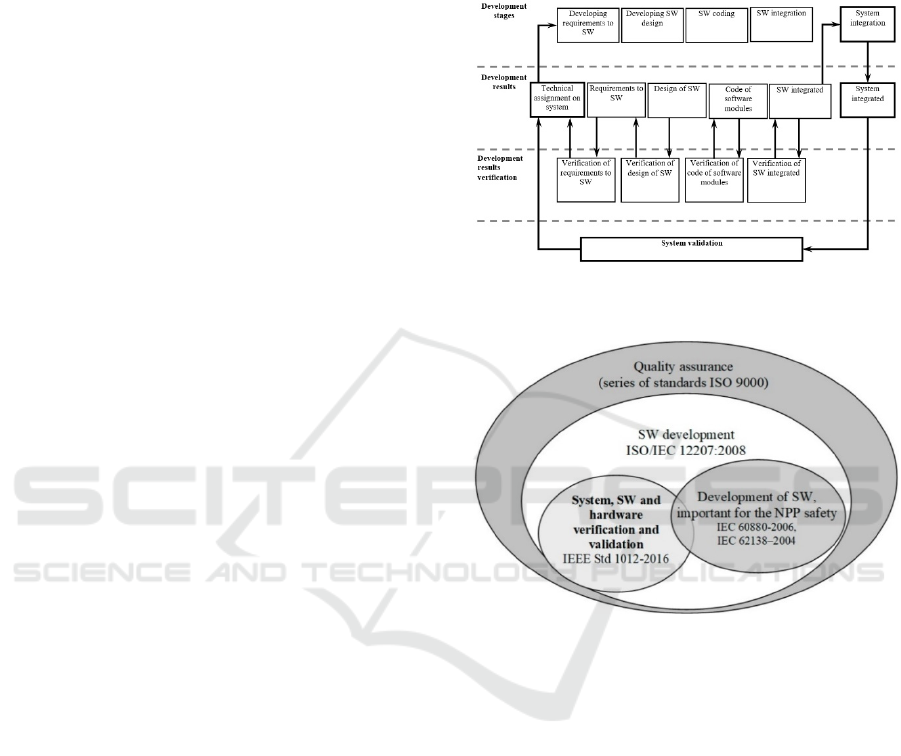
systems. The SW life cycle structure, involving
verification and validation, is displayed in Fig. 1. Fig.
2 displays the place of the software verification and
validation in the context of quality assurance and the
standards hierarchy in the branch of software
development for NPP safety important systems. The
method of complex software verification developed
(Jharko, 2014, 2015, 2018) is based on accounting the
safety standards requirements, integrates SW
verification stages and their attributes, including
personnel involved, procedures, removing
drawbacks, and issued documentation. This method
includes a set of actions on the verification object
analysis, verification planning, as well as stage-by-
software verification method efficiency has been
confirming in the course of works on developing
information and control systems important for the
NPP safety.
Figure 1: Structure of processes of verification and
validation of software.
Figure 2: The place of the software verification and
validation in the quality assurance.
In accordance to standards, the NPP safety
important systems verification is to be implemented
independently of developers. During the safety
analysis, an independent verification and validation
group is to determine the proven system properties
and check it against the correctness, consistency, and
traceability. In this process, the first stage is
determining the safety functions, implementing
which is verifying in a sequel.
Determining and selecting the safety functions
have some particularities. First of all, independent
determining the safety functions is using for
subsequent analysis of the correctness of proving
documents submitted by developers. The SW source
code and SHWC system solutions are support
information, and their analysis can form the
behaviour function contradicting to the
specifications. During the SW safety analysis, it may
occur that the function adopted is not necessary or
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
638

sufficient, when the given safety function is too strict
or the safety proof is impossible, or, in contrast, is too
weak, due to which a finding probability of SW faults
decreases. A way to increase the SW quality within
the applied complex approach is the correctness proof
relating to the formal methods (Pang et al., 2015;
Souri et al., 2018).
3 GENERAL REQUIREMENTS
TO FORMALIZING THE
SAFETY FUNCTION
From the correctness proof, all considered notions
(properties, functions, etc.) are to be formalized,
since, otherwise, to prove somewhat by the use of any
formal methods will be impossible.
The experience of NPP safety important systems
verification has revealed a number of situations, when
assigning the safety function in a formalized form for
some properties does not look possible.
In this case, the solution is a formalized
description of properties of the considered notion as a
task of proving the correctness and determining the
safety function, and in a sequel, an expert conclusion
is done whether the certified property is safe or not.
For this, at the beginning by use of the correctness
proof formalized system properties are determined,
and in a sequel, on their basis, an inference is made
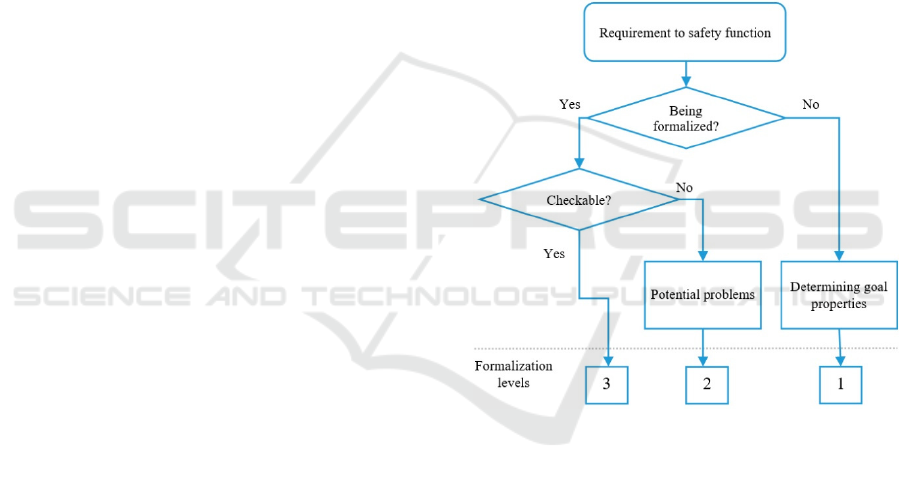
on the system safety. Let us use three formalization
levels:
1) Not-formalized,
2) Formalized,
3) Checkable.
Determining the formalization level is possible to
be represented following the algorithm displayed in
Fig. 3.
The first level is a verbal formulation. Its
drawback is that the necessary in sequel transfer to
the formal level is ambiguous, what may lead to
safety problems and difficulties under the proof. So,
the transfer to the second level is necessary and as
early as possible.
The non-formalized level is initial under the
formulation, is comfortable in communication, does
not require considerable costs, and is abstract.
Besides that, it is widely using in regulatory
documents. However, in the event of consideration of
a specific system and proving its correctness, the
formalization is needed those remove ambiguities,
improve understanding, and can place in an abstract
system for subsequent correctness proof. The
formalized level possesses a property that it can be
written in the form of characters of a formal system.
However, not always a formalized variant may be
checkable (fully or partially), i.e., correspond to the
third formalization level. This level assumes that the
property is to be falsified within available sources for
the proof. An absence of a possibility of checking
may be conditioned by the system or formulation
complexity, limitedness of safety proof sources, or
other factors. The proof correctness may work with
the second formalization level, but an absence of the
check possibility or its limitedness indicate about
potential problems since possibly it will be difficult
to use other verification ways, such as testing,
simulation tests, etc. The necessity itself of
transferring to the third level is coordinating with the
experience of creating reliable and safe systems.
Figure 3: Determining the safety requirement formalization
level.
Any proof is always based on a set of affirmations
(axioms) that are wittingly valid. In sequel, based on
the axioms and by use of rules (logics), a proof is
implemented (a theorem is proven), and an inference
is done with regard to the fact of meeting the system
purpose properties that may be observe, not observed,
or the theorem may be too hard to be proven. A
general scheme of the process described is displayed
in Fig 4. As axioms, such affirmations are chosen that
are maximally invariable and stable. Such
affirmations are to meet a considered abstraction
level. For instance, under proving the SW correctness
in the assembler language, as the axioms affirmations
may be chosen on the basis of the commands
specification and processor statuses. Meanwhile, for
Formalizing the Safety Functions to Assure the Software Quality of NPP Safety Important Systems
639

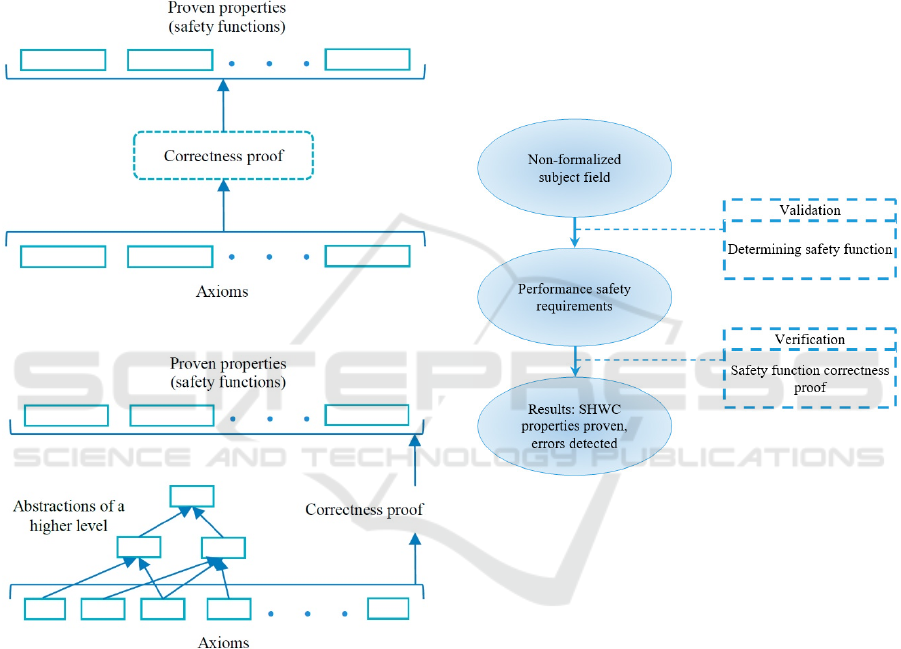
systems possessing a larger complexity, one proposes
to implement the correctness proof on the basis of
determining system properties and forming
abstractions of a higher level (see Fig. 5).
Abstractions of the higher level may involve software
modules, functions, objects, statuses subsets, etc.
Their choice is defined on the basis of the verification
simplification, in other words, a newly formed
abstraction is to be simpler than the entity that it
encapsulates.
Figure 4: A general scheme of proving the correctness.
Figure 5: Correctness proof on the system decomposition
abstractions basis.
A strict axioms formulation is considered as a
powerful tool in the fight against software errors at
stages of the life-cycle.
4 CONDITIONS OF
DETERMINING THE SAFETY
FUNCTION
Formal methods as a correctness proof may be
applied both for ready SW and at early stages of
developing all SHWC, but in any case, one of the first
verification steps is determining the safety function
subject to correctness checking.
The safety function is a formalized condition with
respect to the verified system, implementing which
enables one to make an inference on the performance
safety. For a one SHWC the safety function may be
determined in different manners, and, and selecting a
proven condition may be implemented at different
system life cycle stages. Say, for instance, a safety
function may be determined on the basis of the system
functionality (determining the safety function on the
basis of safety assurance strategy for the entire
system, safety requirements to a considered soft- and
hardware complex and interaction interfaces).
Figure 6: Safety analysis stages.
SW developing and operation say that the later a
fault is detected, the more complicated both its
revealing and removing are, and the more problems it
may provide. Meanwhile, removing errors done
under formulating requirements to a system costs in
dozens time more expensive than errors done under
the implementation (Jharko, 2018). Determining the
safety function, which is related to the solved problem
formalization, is a specification concerning the
correctness proof and possesses the same properties
as the requirements statement under SW
development. Potential errors done under
determining this function negatively influence the
verification quality and may lead to correctness proof
results distortion and, as a consequence, its full
reconsideration. Fig. 6 displays the sequence of the
safety analysis stages with determining the safety
function.
Conditions to determine the safety function are
setting at the validation stage by applied components
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
640

characteristics, safety assurance strategies, and the
experience available. This process is independent of
the subsequent verification; it determines properties
subject to checking and forms initial data, by which
the safety function is setting used in the correctness
proof. If errors make at the validation stage or
behaviour particularities influencing the safety are
not taking into account, then this directly influence
the subsequent verification quality and,
correspondingly, the SW and SHWC quality.
Moreover, no adequate and diverse methods and tools
of the correctness proof can solve problems appeared
during the design, since they work with the same
specification, and the final user only can indicate an
error done under forming the requirements.
Figure 7: Selecting a proven safety function; Domain A –
due to some reasons the system has not implemented the
condition of the proven safety function, but this did not lead
to a dangerous fault; Domain B – The system behaviour
meets the safety function condition.
The world experience of the NPP safety important
systems operation is evidence that faults and
emergencies are the cases due no numerous factors,
meanwhile a considerable part of accidents, due to
(involving) errors done under forming system
requirements.
Under system design, implicit admittances may be
accepted, which directly are not concerned with the
performance safety, but may influence the SHWC
performance as a whole. System performance safety
conditions may be different in a different
environment or performance conditions. Thus of the
validation problems is determining conditions subject
to checking, and particularities of this process are that
after the formalization there is no a univocal criterion
and confidence that the proven function approved is
necessary and sufficient. During subsequent
development and safety analysis one may reveal that
the scopes set are too strict and the correctness proof
is impossible to implement, or, in contrast, are very
weak, due to what the SW errors finding probability
decreases.
NPP safety important systems, as well as other
critically important plants with high operation risk
(Sakrutina, 2017), possesses a complexity that
complicates a formalization of acceptable and safe
behaviour. Due to this, errors may make with a large
probability. To solve the problem, one may determine
such a safety function; in whish, these drawbacks are
absent. Besides that, under the development and
correctness proof, there is no necessity of a strict
selection do the safety function; this may be any
function meeting the conditions in Fig. 7. Thus, the
proven safety function is always to be as strict, or
stricter, than acceptable safe behaviour. Developed
system behaviour is to meet the condition of the
proven safety function.
The NPP safety important systems verification
experience gathered is evidence that determining the
proven safety function of developed and existing
SHWC is to be implemented by:
 The used strategy of the safety assurance,
which the system is to keep within all life cycle;
 Safety requirements to all system;
 Safety requirements to the considered SHWC.
Thus, the verification result is a proof that
properties of the considered software meet the safety
requirements to it and its environment, as well as are
coordinating with the used safety assurance strategy.
Determining the proven safety function may be
implemented on the technical assignment basis on
developed SHWC only, but in this case, it may be a
complex and hairy process. Due to this, a transfer to
proving a more strict safety function is possible,
rather than that was determined due to the safety
requirements and accounting the criteria
completeness of dangerous faults.
Consideration of system requirements to the
safety assurance strategy, safe internal behaviour and
coordination of interaction with external components
enables on faster and more effective to partition the
proven goal safety function on the verification
complexity and improve its quality. The safety
function formulation is not a final solution, and under
a necessity, the safety function may be changed on
any other meeting the conditions displayed in Fig. 7.
The verification experience shows that the transfer to
another safety function should be implemented when
in the new consideration angle the system behaviour
becomes:
Formalizing the Safety Functions to Assure the Software Quality of NPP Safety Important Systems
641

 More deterministic – one may say more
precisely how the system behaves in those or
others situations;
 Less complicated – there are decrease the safe
analysis expenses’ and time required for
understanding processes available in the
system.
5 APPROACHES TO
DETERMINING SAFETY
FUNCTIONS
Fundamental ways of changing the safety function are
its expansion (weakening, weaker definition).
Besides that, the safety function may be changed as a
not severe weakening or enforcing, but in any case, it
is to be within the acceptable safe behaviour (see fig.
7).
Figure 8: Enforcing and weakening the safety functions.
Let us consider three behaviour functions 

, 

,
and 

, each of which depends on the argument
vector 
̅
and has the value domain true/false. Then
enforcing the function 

is the function 

, transfer
to such function 

, under which conditions (1) and
(2) are satisfied
∀














(1)
∃
















(2)
As weakening the function 

, a transfer to such a
function 

is, under which the conditions are
satisfied:
∀














(3)
∃
















(4)
Thus, weakening the function is transfer from one
function 

to other function 

such that always,
when 

, is a truth, then the 

, is truth too, but
meanwhile there exist such truth values of 

, under
which 

is false. Enforcing is the analogous inverse
transfer. Graphically relations between the functions
are displaying in Fig. 8.
Let us consider an example of the safety
functions, selecting which may influence the
correctness proof. Let us assume that there exist
SHWC SW, whose functionality is implemented in
the closed cycle, for which each subsequent
implementing is to be different of preceding, and for
this in the memory the identifier id stored. Let us
assume that the number of cycles is finite, and each
of them is numbered sequentially in time from 1 to n,
and, correspondingly, there exists the number of
identifiers 



,…,


. For the considered
case, let us present several variants of the safety
function. The first function has the form:





,∀

∈,





.
This function guarantees the distinction of the
identifier from preceding one and may be applied for
a safe update of incoming information.
The second safety function guarantees the
identifier uniqueness within all SHWC performance
time from the instant of its launching and may be used
to update information, which is implementing at not
each turn of the full cycle:





,∀



∈,,







.
The next safety function guarantees that each
subsequent identifier is more than preceding one
exactly by 1 and may be utilized to calculate the
number of full cycles between events:





,∀

∈,



1

.
The function 

is more strict than the function 

that, in turn, is more strict than 

.
Verification of a more strict function is more
complicated, than a weak one – this requires more
quantity of resources and not always is possible.
However, if a possibility is available, one
recommends to prove the correctness of the more
strict function, since this has the following positive
effects:
 Obtaining more exact representation about the
system performance – properties and behaviour
are determined more strictly;
 Decreasing the analysed performance
complexity, and due to this, increasing the
errors detection probability;
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
642

 Functions proven may be applied in a sequel
for more effective implementing other
correctness proofs of considered SHWC.
However, in the case of the safety analysis, when
it is impossible to prove the correctness in a proposed
form, or resources for implementing such a works
volume are absent, then weakening the verified
function is possible, what enables one conclude the
SW safety.
Determining the safety functions for
implementing the verification is an essential stage of
the safety analysis and its selection is a compromise
between resources available and proven properties.
The NPP safety important systems verification
6 CONCLUSIONS
For SHWC used in NPP safety important systems, a
problem of assurance of a correct (concerning the
specification), safe, and full meeting the
requirements. Justification of the safety system,
safety, and integrity of specific software is based on
the design and design documents, presented during
the system development, specification analysis
results, algorithms, and implementation. The
approach to determining the safety functions was
applied:
 Under software verification of upper-level
systems of NPP APCS, relating to safety
important systems;
 To reveal software design errors at early
development stages in order decreasing risks of
an appearance of non-regular situations in the
plant’s operation process;
 Under justifying NPP safety important systems
software at all life cycle stages,
moreover, has enabled one to increase the quality of
developed/modified software.
REFERENCES
Akerlund, O., Bieber, P., Boede, E., et al., 2006. ISAAC, a
framework for integrated safety analysis of functional,
geometrical and human aspects. In Proceedings of 3rd
European Congress on Embedded Real-Time Software.
(ERTS ’06), 25-27 January 2006. Toulouse, France.
Barmakov, Yu. N., 2006. Automation tools developed by
VNIIA within the program of development of nuclear
power engineering of Russia. In Automation in
Industry, no. 8, pp. 49-51. (in Russian)
Bozzano, M., Villafiorita, A., Kerlund, O., et al., 2003.
ESACS: An integrated methodology for design and
safety analysis of complex systems. In Proceedings of
the European Safety and Reliability Conference (ESREI
2003), pp. 237-245.
Byvaikov, M. E., Zharko, E. F., Mengazetdinov, N. E.,
Poletykin, A. G., Prangishvili, I. V., Promyslov, V. G.,
2006. Experience from design and application of the
top-level system of the process control system of
nuclear power-plant. In Automation and Remote
Control, vol. 67, no. 5, pp. 735-747.
Cheng, Y., Chao, N., Tian, Z., Zhicheng, Z., Ronghua, Z.,
2014. Quality assurance for a nuclear power plant
simulator by applying standards for safety-critical
software. In Progress in Nuclear Energy, vol. 70, pp.
128-133.
Eoma, H.-s., Park, G.-y., Jang, S.-c., Son, H. S., Kang, H.
G., 2013. V&V-based remaining fault estimation model
for safety–critical software of a nuclear power plant. In
Annals of Nuclear Energy, vol. 51, pp. 38-49.
Joshi, A., Miller, S. P., Whalen, M., Heimdahl, M. P. E.,
2005. A proposal for model-based safety analysis. In
Proceedings of the Digital Avionics Systems
Conference, DASC, vol. 2, p. 13.
Hill, J., Tilley, S., 2010. Creating safety requirements
traceability for assuring and recertifying legacy safety-
critical systems. In Proceedings of the 18th IEEE
International Requirements Engineering Conference,
pp. 297-302.
Jharko, E. Ph., 2003. Problems of management of software
quality. In Proceedings of the International Conference
“System Identification and Control Problems”
SICPRO ’03, Moscow, January 29-31, 2003. Moscow,
V.A. Trapeznikov Institute of Control Sciences, pp. 887-
923. (in Russian)
Jharko, E. Ph., 2014. Evaluation of the Quality of a Program
Code for High Operation Risk Plants. In IFAC
Proceedings Volumes, vol. 47, no. 3, pp. 8060-8065.
Jharko, E., 2015. Towards the quality evaluation of
software of control systems of nuclear power plants:
Theoretical grounds, main trends and problems. In
Proceedings of the 12th International Conference on
Informatics in Control, Automation and Robotics.
Colmar, France, July 21-23, 2015, pp. 471-478.
Jharko, E. Ph., 2018. Towards Quality Assurance under
Developing Safety Important Systems Software for
Nuclear Power Plants. In Proceedings of 2018
International Russian Automation Conference
(RusAutoCon). IEEE, pp. 1-6.
Kogan, I. R., Poletykin, A. G., Promyslov, V. G., Jharko, E.
Ph., 2014. Evolution of APCS of NPP with VVER,
problems, non-solved issues, new threats and possible
directions of the development. In Proceedings of XII
All-Russian Congress on Control Sciences, pp. 4200-
4211. (in Russian)
Leveson, N. G., Cha, S. S., Shimeall, T. J., 1991. Safety
verification of Ada programs using software fault trees.
In IEEE Software, IEEE, vol. 8, no. 4, pp. 48-591.
Maeran, R., Mayaka, J. K., Jung, J. C., 2018. Software
verification process and methodology for the
development of FPGA-based engineered safety features
system Author links open overlay panel. In Nuclear
Engineering and Design, vol. 330, pp. 325-331.
Formalizing the Safety Functions to Assure the Software Quality of NPP Safety Important Systems
643

Mengazetdinov, N. E., Poletykin, A. G., Byvaikov, M. E.,
Promyslov, V. G., Jharko, E. Ph., Smirnov, V. B.,
Akafyev, K. V., 2014. Automation of nuclear power
plants – the experience of the ICS RAS. In Proceedings
of XII All-Russian Congress on Control Sciences, pp.
4219-4236. (in Russian)
Pang, L., Wang, C.-W., Lawford, M., Wassyng, A., 2015.
Formal verification of function blocks applied to IEC
61131-3. In Science of Computer Programming, vol.
113, part 2, pp. 149-190.
Poletykin, A., Jharko, E., Mengazetdinov, N., Promyslov,
V., 2017. Some Issues of Creating the New Generation
of Upper Level Control Systems of NPP APCS. In
Proceedings of the 5th International Conference on
Control, Instrumentation, and Automation (ICCIA
2017, Shiraz, Iran), IEEE, pp. 78-83.
Poletykin, A., 2018. Cyber Security Risk Assessment
Method for SCADA of Industrial Control Systems. In
Proceedings of 2018 International Russian Automation
Conference (RusAutoCon). IEEE, 2018, pp. 1-5.
Promyslov, V. G., 2015. Tool for I&C system Security
Policy Verification. In Proceedings of the 9th
International Conference on Application of Information
and Communication Technologies (AICT 2015, Rostov
on Don), IEEE, pp. 221-224.
Rankin, D. J., Jiang, J., 2011. A Hardware-in-the-Loop
Simulation Platform for the Verification and Validation
of Safety Control Systems. In IEEE Transactions on
Nuclear Science, vol. 58, no. 2, pp. 468-478.
Sakrutina, E., 2017. Some functions of the “Safety
management system” in the transportation area safety
assurance. In Proceedings of the IEEE International
Siberian Conference on Control and Communications
(SIBCON 2017). IEEE, 2017, pp. 1-5.
Smith, D., DeLong, T., Johnson, B. W., 2000. A Safety
Assessment Methodology for Complex Safety-Critical
Hardware/Software Systems. In International Topical
Meeting on Nuclear Plant Instrumentation, Controls,
and Human-Machine Interface Technologies.
Washington, DC, November.
Souri, A., Navimipour, N. J., Rahmani, A. M., 2018.
Formal verification approaches and standards in the
cloud computing: A comprehensive and systematic
review. In Computer Standards & Interfaces, vol. 58,
pp. 1-22.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
644