RACE: Randomized Counter Mode of Authenticated Encryption using

Cellular Automata

Tapadyoti Banerjee

, Bijoy Das

, Deval Mehta

and Dipanwita Roy Chowdhury

Indian Institute of Technology Kharagpur, India

Indian Space Research Organization, SAC Ahmedabad, India

Keywords:

Cellular Automata, Authenticated Encryption, AES-GCM, Counter Mode of Operation.

Abstract:

In this paper, we propose a new Randomized Counter mode of Authenticated Encryption using Cellular Au-

tomata, named as RACE. AES-GCM, the NIST standard Authenticated Encryption scheme is efﬁcient but it is

vulnerable against some of the known attacks. In our design, we try to overcome the limitations of AES-GCM

by exploiting the random evolution of Cellular Automata (CA). Here, the CA is used to make counter values

randomized instead of sequential values used in AES-GCM. In addition, to produce the Message Authenti-

cation Code (MAC), a non-linear CA-based hash-primitive (NASH) is introduced which avoids the complex

Galois ﬁeld multiplication operations of GHASH of AES-GCM. We show that NASH provides more secu-

rity over GHASH against Cycling Attack. Thus, NASH together with AES makes RACE more secure than

AES-GCM with respect to this attack.

1 INTRODUCTION

Authenticated Encryption (AE) refers to the symmet-

ric key based transform whose goal is to achieve pri-

vacy and integrity of the transmitted message in a sin-

gle communication by producing the ciphertext along

with the Message Authentication Code (MAC). AES-

GCM is an AES based Galois/Counter Mode authen-

ticated encryption (McGrew and Viega, 2004) and

considered to be the most efﬁcient NIST standard AE

scheme (Dworkin, 2007). But, the extensive use of

the ﬁnite ﬁeld makes this scheme complex and costly.

Moreover, several attacks (B

ock et al., 2016; Gueron

and Krasnov, 2014; Gueron and Lindell, 2015) are

also identiﬁed against this scheme. In this work, we

try to exploit Cellular Automata (CA) as one of the

crypto primitives to overcome the security issues as

well as the complex Galois ﬁeld multiplication of

GHASH by introducing a new hash-primitive. We

also provide theoretical proof which assures that our

design remains secure.

Since the introduction of the AE scheme by Bel-

lare and Rogaway (Bellare and Rogaway, 2000), the

counter mode of operations (McGrew and Viega,

2004; Whiting et al., 2003) become popular. AES-

GCM, the NIST standard (Dworkin, 2007) also fol-

lows counter mode of operation, but researchers have

pointed out multiple serious security issues. One of

them is the Cycling Attack (Saarinen, 2012) where a

message can be easily forged by swapping any two

blocks. AES-GCM is weak against cycling attack

because of the weak authentication key that has a

small order in the multiplicative group GF(2

128

). Not

only this attack bypasses message authentication with

garbage but also to forges plaintext bits if a polyno-

mial MAC is used in conjunction with the cipher.

This indicates the need of research in the ﬁeld of

authenticated encryption. As a result, NIST together

with the international cryptologic research commu-

nity has initiated an AE competition-CAESAR (Com-

petition for Authenticated Encryption: Security, Ap-

plicability, and Robustness) that boost the research ac-

tivity and public discussion in the ﬁeld of AE and give

many fruitful products (Wu, 2016; Wu and Preneel,

2013). In this context, our motivation is to design

an AE scheme that offers advantages over AES-GCM

and becomes suitable for widespread acceptance with

respect to hardware, as well as software.

In this paper, we propose a new authenticated en-

cryption scheme based on counter mode of operation

using CA. The simple and regular structure of the CA

along with the good random evolution properties are

exploited to overcome the limitations of the Cycling

Attacks (Saarinen, 2012) on AES-GCM. In this con-

struction, a new concept of randomized counter is in-

troduced by using linear CA. On the other hand, to

504

Banerjee, T., Das, B., Mehta, D. and Chowdhury, D.

RACE: Randomized Counter Mode of Authenticated Encryption using Cellular Automata.

DOI: 10.5220/0007971505040509

In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 504-509

ISBN: 978-989-758-378-0

overcome the shortcomings of the GHASH, a Non-

linear CA-based hash-primitive, called NASH is pro-

posed.

Our Contributions:

• RACE, a new authenticated encryption scheme is

proposed which is designed based on the simple

and elegant CA structure.

• The construction uses CA-based random values

instead of the deterministic incremental value in

the counter mode of operation.

• NASH, a new non-linear CA-based hash-

primitive is introduced to avoid the complex

Galois ﬁeld modulo multiplications.

• It has been shown that RACE remains secure over

AES-GCM with respect to the Cycling Attacks.

The rest of the paper is organized as follows. Sec-

tion 2 brieﬂy describes the operation of AES-GCM

and the basics of CA. In section 3, the overall design

of RACE is introduced and described in detail. Sec-

tion 4 claims that RACE is secure over AES-GCM

against Cycling Attacks. Finally, we conclude our

work in section 5.

2 BACKGROUND AND

PRELIMINARIES

In this section, we describe AES-GCM, from which

our RACE is inspired. Later the fundamentals of cel-

lular automata (CA) is provided which is used as the

basic crypto primitive of our proposed design.

2.1 The Galois/Counter Mode of

Operation

AES-GCM (Galois/Counter Mode) (McGrew and

Viega, 2004) is an authenticated encryption algorithm

that provides both conﬁdentiality or privacy and data

authenticity. The basic block diagram of AES-GCM

is shown in Figure 1.

The counter values are encrypted by AES encryp-

tion with key ‘K’ (E

), and this results are EXORed

with the message to produce ciphertext. Successive

counter values are generated by incrementing (incr)

the value of the counter. This scheme uses a hash

function, named GHASH which performs the multi-

plication in GF(2

128

) (mult

) over the hash key ‘H’

which is derived from E

128

). For the sake of sim-

plicity, a case with only a single block of additional

authenticated data (Auth Data 1) and two blocks of

plaintext is shown where ‘len’ denotes the length of

the corresponding data.

Counter 0 incr

Counter 1 incr

Counter 2

⊕

Plaintext 1

Ciphertext 1

⊕

Plaintext 2

Ciphertext 2

⊕ ⊕

mult

Auth Data 1

⊕

mult

⊕

Auth Tag

len(A)||len(C)

Figure 1: Galois/Counter Mode of Operation (McGrew and

Viega, 2004).

2.2 Cellular Automata

Cellular Automata is universally known as a good ran-

dom number generator (Pal Chaudhuri et al., 1997).

It is a discrete lattice of cells which is nothing but

a memory element or ﬂip-ﬂop with combinational

logic function and remains in a particular geome-

try. At each clock pulse, the cells are updated si-

multaneously by using the transition function or rule:

: {0,1}

→ {0,1}, which is deﬁned as the deci-

mal equivalent of the truth table of the function f .

This function takes the present values of a cell and its

neighborhood cells as arguments and performs some

logical operations on them to update the value of that

cell. The next state of the i

cell of a one-dimensional

three-neighborhood CA is: S

t+1

= f (S

i−1

i+1

where S

is the state of i

cell at time t. E.g. consider

Rule 90 and Rule 150 for a one-dimensional CA:

Rule 90 : S

t+1

= S

i+1

⊕ S

i−1

Rule 150 : S

t+1

= S

i+1

⊕ S

i−1

If the cells evolve with different rules instead of

the same rule, it is called hybrid CA. Linear CA is

evolved with linear operations such as EXOR; and

non-linear CA contains linear rules along with some

non-linear operations such as AND/OR. The linear

CA can be converted into non-linear CA by inject-

ing the non-linear function at one/more cells of that

CA along with the rule-vector (Ghosh et al., 2014).

Furthermore, if all the states except one (all 0’s state

for linear CA) lie in a single cycle then this is called

maximal length CA. In this work, we use maximal-

length hybrid CA with both linear and non-linear

rules, called LHCA and NHCA respectively.

RACE: Randomized Counter Mode of Authenticated Encryption using Cellular Automata

505

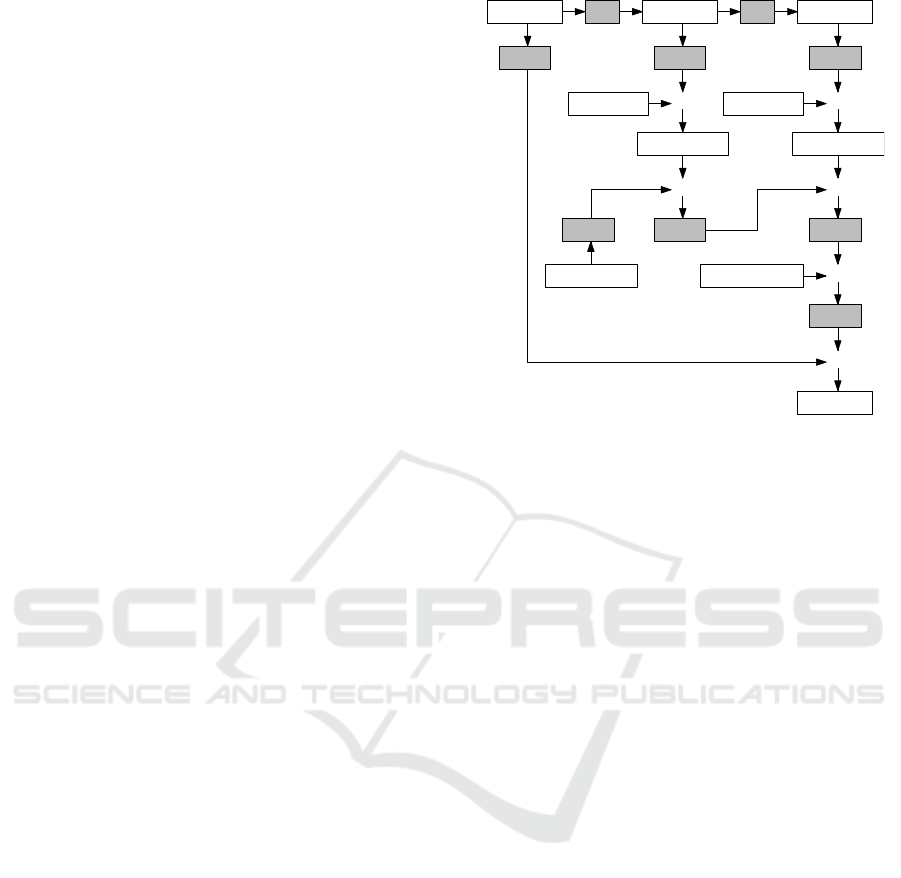
3 RACE: CA-BASED AE SCHEME

The new Randomized Counter mode of Authenticated

Encryption using CA, called RACE is introduced in

this section. The design architecture of RACE is

shown in Figure 2.

LHCA

⊕

NHCA

len(P ) (mod cp)

Auth T ag(T )

LHCA

E E

cntr

⊕

NHCA

⊕

NHCA

AAD

⊕

Figure 2: Design architecture of RACE.

Unlike the sequential counter values as in Counter

Mode of operation, the randomized counter values are

generated by the LHCA from the Initialization Vec-

tor (IV). The ciphertext are produced by EXORing

the message blocks with the encrypted counter val-

ues. For the authentication operation, a hash primitive

is used to generate the Tag. This function uses hash

key which is different from the encryption key.

3.1 RACE Deﬁnition

The following notations are used to present our de-

sign.

len(X): Returns the total number of bits in X

padding(X): X||10

∗

such that len(X||10

∗

) = 128

P: Plaintext message that can be represented as

||p

||... ||p

n−1

||p

∗

, where |p

| = 128 bits for

i = 1,2,3,. . .,n − 1 and 0 < |p

∗

| ≤ 128

IV: 128-bit Initialization Vector

AAD: Additional Authenticated Data can be repre-

sented as A

||A

||... ||A

m−1

||A

∗

where |A

|=128

bits for i = 1,2,3,. . .,m − 1 and 0 < |A

∗

| ≤ 128

C: Ciphertext message can be represented as

||c

||... ||c

n−1

||c

∗

where len(c

) = len(p

) bits

for i = 1,2, 3,. ..,n − 1 and also for len(c

∗

) =

len(p

∗

)

T: 128-bit Authentication Tag

: 128-bit encryption key

: 128-bit hash key

LHCA

(X): State of 128-bit CA after evolving ‘cp’

number of clock pulses on the initial value of 128-

bit X using maximum length LHCA

NHCA

(X): State of 128-bit CA after evolving ‘cp’

number of clock pulses on the initial value 128-bit

X using maximum length NHCA

E(K

, X): The block cipher encryption of the value

X ∈ {0, 1}

128

with the key K

∈ {0, 1}

128

X ⊕ Y: The addition of X and Y

X k Y: The concatenation of two bit strings X and Y

NASH(): Non-linear Cellular Automata based Hash

primitive to produce Authentication Tag

The AE operation takes inputs as IV, K

, P, and AAD,

and gives output as C and T. The authenticated de-

cryption operation takes ﬁve inputs: K

, IV, C, AAD,

and T as deﬁned above. It has only one output, either

the plaintext P or the special symbol FAIL to indicate

that its inputs are not authentic.

During encryption and decryption processes, the

bit strings P, C and AAD are divided into 128-bit

blocks. Assume the unique pair hn,bi with positive

integers such that the length of plaintext is (n-1)×128

+ b, where 0 < b ≤ 128. To sum up, the plaintext

message consists of n blocks. The length of each

block except the last is 128 bit. The last block is

b bit long. The sequence of these plaintext blocks

are p

, p

,... , p

n−1

, p

∗

. The corresponding sequence

of ciphertext blocks are c

,... ,c

n−1

∗

, where the

length of the ﬁnal block c

∗

is b. Similarly, The AAD

is denoted as A

||A

||... ||A

m−1

||A

∗

, where the last

block is d bit long. Assume the unique pair hn,di

with positive integers such that the length of AAD is

(n-1)×128 + d, where 0 < d ≤ 128. We have used

two keys in our proposed scheme; one is encryption

key K

and other is authentication key K

. Moreover,

the K

is generated from K

by running the non-linear

CA for ‘cp’ number of clock cycles. The authenti-

cated encryption operation of RACE is deﬁned by the

following equations based on the above information:

←− {0,1}

128

← NHCA

)

cntr

← LHCA

(IV )

cntr

← LHCA

(cntr

i−1

) //i = 1,2,3,. . .,n

← p

⊕ E(K

,cntr

) //i = 1,2,3,. . .,n − 1

∗

← p

∗

⊕ MSB

(E(K

,cntr

)) //MSB

is Most

Signiﬁcant b bit

T ← NASH(AAD, K

, C) ⊕ E(K

,cntr

)

(1)

The function NASH is deﬁned by NASH(AAD, K

C) = Z

m+n

, where the inputs AAD, K

and C are de-

SECRYPT 2019 - 16th International Conference on Security and Cryptography

506

scribed above, and the variable Z

for i = 0,1, 2,3,... ,

m + n are deﬁned as follows:











, //i = 0

NHCA

i−1

⊕ A

), // i = 1 to m − 1

NHCA

i−1

⊕ A

∗

||10

127−d

), //i = m

NHCA

i−1

⊕ c

i−m

), //i = m + 1 to

m + n − 1

NHCA

len(P)(mod cp)

i−1

⊕ c

∗

||10

127−b

//i = m + n

Successive counter values cntr

are generated us-

ing the function LHCA

(). The randomness of

the counter values generated by CA has successfully

passed the NIST Statistical Test Suite for Random and

Pseudorandom Number Generators (Rukhin et al.,

2001).

3.2 RACE Design

The four main functions of our proposed design are

described as follows:

3.2.1 Randomized Counter Value Generation

Cellular Automata is universally known as

a good Pseudo-Random Number Generator

(PRNG) (Pal Chaudhuri et al., 1997). We have

adopted the maximal-length LHCA to generate the

randomized counter values. A publicly known 128-

bit nonce (should be non-zero string) is considered

as the IV of the LHCA. The counter values are

generated sequentially by applying a ﬁxed number

of clock pulses on the LHCA state. The randomness

of the counter values generated by this method has

successfully passed the NIST Statistical Test Suite

for Random and Pseudorandom Number Generators

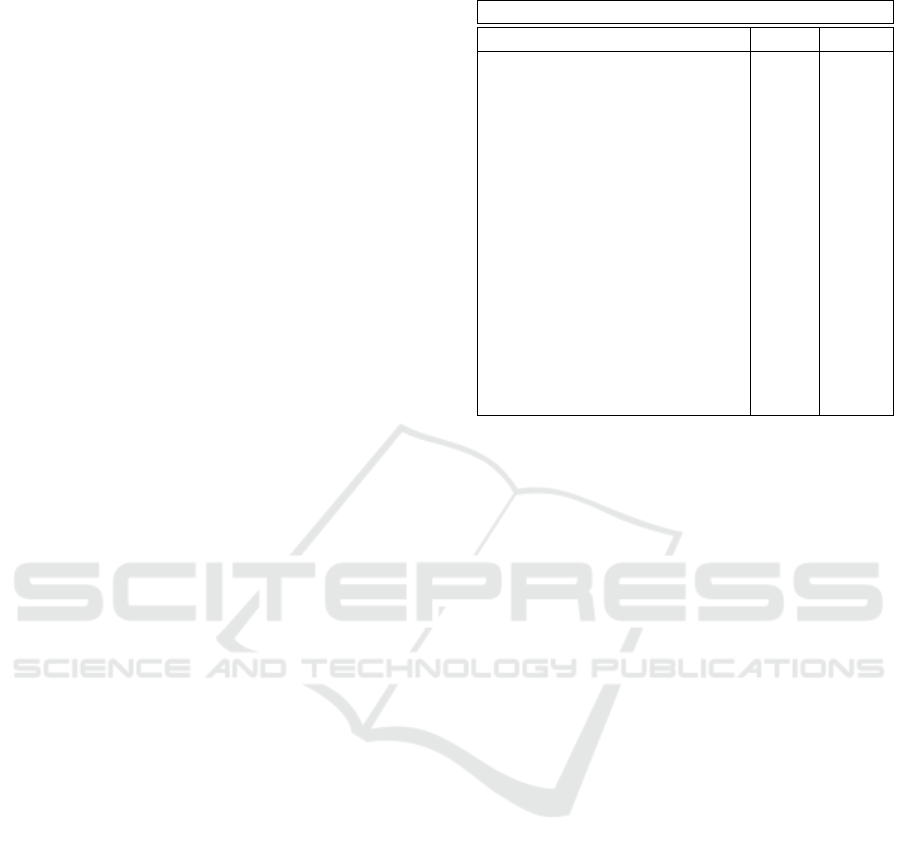
(NIST SP 800-22) (Rukhin et al., 2001). Table 1

shows the ﬁnal analysis report where the minimum

pass rate for the proportion value is 96 for a sample

size = 100 binary sequences with the exception of the

random excursion (variant) test is 65 for a sample

size = 69 binary sequences.

3.2.2 Ciphertext Generation

Recall that the ciphertexts are produced based on the

expression c

= p

⊕E(K

,cntr

), for i = 1,2, . ..,n−1

and for the last block c

∗

← p

∗

⊕ MSB

(E(K

,cntr

)).

In this work, the encryption function E() is imple-

mented using the standard AES-128 (Pub, 2001).

Here, The randomized counter values are encrypted

by AES-128 and then EXORed with the correspond-

ing plaintext/message blocks to produce the cipher-

texts.

Table 1: NIST SP 800-22 test suite for the LHCA.

P-values and the proportion of passing sequences

Test P-Value Proportion

Frequency (Monobit) Test 0.032923 99/100

Frequency Test withen a Block 0.366918 99/100

Runs Test 0.883171 99/100

Test for the Longest Run of Ones in a Block 0.437274 98/100

Binary Matrix Rank Test 0.129620 100/100

Discrete Fourier Transform (Spectral) Test 0.759756 98/100

Non-overlapping Template Matching Test

(avg.)

0.488644 99/100

Overlapping Template Matching Test 0.145326 99/100

Maurer’s “Universal Statistical” Test 0.991468 100/100

Linear Complexity Test 0.637119 100/100

Serial Test (avg.) 0.596405 100/100

Approximate Entropy Test 0.262249 98/100

Cumulative Sums (Cusum) Test (avg.) 0.321921 100/100

Random Excursions Test (avg.) 0.379568 69/69

Random Excursions Variant Test (avg.) 0.298796 69/69

3.2.3 Hash Key Generation

In AE, trying to use same key for both authentica-

tion and encryption is error-prone. To avoid this issue,

RACE uses two different keys; one is for encryption

and another is for authentication. Computation of the

second key i.e. the authentication key K

is expressed

as K

= NHCA

) where K

is the shared key be-

tween sender and receiver.

3.2.4 Authentication Tag Generation

In the reminiscence of the RACE deﬁnition (sec-

tion 3.1), it has been delineated that the authen-

tication tag T is generated by EXORing the en-

crypted counter value and the hash digest i.e., T ←

NASH(AAD, K

, C) ⊕ E(K

,cntr

). The hash value

is achieved using NASH, the proposed non-linear

hash-primitive. In AES-GCM, Galois ﬁeld modulo

multiplication in GHASH has many limitations. Such

as the legitimate message-tag pairs could fail authen-

tication (Gueron and Krasnov, 2014), it uses the same

block cipher key for both encrypt the data and to

generate the hash key which leads a wider classes

of weak-keys (Saarinen, 2011), and so on. In this

work, NASH is proposed to overcome these limi-

tations by exploiting the non-linear CA as a hash-

primitive as presented in section 3.1. Here, simple and

faster NHCA is evolved instead of the complex Ga-

lois ﬁeld multiplication. The randomness of the hash

values generated by this method has also successfully

passed the NIST Statistical Test Suite for Random and

Pseudorandom Number Generators (NIST SP 800-

22) (Rukhin et al., 2001), and the result set is simi-

lar to table 1. The functionality of NASH is depicted

RACE: Randomized Counter Mode of Authenticated Encryption using Cellular Automata

507

in ﬁgure 3. For the sake of simplicity, assume that

only authenticity is needed and there is no need for

conﬁdentiality. So, in this ﬁgure the message is sent

clearly. If conﬁdentiality is required then the message

needs encryption. Figure 3 shows the NASH func-

tionalities with two blocks of plaintext and one block

of AAD.

LHCA

⊕

NHCA

len(P ) (mod cp)

Auth T ag(T )

cntr

NHCA

⊕

NHCA

AAD

⊕

Figure 3: Functional description of NASH.

Here, a randomized counter value cntr

generated

from IV is encrypted by using AES-128. Successively

each message block is EXORed with the output of the

NHCA and the ﬁnal output becomes the state of the

NHCA. For each case, ‘cp’ number of pulses are ap-

plied on the CA. Finally, the authentication tag (Auth

Tag) is achieved by EXORing the value of E

(cntr

)

and the output of the NHCA-chain.

3.3 Design Rationale

This section describes the choice of operations and

parameters in the design of RACE.

• Choice of LHCA: The maximum-length Linear

Hybrid CA is used to generate the randomized

counter values instead of the sequential counter

values. It is used to make the correlation between

the two subsequent counter values as complex and

intricate as possible. In Table 1, it is already

shown that this method produces good random

numbers. The initialization vector of the LHCA

should be a non-zero nonce because the LHCA

will reach to the dead-state for the input of all-

zero state.

• Choice of NHCA: Here, the maximum-length

Non-linear Hybrid CA is used to generate authen-

tication tag instead of complex Galois ﬁeld mod-

ulo calculation used in AES-GCM. It is a well

known fact that CA is a good random number gen-

erator (Pal Chaudhuri et al., 1997), and it is com-

putationally infeasible to ﬁnd the previous state of

a 128 bits NHCA. So, we use this NHCA to gen-

erate the hash key. Additionally, this is also used

to generate the authentication tag.

• Value of ‘cp’: The number of clock pulses (cp)

is determined such that it should be minimum as

well as the CA achieve a good diffusion. Diffu-

sion is calculated by counting the number of bits

affected in the state of the CA after applying one

clock pulse. Analyzing the diffusion values for

both 128 bit LHCA and 128 bit NHCA, it is ob-

served that the CA is totally diffused, i.e., each of

the bits is affected after 63 clock pulses.

• Requirement for ‘len(P) (mod cp)’ number of

pulse in NASH: Consider two plaintext, ‘P’ and

‘P

’, and their corresponding ciphertext ‘C’ and

‘C

’, where c

∗

= 0

127

1 and c

∗

= 0

127

. Thence-

forth, c

∗

becomes c

∗

= 0

127

||1 = 0

127

1 after

padding. So, without len(P) (mod cp) number

of pulse at NHCA, these two ciphertext shall give

same Auth Tag value. So, we try to avoid the mes-

sage forgery attack on this design by super impos-

ing the length of the message.

4 SECURITY OF RACE AGAINST

CYCLING ATTACK

RACE encryption uses AES and authentication is

done by exploiting the properties of nonlinear max-

imum length CA. Here we show that the proposed

design prevents Cycling Attacks, whereas AES-GCM

is vulnerable against this attacks (Saarinen, 2012).

Claim. RACE is secure against Cycling Attack.

Proof. Assume two distinct inputs (AAD, C) and

(AAD

, C

). Let m and n be the number of blocks of

AAD and C respectively, and m

and n

be the number

of blocks of AAD

and C

respectively. Assume w-bit

be the length of each block, and also len(K

) = w. Let

= NHCA

), where NHCA

() and K

are de-

ﬁned previously. Now analyze the probability of the

event that

NASH(K

,AAD,C) ⊕ NASH(K

,AAD

) = S (2)

for some ﬁxed t-bit value S. We assume that these in-

puts are formatted as follows:

AAD = A

||A

||... ||A

, here len(A

) = w for i=1 to m

C = c

||c

||... ||c

, here len(c

) = w for i = 1 to n

AAD

||A

||... ||A

,here len(A

)=w for i=1 to m

= c

||c

||... ||c

, here len(c

) = w for i = 1 to n

Now, we deﬁne D and D

based on the above infor-

mation as follows:

D = NHCA

⊕ NHCA

n−1

⊕.. . ⊕ NHCA

⊕ NHCA

m−1

⊕ . ..⊕ NHCA

⊕ K). ..)))...))

SECRYPT 2019 - 16th International Conference on Security and Cryptography

508

= NHCA

⊕ NHCA

−1

⊕.. . ⊕ NHCA

⊕ NHCA

−1

⊕ . ..⊕

NHCA

⊕ K). ..)))...))

The relation NASH(K

, AAD, C) ⊕ NASH(K

, AAD

) = S results H(K) = 0, since

H(K) = S ⊕ D ⊕ D

(3)

The strings AAD||C and AAD

||C

are distinct. If

cp < (2

− 1) then there are exactly one K for which

H(K) = 0 holds. This follows from the fact that

NHCA

() is maximum length non-linear CA where

the value of NH CA

) will be repeated after 2

−1

clock pulses of operations. So the probability that

H(K) = 0 holds, given that K

is chosen as random

from {0,1}

, is 1/2

(or 2

−w

). Thus, the probabil-

ity that H(K) = 0 holds for any two given messages

(AAD, C) and (AAD

, C

), and a given t-bit value S,

is equal to the probability that NASH(K

, AAD, C) ⊕

NASH(K

, AAD

, C

) = S. So there are 2

(or 2

w−t

)

possible values for which Equation (2) holds with

probability 2

−w

× 2

w−t

=1/2

(or 2

−t

) for any given

values of (AAD, C) and (AAD

, C

), and S∈{0,1}

So, it is clear from the above justiﬁcation that a

minimum of 2

− 1 number of CA clock pulses are

required to get the same CA state.

In case of RACE the length of the authentication tag

(t) is 128 bit.

5 CONCLUSION

This paper presents a new Randomized Counter

mode of Authenticated Encryption Using Cellular

Automata, named as RACE. Here, linear CA are em-

ployed to generate the counter values which provides

randomized counter values instead of sequential val-

ues. Along with this, a non-linear CA-based hash-

primitive named NASH is introduced to generate the

authentication tag. RACE captures the notion of se-

curity and avoids the Galois ﬁeld modulo multiplica-

tion as in AES-GCM. The construction and security

analysis of this scheme implies that it is secure than

AES-GCM against some known attacks, such as Cy-

cling Attacks. Finally, RACE can boost researchers to

concentrate on CA-based designs as a substitute and

faster design approach.

REFERENCES

Bellare, M. and Rogaway, P. (2000). Encode-then-encipher

encryption: How to exploit nonces or redundancy

in plaintexts for efﬁcient cryptography. In Interna-

tional Conference on the Theory and Application of

Cryptology and Information Security, pages 317–330.

Springer.

ock, H., Zauner, A., Devlin, S., Somorovsky, J., and Jo-

vanovic, P. (2016). Nonce-disrespecting adversaries:

Practical forgery attacks on GCM in TLS. IACR Cryp-

tology ePrint Archive, 2016:475.

Dworkin, M. J. (2007). Recommendation for

block cipher modes of operation: Ga-

lois/Counter Mode (GCM) and GMAC. See also

https://nvlpubs.nist.gov/nistpubs/legacy/sp/nistspecial

publication800-38d.pdf. Technical report.

Ghosh, S., Sengupta, A., Saha, D., and Roy Chowdhury,

D. (2014). A scalable method for constructing non-

linear cellular automata with period 2

-1. In Inter-

national Conference on Cellular Automata, pages 65–

74. Springer.

Gueron, S. and Krasnov, V. (2014). The fragility of AES-

GCM authentication algorithm. In 11th International

Conference on Information Technology: New Gener-

ations, ITNG 2014, Las Vegas, NV, USA, April 7-9,

2014, pages 333–337. IEEE.

Gueron, S. and Lindell, Y. (2015). GCM-SIV: Full nonce

misuse-resistant Authenticated Encryption at under

one cycle per byte. In Proceedings of the 22nd ACM

SIGSAC Conference on Computer and Communica-

tions Security, pages 109–119. ACM.

McGrew, D. and Viega, J. (2004). The Ga-

lois/Counter Mode of operation (GCM). See

also http://luca-giuzzi.unibs.it/corsi/Support/papers-

cryptography/gcm-spec.pdf. submission to NIST

Modes of Operation Process, 20.

Pal Chaudhuri, P., Roy Chowdhury, D., Nandi, S., and Chat-

topadhyay, S. (1997). Additive Cellular Automata:

Theory and Applications, volume 1. John Wiley &

Sons.

Pub, N. F. (2001). 197: Advanced Encryption Standard

(AES). Federal information processing standards

publication., 197(441):0311.

Rukhin, A., Soto, J., Nechvatal, J., Smid, M., and Barker,

E. (2001). A Statistical Test Suite for Random and

Pseudorandom Number Generators for Cryptographic

Applications, NIST Special Publication 800-22. Tech-

nical report, Booz-Allen and Hamilton Inc Mclean Va.

Saarinen, M.-J. O. (2011). GCM, GHASH

and Weak Keys. See also https:

//www.iacr.org/archive/fse2012/75490220/75490220

.pdf. IACR Cryptology ePrint Archive, 2011:202.

Saarinen, M.-J. O. (2012). Cycling attacks on GCM,

GHASH and other polynomial MACs and hashes. In

Fast Software Encryption, pages 216–225. Springer.

Whiting, D., Housley, R., and Ferguson, N. (2003).

Counter with CBC-MAC (CCM). See also

https://tools.ietf.org/html/rfc3610. Technical re-

port.

Wu, H. (2016). ACORN: A Lightweight Authenti-

cated Cipher (v3). Candidate for the CAESAR

Competition. See also https://competitions. cr. yp.

to/round3/acornv3. pdf.

Wu, H. and Preneel, B. (2013). AEGIS: A Fast Authenti-

cated Encryption Algorithm. In International Confer-

ence on Selected Areas in Cryptography, pages 185–

201. Springer.

RACE: Randomized Counter Mode of Authenticated Encryption using Cellular Automata

509