Toward Measuring Knowledge Loss due to Ontology Modularization

Andrew LeClair

, Ridha Khedri and Alicia Marinache

Department of Computing and Software, McMaster University, 1280 Main Street West, Hamilton, Canada

Keywords: Ontology, Ontology Modularization, View Traversal, View Extraction, Knowledge Loss, Agent Knowledge,

Agent Reasoning, Autonomous Agents.

Abstract:

This paper formalizes the graphical modularization technique, View Traversal, for an ontology-based system

represented using the Domain Information System (DIS). Our work is motivated by the need for autonomous

agents, within an ontology-based system, to automatically create their own views of the ontology to address the

problems of ontology evolution and data integration found in an enterprise setting. Through DIS, we explore

speciﬁc ontologies that give Cartesian perspectives of the domain, which allows modularization to be a means

for agents to extract views of speciﬁc combinations of data. The theory of ideals from Boolean algebra is

used to formalize a module. Then, with the use of homomorphisms, the quantity of knowledge within the

module can be measured. More speciﬁcally, through the ﬁrst isomorphism theorem, we establish that the loss

of information is quantiﬁed by the kernel of the homomorphism. This constitutes a foundational step towards

theories related to reasoning on partial domain knowledge, and is important for applications where an agent

needs to quickly extract a view that contains a speciﬁc set of knowledge.

1 INTRODUCTION

Conceptualizing ontologies and using them in an en-

terprise setting is a difﬁcult task due to the problems

of data integration (Ziegler and Dittrich, 2004), the

co-ordination of multiple autonomous agents (Huhns

and Singh, 1997), and the evolution of the do-

main (Benomrane et al., 2016; Dietz, 2006). Despite

these problems, there does not yet exist an approach

that properly addresses them. Ontology-based Data

Access (OBDA) attempts to address the issues asso-

ciated with data integration and ontology evolution

(Poggi et al., 2008). The co-ordination of multiple

agents in an ontological setting is studied in several

papers (e.g., (Maedche et al., 2003; Belmonte et al.,

2008; Freitas et al., 2017)).

There is a need in addressing these three tasks

together such that the governing of the domain can

be conducted using an ontology that uses the data

in initial construction or reasoning tasks, such as

in (Nadal et al., 2019). Existing paradigms, such

as OBDA, are used to address the issues of evolv-

ing and heterogeneous data that come from multiple

sources. However, complications arise from updates

to the data. Therefore, restrictions must be placed on

schema changes to not affect the ontology, or on ver-

https://orcid.org/0000-0003-2779-8000

sion controls to control the domain’s evolution. The

problems associated with ontology evolution are fur-

ther demonstrated in (Benomrane et al., 2016), which

discusses the complications introduced with multiple

agents and the current need of manual intervention by

an ontologist.

OBDA and the other approaches formalize their

ontologies using Description Logic (DL), such as in

(Maedche et al., 2003; Motik, 2006; Baader, 2003;

Hustadt et al., 2005; Bao et al., 2009). In (Maedche

et al., 2003) several limitations to DL-based ontolo-

gies are raised. The ﬁrst is the complexity of rea-

soning tasks increasing with the expressivity of DL

fragment or the amount of data used (Motik, 2006;

Baader, 2003). In (Hustadt et al., 2005), it is noted

that the way the existential and universal quantiﬁers

interact with the data can cause the time complexity

of reasoning tasks to rise to exponential time. What

often results is during the design phase, a less expres-

sive fragment of DL is used to avoid the quantiﬁers or

operators, or the amount of data the ontology utilizes

is limited. Additionally, as discussed in (LeClair and

Khedri, 2016), DL only allows for a single context of

the concepts, which further limits the reasoning capa-

bilities, and has resulted in the effort for being able to

capture these contexts with extensions to DL such as

with Package-based DL (Bao et al., 2009). However,

even these are encumbered by the limited expressivity

174

LeClair, A., Khedri, R. and Marinache, A.

Toward Measuring Knowledge Loss due to Ontology Modularization.

DOI: 10.5220/0008169301740184

In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 174-184

ISBN: 978-989-758-382-7

for reasoning inherent to using DL.

This work aims at addressing the issues associ-

ated with an evolving domain, rich with data, and

numerous autonomous agents. To reach this goal,

rather than using DL, we utilize Domain Informa-

tion System (DIS) (Marinache, 2016) to formalize an

ontology-based system. It is with DIS we aim to avoid

monolithic ontologies (discussed in (Maedche et al.,

2003)), and create an optimal ontology-based system

as described in (Jaskolka et al., 2015). We aim to

address domains that have a large set of constantly

evolving data that must be reﬂected in the ontology

that is being used by multiple agents for queries or

other governing tasks. We also make the open world

assumption, therefore, some data elements could be

unspeciﬁed.

In this work we address the particular issues as-

sociated with autonomous agents interacting with an

ontology-based system. DIS provides a means to for-

malize a procedure for the agents to extract a module

from the ontology to ﬁt their needs. The theory of

ideals from Boolean algebra is used to extract smaller

components that are shown to be complete modules.

These customizable views are created through a pro-

cess called modularization. In other words, the views

are modules of the original DIS ontology. The un-

derlying theory of DIS is then used to characterize an

agent’s potential knowledge within the system.

Ontology modularization is an active research

ﬁeld with the aim to ensure the ontologies are us-

able for tractable reasoning tasks, and adhere to es-

tablished engineering principles that promote main-

tainability. Examples of recent modularization efforts

can be seen in (Xue and Tang, 2017; Khan and Keet,

2015; Algergawy et al., 2016; Babalou et al., 2016;

Movaghati and Barforoush, 2016; De Giacomo et al.,

2018). These approaches vary by the ontology for-

malism they modularize on, the components of the

ontology used to modularize (data, concepts, or both),

and what types of modules they produce. The utiliza-

tion of ideals to discuss modularization in the context

of DL has been explored in (Del Vescovo et al., 2011),

but requires rigorous computation. DIS is able to sim-

ply compute ideals using its underlying theory.

The remainder of the paper is as follows. In Sec-

tion 2, we evaluate the work of utilizing ontologies

in multi-agent systems for customizing views, as well

as the literature regarding OBDA. In Section 3, we in-

troduce the necessary mathematical background to fa-

cilitate discussion on the modularization process and

knowledge quantiﬁcation. In Section 4, we provide

the ﬁndings regarding how a DIS-based ontology can

be modularized. In Section 5, we discuss how said

modularization can be used to characterize the poten-

tial knowledge of an agent, followed by a discussion

in Section 6.

2 RELATED WORK

In (Wache et al., 2001), the authors highlight the

need for the ontology of an ontology-based system

to be modularizable so as to avoid the issues associ-

ated with using a monolithic ontology. In addition

to the complications caused by a monolithic ontol-

ogy, in (Jaskolka et al., 2015), the authors discuss the

need to have the ability for several local ontologies to

communicate by using a shared language. Nowadays,

DL, as an ontology formalism, is the standard due

to its wide usage by research teams and several im-

plementations. However, Wache et al. (Wache et al.,

2001) point to multiple limitations with the formal-

ism such as the static nature of the ontologies created,

intractability of reasoning tasks (when using expres-

sive fragments), and tendency to become monolithic.

Thus, we investigate DIS (formally introduced in Sec-

tion 3) as an alternative formalism for an ontology-

based system.

There exist several recent approaches to multi-

agent systems that utilize an ontology at its core (e.g.,

(Pakdeetrakulwong et al., 2016; Kantamneni et al.,

2015; Zhou et al., 2017)). These systems require

agents to have their own ontology, or pieces of a

shared larger ontology, that they can reason on. The

design of agents having their own queries that they

can answer allows for more efﬁcient query answering

as the agent only needs to refer to a smaller, more spe-

ciﬁc ontology. Additionally, it allows for the agents

to collaborate, each with their respective expertise as

determined by the ontology they contain, to answer

more complex queries. However, for collaboration

to occur, the agents must have some shared language

that is provided by an additional ontology that every

agent can communicate through. Although the agents

can efﬁciently answer these small queries, any com-

plex query that requires collaboration will thus suffer

from the issues associated with monolithic ontologies.

The best way to provide each agent with the

needed part of the used large ontology is through

modularizing the ontology into modules that each

agent will utilize. As all modules come from the same

ontology, this mitigates the issue of needing another

ontology to facilitate communication between agents.

However, this requires an ontology that can be broken

into the modules that each agent requires. In other

words, this method requires an ontology that concep-

tualizes the entire domain (rather than a speciﬁc view

for an agent). Examples of such an implementation

Toward Measuring Knowledge Loss due to Ontology Modularization

175

can be found in (Anand et al., 2014; Belmonte et al.,

2008). The modularization techniques that are pro-

posed in these papers are heuristic in nature, not able

to guarantee properties such as knowledge preserva-

tion or correctness. Concerns regarding the modu-

larization process and lack of formal method arise

when considering the use of ontologies that consist of

hundreds or thousands of concepts, such as in (Ash-

burner et al., 2000; Raimond et al., 2007; Brickley

and Miller, 2010; Spackman et al., 1997; Rector et al.,

1996; Bodenreider, 2004; Suchanek et al., 2008).

Regardless of the design approaches used for an

ontology-based system, it will require a full up-

date (recheck for completeness, etc.) whenever an

agent’s ontology changes due to the domain’s evo-

lution (Benomrane et al., 2016). This can be a con-

suming process depending on how often the agents

domain knowledge is expected to change, and can re-

sult in a design where the agents are static and seldom

react to change.

In addition to the complications associated with

ontology evolution, we investigate how the agents can

interact with the data. OBDA is the approach used

by the Semantic Web for linking data to an ontology

(Poggi et al., 2008). OBDA paradigm aims to connect

an ontology layer to a data layer so that rich queries

can be made using the ontology, and answered using

the data. However, it is not a trivial task to create an

ontology from a dataset. The task is described as the

bootstrapping problem (Jim

enez-Ruiz et al., 2015),

and OBDA is mostly considered as read-only as it

puts restrictions on the ability to modify the datasets

and handle updates (Xiao et al., 2018). Additionally,

the query transformation process is not straightfor-

ward, depending on multiple aspects of the ontology,

queries, and data consistency (Bienvenu et al., 2018).

This research seeks to provide a means for agents

to automatically and systematically extract views

from an ontology on-the-ﬂy to achieve the tasks they

are required to do. We seek to have only a single on-

tology that can be modularized to avoid a monolithic

ontology existing at the higher-level. By extracting

them from a single ontology, we ensure that the agents

are able to communicate using the same language. We

also seek to have a system that is adaptable to change

and evolution, allowing for the data that the agents

have to be malleable without the need for modiﬁca-

tion of the ontology itself.

3 MATHEMATICAL

BACKGROUND

In this Section, we present the necessary mathemat-

ical background to communicate how the lattice and

underlying Boolean algebra is utilized in DIS to con-

duct the modularization.

A lattice is an abstract structure that can be de-

ﬁned as either a relational or algebraic structure

(Davey and Priestley, 2002). We provide each deﬁni-

tion, as well as the connection between them, below.

If (L,≤) is a partially ordered set, we deﬁne an

upper bound and lower bound as follows. For an arbi-

trary subset S ⊆ L, we deﬁne an element u ∈ L as an

upper bound of S if s ≤ u for each s ∈ S. Dually, we

deﬁne an element l ∈ L as a lower bound of S if l ≤ s

for each s ∈ S. An upper bound u is deﬁned as a least

upper bound (dually, a lower bound l is deﬁned as a

greatest lower bound) if u ≤ x for each upper bound

x ∈ S (x ≤ l for each lower bound x ∈ S). A least

upper bound is typically referred to as a join, and a

greatest lower bound as a meet. If every two elements

a,b ∈ L have a join, then the partially ordered set is

called a join-semilattice. Similarly, if every two ele-

ments a,b ∈ L have a meet, then the partially ordered

set is called a meet-semilattice. A lattice is a partially

ordered set that is both a join- and meet-semilattice.

An algebraic structure (L, ⊕,⊗), which consists of

a set L and the two binary operators ⊕ and ⊗ that are

commutative, associative, idempotent, and satisfy the

absorption law (i.e., a ⊕ (a ⊗ b) = a ⊗(a ⊕b) = a, for

a,b,c ∈ L).

The relational and algebraic structure can be con-

nected a ≤ b ⇐⇒ (a = a ⊗ b) ⇐⇒ (b = a ⊕ b).

The connection between the relational and alge-

braic deﬁnition of a lattice allows us to freely discuss

relational or algebraic aspects. This is signiﬁcant as

we will be using both the algebraic and relational def-

initions interchangeably in the following sections and

that for simplicity. We will also require the notion of

a sublattice, which is simply deﬁned as a nonempty

subset M of a lattice L that satisﬁes x ⊕ y ∈ M and

x ⊗y ∈ M for all x,y ∈ M. In other words, a sublattice

is a subset of the lattice in which all joins and meets

are preserved in the subset.

We now introduce a distinguished lattice: the

Boolean lattice (Sikorski et al., 1969). A Boolean lat-

tice is deﬁned as a complemented distributive lattice.

A complemented lattice is one that is bounded (in-

cludes a top concept (>) and a bottom concept (⊥)),

and every element a has a complement (an element

b satisfying a ⊕ b = > and a ⊗ b = ⊥). A distribu-

tive lattice is one where the join and meet operators

distribute over each other, in other words, a lattice

KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development

176

L is distributive if for all x, y,z ∈ L, x ⊗ (y ⊕ z) =

(x ⊗ y) ⊕ (x ⊗ z) and x ⊕ (y ⊗ z) = (x ⊕ y) ⊗ (x ⊕ z)

The algebraic structure for the Boolean lattice is

deﬁned as B = (B,⊗,⊕,0, 1,

). The unique elements

0 and 1 are the top and bottom concepts necessary for

the lattice to be bound, and the complement operator

is deﬁned as above for a complemented lattice. In a

ﬁnite Boolean algebra, an atom is deﬁned as an ele-

ment a ∈ B where for any b ∈ B, either a ⊗ b = a or

a ⊗ b = 0. The Boolean algebra (and the correspond-

ing lattice) is thus generated from the power set of the

atoms (Hirsch and Hodkinson, 2002). As a result, all

Boolean algebras with the same number of atoms are

isomorphic to each other.

A notion from Boolean algebra that will be used

for the modularization is the ideal. For a Boolean al-

gebra B with set of elements B, I ⊆ B is called an

ideal in B if I is nonempty and if for all i, j ∈ I and

b ∈ B we have i ⊗ b ∈ I and i ⊕ j ∈ I. In other words,

an ideal is ‘closed-downwards’ such that it is closed

under the lattice meet (⊗) operation.

An ideal is called proper if I 6= {0} or B. We can

also generate an ideal using an element, referred to as

the principal ideal. If we let B be a Boolean algebra,

and b ∈ B, then the principal ideal generated by b is

I(b) = {a ∈ B | a ≤ b}.

3.1 Domain Information System

A DIS is composed of three components: an ontology,

the data, and an operator which maps data to an ontol-

ogy. This separation of data from the ontology grants

us this ability to manipulate the data through adding

or removing records without the need for rechecking

consistency or reconstructing the ontology. Figure 1

graphically shows how the three components interact.

We ﬁrst present the ontology.

Deﬁnition 3.1 (Abstract Ontology). Let C =



C, ⊕,e



be a commutative idempotent monoid.

Let

L =



L,v



be a Boolean lattice, with L ⊆ C, such

that e

∈ L. Let G = {G

def

= (C

)}

∈L

be a set of

rooted graphs at t

We call an abstract ontology the mathematical

structure O

def



C, L,G



We recognize the relation on the set of concepts

L as the partOf relation, denoted by v

. The corre-

sponding Boolean algebra for this structure is deﬁned

as B = (L,⊗,⊕,e

,>,

). The binary operators ⊗ and

A monoid is an algebraic structure that has a set S closed

under a single associative binary operation ·, and a distin-

guished element e ∈ S called the identity. It is denoted by

the triple (S,·,e).

Figure 1: High-level representation of a Domain Informa-

tion System.

⊕ are analogous to the meet and join, but are deﬁned

by the relation v

. The unique elements e

and >

are the bottom and top concepts of the lattice, and are

respectively analogous to 0 and 1. The ⊕ operator

represents the Cartesian product of the concepts, and

it expresses the combination of concepts in the lattice

to form new concepts. The ontology is represented

as the components within the cloud in Figure 1. The

circles represent concepts, and are differentiated by

colour to signify whether they are in the Boolean lat-

tice or a rooted graph.

The second component is the data layer, which is

formalized using a diagonal-free cylindric algebra. Its

operators are indexed with the elements of the carrier

set L of the Boolean lattice. In Figure 1, it is repre-

sented as the dataset.

Deﬁnition 3.2 (Cylindric Algebra). Let A =

(A,+,·,−, 0,1,c

)

k∈L

be a diagonal-free cylindric

algebra (Henkin and Tarski, 1967) such that

(A,+,·,−, 0,1) is a Boolean algebra and c

is an

unary operator on A called cylindriﬁcation, and the

following postulates are satisﬁed for any x,y ∈ A, and

any k, λ ∈ L:

1. c

0 = 0

2. x ≤ c

3. c

(x · c

y) = c

x · c

4. c

x = c

We adopt cylindric algebra to reason on data as it

allows us to go beyond Relational algebra. Cylindri-

ﬁcation operations allow us to handle tuples with un-

deﬁned values (open world assumption) and we can

work on tuples with different length.

Deﬁnition 3.3 (Domain Information System). Let O

be an abstract ontology, A be a diagonal-free cylin-

dric algebra, and a mapping τ : A → L as the type

operator which relates the set A to elements of the

Boolean lattice in O.

We call a Domain Information System the struc-

ture I = (O,A,τ).

Toward Measuring Knowledge Loss due to Ontology Modularization

177

Table 1: Wine Dataset.

Grape Colour Sugar Body Region Winery

Merlot Red Dry Full Niagara Jackson Triggs

Merlot Red Dry Medium Okanagan Jackson Triggs

Pinot Grigio White Dry Medium Niagara Konzelmann

Pinot Grigio White Semi-sweet Medium Niagara Jackson Triggs

Pinot Blanc White Dry Light Okanagan Sperling

Riesling White Semi-sweet Light Niagara Jackson Triggs

. . . . . . . . . . . . . . . . . .

Body

Sugar

Region

Winery

Colour

Grape

Wine

Wine Product

Figure 2: The Boolean lattice for the Wine Ontology.

Figure 1 illustrates this system, with the dataset

and ontology linked by the dashed arrows which rep-

resents the τ operators. In essence, the abstract ontol-

ogy is the conceptual level of the information system.

The Boolean lattice can be mapped to, using the τ op-

erator, from the data that modeled using the cylindric

algebra. In a simpliﬁed way, the abstract ontology is

analogous to the Terminological Box (T-Box) of DL

and the cylindric algebra is the Assertional Box (A-

Box).

In Figure 2, we show a Boolean lattice of a DIS

representation for the Wine Ontology (Noy et al.,

2001). The Boolean lattice is constructed from a

sample data set shown in Table 1. Each attribute

of the data set is a ‘part’ of the concept Wine Prod-

uct, and thus they are atoms of the Boolean lattice.

The remaining concepts are the combinations of these

atoms: the power set. Some combinations hold more

semantic signiﬁcance (as determined by domain ex-

perts), and are signiﬁed by larger hollow nodes. These

concepts can be named, such as Estate being the com-

bination of Region and Winery.

3.2 First Isomorphism Theorem

The ﬁrst isomorphism theorem (Van der Waerden

et al., 1950) is used in this work to quantify knowl-

edge loss from modularization.

Theorem 3.1 (First Isomorphism Theorem). Let R

and S be rings, and let φ : R → S be a ring homo-

morphism. Then:

1. The kernel of φ is an ideal of R,

2. The image of φ is a subring of S, and

3. The image of φ is isomorphic to the quotient ring

R/ker(φ).

In particular, if φ is surjective, then S is isomorphic to

R/ker(φ).

The ﬁrst point introduces the kernel, which is a

structure associated with the homomorphism. If we

deﬁne a homomorphism between rings R and S as φ :

R → S, then the kernel is deﬁned as follows:

ker(φ) = {r ∈ R | φ(r) = 0

} (1)

The kernel is used to measure the non-injectivity

of the homomorphism. It is important to note any

Boolean ring with 1 can be made into a Boolean alge-

bra (Stone, 1936).

4 MODULARIZING THE

ONTOLOGY

From Figure 2, it can be seen that a dataset with even

a relatively small number of attributes results in a

Boolean lattice that is large and possibly unmanage-

able. The Boolean lattice will be of size 2

(where n

is the number of atoms), thus the number of concepts

doubles with each attribute added. Although this can

be partially mitigated with clever database design, it

minimization cannot be assumed. Using the entire

Boolean lattice is both impractical and unreasonable

when considering the motivation of this work: before

addressing the issues of evolution and data integra-

tion, we must employ agents that utilize smaller com-

ponents of the ontology. Simply using the entire on-

tology will result in the same tractability issues that

exist for existing monolithic ontologies. Thus, sound

modularization is necessary to produce views for the

agent(s).

Referring to Figure 2, it can be argued that the

concept Wine Product is composed of two concepts

from closely related domains: the Wine and Estate.

The former is composed of Grape, Colour, Sugar,

and Body whereas the latter is Region and Winery. For

the remainder of this section, we are motivated by be-

ing able to modularize the lattice in Figure 2 as a ﬁrst

step of obtaining modules that a Wine agent and an

Estate agent can use for reasoning purposes. That is

to say, queries regarding a wine would be delegated

to the wine agent, whereas queries about an estate are

delegated to the estate agent. Queries that involve ele-

ments from both would require the co-operation from

both agents. Thus, the modules the agents use need

to preserve the knowledge as though they were still a

part of the original Boolean lattice (i.e., they are com-

plete).

KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development

178

Colour

Sugar

Grape

Body

Taste

Mouthfeel

Style

Wine

Figure 3: The modularization of the Wine Ontology on

Wine.

4.1 Generating a Module With View

Traversal

This work seeks to generate a module using the View

Traversal modularization technique, introduced by

Noy and Musen (Noy and Musen, 2009). It is a graph-

ical modularization technique that aims to produce a

module that contains all information necessary to an-

swer a query (or set of queries). This technique is for-

malized for DIS such that it can produce the Boolean

sublattice as shown in Figure 3. First, we present the

deﬁnition of a module so that modularization can be

explored:

Deﬁnition 4.1 (Module). Given an abstract ontology

O = (C ,L,G), a module M of O is deﬁned as as an

abstract ontology M = (C

) satisfying the

following conditions:

• C

⊆ C

• L

= (L

) such that L

⊆ C

, L

is a

Boolean sublattice of L, and e

∈ L

• G

= {G

| G

∈ G ⊗t

∈ L

}

where C

and C are the carrier sets of C

and C,

respectively.

In other words, a module is a sub-ontology. This

ensures that tasks which can be performed on the on-

tology (e.g., reasoning) can also be performed on a

module. It is evident that abstract ontology given

in Figure 3 conforms to the provided deﬁnition of a

module, if we consider G

View Traversal allows for the freedom to extract a

module on any relation to any depth. To ensure that

the module we extract conforms to the deﬁnition, we

restrict the notion of View Traversal on DIS to only

traverse the partOf relation, and to travel the maxi-

mum distance. In the situation that the desired mod-

ule uses a concept from one of the rooted graphs (i.e.,

does not use the partOf relation), then we ﬁrst de-

termine the concept that is the root of the graph, then

conduct the View Traversal from that concept.

With these restrictions, we claim that the applica-

tion of View Traversal to a Boolean lattice for a given

∈ L is equivalent to the principal ideal generated

by c

, deﬁned below.

Deﬁnition 4.2 (View Traversal Module). For a given

abstract ontology O

def

= (C ,L, G) and starting concept

∈ L, the module M

= (C

) is deﬁned as:

1. L

= (L

) is the principal ideal generated by

2. G

= {G

| G

∈ G ∧t

∈ L

}

3. C

= {c | c ∈ L

T D

∨ ∃(G

| G

∈ G

: c ∈ C

)}

where C

is the carrier set for C

It is possible for a single View Traversal to be cre-

ated from c

. For example, consider the scenario

where we wish to create a single module given two

starting concepts c

= (Colour ⊕ Sugar) and Taste =

(Sugar ⊕ Body). To achieve this, we are required to

extract a single Boolean sublattice that covers both

and Taste. As the deﬁnition of View Traversal

provided uses a single concept, we construct a proxy

starting concept that is the combination of c

and

Taste, i.e., c

= c

⊕ c

. In more general terms, let

be a set of concepts to be modularized on such that

⊆ L, then the starting concept for the View Traver-

sal is deﬁned as

= ⊕(c | c ∈ C

: c) (2)

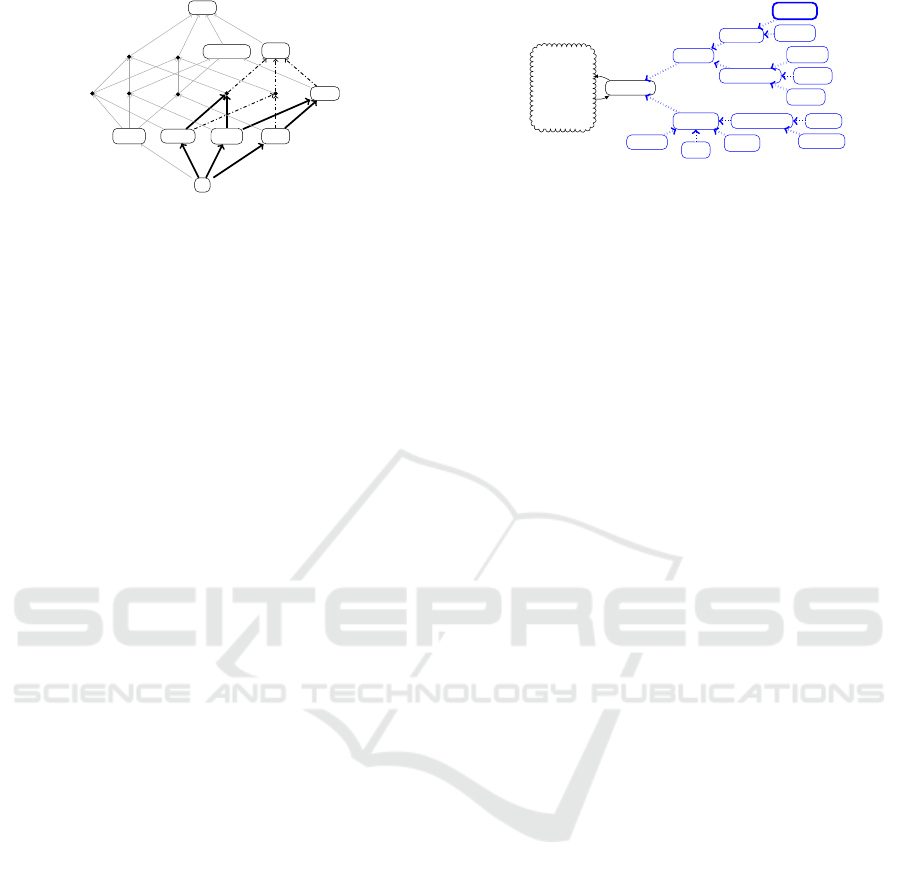
Referring to Figure 4, had we taken two View

Traversals for c

and Taste, we would have acquired

the two modules shown using the bolded black lines.

However, this would provide two distinct modules

rather than just one. By determining a proxy c

, we

produce a single module that represents the informa-

tion that could be built using the existing concepts.

For example, by considering the proxy, we include

the concept Style that would have otherwise been for-

gotten had we taken the union of the two individual

modules (as Noy et al. do in (Noy and Musen, 2009)).

With this method, there exists two trivial scenar-

ios: for c

∈ C

we have c

for disjoint

∈ C

, or we have the joins of concepts in C

produce c

= >. In the former scenario, c

can be

disregarded as according to the deﬁnition of the lat-

tice, c

implies c

⊕ c

= c

. In the latter, the

Boolean lattice of the module will be isomorphic to

Throughout this paper, we adopt the uniform linear no-

tation provided by Gries and Schneider in (Gries and

Schenider, 1993), as well as Dijkstra and Scholten in (Di-

jkstra and Scholten, 1990). The general form of the no-

tation is ?(x | R : P) where ? is the quantiﬁer, x is the

dummy or quantiﬁed variable, R is predicate representing

the range, and P is an expression representing the body of

the quantiﬁcation. An empty range is taken to mean true

and we write ?(x |: P); in this case the range is over all

values of variable x.

Toward Measuring Knowledge Loss due to Ontology Modularization

179

Colour

Sugar

Grape

Body

Taste

Mouthfeel

Style

Wine

Figure 4: Modularization with c

= Colour ⊗ Sugar and

Taste = Sugar ⊗ Body.

the original ontology’s. Although counterintuitive to

modularization, this aligns with the notion of what in-

formation can be built. Such a module implies that all

atoms of the ontology were required.

We now introduce how View Traversal operates

for concepts that belong to one of the rooted graphs

of the ontology (i.e., c

∈ G). The deﬁnition of View

Traversal requires c

∈ L, thus we deﬁne a rooted

View Traversal into the Boolean lattice as the sce-

nario where c

/∈ L. For example, in Figure 5, rooted

graphs have been added to the concept Mouthfeel.

The rest of the Boolean lattice is not shown for eas-

ier viewing. These rooted graphs are created by the

domain experts at the instantiation of the ontology to

enrich the domain by providing additional concepts

that are not comprised of the data that is in Table 1.

For example, since mouthfeel is partOf Wine, we can

say that a wine and opulence are related by associ-

atedWith relationship, but no data from our domain

contains speciﬁc data that corresponds to opulent. If

there existed data for opulent, it would belong to the

Boolean lattice (i.e., our L). With this in mind, we

project a View Traversal on the concept Opulent, i.e.,

= Opulent. As this concept does not belong to the

lattice, we cannot generate the ideal from it. There-

fore, we need to search for the root of the graph to

which opulent belongs and then work out the View

Traversal from it.

Recall that according to the deﬁnition of the

rooted graphs, the root must be a concept in the

Boolean lattice, thus, we can determine the principal

ideal of the root. In the example, Opulent belongs to

a rooted graph which Mouthfeel is the root of, thus,

Mouthfeel would be the root concept, and the ideal

can be generated as before. Additionally, the set of

rooted graphs that belongs to the module will be re-

stricted to only the graphs to which c

belongs. In

the example, the graph that contains Negative would

not be included because it is a different rooted graph.

If both graphs were desired from the View Traver-

sal, the agent would be required to modularize on

a concept that is shared among the graphs, such as

Smoothness. In this scenario, we generate a set of

Mouthfeel

Lattice in

Figure 2

Positive

Negative

Location

Smoothness

Opulent

Angular

Creamy

Buttery

Velvety

Fatty

EarthyAustere

Smoothness Cassis

Charcoal

assocWith

Figure 5: The Wine Ontology enriched with rooted graphs

(i.e., G) with root Mouthfeel.

root concepts,

= {t

| c

∈ C

, where C

is the set of vertices in

}

which is the set of concepts in the Boolean lattice

that are the root of a graph that has queried for View

Traversal. In other words, for each rooted graph that

contains a starting concept for View Traversal, we

take its root. Then, with this set of roots, we conduct

View Traversal as deﬁned in Equation 2. This results

in the following:

Deﬁnition 4.3 (Rooted View Traversal). For a given

abstract ontology O

def

= (C, L,G) and a set of root

concepts C

corresponding to a c

/∈ L, the module

= (C

) is deﬁned as:

1. L

= (L

) is the principal ideal generated by

⊕(c | c ∈ C

: c)

2. G

= {G

| G

∈ G ∧ G

= (C

) ∧ t

∈ L

∧

∃(c

| c

∈ C

∧ c

∈ C

)}

3. C

= {c | c ∈ L

∧ ∃(G

| G

∈ G

: c ∈ C

)}

There are two differences between Deﬁnitions 4.2

and 4.3. The ﬁrst is that the Boolean lattice L

is gen-

erated by the combination of the roots of the graphs

in the set C

rather than the input c

. The second is

that not all graphs are included; we only include the

graphs that c

is one of its vertices.

4.2 Formalization of View Traversal

The modularization of DIS has been so far deﬁned at

the abstract ontology level with Deﬁnitions 4.2 and

4.3. We now deﬁne the DIS that these abstract on-

tologies belong to and the function that produces it.

Deﬁnition 4.4 (View Traversal). For a given DIS

def

= (O,A,τ) and concept c such that c ∈ C, we deﬁne

a View Traversal as a function such that

V T : I × c → M

, where M

= (O

,τ

) satisﬁes:

1. O

is the View Traversal Module generated by c.

2. A

= (A

,+,·,−, 0,1,c

)

k∈L

3. τ

is the restriction of τ to only the elements of A

where L

is the carrier set of the Boolean lattice L

, and A

= {a | a ∈ A ∧ τ(a) ∈ L

KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development

180

We introduce the binary operators of composition

and chaining that are carried over View Traversals.

We show that, similar to the View Traversal in litera-

ture (Noy and Musen, 2009), they are preserved.

Given a DIS I and two View Traversals T

and T

that are modularized on starting concepts c

and c

we deﬁne composition of View Traversals as both T

and T

being applied to I :

∗ T

= V T (I ,c

⊕ c

) (3)

This deﬁnition of composition results in a single

module being produced from multiple View Traver-

sals. Additionally, ∗ is both commutative and asso-

ciative, inheriting the commutativity and associativity

of the join operator it utilizes. It is also trivial to show

the composition of a View Traversal on c

and an-

other View Traversal on c

where c

is equal to

the View Traversal of c

V T (I,c

⊕ c

)

⇐⇒ hc

⇒ c

⊕ c

= c

V T (I,c

)

(4)

The chaining of two View Traversals T

and T

the process of applying T

to the result of T

◦ T

= V T (V T (I , c

),c

) (5)

This deﬁnition of chaining results in the sequen-

tial process of ‘modularizing a modularization’, and

is not necessarily commutative. T

is restricted to the

module produced by T

, and may no longer include

. In this situation, the result would be the empty

DIS, i.e., C = ({},{}, {}).

4.3 Properties of DIS View Traversal

We provide the properties of a module adhering to

Deﬁnition 4.2. We assume c

6= > to avoid the trivial

case of the module being isomorphic to the ontology.

Claim 4.1. The produced Boolean algebra associ-

ated to the Boolean lattice of View Traversal is not a

subalgebra of the Boolean algebra associated to the

Boolean lattice of the ontology.

This is easily proven by showing the lack of

preservation of operators. In particular, the 0-ary op-

erator of > is not preserved in the module’s associated

Boolean algebra.

This claim is signiﬁcant as the Boolean sublattice

(i.e., the module) can be compared to the Boolean lat-

tice of the ontology and be deﬁned as an embedding.

However, as it is not a Boolean subalgebra, the alge-

bras cannot be deﬁned in a similar way as an embed-

ding. This distinction results in the ability to guar-

antee the preservation of the structural information of

the concepts when modularizing (i.e., lattice operators

of join and meet), but not the information pertaining

the additional algebraic operators, summarized in the

following claim.

Claim 4.2. A View Traversal does not preserve the

complement operator of the ontology’s Boolean lat-

tice.

This is trivially proven by demonstrating that in

the View Traversal, e

= c

, but in the ontology, e

>, and due to our earlier stated assumption c

6= >,

this is a contradiction.

The notions of local correctness and complete-

ness are deﬁned in (d’Aquin et al., 2009), and cor-

respond to the logical modularization techniques that

are based on conservative extension. Using these def-

initions, we make the following claim.

Claim 4.3. A View Traversal is locally complete but

not locally correct with respect to the original ontol-

ogy.

The View Traversals completeness follows from

the Boolean lattice being an ideal, which by deﬁni-

tion, must preserve and be closed under the join and

meet operators. However, as shown in Claim 4.2, the

complement is not preserved, and thus the module is

not locally correct.

5 QUANTIFYING KNOWLEDGE

LOSS

An important characteristic of the module is that its

Boolean lattice is the principal ideal generated by c

(or the root starting concept c

). As a result of the

existence of this ideal and the ﬁrst theorem of isomor-

phism (Van der Waerden et al., 1950), there must be a

homomorphism from one Boolean algebra to another

Boolean algebra that this ideal is its kernel.

The homomorphism is from one Boolean algebra

to another such that f : B

→ B

. We deﬁne f as fol-

lows:

f (p) = p ⊗ p

(6)

for every p ∈ B

and an arbitrarily chosen p

∈ B

We remind the reader that the ⊗ operator of a DIS

functions identically to the meet operator (⊗) of tra-

ditional lattices. The kernel is deﬁned as follows:

ker( f ) = {p ∈ B

| f (p) = e

} (7)

To illustrate the utilization of this function, we use

the original Boolean lattice found in Figure 2, and

use Equation 6, setting p

= Estate, where Estate =

Region ⊕Winery. Intuitively, Equation 6 maps every

concept from the original Boolean lattice to Estate or

Toward Measuring Knowledge Loss due to Ontology Modularization

181

Region Winery

Estate

(a) The Boolean lattice

mapped to by f

Grape

Colour

Sugar

Body

Taste

Mouth f eel

Style

Wine

(b) The kernel of f

Figure 6: f (p) = p ⊗ Estate.

one of its parts, populating the kernel with every ele-

ment that maps to e

according to Equation 7. As Es-

tate and all its parts is a subset of the original Boolean

lattice, there will be concepts that map to the same el-

ement (i.e., not be injective).

For example, consider the following three evalua-

tions,

f (Taste) = Taste ⊗ Estate = e

f (Region) = Region ⊗ Estate = Region

f (Winery) = Winery ⊗ Estate = Winery

The function maps any value that is a part of

Estate (such as Region) to itself, and anything that

has no parts of Estate (such as Taste or Grape) to

. With the starting concept c

= Estate, we claim

that the kernel of the function f is composed of

the concept Wine and all its parts, i.e., ker( f ) =

,Grape,Colour,Sugar,Body, . ..}. Figure 6 dis-

plays both Boolean lattices: the one mapped to by f

and the one populated by ker( f ).

The kernel is speciﬁcally the principal ideal gen-

erated by the complement of p

that we denote by

. In our example, Wine is the complement of Estate

(it is the concept that can be created by combining

the atoms that are not partOf Estate). Therefore, the

relationship between p

and the module from View

Traversal can be observed: for any p

∈ B, where

6= c

, the kernel of f corresponds to the mod-

ule generated by c

, or more speciﬁcally, VT (c

) is

equal to the lattice mapped to by f where p

= c

The nature of modularizing an ontology into

smaller components lends itself to the loss of knowl-

edge. The extraction of a smaller part of the ontology

implies something is lost. The relationship between

the kernel and the Boolean algebra mapped to via the

function f embodies this loss of knowledge. If the

kernel is taken to be the module extracted via View

Traversal, then the Boolean algebra mapped to by f

captures the knowledge that is lost. As we associate

with the kernel because it is the result of the modu-

larization, we speak of the knowledge that is kept (or

lost) in terms of the kernel. More speciﬁcally, by as-

sessing and quantifying the size of the kernel, we are

measuring what is being lost due to modularization.

In Figure 6, the concepts of Grape, Colour, and any

combination of them were lost. Thus, from an ontol-

ogist perspective, the manipulation of the homomor-

phism and the kernel allow for the control of what an

agent will know (through the kernel) or what an agent

cannot know (through the Boolean algebra mapped to

via f ).

One can envision a measure for loss of domain

knowledge due to View Traversal proportional to the

number of atoms included in the kernel. In other

words, for a given View Traversal, V T , we say the

percentage of knowledge lost L(V T ) is given as

L(V T ) =

number of atoms in kernel

total number of atoms

× 100 (8)

We can further study this measure, its scale, and give

its laws.

6 DISCUSSION AND FUTURE

WORK

As a consequence of the module produced via View

Traversal not being locally correct, it implies that

what is reasoned from the module may be different

from what is reasoned from the ontology. However,

since the join and meet operators are preserved in the

module, any knowledge deduced in the module using

only those operators will be consistent i.e., the same

knowledge would be deduced in the original ontology.

This is not true for the complement: what they gen-

erate from the complement will be true in the context

of the module, but will not necessarily be when con-

textualized by the ontology. For example, referring

to Figure 6, the complement of Region in the mod-

ule will be Winery. However, in the original ontology

(when all atoms are present), the complement of Re-

gion is not Winery, it is the concept c, deﬁned as

c = Winery ⊕ Grape ⊕Colour ⊕ Sugar ⊕ Body.

We stress that what is generated from the complement

(in the context of the module) is merely incomplete:

the complement computed in the View Traversal will

be a partOf the complement computed in the ontol-

ogy. For example, Winery is a part of the true com-

plement c (as is grape, colour, sugar, and body).

Our approach also comes with a direct usage of

the algebraic notion of a homomorphism associated

to an ideal as a means for measuring the knowledge

that is lost due to only focusing on the module. This is

extremely important as the many questions that are in-

herent to modularization need to have an idea to what

KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development

182

is left behind when you use a module for reasoning

rather than the whole ontology. It is the questions

of knowledge coverage by a module and whether a

set of modules covers the same knowledge that can

be generated using the ontology from which they are

obtained. The kernel associated to a module tells us

about the concepts that we are omitting through mod-

ularization, therefore indirectly telling us about the in-

formation and the domain knowledge we are losing.

Certainly there is still work to be done on explicitly

elaborating this issue. In particular, being able to de-

ﬁne loss in more ways than just the size of the kernel.

Although this provides us with a way of measuring

loss and a way to compare modules based on this, it

does not sufﬁciently capture the idea that there may

exist concepts within the ontology that communicate

more information or knowledge. As far as we know,

we are the ﬁrst to relate the notion of kernel to the part

of knowledge that is lost through modularization. We

illustrated this point using View Traversal techniques.

In this paper, we simply point to this direction as a

viable means for measuring loss of information when

using modularization.

7 CONCLUSION

In this paper, we presented the application of View

Traversal to an ontology represented with DIS. The

utilization of DIS is shown to be advantageous due to

the Boolean algebra allowing for the communication

of the module as the ideal. The Wine Ontology was

utilized as it is a common benchmark for demonstrat-

ing a conceptually rich ontology. With this, we are

able to formally deﬁne what a module is, and how it

can be produced using View Traversal on a starting

concept, c

. With the homomorphism, it is also pos-

sible to create a module that hides a speciﬁc set of

knowledge. This allows for the extraction of a mod-

ule based on what an agent should or should not know.

The knowledge that is lost in the modularization pro-

cess is quantiﬁed using the kernel of the homomor-

phism.

The proposed modularization technique is shown

to ensure the completeness of the module. Due to the

complement operator, the same cannot be said for the

correctness of the module. Extracting a module that

is both complete and correct would result in a subal-

gebra, and correspond to the widely-used techniques

that aim to exhibit conservative extension in DL. Ad-

ditionally, although the kernel quantiﬁes the knowl-

edge that is lost due to modularization, other measure-

ments of knowledge need to be explored. It is com-

mon that certain concepts are more signiﬁcant within

a domain, and the loss of such a concept due to mod-

ularization should be reﬂected in the measurement of

knowledge loss.

REFERENCES

Algergawy, A., Babalou, S., and K

onig-Ries, B. (2016). A

new metric to evaluate ontology modularization. In

SumPre@ ESWC.

Anand, N., van Duin, R., and Tavasszy, L. (2014).

Ontology-based multi-agent system for urban freight

transportation. International Journal of Urban Sci-

ences, 18(2):133–153.

Ashburner, M., Ball, C. A., Blake, J. A., Botstein, D.,

Butler, H., Cherry, J. M., Davis, A. P., Dolinski, K.,

Dwight, S. S., Eppig, J. T., et al. (2000). Gene ontol-

ogy: tool for the uniﬁcation of biology. Nature genet-

ics, 25(1):25.

Baader, F. (2003). The description logic handbook: Theory,

implementation and applications. Cambridge univer-

sity press.

Babalou, S., Kargar, M. J., and Davarpanah, S. H. (2016).

Large-scale ontology matching: A review of the liter-

ature. In Web Research (ICWR), 2016 Second Inter-

national Conference on, pages 158–165. IEEE.

Bao, J., Voutsadakis, G., Slutzki, G., and Honavar, V.

(2009). Package-based description logics. Modular

ontologies, 5445:349–371.

Belmonte, M.-V., P

erez-de-la Cruz, J.-L., and Triguero, F.

(2008). Ontologies and agents for a bus ﬂeet man-

agement system. Expert Systems with Applications,

34(2):1351–1365.

Benomrane, S., Sellami, Z., and Ayed, M. B. (2016). An

ontologist feedback driven ontology evolution with an

adaptive multi-agent system. Advanced Engineering

Informatics, 30(3):337–353.

Bienvenu, M., Kikot, S., Kontchakov, R., Podolskii, V. V.,

and Zakharyaschev, M. (2018). Ontology-mediated

queries: Combined complexity and succinctness of

rewritings via circuit complexity. Journal of the ACM

(JACM), 65(5):28.

Bodenreider, O. (2004). The uniﬁed medical language sys-

tem (umls): integrating biomedical terminology. Nu-

cleic acids research, 32(suppl 1):D267–D270.

Brickley, D. and Miller, L. (2010). Foaf vocabulary speciﬁ-

cation 0.91.

d’Aquin, M., Schlicht, A., Stuckenschmidt, H., and Sabou,

M. (2009). Criteria and evaluation for ontology modu-

larization techniques. Modular ontologies, pages 67–

89.

Davey, B. A. and Priestley, H. A. (2002). Introduction to

lattices and order. Cambridge university press.

De Giacomo, G., Lembo, D., Lenzerini, M., Poggi, A., and

Rosati, R. (2018). Using ontologies for semantic data

integration. In A Comprehensive Guide Through the

Italian Database Research Over the Last 25 Years,

pages 187–202. Springer.

Del Vescovo, C., Parsia, B., Sattler, U., and Schneider, T.

(2011). The modular structure of an ontology: Atomic

Toward Measuring Knowledge Loss due to Ontology Modularization

183

decomposition and module count. In WoMO, pages

25–39.

Dietz, J. L. (2006). What is Enterprise Ontology? Springer.

Dijkstra, E. and Scholten, C. (1990). Predicate Calculus

and Program Semantics. Springer-Verlag New York,

Inc., New York, NY, USA.

Freitas, A., Panisson, A. R., Hilgert, L., Meneguzzi, F.,

Vieira, R., and Bordini, R. H. (2017). Applying on-

tologies to the development and execution of multi-

agent systems. In Web Intelligence, volume 15, pages

291–302. IOS Press.

Gries, D. and Schenider, F. (1993). A Logical Approach to

Discrete Math. Springer Texts And Monographs In

Computer Science. Springer-Verlag, New York.

Henkin, L. and Tarski, A. (1967). Cylindric algebras.

Hirsch, R. and Hodkinson, I. (2002). Relation algebras by

games, volume 147. Gulf Professional Publishing.

Huhns, M. N. and Singh, M. P. (1997). Ontologies for

agents. IEEE Internet computing, 1(6):81–83.

Hustadt, U., Motik, B., and Sattler, U. (2005). Data com-

plexity of reasoning in very expressive description

logics. In IJCAI, volume 5, pages 466–471.

Jaskolka, J., MacCaull, W., and Khedri, R. (2015). Towards

an ontology design architecture. In Proceedings of

the 2015 International Conference on Computational

Science and Computational Intelligence, CSCI 2015,

pages 132–135.

Jim

enez-Ruiz, E., Kharlamov, E., Zheleznyakov, D., Hor-

rocks, I., Pinkel, C., Skjæveland, M. G., Thorstensen,

E., and Mora, J. (2015). Bootox: Practical mapping

of rdbs to owl 2. In International Semantic Web Con-

ference, pages 113–132. Springer.

Kantamneni, A., Brown, L. E., Parker, G., and Weaver,

W. W. (2015). Survey of multi-agent systems for mi-

crogrid control. Engineering applications of artiﬁcial

intelligence, 45:192–203.

Khan, Z. C. and Keet, C. M. (2015). Toward a framework

for ontology modularity. In Proceedings of the 2015

Annual Research Conference on South African Insti-

tute of Computer Scientists and Information Technol-

ogists, page 24. ACM.

LeClair, A. and Khedri, R. (2016). Conto: a prot

e plugin

for conﬁguring ontologies. Procedia Computer Sci-

ence, 83:179–186.

Maedche, A., Motik, B., Stojanovic, L., Studer, R., and

Volz, R. (2003). Ontologies for enterprise knowledge

management. IEEE Intelligent Systems, 18(2):26–33.

Marinache, A. (2016). On the structural link between on-

tologies and organised data sets. Master’s thesis.

Motik, B. (2006). Reasoning in description logics using

resolution and deductive databases. PhD thesis, Karl-

sruhe Institute of Technology, Germany.

Movaghati, M. A. and Barforoush, A. A. (2016). Modular-

based measuring semantic quality of ontology. In

Computer and Knowledge Engineering (ICCKE),

2016 6th International Conference on, pages 13–18.

IEEE.

Nadal, S., Romero, O., Abell

o, A., Vassiliadis, P., and Van-

summeren, S. (2019). An integration-oriented ontol-

ogy to govern evolution in big data ecosystems. Infor-

mation Systems, 79:3–19.

Noy, N. and Musen, M. (2009). Traversing ontologies to

extract views. Modular Ontologies, pages 245–260.

Noy, N. F., McGuinness, D. L., et al. (2001). Ontology

development 101: A guide to creating your ﬁrst ontol-

ogy.

Pakdeetrakulwong, U., Wongthongtham, P., Siricharoen,

W. V., and Khan, N. (2016). An ontology-based multi-

agent system for active software engineering ontol-

ogy. Mobile Networks and Applications, 21(1):65–88.

Poggi, A., Lembo, D., Calvanese, D., De Giacomo, G.,

Lenzerini, M., and Rosati, R. (2008). Linking data

to ontologies. In Journal on data semantics X, pages

133–173. Springer.

Raimond, Y., Abdallah, S. A., Sandler, M. B., and Giasson,

F. (2007). The music ontology. In ISMIR, volume

2007, page 8th. Citeseer.

Rector, A., Rogers, J., and Pole, P. (1996). The galen high

level ontology.

Sikorski, R., Sikorski, R., Sikorski, R., Math

ematicien, P.,

Sikorski, R., and Mathematician, P. (1969). Boolean

algebras, volume 2. Springer.

Spackman, K. A., Campbell, K. E., and C

e, R. A. (1997).

Snomed rt: a reference terminology for health care. In

Proceedings of the AMIA annual fall symposium, page

640. American Medical Informatics Association.

Stone, M. H. (1936). The theory of representation for

boolean algebras. Transactions of the American Math-

ematical Society, 40(1):37–111.

Suchanek, F. M., Kasneci, G., and Weikum, G. (2008).

Yago: A large ontology from wikipedia and wordnet.

Web Semantics: Science, Services and Agents on the

World Wide Web, 6(3):203–217.

Van der Waerden, B. L., Artin, E., and Noether, E. (1950).

Moderne algebra, volume 31950. Springer.

Wache, H., Voegele, T., Visser, U., Stuckenschmidt, H.,

Schuster, G., Neumann, H., and H

ubner, S. (2001).

Ontology-based integration of information-a survey

of existing approaches. In IJCAI-01 workshop: on-

tologies and information sharing, volume 2001, pages

108–117. Seattle, USA.

Xiao, G., Calvanese, D., Kontchakov, R., Lembo, D.,

Poggi, A., Rosati, R., and Zakharyaschev, M. (2018).

Ontology-based data access: A survey. IJCAI.

Xue, X. and Tang, Z. (2017). An evolutionary algo-

rithm based ontology matching system. Journal of

Information Hiding and Multimedia Signal Process-

ing, 8(3):551 – 556. High heterogeneity;Matcher

combination;Matching system;Ontology match-

ing;Optimal model;Recall and precision;Semantic

correspondence;State of the art;.

Zhou, L., Pan, M., Sikorski, J. J., Garud, S., Aditya,

L. K., Kleinelanghorst, M. J., Karimi, I. A., and Kraft,

M. (2017). Towards an ontological infrastructure

for chemical process simulation and optimization in

the context of eco-industrial parks. Applied Energy,

204:1284–1298.

Ziegler, P. and Dittrich, K. R. (2004). Three decades of

data intecration—all problems solved? In Building

the Information Society, pages 3–12. Springer.

KEOD 2019 - 11th International Conference on Knowledge Engineering and Ontology Development

184