AN ADAPTIVE SLIDING-MODE FUZZY CONTROL (ASMFC)
APPROACH FOR A CLASS OF NONLINEAR SYSTEMS
Jian-Hua Zhang and Johann F. Böhme
Signal Theory Group
Department of Electrical Engineering and Information Sciences, Ruhr-Universität Bochum
Bochum 44780, Germany
Keywords: Sliding mode control, Fuzzy controller, TSK fuzzy model, Feedback linearizable systems, Adaptive fuzzy
identification
Abstract: This paper uses the concept of sliding-mode control (SMC), as a special approach in nonlinear control theory,
in aiding the design of a fuzzy controller. The mathematical specifics of the presented approach are given
along with its performance analysis. It was concluded that the new approach with distinctive characteristics
holds potential for coping with difficult control problems for a class of complex (generally nonlinear)
systems.
1 INTRODUCTION
In the previous literature, fuzzy control, especially
adaptive and self-learning fuzzy control, has been
successfully applied for complex nonlinear control
problems (Driankov, Hellendoorn and Reinfrank,
1993; Passino and Yurkovich, 1998; Wang, 1993;
Hwang and Lin, 1992; Takagi and Sugeno, 1983,
1985; Jang, 1992a, 1992b). One of the most
attractive features of adaptive fuzzy control is that
linguistic knowledge elicited from domain expert or
available input-output data set can be conveniently
incorporated into the design process of fuzzy
controller.
In a sliding-mode controller (SMC), the sliding
region is generally a hyper-plane. In the simple case
of 2-D, the sliding region is simply a line. Separated
by this sliding line, control force is switched to its
maximum at one side and minimum at another. In
the theory of SMC, it is usually presumed that the
SMC controller can switch from one extreme to
another extreme arbitrarily fast. Based on this
assumption, the trajectory can remain along this line
once it reaches it. In practice, nevertheless, it is well
known in SMC theory that the trajectory of the
system always chatter around this sliding line, rather
than sliding strictly along it (Hung, Gao and Hung,
1993; Slotine and Li, 1991). Thus the output of the
SMC controller alternates its sign along the switch
line.
The synergism of fuzzy control and SMC has
also been a hot research topic (Palm, 1992; Palm,
Driankov and Hellendoorn, 1996; Palm and Stutz,
2003). One reason, from the perspective of the basic
property of a control system—stability property,
may be that the mathematically strict stability
analysis for a fuzzy controller is hard to establish
and guarantee in general cases, contrarily that for a
sliding-mode controller can be well resolved.
Another advantage offered by the SMC method
includes its capability for decoupling high-
dimensional systems into a body of lower-
dimensional sub-systems to achieve the
dimensionality reduction for a complex multi-input
multi-output (MIMO) control system (Hung, Gao
and Hung, 1993). This advantage may be beneficial
for avoiding the curse of dimensionality inherent in
a fuzzy inference system (FIS) even with moderately
number of input variables (Jang, 1993; Chen and
Tsao, 1989).
In this paper, to improve the transient
performance of fuzzy controller, the state-space of
control system is partitioned into a number of local
cells, across individual cell state-space the sliding
hyper-plane of SMC controller within its cell is
designed separately in an adaptive fashion. The
paper is organized in the following way. Firstly
some basics of SMC are briefly introduced. In
section III, the detailed approach of adaptive sliding-
mode fuzzy control (ASMFC) is developed. Finally
its performance and unique features are discussed.
193
Zhang J. and Böhme J. (2004).
AN ADAPTIVE SLIDING-MODE FUZZY CONTROL (ASMFC) APPROACH FOR A CLASS OF NONLINEAR SYSTEMS.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 193-197
DOI: 10.5220/0001124801930197
Copyright
c
 SciTePress

2 BASICS OF SMC METHOD
Let us consider a class of continuous-time nonlinear
dynamical system which is feedback linearizable
and of the canonical form:
()
()
()
()
(
)
() () () [] ()
() ()
⎪
⎩
⎪
⎨
⎧
=
+=
−−
txty
tbutxtxtxtxftx
nnn
,,,,
21
&
L
(1)
where
[]
⋅f is an unknown continuous function
(generally nonlinear), b>0 is the controller gain,
()
ℜ∈tx is the system’s state variable, and
() ()
ℜ∈ℜ∈ tytu , are the input variable and output
variable of the system, respectively. Our goal is to
force the state vector of the system (1) (where the
superscript
τ
denotes the vector transpose)
() () ()
()
()
[]
τ
txtxtx
n 1
,,,
−
= L
&
tx
to follow a predefined reference trajectory
() () ()
()
()
[]
τ
txtxtx
n
rrrr
1
,,,
−
= L
&
tx .
Define the tracking error vector as the difference
between the actual states and desired states, i.e.,
() () ()
ttt
r
xxe −= (2)
then the control problem can be formalized as: find a
control law
()
tu such that ()
0lim =
∞→
t
t
e
.
A candidate of such a control law is
() () []
(
)
() () ()
twttxFtu
n
r
+++Θ−= emtx
τ
, (3)
where
()
tw is an auxiliary control input to be
determined,
[] ⋅F is a proper function with
sufficiently rich parameter set
Θ used to well
approximate unknown function
[]
⋅f in eqn. (1), i.e.,
fF
ˆ
= may be implemented by an adaptive fuzzy
model (Jang, 1992a; Jang, 1992b; Jang, 1993), and
[]
1,,,
1
L
−
=
nn
mm
τ
m is an properly chosen vector
that controls the performance of the closed-loop
system with the control law (3). With this control
law, the resulting closed-loop system is a linear one
as
()
()
(
)
() ()() ()() []
()
tw
Ffte
n
m
n
emt
n
e
+
Θ−=++
−
+ ,
1
1
txtxL
(4)
Our suggested control approach is formulated as
the following procedures:
1. Use a parameterized adaptive fuzzy model to
approximate
[]
⋅f , i.e., adaptively update the
parameter vector of fuzzy model such that for
()
n
ℜ∈∀ tx and an upper bound of error 0>
ε
,
(
)
[
]
(
)
[
]
., ε ≤−Θ txtx fF (5)
2. Apply the SMC approach to design
(
)
tw to
guarantee the global stability property of the
close-loop system.
Using the standard SMC design approach, define
an error measure below:
(
)
(
)
(
)
()
() etentets
nn
++−+=
−−
L
21
)1( λλ
(6)
where constant
0>
λ
. Then the equation
()
0
=
ts is
called a switching surface in space
n
ℜ on which
(
)
te approaches to zero exponentially, i.e.,
asymptotical tracking performance is achieved.
For simplicity, introduce a kind of differential
operator to express the above differential polynomial
as
() () [] ()
.1,,)1(,
21
1
tente
dt
d
ts
nn
n
L
−−
−
−=
⎟
⎠
⎞
⎜
⎝
⎛
+=
λλλ
(7)
The control law in eqn. (3) guarantees the system
state trajectory, whatever the initial condition may
be, will approach and subsequently maintain on the
sliding surface
(
)
0
=
ts , if the condition
(
)
(
)
(
)
tststs η −≤⋅
&
(8)
holds. Here
η
is a positive constant, which restricts
that the state trajectory hits the sliding surface in a
finite time (Hung, Gao and Hung, 1993; Slotine and
Li, 1991). Thus
(
)
0→te exponentially with a time
constant
(
)
λ
1
−
n .
Taking
[
]
λλλ
τ
,,)1(,,0
21
L
−−
−=
nn
nm (9)
differentiating eqn. (6), and inserting eqn. (5) into it
yield
(
)
(
)
(
)
(
)
(
)
(
)()
., twFfts +
Θ
−
=
txtx
&
(10)
and
(
)
()() ()()()() [] ()
.sgn, stwFf
dt
tsd
+Θ−= txtx (11)
Then condition (8) always maintains if we choose
(
)
(
)
(
)
.sgn stw
η
ε
+
−
=
(12)
By substituting eqns. (9) and (11) into eqn. (3),
eventually we have the control law
(
)
(
)
(
)
[
]
(
)
()()
.sgn
,,)1(,,0,
21
s
tenxFtu
nnn
r
ηε
λλλ
+−
−++Θ−=
−−
Lx
(13)
then the closed-loop system (4) can asymptotically
track the reference state trajectory specified
beforehand with guarantee of global stability
property (Jang, 1992b).
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
194

3 CASE STUDY: A 2-D FEEDBACK
LINEARIZYBLE NONLINEAR
SYSTEM
Consider a 2nd-order system described by state-
space equation
() () () []
)(, tbutxtxftx +=
&&&
(14)
One feasible control law of SMC for 2
nd
-order
system eqn. (14) may be chosen as:
vsgku +⋅−= )(
φ
(15)
where v is an equivalent control used when the
system state lies in the sliding mode, constant
0>k
represents the maximum output of SMC controller.
According to eqn. (6), the switching hyper-plane is
.0=+= ees
λ
&
(16)
There are many ways to define
)(sg
φ
in eqn. (15)
for different purposes. Three candidate functions for
define
)(sg
φ
are given here:
1. Sign function, i.e.,
()
⎩
⎨
⎧
>
<−
==
0for ,1
0for ,1
)sgn(
s
s
ssg
φ
(17)
Introduction of the sign function
)sgn(s often causes
chattering problem for a SMC controller. One way
to alleviate the problem is to use another nonlinear
function below.
2. Saturation function, i.e.,
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤
==
1for ),sgn(
1for ,
)(
φφ
φφ
φ
φ
ss
ss
s
satsg
(18)
where
φ
is a constant that determines the width of
the boundary layer around the switching surface.
In actuality, the control law resulting from this
selection of
)(sg
φ
is a continuous approximation of
the ideal relay control (Hung, Gao and Hung, 1993;
Slotine and Li, 1991). Another possible variant is as
follows.
3. Hyperbolic tangent function, i.e.,
() )tanh(
φ
φ
s
sg =
(19)
In all the above three cases, provided sufficiently
large k, SMC controller of form (15) has been shown
to be asymptotically stable (Hung, Gao and Hung,
1993; Slotine and Li, 1991).
For a 2-D system, the controller structure and the
corresponding control surface are illustrated in
Figure 1.
s
u
k
k−
s
u
k
s
u
φ −
k−
φ
k
k−
Figure 1: Three examples of SMC controllers in 2-D case.
4 ADAPTIVE SLIDING-MODE
FUZZY CONTROL (ASMFC)
From the perspective of optimal control theory,
SMC falls into the category of time sub-optimal
control. As is well known in optimal control theory,
the result of a time optimal control problem for a
regulator with set-point input is a type of Bang-Bang
control with respect to a nonlinear switching curve
shown in Figure 2. Figure 2 also illustrates the
control surface resulting from the nonlinear
switching function.
Since a fuzzy inference system (FIS) can
integrate and coordinate different control algorithms
in a seamless way by using fuzzy decision-making
logic according to the available fuzzy knowledge
and data base, we can directly incorporate the design
conception of SMC into the development of a fuzzy
controller without causing any undesirable effects.
In Takagi-Sugeno-Kang (TSK) fuzzy model, the
output of each fuzzy if-then rule is explicitly and
generally expressed as a linear combination of
controller inputs plus a constant term (Takagi and
Sugeno, 1983; Takagi and Sugeno, 1985; Hoffmann
and Nelles, 2001).
In fact, the rule output can also be a more
generally nonlinear function of the rule input
variables. In this section, we express the output of
each fuzzy rule, i.e., the control output when the
states enter into a local cell space, a switching
AN ADAPTIVE SLIDING-MODE FUZZY CONTROL (ASMFC) APPROACH FOR A CLASS OF NONLINEAR
SYSTEMS
195

function of state vector. In this way, we carefully
design a new adaptive fuzzy controller by borrowing
the notion of SMC, which actually leads to an
adaptive sliding-mode fuzzy control approach
presented in this short paper. In our approach, the
parameters in the output of each fuzzy rule that
covers different cell of state space are determined by
different SMCs that operate over the corresponding
cell state-space, whose concept was proposed by
Chen and Tsao (1989).
e
e
&
sliding line
trajectory
0
trajectory
[state plane]
Figure 2: Nonlinear switching curve and control surface.
For the ASMFC controller, the error and the rate
of error are taken as the its inputs. Its l-th fuzzy if-
then rule in the rule base takes the format of
l
R : if e is
l
F
1
and e
&
is
l
F
2
,
then
)(
l
ll
l
cee
ksatu
φ
λ
++
=
&
(20)
where
l
F
1
and
l
F
2
represent the linguistic label, i.e.,
input fuzzy set, which can be characterized by
proper parameterized membership function defined
over the corresponding universe of discourse.
With only a small number of if-then rules,
ASMFC can generate a complex nonlinear switching
function, which is difficult to achieve by standard
SMC method. Also note that the rule output in
expression (20) need not to be a saturation function,
it could be either a sign function or hyperbolic
tangential function described before.
Figure 3: Fuzzification of error e and its rate e
&
.
In the case of a 2-D system, the switching line
can be either a function of
e , or a function of e
&
. In
this case only a very small number of fuzzy rule
patches are required to cover the switching function
of single variable. Therefore in an ASMFC
controller the number of if-then fuzzy rules is
reduced to a reasonable and manageable amount and
thus the curse of dimensionality arising from multi-
variable fuzzy controller can be avoided.
To approximate the switching curve shown in
Figure 2, we assign 3 linguistic labels (described by
their own properly-parameterized membership
functions) to input variable
e and e
&
, respectively.
The fuzzification of
e and e
&
is illustrated in Figure
3, where symbols ‘ZO’, ’NS’, ’PS’ represent the
corresponding linguistic terms ‘zero’, ‘negative
small’, and ‘positive small’, respectively. In this
case, we partition the universe of discourse of both
input variables into 3 overlapping fuzzy subsets, and
hence we have 9 fuzzy rules in the rule-base of
fuzzy controller and the state space is partitioned
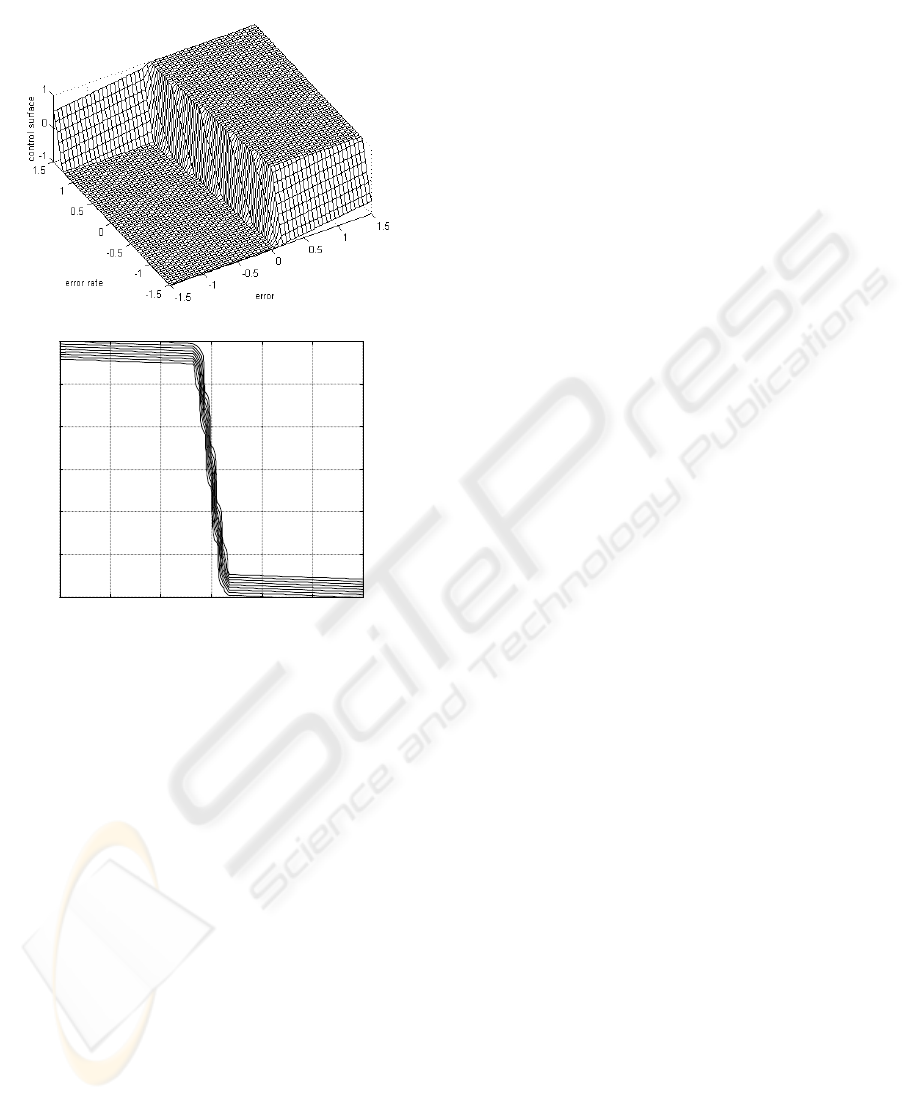
into 9 localized cells. Extensive simulation
experiments have demonstrated that the 9-rule base
suffices to well approximate the desired switching
curve. The control surface and sliding surface are
shown in Figure 4.
e
&
e
PS
ZO
N
S
N
S
ZO
PS
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
196

-1.5 -1 -0.5 0 0.5 1 1.5
-1.5
-1
-0.5
0
0.5
1
1.5
error
error rate
Figure 4: Control surface and sliding surface for an
ASMFC controller with only 9 fuzzy if-then rules.
5 CONCLUSIONS
In this short article an adaptive sliding mode fuzzy
control approach is proposed with some analysis of
its property for addressing nonlinear control
problems. This approach combines the concept of a
branch of nonlinear control theory, namely SMC,
and that of a fuzzy inference system that can
uniformly approximate any nonlinear function with
arbitrary degree of accuracy. In this sense, global
stability of the control system designed by this
approach can be mathematically established (Jang,
1992b; Hung, Gao and Hung, 1993; Slotine and Li,
1991). Nevertheless, be aware that the presented
approach seems only applicable to the class of
nonlinear systems over which the feedback
linearization technique can be performed.
REFERENCES
Chen, Y.-Y. and T.-C. Tsao, 1989. A description of the
dynamic behavior of fuzzy systems, IEEE Trans. Syst.
Man and Cybernet., vol. 19 (4), pp. 745-755.
Driankov, D., H. Hellendoorn, and M. Reinfrank, 1993.
An introduction to fuzzy control, Springer-Verlag,
Berlin/New York/Heidelberg.
Hoffmann, F. and O. Nelles, 2001. Genetic programming
for model selection of TSK-fuzzy systems, J. of
Information Sciences, vol. 136 (4), pp. 7-28.
Hung, J.Y., W. Gao and J.C. Hung, 1993. Variable
structure control: a survey, IEEE Transactions on
Industrial Electronics, vol. 40 (1), pp.2-21.
Hwang, G.-C. and S.-C. Lin, 1992. A stability approach to
fuzzy control design for nonlinear system, Fuzzy Sets
and Systems, vol. 48, pp.279-287.
Jang, J.-S. R., 1992a. Self-learning fuzzy controllers based
on temporal back propagation, IEEE Trans. Neural
Net., vol. 3 (5), pp. 714-723.
Jang, J.-S. R., 1992b. Neuro-fuzzy modeling: architecture,
analyses and applications, Ph.D. dissertation,
Department of Electrical Engineering and Computer
Science, University of California Berkeley, Berkeley,
CA.
Jang, J.-S. R., 1993. ANFIS: adaptive-network-based
fuzzy inference systems, IEEE Trans. Syst. Man and
Cybernet., vol. 23 (3), pp. 665-685.
Palm, R., 1992. Sliding mode fuzzy control, in Proc. of
IEEE International Conference on Fuzzy Systems,
pp.519-526.
Palm, R., D. Driankov, and H. Hellendoorn, 1996. Model-
based fuzzy control, Springer-Verlag, Berlin/New
York/Heidelberg.
Palm, R. and C. Stutz, 2003. Generation of control
sequences for a fuzzy gain scheduler, Int. J. of Fuzzy
systems, vol. 5 (1), pp. 1-10.
Passino, K.M. and S. Yurkovich, 1998. Fuzzy control,
Addison-Wesley Longman Inc..
Slotine, J.J.E. and W. Li, 1991. Applied nonlinear control,
Prentice-Hall, Englewood Cliffs, NJ.
Takagi, T. and M. Sugeno, 1983. Derivation of fuzzy
control rules from human operator’s control actions, in
Proc. of IFAC Symp. Fuzzy Inform., Knowledge
Representation and Decision Analysis, pp. 55-60.
Takagi, T. and M. Sugeno, 1985. Fuzzy identification of
systems and its applications to modeling and control,
IEEE Transactions on Syst. Man and Cybern., vol. 15,
pp.116-132.
Wang, L.-X., 1993. Stable adaptive fuzzy control of
nonlinear systems, IEEE Trans. Fuzzy Syst., vol. 1 (1),
pp. 146-155.
AN ADAPTIVE SLIDING-MODE FUZZY CONTROL (ASMFC) APPROACH FOR A CLASS OF NONLINEAR
SYSTEMS
197