NEW DERIVATION OF THE FILTER AND FIXED-INTERVAL

SMOOTHER WITH CORRELATED UNCERTAIN OBSERVATIONS

S. Nakamori

Department of Technology. Faculty of Education, Kagoshima University

1-20-6, Kohrimoto, Kagoshima 890-0065, Japan

R. Caballero-

Aguila

Departamento de Estad

ıstica e Investigaci

on Operativa, Universidad de Ja

Paraje Las Lagunillas, s/n, 23071 Ja

en, Spain

A. Hermoso-Carazo and J. Linares-P

erez

Departamento de Estad

ıstica e Investigaci

on Operativa, Universidad de Granada

Campus Fuentenueva, s/n, 18071 Granada, Spain

Keywords:

Least-squares estimation, ﬁltering, ﬁxed-interval smoothing, uncertain observations

Abstract:

A least-squares linear ﬁxed-interval smoothing algorithm is derived to estimate signals from uncertain obser-

vations perturbed by additive white noise. It is assumed that the Bernoulli variables describing the uncertainty

are only correlated at consecutive time instants. The marginal distribution of each of these variables, speciﬁed

by the probability that the signal exists at each observation, as well as their correlation function, are known.

The algorithm is obtained without requiring the state-space model generating the signal, but just the covariance

functions of the signal and the additive noise in the observation equation.

1 INTRODUCTION

The problem of estimating a discrete-time signal from

noisy observations in which the signal can be ran-

domly missing is considered. To describe this situa-

tion, the observation equation is formulated multiply-

ing the signal at any sample time by a binary random

variable taking the values one and zero. So, the obser-

vation equation involves both an additive and a mul-

tiplicative noise which models the uncertainty about

the signal being present or missing at each observa-

tion. It is assumed that, for each particular observa-

tion, the probability of containing the signal is known

for the observer.

In many practical situations, the variables mod-

elling the uncertainty in the observations can be as-

sumed to be independent and, then, the distribution

of the multiplicative noise is fully determined by

the probability that each particular observation con-

tains the signal. A different situation, in which the

variables modelling the uncertainty are correlated at

consecutive instants, is considered by Jackson and

Murthy (1976) who, using a state-space approach, de-

rived a least-squares linear ﬁltering algorithm which

allows to obtain the signal estimator at any time from

those in the two preceding instants.

In the last years, the estimation problem in the

aforementioned situations has been investigated under

a more general approach which does not require the

state-space model, but only the autocovariance func-

tion of the signal. Assuming that this function can

be expressed in a semi-degenerate kernel form, algo-

rithms with a simpler structure than the correspond-

ing ones when the state-space model is known have

been obtained for different estimation problems (see

Nakamori et al. (2003a) for the linear ﬁlter and ﬁxed-

point smoother when the uncertainty is modelled by

independent random variables). The situation con-

sidered by Jackson and Murthy (1976) has been also

treated in Nakamori et al. (2003b) under a covariance

approach and ﬁltering and ﬁxed-point smoothing al-

gorithms have been derived for this uncertain obser-

vation model. The aim in this paper is to propose a

ﬁxed-interval smoothing algorithm based on covari-

ance information for this last model.

The ﬁxed-interval smoothing problem appears

when all the measurements of the signal inside a time-

interval are available before proceeding to the esti-

mation. Fixed-interval smoothing techniques have

been applied to stochastic signal processing problems

203

Nakamori S., Caballero-Águila R., Hermoso-Carazo A. and Linares-Pérez J. (2004).

NEW DERIVATION OF THE FILTER AND FIXED-INTERVAL SMOOTHER WITH CORRELATED UNCERTAIN OBSERVATIONS.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 203-207

DOI: 10.5220/0001125702030207

 SciTePress

(Ferrari-Trecate and De Nicolao, 2001, Young and

Pedregal, 1999) as well as to the estimation of time-

variable parameters (Young et al., 2001).

In this paper we treat the least-squares linear

estimation problem and the ﬁxed-interval smooth-

ing algorithm is derived under an innovation ap-

proach. This approach provides an expression for the

smoother as the sum of the ﬁlter and another term,

uncorrelated with it, which can be obtained from a

backward-time algorithm.

The ﬁltering and ﬁxed-interval smoothing algo-

rithms are applied to a simulated observation model

where the signal cannot be missing in two consecutive

observations, situation which can be covered by the

correlation form considered in the theoretical study.

2 ESTIMATION PROBLEM

We consider the least-squares (LS) linear estimation

problem of a discrete-time signal from noisy uncer-

tain observations described by

y(k) = θ(k)z(k) + v(k) (1)

where the involved processes satisfy:

(I) The signal process {z(k); k ≥ 0} has zero mean

and its autocovariance function is expressed in a semi-

degenerate kernel form, that is,

(k, s)=E[z(k)z

(s)]=

A(k)B

(s), 0 ≤ s ≤ k

B(k)A

(s), 0 ≤ k ≤ s

where A and B are known n × M

matrix functions.

(II) The noise process {v(k); k ≥ 0} is a zero-mean

white sequence with known autocovariance function,

E[v(k)v

(s)] = R

(k)δ

(k − s).

(III) The multiplicative noise {θ(k); k ≥ 0}

is a sequence of Bernoulli random variables with

P [θ(k) = 1] =

θ(k) and autocovariance function

(k, s) =

0, |k − s| ≥ 2

E[θ(k)θ(s)] − θ(k)θ(s), |k − s| < 2

(IV) The processes {z(k); k ≥ 0}, {v(k); k ≥ 0}

and {θ(k); k ≥ 0} are mutually independent.

The purpose is to obtain a ﬁxed-interval smooth-

ing algorithm; concretely, assuming that the obser-

vations up to a certain time L are available, our

aim is to ﬁnd recursive formulas which allow to ob-

tain the estimators of the signal, z(k), at any time

k ≤ L. For this purpose, we will use an innova-

tion approach. If by(k, k − 1) denotes the LS lin-

ear estimator of y(k) based on {y(1), . . . , y(k − 1)},

ν(k) = y(k) − by(k, k − 1) represents the innova-

tion contained in the observation y(k), that is, the

new information provided by y(k) after its estima-

tion from the previous observations. It is known that

the LS linear estimator of z(k) based on the observa-

tions {y(1), . . . , y(L)}, which is denoted by bz(k, L),

is equal to the LS linear estimator based on the in-

novations {ν(1), . . . , ν(L)}. The advantage of con-

sidering the innovation approach to address the LS

estimation problem comes from the fact that the in-

novations constitute a white process; then, by denot-

ing Π(i) = E[ν(i)ν

(i)], the Orthogonal Projection

Lemma (OPL) leads to

bz(k, L) =

i=1

E[z(k)ν

(i)]Π

−1

(i)ν(i). (2)

In view of (2), the ﬁrst step to obtain the estimators

is to establish an explicit formula for the innovations,

which is presented in Theorem 1. Afterwards, in the

next section, we present recursive formulas for the

ﬁxed-interval smoother, bz(k, L), k < L, including

that of the ﬁlter, bz(k, k). These formulas have been

derived by decomposing (2) as the ﬁlter and a correc-

tion term uncorrelated with it, and obtaining recursive

expressions for both terms from the OPL.

2.1 Innovation process

When the variables {θ(k); k ≥ 0} modelling the un-

certainty are independent all the information prior to

time k which is required to estimate y(k) is provided

by the one-stage predictor of the signal, bz(k, k − 1).

However, for the problem at hand, the correlation be-

tween θ(k − 1) and θ(k), which must be considered

to estimate y(k), is not contained in bz(k, k − 1). Con-

cretely, as it is indicated in Theorem 1, in this case the

innovation is obtained by a linear combination of the

new observation, the predictor of the signal and the

previous innovation.

Theorem 1. Under hypotheses (I)-(IV), the innova-

tion process associated with the observations given in

(1) satisﬁes

ν(k) = y(k)−

θ(k)A(k)O(k − 1)−K

(k, k − 1)

×A(k)B

(k−1)Π

−1

(k−1)ν(k −1), k ≥ 2

ν(1) = y(1)

where the vectors O(k) are calculated from

O(k) = O(k − 1) + J(k)Π

−1

(k)ν(k), k ≥ 1

O(0) = 0

being

J(k) = θ(k)

(k)−r(k −1)A

(k)

−K

(k, k−1)

×J(k−1)Π

−1

(k−1)B(k −1)A

(k), k ≥ 2

J(1) = θ(1)B

(1)

and Π(k) the covariance matrix of the innovation,

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

204

which is given by

Π(k) = θ(k)A(k)

(k) − θ(k)r(k − 1)A

(k)

−K

(k, k − 1)A(k)B

(k − 1)

×Π

−1

(k − 1)B(k − 1)A

(k)

−

θ(k)K

(k, k − 1)A(k)

J(k − 1)

×Π

−1

(k − 1)B(k − 1) + B

(k − 1)

×Π

−1

(k − 1)J

(k − 1)

(k) + R

(k).

The covariance r(k) of the vector O(k) veriﬁes

r(k) = r(k − 1) + J(k)Π

−1

(k)J

(k), k ≥ 1

r(0) = 0.

3 FIXED-INTERVAL SMOOTHER

Theorem 2. Assuming hypotheses (I)-(IV), the es-

timators of the signal z(k) from the observations

y(1), · · · , y(L), with k ≤ L, are given by

bz(k, L) = bz(k, k) + [B(k) − A(k)r(k)]q

(k, L)

+A(k)J(k)q

(k, L), k < L

bz(k, k) = A(k)O(k), k ≤ L

where q

(k, L) and q

(k, L) can be recursively calcu-

lated, from q

(L, L) = 0 and q

(L, L) = 0, by

(k, L)=

−∆

(k+1)Π

−1

(k+1)J

(k+1)

×q

(k + 1, L) + ∆

(k+1)q

(k + 1, L)

+∆

(k+1)Π

−1

(k+1)ν(k +1), k < L

(k, L) = −∆

(k+1)Π

−1

(k+1)J

(k + 1)

×q

(k + 1, L) + ∆

(k+1)q

(k+1, L)

+∆

(k+1)Π

−1

(k+1)ν(k +1), k < L

with

∆

(k + 1) =

θ(k + 1)A

(k + 1),

∆

(k + 1)=−K

(k+1, k)Π

−1

(k)B(k)A

(k + 1).

3.1 Error covariance matrices

The LS method uses the covariance matrices,

P (k, L), of the estimation errors to measure the good-

ness of the estimators. It is easy to verify that

P (k, L) = K

(k, k) − E[bz(k, L)bz

(k, L)].

Hence, using the expression given in Theorem 2 for

bz(k, L) and the uncorrelation property between each

(k, L), s = 1, 2, and bz(k, k) we have

P (k, L) = P (k, k) − [B(k) − A(k)r(k)]Q

(k, L)

×[B(k) − A(k)r(k)]

−A(k)J(k)Q

(k, L)J

(k)A

(k)

−[B(k) − A(k)r(k)]Q

(k, L)J

(k)A

(k)

−A(k)J(k)Q

(k, L)[B(k) − A(k)r(k)]

where P (k, k), the ﬁltering error covariance matrix,

is given by

P (k, k) = A(k)

(k) − r(k)A

(k)

, k ≤ L.

The matrices Q

(k, L), for s = 1, 2, and Q

(k, L)

are obtained by

(k, L) =F (k + 1)Q

(k + 1, L)F

(k + 1)

+∆

(k + 1)

(k + 1, L) + Π

−1

(k + 1)

×∆

(k + 1)+F (k + 1)Q

(k + 1, L)∆

(k + 1)

+∆

(k + 1)Q

(k + 1, L)F

(k + 1)

(k, L) =∆

(k + 1)Π

−1

(k + 1)

×Q

(k + 1, L)J(k + 1) + Π(k + 1)] Π

−1

(k + 1)

×∆

(k + 1) + ∆

(k + 1)Q

(k + 1, L)∆

(k + 1)

−∆

(k + 1)Π

−1

(k + 1)J

(k + 1)Q

(k + 1, L)

×∆

(k + 1) − ∆

(k + 1)Q

(k + 1, L)J(k + 1)

×Π

−1

(k + 1)∆

(k + 1)

(k, L) =−F (k + 1)Q

(k + 1, L)J(k + 1)

×Π

−1

(k + 1)∆

(k + 1)+∆

(k + 1)Q

(k + 1, L)

×∆

(k + 1)+F (k + 1)Q

(k+1, L)∆

(k, k+1)

−∆

(k + 1)Q

(k + 1, L)J(k + 1)Π

−1

(k + 1)

×∆

(k + 1) + ∆

(k + 1)Π

−1

(k + 1)∆

(k + 1)

for k < L, with initial conditions Q

(L, L) = 0, for

s = 1, 2, and Q

(L, L) = 0, being

F (k + 1) = I

−∆

(k + 1)Π

−1

(k + 1)J

(k + 1).

4 COMPUTER RESULTS

We consider a sequence of independent Bernoulli ran-

dom variables, {γ(k); k ≥ 0}, taking the value one

with probability p and we deﬁne

θ(k) = 1 − γ(k − 1) + γ(k − 1)γ(k), k ≥ 1.

So, the variables θ(k) are also Bernoulli random vari-

ables and, since θ(k) and θ(s) are independent for

|k −s| ≥ 2, they are uncorrelated and hypothesis (III)

is satisﬁed. The common mean of these variables is

θ = 1 − p + p

and its covariance function is given by

(k, s) =

0, |k − s| ≥ 2

−(1 − θ)

, |k − s| < 2

Let z(k) be the signal to be estimated and y(k) the

observation of this signal, deﬁned as in (1) by

y(k) = θ(k)z(k) + v(k)

where v(k) represents the measurement noise.

Since θ(k) = 0 corresponds to γ(k − 1) = 1 and

γ(k) = 0, this fact implies that θ(k + 1) = 1 and,

hence, the possibility of the signal being missing in

two successive observations is avoided. So, the con-

sidered observation model covers those signal trans-

mission models with stand-by sensors, in which any

NEW DERIVATION OF THE FILTER AND FIXED-INTERVAL SMOOTHER WITH CORRELATED UNCERTAIN

OBSERVATIONS

205

failure in the transmission is immediately detected

and the old sensor is then replaced.

We have assumed that the autocovariance function

of the signal is

(k, s) = 1.025641 × 0.95

k−s

, 0 ≤ s ≤ k.

The noise {v(k); k ≥ 0} has been assumed to be a

sequence of independent random variables with

E[v(k)] = 0, R

(k) = 0.7037037.

To show the effectiveness of the algorithm pro-

posed in this paper, we compare the results obtained

from 100 observations of the signal, using different

values of the parameter p.

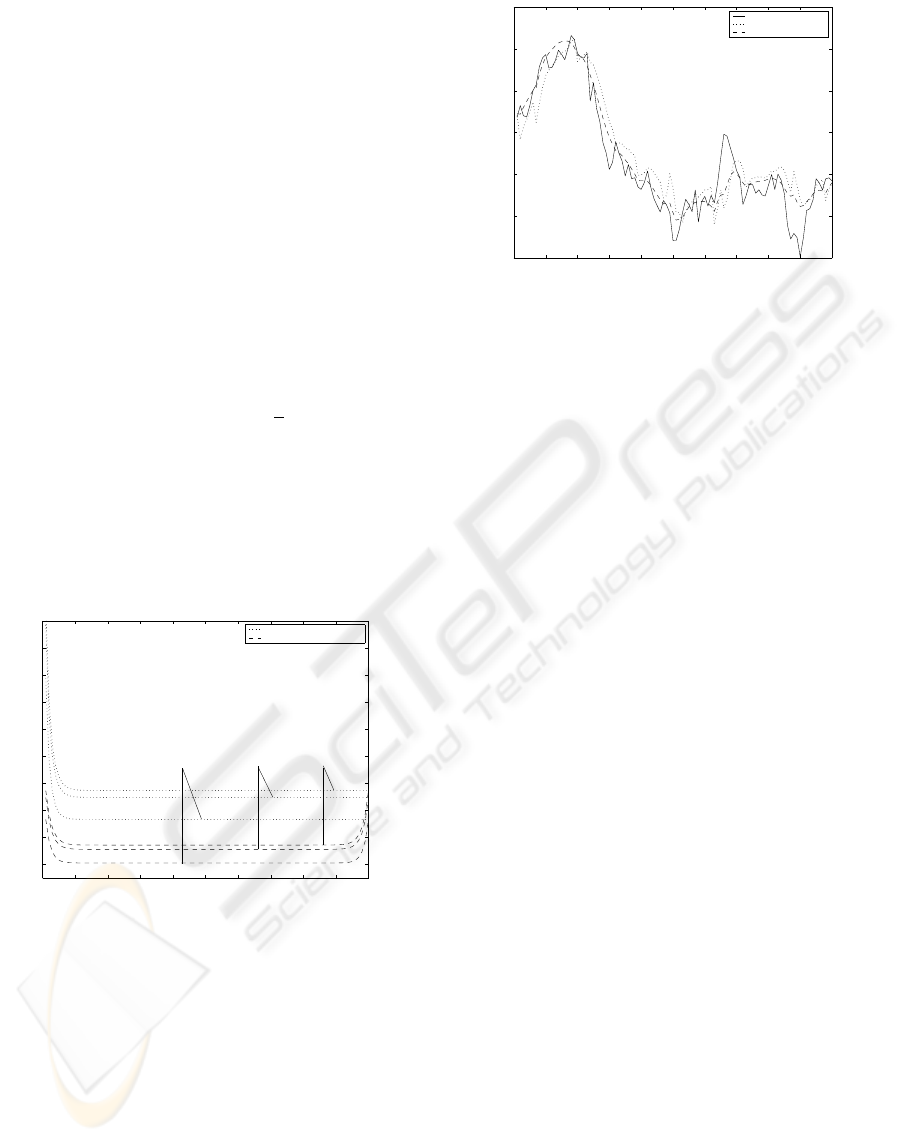
First, the performance of the ﬁlter and ﬁxed-

interval smoother, measured by the error variances,

has been calculated for p = 0.1, 0.3 and 0.5. The

results are displayed in Figure 1 which shows that the

estimators have a better performance as p is smaller,

due to the fact that the mean value, θ, decreases with

p. Moreover, this ﬁgure shows not only that, for

each value of p, the error variances are smaller us-

ing the ﬁxed-interval smoother instead of the ﬁlter,

but also that the improvement with the smoother is

highly signiﬁcant since, even the worst results with

the smoother (p = 0.5) are better than the best ones

with the ﬁlter (p = 0.1). A simulated signal and

0 10 20 30 40 50 60 70 80 90 100

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

0.55

Time k

Filtering error variances

Fixed−interval error variances

p=0.5

p=0.3

p=0.1

Figure 1: Filtering and ﬁxed-interval smoothing error vari-

ances for p = 0.1, 0.3, 0.5.

their ﬁltered and smoothed estimates from 100 ob-

servations simulated with p = 0.1 are displayed in

Figure 2. The result, as expected, is that the smooth-

ing estimates are nearer to the signal and, hence, the

behaviour of the ﬁxed-interval smoother is better than

that of the ﬁlter.

5 CONCLUSION

In this paper, the LS linear ﬁxed-interval smoother is

derived from uncertain observations of a signal, when

0 10 20 30 40 50 60 70 80 90 100

−3

−2

−1

Time k

Signal

Filter

Fixed−interval smoother

Figure 2: Signal, ﬁltering and ﬁxed-interval smoothing es-

timates for p = 0.1.

the Bernoulli random variables characterizing the un-

certainty in the observations are correlated at consec-

utive time instants, for the case of white observation

additive noise. It is not required the knowledge of the

state-space model, but only the covariance matrices

of the processes involved in the observation equation.

The recursive algorithms are derived by an innovation

approach.

The results are applied to a particular model which

includes signal transmission models with stand-by

sensors for the immediate replacement of a failed unit.

ACKNOWLEDGMENT

Supported by the ‘Ministerio de Ciencia y Tec-

nolog

ıa’. Contract BFM2002-00932.

REFERENCES

Young, P. and Pedregal, D. (1999). Recursive and en-bloc

approaches to signal extraction. Journal of Applied

Statistics, 26(1):103–128.

Ferrari-Trecate, G. and De Nicolao, G. (2001). Computing

the equivalent number of parameters of ﬁxed-interval

smoothers. In Proc. 40th IEEE Conf. on Decision and

Control, volume 3, pages 2905–2910.

Jackson, R. N. and Murthy, D. N. P. (1976). Optimal linear

estimation with uncertain observations. IEEE Trans-

actions on Information Theory, May:376–378.

Nakamori, S., Caballero, R., Hermoso, A. and Linares, J.

(2003a). Linear estimation from uncertain observa-

tios with white plus coloured noises using covariance

information. Digital Signal Processing, 13:552–568.

Nakamori, S., Caballero, R., Hermoso, A. and Linares, J.

(2003b). New linear estimations from correlated un-

certain observations using covariance information. In

Proc. Twelfth IASTED Conf. ASM, pages 295–300.

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

206

Young, P. C., McKenna, P. and Bruun, J. (2001). Identi-

ﬁcation of non-linear stochastic systems by state de-

pendent parameter estimation. International Journal

of Control, 74:1837–1857.

NEW DERIVATION OF THE FILTER AND FIXED-INTERVAL SMOOTHER WITH CORRELATED UNCERTAIN

OBSERVATIONS

207