DECENTRALIZED ESTIMATION FOR AGC OF POWER

SYSTEMS

Xue-Bo Chen

School of Electronic & Information Engineering, Anshan University of Science & Technology, Anshan 114044, P. R. China

Xiaohua Li

School of Information Science and Engineering, Northeast University, Shenyang 110004, P. R. China

Srdjan S. Stankovic

University of Belgrade, Belgrade 11000, Yugoslavia

Keywords: Decentralized estimation, Inclusion principle, Automatic generation control

Abstract: A decentralized state estimation

method for automatic generation control (AGC) of interconnected power

systems is proposed in this paper. Based on the Inclusion Principle for linear stochastic systems, the state

space model of the system is decomposed as a group of pair-wise subsystem models. The overlapping

decentralized estimators and fully decentralized estimators are designed for each pair subsystems in the

framework of LQG control schemes. Two types of estimators are considered for the cases of full and

reduced measurement sets in the framework of system closed-loop operations. Simulation results show a

high quality of the AGC scheme based on dynamic controllers with the proposed state estimators.

1 INTRODUCTION

Generally speaking, in power system models, an

overall system with a longitudinal or a loop or a

radial or a network structure can be divided into a lot

of overlapping interconnected subsystems. Tie line

powers, i.e. the sine of the voltage phase angle

differences at the two ends of tie lines connected

with areas, are the interconnections of the

subsystems. It has been found that the decentralized

controllers could be designed based only on local

measurements, especially, the tie line power

between each pair of areas and the frequency in each

area (Chen, 1994; Ohtsuka and Morioka, 1997;

Stankovic et al., 1999). Although the decentralized

control for overlapping interconnected power

systems has attracted considerable attention of

researchers (Chen, 1994; Chen and Stankovic, 1996;

Ikeda et al., 1981; Malik and Hope, 1984/1985;

Ohtsuka and Morioka, 1997; Park and Lee, 1984;

Siljak, 1978 and 1991; Stankovic et al., 1999), the

decentralized state estimation has been treated

mostly within the framework of the dynamic

controllers. The estimators of Kalman filter type are

discussed in (Hodzic and Siljak, 1986), while in

(Ikeda and Siljak, 1986) deterministic systems and

their observers are considered in the case of the

contractibility of dynamic controllers. The inclusion

of observers for deterministic systems has been

considered in (lftar, 1993). Luenberger observers are

considered in (Park and Lee, 1984) separately with

the near optimal decentralized control, since the tie-

line power flow deviations are treated as the

interconnecting states noted as relatively slow.

However, from the practical feasibility point of view,

the area autonomy and decentralized estimator

design of the power system has not been mature.

First of all in this paper, a kind of multi-

ove

rlapping interconnected power system model is

decomposed as a group of pair-wise areas and/or

subsystems (Chen et al., 2002) with only one

overlapping interconnection (the tie-line power)

between the two subsystems. Then, the inclusion of

Kalman filter type estimators is formulated for the

subsystem AGC. Finally, starting from a pair of

electric power subsystems, overlapping and fully

decentralized estimators based on full and reduced

257

Chen X., Li X. and Stankovic S. (2004).

DECENTRALIZED ESTIMATION FOR AGC OF POWER SYSTEMS.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 257-263

DOI: 10.5220/0001126402570263

 SciTePress

measurement sets are formulated. The fully

decentralized scheme used only local area

measurements is based on a separate tie-line power

estimator. Experimental results illustrate the main

features of the proposed estimators applied to AGC.

2 SYSTEM MODEL STRUCTURES

Consider a power system with multi- overlapping

interconnected structures (Siljak, 1978), described

by the linear stochastic continuous-time dynamic

model as follows:

⎪

⎩

⎪

⎨

⎧

iiii

ijj

jijiiiiiii

xCy

xAuBxAx

+Γ++=

∑

≠=

i = 1, 2, …, N, (1)

where,

⎥

⎦

⎤

⎢

⎣

⎡

∑

≠=

ijj

iji

tiii

⎥

⎦

⎤

⎢

⎣

⎡

−

000

jii

[]

bB =

[]

f=Γ

[

]

iii

CdiagC =

, (2)

the vector x

is the state deviations of the i-th area

consisting of 10 components: a

, the valve opening

variation of the steam turbine; P

, P

and P

, the

high, intermediate and low pressure output

variations of steam turbine, respectively; a

, the gate

opening variation of hydro turbine; v

, dashpot

position variation; q, water flow variation of the

hydro-turbine; f, frequency variation; v

, the

deviation of the integral area control error (ACE)

(Calovic, 1972; Malik and Hope, 1984/1985); P

the deviation of the tie-line power exchange

variations between the i-th and other areas; while u

is the deviation of the scalar area control input and ξ

is immeasurable variation of the area load; y

= [P

, f, v, P

]

defined as a vector of the local output

deviations, where P

is the output variation of the

steam turbine and P

is the one of the hydro unit; η

represents the measurement noise vector

corresponding to y

. The parameters and matrices,

such as A

, b

, C

, f

, a

, d

, m

and m

, are constant

and with proper dimensions.

It is obvious that the system (1) constructed by N

interconnected subsystems has the multi-overlapping

interconnections represented by the tie line power

deviations, appearing at the last equation of the state

description:

)(

1 jj

jiii

ijj

ijiei

xmxmP −=

∑

≠=

i = 1, 2,......, N, (3)

where, α

= P

/ P

is a steady load normalization

factor based on area 1, that is α

= 1. The first item

of the sum in (3) is related to the block-diagonal

matrix A

, representing N-1 times overlapping

interconnection of state x

(a part of x

); while the

coefficients of the second item is spread around the

non-block-diagonal matrix A

, j=1,2,...,N, j

≠

representing the interconnections between the i-th

and the j-th area. Because of power mutual

exchanges, the gross tie line power change

deviations in each area have the following relation

as:

∑

iei

. (4)

Decompose the system (1) as a group of pair-wise

subsystems (Chen et al., 2002), i.e. only consider the

i-th subsystem state space model coherent with the j-

th subsystem; therefore, the N(N-1)/2 pair

subsystems can be represented by

⎩

⎨

⎧

iiii

jijiiiiiii

xCy

xAuBxAx

+Γ+

(5)

Where

⎥

⎦

⎤

⎢

⎣

⎡

iji

tiii

⎥

⎦

⎤

⎢

⎣

⎡

−

000

jii

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

258

i = 1, 2, ... , N-1,

j = i+1, i+2,..., N (6)

and the other matrices as in (2). Since the tie line

power equations between the i-th and the j-th

subsystems are of linearly dependent according to

(4), the overlapping interconnected power subsystem

in pairs can be rewritten by

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

jjitjj

jij

jii

iji

tiii

0/00

000

0010

000

αα

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

0000

01000

00100

00010

0000

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

i=1, 2, ... , N-1,

j = i+1, i+2,..., N. (7)

where, dotted lines show the two area models with a

overlapping interconnected part. Thus, the power

system, decomposed from a multi-overlapping

interconnected structure to a group of pair-wise

subsystems (Chen et al., 2002), preserves inherent

interconnected features.

3 INCLUSION OF ESTIMATORS

The centralized design of AGC is typically faced

with both conceptual and computational difficulties,

since the necessary information for control has to be

acquired from power areas and generating plants

spread over large geographic territories. It has been

found that the inclusion principle is a suitable tool

for coping with the problem of decentralized AGC

design. However, the problem has been treated

almost exclusively within the framework of

deterministic models and static state or output

feedback (Siljak, 1991). In this section, we shall

present the inclusion of state estimators for a pair of

subsystem S

, based on the stochastic system

inclusion principle.

For a decentralized state estimation of power

systems, the system (1) can first be decomposed as a

pairs of subsystems (5) or (7). Then, in the case of

(7), consider corresponding estimators E

for S

, in

the Kalman filter form:

: . (8)

]

[

ˆˆ

xCyLBuxAx −++=

Where

is the estimations of state

vector

[

]

TTT

jjjeiiii

of S

xvPvxx =

, L is an estimation

gain matrix, other vectors and matrices are

corresponding to S

. Suppose there is a pair

expansion

(

ijij

for the pair (S

, E

) in the

framework of the input/state/output inclusion, we

state the following:

Definition 1. The pair

(

ijij

includes the pair

, E

) if there exist two pairs of full rank matrices

(U, V), satisfying UV = I

and full rank matrix R

and S, such that for any given initial state vector

]

and input u(t) the conditions [

]

{[x

]

; diag[V,V]}and

)(

{u(t);R}

imply both [x

(t),

)

]

(

{[

)(

]

; diag[U,U]}

and y(t)=C

{

)(

;S} (

tt ≥

∀

t), where E

{ּ} and

{ּ} means strict and weak expansions and C

{ּ}

represents weak contraction (see reference Stankovic

et al., 1999).

Theorem 2. The system

includes the system

, in the sense of Definition 1 if and only if

VAU

RBAU

B=S

BAC

VГR

= ,

ΓΓ

=S S

i = 0, 1, 2, .... (9)

There are two special cases of inclusions, i.e.

restriction and aggregation.

Theorem 3. The estimator E

is a restriction of

the estimator

if the system S

is a restriction of

the system

and

DECENTRALIZED ESTIMATION FOR AGC OF POWER SYSTEMS

259

(VLC =

VCL

)∩(VLR

LRL

together with one of the followings:

(a)

(VB=

)∩ (VL=

(b)

(VBQ=

)∩(VL=

(c)

(VB=

)∩ (VLS= ),

(d)

(VBQ=

)∩(VLS=

where Q and T are full rank matrices.

Theorem 4. The estimator E

is an aggregation

of the estimator

if the system S

is an

aggregation of the system

and

(LCU =

CLU

)∩(LR

= ),

ULRLU

together with one of the followings:

(a)

(BQ=

)∩ (LS=

(b)

(B=

RBU

)∩(LS=

(c)

(BQ=

)∩ (L=

TLU

(d)

(B=

RBU

)∩(L=

TLU

where Q and T are full rank matrices.

4 DECENTRALIZED

ESTIMATION FOR AGC

4.1 Overlapping Decentralized

Estimation

The problem of overlapping structures in the pairs of

subsystems should be solved, i.e. the deviation of the

tie-line power variation of subsystems P

decoupled for each subsystem. The algorithm to

expand a pair of subsystem S

and to get

corresponding estimators E

is that, by imposing the

conditions of inclusion principle presented in the

above, a group of expanding matrices can properly

be chosen, aimed at decomposition of overlapping

part represented by dotted lines in (7), such as:

V=block-diag[I

, (1 1)

, I

T=block-diag[I

, (1 1)

, I

U= block-diag{I

, [

(1-

)], I

S= block-diag{I

, [

(1-

)], I

}, (10)

where, β is a scalar satisfying 0<β<1; the appropriate

complementary matrices M

, M

and M

correspond to the matrices in (7), (8) and satisfy the

equations

MVAUA +=

MVBB +=

MTCUC +=

MVLSL +=

, (11)

such that

and

include the corresponding

matrices of a pair of subsystems and their

estimations, respectively. Although the system S

can become (5) after expanded and modified by

using (10) and (11), it is important to know that the

transform matrices (10) are needed for contractions

to original spaces of each pair subsystems to show

their interconnected relations when the decentralized

estimations and controls are designed.

To formulate overlapping decentralized state

estimation in the framework of LQG control for the

pair subsystems in (7), the non-block diagonal

matrices, such as, A

, j = 1,2,...,N, j i, as

byproducts to be considered after local estimation

and control is established, are neglected. The local

estimation are given by

≠

]

[

ˆˆ

kkkkkkkkk

xCyLuBxAx −++=

k = i, j, (12)

where,

denotes the state estimate vector.

Constructing the estimate gain matrices in the block

diagonal form for the pair of decoupled subsystems

],[

jiD

LLdiagL =

, (13)

and in order to satisfy the estimator restriction and

aggregation conditions for contractions, we modify

the estimator gain matrix from

by adding

∆

relative to A

, j = 1,2,...,N, j i, to the equation

(13) and obtain

≠

⎥

⎦

⎤

⎢

⎣

⎡

−+

××

×××××

×××

××

jjji

LLLLLL

LLLL

4919

4111111141

411141

1949

. (14)

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

260

Overlapping decentralized state estimator L

can be

implemented in the pair subsystems S

by L

TLU

directly, or by L

S =

, VL

indirectly, based on the Theorem 3 and Theorem 4.

4.2 Fully Decentralized Estimation

Although the estimators described above have been

designed in a decentralized way, they are, essentially,

centralized. The desired features for an efficient

decentralized AGC require that each decentralized

dynamic controller and/or estimator should be

applied to its subsystem, using the measurements

only accessible to its own area (Calovic, 1972 and

1984). In order to comply with these requirements, a

modification of the overlapping decentralized

methodology has been done, leading to a fully

decentralized estimator.

The tie-line power variations depend, essentially,

on the states in both the i-th and the j-th areas.

According to (3) and (8), fully decentralized

estimators can be designed, starting from the

estimator of tie-line power variations defined by

)

(

eeme

PPLP −=

(15)

where, L

is an properly chosen constant, adapted to

both dynamics of the tie-line power variations and

the measurement noise. It is obvious that this

estimator is completely autonomous, independent of

the remaining parts of the state vector, having in

mind that the estimators for the remaining parts of

the local state vectors become completely decoupled.

The estimator gain matrix is now modified from (14)

⎥

⎦

⎤

⎢

⎣

⎡

−

××

LLL

4919

1111

1949

000

. (16)

As far as the types of expansion are concerned, fully

decentralized estimator schemes are designed in

parallel with the overlapping decentralized ones.

5 EXPERIMENTAL RESULTS

The efficiency of the described estimation schemes

applied to AGC has been tested by simulation. All

the experiments have been done in the case that the

estimators have been implemented together with the

corresponding gain matrices mapping the state

estimates to the control signals. These gain matrices

have been obtained by using the methodology

(Stankovic et al., 1999), based on expansion,

decomposition to subsystems and the local

application of the LQG optimal design. In order to

get a better practical feeling about the quality of

different estimators, responses to a step load

disturbance in area i have been analyzed.

For the pair of subsystems S

, without losing

generality, assume i = 1, j = 2, let the parameters of

the system matrices in (7) correspond to the

references (Chen, 1994; Calovic, 1984; Stankovic et

al., 1999), and have expanding matrices be (10).

Consider the non-balance case of area 1 and area 2,

that is a steady load normalization factor α

= P

=10. Therefore, choose β = 0.1 and step

disturbance is 0.01 with 5% white noises in ξ

When y

= [P

, P

, f, v, P

]

, i = 1, 2, the estimators

are designed for full measurement sets; while y

= [f,

v, P

]

, i=1,2, the estimators for reduced

measurement sets. The following notation has been

adopted for estimator designs: (1) Overlapping

decentralized (OD) scheme, full measurement sets

(FMS); (2) OD scheme, reduced measurement sets

(RMS); (3) Fully decentralized (FD) scheme, FMS;

(4) FD scheme, RMS. In the case of OD scheme,

=0; and L

=120 for FD.

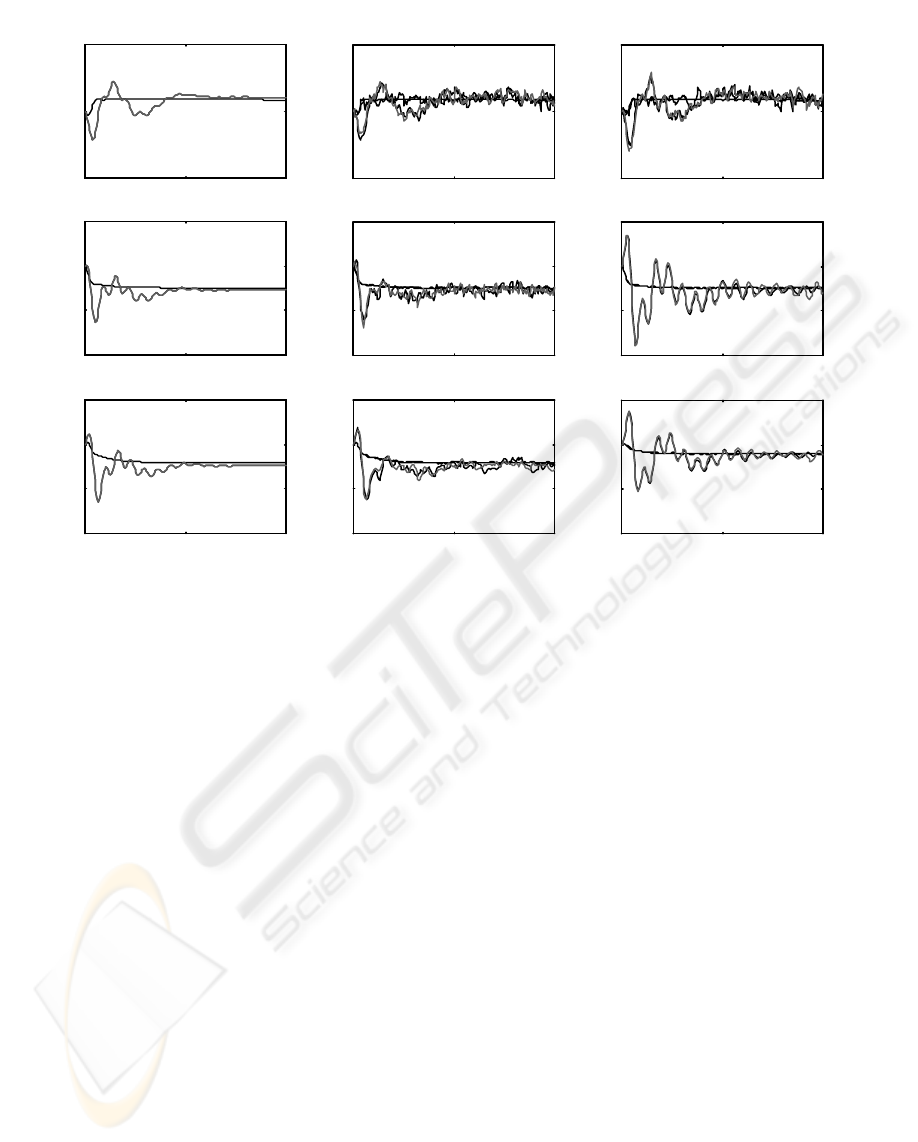
In Figure 1 (a), differences between the globally

optimal estimation errors (obtained by implementing

the globally optimal LQG regulator for the entire

model (7)) and the estimation errors obtained by the

proposed estimators are depicted for f

, P

and f

, all

the noise terms are set to zero, in order to provide a

better insight into the corresponding dynamics.

Smooth overlapped curves are for the cases of 1 and

2, whereas fluctuant overlapped ones for 3 and 4.

Obviously, FD schemes are only slightly inferior to

OD schemes; the number of measurements does not

influence the estimation accuracy significantly.

Figure 1 (b) corresponding to the general situation,

when the stochastic effects are present. It is

interesting to observe that the estimator

decentralization does not degrade the noise

immunity significantly; however, the reduction of

the number of measurements leads in both OD and

FD cases to a visible increase of the estimation error.

This estimator parameter L

plays an important role

in achieving the desired overall system performance.

Figure 1 (c) shows the estimation error differences

when L

= 20 for FD schemes, corresponding to

Figure 1 (b). Obviously, the estimation quality is

deteriorated.

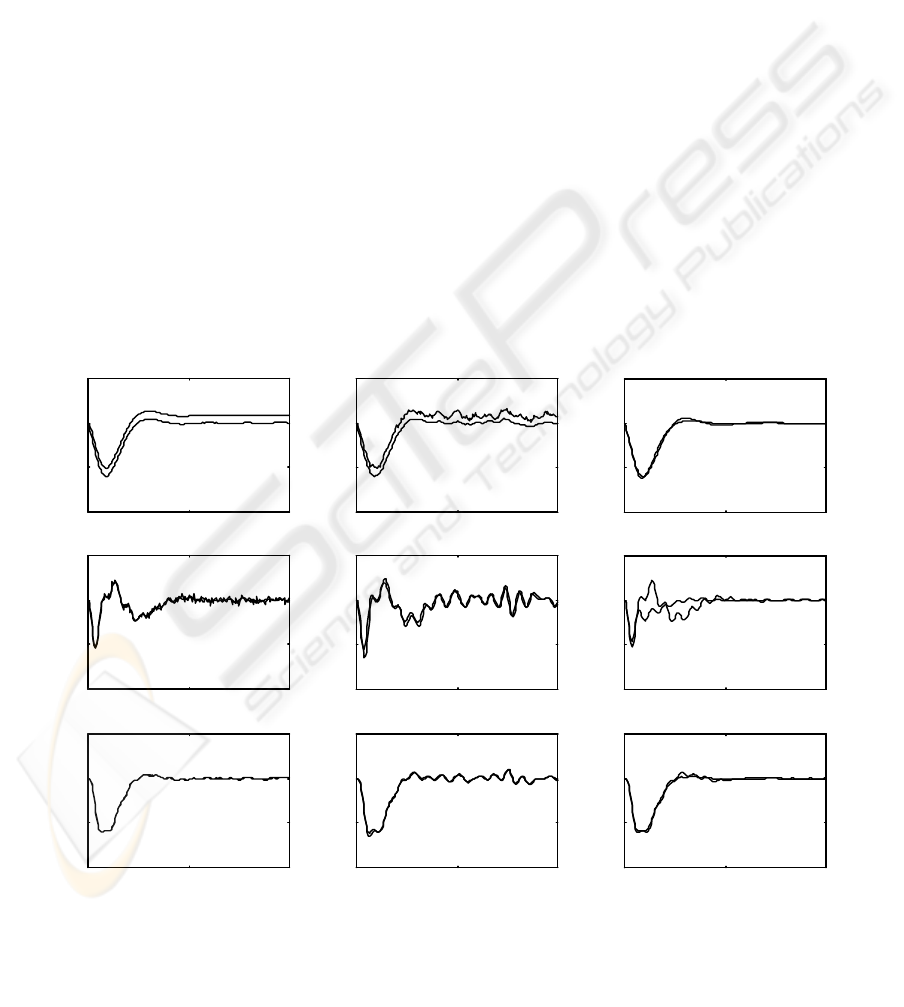
In Figure 2 (a) and Figure 2 (b), the true states

are represented, together with their estimates, for

OD scheme / FMS case and FD scheme / RMS case.

The estimation accuracy is obvious; the bias,

especially pronounced in f

, represents a

DECENTRALIZED ESTIMATION FOR AGC OF POWER SYSTEMS

261

consequence of the step disturbance, and cannot be

eliminated, since it is viewed as a structural change,

which does not affect the steady-state control error

as the integral action is incorporated into the system

model. The estimates P

appear to be very good,

although they are obtained by simple low-pass

filtering. In order to illustrate the performance of the

overall dynamic AGC controllers incorporating the

proposed estimators, The Figure 2 (c) contains the

responses to the step disturbance obtained by the

globally LQG optimal regulator and FD scheme /

FMS case with L

= 120.

6 CONCLUSION

In this paper a decentralized state estimator design

methodology is proposed for AGC of the

overlapping interconnected power system.

Overlapping and fully decentralized estimations for

the system is considered from the point of view of

obtaining possibilities for direct contraction from the

expanded to the original space. The design of the

local estimators is based only on the models of the

corresponding areas and the associated tie lines. The

presented experimental results show a very low

performance degradation caused by decentralization.

-5

x 10

-5

f1/p.u.

-2

-1

x 10

-3

pe/p.u.

-4

-2

x 10

-4

f2/p.u.

t/s.

-5

x 10

-5

f1/p.u.

-2

-1

x 10

-3

pe/p.u.

-2

-1

x 10

-4

f2/p.u.

t/s.

-5

x 10

-5

f1/p.u.

-2

-1

x 10

-3

pe/p.u.

-2

-1

x 10

-4

f2/p.u.

t/s.

(a) (b) (c)

Figure 1: Differences of estimation errors.

ACKNOWLEDGEMENT

This research is supported by the NSFC of China under

grant No. 60074002, and by the USRP of Liaoning

Education Department of China under grant No.

202192057.

REFERENCES

Calovic, M. S., 1972. Linear Regulator Design for A Load

and Frequency Control. IEEE Trans. Power. App. Sys.,

Vol. PAS-9, 2271-2285.

Calovic, M. S., 1984. Automatic Generation Control:

Decentralized Area-Wise Optimal Solution. Electric

Power Systems Research, Vol. 7, 115-139.

Chen, X. -B., 1994. Some Aspects of Control Systems

Design Based on The Inclusion Principle. Ph. D.

dissertation, Univ. of Belgrade.

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

262

Chen, X. -B., Stankovic, S. S., 1996. Overlapping

Decomposition and Decentralized LQG Control for

Interconnected Power Systems. Proc. IEEE SMC’96,

Vol.3. 1904-1909.

Chen, X. -B., Siljak, D. D., Stankovic, S. S., 2002.

Decentralized H

∞

Design of Automatic Generation

Control. Proc. of IFAC 15th World Congress.

Barcelona, Spain, July 21-26, 307-312.

Hodzic, M., Siljak, D.D., 1986. Decentralized Estimation

and Control With Overlapping Information Sets. IEEE

Trans. Aut. Control, Vol. AC-31, 81-86.

lftar, A., 1993. Overlapping Decentralized Dynamic

Optimal Control. Int. J. Contr., Vol. 58, 187-209.

Ikeda, M., Siljak, D. D., 1986. Overlapping Decentralized

Control with Input, State and Output Inclusion. Control

Theory and Advanced Technology, Vol. 2, 155-172.

Ikeda, M., Siljak, D. D., White, D. E., 1981. Decentralized

Control with Overlapping Information Sets. J. Optirniz.

Theory and Appl, Vol. 34, 279-310.

Malik, O. P., Hope, G. S., 1984/1985. Decentralized

Suboptimal Load-Frequency Control of A Hydro-

Thermal Power System Using the State Variable

Model. Electric Power systems Research, Vol. 8, 237-

247.

Ohtsuka, K., Morioka, Y., 1997. A Decentralized Control

System for Stabilizing a Longitudinal Power System

Using Tie-Line Power Flow Measurements. IEEE

Trans. on Power Systems, Vol.12, 1202-1209.

Park Y. M., Lee, K. Y., 1984. Optimal Decentralized Load

Frequency Control. Electric Power systems Research,

Vol. 7, 279-288.

Siljak, D. D., 1978. Large-scale Dynamic Systems:

Stability and Structure. North-Holland, NY.

Siljak, D. D., 1991. Decentralized Control of Complex

Systems. Academic Press, New York.

Stankovic, S. S., Chen, X. -B., Matausek, M. R., Siljak, D.

D., 1999. Stochastic Inclusion Principle Applied To

Decentralized Automatic Generation Control. Int. J.

Contr. Vol. 72, 276-288.

-2

-1

x 10

-3

f1/p.u.

-4

-2

x 10

-3

pe/p.u.

-2

-1

x 10

-3

f2/p.u.

t/s.

-2

-1

x 10

-3

f1/p.u.

-4

-2

x 10

-3

pe/p.u.

-2

-1

x 10

-3

f2/p.u.

t/s.

-2

-1

x 10

-3

f1/p.u.

-4

-2

x 10

-3

pe/p.u.

-2

-1

x 10

-3

f2/p.u.

t/s.

(a) (b) (c)

Figure 2: Estimations and responses.

DECENTRALIZED ESTIMATION FOR AGC OF POWER SYSTEMS

263