PARAMETRIC ESTIMATION OF SINUSOIDS IN NOISE

A comparison between parametric approaches and the definition of a regularized

Smyth algorithm

Aldo Balestrino, Andrea Caiti and Roberto Mati

DSEA – Dept. Electrical Systems and Automation, University of Pisa, Italy

Keywords: Estimation, sinusoids, signals, parametric algorithms

Abstract: A comparison between well-established parametric algorithms and the more recent Smyth algorithm for

estimation of sin

usoidal signals in white noise is presented. The comparison is performed through a pseudo-

Monte Carlo analysis on simulated data. The results obtained show that Smyth algorithm has a slightly

better performance at large Signal-to Noise Ratios. However, when the SNR drops down, the performance

of the Smyth algorithm dramatically decreases. A better performance with respect to both ESPRIT and

Smyth algorithms at low SNR can be obtained by a regularized filtering procedure on the data.

1 INTRODUCTION

The detection of sinusoidal signals embedded in

noise is a classic problem, of wide interest in

numerous applications, from sonar to radar and

tracking problems. The available algorithms can be

classified as parametric and non parametric methods.

The non parametric methods are based on classical

periodogram analysis (Stoica and Moses, 1997).

Parametric methods include Auto Regressive (AR) –

based algorithms and high resolution eigenanalysis

approaches.

Popular eigenanalysis algorithms include MUSIC

(Sc

hmidt, 1983), ESPRIT (Roy and Kailath, 1989)

and the classic Pisarenko algorithm (Pisarenko,

1973). More recently, Smyth has proposed a novel

eigenanalysis algorithm by combining a constrained

Pisarenko approach with an iterative least square

estimator (Smyth, 2000).

The purpose of this paper is to compare the above

entioned algorithms at different Signal to Noise

Ratios (SNR), in order to evaluate pros and cons of

the various approaches. The comparison is done

through a pseudo Monte Carlo method on simulated

data. The results obtained show that the Smyth

algorithm has a slightly better performance with

respect to the other methods at high SNR. At low

SNR, with specific values depending on the number

of different sinusoids to be estimated, MUSIC and

ESPRIT seems to yield the best performance.

The comparison reported is in itself interesting

d valuable, since to the Authors knowledge no

comparison of the traditional methods with the

Smyth approach has appeared in the literature. In

addition to that, the above results have also led to the

definition of a novel estimation algorithm. The novel

approach is essentially an iterated application of the

Smyth algorithm to a succession of regularized data

set. The regularization is obtained as a weighted sum

of the predicted, noise-free data from the previous

step solution with the noise-corrupted

measurements. The data weighting depends on a

regularization parameter which is changed from step

to step in order to reach, in a finite number of steps,

the situation in which the algorithm uses only the

data measurements. The initialization of this filtering

procedure is done with the predicted, noise free

solution obtained from ESPRIT. By using the

simulative approach which has been employed for

the algorithms comparison, it is shown that there

does exist an optimal value of the regularization

parameter such that for this value the proposed

algorithm has performance better than both ESPRIT

and Smyth algorithms.

The paper is organized as follows. In the next

section, a formal state

ment of the problem is given

and the Smyth algorithm is briefly reviewed. In

section 3 the simulative trials and the results

obtained by comparing the performance of ESPRIT,

MUSIC, Pisarenko and Smyth algorithms are

reported. In section 4 the novel regularization

algorithm is presented, and the existence of an

299

Balestrino A., Caiti A. and Mati R. (2004).

PARAMETRIC ESTIMATION OF SINUSOIDS IN NOISE - A comparison between parametric approaches and the deﬁnition of a regularized Smyth

algorithm.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 301-306

DOI: 10.5220/0001128103010306

 SciTePress

optimal continuation parameter is enlightened. In

section 5, some comments on the computational

burden of the various approaches are given, and

future efforts in order to determine algorithmically

the optimal parameter are briefly described. Finally,

some conclusions are given.

2 THE SMYTH PROBLEM AND

THE SMYTH ALGORITHM

It is supposed to have available the measurements:

Kkkwksky

,...,1 , )()()( =+=

∑

(1)

where

are the samples of n

sinusoidal signals, each at the frequency

njks

,...,1 ),( =

ijj

≠≠ if ,

, and is a finite power

white process uncorrelated with the sinusoidal

signals. Given the measurement of

K samples of the

output signal

, and given the knowledge of the

number

n of frequencies present in the measurement,

the problem is to obtain an estimate of the

frequencies

)(kw

)(ky

,...,1 , =

The following estimation procedure has been

introduced by Smyth (Smyth, 2000). The procedure

is composed of three steps. In the first one, a

constrained Pisarenko algorithm is applied. The

estimate thus obtained is used as starting point of the

second step, in which the Osborne-Bresler-

Makovsky (OBM) estimation algorithm is applied

(Bresler and Makovsky, 1986). Finally, the results of

the second step are used to initialize a least square

iterative estimation (Osborne, 1975). The idea

behind the Smyth approach is that the three

algorithms, Pisarenko, OBM and Osborne, are

applied in order of increased sensitivity to the

initialization. So, the least sensitive to the initial

condition is applied as first, while the others are

used to progressively refine the solution.

Formally, let

be the auto correlation matrix of

the measurement signal

; let be the

eigenvector associated to the smallest eigenvalue of

, and let:

)(ky

zczcczc

210

...)( ++=

be the annihilator polynomial whose coefficients are

given by the components of

. By observing that

and must have the same roots, Smyth

has introduced a constrained Pisarenko estimate for

the eigenvector

in the following iterative form: at

each iteration

it must be solved the constrained

least square problem:

)(zc )(

1−

)1()()1(

)( min

cY cc

(2)

where

D is a matrix imposing the root constraint.

Equation (2) is successively solved by Pisarenko,

OBM and Osborne least-square algorithms, using as

starting point the solution obtained in the previous

step.

3 SIMULATIVE EVALUATION OF

THE SMYTH ALGORITHM

In this section a pseudo Monte Carlo simulative

study is presented, reporting the performance

obtained by the Smyth algorithm as compared with

the standard Pisarenko, MUSIC and ESPRIT

algorithms. Results from a non-parametric, FFT-

based, estimation algorithm are also reported. Three

cases are considered. In the first, the signal is

assumed to be composed by a single sinusoid, in the

second by two and in the third by four sinusoids, all

added up with random phases. Gaussian white noise,

is added to the signal, with varying Signal-to-Noise

Ratio (SNR), from –20 up to 40 dB, at 2.5 dB steps.

All simulations have been carried out in Matlab

environment, version 6.5. In each trial, performances

are obtained as follows. For each algorithm, and for

each SNR the signal

y(k) is generated as the sum of

the predefined number of tones plus noise. Then all

the algorithms are applied to

y(k). Such a procedure

is repeated

N = 100 times. The estimated Mean

Square Error from each algorithm is computed as

follows:

()

(

)

∑

−=

MSE

)(

ωωω

(3)

∑

MSEMSE

)(

(4)

where

is the estimate of the j-th frequency in

the

i-th run.

i)(

In the figures reported in the following, the

value in dB of 1/MSE is plotted as a function of the

SNR, so that for each SNR, the higher the y-scale

value, the better is the performance for each

algorithm. Numerically, a normalized sampling time

of 1 second has been used, with a window of K=300

samples. The chosen frequencies have been taken as

= 0.025 Hz,

= 0.062 Hz,

= 0.1021 Hz,

= 0.2848 Hz.

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

300

-20 -10 0 10 20 30 40

100

120

SNR (dB)

1/MSE (dB)

FFT

Pisarenko

MUSIC

ESPRIT

Smyth

Figure 1: Performance results from pseudo Monte Carlo

analysis for the estimation of a single frequency. dash-dot

line: FFT; dashed, with crosses: Pisarenko; continuous

line, with circles: MUSIC; dotted line, with diamonds:

ESPRIT; continuous line with squares: Smyth.

-20 -10 0 10 20 30 40

100

120

SNR (dB)

1/MSE (dB)

FFT

Pisarenko

MUSIC

ESPRIT

Smyth

Figure 2: Performance results from pseudo Monte Carlo

analysis for the simultaneous estimation of two

frequencies; dash-dot line: FFT; dashed, with crosses:

Pisarenko; continuous line, with circles: MUSIC; dotted

line, with diamonds: ESPRIT; continuous line with

squares: Smyth.

In figures 1, 2 and 3 the results obtained in the

estimation of one, two and four sinusoids

respectively are reported.

The results reported show that, at high SNR, the

Smyth approach can lead to some slight

improvement (few dB at the best) with respect to

ESPRIT, which has the best performance among the

standard methods. At low SNR, the performance of

Smyth algorithm drops down quite dramatically;

moreover, at low SNR MUSIC becomes competitive

with ESPRIT, succeeding in obtaining the best

performance in some cases. The behaviour of

MUSIC as a function of the SNR, however, is less

predictable with respect to that of the other methods,

and of ESPRIT in particular, showing weak

correlation among the algorithm performance at

varying SNR.

-20 -10 0 10 20 30 40

100

120

SNR (dB)

1/MSE (dB)

FFT

Pisarenko

MUSIC

ESPRIT

Smyth

Figure 3: Performance results from pseudo Monte Carlo

analysis for the simultaneous estimation of four

frequencies. dash-dot line: FFT; dashed, with crosses:

Pisarenko; continuous line, with circles: MUSIC; dotted

line, with diamonds: ESPRIT; continuous line with

squares: Smyth.

4 SMYTH ESTIMATION WITH

REGULARIZED DATA

The results presented in the previous section have

led to the exploration of a novel procedure in which

the Smyth algorithm is applied to a filtered,

regularized version of the data. The starting

motivation was to increase the performance of the

Smyth algorithm by increasing the SNR by a

process-guided data filtering. As a result, as it will

be shown in the following, a consistent improving in

the performance can be obtained. The proposed data

regularization procedure is the following: the filtered

data are obtained as a weighted sum of the predicted,

noise free data obtained from an estimated solution

(by whatever method) and the noise-corrupted

measurements. In order to generate the noise free

predicted data

, one has to start from the

estimated frequencies; keeping fixed these

frequencies it is possible, through standard Fourier

analysis, to estimate also the phase and amplitude of

these frequency components. This estimate leads to

the estimate

of the time series (1) without the

noise components. The regularized data set is then

obtained as:

)(

)1()()( kykyky

−

(5)

where

≤

is the regularization parameter,

trading off between measurement fidelity and

PARAMETRIC ESTIMATION OF SINUSOIDS IN NOISE - A COMPARISON BETWEEN PARAMETRIC

APPROACHES AND THE DEFINITION OF A REGULARIZED SMYTH ALGORITHM

301

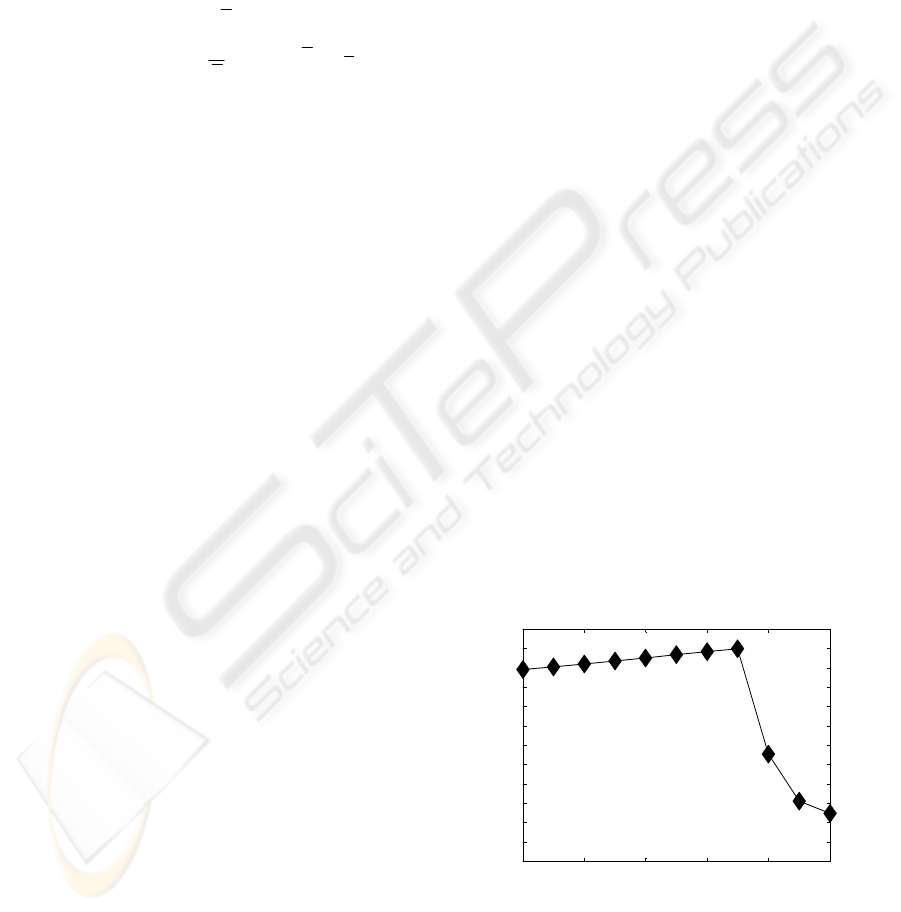
confidence in the estimate. When

the filtered

data are equal to the prediction (complete confidence

in the estimate), when

no filtering is applied

to the measurement.

In applying the Smyth algorithm to the filtered

data of equation (5) one has to select the

regularization parameter. In order to investigate the

algorithm performance as a function of the

regularized parameter, the following procedure has

been applied: the regularization parameter

made varying from 0 to 1 in

1+h steps:

, hh

,...,1,

=+=

−

αα

The noise free predicted data

from

the estimate obtained with parameter

1−h

)(

h−

are used

to generate the filtered data with parameter

accordingly to the equation:

)(

)1()()(

kykyky

ahh

−

−+=

(6)

The Smyth algorithm is applied to this data; then

its results are used to compute a new data prediction,

and the procedure is iterated. The Smyth algorithm

is also intialized with the solution obtained at the

previous step. Substantially, the algorithm is

successively applied to convex combinations of

noise-free data estimates obtained from the previous

step estimation and measurements The procedure is

initialized at step 0 with the ESPRIT algorithm,

whose data prediction is employed to compute the

regularized data with

. The same procedure

described in the previous section has then been

applied to evaluate the performance of the Smyth

algorithm as a function of the regularization

parameter. The results presented report the value in

dB of 1/MSE (equation (4)) against the value of

from 0 to 1, at 0.1 steps. The maximum corresponds

to the optimal regularization parameter. The two

limit cases corresponds to the independent

application of ESPRIT (

) and Smyth ( 1

)

algorithms. A sample of the results obtained are

reported in Figures 4, 5, 6: the figures refer to the

estimation of two sinusoids, at SNR of –5, -10, -20

dB respectively. The results reported show the

existence of an optimal value of the regularization

parameter; the Smyth algorithm, applied with the

initialization process described and with the optimal

regularization parameter, has a performance at low

SNR which is better than that of both the "pure

Smyth" algorithm and ESPRIT. The average

performance gain with respect to ESPRIT of the

regularization approach ranges from the 8 dB of the

–10 dB SNR case (Figure 5) to the 3 dB of the –20

dB SNR case (Figure 6). Note that the performance

gain with respect to the "pure Smyth" algorithm can

be much larger (up to 45 dB, Figure 4). This general

behaviour is systematic in all the simulations test

performed, with sometimes even larger performance

gains.

It is natural to ask what is the optimal

regularization parameter at high SNR. A typical

behaviour is shown in Figure 7, obtained in the case

of estimation of a single tone with SNR of 30 dB:

the optimal value is 1, indicating that the best

performance is given by the unregularized Smyth

algorithm.

It needs to be observed, though, that the

performance curve as a function of the regularization

parameter as determined through the pseudo Monte

Carlo approach does not exhibit any specific

behaviour that can be further exploited. In particular,

Figures 4-6 has been purposely chosen to illustrate

the several different behaviours observed. Figure 4

illustrates the situation in which the experimental

curve exhibits a unique maximum, with monotone

behaviour of the performance curve before and after

the extremal point; Figure 5 shows the presence of

multiple maxima and minima; Figure 6 presents a

case in which, though there does exist a unique

maximum, there is also a minimum within the

regularization interval, and the performance function

does not have a monotone behaviour before the

reaching of the maximum. Moreover, for some

values of the regularization parameter, the

performance is worse with respect to both ESPRIT

and unregularized Smyth. This diversity in the

performance curve behaviour may represent a

serious obstacle to an efficient implementation of a

computational scheme aimed at exploiting the better

performance of the regularized approach. Some

guidelines and critical evaluations toward this goal

are reported in the next section.

0 0.2 0.4 0.6 0.8 1

1/MSE (dB)

regularization parameter

SNR = -5 dB

2 sinusoids

Figure 4: Estimation results obtained from the Smyth

algorithm and the regularization procedure as a function of

the regularization parameter; SNR: -5 dB.

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

302

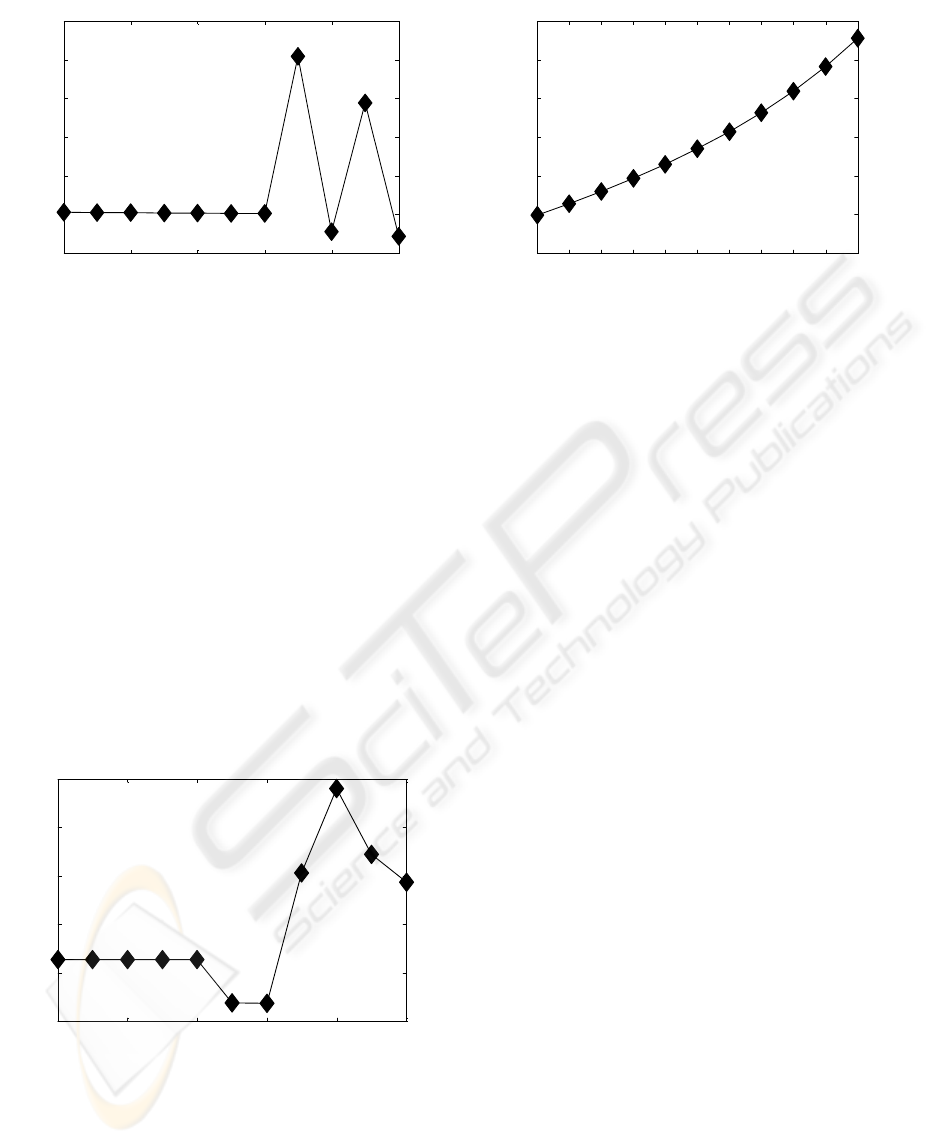
0 0.2 0.4 0.6 0.8 1

1/MSE (dB)

regularization parameter

SNR: -10 dB

2 sinusoids

Figure 5: Estimation results obtained from the Smyth

algorithm and the regularization procedure as a function of

the regularization parameter: SNR: -10 dB.

5 REGULARIZED ALGORITHM:

COMPUTATIONAL ASPECTS

The results reported in section 4 seems promising:

they establish the existence of a regularized Smyth

procedure through which a performance gain of

several dB with respect to ESPRIT can be obtained

by the proper selection of the regularization

parameter. This may lead to a substantial

improvement of the performance curves (Figures 1-

3) at low SNR, where the drop in performance had

been observed. On the other hand, there are some

non trivial computational aspects to be discusses

before the regularization approach can be

successfully implemented in a real life situation.

Figure 6: Estimation results obtained from the Smyth

algorithm and the regularization procedure as a function of

the regularization parameter: SNR: -20 dB

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

1/MSE (dB)

regularization parameter

SNR = 30 dB

1 sinusoid

Figure 7: Estimation results obtained from the Smyth

algorithm and the regularization procedure as a function of

the regularization parameter: SNR: 30 dB.

In particular, the performance curves of Figures

4-6 have been determined with the knowledge of the

true solution, which of course is never available in

practice. A practical implementation may consist in

repeatedly applying the algorithm varying the

regularization parameter over the whole admissible

range, and looking for the best performance by

comparison of the predicted time series with the

measured time domain data. How this is best

accomplished (by direct residual minimization, by

whiteness test on the residual time series, etc.) it is

not clear at the moment. Some preliminary tests with

the residual mean square error show both light and

shadows: in Figure 8 the time domain MSE is

plotted as a function of the regularization parameter

(as before, the plot refers to the quantity 1/MSE in

dB). Figure 8 correspond to the case reported in

Figure 6: -20 dB SNR and 2 unknown sinusoids.

The performance curve measured on the residual in

time domain has the maximum in correspondence of

the same regularization parameter as determined in

the frequency domain with the knowledge of the true

solution; however, the two performance curves do

not have the same behaviour, so that a systematic

exploitation of the time domain curve may also lead

to inaccuracies or undetected mistakes. Additional

considerations are related to the computational

burden of the Smyth approach, either in its "pure"

or regularized version, with respect to the attainable

performance gain. In Table 1 the mean computation

time of ESPRIT and of the Smyth algorithm, taken

over the 100 simulations described in Section 3, are

reported. The computation time refers to our Matlab

implementation running on a Pentium 4 PC, 2.4

GHz clock, under Windows XP operating system.

0 0.2 0.4 0.6 0.8 1

1/MSE (dB)

regularization parameter

SNR: -20 dB

2 sinusoids

PARAMETRIC ESTIMATION OF SINUSOIDS IN NOISE - A COMPARISON BETWEEN PARAMETRIC

APPROACHES AND THE DEFINITION OF A REGULARIZED SMYTH ALGORITHM

303

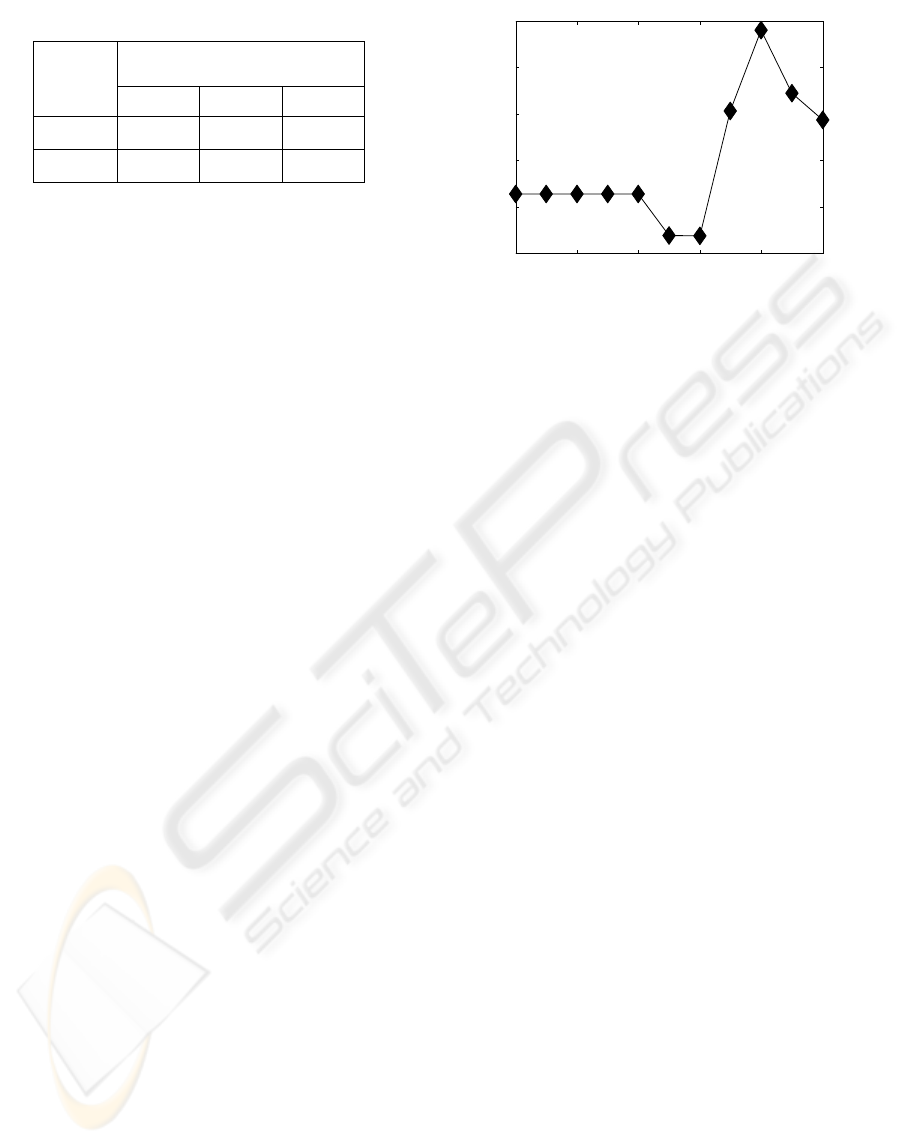
Table 1: comparison between ESPRIT and Smyth

algorithm computation times

Mean computation time (ms)

1 freq. 2 freq. 4 freq.

ESPRIT 9.9 10.2 8.5

SMYTH 41.6 77.4 105.4

The regularized Smyth algorithm consists of the

successive application of several Smyth algorithms,

with in addition the computational effort of

computing the new data set through Equation (6). So

there may as well be a factor of 100 in the

computational speed in favour of ESPRIT.

6 CONCLUSIONS

The paper has concentrated on two main topics: a

pseudo Monte Carlo evaluation of standard

parametric algorithms with respect to the Smyth

algorithm; an investigation of an innovative

regularization technique to improve the performance

of the Smyth algorithm at low SNR. The evaluation

study has shown that the Smyth algorithm can lead

to a slightly better performance with respect to

ESPRIT (the best among the standard parametric

algorithms tested) at high SNR. The Smyth

performance drops down dramatically at low SNR,

with a SNR threshold that is higher the greater the

number of sinusoids to be estimated. It has been

shown that, with the regularization approach

introduced, the Smyth algorithm is capable to

improve consistently its performance at low SNR,

with respect to its own performance, and also with

respect to ESPRIT. In particular, performance gains

up to 10 dB have been obtained. The results reported

are an experimental verification of the existence of

an optimal regularization parameter. Steps toward

the definition of an algorithm for the search of the

optimal parameter have been reported, as well as the

computational issues to be taken into account.

0 0.2 0.4 0.6 0.8 1

1/MSE (dB)

regularization parameter

SNR: -20 dB

2 sinusoids

Figure 8: Performance results computed from the time

domain residual as a function of the regularization

parameter: SNR: -20 dB

REFERENCES

Bresler, Y., Macovsky, A., 1986. Exact maximum

likehood parameter estimation of superimposed

exponential signals in noise.

IEEE Trans. Acoustic,

Speech, Signal Processing

, vol. 34, pp.1081-1089.

Osborne M.R., 1975. Some special nonlinear least square

problems.

SIAM J. Numer. Anal., vol. 12, pp.571-592.

Pisarenko, V.F., 1973. The retrieval of harmonics from

covariance functions,

Geophys. J. R. Astr. Soc., vol.

33, pp.347-366.

Roy, R., Kailath T., 1989. ESPRIT – Estimation of signal

parameters via rotational invariant techniques,

IEEE

Trans. Acoust. Speech Sig. Proc.

, vol. 37, pp. 984-995.

Schmidt R.O., 1983. A signal subspace approach to

multiple emitter location and spectral estimation,

Ph.D. thesis, Stanford University, Stanford, CA.

Smyth G.K., 2000. Employing symmetry constraints for

improved frequency estimation by eigenanalysis

methods,

Technometrics, n. 42, pp. 277-289.

Stoica, P., and Moses, R., 2000.

Introduction to spectral

analysis

, Prentice-Hall.

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

304