HIERARCHICAL MODAL CONTROL OF A NOVEL

MANIPULATOR

Clarence W. de Silva, Jian Zhang

Department of Mechanical Engineering, University of British Columbia, Vancouver, BC, Canada

Keywords: Deployable manipulator, Intelligent tuning, Modal control

Abstract: This paper focuses on the development and implementation of an intelligent hierarchical controller for the

vibration control of a deployable manipulator. The emphasis is on the use of knowledge-based tuning of the

low-level controller so as to improve the performance of the system. To this end, first a fuzzy inference

system (FIS) is developed. The FIS is then combined with a conventional modal controller to construct a

hierarchical control system. Specifically, a knowledge-based fuzzy system is used to tune the parameters of

the modal controller. The effectiveness of the hierarchical control system is investigated through numerical

simulation studies. Examples are considered where the system experiences vibrations due to initial

disturbance at the flexible revolute joint or due to maneuvers of a deployable manipulator. The results show

that the knowledge-based hierarchical control system is quite effective in suppressing vibrations induced

due to the above mentioned disturbances. Results suggest that performance of the modal controller could be

significantly improved through knowledge-based tuning.

1 INTRODUCTION

Among the fundamental developments in the

modern control theory are the two sets of analytical

results that underlie the linear quadratic regulator

(LQR) and eigenstructure assignment regulator

(EAR). Design and implementation of practical

control of flexible structures have been

accomplished using both the design techniques

(Junkins, 1993). In the LQR approach, the central

feature is the minimization of a quadratic

performance index, subject to a linearized system

model. However, a major drawback of the LQR is

that it has no direct control of the system

eigenstructure, which determines not only the level

of stability but also the specific nature of the

response to a control input (e.g., a step function).

The LQR method does not involve the assignment of

the system eigenstructure in a specified manner.

Consequently, it is desirable to employ a control

strategy that has the capability to modify the system

eigenstructure appropriately to meet specified

requirements. Such a control approach would prove

more effective if the capability of the parameter

tuning is available as well. To this end, a modal

control strategy is introduced here. An intelligent

control system, which combines a modal controller

and a fuzzy tuning structure, is developed to

‘intelligently’ assign the system eigenstructure so as

to obtain better performance of the controller in

terms of response speed, overshoot, and steady state

offset. Simulation studies have been carried out

using this intelligent control system to suppress

vibrations of a ground-based deployable

manipulator. The approach may be conveniently

applied to a space-based manipulator as well.

2 CONTROL SYSTEM

DEVELOPMENT

2.1 Eigenvalue Assignment

A linear system may be expressed in the state-space

form as

+xAxBu

, (1)

where the time-dependent state vector

contains

generalized coordinates and their first time

derivatives of the system. The square matrix A is

composed of the matrices of mass, damping and

stiffness. The term B

(t) represents the effect of a

control action, with

u (t) and B being the control

force (torque) vector and actuator placement matrix,

206

de Silva C. and Zhang J. (2004).

HIERARCHICAL MODAL CONTROL OF A NOVEL MANIPULATOR.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 206-213

DOI: 10.5220/0001128302060213

 SciTePress

respectively. As is normally the case in such studies,

all states are assumed to be available thus making

the system observable. By introducing state

feedback, the control input u

can be written as

=−uKx

. (2)

Thus one obtains a closed loop system

(- )

=xABKx

. (3)

In Equation (3), matrix

BK decides the

modal parameters of the closed loop system, such as

the modal frequencies, damping ratios and mode

shapes. A relation exists, between the modal

parameters of the system and the eigen-parameters

of matrix

A-BK, as eigen-parameters decide the

controlled behavior of the closed loop system

(Nishitani,1998), Equation (3). To obtain the relation

explicitly, it is useful to define some notations.

Assuming

A-BK to be a matrix of real-numbers, the

eigenvalues and eigenvectors of

A-BK appear as

conjugate pairs. Let

21i

−

and

be the ith pair of

eigenvalues, and

21i−

and

be the corresponding

ith pair of eigenvectors. Also let

ωζ

and n

denote, respectively, the modal frequency, damping

ratio and mode shape of the

ith mode. Then we have:

j1- ;

iiiii

λζωωζ

−

=− + −

=− −

;

⎫

⎬

⎭

and

21 2

;

ii ii

λλ

−

⎧⎫ ⎧

⎨⎬ ⎨

⎩⎭ ⎩

;

for

i = 1 to n , (4)

where j =

1−

, and n is the number of degrees of

freedom of the system.

Equation (4) gives a one-to-one mapping

between the system modal parameters and the eigen-

parameters of matrix A

-BK. Therefore, if the modal

parameters

and

ωζ

are specified in the

domain, one can calculate the corresponding

eigenvalues and eigenvectors for the closed loop

system using Equation (4). Moreover, according to

Equation (3), if one can modify and assign the

eigenstructure at desired values by selecting proper

feedback matrix K, the modal property of the system

can be modified accordingly. This is the essence of

the modal control procedure. It is also the reason

why modal control is also called eigenvalue

assignment control.

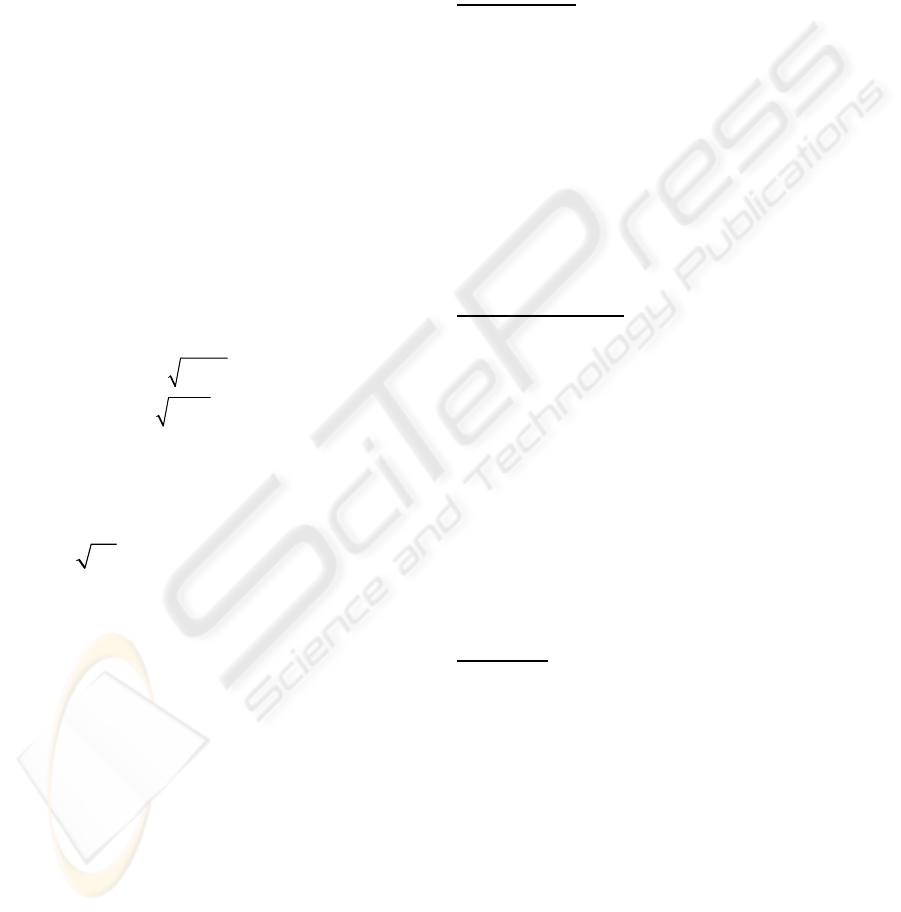
2.2 Hierarchical Structure

The control system developed for the deployable

manipulator system has a three-level structure. This

hierarchical form combines the advantages of a crisp

controller, i.e. a modal controller, with those of a

soft, knowledge-based, supervisory controller. The

overall structure can be developed into three main

layers (de Silva, 1995).

Bottom Layer

The bottom layer deals with information coming

from sensors attached to the system. This type of

information is characterized by a large amount of

high resolution data points produced and collected at

high frequency. The crisp controller used is a state

feedback regulator with feedback gain matrix

determined using the eigenstructure assignment

approach. The control algorithm can be described as:

;

- ;

xAxBu

uKx

(5)

where u is the control action and K the feedback

matrix.

Intermediate Layer

The data processing for monitoring and

evaluation of the system performance occurs in the

intermediate layer. Here high-resolution, crisp data

from sensors are filtered to allow representation of

the current state of the manipulator. This servo-

expert layer acts as an interface between the crisp

controller, which regulates the servomotors at the

bottom layer, and the knowledge-based controller at

the top layer. The intermediate layer handles such

tasks as performance specification, response

processing, and computation of performance indices.

This stage involves, for example, averaging or

filtering of the data points, and computation of the

rise time, overshoot, and steady state offset.

Top Layer

The knowledge base and the inference engine in

the uppermost layer are used to make decisions that

achieve the overall control objective, particularly by

improving the performance of low-level direct

control. This layer can serve such functions as

monitoring the performance of the overall system,

assessment of the quality of operation, tuning of the

low-level controllers, and general supervisory

control. In this layer, there is a high degree of

information fuzziness and a relatively low control

bandwidth. Figure 1 presents the hierarchical

structure of the three-level control system.

HIERARCHICAL MODAL CONTROL OF A NOVEL MANIPULATOR

207

2.3 Performance Specification,

Evaluation, and Classification

The desired performance of the system is specified

in terms of the following time domain parameters:

• Rise time ( );

RST

• Overshoot, if underdamped ( );

OVS

• Offset at steady state ( ).

OFS

These three parameters are used to present the

desired performance of the system. The rise-time is

chosen as the time it takes for the response to reach

95% of the desired steady-state response. The

overshoot is calculated at the first peak of the

response. The steady-state offset is computed by

taking the difference between the average of the last

third of the response and the desired response.

The corresponding time domain parameters are

obtained from the response of the actual system,

with the subscript

r referring to the real system

response as:

, , and . Once

evaluated, the parameters of the real system are

compared with the desired ones to get the index of

deviation. For each performance attribute, an index

of deviation is calculated using the following

equation,

RST

OVS

OFS

Index of deviation of attribute = 1

−

i desired attribute

i actual attribute

(6)

The index is defined in such a way that the value of

1 corresponds to the worst-case performance, while

zero means the actual performance of the system, for

that particular attribute, exactly meets the

specification. The indices are calculated according

to:

RST

RST ERR

RST

=− = 1)

; (7)

OVS

OVS ERR

OVS

=− =

(2)

; (8)

OFS

OFS ERR

OFS

=− =

(3)

. (9)

These indices represent the performance of the

system and hence should correspond to the context

of the rulebase of system tuning. The index of

deviation is therefore fuzzified into membership

values according to the five selected primary fuzzy

states: Highly Unsatisfactory (HIUN), Needs

Improvement (NDIM), Acceptable (ACCP), In

Specification (INSP) and Over Specification

(OVSP). In order to obtain a discrete set of

performance indices K(i), threshold values TH(i) are

defined for each index of deviation over the interval

∞

to 1, as given in Table 1.

Table 1: Mapping from the index of deviation to a discrete

performance index

The performance indices obtained in this

manner are the input to a Fuzzy Inference System

(FIS) which tunes the modal frequencies and

damping ratios of the closed-loop system. The

output from FIS is the tuning action that is used to

update modal frequencies and modal damping ratios

Discrete

Performance

Index K(i)

Index of Deviation

5 ERR(i) < 0

0 < ERR(i)

TH(1)

≤

TH(1)

≤

ERR(i) TH(2)

≤

TH(2)

ERR(i) TH(3)

≤ ≤

TH(3)

≤

ERR(i)

≤

Information

Abstraction

Intelligent

erviso

−

Bottom La

Intermediate

Layer

Top Layer

Response

Direct

Controller

Manipulator

Figure 1: Schematic representation of the three-level controller.

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

208

of the closed-loop system. Therefore, closed-loop

poles can be modified correspondingly.

2.4 Fuzzy Tuner Layer

At the highest level of the hierarchical structure,

there is a knowledge base for tuning a crisp

controller. This knowledge may originate from

human experts or some form of archives, and is

expressed as linguistic rules containing fuzzy terms.

For each status (context) of the system, a

conceptual abstraction is computed, and the expert

knowledge is transformed into a mathematical form

by the use of the fuzzy set theory and fuzzy logic

operations. A Fuzzy Inference System (FIS) has

been built using the Matlab Toolbox to this end. To

construct the system, one must first assign a

membership function to each of the performance

indices and tuning parameters. Then the knowledge

base should be created. Taking performance indices

as the input, Fuzzy Inference System carries out

such tasks as fuzzification of the performance

indices, operations of the fuzzy set, and defuzzifying

of the tuning actions. The output of the FIS is a crisp

tuning action corresponding to numerical context

values of the system condition.

The tuned parameters are chosen to be the

modal frequencies and modal damping ratios. As

mentioned before, eigenstructure of the closed loop

system plays a key role in determining the system

performance. Required performance can be achieved

by properly assigning the system eigenstructure.

There are relationships between system

eigenstructure and system modal parameters

(Equation 4). They provide a way to modify the

eigenstructure by tuning modal frequencies and

modal damping ratios. These modal parameters are

physically meaningful and hence chosen as the tuned

parameters.

and

represent the modal

frequency and damping ratio, respectively, the

relationship between modal parameters and system

eigenstructure is given by Equation (4). At each

tuning step, the values of

thi

and

are updated

according to the tuning actions obtained from the

Fuzzy Inference System (FIS). Once updated, the

new values of parameters

and

are used to

determine the new desired eigrnstructure of the

system. Relations used for updating

and

are:

;

new old

ii iis

new old

ii iise

ωω ωω

ζζ ζζ

=+∆

(10)

where the subscript ‘new’ denotes the updated value

and ‘old’ refers to the previous value. The

incremental action taken by the fuzzy controller is

denoted by

∆

and

∆

. Parameters

isen

and

isen

are introduced to adjust sensitivity of tuning,

when needed.

2.5 Construction of Fuzzy Inference

System

The expert tuning knowledge for a modal controller

may utilize heuristics such as those given in Table 2.

One may define the primary fuzzy sets for the

performance indices for each context variable (i.e.,

RST, OVS, and OFS) as given in Table 3. Fuzzy

tuning variables are defined as follows:

DFREQ

= Change in the modal frequency;

thi

DDAMP

= Change in the modal damping ratio.

thi

Each tuning variable may be expressed with fuzzy

sets and representative numerical values that are

listed in Table 4. The rulebase for control parameter

tuning is given in Figure 2.

Table 2: Heuristics of modal control tuning.

Actions for Performance

Improvement

Context

Modal

Frequency

Modal

Damping

Ratio

Rise Time (RST) Increase Decrease

Overshoot (OVS) ------ Increase

Offset (OFS) Increase Decrease

Table 3: Fuzzy labels of performance indices

Context Fuzzy Set Perform.

Index

Notation Fuzzy Value

1 HIUN Highly Unsatisfactory

2 NDIM Needs Improvement

3 ACCP Acceptable

4 INSP In Specification

5 OVSP Over-Specification

Triangular membership functions for the

performance attributes RST, OVS, OFS and for the

fuzzy tuning actions DFREQ

, DDAMP

are given

in Figure 3 and Figure 4, respectively. Each fuzzy

action or condition quantity has a representative

HIERARCHICAL MODAL CONTROL OF A NOVEL MANIPULATOR

209

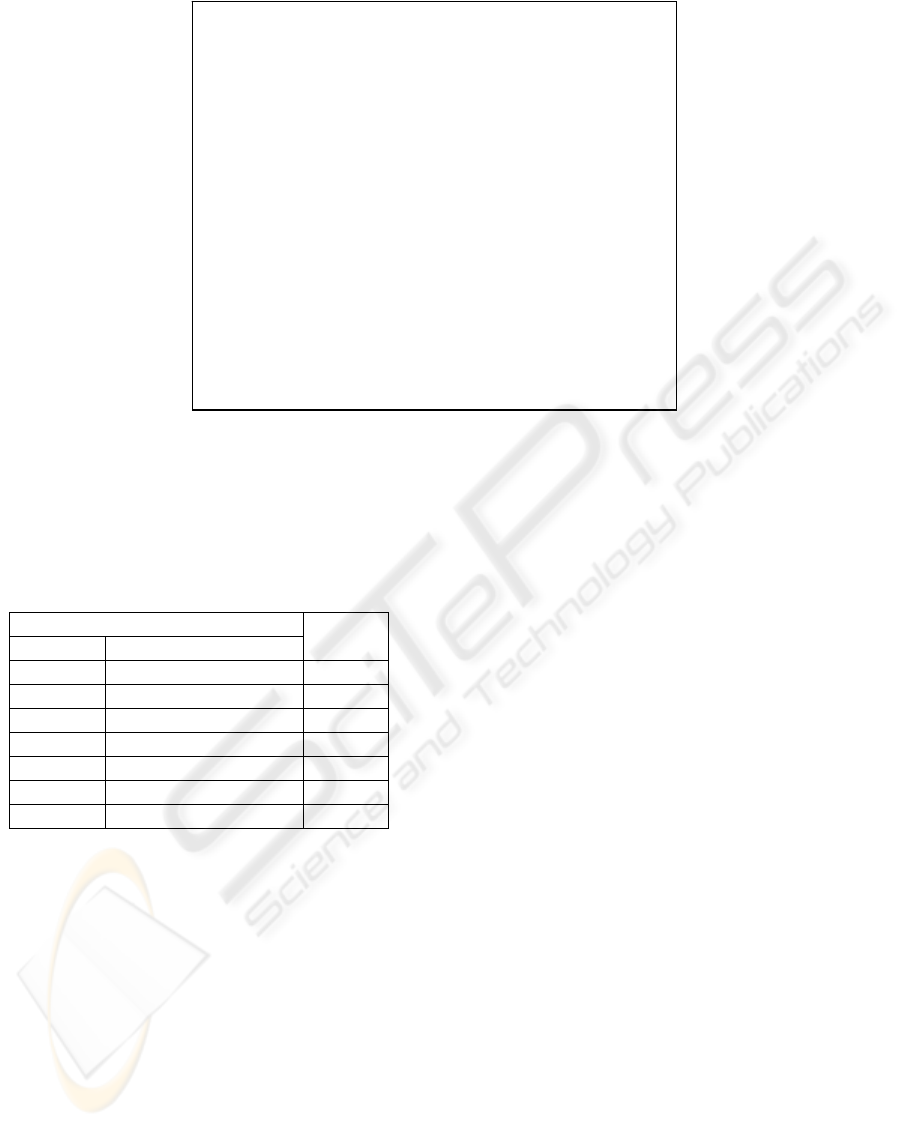
value, which is assigned a membership grade equal

to unity. The decreasing membership grade around

that representative value introduces a degree of

fuzziness.

Table 4: Tuning fuzzy sets and representative numerical

values

Tuning Fuzzy Set

Notation Fuzzy Value

Integer

Value

PL Positive Large 3

PM Positive Moderate 2

PS Positive Small 1

ZR Zero 0

NS Negative Small -1

NM Negative Moderate -2

NL Negative Large -3

3 GROUND-BASED SIMULATION

3.1 Modeling of a Ground-Based

Manipulator System

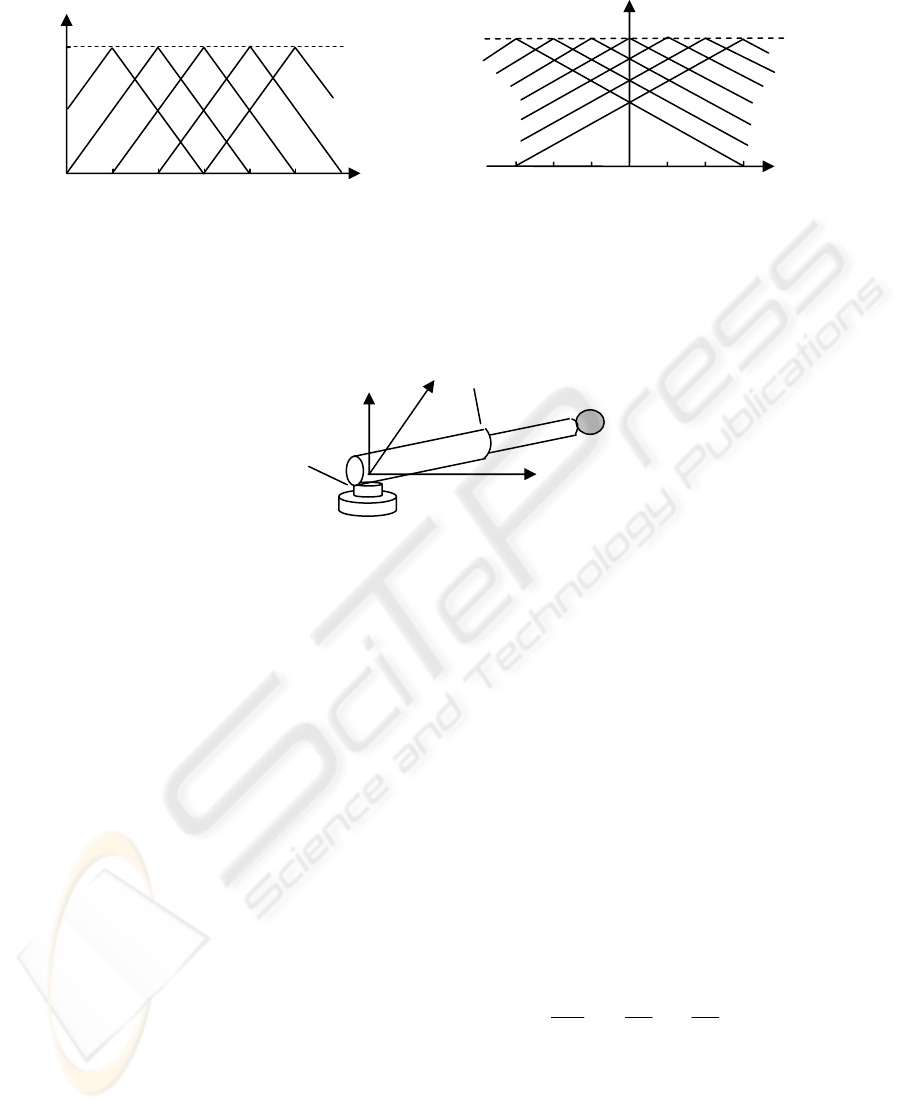
The ground-based manipulator system considered

for fuzzy tuning modal control is shown in Figure 5.

The system consists of a single module manipulator

carrying a point-mass payload held by the end

effector. The module has two rigid links. The first

link undergoes slewing motion through a flexible

revolute joint. The other link can be deployed and

retrieved by the rigid prismatic joint. The motion of

the manipulator is confined to the horizontal plane,

i.e. the gravity effects are not present.

The revolute joint is considered flexible. It is

modeled by a linear torsional spring, with stiffness

K, that connects the rotor of the servomotor to the

slewing link. The angular motion of the rotor with

respect to stator is denoted by

. The angular

deformation of the torsional spring is given by

Thus

αβ

is the total angular displacement of

the slewing link.

3.2 Control System and Simulation

Results

As mentioned before, the hierarchical structure used

combines the advantages of a crisp modal controller

with those of a soft, knowledge-based, supervisory

controller. The three layers of the structure

implement such tasks as collection of information

coming from sensors, data processing and

information abstraction, as well as general

supervisory control.

This hierarchical control system is used to

suppress the vibrations of the manipulator system

described in Figure 5. The effectiveness of the

control system is assessed by studying suppression

of vibrations caused by different disturbances. In the

first two cases, the initial disturbances at the flexible

joint of the manipulator are considered. The length

of the module may be specified at a fixed value

through the Lagrange multiplier. Therefore, the

subsystem considered for control simulation has two

Figure 2: Rulebase for the control parameter tuning.

If RST is HIUN, then DFREQ

is PL, DDAMP

is NM,

or If RST is NDIM, then DFREQ

is PM, DDAMP

is NS,

or If RST is ACCP, then DFREQ

is PM, DDAMP

is ZR,

or If RST is INSP, then DFREQ

is ZR, DDAMP

is ZR,

or If RST is OVSP, then DFREQ

is NS, DDAMP

is ZR,

or If OVS is HUIN, then DFREQ

is NM, DDAMP

is PL,

or If OVS is NDIM, then DFREQ

is NS, DDAMP

is PM,

or If OVS is ACCP, then DFREQ

is ZR, DDAMP

is PS,

or If OVS is INSP, then DFREQ

is ZR, DDAMP

is ZR,

or If OVS is OVSP, then DFREQ

is PS, DDAMP

is NS,

or If OFS is HIUN, then DFREQ

is PM, DDAMP

is NS,

or If OFS is NDIM, then DFREQ

is PS, DDAMP

is NS,

or If OFS is ACCP, then DFREQ

is ZR, DDAMP

is NS,

or If OFS is INSP, then DFREQ

is ZR, DDAMP

is ZR,

or If OFS is OVSP, then DFREQ

is NS, DDAMP

is ZR,

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

210

degrees of freedom, with

,,,

βαβ

as the system

state variables. The parameters for the first

simulation case are given in Figure 6.

The initial feedback control gain is determined

using the Linear Quadratic Regulator (LQR). Based

on this, tuning action takes place. The tuning process

involves analysis of the response to an initial

disturbance listed in Figure 7, with respect to the

performance requirements of rise time, overshoot,

and steady-state error. The feedback gain matrix is

updated by the supervisory controller accordingly.

Figure 7(a) shows the system response when

controlled using the LQR strategy. The initial

displacement (= 2°) of the torsional spring at the

revolute joint results in vibrations at

and

. The

suppression of the vibrations can be observed due to

the application of the LQR controller. As can be

seen, the convergence speed is slow in this case, and

significant vibration remains after 10 seconds.

Figure 7(b) shows the results after fuzzy tuning is

applied. It can be observed that the convergence

speed is much faster compared to that in the LQR

controlled case. Within 4 seconds, the vibrations in

each degree of freedom are eliminated. Further

more, the peak amplitudes of the vibrations are

sign

hnique (FLT). The desired profiles

are described as

ificantly reduced.

In the above case, the response of a ground-

based deployable manipulator, experiencing

vibrations due to the initial disturbance at the

revolute joint, was studied. To further evaluate the

effectiveness of the hierarchical control system, a

case of simultaneous 30° slew and 0.5 m deployment

in 10 seconds was considered. Now the slew motion

at the revolute joint and deployment at the prismatic

joint are controlled using the nonlinear Feedback

Linearization Tec

() sin

τπ

ττ

τπτ

⎧

⎫

∆

⎛⎞

=−

⎨

⎬

⎜⎟

∆∆

⎝⎠

, (11)

whe

of coo

⎩⎭

is the specified set rdinates ( ,l

);

∆

is its desired variation (

, l

∆∆

);

is the time;

and ∆

is the time required for the maneuver.

-3 -2

-1

Figure 4: Membership functions for the fuzzy

tuning actions

Membership

Grade

Tuning

Action

HIUN

NDIM

ACCP

INSP

OVS

Figure 3: Membership functions for the fuzzy

performance attributes

Membership

Grade

Performance

Attribute

Figure 5: Configuration of the single-module manipulator with

revolute and prismatic joints

Base

Flexible Revolute

Join

Prismatic

Joint

Payload

HIERARCHICAL MODAL CONTROL OF A NOVEL MANIPULATOR

211

As can be expected, the large scale motions at

both revolute and prismatic joints would result in

vibration at the revolute joint, and this would persist

if damping is not present in the system. This

suggests a need for active control to suppress the

maneuver-induced vibration. To that end, two

control approaches are considered: the LQR and

Tuned Modal Control. They are applied after the

FLT- regulated maneuver is completed. Figure 8 (a)

shows the system response when controlled by the

combined FLT/LQR procedure. The rigid degrees of

freedom are regulated very well within the first 10

seconds by the FLT. After that, the LQR is applied

to suppress the maneuver-induced vibrations at the

flexible revolute joint. It is apparent that the LQR is

effective but its convergence speed is slow. Figure 8

(b) shows the system response when the

combination of the FLT and Tuned Modal Control is

employed. To obtain faster convergence speed,

tuning action is carried out based on the LQR

feedback gain matrix. It can be seen from Figure 8

(b) that, after a few tuning steps, much faster

convergence speed is achieved. The vibrations at the

flexible revolute joint are quickly eliminated right

after completion of the maneuver, without any

oscillations. Therefore, the developed knowledge-

based tuning system is quite effective in improving

the controller performance in presence of

maneuvers. It should be pointed out that, by

changing weight matrix of the LQR, a faster

response than that shown in Figure 8 (a) may be

achievable. However it is still significant to evaluate

the effectiveness of the ‘intelligent’ tuning system in

improving the controller performance.

4 CONCLUDING REMARKS

In this paper, a knowledge-based hierarchical control

system was developed for the vibration control of a

manipulator system. For this purpose, first a fuzzy

inference system (FIS) was established. The FIS was

then combined with a crisp modal controller to

construct a hierarchical control system.

The effectiveness of the hierarchical control

system was investigated through two simulation

cases. In the first case, the system was experiencing

vibration due to an initial disturbance at the revolute

joint. The second case considered a system going

through a simultaneous slew and deployment

maneuver. The results showed that the knowledge-

based tuning system developed here was quite

effective. It was found that the performance of a

modal controller for a manipulator could be

significantly improved through knowledge-based

tuning. On this basis one might conclude that

additional tuning of the controller parameters could

significantly improve the performance of a modal

controller in general.

System Parameters

Slewing link:

= 1.0 m

= 2.0 kg

Deployable link:

= 1.0 m

= 2.0 kg

Payload:

= 3.0 kg

Joint stiffness:

K = 80 Nm/rad

Rotor inertia:

J = 2 kg-

Specified Coordinates

l = 1.5 m

(i.e., length is held fixed.)

Initial Conditions

(0) 0

= , ; (0) 2

(0) (0) 0.

αβ

Figure 6: Parameters for the ground-based simulation.

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

212

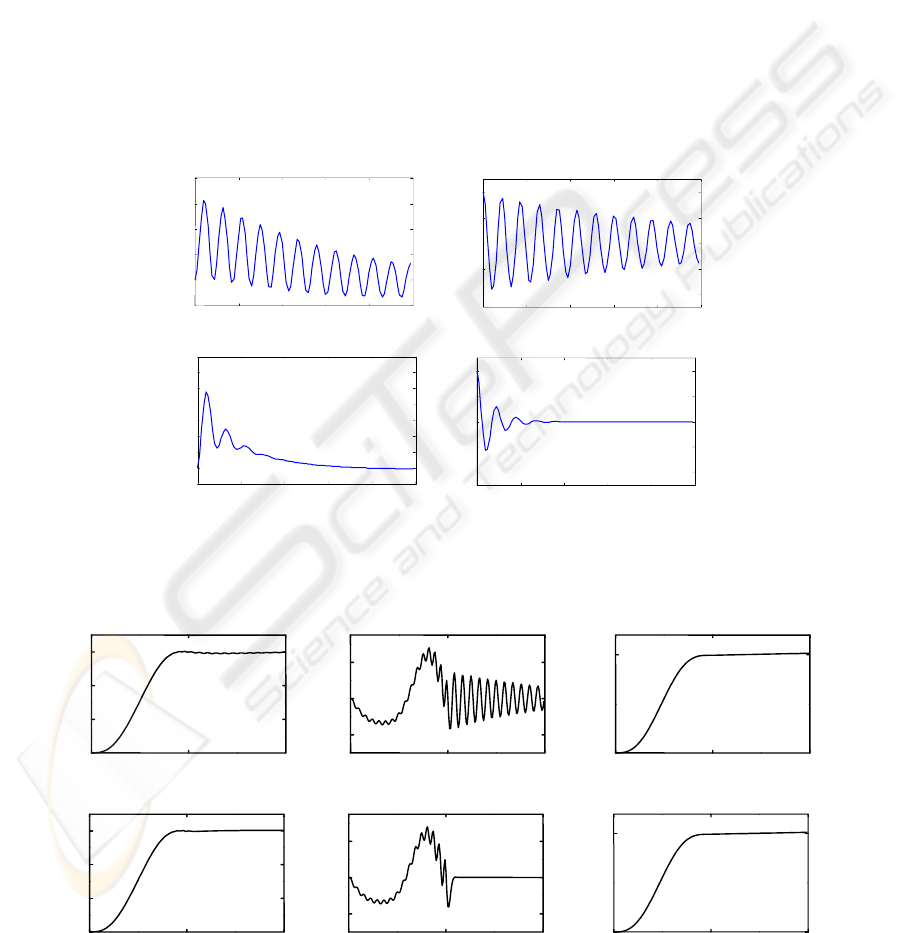
Figure 7: System response to an initial displacement at the revolute joint:

(a) controlled by LQR; (b) controlled by hierarchical controller.

Time, s

0 2

8 10

-2

-1

0 2 4 6 8 10

-1

(a)

2 4 6

Time, s

-2

-1

0 8

(

)

ACKNOWLEDGEMENT

Funding for the work reported in this paper has

come from the Natural Sciences and Engineering

Research Council of Canada.

REFERENCES

Junkins, J.L., 1993. Introduction to Dynamics and

Control of Flexible Structures, American Institute of

Aeronautics and Astronautics, Inc., Washington,

DC, U.S.A., pp. 235-265.

Nishitani, A., 1998. Application of Active Structural

Control in Japan, Progress in Structural Engineering

and Materials, Vol. 3, pp. 301-307.

de Silva, C. W., 1995. Intelligent Control: Fuzzy Logic

Applications, CRC Press, Boca Raton, FL, U.S.A.

Goulet, J. F., 1999. Intelligent Hierarchical Control of a

Deployable Manipulator, M.A.Sc. Thesis,

Department of Mechanical Engineering, University

of British Columbia. Vancouver, B.C.

de Silva, C.W., 2000. Vibration Fundamentals and

Practice, CRC Press, Boca Raton, FL, U.S.A.

Caron, M., Modi, V. J., Pradhan, S., de Silva, C. W., and

Misra, A.K., 1998. Planar Dynamics of Flexible

Manipulators with Sewing and Deployable Links,

Journal of Guidance, Control, and Dynamics, Vol.

24, pp. 572-580.

Time, s

0.2

l, m

(a)

(b)

Figure 8: System response while going through a maneuver:

(a) controlled by the FLT/LQR;

(b) controlled by the FLT/Tuned Modal Control.

0.2

l, m

HIERARCHICAL MODAL CONTROL OF A NOVEL MANIPULATOR

213