HYBRID CONTROL DESIGN FOR A ROBOT MANIPULATOR

IN A SHIELD TUNNELING MACHINE

Jelmer Braaksma, Ben Klaassens, Robert Babu

ska

Delft Center for Systems and Control, Delft University of Technology

Mekelweg 2, 2628 CD Delft, the Netherlands

Cees de Keizer

IHC Systems B.V., P.O. Box 41, 3360 AA Sliedrecht, the Netherlands

Keywords:

Robotic manipulator, shield tunneling, hybrid control, collision, environment model, feedback linearization.

Abstract:

In a novel shield tunneling method, the tunnel lining is produced by an extrusion process with continuous

shield advance. A robotic manipulator is used to build the tunnel supporting formwork, consisting of rings

of steel segments. As the shield of the tunnel-boring machine advances, concrete is continuously injected in

the space between the formwork and the surrounding soil. This technology requires a fully automated ma-

nipulator, since potential human errors may jeopardize the continuity of the tunneling process. Moreover, the

environment is hazardous for human operators. The manipulator has a linked structure with seven degrees of

freedom and it is equipped with a head that can clamp the formwork segment. To design and test the controller,

a dynamic model of the manipulator and its environment was ﬁrst developed. Then, a feedback-linearizing hy-

brid position-force controller was designed. The design was validated through simulation in Matlab/Simulink.

Virtual reality visualization was used to demonstrate the compliance properties of the controlled system.

1 INTRODUCTION

With conventional shield tunnel boring machines

(TBM), the tunnel lining is built of pre-fabricated

concrete segments (Tanaka, 1995; K. Kosuge et al.,

1996). These segments must be transported from the

factory to the construction site, which requires con-

siderable logistics effort. Delays in delivery and dam-

age of the segments during their transport are not un-

common.

To improve the process, IHC Tunneling Systems

are developing a novel shield tunneling method in

which the tunnel lining is produced by extruding con-

crete in the space between the drilled hole and the

supporting steel formwork. This formwork is built of

rings, each consisting of eight segments.

The main functions of the formwork are: i) sup-

port the extruded concrete tunnel lining until it is

hardened and becomes self-supporting, ii) provide the

thrust force to the TBM shield which actually exca-

vates the tunnel. The thrust is supplied by 16 indi-

vidually controlled hydraulic thrust cylinders, evenly

spread around the shield’s circumference.

A robotic manipulator (erector) is used to place the

segments at the desired position. The erector is a

linked robot mounted such that it can rotate around

the TBM spine, see Fig. 1. It is equipped with a head

that clamps the segment and picks it up from the con-

veyer. At the back end of the TBM, the concrete is al-

ready hardened and the formwork can be dismantled

by a similar manipulator (derector). The segments

are cleaned and inspected for possible damage before

they can be transported to the front end of the TBM

and re-used.

As in the proposed method the tunnel-boring pro-

cess is continuous (maximum speed of 2 m/h), the

segments have to be placed within a limited time

interval, and simultaneously with the TBM forward

movement. To comply with the stringent timing re-

quirements and to ensure the continuity of the boring

process, the erector must be controlled automatically

(as opposed to the current practice of using operator-

controlled manipulators). By automating the process,

the probability of a human error is limited and also

the hazard for the operator is considerably reduced.

The controller of the erector must guarantee stable

and safe operation in three different modes (Fig. 2):

1. The segment is in free space and the main task is to

bring it close to the desired position.

2. The segment is in contact with the hydraulic thrust

cylinders which push it toward the already placed

formwork ring.

185

Braaksma J., Klaassens B., Babuška R. and Keizer C. (2004).

HYBRID CONTROL DESIGN FOR A ROBOT MANIPULATOR IN A SHIELD TUNNELING MACHINE.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 185-192

DOI: 10.5220/0001128901850192

 SciTePress

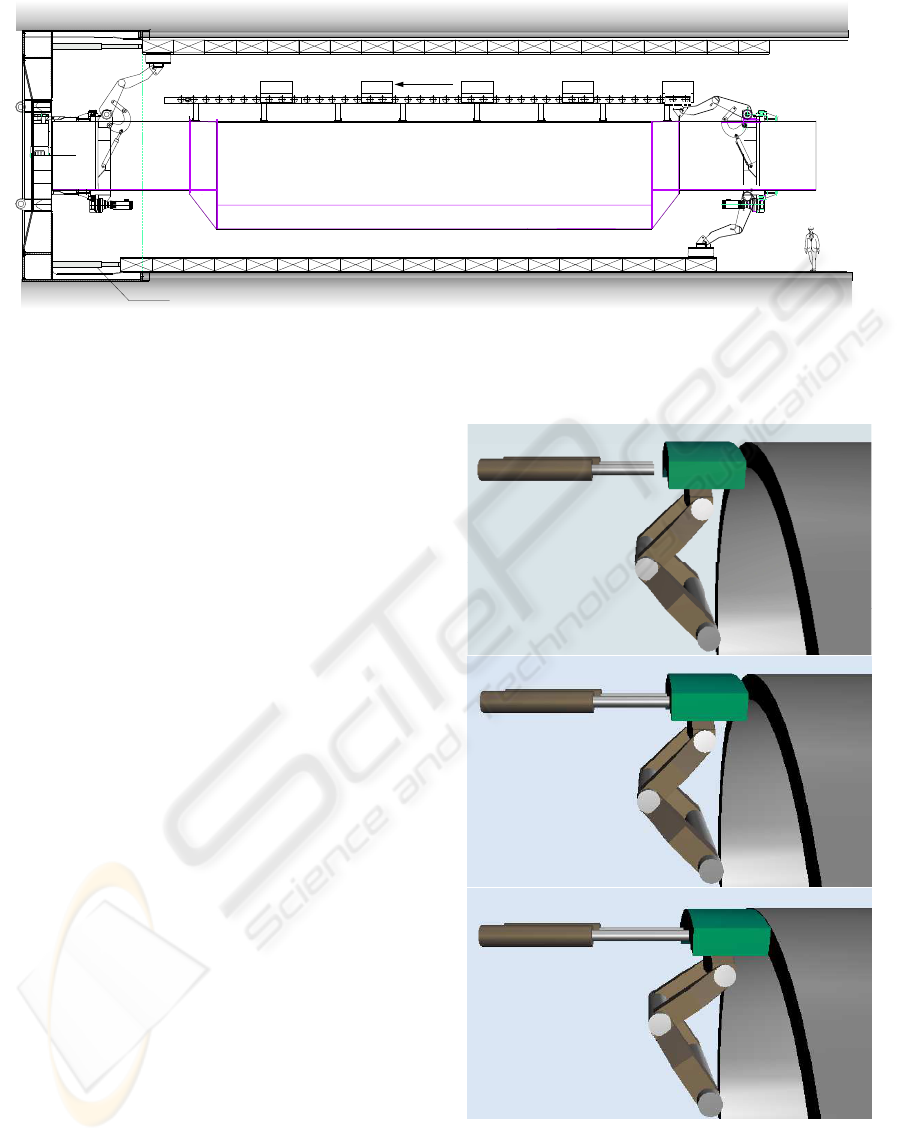
erector

conveyer

derector

formwork

hydraulic thrust cylinders

spine

shield

concrete

Figure 1: Cross-section of the shield tunneling machine. Two working conﬁgurations of the derector are shown.

3. The segment is in contact with the hydraulic thrust

cylinders and the formwork ring. The force deliv-

ered by the thrust cylinders will align the segment

in the desired position.

While the ﬁrst mode is characterized by traditional

trajectory-following control, the latter two modes re-

quire compliant control, capable of limiting the con-

tact forces and correcting a possible mis-alignment

due to a different orientation of the segment and the

already placed ring. Note that no absolute measure-

ment of the segment position is available, it can only

be indirectly derived from the measurements of the

individual angles of the manipulator links.

To analyze the process and to design the control

system, a detailed dynamic model of the erector has

been developed. This model includes collision mod-

els for operation modes 2 and 3. A hybrid control

scheme is then applied to control certain DOFs by

a position control law and the remaining ones by a

force control law. Input-output feedback linearization

is applied in the joint space coordinates. Simulation

results are reported.

2 MODELING

The mathematical model consists of three parts: the

manipulator, the environment and the hydraulic thrust

cylinders. This section describes these elements one

by one.

2.1 Manipulator model

The erector was designed as a linked structure with

three arms and a ﬁne-positioning head, see Fig. 3. The

ﬁrst arm is attached to the base ring (body0) that can

rotate around the spine. This ring is actuated by an

electric motor. The arms are actuated by hydraulic

Hydraulic push actuators

Manipulator

Segment to be placed

Ring, already built

Figure 2: The erector manipulates segments in three differ-

ent modes: in free space (top), in contact with the hydraulic

thrust cylinders (middle), in contact with the trust cylinders

and the segment ring (bottom).

ICINCO 2004 - ROBOTICS AND AUTOMATION

186

actuators (not modeled here). At the top of the third

arm (body3), the head is attached, which has three de-

grees of freedom (DOF). The entire manipulator has

seven DOF (q

to q

) in total.

(pitch)

(yaw)

(roll)

Spine

body2

body1

body0

body3

head

Figure 3: The structure and the corresponding degrees of

freedom of the erector.

The bodies are assumed rigid bodies and the DOF

in body0 is not taken into account. This is justiﬁed,

as the rotation around the spine is ﬁxed during the

positioning of the head. Angle q

is still an input to

the model, ﬁxed to a value between 0 and 2 π rad. The

control inputs of the robot are assumed to be perfect

torque/force generators in the joints.

The dynamic equation for the manipulator is:

D(q)

q + C(q,

q + F

q + φ(q) = τ − J

(q)

(1)

where f is the vector of contact forces between the

hydraulic thrust cylinders and the segment plus the

contact forces between the segment and the ring. The

matrix D(q) is the inertia matrix, C(q,

q) is the Cori-

olis and centrifugal matrix, F

is the friction matrix

and φ(q) is the gravity vector. J

is the Jacobian

from frame b4 to frame 0, and q is the vector of the

joint angles. The manipulator is actuated with the

torque/force vector τ .

2.2 Environment model

The environment consists of the segment ring (Fig. 4).

An accurate environment model, very important to

the contact tasks in robotics, is usually difﬁcult to

obtain in an analytic form. In the literature, usu-

ally a simpliﬁed linear model is used (Vukobratovi

Figure 4: Two consecutive rings of the formwork. Each ring

consists of eight segments.

1994). The environment is modeled as a mass-spring-

damper-system. The surface of the segment’s side is

considered ﬂat and only the normal force acting on the

side of the segment is taken into account. Tangential

friction forces are neglected. The collision detection

is implemented with the following smooth switching

function

g(x) =

atan(α(x − x

)) +

(2)

where α is the steepness of the function, x is the po-

sition of the segment and x

is the position of the en-

vironment. The environment force is described by the

following equation:

= g(x)(K

(x − x

) + D

( ˙x − ˙x

)) (3)

For stationary environments, equation (3) can be sim-

pliﬁed by taking ˙x

= 0. K

is the stiffness and D

is the damping.

hydraulic

push actuators

COG

segment

formwork ring

{ }C

Figure 5: Decomposition of contact force f

In the Cartesian space, the dynamic behavior de-

pends on the direction vector of the force and the lo-

cation of the collision. Fig. 5 shows an unaligned col-

lision of the segment with the formwork ring. In this

HYBRID CONTROL DESIGN FOR A ROBOT MANIPULATOR IN A SHIELD TUNNELING MACHINE

187

ﬁgure, a transformation is applied, which decomposes

a force f

into a force f

and torque τ acting on the

center of gravity (COG). The following formulas can

be applied.

= f

(4)

τ = r × f

(5)

where r points to the place where the force acts. The

above derivation is valid for a body moving in free

space. The transformation of the force and torque to

the joint torque is achieved using the principle of vir-

tual work, see (Spong and Vidyasagar, 1989). The

following formula for the joint torques can be derived

= J

(q)

0 R

f with f =

(6)

where R

transforms the force expressed in the seg-

ment body frame to the base frame, J

(q) is the Ja-

cobian which transforms the joint speeds to the lin-

ear/rotational speeds in the base frame and τ

is a

vector with joint torques/forces.

2.3 Hydraulic thrust cylinders

The model consists of a collision model and a hy-

draulic model. The collision model must detect the

collision between the hydraulic thrust cylinders and

the formwork ring, which means that the model must

detect whether the tips are contacting the segment

body (body4). If there is a collision, the magnitude of

the force can be calculated with the scheme explained

in Section 2.2.

The shape of a segment is illustrated in Fig. 6. The

segment (body4) is a part of a hollow cylinder. For

a controlled collision, the y coordinate of tip of the

hydraulic thrust cylinders must be between the inner

radius r

and the outer radius r

, and within the range

ϕ, see Fig. 6. The kinematic transformation of two

hydraulic thrust cylinders tips to the C

frame is used

to detect collision.

}

side view

body4

Figure 6: The dimensions of the segment (body4).

When the actuators come into contact with the seg-

ment, this will result in a force and torque as ex-

plained in Fig. 5. Only the normal force acting on the

segment is simulated. The error between the segment

and the thrust cylinders is at most 3 degrees, satisfying

the assumption to neglect the tangential force. The

force and torque in the C

frame, are calculated with

the following equations. Let H

and H

be the ho-

mogeneous transformations from the thrust cylinder

frames (C

, C

) to C

. The two force and torque

vectors can be calculated as follows

= |f

|[0 1 0]

= (H

[0 0 0 1]

)

123

= r

× f

(7)

= |f

|[0 1 0]

= (H

[0 0 0 1]

)

123

= r

× f

. (8)

where the subscript 123 refers to the ﬁrst three ele-

ments. These forces and torques in the body frame

can be transformed to the joint torques by means of

the principle of virtual work (6).

3 HYBRID CONTROLLER

The manipulator in free space is position controlled,

but when it is in contact with the environment, the lat-

eral motion and rotation become constrained. When

the segment is pushed by the hydraulic thrust cylin-

ders, stable contact between the thrust cylinders and

the segment is maintained by controlling the contact

force (Fig. 7). When the segment comes into contact

with the segment ring, it aligns to the desired orienta-

tion and position. During the transition between the

modes it is required that the contact forces are lim-

ited. An impedance controller gives the manipulator

the desired compliant behavior (Hogan, 1985).

Hydraulic

push

actuators

Segment

ring

}

Figure 7: Top view of the segment.

ICINCO 2004 - ROBOTICS AND AUTOMATION

188

A control scheme known as a hybrid position force

controller of (Raibert and Craig, 1981) allows to spec-

ify for each DOF the type of control. The frame in

which the segment is controlled is positioned such

that the direction, in which the position is controlled,

is perpendicular to the direction in which the force is

controlled. This frame is called the constraint frame.

In our case the constraint frame is aligned with the

two thrust cylinder frames (see Fig. 7). In this sit-

uation, the yaw, y, and the pitch, z, DOFs are con-

strained. We choose for the y degree of freedom a

force controller to assure contact. For the other po-

sition constrained degrees of freedom an impedance

controller is chosen which guarantees compliant be-

havior.

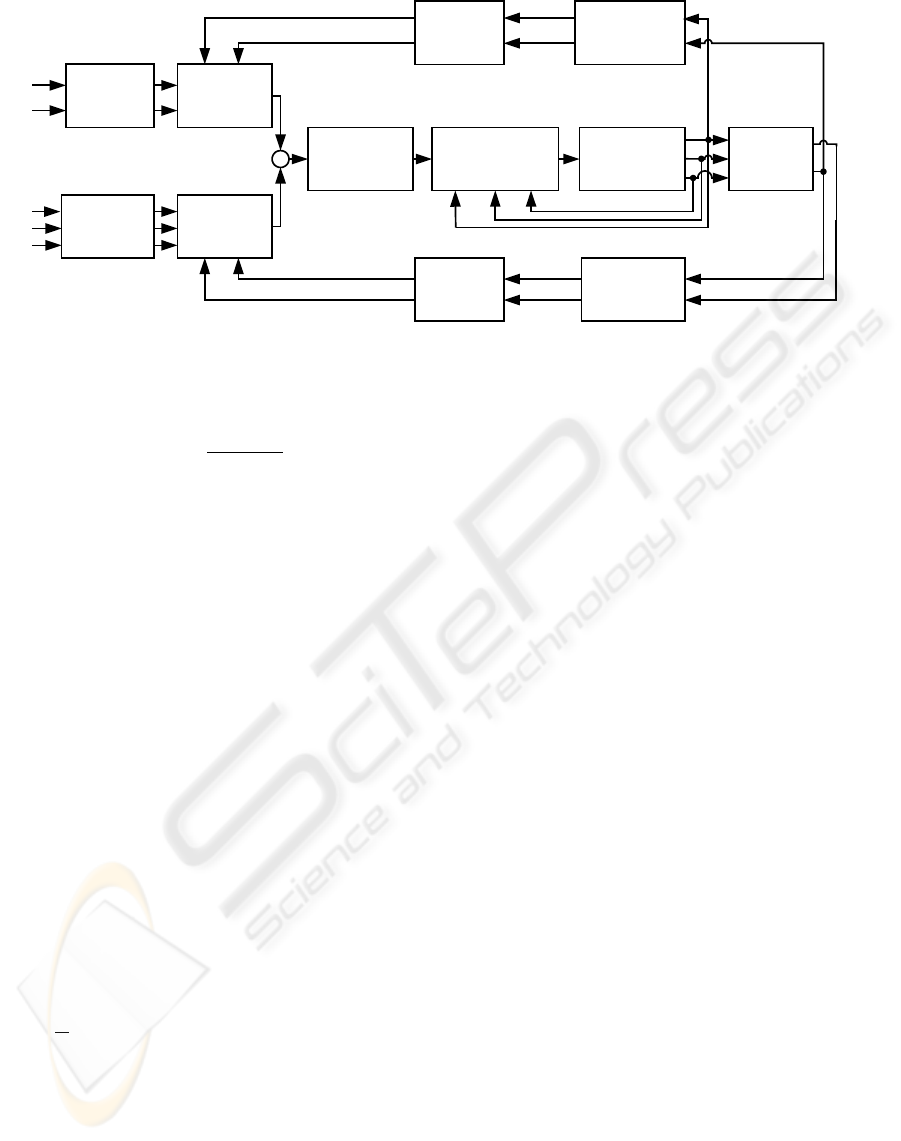
The controller consists of four blocks: feedback

linearization, transformation of sensor data (kinemat-

ics, Jacobian and coordinate transform), selection ma-

trix and the controllers (see Fig. 8).

The coordinate-transform block transforms the data

f, x, R, v and ω from the base frame to the constraint

frame and vice versa, where f is the measured force, x

is the position of the segment, R is the rotation matrix

which deﬁnes the orientation of the segment, v is the

linear speed of the segment and ω is the angular speed

of the segment. The inputs of the force controller are

and

, which are the desired force and it’s deriva-

tive. The inputs of the position controller are x

and

, which are the desired position, velocity and

acceleration respectively. The vector a is the resolved

acceleration vector and τ is the torque/force vector

for the manipulator.

3.1 Feedback linearization

The following controller is used for feedback lin-

earization (Siciliano and Villani, 1999)

τ =

D(q)u +

C(q,

q +

φ(q) + J

(q)

(9)

where u is the new acceleration control input. Sub-

stituting (9) into (1) and assuming perfect modeling

results in the following system

q = u (10)

The goal of the controller is to control the manipulator

in the constraint frame to its desired values.

The Jacobian transforms the joint velocities to the

linear and rotational speeds. The Jacobian is given by

= J

(q)

q (11)

Differentiating (11) gives

x = J

(q)

q +

(q)

q (12)

which represents the relationship between the joint

acceleration and the segment’s linear and rotational

speed. A new control input can now be chosen as

u = (J

(q))

−1

a −

(q)

. (13)

Substitute (13) into (10) and the result into (12), as-

suming perfect modeling and perfect force measure-

ment, leads to the following total plant model

x = a = a

+ a

(14)

where a is the resolved acceleration in the base frame

and a

, a

are the outputs of the position controller

and force controller in the base frame. The vector a

can be partitioned into linear acceleration a

and an-

gular acceleration a

. Likewise, a

can be partitioned

into linear acceleration a

and angular acceleration

. (15)

3.2 Transformation of sensor data

The different positions and speeds are measured in the

joints of the manipulator. The force is measured us-

ing a force sensor, located in the manipulator head. To

control the manipulator in Cartesian space these mea-

surements must be transformed to a Cartesian frame.

This is done with the kinematic matrix and the Jaco-

bian matrix. The frame in which the manipulator is

controlled is the constraint frame.

3.3 Selection matrix

The DOF for position control and for force control

can be selected. This is done by multiplying the

force/torque vector by a diagonal selection matrix S

and the position/velocity vector by I − S, with I the

identity matrix. For a DOF that is position controlled

= 0 and for a force controlled DOF S

= 1. For a

manipulator moving in free space the selection matrix

is a zero matrix, meaning position control.

To make sure that the switch between the two sit-

uations is in a controlled manner, the switch function

of the selection matrix must be smooth. The time of

switching in unknown, so the switch should be trig-

gered by the contact force (Zhang et al., 2001).

) =

− f

ref 1

, if f

≥ 0

ref 2

− f

, if f

< 0

(16)

The smooth switch function can now be deﬁned as

0, if Φ

) < 0

1 − sech(αΦ

)), otherwise

(17)

HYBRID CONTROL DESIGN FOR A ROBOT MANIPULATOR IN A SHIELD TUNNELING MACHINE

189

Feedback

linearization &

Cartesian to joint

space transformation

Coordinate

transform

Manipulator

Environment

Coordinate

transform

Position

controller

Selection

matrix

Selection

matrix

Force

controller

Coordinate

transform

Kinematics

Jacobian

Selection

matrix

Selection

matrix

Figure 8: Block diagram of the hybrid position force controller.

with

sech(x) =

+ e

−x

(18)

The value α determines the steepness of the curve,

and f

ref 1

, f

ref 2

are the upper and lower threshold

values respectively. The steepness α should be chosen

such that the S

= 1, when the desired contact force

is reached. The force in the y DOF (in the constraint

frame) is chosen to switch from position control to

force/impedance control.

3.4 Position control

For the linear and decoupled system (14), the follow-

ing control can be used in order to give the system the

desired dynamics (Siciliano and Villani, 1999).

+ D

(

−

x) + P

− x) (19)

+ D

(ω

− ω) + P

(20)

This is a PD controller for the position controlled

DOF, where R

transforms the quarternion error ²

from the C

frame to the constraint frame. The ma-

trices D

and D

are the diagonal damping matri-

ces, and P

and P

are the proportional gain matrices.

Substituting (19) and (20) into (14) assuming perfect

modeling gives the total plant model

¨x =

¨x

+ D

( ˙x

− ˙x) + P

− x)

+ D

(ω

− ω) + P

(21)

3.5 Force control

The force controller has an inner position/orientation

loop within the force loop. For the position loop, the

following PD-controller is chosen (Siciliano and Vil-

lani, 1999).

= −D

x + P

− x) (22)

where x

− x is the difference between x

the

output of the force loop and the measured posi-

tion/orientation x and P

is the proportional matrix

gain and D

is damping gain. For the force loop a

proportional-integral (PI) control is chosen

= P

−1

− f ) + P

− f )dς

(23)

where P

is the proportional gain, P

is the inte-

gral gain, f

is the desired force and f is the measured

force. The P

−1

in (23) has been introduced to make

the resulting force and moment control action in (22)

independent of the choice of the proportional gain on

the position and orientation.

3.6 Impedance control

For the impedance controlled DOF the following con-

trol law can be chosen (Siciliano and Villani, 1999)

+ M

−1

(

−

x) + P

− x) − f

)

+ M

−1

(ω

− ω) + P

− f

)

(24)

with M

and M

positive deﬁnite matrix gains,

leading to

(

−

x) + D

(

−

x) + P

− x) = f

(25)

(

−

ω) + D

(ω

− ω) + P

= f

(26)

Equations (25) and (26) allow specifying the manipu-

lator dynamics through the desired impedance, where

the translational impedance is speciﬁed by M

, D

and P

and the rotational impedance is speciﬁed by

, D

and P

ICINCO 2004 - ROBOTICS AND AUTOMATION

190

3.7 Simulation results

The rotation around the spine is ﬁxed during ﬁne po-

sitioning at q

= 0. The segment ring has a different

orientation than the segment; it is rotated around the

yaw axis by 0.05 radians. In order to take model un-

certainties into account, errors are introduced in the

model. For the dynamic parameters such as inertia an

error of 10% is introduced and for length and posi-

tions an error of 1% is introduced. As it is impossible

to simulate all combination of parameter errors, the

errors are randomly chosen for every simulation.

In the position loop, the P-gain is chosen P

= 10I.

This corresponds with a natural frequency of 3.2 rad/s

and for the D-gain D

= 6.3I and this corresponds

to a damping ratio of 1. For the pitch and roll axes

the same gains P

= 10I and D

= 6.3 are used.

The desired force input is 500 N. The position loop in

the force controller has also a P-gain of P

= 10I

and a D-gain of D

= 6.3I. The P-gain of the force

controller is P

p = 5 · 10

−3

I and the I-gain is set

= 5 · 10

−3

I. The parameters of the impedance-

controlled DOFs are given by M

= 100I, D

250I and P

= 500I for the z DOF and M

= 300I,

= 50000I and P

= 100I for rotational DOF.

At t=0 s the manipulator is in position control, and

there is no contact between the segment and the envi-

ronment. The thrust cylinders start moving and get in

contact with the segment at t=4.8 s. The manipulator

switches to force/impedance control and moves fur-

ther with the same speed as the hydraulic thrust cylin-

ders (see Fig. 9). The y position of the environment is

at y = 0.25 m. When the segment contacts the envi-

ronment at t = 8 s, the segment aligns with the envi-

ronment as shown in Fig. 10. This contact gives rise to

a torque τ

of 800 Nm in the head, which is measured

by the force sensor (Fig. 11). This torque is caused by

the damping term in the impedance controller. The

rotational speed is 0.0017 rad/s the damping term is

50000, the torque is then 0.0017 × 50000 = 833 Nm.

The simulations are repeated 50 times, each time

the parameters in the controller’s internal model are

chosen randomly. In Fig. 11 and Fig. 12, the measure-

ments of the force sensor are plotted. The magnitude

of the force in the y DOF is not inﬂuenced; the time

of impact varies due to the parameter changes. The

torque around the z axis is inﬂuenced by the parame-

ter change.

4 CONCLUSIONS

A dynamic model of the manipulator and its environ-

ment has been successfully derived and implemented

in Matlab/Simulink. The control requirements have

5 10 15 20 25 30

4.2

4.3

4.4

x[m]

time(s)

Position of segment Center of Grafity

5 10 15 20 25 30

0.1

0.2

y[m]

time(s)

5 10 15 20 25 30

−0.1

−0.05

0.05

0.1

z[m]

time(s)

Figure 9: Position of the segment.

5 10 15 20 25 30

0.02

0.04

Roll[rad]

time(s)

Roll Pitch and Yaw angles of the segment

5 10 15 20 25 30

−0.04

−0.02

Pitch[rad]

time(s)

5 10 15 20 25 30

0.02

0.04

Yaw[rad]

time(s)

Figure 10: Orientation of the segment.

0 5 10 15 20 25 30

200

400

600

800

1000

1200

1400

Linear force[N]

time(s)

0 5 10 15 20 25 30

−400

−200

200

400

600

800

1000

Torque[Nm]

time(s)

Figure 11: Force measurement in the segment force sensor

(one simulation run).

HYBRID CONTROL DESIGN FOR A ROBOT MANIPULATOR IN A SHIELD TUNNELING MACHINE

191

Figure 12: Force measurement in the segment force sensor

(50 simulation runs).

been met by using a combination of a force con-

troller, an impedance controller and a position con-

troller. The position precision is 0.01 m and for the

orientation the precision is 0.005 rad (0.3 degrees)

The hybrid controller is based on feedback lin-

earization to make the system linear and decoupled.

The feedback linearization is an inverse model of the

manipulator. If the dynamic parameters in the feed-

back linearization are within 10% accuracy and the

dimensional parameter are within 1% accuracy, a sta-

ble hybrid controller is obtained in simulations.

The position loops in the hybrid controller consist

of a PD-controller. The P and the D gains are tuned

by applying the following rules. When the natural fre-

quency ω and the damping ratio ζ are known, then the

P-gain is deﬁned by ω

and the D-gain is deﬁned by

2ζω.

It is assumed that the manipulator head is equipped

with a six DOF force sensor. If this is not possible

in the mechanical design, the possibility must be in-

vestigated of estimating the force, by measuring the

pressures in the hydraulic actuators.

REFERENCES

Hogan, N. (1985). Impedance control: An approach to ma-

nipulation: Part i - theory, part ii - implementation,

part iii - applications. ASME Journal of Dynamic Sys-

tems, Measurement, and Control, 107:1–24.

K. Kosuge et al. (1996). Assembly of segments for shield

tunnel excavation system using task-oriented force

control of parallel link mechanism. IEEE.

Raibert, M. and Craig, J. (1981). Hybrid position/force con-

trol of manipulators. J of Dyn Sys, Meas, and Cont.

Siciliano, B. and Villani, L. (1999). Robot Force Control.

Kluwer Academic Publishers.

Spong, M. W. and Vidyasagar, M. (1989). Robot Dynamics

and Control. John Wiley & Sons.

Tanaka, Y. (1995). Automatic segment assembly robot for

shield tunneling machine. Microcomputers in Civil

Engineering, 10:325–337.

Vukobratovi

c, M. (1994). Contact control concepts in ma-

nipulation robotics-an overview. In IEEE Transac-

tions on industrial electronics, vol. 41, no. 1, pages

12–24.

Zhang, H., Zhen, Z., Wei, Q., and Chang, W. (2001).

The position/ force control with self-adjusting select-

matrix for robot manipulators. In Proceedings of the

2001 IEEE International Conference on Robotics &

Automation. Department of Automatic Control, Na-

tional University of Defense Technology.

ICINCO 2004 - ROBOTICS AND AUTOMATION

192