ADAPTIVE MIMO MULTI-PERIODIC REPETITIVE CONTROL
SYSTEM:
LIAPUNOV ANALYSIS
H. Dang*, D.H. Owens
Department of Automatic Control and Systems Engineering ,The University of Sheffield
Mappin Street, Sheffield, S1 3JD, United Kingdom
Keywords:
Almost
Strictly Positive/Negative Real, Multi-periodic Repetitive Control, Adaptive Control, Lyapunov Anal-
ysis.
Abstract:
This paper presents a simple feed forward adaptive multi-periodic repetitive control scheme for the
ASPR(Almost Strictly Positive Real) or ASNR(Almost Strictly Negative Real, See Appendix for definition)
plant to asymptotically track/reject multi-periodic reference/disturbance signals. The lyapunov stability anal-
ysis is given. This is an extension work of the lyapunov stability analysis for multi-periodic repetitive control
system under a positive real condition. A simulation is included. The extension of the lyapunov stability anal-
ysis to ASPR or ASNR plant under certain non-linear perturbations and an exponential stability scheme are
discussed as well. Finally an adaptive proportional plus multi-periodic repetitive control scheme is proposed.
1 INTRODUCTION
For a system to track/reject periodic refer-
ence/disturbance signal, repetitive control was
developed several years ago. This control method,
which is based on the internal model principle, has
proven to be very effective in practical applications.
In most existing repetitive control approaches (Dixon
W. E., 2001; Hara S. and M., 1988; Horowitz R.,
1991; Jiang Y.A., 1995; Owens D.H. and S.P.,
2002; Owens D.H. and S.P., 2003), the asymptotic
convergence of the state to the origin and internal
stability of the system are guaranteed under some
strict assumption on the dynamic system. Hara
derived the sufficient conditions for the stability of
repetive and modified repetitive control systems by
applying the small gain theorem and the stability
theorem for time-lag systems. It is shown that the
plant P (s) should satisfy kf (s)(1 − P (s))k
∞
< 1
where f (s) is a low-pass filter introduced to improve
the system stability at a cost of losing tracking
accuracy at high frequencies. Owens et al gave
the lyapunov stability analysis and proved that
asymptotic/exponential stability is guaranteed if the
linear plant is positive real/strictly positive real or the
nonlinear plant is passive/strictly passive. Similar
lyapunov stability analysis was done (Dixon W. E.,
2001; Horowitz R., 1991; Jiang Y.A., 1995) and
some strict assumptions, which are actually passive
condition as in (Owens D.H. and S.P., 2003), were
made on the nominal system of the plant. In this
paper, we will alleviate such restrictive assumptions
on the plant to some extent.
In many cases, the reference/disturbance periodic
signals may contain different fundamental frequen-
cies and the ratio of these frequencies can be ir-
rational. So the so-called multi-periodic repeti-
tive control was analysed by several authors (G.,
1997; Weiss G., 1999; Owens D.H. and S.P., 2002;
Owens D.H. and S.P., 2003; Li L.M. and S.P.,
2002). Weiss gave a H
∞
stability condition based on
input-output transfer function for linear SISO/MIMO
single/multi-periodic system. The lyapunov stability
analysis is given by Owens and it is studied by Li
that a feed forward and feedback compensation can
be employed when the real plants are not necessarily
positive real. However, the method in (Li L.M. and
S.P., 2002) needs some plant parameter information
and such information is based on off-line frequency
domain system identification of a particular system.
Also the plant is restricted to be minimum phase,
strictly proper and with relative degree one and posi-
tive high-frequency gain, which actually is an ASPR
plant.
Adaptive repetitive control design and implemen-
tation, which includes internal model principle, have
Dang H. and H. Owens D.
ADAPTIVE MIMO MULTI-PERIODIC REPETITIVE CONTROL SYSTEM: LIAPUNOV ANALYSIS.
DOI: 10.5220/0001129102490256
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics (ICINCO 2004), pages 249-256
ISBN: 972-8865-12-0
Copyright
c
 2004 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
249

been discussed by many authors (G, 1996; Jiang Y.A.,
1995; Sun Z., 2000; Tomizuka M., 1989; Tsao T.,
1994; Tzou Y., 1999; X.D. and J.P., 1998) both in
the discrete-time and continuous-time domain. Most
of them (G, 1996; Sun Z., 2000; Tomizuka M.,
1989; Tsao T., 1994; Tzou Y., 1999) are indirect
adaptive control algorithms. Several estimation al-
gorithms were used to identify the plant models and
certainty equivalence principles were applied to de-
sign the adaptive control schemes. On the other hand,
Jiang gave a direct adaptive control scheme and ap-
plied an adaptively adjusted gain in the feedback con-
troller when the upper bound of the plant uncertainty
exists, however unknown. Ye designed a global adap-
tive control of a class of nonlinear systems when the
signs of certain system parameters are unknown for
learning control system.
In this paper we will use the non-identifier-based
direct adaptive control technique (A., 1993) to design
adaptive controllers for a class of ASPR or ASNR
MIMO LTI systems, which actually are minimum-
phase, with relative degree m and unknown high-
frequency gain, to track/reject multi-periodic refer-
ence/disturbance signals. The Lyapunov stability
analysis is applied.
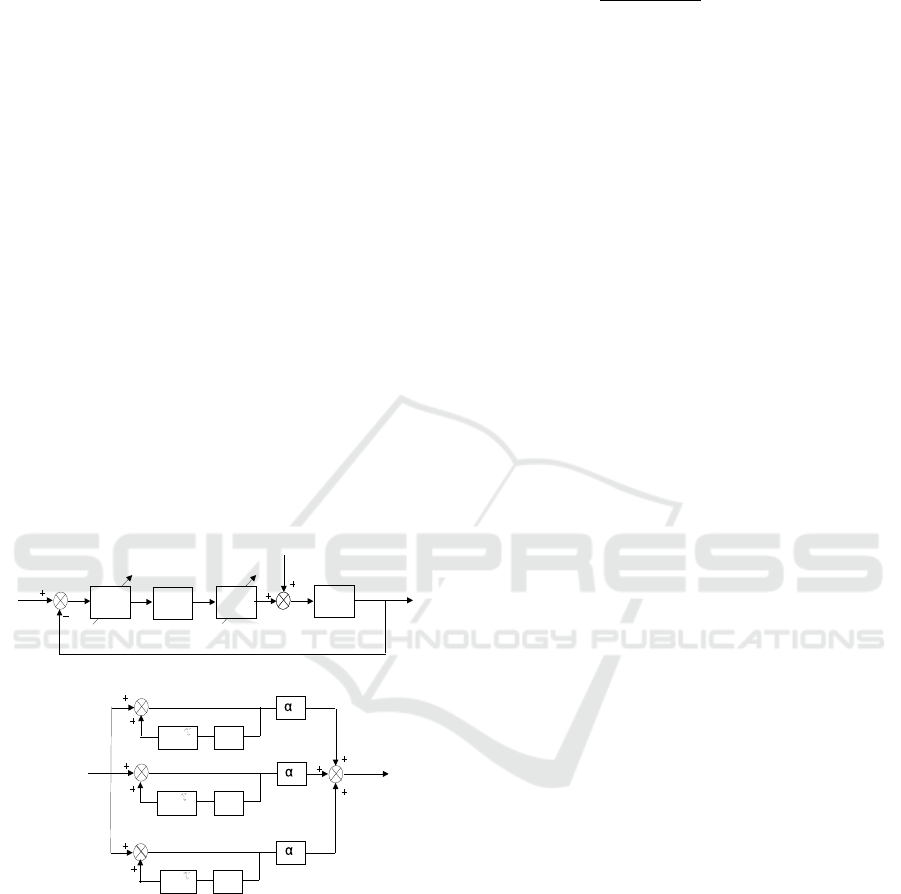
The adaptive MIMO multi-periodic repetitive con-
trol system is shown in Figure 1. The R, D, Y, U, E are
C (s)
1
C (s)
2
M(s)
G(s)
R E
U
D
Z
Y
W (s)
1
W (s)
2
W (s)
p
M(s):
V
p
V
2
V
1
Z
p
Z
2
Z
1
1
2
P
e
-S
1
e
-S
e
-S
2
P
Figure 1: Adaptive MIMO multi-periodic repetitive control
system
reference, disturbance, output, control input and error
respectively. The plant
P
G
is finite-dimensional, lin-
ear time-invariant and described by
˙x(t) = Ax(t) + B(u(t) + d(t))
y(t) = Cx(t), x(0) = x
0
(1)
where x(t) ∈ R
n
, u(t) ∈ R
m
, y(t) ∈ R
m
and the di-
mensions of constant matrices A, B, C are n×n, n ×
m, m × n respectively. Both reference r(t) and dis-
turbance d(t) are multi-periodic with components of
period τ
i
, i = 1, ..., p. These periods are assumed
known. The multi-periodic repetitive controller is
M(s) =
P
p
i=1
α
i
I
1−W
i
(s)e
−sτ
i
, we select
P
p
i=1
α
i
= 1
without loss of generality. W
i
(s) is a low-pass fil-
ter. C
1
(s), C
2
(s) are both feed forward matrix gains
given in the following sections designed to guarantee
the Lyapunov stability of the whole system including
the plant.
The paper is organized as follows. In section 2,
we introduce a simple high constant feed forward
gain, which realizes the stability of the multi-periodic
repetitive control system for an ASPR plant. In sec-
tion 3, we adopt an adaptive feed forward gain, which
alleviate the assumption made in section 2. In sec-
tion 4, the general problem is solved for the ASPR or
ASNR plant and here we introduce a Nussbaum-type
feed forward gain. Simulation results are presented
in section 5. Section 6 discusses the extension of the
lyapunov analysis to the ASPR or ASNR plant un-
der certain non-linear perturbations. Section 7 gives
an exponential stabilization control scheme via expo-
nential weighting factor. Section 8 gives an adap-
tive proportional plus multi-periodic repetitive con-
trol scheme. For every control schemes, the Lyapunov
stability proof is given. Finally in section 9, conclu-
sions are given.
2 STABILIZATION BY HIGH
CONSTANT FEED FORWARD
GAIN
In this section, we will show that applying a enough
high constant feed forward gain can make the multi-
periodic repetitive control system to be lyapunov sta-
ble when the plant is ASPR.
Assume the MIMO, LTI plant
P
G
is ASPR, that is
there exists an unknown constant matrix λ
∗
∈R
m×m
such that the closed-loop system (A − Bλ
∗
C, B, C)
satisfies the strict-positive-realness conditions, that is
P (A − Bλ
∗
C) + (A − Bλ
∗
C)
T
P < −Q
P B = C
T
(2)
where the P, Q are positive definite matrix. An ASPR
plant G(s) has a strictly minimum-phase m×m trans-
fer matrix of relative degree m(n poles and n − m ze-
ros). If G(s) has the minimal realization (A, B, C),
then CB > 0(positive definite).
Theorem 1 Consider the ASPR system
P
G
de-
scribed by (1). Suppose that both reference r(t) and
disturbance d(t) are identically zero. The feed for-
ward gain C
1
(s) = kΓ and C
2
(s) = Γ , where
k is a positive constant selected to be larger than
γ := kλ
∗
T
+ λ
∗
k and Γ ∈ R
m×m
is a matrix such
that Γ + Γ
T
> 0. Γ is selected to be I
m×m
without
Special Session on Analytical and Simulation Methods for Complex Systems 2004 - Special Session on Analytical and Simulation Methods
for Complex Systems
250

loss of generality. Then the multi-periodic repetitive
system in Figure 1 is globally asymptotically stable in
the sense that the state x(.) ∈ L
n
∞
[0, ∞), control sig-
nal v
i
(.) ∈ L
m
2
[0, ∞), and output y(.) ∈ L
m
2
[0, ∞).
Proof: Assume
˙x
W
i
(t) = A
W
i
x
W
i
(t) + B
W
i
v
i
(t)
z
i
(t) = C
W
i
x
W
i
(t)
(3)
is a minimal realization of strictly bounded real
W
i
(s). Then according to Corollary 1 and the in-
equality (10) in (Owens D.H. and S.P., 2002), we
have (x
T
W
i
P
W
i
x
W
i
)
0
≤ µ
2
v
T
i
v
i
− z
T
i
z
i
, where 0 <
µ < 1 is a constant. Introduce a positive definitive
Lyapunov function V of the form
V = x
T
P x+
1
k
p
X
i=1
α
i
(
Z
t
t−τ
i
kz
i
(θ)k
2
dθ+x
T
W
i
P
W
i
x
W
i
)
(4)
The system (1) can be rewritten as follows:
˙x(t) = (A − Bλ
∗
C)x(t) + Bv(t) + Bλ
∗
y(t)
y(t) = Cx(t), z(t) :=
P
p
i=1
α
i
v
i
(5)
By differentiating V along (5), using (2) and z
i
(t −
τ
i
) = v
i
(t) + k(t)y(t), we have
dV
dt
< −x
T
Qx − (k − γ)y
T
y −
1−µ
2
k
P
p
i=1
α
i
v
T
i
v
i
(6)
Integrating (6) and using (4) and the positivity of V
yield
V (0) > V (t) +
R
t
0
x
T
Qxdt +
R
t
0
(k − γ) kyk
2
dt
+
R
t
0
1−µ
2
k
P
p
i=1
α
i
v
T
i
v
i
dt
(7)
from which x(.) ∈ L
n
∞
[0, ∞),v
i
(.) ∈ L
m
2
[0, ∞) and
y(.) ∈ L
m
2
[0, ∞), which proves the result. ¤
3 STABILIZATION BY ADAPTIVE
FEED FORWARD GAIN
In section 2, we assume γ is known. It is a restrictive
assumption which will be excluded in this section by
applying an adaptive feed forward gain k(t).
Theorem 2 Consider the ASPR system
P
G
de-
scribed by (1). Suppose that both reference r(t)
and disturbance d(t) are identically zero. The feed-
forward gain C
1
(s) = k(s)Γ and C
2
(s) = Γ ,
where k(t) is an adaptive scale gain with adaptive
law
˙
k(t) = e
T
(t)e(t), k(0) > 0, Γ = I
m×m
. Then
the adaptive multi-periodic repetitive system in Fig-
ure 1 is globally asymptotically stable in the sense
that x(.) ∈ L
n
∞
[0, ∞), v
i
(.) ∈ L
m
2
[0, ∞), y(.) ∈
L
m
2
[0, ∞), k(.) ∈ L
∞
[0, ∞) and lim
t→∞
k(t) =
k
∞
< ∞.
Proof: The proof is an extension of that in section 2.
By differentiating (4) we have
dV
dt
< −x
T
Qx − (k − γ)y
T
y −
1−µ
2
k
P
p
i=1
α
i
v
T
i
v
i
−
1
k
2
dk
dt
P
p
i=1
α
i
(
R
t
t−τ
i
kz
i
(θ)k
2
dθ + x
T
W
i
P
W
i
x
W
i
)
(8)
Integrating (8) and using the adapting law
˙
k(t) =
e(t)
T
e(t) = y(t)
T
y(t) yields
V (t
0
) − V (0) < −
R
t
0
0
x
T
Qxdt −
R
k(t
0
)
k(0)
(τ − γ)dτ−
R
t
0
0
1
k
2
dk
dt
P
p
i=1
α
i
(
R
t
t−τ
i
kz
i
(θ)k
2
dθ + x
T
W
i
P
W
i
x
W
i
)dt
−
R
t
0
0
1−µ
2
k
P
p
i=1
α
i
v
T
i
v
i
dt
(9)
We will establish k(t) ∈ L
∞
[0, t
0
) by contradiction.
Suppose k(t) 6∈ L
∞
[0, t
0
), the term −
R
k(t
0
)
k(0)
(τ −
γ)dτ = −[
k(t
0
)
2
2
− γk(t
0
) −
k(0)
2
2
+ γk(0)] will be
negative infinity. The other items of the right part
of (9) are definitely negative due to
dk(t)
dt
≥ 0 and
0 < µ < 1 , hence contradicting the non-negativity
of the left hand side of (9). Therefore, we have
k(t) ∈ L
∞
[0, t
0
) .
When t
0
= ∞ , we have k(t) ∈ L
∞
[0, ∞).
Due to the monotonic increase of k(t), we have
lim
t→∞
k(t) = k
∞
< ∞. Also we have x(.) ∈
L
n
∞
[0, ∞), v
i
(.) ∈ L
m
2
[0, ∞) and y(.) ∈ L
m
2
[0, ∞)
as before, which proves the result. ¤
4 STABILIZATION VIA
NUSSBAUM-TYPE SWITCHING
In some case, CB, which is called control direc-
tion in (X.D. and J.P., 1998), is non-zero, however
not definitely positive and we don’t know the sign
of CB. Such plant
P
G
can be called ASPR or
ASNR, that is there exists an unknown positive def-
inite matrix λ
∗
such that the closed-loop system (A −
σBλ
∗
C, σB, C) satisfies the strict-positive-realness
conditions, where σ := sign(CB) is assumed un-
known.
Now we introduce a Nussbaum-type adaptive con-
troller as follows:
u(t) = N (λ(t))Γz(t) (10)
Γ = I
m×m
, N(.) : R → R is any continuous func-
tion of Nussbaum type (R.D., 1983), that is, N (.)
has the properties sup
k>k
0
1
k−k
0
R
k
k
0
N(τ )dτ = +∞
and inf
k>k
0
1
k−k
0
R
k
k
0
N(τ )dτ = −∞. For example,
N(.) : τ → τ
2
cos τ suffices.
Theorem 3 Consider the ASPR or ASNR system
P
G
described by (1). The feedforward gain C
1
(s) =
ADAPTIVE MIMO MULTI-PERIODIC REPETITIVE CONTROL SYSTEM: LIAPUNOV ANALYSIS
251

k(s)Γ and C
2
(s) = N(s)Γ , where k(t) and λ(t) are
both adaptive scalar gains with adaptive law
˙
k(t) =
e(t)
T
e(t), k(0) > 0 and
˙
λ(t) = e(t)
T
z(t), λ(0) ≥ 0.
Then the adaptive multi-periodic repetitive system in
Figure 1 is globally asymptotically stable in the sense
that x(.) ∈ L
n
∞
[0, ∞), e(.) ∈ L
m
2
[0, ∞), λ(.) ∈
L
∞
[0, ∞), k(.) ∈ L
∞
[0, ∞) and lim
t→∞
k(t) =
k
∞
< ∞.
Proof: We set the low-pass filter W
i
(s) to be 1. The
system can be rewritten as follows:
˙x(t) = (A − σBλ
∗
C)x(t) + B[N(λ)z(t) + d(t)]
+σBλ
∗
y(t)
y(t) = Cx(t), z(t) =
P
p
i=1
α
i
z
i
(t)
(11)
Also due to the minimum phase property of
P
G
,
there exists an invariant set, made up of periodic tra-
jectoris vanishing with r(t) and d(t), which is con-
tained in the ker of the output. That is, if the control
input u
∞
is carefully selected under some state x
∞
,
the output of the system output y
∞
will be r. So we
have
˙x
∞
(t) = Ax
∞
(t) + Bu
∞
(t)
r(t) = Cx
∞
(t)
(12)
Then we define e(t) := r (t)−y(t), e
x
(t) := x
∞
(t)−
x(t), we have
˙e
x
(t) = (A − σBλ
∗
C)e
x
(t) + σBλ
∗
e(t)
−BN (λ)z(t) − Bd(t) + Bu
∞
(t)
e(t) = Ce
x
(t)
(13)
Similar to d(t) =
P
p
i=1
α
i
d
i
(t), we have u
∞
(t) =
P
p
i=1
α
i
u
∞i
(t). Introducing a positive definite lya-
punov function V:
V = e
T
x
P e
x
+
1
k
P
p
i=1
α
i
R
t
t−τ
i
kez
i
(θ)k
2
dθ
ez
i
(θ) := z
i
(θ) − σu
∞i
(θ) + σd
i
(θ)
(14)
By differentiating V, we have
dV
dt
< −e
T
x
Qe
x
− (2σN(λ) − 2)z
T
e − (k − γ)e
T
e
−
1
k
2
dk
dt
P
p
i=1
α
i
R
t
t−τ
i
kez
i
(θ)k
2
dθ
(15)
Integrating (15) and using law
˙
k(t) = e(t)
T
e(t),
˙
λ(t) = e(t)
T
z(t) yield
V (t
0
) − V (0) < −
R
t
0
0
e
T
x
Qe
x
dt −
R
k(t
0
)
k(0)
(τ − γ)dτ
−
R
λ(t
0
)
λ(0)
(2σN(τ) − 2)dτ
−
R
t
0
0
1
k
2
dk
dt
P
p
i=1
α
i
R
t
t−τ
i
kez
i
(θ)k
2
dθdt
(16)
Suppose λ(t) 6∈ L
∞
[0, t
0
), k(t) 6∈ L
∞
[0, t
0
),
the term −
R
λ(t
0
)
λ(0)
(2σN(τ) − 2)dτ will take arbi-
trary large negative or positive value when λ(t
0
) =
∞ according to Theorem A.1 in Appendix. For
example, if we select N (λ) = λ
2
cos λ and
λ(0) = 0 without loss of generality, then we have
−
R
λ(t
0
)
0
(2σN(τ) − 2)dτ = −2σ[λ(t
0
)
2
sin λ(t
0
) +
2λ(t
0
) cos λ(t
0
) −2 sin λ(t
0
)] + 2λ(t
0
) and it will
take arbitrary large negative or positive value when
λ(t
0
) = ∞ . So when it takes arbitrary large neg-
ative, the right hand side of (16) will be negative,
hence contradicting the non-negativity of the left hand
side of (16). Therefore, we have λ(t) ∈ L
∞
[0, t
0
),
k(t) ∈ L
∞
[0, t
0
).
When t
0
= ∞ , we have λ(t) ∈ L
∞
[0, ∞), k(t) ∈
L
∞
[0, ∞). As in section 3, we have lim
t→∞
k(t) =
k
∞
< ∞, x(t) ∈ L
n
∞
[0, ∞) and e(t) ∈ L
m
2
[0, ∞),
which proves the result. ¤
It should be pointed out that we can’t prove that
lim
t→∞
λ(t) = λ
∞
< ∞ although the simulation
seems to show λ converges. Also for above analy-
sis we don’t assume that reference r(t) and distur-
bance d(t) are identically zero. In that case, W
i
(s)
can only be set as 1 because otherwise ez
i
(t) = z
i
(t)−
σu
∞i
(t) + σd
i
(t) doesn’t satisfy the same evolution
equation as z
i
(t). It’s easy to understand because
zero-tracking/full-rejection will be lost when W
i
(s)
isn’t equal to 1.
5 SIMULATION
For sake of simplicity, a SISO system is examined to
illustrate the control system performance. The ASPR
or ASNR plant under control is described as (1) where
A =
µ
−1 1
2 0
¶
, B =
µ
±1
0
¶
, C = (
1 0.5
),
x(0) =
µ
1
−1
¶
or G(s) =
±(s+1)
(s−1)(s+2)
. The refer-
ence is r = r
1
+ r
2
, where r
1
= sin ω
1
t +1.5 sin 5ω
1
t,
r
2
= sin ω
2
t and ω
1
= 0.2 × 2πrad/sec, ω
2
=
0.3 × 2πrad/sec. The disturbance is a square wave
at a period of 7Hz and with peak value ±2. A square
wave is chosen to indicate the scheme can cope with
signals with infinite frequency content. The weight-
ings are chosen to be 0.4, 0.4, 0.2(for the disturbance
rejection repetitive sub-controller). We select k(0) =
1, λ(0) = 0, W
i
(s) = 1 and N(λ) = λ
2
cos(λ).
The simulation result is given in Figure 2 and 3. Fig-
ure 2 is for G(s) =
(s+1)
(s−1)(s+2)
and Figure 3 is for
G(s) =
−(s+1)
(s−1)(s+2)
. The simulation result shows that
the control scheme is capable for the ASPR or ASNR
plant to asymptotically track/reject a multi-periodic
reference/disturbance signal.
Special Session on Analytical and Simulation Methods for Complex Systems 2004 - Special Session on Analytical and Simulation Methods
for Complex Systems
252

0 10 20 30 40 50 60 70 80 90 100
−3
−2
−1
0
1
2
3
4
5
6
7
t: second
e
0 10 20 30 40 50 60 70 80 90 100
−20
−10
0
10
20
30
40
t: second
N(lambda)
Figure 2: Error e(t) and Nussbaum-type gain N (λ) for
ASPR plant
0 10 20 30 40 50 60 70 80 90 100
−12
−10
−8
−6
−4
−2
0
2
4
t: second
e
0 10 20 30 40 50 60 70 80 90 100
−100
−50
0
50
t: second
N(lambda)
Figure 3: Error e(t) and Nussbaum-type gain N (λ) for
ASNR plant
6 EFFECT OF NON-LINEAR
PERTURBATION
The above lyapunov stability can be extended to the
system under certain non-linear perturbations. The
plant is described by
˙x(t) = Ax(t) + B(u(t) + d(t)) + g
1
(t, x(t))
+g
2
(t, y(t)) + d
0
(t)
y(t) = Cx(t)
(17)
The nominal system is ASPR or ASNR as in section 4
and the non-linear perturbations satisfy
g
1
(., .) : R × R
n
→ R
n
, kg
1
(t, x)k ≤ ˆg
1
kxk
g
2
(., .) : R × R
m
→ R
n
, kg
2
(t, y)k ≤ ˆg
2
kyk
d
0
(.) ∈ L
n
2
[0, ∞)
(18)
Here g
1
(., .), g
2
(., .), d
0
(.) are assumed to be Carathe-
dory function, which, for some unknown ˆg
1
, ˆg
2
≥ 0,
are linearly bounded for almost all t ∈ R and for all
x ∈ R
n
, u, y ∈ R
m
.
Theorem 4 Consider the system
P
G
described by
(17) and (18). Suppose that both reference r(t) and
disturbance d(t) are identically zero. Then the adap-
tive multi-periodic non-linear repetitive system in
Figure 1 where the feedforward gain C
1
(s) = k(s)Γ
and C
2
(s) = N (s)Γ with
˙
k(t) = e(t)
T
e(t), k(0) > 0
,
˙
λ(t) = e(t)
T
z(t), λ(0) ≥ 0 is globally asymptoti-
cally stable in the sense that x(.) ∈ L
n
∞
[0, ∞), y(.) ∈
L
m
2
[0, ∞), λ(.) ∈ L
∞
[0, ∞), k(.) ∈ L
∞
[0, ∞) and
lim
t→∞
k(t) = k
∞
< ∞.
Proof: We set the low-pass filter W
i
(s) to be 1 for
sake of simplicity. The proof is similar to that in sec-
tion 4 and here we only outline below. Introducing a
positive definite lyapunov function V:
V = x
T
P x +
1
k
p
X
i=1
α
i
Z
t
t−τ
i
kz
i
(θ)k
2
dθ (19)
Differentiating V along (17) yield
(x
T
P x)
0
< −x
T
Qx + 2σN(λ)z
T
y + γy
T
y + 2ˆg
1
kP k kxk
2
+2ˆg
2
kP k kxk kyk + 2 kP k
°
°
°
d
0
°
°
°
kxk
≤ −x
T
ˆ
Qx + 2σN(λ)z
T
y + (γ + ˆg
2
kP k a
2
1
)y
T
y
+ kP k a
2
2
°
°
°
d
0
°
°
°
2
ˆ
Q := Q − (2ˆg
1
+ ˆg
2
a
−2
1
+ a
−2
2
) kP k I, a
1
, a
2
> 0
1
k
(
P
p
i=1
α
i
R
t
t−τ
i
kz
i
(θ)k
2
dθ)
0
= −2z
T
y − ky
T
y −
1
k
2
dk
dt
P
p
i=1
α
i
R
t
t−τ
i
kz
i
(θ)k
2
dθ
dV
dt
< −x
T
ˆ
Qx − (2σN(λ) − 2)z
T
(−y)
−(k − γ − ˆg
2
kP k a
2
1
)y
T
y
−
1
k
2
dk
dt
P
p
i=1
α
i
R
t
t−τ
i
kz
i
(θ)k
2
dθ + kP k a
2
2
°
°
°
d
0
°
°
°
2
(20)
When the linear bounds ˆg
1
, ˆg
2
> 0 are sufficiently
small in terms of the system entries (A, B, C) and
a
1
, a
2
> 0 are chosen to be sufficiently large so that
ˆ
Q is also positive definite. Integrating (20) yields
V (t
0
) − V (0)
< −
R
t
0
0
x
T
ˆ
Qxdt −
R
k(t
0
)
k(0)
(τ − γ − ˆg
2
kP k a
2
1
)dτ
−
R
λ(t
0
)
λ(0)
(2σN(τ) − 2)dτ +
R
t
0
0
kP k a
2
2
°
°
°
d
0
°
°
°
2
dt
−
R
t
0
0
1
k
2
dk
dt
P
p
i=1
α
i
R
t
t−τ
i
kz
i
(θ)k
2
dθdt
(21)
ADAPTIVE MIMO MULTI-PERIODIC REPETITIVE CONTROL SYSTEM: LIAPUNOV ANALYSIS
253

The item
R
t
0
0
kP k a
2
2
°
°
°
d
0
°
°
°
2
dt is bounded as d
0
(.) ∈
L
2
[0, ∞). Therefore, it can be shown that λ(.) ∈
L
∞
[0, ∞), k(.) ∈ L
∞
[0, ∞),y(.) ∈ L
m
2
[0, ∞)
,x(.) ∈ L
n
∞
[0, ∞) and lim
t→∞
k(t) = k
∞
< ∞ as
before, which proves the result. ¤
7 EXPONENTIAL
STABILIZATION VIA
EXPONENTIAL WEIGHTING
FACTOR
It has been proved that asymptotical stability of adap-
tive multi-periodic repetitive control system can be
guaranteed if the plant
P
G
is ASPR or ASNR. While
when it strictly satisfies a ASPR or ASNR condition,
now we show that the system is exponentially sta-
ble when modifying the adaptive scheme. Accord-
ing to definition A.1 and A.3 in Appendix, each al-
most strictly positive real system is almost ² -strictly
positive real for some sufficiently small but unknown
²
∗
> 0, that is, (A + ²
∗
I, σB, C) is Almost Strictly
Positive Real. Our aim is to find ²
∗
> 0 adaptively by
using an exponential weighting factor tuned by k(t).
We introduce a function ²(k(t))(for example
0.1
k(t)+1
)
with following properties: i) ²(k(t)) > 0 for all
k(t) > 0. ii) It is non-increasing for all k(t) > 0.
iii) lim
t→∞
²(k(t)) = ²
∞
> 0.
Theorem 5 Consider the system
P
G
described by
(1). Suppose that both reference r(t) and distur-
bance d(t) are identically zero. Then the adaptive
multi-periodic repetitive system in Figure 1 where
the feedforward gain C
1
(s) = k(s)Γ and C
2
(s) =
N(s)Γ with
˙
k(t) = e
²
(t)
T
e
²
(t), k(0) > 0 ,
˙
λ(t) = e
²
(t)
T
z
²
(t), λ(0) ≥ 0 by denoting x
²
(t) :=
e
²(k(t))t
x(t) is globally exponentially stable in the
sense that x(.) ∈ L
n
∞
[0, ∞), y (.) ∈ L
m
2
[0, ∞),
λ(.) ∈ L
∞
[0, ∞), k(.) ∈ L
∞
[0, ∞), lim
t→∞
k(t) =
k
∞
< ∞ , lim
t→∞
²(k(t)) = ²
∞
> 0 and also
kx(t)k ≤ M
1
e
−²t
for all t ≥ 0 and some M
1
>
0, ² > 0.
Proof: With the notation x
²
(t) := e
²(k(t))t
x(t), the
plant can be written as
˙x
²
(t) = [A + ²
∗
I − σBλ
∗
C]x
²
(t) + N(λ)Bz
²
(t)
+[²(k(t)) − ²
∗
+
d²(k(t))
dt
t + σBλ
∗
C]x
²
(t)
y
²
(t) = Cx
²
(t), z
²
(t) =
P
p
i=1
α
i
v
i
²
(t)
(22)
Also we have
z
T
i²
(t − τ
i
)z
i²
(t − τ
i
)
= e
2²(k(t−τ
i
))(t−τ
i
)
z
T
i
(t − τ
i
)z
i
(t − τ
i
)
≥e
2²(k(t))(t−τ
i
)
z
T
i
(t − τ
i
)z
i
(t − τ
i
)
= e
−2²(k(t))τ
i
(v
i²
+ ky
²
)
T
(v
i²
+ ky
²
)
≥e
−2²(k(0))τ
(v
i²
+ ky
²
)
T
(v
i²
+ ky
²
)
τ := max(τ
i
)
(23)
Introducing a positive definite lyapunov function V :
V = x
T
²
P x
²
+
1
k
P
p
i=1
α
i
M(t)
M(t) :=
R
t
t−τ
i
kz
i²
(θ)k
2
dθ + x
T
W
i
²
P
W
i
x
W
i
²
(24)
Differentiating V along (22) and using (23) yields
dV
dt
< −x
T
²
Qx
²
− 2²
∗
x
T
²
P x
²
+ 2²(k)x
T
²
P x
²
+2
d²(k)
dt
tx
T
²
P x
²
+ (γ − ke
−2²(k(0)τ
)y
T
²
y
²
+(2e
−2²(k(0))τ
− 2σN(λ))(−y
²
)
T
v
²
−
1
k
(e
−2²(k(0))τ
− µ
2
)
P
p
i=1
α
i
v
T
i²
v
i²
−
1
k
2
dk
dt
P
p
i=1
α
i
M(t)
(25)
Integrating (25) and using the adaptive law yields
V (t
0
) − V (0)
< −
R
t
0
0
x
T
²
Qx
²
dt − 2
R
t
0
0
(²
∗
− ²(k))x
T
²
P x
²
dt
+2
R
t
0
0
d²(k)
dt
tx
T
²
P x
²
dt +
R
k(t
0
)
k(0)
(γ − se
−2²(k(0))τ
)ds
+
R
λ(t
0
)
λ(0)
(2e
−2²(k(0))τ
− 2σN(s))ds
−
R
t
0
0
1
k
2
dk
dt
P
p
i=1
α
i
M(t)dt
+
R
t
0
0
1
k
P
p
i=1
α
i
(µ
2
− e
−2²(k(0))τ
)z
T
i²
z
i²
dt
(26)
Suppose λ(.) /∈ L
∞
[0, ∞), k(.) /∈ L
∞
[0, ∞). As-
sume ²(k (0)) > ²
∗
, −2
R
t
0
0
(²
∗
− ²(k))x
T
²
P x
²
dt is
definitely negative. When ²(k(0)) ≤ ²
∗
, −2
R
t
0
0
(²
∗
−
²(k))x
T
²
P x
²
dt = −2
R
t
1
0
(²
∗
− ²(k))x
T
²
P x
²
dt −
2
R
t
0
t
1
(²
∗
− ²(k))x
T
²
P x
²
dt, where ²(k(t
1
)) = ²
∗
. Ac-
cording to Theorem A.2 in Appendix and without
loss of generality, we can assume x
²
= (y
T
²
, η
T
²
)
T
,
so then P =
µ
(σCB)
−1
0
0 P
4
¶
. Due to y
²
(.) ∈
L
∞
[0, t
1
) and A
4
is asymptotically stable, we have
η
²
(.) ∈ L
∞
[0, t
1
), then −2
R
t
1
0
(²
∗
− ²(k))x
T
²
P x
²
dt
is a positive finite. So −2
R
t
0
0
(²
∗
− ²(k))x
T
²
P x
²
dt is
negative infinity. +
R
k(t
0
)
k(0)
(γ − se
−2²(k(0))τ
)ds is neg-
ative infinity and +
R
λ(t
0
)
λ(0)
(2e
−2²(k(0))τ
− 2σN (s))ds
is arbitrarily negative or positive infinity as before.
When we select k(0) so that |e
−²(k(0))τ
| < µ,
+
R
t
0
0
1
k
P
p
i=1
α
i
(µ
2
− e
−2²(k(0))τ
)z
T
i²
z
i²
dt is nega-
tive. The other items are definitely negative due to
Special Session on Analytical and Simulation Methods for Complex Systems 2004 - Special Session on Analytical and Simulation Methods
for Complex Systems
254

dk
dt
≥ 0 and
d²
dt
≤ 0. So when +
R
λ(t
0
)
λ(0)
(2e
−2²(k(0))τ
−
2σN(s))ds takes arbitrarily negative, the right hand
side of (26) will be negative, hence contradicting
the non-negativity of the left hand side. Then from
R
+∞
0
x
T
Qxdt ≤
R
+∞
0
x
T
²
Qx
²
dt ≤ +∞, we have
x(.) ∈ L
n
∞
[0, ∞). Similar as before, we have y(.) ∈
L
m
2
[0, ∞), λ(.) ∈ L
∞
[0, ∞), k(.) ∈ L
∞
[0, ∞)
and lim
t→∞
k(t) = k
∞
< ∞. Then we have
lim
t→∞
²(k(t)) = ²
∞
> 0. As x
²
(t) is uniformly
bounded such that kx
²
(t)k ≤ M
1
, we have kx(t)k ≤
M
1
e
−²t
for some M
1
> 0, ² > 0, which indicates
exponential stability of the state. ¤
However, perfect zero-tracking/full-rejecting for
periodic reference/disturbance signals will be lost if
the low-pass filter is not selected to be 1. So the
state can only exponentially decrease to a bound as
kx(t)k ≤ M
1
e
−²t
+ M
2
for all t ≥ 0 and some
M
1
> 0, M
2
> 0, ² > 0. Now we need to revise
the adaptive scheme of k(t) as
˙
k(t) =
½
ke(t)k(ke(t)k − δ) if ke(t)k ≥ δ
0 if ke(t)k < δ
to prevent the divergence of adaptive gain k(t).
8 ADAPTIVE PROPORTIONAL
PLUS MULTI-PERIODIC
REPETITIVE CONTROL
SYSTEM
Theorem 6 Consider the ASPR or ASNR system
P
G
described by (1). Suppose that both reference r(t)
and disturbance d(t) are identically zero. Then
the adaptive multi-periodic repetitive system in Fig-
ure 4 with k
1
being a positive constant,
˙
k
2
(t) =
e(t)
T
e(t), k
2
(0) > 0 and
˙
λ(t) = e(t)
T
z(t) +
k
1
k
2
(t)e(t)
T
e(t), λ(0) ≥ 0 is globally asymptoti-
cally stable in the sense that x(.) ∈ L
n
∞
[0, ∞), y(.) ∈
L
m
2
[0, ∞), λ(.) ∈ L
∞
[0, ∞) , k
2
(.) ∈ L
∞
[0, ∞) and
lim
t→∞
k
2
(t) = k
2∞
< ∞.
K
2
N(s)
M(s)
G(s)
R E
U
D
Z
Y
K
1
Figure 4: Adaptive MIMO proportional plus multi-periodic
repetitive control system
Proof: We set the low-pass filter W
i
(s) to be 1 for
sake of simplicity. Introducing a positive definite lya-
punov function V:
V = x
T
P x +
1
k
2
p
X
i=1
α
i
Z
t
t−τ
i
kz
i
(θ)k
2
dθ (27)
By differentiating V we have
dV
dt
< −x
T
Qx − (k
2
+ 2k
1
k
2
− γ)y
T
y
−(2σN(λ) − 2)(k
1
k
2
y
T
y − z
T
y)
−
1
k
2
2
dk
2
dt
P
p
i=1
α
i
R
t
t−τ
i
kz
i
(θ)k
2
dθ
(28)
Integrating (28) yields
V (t
0
) − V (0)
< −
R
t
0
0
x
T
Qxdt −
R
k
2
(t
0
)
k
2
(0)
(τ + 2k
1
τ − γ)dτ
−
R
λ(t
0
)
λ(0)
(2σN(τ) − 2)dτ
−
R
t
0
0
1
k
2
2
dk
2
dt
P
p
i=1
α
i
R
t
t−τ
i
kz
i
(θ)k
2
dθdt
(29)
Similar to that in section 4, we can conclude x(.) ∈
L
n
∞
[0, ∞), y(.) ∈ L
m
2
[0, ∞), λ(.) ∈ L
∞
[0, ∞),
k
2
(.) ∈ L
∞
[0, ∞) and lim
t→∞
k
2
(t) = k
2∞
< ∞,
which proves the result. ¤
Also the simulation results show that a higher pro-
portional gain k
1
is helpful for the performance.
9 CONCLUSION
A kind of adaptive MIMO multi-periodic repetitive
control system is studied. The stability is analysed in
the sense of lyapunov stability. The adapting gains are
proved to be bounded and the error decays asymptot-
ically to zero. The similar lyapunov stability anal-
ysis is also extended to ASPR or ASNR plant un-
der certain non-linear perturbations. It is also shown
that exponential stability can be guaranteed by mod-
ifying the adaptive schemes. Finally, an proportional
plus adaptive multi-periodic repetitive control system
is proposed and its stability is proven in the sense of
lyapunov stability as well.
APPENDIX
Theorem A. 1 (X.D. and J.P., 1998). Let V (t) and
k(t) be smooth functions defined on [0, +∞) with
V (t) ≥ 0, ∀t ∈ [0, +∞) , N (t) a Nussbaum-type
function, and b a nonzero constant. If the following
inequality holds: V (t)≤
R
k(t)
0
[bN(ω)+1]dω+c, ∀t ∈
[0, +∞) where c is an arbitrary constant, then V (t),
k(t) and
R
k(t)
0
[bN(ω) + 1]dω must be bounded on
[0, +∞) .
ADAPTIVE MIMO MULTI-PERIODIC REPETITIVE CONTROL SYSTEM: LIAPUNOV ANALYSIS
255

Theorem A. 2 (A., 1993). Consider the system (1)
with det(CB) 6= 0 and let V ∈ R
n×(n−m)
de-
note a basis matrix of kerC. It follows that S :=
[B(CB)
−1
, V ] has the inverse S
−1
= [C
T
, N
T
]
T
,
where N := (V
T
V )
−1
V
T
[I
n
−B(CB)
−1
C]. Hence
the state space transformation (y
T
, η
T
)
T
= S
−1
x =
((Cx)
T
, (Nx)
T
)
T
converts (1) into
˙y(t) = A
1
y(t) + A
2
η(t) + CB(u(t) + d(t))
˙η(t) = A
3
y(t) + A
4
η(t)
(30)
Here A
1
∈ R
m×m
, A
2
∈ R
m×(n−m)
, A
3
∈
R
(n−m)×m
, A
4
∈ R
(n−m)×(n−m)
, so that
µ
A
1
A
2
A
3
A
4
¶
= S
−1
AS
If (A, B, C) is minimum phase, then A
4
in (30) is
asymptotically stable.
Definition A. 1 Almost Strictly Positive Real: A sys-
tem
˙x(t) = Ax(t) + Bu(t)
y(t) = Cx(t) + Du(t), x(0) = x
0
(31)
where (A, B, C, D )∈R
n×n
×R
n×m
×R
m×n
×R
m×m
,
is called Strictly Positive Real, if it satisfies equation
(32) for µ > 0 and we say it is Almost Strictly
Positive Real, if there exists a K∈R
m×m
, so that
the feedback u(t) = −Ky(t) + r(t) yields a Strictly
Positive Real system.
P A + A
T
P = −QQ
T
− 2µP
P B = C
T
− QW
W
T
W = D + D
T
(32)
Definition A. 2 Almost Strictly Negative Real: The
system G(s) defined by (31) is called Almost Strictly
Negative Real, if −G(s) is a Almost Strictly Positive
Real system.
Definition A. 3 Almost ²-Strictly Positive/Negative
Real: Let ² > 0, the system (31) is called ²-Strictly
Positive Real, if it satisfies equation (32) for µ > ²
and we say it is Almost ²-Strictly Positive Real, if
there exists a K∈R
m×m
, so that the feedback u(t) =
−Ky(t)+r(t) yields a ²-Strictly Positive Real system.
It is called Almost ²-Strictly Negative Real, if −G(s)
is a Almost ²-Strictly Positive Real system.
REFERENCES
A., I. (1993). Non-Identifier-Based High-Gain Adaptive
Control, Lecture Notes in Control and Information
Sciences 189. Springer-Verlag, London, 1st edition.
Dixon W. E., Zergeroglu E., D. D. C. B. (Sep, 2001). Repet-
itive learning control: A lyapunov-based approach. In
Proceedings of the 2001 International Conference on
Control Applications, Mexico City, Mexico.
G, H. (1996). Adaptive suppression of vibrations: A repet-
itive control approach.
G., W. (1997). Repetitive control systems: old and new
ideas.
Hara S., Yamamoto Y., O. T. and M., N. (1988). Repetitive
control system: A new type servo system for periodic
exogenous signals.
Horowitz R., Messner W., M. J. B. (1991). Exponential
convergence of a learning controller for robert manip-
ulators.
Jiang Y.A., Clements D.J., H. T. (Dec, 1995). Adaptive
repetitive control of nonlinear systems. In Proceed-
ings of the 34th Conference on Decidion and Control,
New Orleans, LA.
Li L.M., O. D. and S.P., B. (2002). Multi-periodic repetitive
control system part ii: Robustness and practical issues.
Owens D.H., L. L. and S.P., B. (2002). Multi-periodic repet-
itive control system part i: A liapunov analysis for
mimo systems.
Owens D.H., L. L. and S.P., B. (2003). Multi-periodic non-
linear repetitive control: Feedback stability analysis.
R.D., N. (1983). Some remarks on a conjecture in parameter
adaptive control.
Sun Z., T. T. (2000). Adaptive control with asymptotic
tracking performance and its application to an electro-
hydraulic servo system.
Tomizuka M., Tsao T., C. K. (1989). Analysis and synthesis
of discrete-time repetitive controllers.
Tsao T., T. M. (1994). Robust adaptive and repetitive digital
tracking control and application to a hydraulic servo
for noncircular marching.
Tzou Y., Jung S., Y. H. (1999). Adaptive repetitive control
of pwm inverters for very low thd ac-voltage regula-
tion with unknown loads.
Weiss G., H. M. (1999). Repetitive control of mimo systems
using h
∞
design.
X.D., Y. and J.P., J. (1998). Adaptive nonlinear design with-
out a priori knowledge of control directions.
Special Session on Analytical and Simulation Methods for Complex Systems 2004 - Special Session on Analytical and Simulation Methods
for Complex Systems
256