
TRACKING OF EXTENDED CROSSING OBJECTS USING THE
VITERBI ALGORITHM
Andreas Kr
¨
außling, Frank E. Schneider and Dennis Wildermuth
Research Establishment for Applied Sciences (FGAN)
Wachtberg, Germany
Keywords:
Multiple target tracking, expanded objects, Viterbi algorithm, crossing targets.
Abstract:
Tracking, which means determining the positions of the humans in the surrounding, is one of the goals in the
field of mobile robots that operate in populated environments. This paper is concerned with the special problem
of tracking expanded objects under such constraints. A solution in form of a Viterbi based algorithm, which
can be useful for real–time systems, is presented. Thus a Maximum–a–posteriori (MAP) filtering technique
is applied to perform the tracking process. The mathematical background of the algorithm is proposed. The
method uses the robots’ sensors in form of laser range finders and a motion and observation model of the
objects being tracked. The special problem of the crossing of two expanded objects is considered. The
mathematical background for this problem is enlightened and a solution for it in form of a heuristic algorithm
is proposed. This algorithm is tested on simulated and real data.
1 INTRODUCTION
When tracking people and other expanded objects in
densely populated surroundings with robot–borne de-
vices like laser scanners or sonar the situation is usu-
ally as follows: there are a lot of readings from ob-
stacles like walls or other targets and only some read-
ings from the object itself. The problem of allocation
of data obtained from the just now accounted target is
referred to as the problem of data association in the lit-
erature. Therefore, the tracking algorithm uses a gate
which separates the signals belonging to the current
target from other signals as a solution to this prob-
lem. A second feature of all algorithms for tracking
vast objects should be the description of shape and
extension of the objects. Finally, an estimate for the
centre of the object has to be computed. For this pur-
pose two antithetic methods can be used. First, all
points that have passed the gate successfully can be
used for the calculation of the estimate in terms of a
weighted mean. Second, only the point that fits best
to the previous data can be used for the further cal-
culations. In this paper we picture the Viterbi algo-
rithm as an example for the latter of these two meth-
ods. The Viterbi algorithm has been introduced in
(Viterbi, 1967), a good description of it is given in
(Forney, 1973). It has already been recommended for
tracking punctiform targets in clutter (Quach and Far-
rooq, 1994) and has also been introduced for tracking
expanded objects and evaluated on real and simulated
data in (Kr
¨
außling et al., 2004).
In this paper we focus on the special problem of
tracking two expanded objects which are crossing.
This means that the gates of the two objects are inter-
secting. The problem of two crossing targets is a com-
mon challenge in the field of multiple target tracking
(MTT). In this case the Viterbi algorithm, as it has
been proposed in (Kr
¨
außling et al., 2004), often fails
to track the two objects when their paths get separated
again. Our research has shown that this is an impor-
tant drawback of all tracking algorithms introduced so
far for expanded objects, for example Koch’s EM al-
gorithm (Koch and Stannus, 2003). This often occurs
when one target is occluded at least partially by the
other. Hence in this paper a heuristic algorithm is in-
troduced, that is capable of handling the special prob-
lem of the crossing of two expanded objects, based on
a special feature of our implementation of the Viterbi
algorithm. The crossing of two objects is also a well
known problem in people tracking which frequently
occurs since persons move together, talk to each other,
and then separate again.
This paper is organized as follows. In section 2 re-
lated work in the field of tracking using mobile robots
142
Kräußling A., E. Schneider F. and Wildermuth D. (2004).
TRACKING OF EXTENDED CROSSING OBJECTS USING THE VITERBI ALGORITHM.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 142-149
DOI: 10.5220/0001129601420149
Copyright
c
SciTePress

is presented. Section 3 describes the model used and
gives details of the Viterbi algorithm, as we use it for
tracking expanded objects. In section 4 a mathemati-
cal dicussion of the problem of tracking two crossing
expanded targets is given. Furthermore, our heuris-
tic solution is proposed. Section 5 describes the ex-
periments and simulations. Finally, in section 6 the
summarized results and an outlook on future work are
presented.
2 RELATED WORK
Tracking people, e.g. for surveillance, is a well stud-
ied problem in machine vision (Sclaroff and Rosales,
1998). Common attempts to track people are inspired
by the need in humanoid robotics to react to human
beings. A new approach of tracking objects, that has
rapidly gained popularity in mobile robotics during
the last years, uses laser range finders. Earlier work
uses occupancy grids and linear extrapolation of oc-
cupancy maps to estimate trajectories (Elfes et al.,
1999). Newer methods involve the use of advanced
trajectory estimation algorithms (Fod et al., 2001).
Laser sensing differs significantly from vision in ways
that can be exploited for tracking. In vision, vari-
ables like colour, intensity, and depth are available.
In contrast, lasers are restricted to one plane of the
observable space. Most of the useful information for
tracking is in just one parameter – the range to the
nearest obstacle over an arc. The range measurements
are, however, of high accuracy, especially in compar-
ison with other range sensors such as ultrasound or
infra red. Thus, lasers have rapidly gained popular-
ity for mobile robotic applications such as collision
avoidance, navigation, localization, and map building
(Thrun, 1999), (Thrun et al., 1999). The problem of
estimating the position of moving objects is an impor-
tant problem in mobile robotics. This ability allows a
robot to adapt its velocity to the speed of people in
the environment and to improve its collision avoid-
ance behaviour in situations in which the trajectory of
the robot crosses the path of a human (Sclaroff and
Rosales, 1998). In this context the work of Schulz
(Schulz et al., 2001) is very notable. He combined
the ideas of Joint Probabilistic Data Association Fil-
tering (JPDAF) (Bar-Shalom and Tse, 1975), (Fort-
mann et al., 1983) with Particle Filtering (Gordon
et al., 1993), (Pitt and Shephard, 1999) and called his
method Sample–based Joint Probabilistic Data As-
sociation Filtering (SJPDAF). Thereby, he is able to
assign the measurements to the tracked objects and
to reproduce multimodal densities, a major improve-
ment for example when handling obstacles.
The problem of two crossing targets has been stud-
ied for the first time in (Fortmann et al., 1983). In this
work the problem of tracking two punctiform cross-
ing targets in clutter, as it occurs for example in the
field of aerial surveillance, has been investigated. It
has been shown there that with the classical PDAF al-
gorithm introduced in (Bar-Shalom and Tse, 1975) or
with the nearest neighbour algorithm the objects are
not tracked correctly after the crossing. In the case
of the PDAF algorithm both objects are tracked in the
middle of the connection line of the true positions af-
ter the crossing. In the case of the nearest neighbour
algorithm both objects are tracked close to the true
positions of the same object after the crossing. Be-
cause of these difficulties in (Fortmann et al., 1983) a
new algorithm in form of the Joint Probabilistic Data
Association Filter has been proposed which performs
well under the constraints of the crossing of two punc-
tiform targets.
3 MATHEMATICAL
BACKGROUND OF THE
VITERBI ALGORITHM
3.1 The Model
The dynamics of the object to be observed and the
observation process itself are modeled as customary
by
x
k
= Ax
k−1
+ w
k−1
(1)
and
z
k
= Bx
k
+ v
k
. (2)
Thereby x
k
is the object state vector at time k, A is
the state transition matrix, z
k
is the observation vec-
tor at time k and B is the observation matrix. Fur-
thermore, w
k
and v
k
are supposed to be zero mean
white Gaussian noises with E(w
i
(w
j
)
)=Qδ
ij
,
E(v
i
(v
j
)
)=Rδ
ij
and E(w
i
(v
j
)
)=0, which
means the measurement noise and the process noise
are uncorrelated. In these equations the object is sup-
posed to be punctiform. Nevertheless, the model will
also be helpful for the description of an expanded tar-
get. In this case x
k
will get the state vector of the
centre of the target at time k. Since the motion of
a target has to be described a two dimensional kine-
matic model is used. Therefore it is
x
k
=(
x
1
x
2
˙x
1
˙x
2
)
, (3)
A =
⎛
⎜
⎝
10 ∆T 0
01 0 ∆T
00e
−∆T/Θ
0
00 0 e
−∆T/Θ
⎞
⎟
⎠
, (4)
Q = ρ
2
e
−2∆T/Θ
⎛
⎜
⎝
0000
0000
0010
0001
⎞
⎟
⎠
, (5)
TRACKING OF EXTENDED CROSSING OBJECTS USING THE VITERBI ALGORITHM
143

B =
1000
0100
, (6)
and
R = δ
10
01
. (7)
Thereby x
1
and x
2
are the Cartesian coordinates of
the target and ρ and Θ are parameters that are mod-
eling the acceleration of the target. A small Θ and
a large ρ correspond to a large acceleration. ∆T is
the temporal interval between two consecutive mea-
surements. In the calculations Θ=3, ρ =40and
δ = 1000 are used.
3.2 The Gate
The gate is realised with the help of the Kalman fil-
ter (Kalman, 1960) (Maybeck, 1979) (Shumway and
Stoffer, 2000), which makes a prediction y(k +1|k)
for the measurement of the object based on the last
estimate x(k|k) for its position via the formulae
x(k +1|k)=Ax(k|k) (8)
and
y(k +1|k)=Bx(k +1|k). (9)
Thereby x(k|l) is the estimate for x at time k based on
the observations up to time l. Then the Mahalanobis
distance
λ =(z
i
(k +1)− y(k +1|k))
· [S(k + 1)]
−1
·
·(z
i
(k +1)− y(k +1|k)) (10)
with the innovations covariance S(k +1)from the
Kalman filter is computed for every sensor reading
z
i
(k +1)at time k +1. The Mahalanobis distance has
been introduced in (Mahalanobis, 1936). In contrast
to the Euclidian distance it incorporates the different
uncertainnesses in the varying directions. To illustrate
this one can think of S(k +1)as a diagonal matrix.
A greater uncertainty in a direction then results in a
greater associated diagonal entry in S(k +1)and thus
in a smaller associated diagonal entry in [S(k +1)]
−1
.
Consequently deviations from y(k +1|k) in this di-
rection will be multiplicated with a smaller factor
and thus will be weighted less in the calculation of
the Mahalanobis distance. More precisely, the points
with the same Mahalanobis distance are lying on the
surface of an ellipsoid with the semi–major axis in the
direction of the greater uncertainty (see also the next
paragraph). In our experiments λ =4has been used.
Deviant from the Kalman filter the Matrix S(k +1)
is computed as
S(k +1)=BP(k +1|k)B
+ R + E(k) (11)
with the matrix E(k), that describes the shape and the
extension of the object in order to account for these
attributes. A detailed description of the matrix E(k)
will be given in the next paragraph. The recursion
formula for P (k +1|k) is
P (k +1|k)=AP (k|k)A
+ Q. (12)
λ is χ
2
distributed with two degrees of freedom, so
a χ
2
test is used. All sensor readings with a λ lower
than a given threshold are passing the gate.
3.3 The Extension of the Object
To describe the extension of the tracked object a pos-
itive definite matrix can be used, because for a pos-
itive definite matrix P and a given >0 all points
y with y
Py = are lying on the surface of an el-
lipsoid with the origin as the centre (Torrieri, 1984).
So shape, orientation, and extension of the objects are
approximated by an ellipsoid. The appropriate posi-
tive definite matrix is computed as follows. At first
it is assumed that all points that have passed the gate
successfully are originated from the target, so that it is
reasonable to use all these points for the computation
of the matrix E(k). Hence the covariance of these
points which is positive definite is computed and used
as the matrix E(k).
3.4 The Viterbi Algorithm
The Viterbi algorithm (Viterbi, 1967) is a recursive al-
gorithm. Thus as an initialisation x(0|0), P (0|0) and
E(0), that describe the object at the beginning, are
used. Now a description of a single step of the recur-
sion is given. The Viterbi algorithm uses a directed
graph to determine the optimal sequence of measure-
ments for a given set of measurements Z
T
. Thereby,
it is Z
T
= {Z
k
}
T
k=1
, and Z
k
= {z
k,j
} is the set of
selected measurements z
k,j
at time k. The selected
measurements correspond to the nodes in the graph.
Given the selected measurements Z
k
at time k, the set
of selected measurements at time k +1is computed
as follows.
For every measurement z
k,j
the gate is applied to
the measurements at time k +1. That results in the
sets Z
k+1,j
of measurements which have passed the
particular gate for the measurement z
k,j
successfully.
The set Z
k+1
= {z
k+1,i
}
i
of selected measurements
z
k+1,i
at time k+1is then just the union of these sets,
i.e. it is
Z
k+1
= ∪
j
Z
k+1,j
. (13)
In the next step for every selected measurement
z
k+1,i
its predecessor is identified. For this purpose
only those selected measurements z
k,j
whose gates
have been passed by z
k+1,i
successfully are consid-
ered (this technique is due to (Pulford and Scala,
1995)). For each of these measurements z
k,j
the
length d
k+1,j,i
of the path from x(0|0) to z
k+1,i
ICINCO 2004 - ROBOTICS AND AUTOMATION
144

through z
k,j
is calculated.
d
k+1,j,i
= d
k,j
+ a
k+1,j,i
(14)
is used. Thereby, d
k,j
is the length of the path that
ends in the node z
k,j
. a
k+1,j,i
is the distance between
the nodes z
k,j
and z
k+1,i
.Fora
k+1,j,i
a
k+1,j,i
=
1
2
ν
k+1,j,i
[S
k+1,j
]
−1
ν
k+1,j,i
+
+ln
|2πS
k+1,j
|
(15)
is used. ν
k+1,j,i
is the innovation defined as
ν
k+1,j,i
= z
k+1,i
− y
j
(k). (16)
In doing so S
k+1,j
and y
j
(k) are the innovations co-
variance respectively the prediction evaluated by the
Kalman filter based on the nodes or the measurements
{z
l,i(l,j)
}
k
l=1
belonging to the path ending in z
k,j
. The
sequence
Z
k,j
= {z
l,i(l,j)
}
k
l=1
(17)
of these nodes is called the tracking history belong-
ing to the node z
k,j
and the tracking histories define
an association τ which assignes to every j and l ≤ k
a measurement z
l,i(l,j)
. Thereby the same measure-
ment can be associated to more than one tracking his-
tory and not all measurements have to be associated.
This proceeding causes
p(z
k+1,i
|Z
k,j
)=exp(−a
k+1,j,i
) (18)
and therefore with Bayes’ rule as well
p(Z
k,j
|Z
0
)=exp(−d
k,j
) (19)
with Z
0
= x(0|0),P(0|0),E(0). Finding the track-
ing histories with the minimal distance corresponds
therefrom strictly to determining the tracking history
with the maximal likelihood. Furthermore it is with
Bayes’ law for a association τ of the measurements
p(τ|Z
T
)=
p(Z
T
|τ)p(τ)
p(Z
T
)
. (20)
Thereby, p(Z
T
) is a normalization constant. p(τ) is
the prior probability of the association τ . In the ab-
sence of prior information one usually assumes the
priors to be equal for all associations. In this case
searching for the association τ with the most likely
posterior probability p(τ |Z
T
) coincides with maxi-
mizing the likelihood function p(Z
T
|τ) of the mea-
surements over all associations.
The predecessor of z
k+1,i
is now just the node z
k,j
,
by which d
k+1,j,i
is kept at a minimum. For this
node it is written z
k,i(k,j)
. With the appendant pre-
dictions x(k +1|k)
i
, P (k +1|k)
i
and y(k +1|k)
i
then the Kalman filter is used to get the estimates
x(k +1|k +1)
i
and P (k +1|k +1)
i
using the well
known equations from Kalman filtering
x(k +1|k +1)
i
= x(k +1|k)
i
+ W
k+1,i
·
·(z
k+1,i
− y(k +1|k)
i
) (21)
and
P (k +1|k +1)
i
=[I − W
k+1,i
B]P (k +1|k)
i
(22)
with the Kalman gain
W
k+1,i
= P (k +1|k)
i
B
S
−1
i
(k +1). (23)
In doing so the subscript i at the matrices P (k +1|k),
S(k +1), P (k +1|k +1) and W
k+1
traces back to the
different matrices E(k) used in equation 11. Accord-
ing to this these matrices depend on the measurements
Z
T
aberrant from the customary Kalman filter.
Thus the description of one step of the recursion is
finished.
4 CROSSING EXTENDED
OBJECTS
4.1 Mathematical background
First a mathematical description of the problem of
tracking two expanded objects is given. An expanded
object is defined as an object that can be the origin of
more than one measurement. A crossing of two ob-
jects is defined by the fact that the validation gates of
the two objects are intersecting. Each measurement of
the intersection can then be associated with both tar-
gets. The full association θ of the n measurements in
this intersection can be represented by a binary n × 2
indicator matrix Ω(θ), i.e. a matrix with entries 1 or 0.
If Ω(θ)
ij
=1, measurement i is associated with tar-
get j by the association θ, otherwise not. Since there
is no clutter in our application each measurement in
the intersection has to be associated with exactly one
target. Therefore, the sum of the entries of each row
of Ω has to be one and the sum of all entries has to be
equal to n. Since we are dealing with expanded ob-
jects, the sum of the entries of a column of Ω can vary
from 0 to n. This is different from the case of punc-
tiform targets, where this sum can only be 1 or 0. In
the case of an expanded target a sum of n means that
all measurements in the intersection are caused by the
corresponding target, and a sum of 0 means that all
measurements come from the other target. θ
k
refers
to the association θ at time k. The association history
(θ
1
,...,θ
k
) is referred to as θ
k
.
As discussed in the previous section, the Viterbi al-
gorithm developes the probability p(Z
k,j
) to the max-
imum. For two crossing targets the MAP estimate
is calculated as follows. For each association θ
k
the
TRACKING OF EXTENDED CROSSING OBJECTS USING THE VITERBI ALGORITHM
145

Viterbi algorithm is run for each measurement z
k,j
to find the tracking history that minimizes the corre-
sponding distance. Thereafter the sum over all dis-
tances is calculated. The MAP estimate then corre-
sponds to that association, for which this sum reaches
its minimum. This approach implies that the likeli-
hoods p(θ
k
) for all associations are equal. Thus, this
procedure can obviously be improved by consider-
ing different likelihoods p(θ
k
) for these associations.
Since the associations θ
k
are mutually exclusive and
exhaustive, the law of total probability leads to
p(Z
k,j
)=
θ
k
p(Z
k,j
,θ
k
) (24)
and with Bayes’ rule it is
θ
k
p(Z
k,j
,θ
k
)=
θ
k
p(Z
k,j
|θ
k
)p(θ
k
). (25)
In order to find the improved MAP solution we have
to calculate p(θ
k
) for every θ
k
, and to maximise
p(Z
k
|θ
k
) using the Viterbi algorithm as proposed in
the previous section.
In practice this approach is infeasible for several
reasons. First, if the number of measurements in the
intersection of the validation gates is n then there are
2
n
possible associations θ
k
. A typical example for n
in our application is 10. So, since 2
n
is 1024, there
might be some hundreds of associations to deal with.
Therefore, the calculation of the exact Bayesian solu-
tion in form of the Gaussian sum
θ
k
p(Z
k
|θ
k
)p(θ
k
)
often cannot be obtained efficiently. Second, the cal-
culation of the likelihood p(θ
k
) is difficult, because it
depends on the shape, the extension and the orienta-
tion of the two crossing objects. Furthermore, there
is no guarantee that the two objects will be separated
after the crossing by this Bayesian approach. Conse-
quently, we tried to develop a heuristic solution for
this problem.
As in the case of a single target in clutter there ex-
ists an optimal Bayesian approach. With the stacked
state vector x(k)=
x
1
(k)
x
2
(k)
it is
E[x(k)|Z
k
]=
θ
k
E[x(k),θ
k
|Z
k
]=
=
θ
k
E[x(k)|θ
k
,Z
k
]p(θ
k
|Z
k
). (26)
The expected value E[x(k)|θ
k
,Z
k
] could be approx-
imated by known techniques (see the next paragraph
for details), but the probabilities p(θ
k
|Z
k
) again can-
not be efficiently calculated. Moreover, because a
crossing lasts for about ten time steps there would
be about 1000
10
=10
30
association histories to con-
sider. A method which runs a Viterbi algorithm for
each association history θ
k
and looks for the associ-
ation history with the minimal sum of distances pro-
duces unattainable computational costs.
An algorithm similar to the PDAF algorithm for
punctiform targets in clutter can be constructed as fol-
lows: it is
E[x(k)|Z
k
]=
θ
k
E[x(k),θ
k
|Z
k
]=
=
θ
k
E[x(k)|θ
k
,Z
k
]p(θ
k
|Z
k
). (27)
Thereby, E[x(k)|θ
k
,Z
k
] can again be approximated
by known techniques based on the estimate E[x(k −
1)|Z
k−1
]. More precisely, the Kalman filter can be
run for each of the two targets with a weighted av-
erage of the measurements z
k,j
. The weights can be
calculated using the normal distribution as in (Koch
and Stannus, 2003) via the formula
α
t
l
=
N(ν
t
k,l
;0,R)
l,Ω(θ
k
)
l,t
=1
N(ν
t
k,l
;0,R)
(28)
or similar as in (Bar-Shalom and Tse, 1975) via the
formula
α
t
l
=
N(ν
t
k,l
;0,S
t
(k))
l,Ω(θ
k
)
l,t
=1
N(ν
t
k,l
;0,S
t
(k))
. (29)
These algorithms are equivalent to running a Kalman
filter for each target t ∈{1, 2} with the combined
innovation
ν
t
k
=
θ
k
m
l=1,Ω(θ
k
)
l,t
=1
p(θ
k
|Z
k
)α
t
l
Ω(θ
k
)
l,t
ν
t
k,l
.
(30)
Finally, an algorithm similar to the JPDAF algo-
rithm for the crossing of two punctiform targets in
clutter can be constructed as follows: for each target
t a Kalman filter is run with the innovations
ν
t
k
=
m
j=1
β
t
j
ν
t
k,j
. (31)
Thereby, m is the number of measurements z
k,j
in the
intersection, β
t
j
is the posterior probability that mea-
surement z
k,j
originated from target t and ν
t
k,j
is the
innovation z
k,j
− y(k|k − 1)
t
. The predicted mea-
surement y(k|k − 1)
t
is calculated by the equations
of Kalman filtering based on the last estimated state
vector x(k − 1|k − 1)
t
of target t and, furthermore, it
is
β
t
j
=
θ
k
p(θ
k
|Z
k
)Ω(θ
k
)
jt
. (32)
p(θ
k
|Z
k
) can be aproximated via the formula
p(θ
k
|Z
k
)=
1
c
2
t=1
ICINCO 2004 - ROBOTICS AND AUTOMATION
146

j|Ω(θ
k
)
j,t
=1
exp[(z
k,j
− y(k|k − 1)
t
)
·
·{S
t
(k)}
−1
(z
k,j
−y(k|k − 1)
t
)]
1
|2πS
t
(k)|
1/2
. (33)
Thereby c is a normalisation constant. The last equa-
tion can be derived similar to the corresponding equa-
tion of the JPDA filter. This algorithm is then equiv-
alent to running a kalman filter with the combined in-
novation
ν
t
k
=
θ
k
m
j=1
p(θ
k
|Z
k
)Ω(θ
k
)
lt
ν
t
k,j
. (34)
4.2 A heuristic approach
Our approach to deal with two crossing expanded tar-
gets relies on a specific feature of the Viterbi algo-
rithm. The Viterbi algorithm is able to cope with bi-
modal probability densities to some degree. It has
this feature in common with Schulz’ SJPDAF algo-
rithm proposed in (Schulz et al., 2001). But while
Schulz’ algorithm uses particle filtering and thus has
to deal with several hundreds of points, the Viterbi
algorithm in our application only handles a few (typ-
ically between 3 and 12) points. Additionally, these
points contain some information about the surface of
the tracked objects as proposed in (Kr
¨
außling et al.,
2004). If a crossing between two targets occurs the
Viterbi algorithm shows the following behaviour. As
soon as the crossing occurs the algorithm tracks all
points originated from both objects simultaneously.
When the crossing is over, these points are again sep-
arated into two distinct clouds. The two clouds of
points are still tracked simultaneously. Our heuris-
tical approach now is based one some observations
from our experiments and consists of three different
steps:
1. At every time step k a binary matrix in form of an
upper triangular matrix is calculated. The elements
a
ij
of this matrix are set to 1, if the gates of the
objects i and j intersect, otherwise they are set to 0.
Once a crossing has been detected the element a
ij
remains 1 until the end of the crossing is recognized
in step 2.
2. For each pair of targets i and j with a
ij
=1it is
examined whether the crossing has finished. This
is done by testing if the points have dispersed into
two distinct clouds with a minimum Euclidian dis-
tance. For people tracking this is the case when
there are at least two points with a minimal Euclid-
ian distance of 300 cm. This is due to the fact, that
the maximal distance of the points on the two dif-
ferent legs of a person in human walking can be
assumed to not exceed 150 cm. In our experiments
the value of 300 cm worked well also with regard to
the problem that the gates of the two targets should
not intersect again once the end of the crossing has
been detected.
3. As soon as the end of the crossing has been ob-
served the two corresponding clouds have to be
separated and assigned to the two objects. In order
to do so an arbitrarily chosen point of the combined
cloud is assigned to the object with the lower index.
Then, for every other point it is determined wether
the Euclidian to the first point is larger or lower
than 150 cm. In the first case it is assigned to the
object with the higher index and otherwise to that
with the lower one. Of course, since the first point
is arbitrarily chosen the two objects might be inter-
changed after the crossing by this procedure. But in
our opinion there is no general solution to this prob-
lem which is based only on laser distance informa-
tion. An improvement over this approach can eas-
ily be achieved in the case of additional knowledge
about the objects. For example, different reflecting
power of the laser beams could be due to the fact
that two persons are wearing differently coloured
trousers. Or, in the case of one human and one cir-
cular robot, the different shapes could be used in
order to correctly identify the separated objects.
Finally, at the end of the tracking process for each
object the path with the minimum length of the path
is determined and the Kalman smoother (Shumway
and Stoffer, 2000) is applied for the estimated state
vector via the formula
x(t − 1|n)=x(t − 1|t − 1)+
+J
t−1
(x(t|n) − x(t|t − 1)). (35)
Thereby it is
J
t−1
= P (t − 1|t − 1)A
[P (t|t − 1)]
−1
. (36)
The backward recursion for the estimates x(t − 1|n)
is initialised with the estimate x(n|n) of the Kalman
filter for the final time step n.
5 EXPERIMENTS AND
SIMULATIONS
The new approach has been tested on simulated data
and on data provided by a real experiment. In both
cases the new algorithm was able to separate the two
targets after the crossing successfully whereas the
original algorithm as proposed in (Kr
¨
außling et al.,
2004) failed to achieve this goal (see figure 1). In
simulation the motion of two robots of radius 26 cm
is explored. The lower robot is moving from left to
right and the upper robot is moving in the opposite
direction. In the middle of the two paths the cross-
ing occurs. During the crossing the estimate for the
TRACKING OF EXTENDED CROSSING OBJECTS USING THE VITERBI ALGORITHM
147
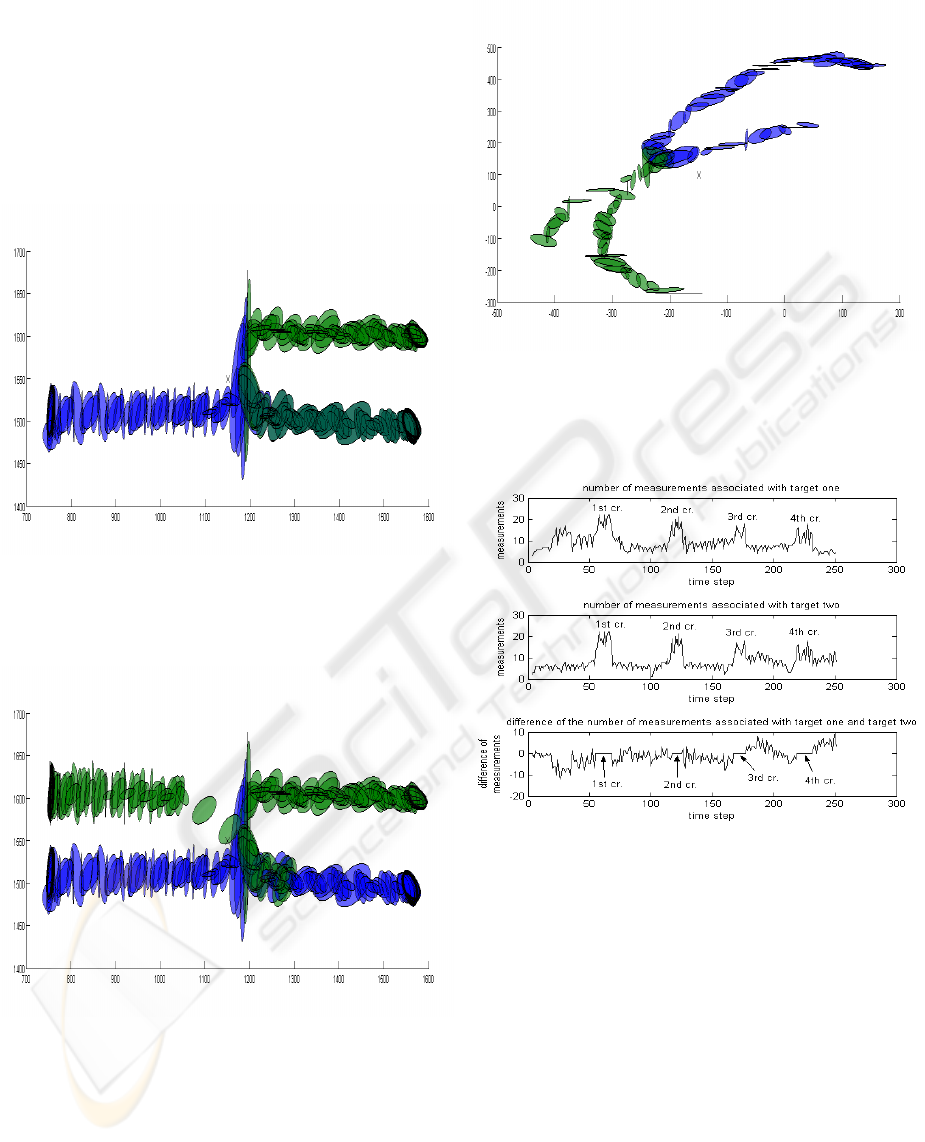
extension of the targets is increasing. The isolated es-
timate in the path of the upper target when using the
improved algorithm (see figure 2) is due to the fact
that the Kalman smoother is used. Otherwise there
would be a gap between the region where the cross-
ing takes place and the region where the upper target
is tracked again after the crossing. In this example the
two targets are assigned correctly after the crossing.
Figure 1: Simulated Data, tracked with the original algo-
rithm.
Figure 2: Simulated Data, tracked with the improved algo-
rithm.
In the second example, which uses real data of two
walking persons, the assignment after the crossing is
wrong (see figure 3). But again, the two objects are
separated well after the crossing has finished.
Finally, to illustrate the special features of the im-
proved algorithm, we investigate the processing of
four consecutive crossings with this algorithm (see
Figure 3: Real data, tracked with the improved algorithm.
Figure 4: Real data, tracked with the improved algorithm.
figure 4). As the first two diagrams in figure 4 show,
the number of measurements associated with each tar-
get grows rapidly when a crossing occurs. This is
due to the fact, that the measurements of both of the
targets are associated with each target. When the
improved algorithm separates the targets again after
the crossing, the number of measurements associated
with each of the targets consequently declines rapidly.
The third diagram in figure 4 shows, during a cross-
ing all of the measurements associated with one of
the targets are associated with each of the two targets,
so that the difference of the number of measurements
associated with each of the targets equals zero.
ICINCO 2004 - ROBOTICS AND AUTOMATION
148

6 CONCLUSION AND FUTURE
WORK
In this paper a new method for tracking expanded ob-
jects as an application of the Viterbi algorithm has
been introduced. The special problem of tracking two
crossing targets has been investigated qualitatively.
The mathematical background of this topic has been
analysed briefly. A solution to the problem in form of
a heuristic approach has been suggested and evaluated
on simulated and real data. It has been demonstrated
by means of these examples that the new algorithm
performs well under general conditions.
A more detailed and advanced analysis of the math-
ematical description of crossing targets together with
further experiments might be the content of a consec-
utive journal paper.
ACKNOWLEDGEMENTS
We want to thank Dr Martin Ulmke from the depart-
ment SDF at the FGAN for drawing our attention
to the fact, that particle filters can represent bimodal
probability distributions. From this we recognized
that our implementation of the Viterbi algorithm has
a comparable property and that this characteristic can
be used to develop a robust algorithm for the problem
of expanded crossing targets. Furthermore we want
to thank Dr Koch, the department head of SDF, for a
lot of helpful suggestions about the philosophy of a
tracking algorithm.
REFERENCES
Bar-Shalom, Y. and Tse, E. (1975). Tracking in a cluttered
environment with probabilistic data association. Au-
tomatica, Volume 11, pp. 451–460.
Elfes, A., Prassler, E., and Scholz, J. (1999). Tracking peo-
ple in a railway station during rush hour. In Proc.
of the International Conference on Computer Vision
(ICVS), pages 13–15, Las Palmas, Spain. Springer
Verlag.
Fod, A., Howard, A., and Mataric, M. J. (2001). Laser–
based people tracking. Technical report, Computer
Science Department, University of Southern Califor-
nia, Los Angeles, USA.
Forney, Jr., G. D. (1973). The viterbi algorithm. In Proceed-
ings of the IEEE, volume Volume 61, pages 268–278.
Fortmann, T. E., Bar-Shalom, Y., and Scheffe, M. (1983).
Sonar tracking of multiple targets using joint proba-
bilistic data association. IEEE Journal Of Oceanic
Engineering, Volume OE–8(Number 3).
Gordon, N., Salmond, D., and Smith, A. (1993). A novel
approach to nonlinear/non–gaussian bayesian state es-
timation. IEEE Proceedings F, Volume 140(Number
2):107–113.
Kalman, R. E. (1960). A new approach to linear filtering
and prediction problems. Transactions of the ASME,
Journal Basic Engineering, Volume 82:34–45.
Koch, W. and Stannus, W. (2003). A new application of
the em algorithm: Robot–borne extended object track-
ing. Technical Report Number 66, Research Institute
for Communication, Information Processing and Er-
gonomics of the Research Establishment of Applied
Sciences (FGAN), Wachtberg, Germany.
Kr
¨
außling, A., Schneider, F. E., and Wildermuth, D. (2004).
Tracking expanded objects using the viterbi algo-
rithm. to be published in the Proceedings of the IEEE
Conference on Intelligent Systems, Varna, Bulgaria.
Mahalanobis, P. C. (1936). On the generalized distance in
statistics. In Proc. Natl. Inst. Science, volume Volume
12, pages 49–55, Calcutta, India.
Maybeck, P. S. (1979). Stochastic Models, Estimation, and
Control. Academic Press, New York, San Francisco,
London.
Pitt, M. and Shephard, N. (1999). Filtering via simulation:
auxiliary particle filters. Journal of the American Sta-
tistical Association, Volume 994(Number 446).
Pulford, G. W. and Scala, B. L. (1995). Over–the–horizon
radar tracking tracking algorithm using the viterbi al-
gorithm – third report to high frequency radar divi-
sion. Technical report, Cooperative Research Centre
for Sensor Signal and Information Processing, Univer-
sity of Melbourne, Australia.
Quach, T. and Farrooq, M. (1994). Maximum likelihood
track formation with the viterbi algorithm. In Pro-
ceedings of the 33rd Conference on Decision and
Control, Lake Buena Vista, FL, USA.
Schulz, D., Burgard, W., Fox, D., and Cremers, A. B.
(2001). Tracking multiple moving objects with a mo-
bile robot. In Proceedings of the 2001 IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition (CVPR 2001), Kauai, Hawaii, USA.
Sclaroff, S. and Rosales, R. (1998). Improved tracking of
multiple humans with trajectory prediction and occlu-
sion modeling. In IEEE Conference on Computer Vi-
sion and Pattern Recognition, Workshop on the inter-
pretation of Visual Motion, Santa Barbara, CA, USA.
Shumway, R. H. and Stoffer, D. S. (2000). Time Series
Analysis and Its Applications. Springer.
Thrun, S. (1999). Learning metric–topological maps for
indoor mobile robot navigation. Artificial Intelligence,
(Number 1):21–71.
Thrun, S., Fox, D., and Burgard, W. (1999). Markov lo-
calization for mobile robots in dynamic environments.
Artificial Intelligence, (Number 11):391–427.
Torrieri, D. J. (1984). Statistical theory of passive location
systems. IEEE Transactions on Aerospace and Elec-
tronic Systems, Volume AES–20(Number 2).
Viterbi, A. J. (1967). Error bounds for convolutional codes
and an asymptotically optimum decoding algorithm.
IEEE Transactions On Information Theory, Volume
IT–13(Number 2).
TRACKING OF EXTENDED CROSSING OBJECTS USING THE VITERBI ALGORITHM
149
