DYNAMIC STRUCTURE CELLULAR AUTOMATA

IN A FIRE SPREADING APPLICATION

Alexandre Muzy, Eric Innocenti, Antoine Aïello, Jean-François Santucci, Paul-Antoine Santoni

University of Corsica

SPE – UMR CNRS 6134

B.P. 52, Campus Grossetti, 20250 Corti. FRANCE.

David R.C. Hill

ISIMA/LIMOS UMR CNRS 6158

Blaise Pascal University

Campus des Cézeaux BP 10125, 63177 Aubière Cedex. FRANCE.

Keywords: Systems modeling, Discrete event systems, Multi-formalism, Fire spread, cellular automata.

Abstract: Studying complex propagation phenomena is usually

performed through cellular simulation models.

Usually cellular models are specific cellular automata developed by non-computer specialists. We attempt

to present here a mathematical specification of a new kind of CA. The latter allows to soundly specify

cellular models using a discrete time base, avoiding basic CA limitations (infinite lattice, neighborhood and

rules uniformity of the cells, closure of the system to external events, static structure, etc.). Object-oriented

techniques and discrete event simulation are used to achieve this goal. The approach is validated through a

fire spreading application.

1 INTRODUCTION

When modeling real systems, scientists cut off

pieces of a biggest system: the world surrounding us.

Global understanding of that world necessitates

connecting all these pieces (or subsystems),

referencing some of them in space. When the whole

system is complex, the only way to study its

dynamics is simulation.

Propagation phenomena as fire, swelling, gas

propagation,

(…) are complex systems. Studying

these phenomena generally leads to divide the

propagation space in cells, thus defining a cellular

system.

Developed from the General Systems Theory

esarovic and Takahara, 1975), the Discrete Event

Structure Specification (DEVS) formalism (Zeigler

et al., 2000) offers a theoretical framework to map

systems specifications into most classes of

simulation models (differential equations,

asynchronous cellular automata, etc.). For each

model class, one DEVS sub-formalism will allow to

faithfully specify one simulation model. As

specification of complex systems often needs to

grasp different kinds of simulation models,

connections between the models can be performed

using DEVS multi-formalism concepts.

Another DEVS advantage relates to its ability in

oviding discrete event simulation techniques, thus

enabling to concentrate the simulation on active

components and resulting in performance

improvements.

Precise and sound definition of propagation

need

s to use models from physics as Partial

Differential Equations (PDEs). These equations are

then discretized leading to discrete time simulation

models. These models are generally simulated from

scientists by using specific Cellular Automata (CA).

As defined in (Wolfram, 1994), standard CA consist

of an infinite lattice of discrete identical sites, each

site taking on a finite site of, for instance, integer

values. The values of the sites evolve in discrete

143

Muzy A., Innocenti E., Aïello A., Santucci J., Santoni P. and C. Hill D. (2004).

DYNAMIC STRUCTURE CELLULAR AUTOMATA IN A FIRE SPREADING APPLICATION.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 143-151

DOI: 10.5220/0001129801430151

 SciTePress

time steps according to deterministic rules that

specify the value of each site in terms of the values

of neighboring sites. CA may thus be considered as

discrete idealizations of PDEs. CA are models where

space, time and states are discrete (Jen, 1990).

However, definition of basic CA is too limited to

specify complicated simulations (infinite lattice,

neighborhood and rules uniformity of the cells,

closure of the system to external events, discrete

state of the cells, etc.). Scientists often need to

modify CA’s structure for simulation purposes

(Worsch, 1999).

We extend here basic CA capabilities by using

object-oriented techniques and discrete event

simulation (Hill, 1996). A mathematical

specification of the approach is defined using the

Dynamic Structure Discrete Time System

Specification (DSDTSS) formalism (Barros, 1997).

This formalism allows dynamically changing the

structure of discrete time systems during the

simulation. These new CA are called the Dynamic

Structure Cellular Automata (DSCA).

DSCA have been introduced in (Barros and

Mendes, 1997) as a formal approach allowing to

dynamically change network structures of

asynchronous CA. Using an asynchronous time

base, cells were dynamically instantiated or

destroyed during a fire spread simulation.

The scope here is to extend basic CA capabilities

using a discrete time base. If previous DSCA were

dedicated to discrete event cellular system

specification, we extend here the DSCA definition to

discrete time cellular system specification.

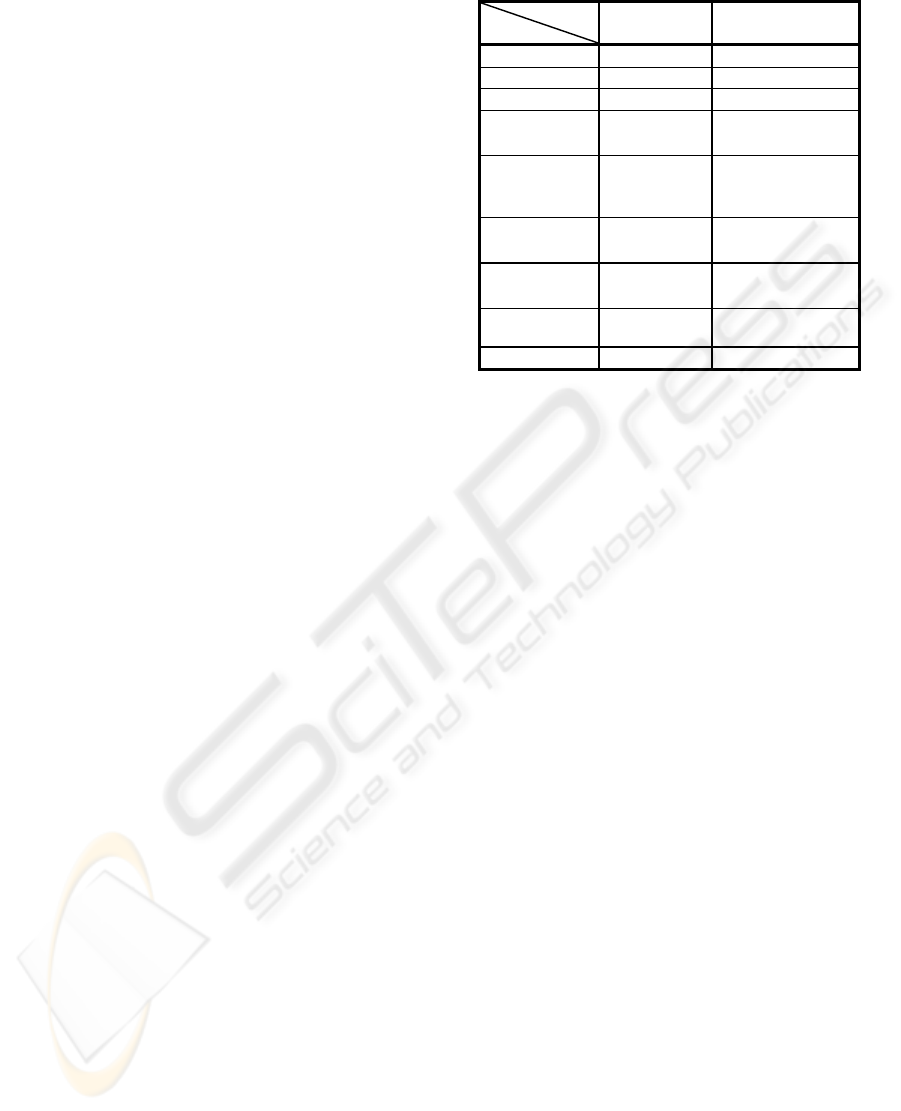
Table 1 sums up the advantages of the DSCA in

relation to basic CA. In DSCA, each cell can contain

different behaviors, neighborhoods and state

variables. Rules and neighborhoods of the cells can

dynamically change during the simulation. Each cell

can receive external events. During the simulation,

the computing of state changes is limited to active.

Finally, a global transition function allows the

specification of the DSCA global behaviors.

Table 1: DSCA extensions

Basic CA DSCA

Time discrete Discrete

Space discrete Discrete

State discrete Continuous

Closure to

external events

- +

Different

variables per

cell

- +

Rules

uniformity*

- +

Neighborhood

uniformity*

- +

Activity

tracking*

Global function - +

*at simulation time

The DSCA definition is validated against a fire

spreading application. Recent forest fires in Europe

(Portugal, France and Corsica) and in the United

States (California) unfortunately pinpoint the

necessity of increasing research efforts in this

domain. Fires are economical, ecological and human

catastrophes. Especially as we know that present

rising of wild land surfaces and climate warming

will increase forest fires.

Modeling such a huge and complex phenomenon

obviously leads to simulation performance

overloadings and design problems.

Simulation model reusability has to face to the

complicated aspects of both model implementations

and model modifications. Despite a large number of

cells, simulation has to respect real time deadlines to

predict actual fire propagations. Hence, this kind of

simulation application provides a powerful

validation to our work.

This study is organized as follows. First some

formalisms background is provided. Then two

sections present the DSCA modeling and simulation

principles. After, simulation results of a fire

spreading application are provided. Finally, we

conclude and make some prospects.

2 BACKGROUND

A formalism is a mathematical description of a

system allowing to guide a modeler in the

specification task. The more a formalism fits to a

system class, the more simple and accurate it will be.

Efficiently modeling complex systems often

implies the need to define subsystems using different

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

144

formalisms. Connections between the different

formalisms can then be achieved through a multi-

formalism to perform the whole system

specification.

In this study, subsystems are specified using

DEVS, DTSS (Discrete Time System Specification)

and DSDTSS formalisms. Connections between the

different models are achieved using a Multi-

formalism Network (MFN). A structure description

of each model is provided hereafter.

A DEVS atomic model is a structure:

DEVS = (X, Y, Q, q

, δ

int

, δ

ext

, λ, t

)

where X is the input events set, Q is the set of state,

is the initial state, Y is the output events set, δ

int

Q is the internal transition function, δ

ext

: Q×X

Q is the external transition function,

: Q

the output function, t

is the time advance function.

DSDTSS basic models are DTSS atomic model:

DTSS = (X, Y, Q, q

, h)

where X, Y are the input and output sets, Q is the

set of state, q

is the initial state,

: Q×X

Q is

the state transition function,

: Q

Y is the

output function (considering a Moore machine) and

h is a constant time advance.

At a periodic rate, this model checks its inputs

and, based on its state information, produces an

output and changes its internal state.

The network of simple DTSS models is referred

to as a Dynamic Structure Discrete Time Network

(DSDTN) (Barros, 1997). We introduce here input

and output sets to allow connections with the

network. Formally, a DSDTN is a 4-tuple:

DSDTN = (X

DSDTN

, M

)

where X

DSDTN

is the network input values set, Y

DSDTN

is the network input values set,

is the name of the

DSDTN executive, M

is the model of the executive

The model of the executive is a modified DTSS

defined by the 8-tuple:

= (X

, q

, Y

)

where

: Q

is the structure function, and

the set of network structures. The transition function

computes the executive state q

. The network

executive structure

, at the state q

∈

is given by

) = (D, {M

}, {I

}, {Z

i,j

}), for all i

∈

D, M

, Q

, q

0,i

, Y

), where D is the set of model

references, I

is the set of influencers of model i, and

i,j

is the i to j translation function.

Because the network coupling information is

located in the state of the executive, transition

functions can change this state and, in consequence,

change the structure of the network. Changes in

structure include changes in model interconnections,

changes in system definition, and the addition or

deletion of system models.

Formally, a multiformalism network (Zeigler et

al., 2000) is defined by the 7-tuple:

MFN = (X

MFN

, D, {M

}, {I

}, {Z

i,j

},select)

where X

MFN

discr

×X

cont

is the network input values

set, X

discr

and X

cont

are discrete and continuous input

sets, Y

MFN

discr

×Y

cont

is the network input values

set, Y

discr

and Y

cont

are discrete and continuous output

sets, D is the set of model references,

For each i

∈

is are DEVS, DEVN, DTSN, DTSS,

DESS, DEV&DESS or other MFN models.

As DSDTSS proved to be closed under

coupling, M

can also be dynamic structure

models or networks,

is the set of influencers of model i,

i,j

is the i to j translation function,

select is the tie-breaking function.

3 DSCA MODELLING

Models composing a DSCA are specified here using

the previous model definitions. As described in the

modeling part of Figure 1, external events are

simulated using a DEVS atomic model: the

Generator. The latter can asynchronously generate

data information to the DSCA during the simulation.

The cell space is embedded in a DSDTN. Each cell

is defined as a DTSS model. Using its transition

function, the DSCA executive model (containing

every cells) achieves changes in structure directly

accessing to the attributes of cells. A mathematical

description of each model is provided here after.

We define the MFN by the structure:

MFN = (X

MFN

, D, {M

}, {I

}, {Z

i,j

}, select)

where D={G,DSDTN}, M

= (X

, Q

, q

0,G

, Y

), M

DSDTN

=DSDTN, I

={}, I

DSDTN

={G}, and

DSDTN,MFN

: Y

DSDTN

MFN

, Z

G,DSDTN

: Y

DSDTN

DYNAMIC STRUCTURE CELLULAR AUTOMATA IN A FIRE SPREADING APPLICATION

145

We define the DSDTN by the structure:

DSDTN = (X

DSDTN

, Y

DSDTN

, DSCA, M

DSCA

)

where

) = (D, {M

}, {I

}, {Z

i,j

}), where

D={(i,j) / (i,j)

∈

}, M

ℑ

DSCA

= (X

DSCA

, Q

DSCA

0,DSCA

, Y

DSCA

), I

DSCA

={DSDTN},

cell

={cell

,DSDTN}. Where I

cell

= {I

/ k

∈

[0,m], l

∈

[0,n]} is the neighbourhood set (or the set of

influencers) of the cell as defined in (Wainer and

Giambiasi, 2001). It is a list of pairs defining the

relative position between the neighbours and the

origin cell. I

= {(i

) /

∀

∈

cell

, p

∈

[1,η

], i

∈

Z ; |k- i

| ≥ 0 |l- j∧

| ≥ 0 ∧ η

∈

cell

}, and η

∈

cell

is the neighborhood size.

cell,DSCA

: Y

cell

ÆY

DSCA

, Z

DSCA,DSDTN

DSCA

ÆY

DSDTN

, Z

DSDTN,DSCA

: X

DSDTN

ÆX

DSCA

DSCA,cell

: X

DSCA

cell

For the implementation, ports are defined:

=Px

DSDTN

=Px

DSCA

={data}

DSCA

=Py

DSDTN

=Py

MFN

={state}

cell

=Py

cell

={(i,j)}

We specify each cell as a special case of DTSS

model:

cell=(X

cell

, Q

cell

, q

cell

, Y

cell

)

where X

cell

is an arbitrary set of input values, Y

cell

an arbitrary set of output values, q

0,cell

is the initial

state of the cell and

∈

cell

is given by:

q=((i,j), state, N, phase),

(i,j)

∈

, is the position of the cell,

ℑ

state is the state of the cell,

= {N

/ k

∈

[0,m], l

∈

[0,n]}. N is a list of

states N

of the neighboring cells of coordinates

(k,l),

phase = {passive, active} corresponds to the

name of the corresponding dynamic behavior.

For numerous adjacent active cells, the active

phase can be decomposed in ‘testing’ and

‘nonTesting’ phases. The use of these phase is

detailed in section 5.

cell

: Q

cell

×X

cell

: Q

cell

4 DSCA SIMULATION

As depicted in Figure 2, implementation of discrete

event models consists in dividing a transition

function

of a model according to event types ev

issued from a set of possible event types S

. The

transition function then depends on the event types

the model receives.

Model d

= {ev

, ev

, … , ev

}

)

case S

: call event-routine

…

: call event-routine

Figure 2: Discrete event model implementation

(Zeigler et al., 2000)

The DSCA receives data from the Generator.

These data represent external influences of the

DSCA. During the simulation, information is

embedded in messages and transits through the data

and state ports. Messages have fields [Message type,

Time, Source processor, Destination port, Content],

where Content is a vector of triplets [Event type,

Value, Coordinate port]. When a DSCA receives a

message on its data port, the corresponding

Aggregated Network Simulator (AN Simulator)

scans the Content vector and according to the

Coordinate port, sends the [Event type, Value] pairs

to the concerned cells. A vector of pairs [Event type,

Value] can be sent to a cell port. Then, according to

the Event type a cell receives, it will update the

concerned attributes, executing the concerned

transition function.

The simulation tree hierarchy is described in the

simulation part on the right side of Figure 1. Except

for the Root and DTSS interface, all nodes of the tree

are processors attached to models. The processors

manage with message exchanges and execution of

model functions. Each processor is automatically

generated when the simulation starts.

The Coordinator pilots the MFN model, the

simulator SimG pilots the Generator, the DSDTN

model and the DSDTN models are piloted by the

Aggregated Network Simulator (AN Simulator).

Algorithms of the DSCA simulators can be found in

(Muzy et al., 2003). Algorithms of basic DEVS

simulators and DTSS interfaces can be found in

(Zeigler et al., 2000).

The Root processor supervises the whole

simulation loop. It updates the simulation time and

activates messages at each time step. For the

Coordinator, the DTSS interface makes the

Aggregated Network simulator seen as a DEVS

atomic simulator. This is done by storing all

messages arriving at the same time step and then by

calculating the new state and output of the DSCA

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

146

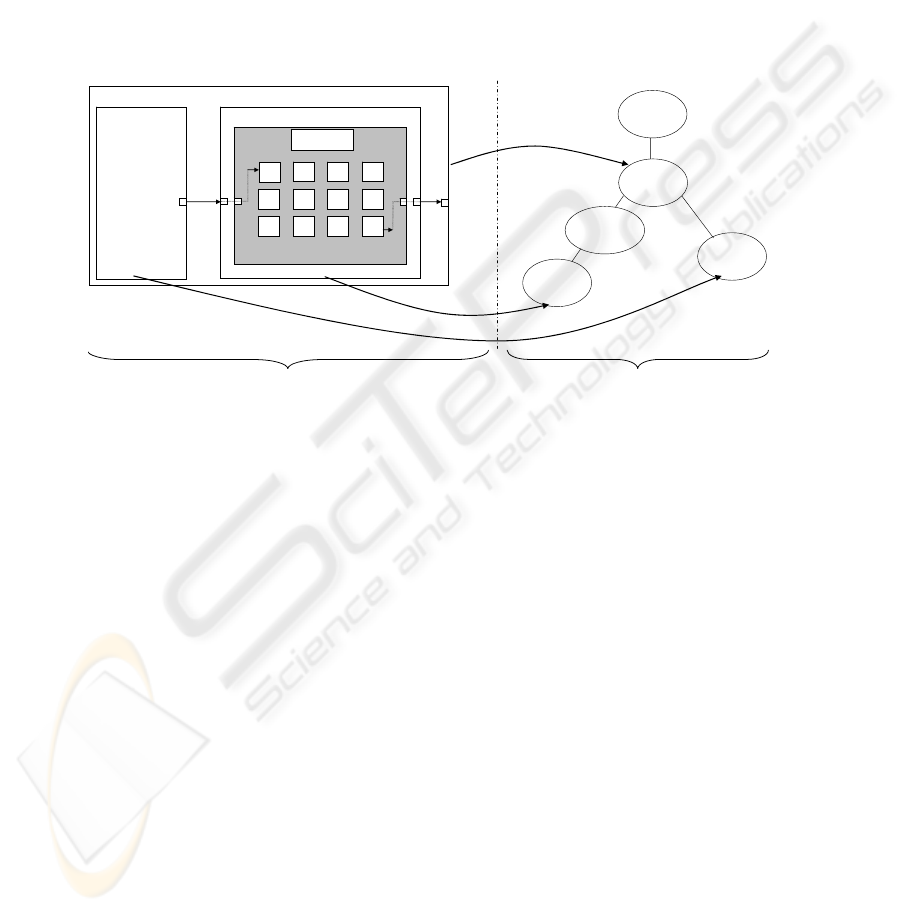
when receiving an internal transition message. The

simulation tree thus respects the DEVS bus

principle. That means that whatever DEVS model

can be appended to the simulation tree.

5 ACTIVITY TRACKING

Using discrete event cellular models, activity

tracking can be easily achieved (Nutaro et al., 2003).

Active cells send significant events to be reactivated

or to activate neighbors at next time step. However,

pure discrete event models proved to be inefficient

for discrete time system simulation (Muzy et al.,

2002). Interface configurations and message

management produce simulation overheads,

especially for numerous active components.

For discrete time systems, we know that each

component will be activated at each time step.

Moreover, in CA, states of cells directly depend on

the states of their neighbors. To optimize the

simulation, messages between the cells have to be

canceled and simulation time advance has to be

discrete. However, a new algorithm has to be

defined to track active c

ells.

Coordinator

SimG

DTSS-interface

Root

AN Simulator

DSDTN

MFN

Generator

data data

state

DSCA

Cell

…

states

(0,0)

(m,n)

modelling simulation

Figure 1: DSCA modeling and simulation

To focus the simulation on active cells, we use

the basic principles exposed in (Zeigler et al.,

2000) to predict whether a cell will possibly

change state or will definitely be left unchanged in

a next global state transition: “a cell will not

change state if none of its neighboring cells

changed state at the current state transition time”.

Nevertheless, to obtain optimum performance

the entire set of cells cannot be tested. Thereby, an

algorithm, which consists in testing only the

neighborhood of the active bordering cells of a

propagation domain, has been defined for this type

of phenomena.

To be well designed, a simulation model should

be structured so that all information relevant to a

particular design can be found in the same place.

This principle enhances models modularity and

reusability making easier further modifications.

Pure discrete event cells are all containing a

micro algorithm, which allows to focus the whole

simulation loop on active cells. We pinpointed

above the inefficiency of such an implementation

for discrete time simulation. An intuitive and

efficient way to achieve activity tracking in

discrete time simulation is to specify this particular

design at one place. As depicted in Figure 3, the

activity tracking algorithm is located in the global

transition function of the DSCA, in charge of the

structure evolution of the cell space.

Cells are in ‘testing’ phases when located at the

edge of the propagation domain, ‘nonTesting’

when not tested at each state transition and

‘quiescent’ when inactive.

A propagation example is sketched in Figure 4

for cardinal and adjacent neighborhoods. In our

algorithm, only the bordering cells test their

neighborhood, this allows to reduce the number of

testing cells.

The result of the spreadTest(i,j,nextState)

function of Figure 3, depends on the state of the

tested cells. If this state fulfils a certain condition

defined by the user, the cell becomes ‘nonTesting’

and new tested neighboring are added to the set of

active cells. The transition function receives x

messages from the Generator corresponding to

external events. The x

messages contain the

coordinates of the cells influenced by the external

event. If the coordinates are located in the domain

DYNAMIC STRUCTURE CELLULAR AUTOMATA IN A FIRE SPREADING APPLICATION

147

calculation, the state of the cell is changed by

activating its transition function with the new

value. Otherwise, new cells are added to the

propagation domain.

t+h

t+2h

quiescent

non testing

testing

active

//’Q’ is for the quiescent phase,

//’T’ for the testing one and ‘N’ for

//the nonTesting one

Transition Function(x

)

For each cell(i,j) Do

If(cellPhase(i,j)==’Q’) Then

removeCell(i,j)

Endif

If(cellPhase(i,j)==’T’) Then

If (cellNearToBorder(i,j)) Then

setSpreadStateCell(i,j,’N’)

Else

If(spreadTest(i,j,nextState))Then

setCellPhase(i,j,‘N’)

addQuiescentNeighboringCells(i,j)

EndIf

EndFor

If(x

message is not empty)

If(cells in the propagation domain) Then

cell(i,j).transitionF(newState)

change the cell states //

Else

addNewCells()

EndIf

EndTransitionFunction()

Figure 3: Transition function of the DSCA

For efficiency reasons, the simulation engine

we developed has been implemented in C++ and

dynamic allocation has been suppressed for some

classes. Indeed, for significant numbers of object

instantiation/deletion dynamic allocation is

inefficient and we have designed a specialized

static allocation (Stroustrup, 2000). A pre-

dimensioning via large static arrays can be easily

achieved thanks to current modern computer

memory capabilities.

The state of the executive model is a matrix of

cellular objects. References on active cells are

stored in a vector container. A start-pointer and an

end-pointer are delimiting the current calculation

domain on the vector. Thus initial active cells that

are completely burned during a simulation run can

be dynamically ignored in the main loop. At each

time step, by modifying the position of pointers,

new tested cells can be added to the calculation

domain and cells that return in a quiescent state are

removed from the former.

Figure 4: Calculation domain evolution

6 FIRE SPREADING

APPLICATION

The simulation engine we use has been proved to

achieve real-time simulation (Muzy et al., 2003).

Moreover, we use a mathematical fire spread

model already validated and presented in (Balbi et

al., 1998). In this model, a Partial Differential

Equation (PDE) represents the temperature of each

cell. A CA is obtained after discretizing the PDE.

Using the finite difference method leads to the

following algebraic equation:

(1)

dTeTTbTTaT

)(

0,1,1,,1,1

)()( +++++=

−−

+−+−

where T

is the grid node temperature. The

coefficients a, b, c and d depend on the time step

and mesh size considered, t is the real time, t

the

real ignition time (the time the cell is ignited) and

is the initial combustible mass.

Figure 5 depicts a simplified temperature curve

of a cell in the domain. We consider that above a

threshold temperature T

, the combustion occurs

and below a temperature T

, the combustion is

finished.

The end of the real curve is purposely neglected

to save simulation time. Four states corresponding

to the behavior of each cell behavior are defined

from these assumptions. The four states are:

‘unburned’, ‘heating’, ‘onFire’ and ‘burned’.

(Ta, tig)

Tf = 333 K

Tig = 573 K

T (Kelvin)

heating

burned

onFire

unburned

Figure 5: Simplified temperature curve of a cell behavior

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

148

Figure 6 depicts a fire spreading in a Corsican

valley, generated using the OpenGL graphics

library. By looking at this picture we easily

understand that simulation has to focus only on a

small part of the whole land. Actually, areas of

activity just correspond to the fire front, and to the

cells in front of the latter (corresponding to cells in

one of the following states: ‘heating’ or ‘onFire’ ).

Figure 6:

3D Visualization of fire spreading

X(cells)

Y(cells)

25 50 75 10

100

(

)

Y(cells)

25 50 75 100

100

X(cells)

Y(cells)

25 50 75 100

100

X(cells)

Y(cells)

25 50 75 10

100

Figure 7: Fire ignitions and propagation

During a fire spreading, flying brands ignite

new part of lands away from the fire. This is an

important cause of fire spreading. However,

tracking activity of flying brands is difficult.

Firstly, because flying brands occur whenever

during the simulation time. Secondly, because they

occur far away from the calculation domain, thus

new calculation allocations need to be created

dynamically.

Figure 7 represents a case of multi-ignitions

during the simulation. Simulation starts with one

ignition on the center of the propagation domain.

Then, at time t=7s, a second ignition occurs on the

top right corner of the propagation domain.

Finally, at t=12s, two new ignitions occur on the

right and left bottom of the propagation domain.

The last picture shows the multiple fire fronts

positions at t=70s.

Figure 8 describes the DSCA state transitions in

a fire spread simulation. First the simulation starts

with the first ignition, which is simulated by an

output external event of the Generator of Figure 1.

Then the main simulation loop calculating the fire

front position is activated. The latter consists in

calculating the temperature of cells. After,

according to the calculated temperatures, the

calculation domain is updated. For each cell of the

calculation domain, the temperature is calculated

using equation (1), according to the state of the

cells. The calculation domain is updated using the

algorithm described in Figures 3 and 4. Phase

transitions depend on the temperature of cells.

At the initialization, only one calculation

domain corresponding to the one described in

Figure 4 is generated. Bordering cells of the

calculation domain are in a ‘testing’ phase and

DYNAMIC STRUCTURE CELLULAR AUTOMATA IN A FIRE SPREADING APPLICATION

149

non-bordering cells in a ‘nonTesting’ one.

Remaining cells are ‘quiescent’. If the temperature

of a ‘testing’ cell fulfills a certain threshold

temperature T

, the testing cell will pass in the

‘nonTesting’ phase and neighboring ‘testing’ cells

will be added to the calculation domain. In the fire

spread case, this threshold can be fixed slightly

over the ambient temperature.

During the simulation, the Generator simulates

the flying brands by sending external events. When

the DSCA receives the events and updates the

calculation domain.

ignition

!endSimulationTime

!inactivity

igniting

activity

tracking

new cells'

temperature

inactive

testing

non

testing

remove

cell

add

neighbors

unburned

burning

burned

bordering cell non bordering cell

T <= TfT >= Tt

T >= Tig

T <= Tf

T >= Tt

dTTTbTTaT

,1,1,,1,1

)()( ++++=

+−+−

)(

0,1,1,,1,1

.)()(

tigtk

edTTTbTTaT

−−

+−+−

+++++=

aji

TT =

calculating

cells'

temperature

Calculating

flame front

position

Internal input

ttt

∆

Figure 8: Transition state diagram

The resulting activity tracking is showed in

Figure 9. We can notice that active cells

correspond to the fire front lines, not to the burned

and non-heated areas.

Figure 9: Activity tracking

7 CONCLUSION

Considering the previous discrete event DSCA

(Barros and Mendes, 1997), new well-designed

and complementary discrete time DSCA have been

defined here. These two methodologies allow to

faithfully guide modelers for modeling and

simulating discrete event and discrete time cellular

simulation models.

X(cells)

Y(cells)

25 50 75 100

100

DSCA allow to simulate a large range of

complicated cellular models. Complex phenomena

can be simulated thanks to basic CA simplicity.

We hope that even more complex phenomena will

be able to be simulated thanks to DSCA. To be

well understood and widely applied, DSCA

definition has to be as clear and simple as possible.

Clearness and simplification of DSCA

specification will remain our objective.

Another objective will be to improve DSCA

specification using new experiments. To achieve

this goal, complexity of fire spread remains an

infinite challenge for DSCA simulation. We plan

now to extend the DSCA specification to the

simulation of implicit-time models.

Another important validation of our approach

concerns network structure changes. Here again, a

fire spread model taking into account wind effects

(Simeoni et al., 2003) will allow us to validate

DSCA network structure changes. This model

actually needs to dynamically change the

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

150

neighborhood of burning cells according to the fire

front shape.

ACKNOWLEDGMENTS

We would like to thank our research assistant

Mathieu Joubert, for his technical support and for

his C++ implementation of the 3D visualization

tool using OpenGL.

REFERENCES

Balbi, J. H., P. A. Santoni, and J. L. Dupuy, 1998.

Dynamic modelling of fire spread across a fuel bed.

Int. J. Wildland Fire, p. 275-284.

Barros, F. J., 1997. Modelling Formalisms for Dynamic

Structure Systems. ACM Transactions on Modelling

and Computer Simulation, v. 7, p. 501-515.

Barros, F. J., and M. T. Mendes, 1997. Forest fire

modelling and simulation in the DELTA

environment. Simulation Practice and Theory, v. 5,

p. 185-197.

Hill, D. R. C., 1996. Object-oriented analysis and

simulation, Addison-Wisley Longman, UK, 291 p.

Jen, E., 1990. A periodicity in one-dimensional cellular

automata. Physica, v. 45, p. 3-18.

Mesarovic, M. D., and Y. Takahara, 1975. General

Systems Theory: A mathematical foundation,

Academic Press. New York.

Muzy, A., E. Innocenti, F. Barros, A. Aïello, and J. F.

Santucci, 2003. Efficient simulation of large-scale

dynamic structure cell spaces. Summer Computer

Simulation Conference, p. 378-383.

Muzy, A., G. Wainer, E. Innocenti, A. Aiello, and J. F.

Santucci, 2002. Comparing simulation methods for

fire spreading across a fuel bed. AIS 2002 -

Simulation and planning in high autonomy systems

conference, p. 219-224.

Nutaro, J., B. P. Zeigler, R. Jammalamadaka, and S.

Akrekar, 2003. Discrete event solution of gaz

dynamics winthin the DEVS framework: exploiting

spatiotemporal heterogeneity. Intrnational

conference for computational science.

Simeoni, A., P. A. Santoni, M. Larini, and J. H. Balbi,

2003. Reduction of a multiphase formulation to

include a simplified flow

in a semi-physical model of fire spread across a fuel bed.

International Journal of Thermal Sciences, v. 42, p.

95–105.

Stroustrup, B., 2000. The C++ Programming Language,

1029 p.

Wainer, G., and N. Giambiasi, 2001. Application of the

Cell-DEVS paradigm for cell spaces modeling and

simulation. Simulation, v. 76, p. 22-39.

Wolfram, S., 1994. Cellular automata and complexity:

Collected papers, Addison-Wesly.

Worsch, T., 1999. Simulation of cellular automata.

Future Generation Computer Systems, v. 16, p. 157-

170.

Zeigler, B. P., H. Praehofer, and T. G. Kim, 2000.

Theory of modelling and simulation, Academic

Press.

DYNAMIC STRUCTURE CELLULAR AUTOMATA IN A FIRE SPREADING APPLICATION

151