TABU SEARCH STRATEGIES IN SCHEDULING PROBLEM IN

FLEXIBLE MANUFACTURING SYSTEM

Considering tool switches and number of setups

Antonio Gabriel Rodrigues, Arthur Tórgo Gómez

Mastes in Computer Applied, Unisinos University, Av. Unisinos 950, São Leopoldo,Rio Grande do Sul, Brazil

Keywords: Tabu Search, Scheduling Problem, Flexible Man

ufacturing Systems.

Abstract: In this paper it’s investigated the impact of the Tabu List size, neighborhood generation approach and the

managing of the decision variables of the Objective Function in the quality of a Tabu Search solution to the

Scheduling Problem applied to a Flexible Manufacturing System. It was used a Part Scheduling Model,

which starts with qualitatively different initial solutions that yields experiments in which it’s observed the

Tabu List size influence in the results quality, according to the pre-defined Objective Function variables

contribution. This Model creates a schedule in a Flexible Manufacturing System, considering resident

tooling concepts, production turns, Part Selection, Machine Magazine Constraints and Due-dates. Numerical

results show relations among neighborhood strategies and the Tabu List size behavior considering initial

solutions and contribution managing of the Objective Function variables.

1 INTRODUCTION

In this paper the impact of the Tabu List size is

analyzed in the solution’s quality in the Scheduling

Problem applied to a Flexible Manufacturing System

(FMS). Its considered initials solutions approaches,

neighborhood generation and the managing of the

decision variables of a Objective Function. In order

to do so, two classic problems are studied: the Part

Selection Problem and the Scheduling Problem.

The FMS is the highest degree in automation of a

anufacturing system (Kaighobadi and Venkatech,

1993). Among several definitions, it can be said the

FMS possesses high degree of distributed data

processing and automated material flow, using

computer-controlled CNC/DNC machines, assembly

cells, robots and inspection machines (Dorf and

Kusiak, 1994; Kusiak, 1992).

The studied problems are solved with Cluster

nalysis techniques (Kusiak and Chow, 1986),

Dispatching rules (Kusiak, 1992) and Tabu Search

(Glover and Laguna, 1997).

Based in these techniques, a Part Scheduling Model

was de

veloped, with which experiments were

accomplished.

The Problems and the contemplated techniques are

resented in the section 2. In the section 3 it is

described the Part Scheduling Model. The

accomplished experiments are described in section 4

and the conclusions are showed section 5.

2 PROBLEMS AND TECHIQUES

CONTEMPLATED

The Part Selection Problem can be defined as a

technique in which similar parts are grouped

according to similar attributes of design and

production processes (Groover, 2001), respecting

environmental and machining constraints (Kusiak

and Chow,1986; Bedworth et al,1991). Similar parts

are grouped in Part Families, where each Part

Family possesses similar design/process

characteristics. In this work, the type of tool that

processes a part is the attribute used to generate the

Part Families (PF).

To solve this problem it’s used a Part Selection

odel (Rodrigues et al, 1999) which is based in the

Cluster Identification Algorithm created by Kusiak

and Chow (Gómez,1993). This model uses a binary

part-tool incidence matrix formulation to create PFs

and considers the tool sharing among PFs

(Gómez,1993). For the model’s performance

improvement, dynamic programming approach was

used.

Rodrigues A. and Gómez A. (2004).

TABU SEARCH STRATEGIES IN SCHEDULING PROBLEM IN FLEXIBLE MANUFACTURING SYSTEM - Considering tool switches and number of

setups.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 20-26

DOI: 10.5220/0001130200200026

 SciTePress

The Scheduling Problem (Kusiak and Chow, 1986)

can be defined in scheduling parts in processing

machines respecting its due dates. Other objectives

can be considered, such as minimizing throughput,

minimizing work in process and so on (Kusiak and

Chow, 1986). In this paper, the Scheduling Problem

approach concerns to the production batch

processing time reduction, through the minimization

of the number of machine stops for tool switching

(setup). The schedule generated should respect the

production turn time, or, it cannot have in processing

after the end of each turn.

To solve the Scheduling Problem, a Tabu Search

approach was proposed (Hertz, 1991; Glover, 1989).

This technique has been applied in combinatorial

optimisation problems, such as Travel Salesman

Problem, Time Tabling Problem, Job Shop

Scheduling Problem (Hertz, 1991; Glover, 1989;

Widmer, 1991). Tabu Search deals to find a better

solution exploring the feasible solution space.

Starting with an initial solution, Tabu Search

successively generates a set of feasible solutions by

well-defined moves approaches, in which a local

optimal is found. This local optimal becomes the

starting point for a new iteration. Among the

iterations, the best result found is stored. Each move

that leads to a local optimal is stored in a circular list

of forbidden (or tabu) moves, called Tabu List. The

stop criterion is defined as a number of interactions

without improvement occurrence in the best solution

found (nbmax) (Glover,1989; Gómez et al,2002).

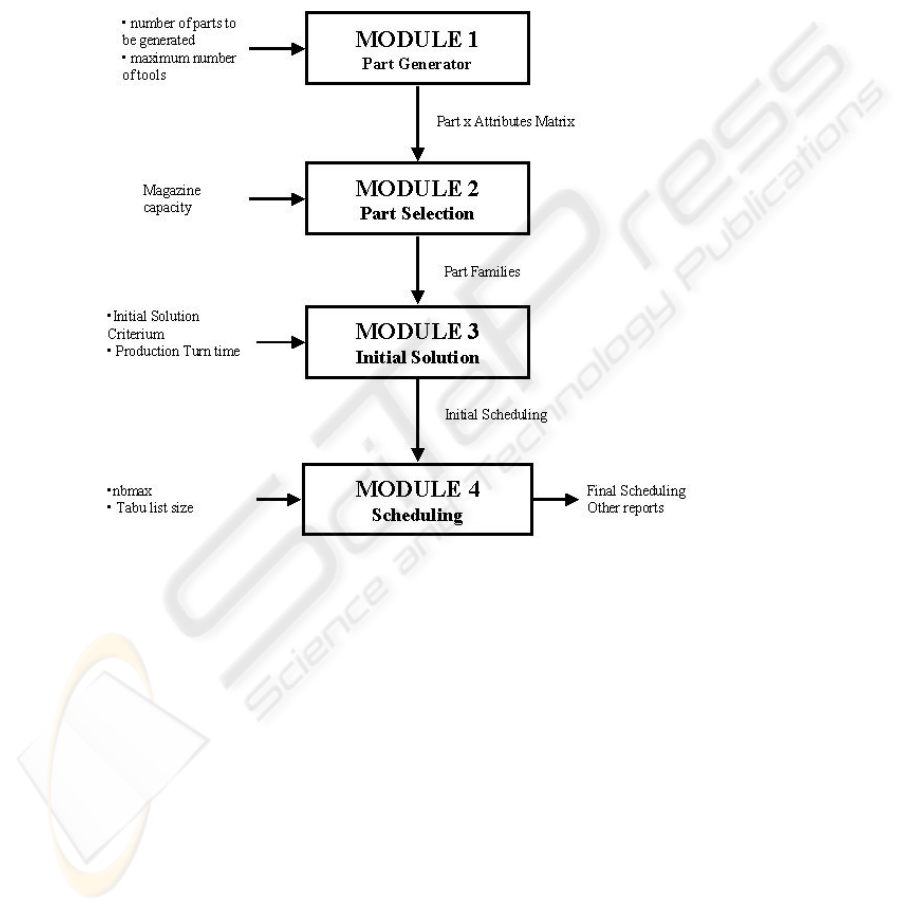
3 MODEL ARCHITECTURE

The Part Scheduling Model (Gómez et al,2002)

deals to generate a schedule of a part set in a flexible

machine (Hwang e Shogan, 1987) considering

productions turns, minimizing the setup number.

The model’s representation is showed in Figure 1.

Figure 1: Part Scheduling Model architecture.

Each module in Figure 1 represents a specialized

algorithm and the flow among the modules shows

the execution sequence. The modules are described

following:

Part Generator Module: this module creates data for

experiments. These data are part-tool incidence

matrixes, which are the Part Selection Module input.

Part Selection Module: it applies the Part Selection

Algorithm (Kusiak e Chow,1986) in the parts that it

receive as input. These parts are grouped in PFs

according to the tool-type (Rodrigues and Gómez,

2000), taking in account the tool sharing among

PFs. An example of PF generation is shown in the

Figure 2;

Dispatching Rules Module: starting with a set of

parts grouped in PFs, this module generates a initial

scheduling of parts in the machine based in the

following criterions: Random, Part Family Sorting,

TABU SEARCH STRATEGIES IN SCHEDULING PROBLEM IN FLEXIBLE MANUFACTURING SYSTEM -

Considering tool switches and number of setups

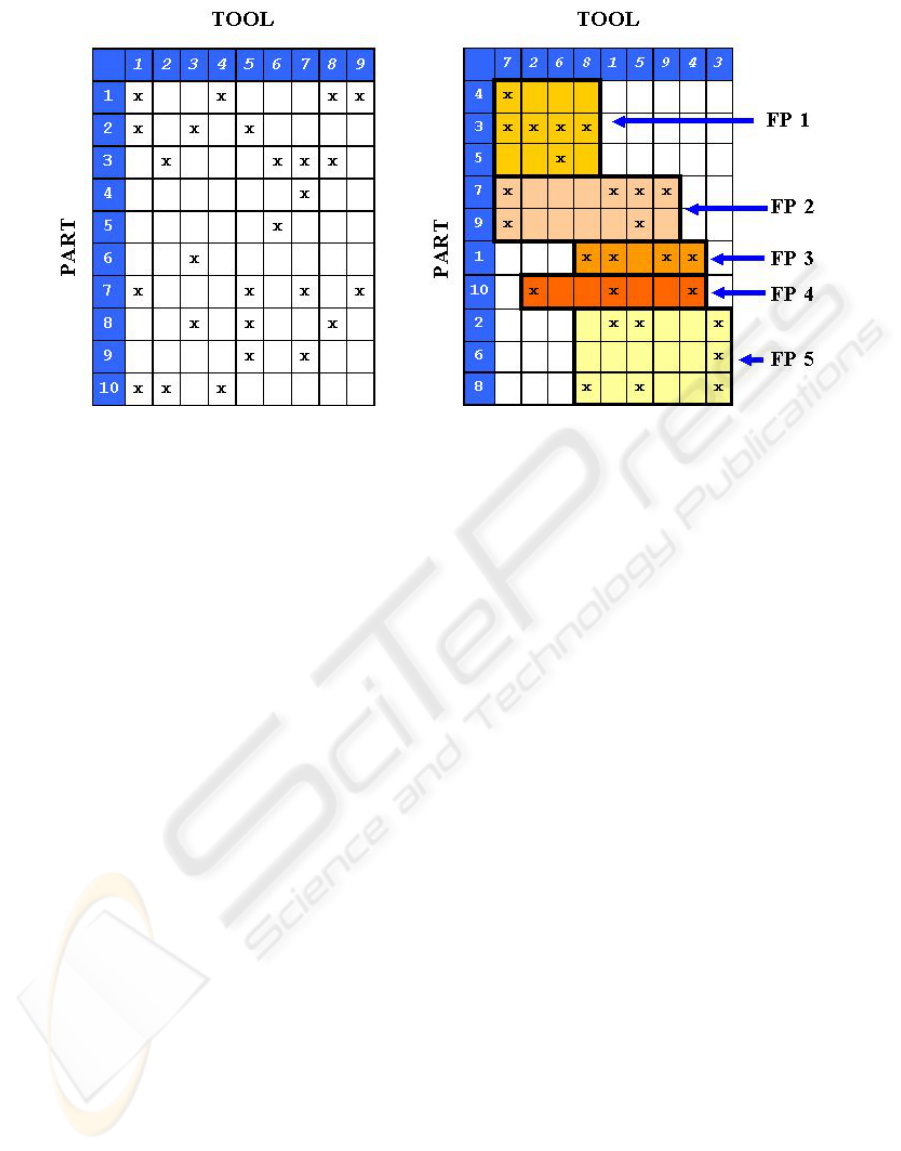
Figure 2: Part-tool incidence Matrix and Part Selection.

Most dissimilar Resources, Most Similar Family

Resources and Larger Process-time First (Gómez et

al, 2002);

Tabu Search Module: starting with a initial solution,

the Tabu Search Algorithm generates a schedule that

reduces the production time through minimizing the

number of setups and the number of tool switches.

Its considered part batching and production turn

time. The Objective Function considered is the

following:

∑∑∑

−

++=

)(min

iii

BTimeSetTSwtxf

Where:

TSwt

: tool switches in batch i;

Set

: number of setups;

BTime

: processing time of the batch i;

n = total of batches;

The neighborhood generation approaches

considered are batch swap (where the two batches

are shifted from its turns) and batch insertion (where

a batch is removed from its turn and inserted into

another) (Rodrigues and Gómez, 2001). The Tabu

Search Algorithm implemented is shown following.

Begin

Initialise TList empty;

Initialise niter;

Initialise biter;

Initialise nbmax;

Load Initial Solution s;

Upload bs with init;

While (niter – biter < nbmax) do

Generate neighborhood V(s)

starting with s;

Calculate F(s) for each s

generated;

Find s* of V(s) that minimizes

F(s);

If (s* is not in TList) then

Bs = s*;

Biter = niter;

End_if

s = s*;

increment niter;

End_while;

End

Where:

TList: tabu list;

Niter: iteration counter;

Bs: best solution found;

Biter: iteration when a better solution was found;

Nbmax: number of iterations with no improvement

of bs;

F(s) parts processing time calculus;

V(s): neighborhood of solutions;

s: a solution in V;

s*: better solution in V;

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

4 EXPERIMENTS

The model’s implementation was made in C++

language, using GCC compiler in a GNU-Linux

operational system. A Pentium III 833Mhz 128MB

RAM was used to perform the experiments batches.

A experiment batch consists that follows: the Part

Generator Module starts creating 10 par-tool

incidence matrixes with 90 parts versus 10 tools

dimension, respecting the 4 tools magazine

constraints. Each one of the five dispatching rules

receives as input the 10 matrixes and it generates a

set of initial solutions. All those initial solutions are

used by the Tabu Search Module, witch is executed

considering independently the two neighborhood

generation approaches and the Tabu List size

variation. The nbmax number was set in 120

iterations without improvement in the global result

and the Tabu List size were varied in 10, 50 and 100

positions. For each batch of experiments, the

analysis of the number of tool switches and the

number of setups is done separately.

In the following tables the statistics obtained with

the experiments are presented. Those statistics are

referring to the averages of setups number and tool

switches number of the initial solutions (generated

by Dispatching Rules) and final solutions (generated

by Tabu Search) and to the variation of the Tabu List

size. The tables 1,2 and 3 refer to the accomplished

experiments being considered the number of setups

and the tables 4, 5 and 6 consider the number of tool

switches.

The initial solutions are shown briefly: RAN

(Random Initial Solution), FAM (Part Family Initial

Solution Based), PMSR (Part Family Most Similar

Resources), MDR (Most Dissimilar Resources) and

LPTF (Larger Process Time First).

Table abbreviations:

istn = number of tool switches of the initial solution;

fstn = number of tool swsitches of the final solution;

issn = number of setups of the initial solution;

fssn = number of setups of the final solution;

std = stander deviation;

Table 1: Average of the initial and final number of setups and number of tool switches for the dispatching rules, with Tabu

List size set in 10 position and considering only the machine setup.

Initial Solutions Batch swap Batch insertion

Istn std issn std fstn std fssn std fstn std fssn std

FAM 40,4 4,22 21,9 2,23 39,8 4,92 20,2 2,66 39,8 4,92 20,2 2,66

LPTF 198,1 13,16 82,9 2,47 53,1 7,74 21,3 2,75 51,5 6,82 20,6 2,72

MDR 214,5 15,57 86,6 1,17 50,2 6,46 21,2 3,01 49,2 8,79 19,7 3,02

PMSR 28,1 2,64 20,5 2,55 27,9 3,21 19,6 3,03 27,7 3,40 19,7 2,98

RAN 200,5 13,54 77,7 20,39 51,1 5,86 20,8 2,57 50 8,26 20,1 2,77

Table 2: Average of the initial and final number of setups and number of tool switches for the dispatching rules, with Tabu

List size set in 50 position and considering only the machine setup.

Initial Solutions Batch swap Batch insertion

Istn std issn std fstn Std fssn std fstn std fssn std

FAM 40,4 4,22 21,9 2,23 39,5 5,05 19,8 2,74 39,8 4,92 20,2 2,66

LPTF 198,1 13,16 82,9 2,47 52,4 8,22 20,8 2,90 50,8 7,21 20,4 2,59

MDR 214,5 15,57 86,6 1,17 50,1 6,38 21,1 2,96 49 8,87 19,6 3,03

PMSR 28,1 2,64 20,5 2,55 27,9 3,21 19,6 3,03 27,7 3,40 19,7 2,98

RAN 200,5 13,54 77,7 20,39 49,6 8,47 20,5 2,59 49,8 8,07 20 2,62

TABU SEARCH STRATEGIES IN SCHEDULING PROBLEM IN FLEXIBLE MANUFACTURING SYSTEM -

Considering tool switches and number of setups

Table 3: Average of the initial and final number of setups and number of tool switches for the dispatching rules, with Tabu

List size set in 100 position and considering only the machine setup.

Initial Solutions Batch swap Batch insertion

Istn std issn std fstn std fssn std fstn std fssn std

FAM 40,4 4,22 21,9 2,23 39,5 4,99 20 2,75 39,8 4,92 39,8 4,92

LPTF 198,1 13,16 82,9 2,47 52,4 8,13 20,7 2,83 50,8 7,21 50,8 7,21

MDR 214,5 15,57 86,6 1,17 50,1 6,38 21,1 2,96 49 8,87 49 3,03

PMSR 28,1 2,64 20,5 2,55 27,9 3,21 19,6 3,03 27,9 3,40 27,9 3,35

RAN 200,5 13,54 77,7 20,39 49,6 8,47 20,4 2,67 49,8 8,07 49,8 2,62

Table 4: Average of the initial and final number of setups and number of tool switches for the dispatching rules, with Tabu

List size set in 10 position and considering only the tool switches.

Initial Solutions Batch swap Batch insertion

istn std issn std fstn Std fssn std fstn std fssn std

FAM 40,4 4,22 21,9 2,23 34,8 3,77 20 2,79 32,7 2,31 20,1 2,69

LPTF 198,1 50,41 82,9 2,47 40,8 7,83 23,1 5,00 32,3 2,11 20,4 2,41

MDR 214,5 15,57 86,6 1,17 38,7 3,92 22,2 3,16 32,3 2,58 20,2 2,86

PMSR 28,1 2,64 20,5 2,55 26,9 3,11 19,8 2,86 26,6 2,88 19,6 3,03

RAN 200,5 13,54 84 2,21 41,1 7,02 22,5 3,72 33,6 2,55 20,2 2,82

Table 5: Average of the initial and final number of setups and number of tool switches for the dispatching rules, with Tabu

List size set in 50 position and considering only the tool switches.

Initial Solutions Batch swap Batch insertion

istn std issn std fstn std fssn std fstn std fssn std

FAM 40,4 4,22 21,9 2,23 34,1 3,45 20 2,79 31,5 2,59 19,9 2,69

LPTF 198,1 50,41 82,9 2,47 37,9 5,09 21,6 2,80 31,9 2,56 20,1 2,81

MDR 214,5 15,57 86,6 1,17 37,7 4,06 21,7 3,16 30,7 2,91 19,7 2,98

PMSR 28,1 2,64 20,5 2,55 26,9 3,11 19,8 2,86 26,3 2,87 19,6 3,03

RAN 200,5 13,54 84 2,21 37,8 6,11 21,3 2,75 33 2,49 20,2 2,82

Table 6: Average of the initial and final number of setups and number of tool switches for the dispatching rules, with Tabu

List size set in 100 position and considering only the tool switches.

Initial Solutions Batch swap Batch insertion

Istn std issn std fstn std fssn std fstn std fssn std

FAM 40,4 4,22 21,9 2,23 34,2 3,46 20 2,79 30,9 3,28 19,9 2,69

LPTF 198,1 50,41 82,9 2,47 37,1 3,51 21,2 2,44 31,8 2,57 20,1 2,81

MDR 214,5 15,57 86,6 1,17 37,4 4,01 21,3 3,16 31 2,49 19,8 2,82

PMSR 28,1 2,64 20,5 2,55 26,9 3,11 19,7 2,98 26,7 3,23 20,3 3,40

RAN 200,5 13,54 84 2,21 37,9 7,19 21,1 2,69 33,2 2,49 20,2 2,82

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

Can be noticed in these experiments that the

approach of neighborhood generation based on

batch insertion moves promotes a better Tabu

Search performance compared to the approach batch

swap based. That is due to the fact the move type

accomplished in the batch insertion generates a

richer neighborhood than the one generated by batch

swap approach, taking to a better result. The batch

insertion approach needs a larger number of moves

to find a qualitatively superior result (according to

the number of tool switches) to the result found by

batch swap approach (Rodrigues and Gómez, 2001).

For the Dispatching rules RAN, MDR and LPTF,

which generate worse initial solutions, the increase

of the Tabu List size has positive impact in the Tabu

Search performance, therefore it extends the search

in the solutions space.

The initial solutions approaches that present better

results were the PMSR and FAM, which as it can be

seen in previous works (Gómez et al,2002). The

Tabu List size increasing did not bring significant

performance improvements in Tabu Search that have

as initial solutions those approaches, independent of

used neighborhood generation approach. Those

Dispatching Rules generate a result very close to the

better solution, so the necessary number of iterations

to find it becomes smaller. To the Dispatching rules

RAN, MDR and LPTF, which generates worse

initial schedules (faraway from the better solution),

the increase of the Tabu List has a positive impact,

therefore it extends the search, escaping from local

optima.

It is also noticed in the experiments that the

contribution of the decision variable of the Objective

Function tool switches is more significant in the

reduction of the batch processing time, generating

better results than the ones generated for the setups

number variable contribution. The variable change

of tools considers the resource sharing among PFs,

factor that relieve in the setup time reduction,

assuring better solutions.

5 CONCLUSIONS

In this paper it was developed a Part Scheduling

Model in which it was observed the Tabu List size

variation and its influence in the Tabu Search

perfomance. In the Tabu Search Algorithm, two

approaches of neighborhood generation were used:

(the batch insertion and the batch swap approaches).

The initial solutions were based in five Dispatching

rules (RAN, MDR, PMSR, FAM, LPTF). In the

accomplished experiments, the Tabu List size was

varied.

It could be observed that the batch insertion

approach promotes better Tabu Search Performance

due to generation of a richer neighborhood in

comparison to the batch swap approach. That leads

to a larger number of iterations to find the better

result. The Tabu List variation has positive impact in

the batch swap approach, doing with its performance

went as good as the one of the batch insertion

approach.

The initial solutions that more contribute to the Tabu

Search performance improvement are PMSR and

FAM, therefore these rules take into account the

resource sharing among PFs. The Tabu List size

variation has positive impact in dispatching rules

that generates worse initial solutions (RAN, MRD,

LPTF), because with the search diversification, a

larger number of solutions in the neighborhood is

visited, escaping of the local optimum.

To solve the Scheduling Problem, can be opted by

the use of a more flexible approach of neighborhood

generation (batch insertion approach), having as

initial solution a Dispatching Rule that takes into

account the resource sharing among PFs (PMSR and

FAM), which is important factor for the batch

processing time minimization. The batch swap

approach needs a larger number of iterations to

reach a better result like the one found by the batch

insertion approach. To this approach, the Tabu List

would not need to store a larger number of forbidden

moves.

In case the approach of neighborhood generation

cannot be flexible and the initial solution cannot take

into account the resource sharing, a larger Tabu List

will act diversifying the space search, leading to a

better result.

REFERENCES

Bedworth, D. D., Henderson, M. R., Wolfe, P.M., 1991.

Computer Integrated Design and Manufacturing,

McGraw-Hill.

Dorf, R., Kusiak, A., 1994. Handbook of Design,

Manufacturing and Automation, John Wiley and Sons.

Glover, F., 1989. Tabu Search: Part I, ORSA Journal of

Computing.

Glover, F., Laguna, M., 1997. Tabu Search, Kluwer

Academic, Boston.

Gómez, A. T., 1993. Aplicação de Otimização

Combinatória em Sistemas de Manufatura Flexíveis,

INPE, São Paulo, Brazil.

Gómez, A. T., Rodrigues, A. G., Hoffmann, L. T., 2002.

Análise da Performance de um Modelo de

Escalonamento Baseado em Pesquisa Tabu aplicado a

um Sistema de Manufatura Flexível. In LAPTEC 2002,

3rd Congress of Logic Applied to Technology.

TABU SEARCH STRATEGIES IN SCHEDULING PROBLEM IN FLEXIBLE MANUFACTURING SYSTEM -

Considering tool switches and number of setups

Hertz, A., 1991. Tabu Search for large Timetabling

Problems, European Journal of Operational Research.

Kaighobadi, M., Venkatesh, K., 1993. Flexible

Manufacturing Systems: An Overview, International

Journal of Operations & Production Management.

Kusiak, A., Chow, W. S., 1986. Efficient Solving of

Group Technology Problem, University of Manitoba,

Winnipeg.

Kusiak, A., 1992. Intelligent Design and Manufacturing,

John Wiley and Sons.

Rodrigues, A. G., Araújo, R. S., 1999. Modelagem de

Sistemas de Manufatura Flexíveis considerando

restrições físicas e temporais. In CRICTE´99,

Congresso Regional de Iniciação Científica e

Tecnológica em Engenharia, Santa Maria, Rio Grande

do Sul, Brazil.

Rodrigues, A. G., Gómez, A. T., 2000. Utilização de

metaheurísticas para a modelagem de Problemas de

Seleção de Partes e Scheduling em um Sistema de

Manufatura Flexível, Scientia, São Leopoldo, Rio

Grande do Sul, Brazil.

Rodrigues, A. G., Gómez, A. T., 2001. Utilização de

Pesquisa Tabu no Escalonamento de um Sistema de

Manufatura Flexível. In CRICTE’2001, Congresso

Regional de Iniciação Científica e Tecnológica em

Engenharia, Ijuí, Rio Grande do Sul, Brazil.

Widmer, M., 1991. Job Shop Scheduling with Tooling

Constraints: a Tabu Search Approach. Journal of

Manufacturing.

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION