BEST-ACTION PLANNING FOR REAL-TIME RESPONSE

An approach in ORICA

Tariq Ali Omar, Ana Simonet, Michel Simonet

Osiris Team, TIMC-IMAG Laboratory, La Tronche Cedex, France

Keywords: Real-time control, Artificial Intelligence, Planning.

Abstract: A planner for real-time response aims at building a plan to safely guide the world to its goal state by

guaranteeing response deadlines. Ideally, it should find the paths most suitable for guaranteeing real-time

behaviour and goal achievement. To achieve this ideal behaviour, it must possess maximum information

about the world behaviour and be able to plan the responses of the system under-control to its advantage. It

should be able to reason about one path with respect to the other, based on the execution duration, the

amount of resources used and the system safety. In this paper, we present the ORICA (OSIRIS

real-time

intelligent control architecture) real-time response planner, which builds plans that permit the real-time

system to strive to achieve its goal in un-guaranteed environment behaviour, while still ensuring system

safety. It does heuristic reasoning for comparison of different paths when a choice of path is possible.

1 INTRODUCTION

Like most classic AI problems, a real-time AI

system for control application is given the current

world state and it plans actions to lead the world to a

goal state. However, it needs to combine the

properties of predictability and response deadline

guarantee of a real-time system with the intelligent

reasoning. Thus, it must provide the best response

that can satisfy the given response-time deadline and

safely lead the system to its goal.

Different approaches have been used to handle this

problem. Precompiled structures using search-based

reasoning are predictable, but impractical for

complex world problems. Reactive behaviour of

reasoning and selecting a response within the

deadline, like “Anytime” and “design-to-time”

(Garvey, 96) algorithms are useful but compromise

the response precision to respect the response

deadline. Planning systems like PRS (Ingrand, 01)

and CIRCA (Goldman, 00) build plans of responses

that can take the world to the goal state.

Planning systems can permit more organized

response to world events through reasoning over the

future possible world behaviour. The responses can

be selected based on their usefulness under a given

situation.

Ideally, the best response plan for a real-time

control application is the one that can lead the world

to its desired goal state safely by meeting all

response deadlines and minimizes system resource

occupation. Two important factors affecting the

quality of reasoning of a planner are:

1. Knowledge representation semantics for real-

time world behaviour and ease of reasoning about

temporal deadlines and responses.

2. Heuristic measure of different factors to

determine most suitable real-time response paths,

i.e., cost of execution, safety etc.

In this paper, we present the real-time response path-

planner, as implemented in ORICA. The AI

planning module of ORICA is very similar to that of

CIRCA, but supports augmented knowledge

representation semantics, threat perception and

heuristic reasoning for planning the best real-time

response.

In the following sections, we discuss how the

ORICA planner handles the best-action selection

problem through its knowledge representation

semantics, reasoning around threat of failure and

heuristic measurement of the quality of paths that

are lead to by a selected response action.

2 REASONING ABOUT REAL-

TIME WORLD BEHAVIOUR

ORICA uses a states space planner (SSP) which

starts from the initial world state and identifies all

reachable states, i.e., the states that can be reached

through fireable transitions from the current state. A

OSIRIS is an implementation of the p-type model

presented by (Simonet,94)

306

Ali Omar T., Simonet A. and Simonet M. (2004).

BEST-ACTION PLANNING FOR REAL-TIME RESPONSE - An approach in ORICA.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 306-309

DOI: 10.5220/0001130803060309

 SciTePress

transition is defined by a set of preconditions and

postconditions. It is said to be applicable from a

state if its preconditions are satisfied by the state.

The planner recursively identifies all reachable

states from each state and plans actions when

possible in order to guide the world towards the goal

state. An applicable transition from a state may lead

to a failure state, e.g., a robot falling off a cliff. To

ensure system safety, the planner guarantees that no

failure transition fires from a state.

ORICA uses the world state space model as

presented below, to define the real-time behaviour of

the world.

2.1 World State Space Representation

World state space is a set of possible world states.

Each state has transitions leading to other states.

where S is finite set of world states,

and where T is the set of all possible

world transitions then:

Sss ∈

, ss ≠ Tt ∈

t :s

→s

and ,

1 2

)( st =∇ )( st =

ℜ

where

and ℜ are the domain and range functions

on a transition. ORICA segregates the transitions

into five categories, as given below:

∇

arttree

tttttT UUUU=

Each transition t has two time intervals min∆(t)

and max∆(t), measured from the instant the world

enters

(t). The former represents the minimum

duration after which t can fire, and the latter the

maximum duration before which t must fire. Their

respective min∆ and max∆ are given as:

∇

where 0 < firing time < ∞, bect(t

) and wcet(t

)

represent the best-case and the worst-case execution

times of the action transition. The event, temporal

and guaranteed temporal transitions, represent the

environmental events. An event transition may fire

at any instant as the world enters the domain state.

However, it is not guaranteed to fire. A temporal

transition is guaranteed not to fire before a finite

time delay, while a guaranteed temporal transition is

guaranteed to fire between min∆ and max∆ delays.

The guaranteed event and action transitions

represent the agent’s responses. The guaranteed

event guarantees that the system will react at

predefined deadline after the domain state of the

transition is reached. The action guarantees that the

system will respond before a finite time deadline.

Two types of sub-regions are defined in the

world state space, i.e., the safe region and the threat

region. The “safe region” is a set of “safe states”

from which direct failure is impossible. The threat

region consists of the failure states and “threat

states”, states from which failure is possible.

The AI planner may build a plan leading to a

state inside a threat region, in order to achieve the

goal. However, it must ensure that a guaranteed path

will take the world to safe region by pre-empting the

failure transitions in the threat region. This is done

by planning a guaranteed transition, i.e., an action, a

guaranteed event or a guaranteed temporal

transition, which will fire before failure can occur,

i.e.,

max∆(gt(s)) < min∆(ttf (s))

where gt(s) and ttf(s) are respectively guaranteed

and temporal transition to failure from state s.

A guaranteed event is like a watch-dog timer set

when the world reaches its domain state. It enables

the system to modify its beliefs about the world state

when no external event occurs by a finite time.

2.3 Dependent Temporal Transitions

to Failure

All transitions inside a threat region, taking the

world from a threat state to another, consume a finite

amount of time (except for an event transition which

may be instantaneous). Inside the threat region the

world moves towards a failure.

The time to failure from a threat state is

represented as a dependent temporal transition to

failure (dttf) and ORICA states that it depends on the

length of previous transitions in the threat region and

their effect on the cause leading to failure (Omar,

04), e.g., throwing water on fire may reduce its

spread but throwing oil will speed it up.

Transition Symbol min∆ max∆

Event t

0 ∞

Guaranteed event t

firing time firing time

Temporal t

> 0 ∞

Guaranteed

temporal

> 0 < ∞

Action t

bcet(ta) Sensing

delay+wcet(ta)

If the previous state s

i-1

is more threatening than

the currents state s

then the time to failure from the

current state is given as:

∆

))((min

sdttf

))((max

))((min

−

∆−

⎥

⎦

⎤

⎢

⎣

⎡

∆

×∆

sttf

Otherwise it is given as:

⎥

⎦

⎤

⎢

⎣

⎡

∆

∆−

×∆=∆

−

))((min

))((max

))((min))((min

sttf

stX

sttfsdttf

BEST-ACTION PLANNING FOR REAL-TIME RESPONSE - An approach in ORICA

307

Where

⎭

⎬

⎫

⎩

⎨

⎧

≤≤∆

=∆

−

niforsdttf

iforsttf

3))((min

2))((min

The dependent temporal transition relationship

exists only when the world moves from a threat state

to another threat state, within the same threat region.

3 HEURISTIC ACTION QUALITY

MEASUREMENT

The choice of the best action from a set of actions

possible from a state does not only depend on the

action’s execution length, resource utilization and

safety of the destination state, but also on the paths it

leads to.

Since, the “brute force” approach of tracing all

paths from all possible actions is a costly operation

in resource and time, a heuristic approach of “N-step

look ahead” is used by the ORICA planner. It does

depth-wise path search to the next N states and

calculates “cost of path-section” for each of the

paths based on their safety, execution length and

length of actions employed. Action leading to least

average cost paths is selected.

3.1 Threat Factor

The threat factor for a path section is defined as

“how close the world gets to failure, while moving

along that path”. It is calculated as the sum of the

costs of successive transitions inside the threat

region. The higher the threat factor, the shorter will

be the real-time response deadline, leading to more

load on system resources to detect and react to the

states along that path. It is represented as TF(Pi) for

a path-section Pi and calculated as:

∑

∆

sdeadline

PTF

)(

)(max

)(

where P

is a path composed of n successive

threat states and deadline(si) is the shortest time to

failure from the state si.

The TF(P

) is a positive value and varies in the

interval [0,1]. The threat factor equal to one

guarantees that the path will lead to failure.

3.2 Length Factor

The length factor for a path section measures “the

maximum time taken to cover that path section”.

The maximum length of all fireable transitions from

a state is less than the max∆ of the first guaranteed

transition in the set or the shortest time to failure

from the state (state deadline).

The length factor LF(P

) is thus given as:

)(max*

)(max

)(

max

PLF

∆

∑

where P

is a path section composed of n states,

max∆(s

) is the maximum time for which the world

can stay in the state si and t

max

is the maximum finite

length transition in the set of all transitions of

knowledge base.

3.3 Actions Factor

The actions factor is a measure of “length of all

actions along the path section”. It is important as the

real-time execution system must detect the state in

time to take the necessary planned action and meet

the response deadline. Shorter actions factor means

either less actions or actions with less execution

length, limiting the occupation of system resources.

It is given as:

)(

max

awcetn

awcet

PAF

∑

where n is the number of action states in the

path-section and a

max

is the action with the

maximum worst case execution time in the set of all

actions in the knowledge base.

3.4 Cost of the path-section

The above three factors permit a heuristic measure

of quality of a path section for real-time response.

Their weighed sum gives the cost of a path-section:

[

]

[

][ ]

CBA

PAFCPLFBPTFA

iii

×+×+×

)()()(

)(

where the values of the constants A,B and C are

assigned empirically. ORICA assigns higher priority

to the threat factor to ensure safe real-time behaviour

and hence assigns A twice the value of B and C.

For all possible responses from the current state,

an average cost of all paths originating from it is

calculated and the response with least cost is

selected. However, being heuristic calculation

limited to N states, the selected response does not

guarantee safety and goal achievement over the

complete path. If a path fails, either because it does

not take the system to the goal or it cannot guarantee

safety, then the planner backtracks to a previous

state and selects the second best response from it.

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

308

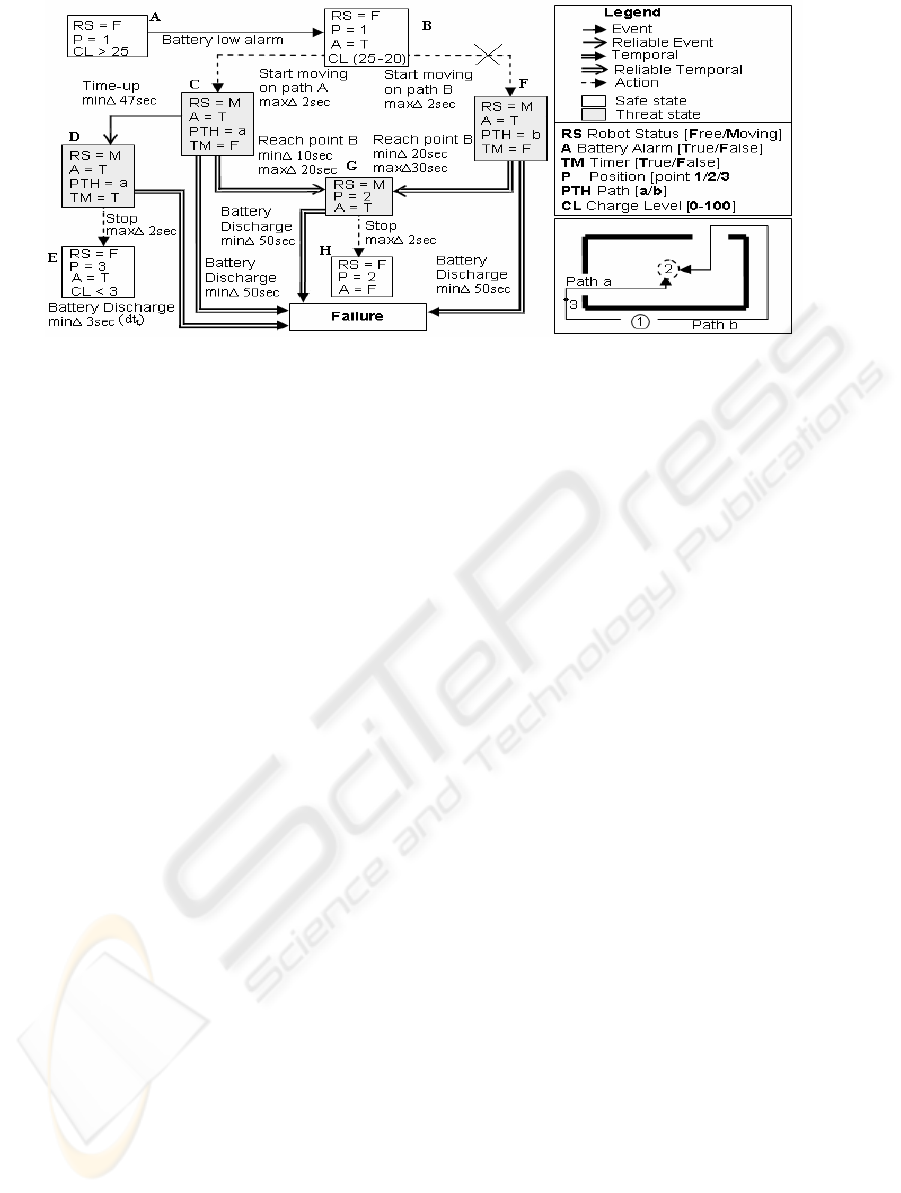
Figure 2: Planning for a robot to move from point 1 to 2.

4 EXAMPLE

To demonstrate the reasoning capability of the

ORICA planner we consider a mobile robot at point

1. It receives a “low battery” event (passage from

state A to state B). It must reach point 2 (see bottom

right box in figure 2) to charge its batteries. The

knowledge about the robot can only guarantee

minimum motion duration before the batteries

discharge completely, based on charge level of the

batteries. However, complete discharge is a failure

condition which it must avoid.

The planner starts building a plan to reach point

2. The reliable temporal transitions from state C and

F guarantee that the robot will reach point 2 before

failure (i.e., 20 sec and 30 sec). The two paths

B,C,G,H and B,F,G,H will have same threat and

action factor but the length factor will be less for the

path B,C,G,H and hence the planner will select it.

If the knowledge base cannot guarantee the

passage of the robot from state C to state G before

the transition to failure occurs (i.e., a temporal

transition exists between state C and state G, instead

of the reliable temporal transition) then the planner

will build a guaranteed event transition from state C

to state D. Since state C and D are in same threat

region, the dependent temporal transition from state

D to failure will have a min∆ equal to 3 seconds (50

- 47). The action transition from D to E is

guaranteed to fire in 2 seconds, thus it will pre-empt

the dependent transition to failure, preserving the

safety of the robot, even though the goal is not

reached.

Thus, although the knowledge base was not able

to guarantee that the robot could reach its goal,

because of imprecise knowledge of the path length

the planner still made it possible for the robot to

strive to reach point 2, while ensuring that the failure

is avoided at all costs.

5 SUMMARY AND FUTURE

WORK

We have presented the ORICA planner for real-time

response planning with its knowledge representation

semantics and heuristic reasoning. The planner can

build plans to permit the agent to strive to reach its

goal without compromising safety, when no

guaranteed path is available. The heuristic analysis

permits a piece-wise comparison of paths based on

factors most useful for real-time response.

Current implementation of ORICA has a Java

based AI module for reasoning and planning while

the real-time module is being built in C and will run

on a QNX platform. Our future objectives include

testing the model in real environment and comparing

our results with the other real-time AI models.

REFERENCES

Ingrand F. Olivier D. Extending Procedural Reasoning

toward Robot Actions Planning, IEEE ICRA 2001,

Seoul, South Korea.

Garvey, A., Lesser, V.. Design-to-time Scheduling and

Anytime Algorithms. In SIGART Bulletin, Volume 7,

Number 3. January, 1996.

Simonet A., Simonet M., Objects with Views and

Constraints : from Databases to Knowledge Bases,

OOIS'94, D. Patel, Y. Sun and S. Patel eds, London,

Springer Verlag, Dec. 1994, pp 182-197.

Goldman R. P., Musliner D. J., and Pelican M. J., Using

Model Checking to Plan Hard Real-Time Controllers,

Proc. AIPS Workshop on Model-Theoretic

Approaches to Planning, April 2000.

Omar T. A., M. Simonet, A. Simonet, Threat Perception in

Planning for Real-Time Response. To be published in

proceedings of CSIMTA, 2004.

BEST-ACTION PLANNING FOR REAL-TIME RESPONSE - An approach in ORICA

309