A STOCHASTIC OFF LINE PLANNER OF OPTIMAL DYNAMIC

MOTIONS FOR ROBOTIC MANIPULATORS

Taha Chettibi, Moussa Haddad, Samir Rebai

Mechanical Laboratory of Structures, EMP, B.E.B., BP17, 16111, Algiers, Algeria

Abd Elfath Hentout

Laboratory of applied mathematics, EMP, B.E.B., BP17, 16111, Algiers, Algeria

Keywords: Robotic manipulator, Motion planning, Sto

chastic optimization, Obstacles avoidance.

Abstract:

We propose a general and simple method that handles free (or point-to-point) motion planning problem for

redundant and non-redundant serial robots. The problem consists of linking two points in the operational

space, under constraints on joint torques, jerks, accelerations, velocities and positions while minimizing a

cost function involving significant physical parameters such as transfer time and joint torque quadratic

average. The basic idea is to dissociate the search of optimal transfer time T from that of optimal motion

parameters. Inherent constraints are then easily translated to bounds on the value of T. Furthermore, a

stochastic optimization method is used which not only may find a better approximation of the global

optimal motion than is usually obtained via traditional techniques but that also handles more complicated

problems such as those involving discontinuous friction efforts and obstacle avoidance.

1 INTRODUCTION

Motion planning constitutes a primordial phase in

the process of robotic system exploitation. It is a

challenging task because the robot behaviour is

governed by highly non linear models and is

subjected to numerous geometric, kinematic and

dynamic constraints (Latombe, 1991) (Angeles,

1997) (Chettibi, 2001). Two categories of motions

can be distinguished (Angeles, 1997) (Chettibi,

2000). The first covers motions along prescribed

geometric path and correspond, for example, to

continuous welding or glowing operations (Bobrow,

1985) (Kang, 1986) (Pfeiffer, 1987) (Chettibi,

2001b). The second, which is the focus of this

paper, concerns point-to-point (or free) motions

involved, for example, in discrete welding or pick-

and-place operations (Bessonnet, 1992) (Mitsi,

1995) (Lazrak, 1996) (Danes, 1998) (Chettibi,

2001a). In general, many different ways are

possible to perform the same task. This freedom of

choice can be exploited judiciously to optimize a

given performance criterion. Hence, motion

generation becomes an optimization problem. It is

here referred to as the optimal free motion planning

problem (OFMPP).

In the specialized literature, various resolutions

ethods have been proposed to handle the OFMPP.

They can be grouped in two main families; namely:

direct and indirect methods (Hull, 1997) (Betts,

1998). The indirect methods are, in general,

applications of optimal control theory and in

particular Pontryagin Maximum Principle (PMP)

(Pontryagin, 1965). Optimality conditions are stated

under the form of a boundary value problem that is

generaly too difficult to solve (Bessonnet, 1992)

(Lazrak, 1996) (Chettibi, 2000). Several techniques,

such as the phase plane method (Bobrow, 1985)

(Kang, 1986) (Jaques, 1986) (Pfeiffer, 1987), exploit

the structure only of the optimal solution given by

PMP and get numerical solutions via other means.

In general, such techniques are applied to limited

cases and have several drawbacks resumed below:

 Th

ey require the solution of a N.L multi-point

shooting problem (David, 1997) (John, 1998 ),

 They re

quire analytical computing of gradients

(Lazrak, 1996) (Bessonnet, 1992),

121

Chettibi T., Haddad M., Rebai S. and Hentout A. (2004).

A STOCHASTIC OFF LINE PLANNER OF OPTIMAL DYNAMIC MOTIONS FOR ROBOTIC MANIPULATORS.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 121-128

DOI: 10.5220/0001132301210128

 SciTePress

 The region of convergence may be small

(Chettibi, 2001) (Lazrak, 1996),

 Path inequality are difficult to handle (Danes,

1998),

 They introduce new variables known as co-state

variables that are, in general, difficult to estimate

(Lazrak, 1996) (Bessonnet, 1992) (Danes, 1998)

(Pontryagin, 1965).

 In minimum time transfer problems, they lead to

discontinuous controls (bang-bang) that may

create many practical problems (Ola, 1994)

(Chettibi, 2001a). In fact, the controller must

work in saturation for long periods. The optimal

control leaves no control authority to compensate

for any tracking error caused by either unmodeled

dynamics or delays introduced by the on-line

feedback controller

To overcome these difficulties, direct methods have

been proposed. They are based on discretisation of

dynamic variables (states, controls). They seek to

solve directly a parameter optimization problem.

Then, N.L. programming (Tan, 1988) (Martin, 1997)

(Martin, 1999) (Chettibi, 2001a) or stochastic

optimization techniques (Chettibi, 2002b) are

applied to compute optimal values of parameters.

Other ways of discretisation can be found in

(Richard, 1993) (Macfarlane, 2001). These

techniques suffer, however, from numerical

explosion when treating high dimension problems.

Although they have been used successfully to solve

a large variety of problems, techniques based on

N.L. programming (Fletcher, 1987) (David, 1997)

(Danes, 1998) (John, 1998) (Chettibi, 2000) have

two essential drawbacks:

 They are easily attracted by local minima ;

 They generally require information on gradiant and

hessian that are difficult to get analytically. In

addition, continuity of second order must be

ensured, while realistic physical models may

include some discontinuous terms (frictions).

In parallel to these methods, that take into

account both kinematics and dynamics aspects of the

problem, numerous pure geometric planners have

been proposed to find solutions for the simplified

problem that consists of finding only feasible

geometric paths (Piano movers problem) (Latombe,

1991) (Overmars, 1992) (Barraquand, 1992)

(Kavraki, 1994) (Barraquand, 1996) (Kavraki, 1996)

(Latombe, 1999) (Garber, 2002). In spite of this

simplification, the problem still remains quite

complex with exponential computational time in the

degree of freedom (d.o.f.). Of course, any extension

(presence of obstacles, for example) adds in

computational complexity. Even so, various

practical planners have been proposed. Reference

(Latombe, 1991) gives an excellent overview of

early methods (before 1991) such as: potential field,

cell decomposition and roadmap methods, some of

which have shown their limits. For instance, a

potential field based planner is quickly attracted by

local minima (Khatib, 1986) (Latombe, 1991)

(Barraquand, 1992). Cell decomposition methods

often require difficult and quite expensive geometric

computations and data structures tend to be very

large (Latombe, 1991) (Overmars, 1992). The key

issue for roadmap methods is the construction of the

roadmap. Various techniques have been proposed

that produce different sorts of roadmaps based on

visibility and Voronoi graphs (Latombe, 1991).

During the last decade, interest was given to

stochastic techniques to solve various forms of

optimal motion planning problems. In particular,

powerful algorithms were proposed to solve the

basic geometric problem. Probabilistic roadmaps

(PRM) or Probabilistic Path Planners (PPP) were

introduced in (Overmars, 1992) (Barraquand, 1996)

(Kavraki, 1994) (Kavraki, 1996) and applied

successfully to complex situations. They are

generally executed in two steps: first a roadmap is

constructed, according to a stochastic process, then

the motion planning query is treated. Due to the

power of this kind of schemes, many perspectives

are expected as shown in (Latombe, 1999).

However, there are few attempts to apply them to

solve the complete OFMPP. References (LaValle,

1998) (LaValle, 1999) propose the method of

Rapidly exploring Random Trees (RRTs) as an

extention of PPP to optimize feasible trajectories for

NL systems. Dynamic model and inherent

constraints are taken into account.

In (Chettibi, 2002a), we introduced a different

scheme using a sequential stochastic technique to

solve the OFMPP. We present here this simple and

versatile method and how it can be used to handle

complex situations involving both friction efforts

and obstacle avoidance.

2 PROBLEM STATEMENT

Let us consider a serial redundant or non-redundant

manipulator with n d.o.f.. Motion equations can be

derived using Lagrange's formalism or Newton-

Euler formalism (Dombre, 1988) (Angeles, 1997):

(

)

(

)()

=++ qGqqQqqM

&&&

(1a),

q, and are respectively joints position, velocity,

acceleration vectors. M(q) is the inertia matrix.

) is the vector of centrifugal and Coriolis

forces in which joints velocities appear under a

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

122

quadratic form. G(q) is the vector of potential

forces and

is the vector of actuator efforts.

In order to make the dynamic model more realistic,

we may introduce, for the i

joint, friction efforts as

follows:

)())(()())((

))(),(()())((

ttqsignFtqFtqG

tqtqQtqtqM

jij

=+++

∑

&&&

(1b),

and are, respectively, sec and viscous

friction coefficients of the i

joint.

The robot is required to move freely from an initial

state P

to a final state P

, both of which are specified

in the operational space. In addition to solving for

(t) and transfer time T, we must find the trajectory

defined by q(t) such as the initial and the final state

are matched, constraints are respected and a cost

function is minimized.

The cost function adopted here is a balance

between transfer time T and the quadratic average of

actuator efforts:

∫

∑

⎟

⎠

⎞

⎜

⎝

⎛

−

max

obj

)t(

(2).

is a weighting coefficient chosen from [0,1] and

according to the relative importance we would like

to give to the minimization of T or to the quadratic

average of actuator efforts. The case

µ =

1 corresponds to the optimal time free motion

planning problem.

Constraints that must be satisfied during the

entire transfer (0 ≤ t ≤ T) are summarized bellow:

for i = 1, …, n we have bounds on:

- Joint torques:

()

max

ττ

≤ (3a);

- Joint jerks :

()

max

qtq

&&&&&&

≤

(3b);

- Joint accelerations:

()

max

qtq

&&&&

≤ (3c);

- Joint velocities:

()

max

qtq

≤ (3d);

- Joint positions:

()

max

qtq ≤ (3e).

Of course, non-symmetrical bounds on the above

physical quantities can also be handled without any

new difficulty.

Relations (3a, b, c, d and e) traduce the fact that

not all motions are tolerable and that power

resources are limited and must be used rationally in

order to control correctly the robot dynamic

behavior. Also, since joint position tracking errors

increase with jerk, constraints (3b) are introduced to

limit excessive wear and hence to extend the robot

life-span (Latombe, 1991) (Piazzi, 1998)

(Macfarlane, 2001).

In the case where obstacles are present in the

robot workspace, motion must be planned in such a

way collision is avoided between links and

obstacles. Therefore, the following constraint has to

be satisfied :

C(q)=False (3f).

The Boolean function C indicates whether or not the

robot at configuration q is in collision with an

obstacle. This function uses a distance function

D(q) that supplies for any robotic configuration the

minimal distance to obstacles.

3 REFORMULATION OF THE

PROBLEM

The normalization of the time scale, initially used to

make the problem with fixed final time, is exploited

to reformulate the problem and to make it propitious

for a stochastic optimization strategy. Details are

shown bellow.

3.1 Scaling

We introduce a normalized time scale as follows:

T.xt

with (4).

[]

1,0∈x

Hereafter, we will use the prime symbol to indicate

derivations with respect to x :

(

)

(

)

,",'

xqd

xdq

q ==

()

xqd

q =

(5).

Relations (1a) and (1b) can be written as follows:

(1a)

⇒

()

iii

x +=

(6a)

(1b)

⇒

)(

qsignFqF

iiii

′

++=

(6b)

where:

()

(

)

max

, =

jij

QqM +

∑

(7)

and:

max

(8)

A STOCHASTIC OFF LINE PLANNER OF OPTIMAL DYNAMIC MOTIONS FOR ROBOTIC MANIPULATORS

123

3.2 Cost function

With the previous notations, the cost function (2)

becomes without friction efforts:

⎟

⎠

⎞

⎜

⎝

⎛

++=

STF

obj

(9),

Where S

, S

and S

are given by:

()

∫

∑

∫

∑

∫

∑

−

−=

−

dxHS

dxGHS

dxGS

(10).

It must be noted that S

, S

and S

are real

coefficients that do depend on the joint evolution

profile q(x) but that do not depend on T. Also, S

and S

are always positive. Expression (9)

represents a family of curves whose general shape,

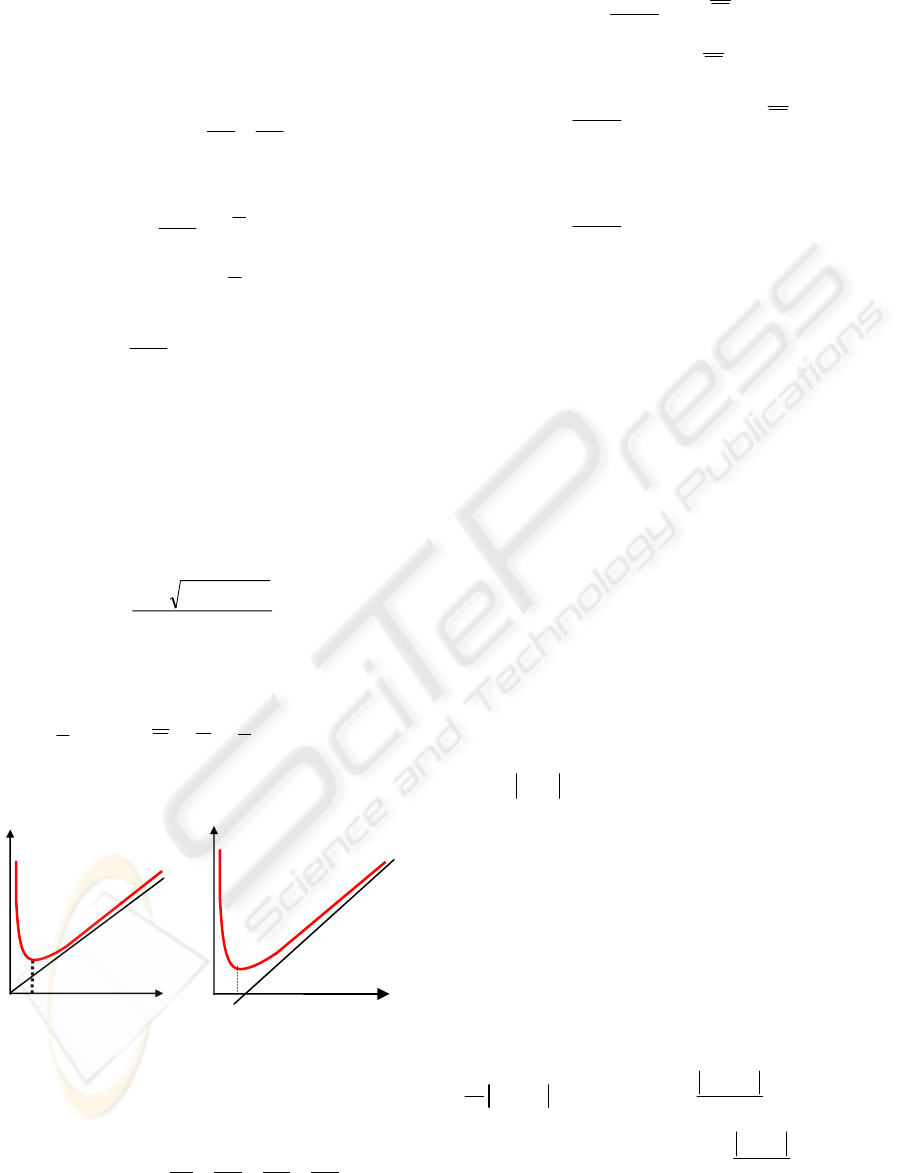
for any feasible motion, is shown in figure 1a. The

minimum of each of these curves is reached when T

takes on the value T = T

given by :

2/1

⎟

⎠

⎞

⎜

⎝

⎛

SSSS

(11).

If friction efforts are taken into account, we

introduce the following quantities:

qFK

′

)(qsignFGG

iii

′

(12)

The expression of (2) becomes then :

⎟

⎠

⎞

⎜

⎝

⎛

++++=

STF

obj

(13)

where:

()

∫

∑

∫

∑

∫

∑

∫

∑

∫

∑

−

−=

−

−=

−

)1(

λµ

dHS

dKHS

dGHKS

dGKS

dGS

iii

(14)

For a given profile q(x), (13) represents a family of

curves whose general shape is shown in figure 1b,

but now the asymptotic line intersects the time axis

. Furthermore, T

/SS - T =

has to be

computed numerically since (11) is no longer

applicable.

3.3 Effects of constraints

Constraints imposed on the robot motion will be

handled sequentially within the iterative process of

minimization described in the next section. Already,

we can group constraints into several categories

according to the stage of the iterative process at

which they will be handled.

3.3.a Constraints of the first category

In the first category, we have constraints that will

not add any restriction on the value of T. For

example, joint position constraints (3e) become:

(

)

[]

nixqxq

,,11,0

max

K=∈∀≤ (15),

and those due to obstacles presence (3f) become :

C(q(x))=False

[]

1,0∈

∀

(16)

In both cases, only the joint position profiles q(x) are

determinant.

3.3.b Constraints of second category

In the second category, we have constraints that can

be transformed into explicit lower bounds on T. For

example joint velocity constraints lead to:

()

Tqxq

,...,1

max

=≥⇒≤

so:

TT ≥

[]

()

⎥

⎦

⎤

⎢

⎣

⎡

max

1,0,,1

maxmax

(17).

Joint acceleration and jerk constraints are

transformed in the same way to give:

Figure 1. General shape of the cost function;

(a) without friction efforts , (b) with friction efforts

obj

-S

Fig. 1a

Fig. 1b

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

124

For accelerations:

≥

[]

()

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

2/1

max

1,0,,1

maxmax

(18),

Figure 3: New exploration region defined by

a new lower value of F

best

obj

Last

best

and for jerks:

T≥T

[]

()

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

3/1

max

1,0,,1

maxmax

(19).

&&&

Thus, (17), (18) and (19) define three lower bounds

on transfer period. In consequence; T must satisfy

the following condition:

≥

T* , T*=max(T

, T

) (20),

This type of constraints defines a forbidden region

as shown in figure 2. Note that two cases are

possible.

3.3.c Constraints of third category

In the third category, we have constraints that can be

transformed into explicit bilateral bounds on T. For

example those imposed on the value of joint torques

(3a) define, in general, bracketing bounds on T,

namely: T

and T

. In consequence,

T∈[T

, T

] (21).

A fourth category might be included and would

concern any other constraint that does add

restrictions on T but that cannot be easily translated

into simple bounds on T.

4 STRATEGY OF RESOLUTION

The iterative process of minimization proposed here

includes the following steps:

Step 1: Generate a random (or guessed) temporal

evolution shape q

(x) for each of the joint variables,

taking into account any constraints of the first

category (15), (16) as well as any conditions

imposed on the initial and the final state.

Step 2: Get the S coefficients from (10) or (14) and

from (11) or by numerical means. If F(T

) is

greater than F

best

obtained so far, then there is no

need to continue and hence, return to Step 1.

Otherwise, a first bracketing interval [T

, T

] is

deduced (Fig. 3) in which F is decreasing from T

and increasing from T

to T

The remaining steps will simply consist of changing

, T

or T

while keeping this bracketing.

Step 3: Get T

, T

from (17, 18, 19) and T* from

(20). If T* > T

then return to Step 1 else modify T

and/or T

according to Fig. 2. That is: in case (a) T

← T* while in (b) T

← T* and T

← T*.

Step 4: Get [T

, T

] from (21). If T

> T

or T

< T

then return to Step 1. Otherwise, we have a

new improved F

best

If T

∈ [T

, T

] then

best

← F(T

)

Else if T

< T

then

best

← F(T

)

Else

best

← F(T

)

End if

The above steps can be imbedded in a stochastic

optimization strategy to determine better profiles

(x), i = 1,… n, leading to lower values of the

objective function.

One way to get a guessed temporal evolution shape

(x) for the joint variables, at any stage of

optimization process, is to use randomly generated

clamped cubic spline functions with nodes

distributed for x ∈ [0,1] (Fig. 4).

obj

Case b: T

Case a: T

Forbidden

region

Forbidden

region

Figure 2: Bounds on transfer time value due to constraints of

second category

A STOCHASTIC OFF LINE PLANNER OF OPTIMAL DYNAMIC MOTIONS FOR ROBOTIC MANIPULATORS

125

(x)

Free Nodes uniformly

distributed

Figure 4: Approximation of joint position temporal

evolution

max

Admissible interval

5 NUMERICAL RESULTS

We consider here a redundant planar robot

constituted of four links connected by revolute

joints. The corresponding geometric and inertial

characteristics are listed in Appendix A. It is asked

to move among two static obstacles disposed in it’s

work space at respectively (2, 1.5) and (-1.5, 1.5)

with both unity radius. The robot begin at (π/4, -π/2,

π/4, 0) and stops at (π/2, 0, 0, 0). Boundary

velocities are null. The numerical results are

obtained with µ=0.5 for both cases: with and

without friction efforts. The corresponding optimal

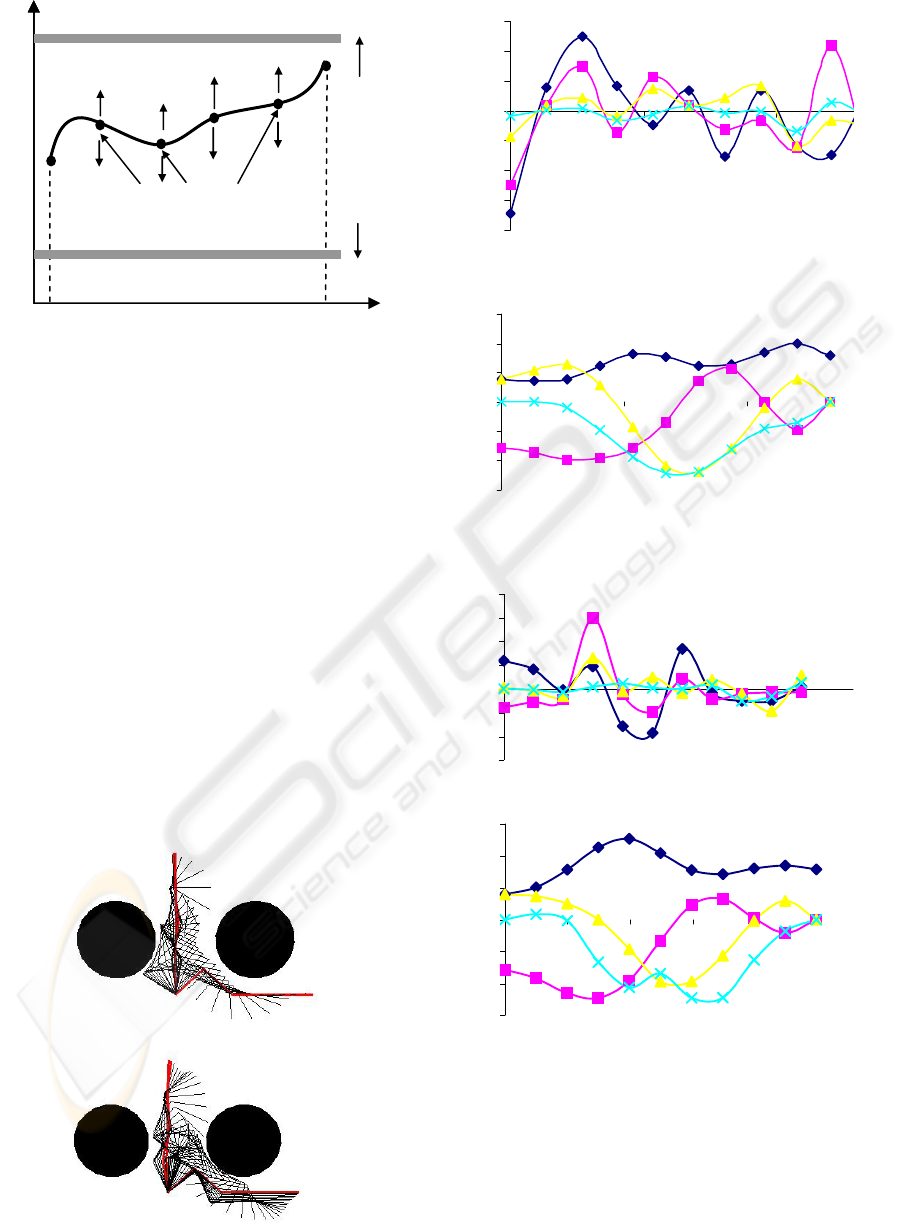
motions are depicted in Figures 5a, b, c, d, e and f.

In fact, without introducing friction effort we get :

obj

= 2.7745(s) and T

opt

= 4.9693 (s).In the

presence of friction efforts we get a different result:

obj

= 3.1119 (s) and T

opt

= 5.3745 (s). Hence, to

achieve the same task, we need more time and more

effort in the presence of friction efforts.

-40

-30

-20

-10

024

Figure 5c: Evolution of joint torques with friction

effect

-3

-2

-1

024

Figure 5d. Evolution of joint positions with friction

effect

-30

-20

-10

024

Figure 5e: Evolution of joint torques without

friction effect

-3

-2

-1

012345

Figure 5a: Aspect of motion without friction effect

Figure 5f: Evolution of joint positions without

friction effect

6 CONCLUSION

In this paper we have presented a simple trajectory

planner of point-to-point motions for robotic arms.

The problem is highly non-linear due first to the

complex robot dynamic model that must be verified

during the entire transfer, then to the non-linearity of

Figure 5b: Aspect of motion with friction effect

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

126

the cost function to be minimized and finally to

numerous constraints to be simultaneously

respected. The OFMPP is originally an optimal

control one and has been transformed into a

parametric optimization problem. The optimization

parameters are time transfer T and the position of

nodes defining the shape of joint variables. The

research of T has been separated from that of the

others parameters in order to make the computing

process efficient and to handle constraints easily by

transforming them into explicit bounds on T possible

values. In fact, the various possible constraints have

been regrouped in four families according to their

possible effects on T values and then have been

handled sequentially during each optimization step.

Nodes, defining q(x) shape, are connected by cubic

spline functions and their positions are perturbed

inside a stochastic process until the objective

function value is sufficiently reduced while all

constraints are all satisfied. This ensured smoothness

of resulted profiles. The objective function has been

written under a weighting form permitting to make

balance between reducing T and magnitude of

implied torques.

Numerical examples, where a stochastic

optimization process, implementing the proposed

approach, has been used along with cubic spline

approximations, and dealing with complex

problems, such as those involving discontinuous

friction efforts and obstacle avoidance, have been

presented to show the efficiency of this technique.

Others successful tests have been made in parallel

for complex robotic architectures, like biped robots,

will be presented in a future paper.

ACKNOWLEDGEMENTS

We thank Prof. H. E. Lehtihet for his suggestions

and helpful discussions.

REFERENCES

Angeles J., 1997, Fundamentals of robotic mechanical

systems. Theory, methods, and algorithms,” Springer

Edition.

Barraquand J., Langlois B., Latomb J. C., 1992, Numerical

Potential Field Techniques for robot path planning,

IEEE Tr. On Sys., Man, and Cyb., 22(2):224-241.

Barraquand J., Kavraki L., Latombe J. C., Li T. Y.,

Motwani R., Raghavan P., 1996, A random Sampling

Scheme for path planning, 7

Int. conf. on Rob.

Research ISRR.

Bobrow J.E., Dubowsky S., Gibson J.S., 1985, Time-

Optimal Control of robotic manipulators along

specified paths, The Int. Jour. of Rob. Res., 4 (3), pp.

3-16.

Bessonnet G., 1992, Optimisation dynamique des

mouvements point à point de robots manipulateurs,

Thèse d’état, Université de Poitiers, France.

Betts J. T., 1998, Survey of numerical methods for

trajectory optimization, J. Of Guidance, Cont. & Dyn.,

21(2), 193-207.

Chen Y., Desrochers A., 1990, A proof of the structure of

the minimum time control of robotic manipulators

using Hamiltonian formulation, IEEE Trans. On Rob.

& Aut. 6(3), pp388-393.

Chettibi T., 2000, Contribution à l'exploitation optimale

des bras manipulateurs, Magister thesis, EMP,

Algiers, Algeria.

Chettibi T., 2001a, Optimal motion planning of robotic

manipulators, Maghrebine Conference of Electric

Engineering, Constantine, Algeria.

Chettibi T., Yousnadj A., 2001b, Optimal motion planning

of robotic manipulators along specified geometric

path, International Conference on productic, Algiers.

Chettibi T., Lehtihet H. E., 2002a, A new approach for

point to point optimal motion planning problems of

robotic manipulators, 6th Biennial Conf. on

Engineering Syst. Design and Analysis (ASME ),

Turkey, APM10.

Chettibi T., 2002b, Research of optimal free motions of

manipulator robots by non-linear optimization,

Séminaire international sur le génie Mécanique, Oran,

Algeria.

Danes F., 1998, Critères et contraintes pour la synthèse

optimale des mouvements de robots manipulateurs.

Application à l’évitement d’obstacles, Thèse d’état,

Université de Poitiers.

Dombre E. & Khalil W., 1988, Modélisation et commande

des robots, First Edition, Hermes.

Fletcher R., 1987, Practical methods of optimization,

Second Edition, Wiley Interscience Publication.

Garber M., Lin. M.C., 2002, Constrained based motion

planning for virtual prototyping, SM’02, Germany.

Glass K., Colbaugh R., Lim D., Seradji H., 1995, Real

time collision avoidance for redundant manipulators,

IEEE Trans. on Rob. & Aut., 11(3), pp 448-457.

Hull D. G., 1997, Conversion of optimal control problems

into parameter optimization problems, J. Of Guidance,

Cont. & Dyn., 20(1), 57-62.

Jaques J., Soltine E., Yang H. S., 1989, Improving the

efficiency of time-optimal path following algorithms,

IEEE Trans. on Rob. & Aut., 5 (1).

Kang G. S., McKay D. N., 1986, Selection of near

minimum time geometric paths for robotic

manipulators, IEEE Trans. on Aut. & Contr., AC31(6),

pp. 501-512.

Kavraki L., Latombe J. C., 1994, Randomized

Preprocessing of Configuration Space for Fast Path

Planning, Proc. Of IEEE Int. Conf. on Rob. & Aut., pp.

2138-2139, San Diego.

Kavraki L., Svesta P., Latombe J. C., Overmars M., 1996,

Probabilistic Roadmaps for Path Planning in High

Dimensional Configuration space, IEEE trans. Robot.

Aut., 12:566-580.

A STOCHASTIC OFF LINE PLANNER OF OPTIMAL DYNAMIC MOTIONS FOR ROBOTIC MANIPULATORS

127

Khatib O., 1986, Real-time Obstacle Avoidance for

Manipulators and Mobile Robots, Int. Jour. of Rob.

Research, vol. 5(1).

Latombe J. C., 1991, Robot Motion Planning, Kluwer

Academic Publishers.

Latombe J. C., 1999, Motion planning: A journey of,

molecules, digital actors and other artifacts, Int. Jour.

Of Rob. Research, 18(11), pp 1119-1128.

LaValle S. M., 1998, Rapidly exploring random trees: A

new tool for path planning, TR98-11, Computer

Science Dept., Iowa State University.

http://janowiec.cs.iastate.edu/papers/rrt.ps.

LaValle S. M., Kuffner J. J., 1999, Randomized

kinodynamic planning, Proc. IEEE Int. Conf. On Rob.

& Aut., pp 473-479.

Lazrak M., 1996, Nouvelle approche de commande

optimale en temps final libre et construction

d’algorithmes de commande de systèmes articulés,

Thèse d’état, Université de Poitiers.

Macfarlane S., Croft E. A., 2001, Design of jerk bounded

trajectories for on-line industrial robot applications,

Proceeding of IEEE Int. Conf. on rob. & Aut. pp 979-

984.

Martin B. J., Bobrow J. E., 1997, Minimum effort motions

for open chain manipulators with task dependent end-

effector constraints, Proc. IEEE Int. Conf. Rob. & Aut.

Albuquerque, New Mexico, pp 2044-2049.

Martin B. J., Bobrow J. E., 1999, Minimum effort motions

for open chain manipulators with task dependent end-

effector constraints, Int. Jour. Rob. of Research, 18(2),

pp.213-224.

Mao Z. , Hsia T. C., 1997, Obstacle avoidance inverse

kinematics solution of redundant robots by neural

networks, Robotica, 15, 3-10.

Mayorga R. V., 1995, A framework for the path planning

of robot manipulators, IASTED third Int. Conf. on

Rob. and Manufacturing, pp 61-66.

Mitsi S., Bouzakis K. D., Mansour G., 1995, Optimization

of robot links motion in inverse kinematics solution

considering collision avoidance and joints limits,

Mach. & Mec. Theory,30 (5), pp 653-663.

Ola D., 1994, Path-Constrained robot control with limited

torques. Experimental evaluation, IEEE Trans. On

Rob. & Aut., 10(5), pp 658-668.

Overmars M. H., 1992, A random Approach to motion

planning, Technical report RUU-CS-92-32, Utrecht

University.

Piazzi A., Visioli A., 1998, Global minimum time

trajectory planning of mechanical manipulators using

internal analysis, Int. J. Cont., 71(4), 631-652.

Pfeiffer F., Rainer J., 1987, A concept for manipulator

trajectory planning, IEEE J. of Rob. & Aut., Ra-3 (3):

115-123.

Powell M. J., 1984, Algorithm for non-linear constraints

that use Lagrangian functions, Mathematical

programming, 14, 224-248.

Pontryagin L., Boltianski V., Gamkrelidze R.,

Michtchenko E., 1965,

Théorie mathématique des

processus optimaux, Edition Mir.

Rana A.S., Zalazala A. M. S., 1996, Near time optimal

collision free motion planning of robotic manipulators

using an evolutionary algorithm, Robotica, 14, pp 621-

632.

Richard M. J., Dufourn F., Tarasiewicz S., 1993,

Commande des robots manipulateurs par la

programmation dynamique, Mech. Mach. Theory,

28(3), 301-316.

Rebai S., Bouabdallah A., Chettibi T., 2002, Recherche

stochastique des mouvements libres optimaux des bras

manipulateurs, Premier congrès international de génie

mécanique, Constantine, Algérie.

Tan H. H., Potts R. B., 1988, Minimum time trajectory

planner for the discrete dynamic robot model with

dynamic constraints, IEEE Jour. Of Rob. & Aut. 4(2),

174-185.

Appendix A: Characteristics of the 4R robot.

Joint N° 1 2 3 4

α (rad)

0 0 0 0

d(m) 0 1 1 1

r(m) 0 0 0 0

a(m) 0 0 0 0

M(kg) 5 4 3 2

Izz(kg.m

) 1 0.85 0 0

τ(N.m)

25 20 15 5

(N.m) 0.7 0.2 0.5 0.2

(N.m.s) 1 0.2 0.5 0.2

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

128