AN EVOLUTIONARY APPROACH TO NONLINEAR

DISCRETE-TIME OPTIMAL CONTROL WITH

TERMINAL CONSTRAINTS

Yechiel Crispin

Department of Aerospace Engineering

Embry-Riddle University

Daytona Beach, FL 32114

Keywords: Optimal Control, Genetic Algorithms

Abstract: The nonlinear discrete-time optimal control problem with terminal constraints is treated using a new evolutionary

approach which combines a genetic search for finding the control sequence with a solution of the initial value

problem for the state variables. The main advantage of the method is that it does not require to obtain the

solution of the adjoint problem which usually leads to a two-point boundary value problem combined with an

optimality condition for finding the control sequence. The method is verified by solving the problem of discrete

velocity direction programming with the effects of gravity and thrust and a terminal constraint on the final

vertical position. The solution compared favorably with the results of gradient methods.

1 INTRODUCTION

A continuous-time optimal control problem consists

of finding the time histories of the controls and the

state variables such as to maximize (or minimize) an

integral performance index over a finite period of

time, subject to dynamical constraints in the form of

a system of ordinary differential equations (Bryson,

1975). In a discrete-time optimal control problem,

the time period is divided into a finite number of

time intervals of equal time duration . The?X

controls are kept constant over each time interval.

This results in a considerable simplification of the

continuous time problem, since the ordinary

differential equations can be reduced to difference

equations and the integral performance index can be

reduced to a finite sum over the discrete time

counter (Bryson, 1999). In some problems,

additional constraints may be prescribed on the final

states of the system. In this paper, we concentrate on

the discrete-time optimal control problem with

terminal constraints.Modern methods for solving the

optimal control problem are extensions of the

classical methods of the calculus of variations (Fox,

1950).

These methods are known as indirect methods and

are based on the maximum principle of Pontryagin,

which is astatement of the first order necessary

conditions for optimality, and results in a two-point

boundary value problem (TPBVP) for the state and

adjoint variables (Pontryagin, 1962). It has been

known, however, that the TPBVP is much more

difficult to solve than the initial value problem

(IVP). As a consequence, a second class of solutions,

known as the direct method has evolved.

For example, attempts have been made to recast the

original dynamic problem as a static optimization

problem, also known as a nonlinear programming

(NLP) problem.

This can be achieved by parameterisation of the

state variables or the controls, or both. In this way,

the original dynamical differential equations or

difference equations are reduced to algebraic

equality constraints. The problems with this

approach is that it might result in a large scale NLP

problem which has stability and convergence

problems and might require excessive computing

time. Also, the parameterisation might introduce

spurious local minima which are not present in the

original problem.

Crispin Y. (2004).

AN EVOLUTIONARY APPROACH TO NONLINEAR DISCRETE-TIME OPTIMAL CONTROL WITH TERMINAL CONSTRAINTS.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 49-57

DOI: 10.5220/0001134700490057

 SciTePress

Several gradient based methods have been

proposed for solving the discrete-time optimal

control problem (Mayne, 1966). For example,

Murray and Yakowitz (Murray, 1984) and

(Yakowitz, 1984) developed a differential dynamic

programming and Newton's method for the solution

of discrete optimal control problems, see also the

book of Jacobson and Mayne (Jacobson, 1970),

(Ohno, 1978), (Pantoja, 1988) and (Dunn, 1989).

Similar methods have been further developed by

Liao and Shoemaker (Liao, 1991). Another method,

the trust region method, was proposed by Coleman

and Liao (Coleman, 1995) for the solution of

unconstrained discrete-time optimal control

problems. Although confined to the unconstrained

problem, this method works for large scale

minimization and is capable of handling the so

called hard case problem.

Each method, whether direct or indirect,

gradient-based or direct search based, has its own

advantages and disadvantages. However, with the

advent of computing power and the progress made

in methods that are based on optimization analogies

from nature, it became possible to achieve a remedy

to some of the above mentioned disadvantages

through the use of global methods of optimization.

These include stochastic methods, such as simulated

annealing (Laarhoven, 1989), (Kirkpatrick, 1983)

and evolutionary computation methods (Fogel,

1998), (Schwefel, 1995) such as genetic algorithms

(GA) (Michalewicz, 1992a), see also (Michalewicz,

1992b) for an interesting treatment of the linear

discrete-time problem.

Genetic algorithms provide a powerful

mechanism towards a global search for the

optimum, but in many cases, the convergence is very

slow. However, as will be shown in this paper, if the

GA is supplemented by problem specific heuristics,

the convergence can be accelerated significantly. It

is well known that GAs are based on a guided

random search through the genetic operators and

evolution by artificial selection. This process is

inherently very slow, because the search space is

very large and evolution progresses step by step,

exploring many regions with solutions of low

fitness. What is proposed here, is to guide the search

further, by incorporating qualitative knowledge

about potential good solutions. In many problems,

this might involve simple heuristics, which when

combined with the genetic search, provide a

powerful tool for finding the optimum very quickly.

The purpose of the present work, then, is to

incorporate problem specific heuristic arguments,

which when combined with a modified hybrid GA,

can solve the discrete-time optimal control problem

very easily. There are significant advantages to this

approach. First, the need to solve the two-point

boundary value problem (TPBVP) is completely

avoided. Instead, only initial value problems (IVP)

are solved. Second, after finding an optimal

solution, we verify that it approximately satisfies the

first-order necessary conditions for a stationary

solution, so the mathematical soundness of the

traditional necessary conditions is retained.

Furthermore, after obtaining a solution by direct

genetic search, the static and dynamic Lagrange

multipliers (the adjoint variables) can be computed

and compared with the results from a gradient

method. All this is achieved without directly solving

the TPBVP. There is a price to be paid, however,

since, in the process, we are solving many initial

value problems (IVPs). This might present a

challenge in advanced difficult problems, where the

dynamics are described by a higher order system of

ordinary differential equations, or when the

equations are difficult to integrate over the required

time interval and special methods are required. On

the other hand, if the system is described by

discrete-time difference equations that are relatively

well behaved and easy to iterate, the need to solve

the initial value problem many times does not

represent a serious problem. For instance, the

example problem presented here , the discrete

velocity programming problem (DVDP) with the

combined effects of gravity, thrust and drag,

together with a terminal constraint (Bryson, 1999),

runs on a 1.6 GHz pentium 4 processor in less than

a minute of CPU time.

In the next section, a mathematical formulation

of the optimal control problem is given. The

evolutionary approach to the solution is then

described. In order to illustrate the method, a

specific example, the discrete velocity direction

programming (DVDP) is solved and results are

presented and compared with the results of an

indirect gradient method developed by Bryson

(Bryson, 1999).

2 OPTIMAL CONTROL OF

NONLINEAR DISCRETE TIME

DYNAMICAL SYSTEMS

In this section, we describe a formulation of the

nonlinear discrete-time optimal control problem

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

subject to terminal constraints. Consider the

nonlinear discrete-time dynamical system described

by a system of difference equations with initial

conditions

(1) B0B?Ð3  "Ñ œ Ò Ð3Ñß Ð3Ñß 3Ó

(2) BBÐ!Ñ œ

where is the vector of state variables,B − ‘

? −ß:8‘

is the vector of control variables and

3−Ò!ßR"Ó is a discrete time counter. The

function is a nonlinear function of the state0

vector, the control vector and the discrete time ,3

i.e., x x . Define a performance0 ÀÈ‘‘‘‘

8: 8

index

(3)

N Ò Ð3Ñß Ð3Ñß 3ß R Ó œ Ò ÐR ÑÓ  PÒ Ð3Ñß ÐB? B B?9



3œ!

R"

3Ñß 3Ó

where

9‘ ‘ ‘ ‘ ‘ ‘ÀÈ PÀ È

88:

, x x

Here is the Lagrangian function and is aP Ò ÐRÑÓ9 B

function of the terminal value of the state vector

BÐRÑ. Terminal constraints in the form of

additional functions of the state variables are<

prescribed as

(4) <<Ò ÐRÑÓœ! À È 5Ÿ8B ‘‘

The optimal control problem consists of finding the

control sequence such as to maximize (or?Ð3Ñ

minimize) the performance index defined by (3),

subject to the dynamical equations (1) with initial

conditions (2) and terminal constraints (4). This is

known as the Bolza problem in the calculus of

variations (Bolza, 1904).

In an alternative formulation, due to Mayer, the

state vector ( ) is augmented by anB ß 4 − "ß 8

additional variable which satisfies theB

8"

following initial value problem:

(5) B Ð3  "Ñ œ B Ð3Ñ  PÒ Ð3Ñß Ð3Ñß 3Ó

8" 8"

(6) BÐ!Ñœ!

8"

The performance index can then be written as

(7)

N ÐR Ñ œ Ò ÐR ÑÓ  B ÐR Ñ ´ Ò ÐR ÑÓ99BB

8"

+ +

where is the augmented stateBB

œÒ B Ó

8"

vector and the augmented performance function.9

In this paper, the Meyer formulation is used.

Define an augmented performance index with

adjoint constraints and adjoint dynamical<

constraints ( ) , with0B ? BÐ3Ñß Ð3Ñß 3  Ð3  "Ñ œ !

static and dynamical Lagrange multipliers and ,/-

respectively.

(8) N œ   Ð!ÑÒ  Ð!ÑÓ 

9 /< - BB

 Ð3  "ÑÖ Ò Ð3Ñß Ð3Ñß 3Ó  Ð3  "Ñ×



3œ!

R"

- 0B ? B

Define the Hamiltonian function as

(9) LÐ3Ñ œ Ð3  "Ñ Ò Ð3Ñß Ð3Ñß 3Ó-

0B ?

Rewriting the augmented performance index in

terms of the Hamiltonian, we get

(10)

N œ   ÐRÑ ÐR Ñ  Ð!Ñ 

XX X

9 /< - -BB

 ÒLÐ3Ñ  Ð3Ñ Ð3ÑÓ



3œ!

R"

- B

A first order necessary condition for to reach aN

stationary solution is given by the discrete version of

the Euler-Lagrange equations

(11)

Ð3Ñ œ L Ð3Ñ œ Ð3  "Ñ Ò Ð3Ñß Ð3Ñß 3Ó

0B ?

with final conditions

(12) -/<

ÐR Ñ œ 9

and the control sequence satisfies the?Ð3Ñ

optimality condition:

(13) L Ð3Ñ œ Ð3  "Ñ Ò Ð3Ñß Ð3Ñß 3Ó œ !

0B ?

Define an augmented function asF

(14) F9œ/<

AN EVOLUTIONARY APPROACH TO NONLINEAR DISCRETE - TIME OPTIMAL CONTROL WITH TERMINAL

CONSTRAINTS

Then, the adjoint equations for the dynamical

multipliers aregiven by

(15)

Ð3Ñ œ L Ð3Ñ œ Ð3  "Ñ Ò Ð3Ñß Ð3Ñß 3Ó

0B ?

and the final conditions can be written in terms of

the augmented function F

(16) -/<

ÐR Ñ œ œ F9

BB B

If the indirect approach to optimal control is used,

the state equations (1) with initial conditions (2)

need to be solved together with the adjoint equations

(15) and the final conditions (16), where the control

sequence is to be determined from the?Ð3Ñ

optimality condition (13). This represents a coupled

system of nonlinear difference equations with part of

the boundary conditions specified at the initial time

3œ! and the rest of the boundary conditions

specified at the final time . This is a nonlinear3œR

two-point boundary value problem (TPBVP) in

difference equations. Except for special simplified

cases, it is usually very difficult to obtain solutions

for such nonlinear TPBVPs. Therefore, many

numerical methods have been developed to tackle

this problem, see the introduction for several

references.

In the proposed approach, the optimality

condition (13) and the adjoint equations (15)

together with their final conditions (16) are not used

in order to obtain the optimum solution. Instead, the

optimal values of the control sequence are?Ð3Ñ

found by genetic search starting with an initial

population of solutions with values of randomly?Ð3Ñ

distributed within a given domain. During the

search, approximate, less than optimal values of the

solutions are available for each generation.?Ð3Ñ

With these approximate values known, the state

equations (1) together with their initial conditions

(2) are very easy to solve, by a straightforward

iteration of the difference equations from to3œ!

3œR". At the end of this iterative process, the

final values are obtained, and the fitnessBÐRÑ

function can be determined. The search than seeks

to maximize the fitness function such as to fulfillJ

the goal of the evolution, which is to maximize

NÐRÑ, as given by the following Eq.(17), subject to

the terminal constraints , as defined<Ò ÐRÑÓœ!B

by Eq.(18).

(17) maximize N ÐR Ñ œ Ò ÐR ÑÓ9 B

subject to the dynamical equality constraints, Eqs.

(1-2) and to the terminal constraints (4), which are

repeated here for convenience as Eq.(18)

(18) <<Ò ÐRÑÓœ! À È 5Ÿ8B ‘‘

Since we are using a direct search method, condition

(18) can also be stated as a search for a maximum,

namely we can set a goal which is equivalent to (18)

in the form

(19) maximize N ÐRÑ œ  Ò ÐRÑÓ Ò ÐRÑÓ

The fitness function can now be defined byJ

(20) J ÐR Ñ œ N ÐR Ñ  Ð"  ÑN ÐR Ñ œαα

œ Ò ÐR ÑÓ  Ð"  Ñ Ò ÐRÑÓ Ò ÐR ÑÓα9 αBBB ,<<

with and determined from theα − Ò!ß "Ó ÐRÑB

following dynamical equality constraints:

(21) ,B0B?Ð3  "Ñ œ Ò Ð3Ñß Ð3Ñß 3Ó

3−Ò!ßR"Ó

(22) BBÐ!Ñ œ

3 DISCRETE VELOCITY

DIRECTION PROGRAMMING

FOR MAXIMUM RANGE WITH

GRAVITY AND THRUST

In this section, the above formulation is applied to a

specific example, namely, the problem of finding the

trajectory of a point mass subjected to gravity and

thrust and a terminal constraint such as to achieve

maximum horizontal distance, with the direction of

the velocity used to control the motion. This

problem has its roots in the calculus of variations

and is related to the classical Brachistochrone

problem, in which the shape of a wire is sought

along which a bead slides without friction, under the

action of gravity alone, from an initial point ÐB ß C Ñ

to a final point in minimum time . TheÐB ß C Ñ >

00 0

dual problem to the Brachistochrone problem

consists of finding the shape of the wire such as the

bead will reach a maximum horizontal distance B

in a prescribed time . Here, we treat the dual>

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

problem with the added effects of thrust and a

terminal constraint where the final vertical position

is prescribed. The more difficult problem, where

the body is moving in a viscous fluid and the effect

of drag is taken into account was also solved, but

due to lack of space, the results will be presented

elsewhere. The reader interested in these problems

can find an extensive discussion in Bryson's book

(Bryson,1999).

Let point O be the origin of a cartesian system of

coordinates in which is pointing to the right and BC

is pointing down. A constant thrust force isJ

acting along the path on a particle of mass which7

moves in a medium without friction. A constant

gravity field with acceleration is acting downward1

in the positive direction. The thrust acts in theC

direction of the velocity vector and its magnitudeZ

is , i.e. times the weight . TheJœ+71 + 71

velocity vector acts at an angle with respect toZ #

the positive direction of . The angle , whichB #

serves as the control variable, is positive when Z

points downward from the horizontal. The problem

is to find the control sequence to maximize the#Ð>Ñ

horizontal range in a given time , provided theB>

particle ends at the vertical location . In otherC

words, the velocity direction is to be#Ð>Ñ

programmed such as to achieve maximum range

and fulfill the terminal constraint . The equationsC

of motion are

(23) .Z Î.> œ 1Ð+  =38 Ð>ÑÑ#

(24) .BÎ.> œ Z -9= Ð>Ñ#

(25) .CÎ.> œ Z =38 Ð>Ñ#

with initial conditions

(26) , Z Ð!Ñ œ ! BÐ!Ñ œ !ß CÐ!Ñ œ !

and final constraint

(27) .CÐ> Ñ œ C

We would like to formulate a discrete time version

of this problem. The trajectory is divided into a

finite number of straight line segments of fixedR

time duration , along which the?Xœ>ÎR

direction is constant. We can increase such as# R

to approach the solution of the continuous trajectory.

The velocity is increasing under the influence ofZ

a constant thrust and gravity . The problem+1 1=38#

is to determine the control sequence at points #Ð3Ñ 3

along the trajectory, where , such as to3−Ò!ßR"Ó

maximize at time , arriving at the same time at aB>

prescribed elevation . The time at the end of eachC

segment is given by , so can be viewed>Ð3Ñ œ 3 X 3?

as a time step counter at point . Integrating the3

first equation of motion, Eq.(17) from a time

>Ð3Ñ œ 3 X >Ð3  "Ñ œ Ð3  "Ñ X?? to , we get

(28) ZÐ3"ÑœZÐ3Ñ1Ò+=38 Ð3ÑÓ X#?

Integrating the velocity over a time interval ,ZX?

we obtain the length of the segment ?.Ð3Ñ

connecting the points and .33"

(29)

?? #?.Ð3Ñ œ Z Ð3Ñ X  1Ò+  =38 Ð3ÑÓÐ X Ñ

Once is determined, it is easy to obtain the?.Ð3Ñ

coordinates and asBC

(30) BÐ3  "Ñ œ BÐ3Ñ  .Ð3Ñ-9= Ð3Ñ œ?#

œ BÐ3Ñ  Z Ð3Ñ-9= Ð3Ñ X #?

 1Ò+  =38 Ð3ÑÓ-9= Ð3ÑÐ X Ñ

##?

(31) CÐ3  "Ñ œ CÐ3Ñ  .Ð3Ñ=38 Ð3Ñ œ?#

œ CÐ3Ñ  Z Ð3Ñ=38 Ð3Ñ X #?

 1Ò+  =38 Ð3ÑÓ=38 Ð3ÑÐ X Ñ

##?

We now develop the equations in nondimensional

form. Introduce the following nondimensional

variables denoted by primes:

(32) , , ,>œ>> Zœ1>Z Bœ1>B

ww#w

Cœ1> C

Since , the nondimensional time is>Ð3Ñ œ 3> ÎR

>Ð3Ñœ3ÎR

. The time interval was defined as

??Xœ>ÎRœ>Ð XÑ

, so the nondimensional

time interval becomes . SubstitutingÐ X Ñ œ "ÎR?

the nondimensional variables in the discrete

equations of motion and omitting the prime

notation, we obtain the nondimensional state

equations:

AN EVOLUTIONARY APPROACH TO NONLINEAR DISCRETE - TIME OPTIMAL CONTROL WITH TERMINAL

CONSTRAINTS

(33) Z Ð3  "Ñ œ Z Ð3Ñ  Ò+  =38 Ð3ÑÓÎR#

(34) BÐ3  "Ñ œ BÐ3Ñ  Z Ð3Ñ-9= Ð3ÑÎR #

 Ò+  =38 Ð3ÑÓ-9= Ð3ÑÎR

(35) CÐ3  "Ñ œ CÐ3Ñ  Z Ð3Ñ=38 Ð3ÑÎR #

 Ò+  =38 Ð3ÑÓ=38 Ð3ÑÎR

with initial conditions

(36) , Z Ð!Ñ œ ! BÐ!Ñ œ !ß CÐ!Ñ œ !

and terminal constraint

(37) CÐRÑ œ C

The optimal control problem now consists of finding

the sequence such as to maximize the range#Ð3Ñ

BÐRÑ, subject to the dynamical constraints (33-35),

the initial conditions (36) and the terminal

constraint (37), where is in units of and theC1>

final time is given.>

4 NECESSARY CONDITIONS FOR

ANOPTIMUM

In this section we present the traditional indirect

approach to the solution of the optimal control

problem, which is based on the first order necessary

conditions for an optimum. First, we derive the

Hamiltonian function for the above DVDP problem.

We then derive the adjoint dynamical equations for

the adjoint variables (the Lagrange multipliers) and

the optimality condition that needs to be satisfied by

the control sequence . Since we have used the#Ð3Ñ

symbol for the horizontal coordinate, we denoteB

the state variables by . So the state vector for this0

problem is

0 œÒZ B CÓ

The performance index and the terminal constraint

are given by

(38) NÐR Ñ œ Ò ÐR ÑÓ œ BÐR Ñ9 0

(39) <<ÐR Ñ œ Ò ÐR ÑÓ œ CÐR Ñ  C œ !0

The Hamiltonian is defined byLÐ3Ñ

(40)

LÐ3Ñ œ Ð3  "ÑÖZ Ð3Ñ  Ò+  =38 Ð3ÑÓÎR ×-#



 Ð3  "ÑÖBÐ3Ñ  Z Ð3Ñ-9= Ð3ÑÎR -#

 Ò+  =38 Ð3ÑÓ-9= Ð3ÑÎR × 

 Ð3  "ÑÖCÐ3Ñ  Z Ð3Ñ=38 Ð3ÑÎR -#

 Ò+  =38 Ð3ÑÓ=38 Ð3ÑÎR ×

The augmented performance index is given by

(41) F9 /œ  œ BÐRÑ  ÒCÐR Ñ  C Ó/<

The discrete Euler-Lagrange equations are derived

from the Hamiltonian function:

(42) --

Ð3Ñ œ L Ð3Ñ œ Ð3  "Ñ 

 -9= Ð3Ñ Ð3  "ÑÎR  =38 Ð3Ñ Ð3  "ÑÎR#- #-

(43) --

Ð3Ñ œ L Ð3Ñ œ Ð3  "Ñ

(44) --

Ð3Ñ œ L Ð3Ñ œ Ð3  "Ñ

It follows from the last two equations that the

multipliers and are constant. The final--

Ð3Ñ Ð3Ñ

conditions for the multipliers are obtained from the

augmented function .F

(45)

-F9/<

ZZ Z

ÐR Ñ œ ÐR Ñ œ ÐR Ñ  ÐR Ñ œ !

-F9/<

BB B

ÐR Ñ œ ÐR Ñ œ ÐRÑ  ÐR Ñ œ "

-F9/</

CC C

ÐR Ñ œ ÐR Ñ œ ÐR Ñ  ÐRÑ œ

Since and are constant, they can be set equal--

to their final values:

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

(46) ,--

Ð3Ñ œ ÐR Ñ œ "

-- /

Ð3Ñ œ ÐR Ñ œ

With the values given in (46), the equation for -

Ð3Ñ

becomes

(47)

-- # /#

Ð3Ñ œ Ð3  "Ñ  -9= Ð3ÑÎR  =38 Ð3ÑÎR

with final condition

(48) -

ÐR Ñ œ !

The required control sequence is determined#Ð3Ñ

from the optimality condition

(49)

L Ð3Ñ œ Ð3  "Ñ-9= Ð3ÑÎR  Z Ð3Ñ=38 Ð3ÑÎ

-# #

R  +=38 Ð3ÑÎÐ#R Ñ  -9=Ð# Ð3ÑÑÎÐ#R Ñ ##

 Z Ð3Ñ-9= Ð3ÑÎR  +-9= Ð3ÑÎÐ#R Ñ/# /#

 =38Ð# Ð3ÑÑÎÐ#R Ñ œ !/#

Ð3  "Ñ is determined by the adjoint equation (47)

and the Lagrange multiplier is determined from/

the terminal equality constraint .CÐRÑ œ C

5 AN EVOLUTIONARY

APPROACH TO OPTIMAL

CONTROL

We now describe the direct approach using genetic

search. As was mentioned in Sec. , there is no need

to solve the two-point boundary value problem

described by the state equations (33-35) and the

adjoint equation (47), together with the initial

conditions (36), the final condition (48), the

terminal constraint (37) together with the optimality

condition (49) for the optimal control . Instead,#Ð3Ñ

the direct evolutionary method allows us to evolve a

population of solutions such as to maximize the

objective function or fitness function . TheJÐRÑ

initial population is built by generating a random

population of solutions , ,#Ð3Ñ 3 − Ò!ß R  "Ó

uniformly distributed within a domain ,##−Ò

min

##1

max max

ÓœÎ#. Typical values are and either

#1#

min min

œ Î# œ! or depending on the

problem. The genetic algorithm evolves this initial

population using the operations of selection,

mutation and crossover over many generations such

as to maximize the fitness function:

(50) J ÐR Ñ œ N ÐR Ñ  Ð"  ÑN ÐR Ñ œαα

œ Ò ÐR ÑÓ  Ð"  Ñ Ò ÐR ÑÓ Ò ÐR ÑÓα9 α0<0<0 ,

with and and given by:α − Ò!ß "Ó N ÐRÑ N ÐRÑ

(51) NÐR Ñ œ Ò ÐR ÑÓ œ BÐR Ñ9 0

(52) N ÐRÑ œ Ò ÐRÑÓ œ ÐCÐRÑC Ñ

< 0

For each member in the population of solutions, the

fitness function depends on the final values BÐRÑ

and , which are determined by solving theCÐRÑ

initial value problem defined by the state equations

(33-35) together with the initial conditions (36).

This process is repeated over many generations.

Here, we run the genetic algorithm for a

predetermined number of generations and then we

check if the terminal constraint (52) is fulfilled. If

the constraint is not fulfilled, we can either increase

the number of generations or readjust the weight

α − Ò!ß "Ó. After obtaining an optimal solution , we

can check the first order necessary conditions by

first solving the adjoint equation (47) with its final

condition (48). Once the control sequence is known,

the solution of (47-48) is obtained by direct iteration

backwards in time. We then check to what extent

the optimality condition (49) is fulfilled by

determining for andL Ð3Ñ œ /Ð3Ñ 3 − Ò!ß R  "Ó

plotting the result as an error measuring the/Ð3Ñ

deviation from zero.

The results for the DVDP problem with gravity and

thrust, with and the terminal constraint+ œ !Þ&

Cœ!Þ"

are shown in Figs.(1-3). A value of

α œ!Þ!"was used. Fig.1 shows the evolution of the

solution over 50 generations. The best fitness and

the average fitness of the population are given. In all

calculations the size of the population was 50

members.

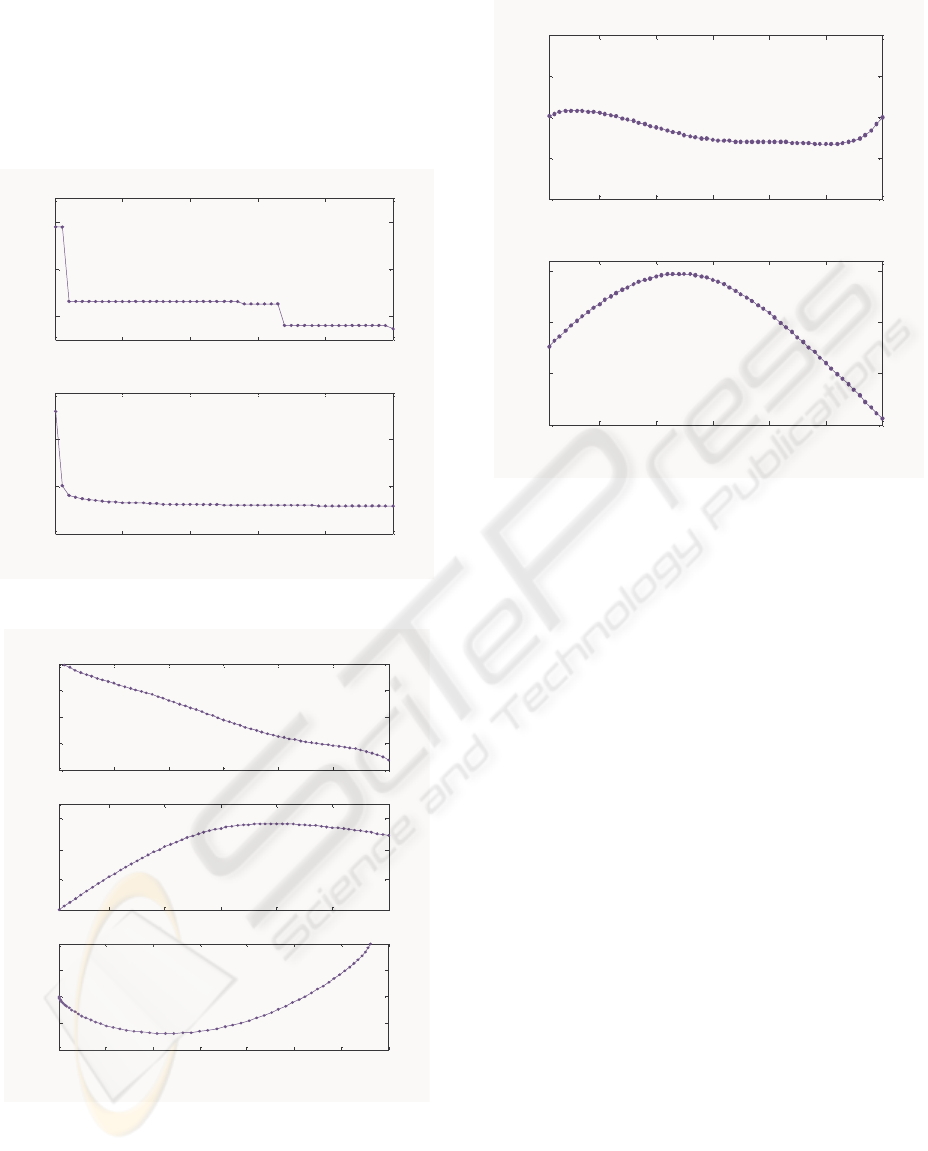
The control sequence , the velocity and#Ð3Ñ Z Ð3Ñ

the optimal trajectory are given in Fig.2 where the

sign of is reversed for plotting. The trajectoryC

obtained here was compared to that obtained by

Bryson (Bryson, 1999) using a gradient method and

the results are similar. In Fig.3 we plot the

expression for as given by.LÎ. Ð3Ñ#

the right-hand side of Eq.(49). Ideally, this should

be equal to zero at every point . However, since we3

AN EVOLUTIONARY APPROACH TO NONLINEAR DISCRETE - TIME OPTIMAL CONTROL WITH TERMINAL

CONSTRAINTS

are not using (49) to determine the control

sequence, we obtain a small deviation from zero in

our calculation. Finally, after determining the

optimal solution, i.e. after the control and the

trajectory are known, the adjoint variable can-

Ð3Ñ

be estimated by using Eqs.(47-48). The result is

shown in Fig.3.

0 10 20 30 40 50

-3.22

-3.2

-3.18

x 10

-3

Best f

0 10 20 30 40 50

-3.5

-3

-2.5

-2

x 10

-3

Generations

Average f

Figure 1: Convergence of the DVDP solution with gravity

and thrust, and terminal constraint + œ !Þ& C œ  !Þ"

0 10 20 30 40 50 60

-1

-0.5

0.5

gama / (pi/2)

10 20 30 40 50 60

0.2

0.4

0.6

V / g t

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

-0.1

-0.05

0.05

0.1

x / (g t

)

y / (g t

)

Figure 2: The control sequence , the velocity and#Ð3Ñ Z Ð3Ñ

the optimal trajectory for the DVDP problem with gravity

1 + œ !Þ& C œ  !Þ", thrust and terminal constraint .

The sign of is reversed for plottingC

10 20 30 40 50 60

-0.02

-0.01

0.01

0.02

10 20 30 40 50 60

0.5

1.5

LambdaV

Figure 3: The error measuring the deviation of the/Ð3Ñ

optimality condition from zero, and theLÐ3Ñœ/Ð3Ñ

adjoint variable as a function of the discrete-time-

Ð3Ñ

counter . DVDP with gravity and thrust, . Here3+œ!Þ&

Rœ'!time steps

6 CONCLUSIONS

A new method for solving the discrete-time optimal

control problem with terminal constraints was

developed. The method seeks the best control

sequence diretly by genetic search and does not

make use of the first-order necessary conditions to

find the optimum. As a consequence, the need to

develop a Hamiltonian formulation and the need to

solve a difficult two-point boundary value problem

for finding the adjoint variables is completely

avoided. This has a significant advantage in more

advanced and higher order problems where it is

difficult to solve the TPBVP with large systems of

differential equations, but when it is still easy to

solve the initial value problem (IVP) for the state

variables. The method was demonstrated by solving

a discrete-time optimal control problem, namely, the

DVDP or the discrete velocity direction

programming problem that was pioneered by Bryson

using both analytical and gradient methods. This

problem includes the effects of gravity and thrust

and was solved easily using the proposed approach.

The results compared favorably with those of

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

Bryson, who used analytical and gradient

techniques.

REFERENCES

Bryson, A. E. and Ho, Y. C., Applied Optimal Control,

Hemisphere, Washington, D.C., 1975.

Bryson, A.E., Dynamic Optimization, Addison-Wesley

Longman, Menlo Park, CA, 1999.

Coleman, T.F. and Liao, A., An efficient trust region

method for unconstrained discrete-time optimal

control problems, Computational Optimization and

Applications, 4, pp. 47-66, 1995.

Dunn, J., and Bertsekas, D.P., Efficient dynamic

programming implementations of Newton's method for

unconstrained optimal control problems, J. of

Optimization Theory and Applications, 63 (1989), pp.

23-38.

Fogel, D.B., Evolutionary Computation, The Fossil

Record, IEEE Press, New York, 1998.

Fox, C., An Introduction to the Calculus of Variations,

Oxford University Press, London, 1950.

Jacobson, D. and Mayne, D. , Differential Dynamic

Programming, Elsevier Science Publishers, 1970.

Kirkpatrick, and Gelatt, C.D. and Vecchi, Optimization

by Simulated Annealing, Science, 220, 671-680,

1983.

Laarhoven, P.J.M. and Aarts, E.H.L., Simulated

Annealing: Theory and Applications, Kluwer

Academic, 1989.

Liao, L.Z. and Shoemaker, C.A., Convergence in

unconstrained discrete-time differential dynamic

programming, IEEE Trans. Automat. Contr., 36, pp.

692-706, 1991.

Mayne, D., A second-order gradient method for

determining optimal trajectories of non-linear discrete

time systems, Intnl. J. Control, 3 (1966), pp. 85-95.

Michalewicz, Z., Genetic Algorithms + Data Structures =

Evolution Programs, Springer-Verlag, Berlin, 1992a.

Michalewicz, Z., Janikow, C.Z. and Krawczyk, J.B., A

Modified Genetic Algorithm for Optimal Control

Problems, Computers Math. Applications, 23(12), pp.

83-94, 1992b.

Murray, D.M. and Yakowitz, S.J., Differential dynamic

programming and Newton's method for discrete

optimal control problems, J. of Optimization Theory

and Applications, 43, pp. 395-414, 1984.

Ohno, K., A new approach of differential dynamic

programming for discrete time systems, IEEE Trans.

Automat. Contr., 23 (1978), pp. 37-47.

Pantoja, J.F.A. de O. , Differential Dynamic Programming

and Newton's Method, International Journal of

Control, 53: 1539-1553, 1988.

Pontryagin, L. S. Boltyanskii, V. G., Gamkrelidze, R. V.

and Mishchenko, E. F., The Mathematical Theory of

Optimal Processes, Moscow, 1961, translated by

Trirogoff, K. N. Neustadt, L. W. (Ed.), Interscience,

New York, 1962.

Schwefel H.P., Evolution and Optimum Seeking, Wiley,

New York, 1995.

Yakowitz, S.J., and Rutherford, B., Computational

aspects of discrete-time optimal control, Appl. Math.

Comput., 15 (1984), pp. 29-45.

AN EVOLUTIONARY APPROACH TO NONLINEAR DISCRETE - TIME OPTIMAL CONTROL WITH TERMINAL

CONSTRAINTS