A DISTURBANCE COMPENSATION CONTROL FOR AN

ACTIVE MAGNETIC BEARING SYSTEM BY A MULTIPLE

FXLMS ALGORITHM

Min Sig Kang

Department of mechanical engineering, Kyungwon University, Sungnam, Kyunggido, KOREA

Joon Lyou

Dept. of Electronics Eng., Chungnam National Univ., Daejeon 305-764, KOREA

Keywords: Active magnetic bearing, Multiple filtered-x least mean square algorithm, Acceleration feedforward

compensation

Abstract: In this paper, a design technique is proposed for a disturbance feedforward compensation control to

attenuate disturbance responses in an active magnetic bearing system, which is subject to base motion. To

eliminate the sensitivity of model accuracy to disturbance responses, the proposed design technique is an

experimental feedforward compensator, developed from an adaptive estimation, by means of the Multiple

Filtered-x least mean square (MFXLMS) algorithm. The compensation control is applied to a 2-DOF active

magnetic bearing system subject to base motion. The feasibility of the proposed technique is illustrated, and

the results of an experimental demonstration are shown.

1 INTRODUCTION

Active magnetic bearing (AMB) systems are

increasingly used in industrial applications. Unlike

conventional bearings, AMB systems utilize

magnetic fields to levitate and support a shaft in an

air-gap within the bearing stator. When compared to

conventional mechanical bearings, AMB offers the

following unique advantages: non-contact,

elimination of lubrication, low power loss, and

controllability of bearing dynamic characteristics.

Recently, interest has increased regarding the

application of AMB systems to the sight

stabilization systems mounted on moving vehicles.

When a vehicle is undergoing angular motion, the

mirror axis of sight rotates relative to the vehicle, to

stabilize the line of sight. In such systems, the

friction of mechanical bearings that support the

mirror axis may cause tracking errors and, hence,

may deteriorate the quality of an image obtained

through electro-optical equipment. To eliminate the

undesirable effects of friction, an AMB system is

used instead of mechanical bearings.

The main problem of a sight system levitated

and stabilized by an AMB is the image scattering

caused by base motion. One solution for reducing

the effects of base motion is to expand the

bandwidth of the control system by using feedback

controls (Cole, 1998) such as PID control, state

feedback control,

∞

control, and so on. A

controller with a wider bandwidth, however,

requires a higher sampling frequency, which often

induces a mechanical resonance.

An alternative approach for disturbance

attenuation is a feedforward compensation of the

base acceleration. The effectiveness of this approach

has been demonstrated in the field of hard disk

drives, which are also subject to base motion

(Jinzenji, 2001). Suzuki (1998) developed

feedforward compensation based on a dynamic

model of the AMB system and showed that

increases in the vibration rejection can be achieved.

In practice, however, a dynamic model is not

reliably accurate, because of many problems

associated with it, such as the non-linearity of AMB,

approximation errors of the discrete equivalent to a

continuous transfer function, and sensor dynamics.

Motivated to overcome these problems, in this

work an alternative technique is proposed: a non-

model based acceleration feedforward compensation

control developed from an adaptive estimation, by

means of the multiple filtered-x least mean square

264

Kang M. and Lyou J. (2004).

A DISTURBANCE COMPENSATION CONTROL FOR AN ACTIVE MAGNETIC BEARING SYSTEM BY A MULTIPLE FXLMS ALGORITHM.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 264-269

DOI: 10.5220/0001135102640269

 SciTePress

(MFXLMS) algorithm (Kuo, 1996; White, 1997).

The performance and the effectiveness of the

proposed technique are demonstrated on a 2-DOF

AMB system subject to base motion.

2 SYSTEM MODEL

The test rig used in this paper is an AMB system of

2-DOF shown in Fig. 1. Figure 2 is the photograph

of the test rig. The test rig consists of two sets of

AMB(left AMB: AMB-1, right AMB:AMB-2) and a

circular shaft. Each end of the shaft is tied up by

string wire such that the shaft moves only in the

vertical plane. Each electromagnet is attached rigidly

to each shaker(B&K-4808), which generates base

motion resembling the vehicle motion. Two non-

contacting proximity displacement sensors(AEC-

5505) measure each air gap between the probe tip

and the shaft surface, and the vertical acceleration of

each electromagnet is measured by each

accelerometer(Crossbow, CX04LP1Z).

Displacement

Sensor

Accelerometer

Shaker 2

Shaker 1

- I

−

Figure 1: Schematic diagram of test rig

From the free-body diagram of the system in Fig.

3, the equation of motion is given by

1212 1212

yyzz yyzz

+++ −+−+

⎧⎫⎧

−

⎨⎬⎨

+++ −+−

⎩⎭⎩

⎧⎫

⎨⎬ ⎨ ⎬

⎩⎭

   

⎫

⎬

⎭

(1)

where m and J are the mass and the mass moment of

inertia about the mass center of the shaft.

, and

y z



mean the air gap, the vertical acceleration and the

actuating force, respectively. The subscripts 1 and 2

denote the positions of the AMB-1 and the AMB-2,

respectively. This definition is consistent hereafter.

Figure 2: Photograph of test rig

Figure 3: Free-body diagram of the levitated axis

The magnetic attractive force is approximately

proportional to the square of the coil current and

inversely proportional to the square of gap. However

the nonlinearity of the magnetic attractive force

against the coil current is decreased with the bias

current added to the coil current. Consequently the

linearized model is given by

cd ic

Ky Ki

(2)

where

is the displacement stiffness and is

the current stiffness.

Since the time constant of the power amplifier-

magnet coil can be designed to be small enough by

current feedback control, the control current

i can

be assumed to be proportional to the applied voltage,

, to the amplifier, i.e.

iKu

(3)

where

is the gain of the amplifier.

Substituting eqs. (2) and (3) into eq. (1) gives the

linearized AMB system model as follows:

1211

()()

K J ma K J ma

KJmaKJma

K J ma K J ma u z g

uzg

KJma KJma

⎡⎤

+−

⎧⎫ ⎧⎫

⎢⎥

−

⎨⎬ ⎨⎬

⎢⎥

−+

⎩⎭ ⎩⎭

⎣⎦

⎡⎤

+−

⎧⎫⎧ ⎫

⎢⎥

=−

⎨⎬⎨ ⎬

⎢⎥

−+

⎩⎭⎩ ⎭

⎣⎦



(4)

A DISTURBANCE COMPENSATION CONTROL FOR AN ACTIVE MAGNETIC BEARING SYSTEM BY A

MULTIPLE FXLMS ALGORITHM

265

It is clear from eq.(4) that the system is open-

loop unstable, and the base acceleration and the

gravitational force disturb the system.

3 CONTROLLER DESIGN

The system model in eq. (4) can be represented by

the state space equation as

fdBuAqq −−+=



(5)

{}

1212

qyyyy=



{

}

uuu

dzz=

⎡⎤

⎣⎦

 

gg=

⎡

⎤

⎣

⎦

(6)

Since this system has no integrator, the state

feedback control with integral is applied to eliminate

the steady state error due to the gravity force.

kKqu −−= (7)

where K and

k are the state feedback gain vectors,

and

is the integration of y

and y

, i.e.,

{}



The feedback gains in eq.(7) can be design from

various kinds of schemes. The closed-loop system

stabilized by eq. (7) can be represented in discrete

time domain as

111

11111122

11112 2

111

22211222

21 1 22 2

()() ()() ()()

()() ()()

( ) () ( ) () ( ) ()

()() ()()

qykBqukBquk

Cq dkCq dk

qykBqukBquk

CqdkCqdk

−−−

−−

−−−

−−

(8)

where variables with the index k mean the sampled

variables.

()

−

(

)

−

and are the

system polynomials.

is the one step delay

operator.

()

−

1−

A general compensator for the system in eq.(8) is

defined by

1111 122

2211222

() ( ) () ( ) ()

() ()() ()()

uk W q dk W q d k

uk W q dk W q dk

−−

(9)

Applying the compensator, eq.(9), to the system,

eq.(8), yields the compensated system of the form

1 1 11 11 12 21 11 1

11 12 12 22 12 2

() ()

()

yk BW BW C dk

BW BW C d k

=++

⎡⎤

⎣⎦

+++

⎡⎤

⎣⎦

2 2 21 11 22 21 21 1

21 12 22 22 22 2

() ()

()

yk BW BW C dk

BW BW C d k

=++

⎡⎤

⎣⎦

+++

⎡⎤

⎣⎦

(10)

Obviously, the perfect disturbance cancelling

compensators

, , , are derived from

⎧

⎫

⎪

⎨

⎬

⎪

⎩⎭

22 11 12 21

21 11 11 21

22 12 12 22

11 22 12 21

21 12 11 22

BC BC

BB BB

BC BC

−

⎧

⎫

⎪

−+

⎪

⎨

⎬

−

⎪

−+

⎩⎭

(11)

Since the compensators given in eq.(11) are

designed from the system model, the compensation

performance should be sensitive to the accuracy of

the model. In practice, however, this kind of perfect

cancelling based on the model is not expected

because of the problems such as inaccuracy of

dynamic model, approximation error of a discrete

equivalent to a continuous transfer function, and

sensor dynamics. Motivated by these problems, an

explicit optimal feedforward compensator design

technique is proposed in this paper. By this

technique, the feedforward compensator design can

be separated into two parts.

1) Disturbance cancelling control for single

harmonic base motion

It is clear from eq. (11) that the response to a

harmonic base motion of the frequency

can be

exactly nullified by choosing the polynomial

()

−

as the first order polynomial satisfying the

relation

121 *

,, 1,2

jw T jw T

ij ij ij ij

qe qe

Wwwq W ij

−

⎡⎤

=+ = =

⎣⎦

(12)

where is the sampling interval.

Nullifying disturbance response by using

feedforward compensator means physically

matching the impedance from the base motion to the

air-gap with the impedances from the base motions

to the air-gaps through the AMB dynamics and of

the feedforward compensators, so that the

disturbance can be perfectly cancelled. However

compensator design from the model is not suitable

for practical applications. To get rid of the problems

associated with the inaccurate model, adaptation of

the feedforward compensator is proposed. This

technique is an explicit design through experiments

by using a multiple-FXLMS algorithm. The FXLMS

algorithm has been extensively used in the field of

active noise control(Kuo, 1996; Widrow and Stearns,

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

266

1985)). Figure 4 shows an example of the multiple-

FXLMS algorithm to estimate the compensator

polynomial

. The parameters of the

compensators are estimated from the following

update equation.

Figure 4: MFLMS algorithm for estimating

)(

−

()

(1) ()

(1)

()

(1) ()

()

(1)

()

ˆˆ ˆ

() () ( 1), () (),,, 1

ij ij

mm m m

ij ij ij ij m

wk wk

Dkdk dk dk dkijm

⎧⎫

⎪⎪

⎨⎬

⎧⎫⎧⎫

⎪⎪

−

⎪⎪⎪⎪

⎩⎭

⎨⎬⎨⎬

⎪⎪⎪⎪

⎩⎭⎩⎭

⎧⎫

⎪⎪

⎨⎬

⎪⎪

−

⎩⎭

=+− = =,2

(13)

where

and

are the update gains,

(

)

−

and

(

)

−

are the estimated system polynomials. All

the compensator polynomials are estimated

simultaneously from eq. (13).

By applying the MFXLMS algorithm meanwhile

the exciters generate a stationary single harmonic

base motion, the control parameters

and in

eq. (13) are estimated.

Since the base motion is single harmonic of

frequency

, the Fourier transforms

(

)

and

(

)

of and , respectively, would yield the

relation

12r

() (

)

jDj

αω

, where

is a complex

number which represents the magnitude and phase

relations between

and

. The estimated

polynomials are not unique but satisfy two

independent relations in the following

11 12 11 12 1

21 22

ˆˆ

WW WW

αα

⎧⎫⎧⎫

⎧⎫

⎪⎪⎪⎪ ⎪⎪⎪⎪

+= +=

⎨⎬⎨⎬ ⎨⎬⎨⎬⎨

⎩⎭

⎪⎪⎪⎪

⎩⎭⎩⎭

⎬

(14)

Thus it is necessary to have at least two sets of

polynomials estimated from the experiments where

and

have the same frequency but have

different relations. For example, if a set of

polynomials is estimated from the experiment where

d d

then one can determine

and

from

eq.(14) as

11 12 1

21 22

ˆˆ

⎧⎫⎧⎫

⎧

⎫

⎪

⎪⎪ ⎪⎪ ⎪

⎨

⎬⎨ ⎬⎨ ⎬

⎪

⎪⎪ ⎪⎪ ⎪

⎩⎭

⎩⎭⎩⎭

(15)

MFXLMS

)(

−−

+= qwwqW

() sin

dk M k T

Similarly, from another set of estimated

polynomials obtained from another experiment

where

αα

≠

and

are obtained as

11 12 1

21 22

ˆˆ

⎧⎫⎧⎫

⎧

⎫

⎪

⎪⎪ ⎪⎪ ⎪

⎨

⎬⎨ ⎬⎨ ⎬

⎪

⎪⎪ ⎪⎪ ⎪

⎩⎭

⎩⎭⎩⎭

(16)

From eqns. (14)-(16), the compensator

polynomials that perfectly cancel any stationary

harmonic base disturbance of the specified

frequency

can be determined as

11 1

21 1 2

12 1

22 2

010

001

010

001

−

⎧

⎫⎧

⎡⎤

⎫

⎪

⎪⎪

⎢⎥

⎪

⎪⎪⎪

⎪

⎢⎥

⎪⎪

⎨

⎬

⎢⎥

⎨⎬

⎪

⎪⎪

⎢⎥

⎪

⎪⎪

⎢⎥

⎣⎦

⎪

⎪⎪

⎩⎭ ⎩⎭

⎪

(17)

Repeating the above experimental procedures by

changing the base motion frequency, sets of perfect

cancelling compensator polynomials for each

frequency are obtained.

2) Model fitting in frequency domain

From the sets of compensator parameters for each

specified frequency, the FRF(frequency response

function) of the disturbance cancelling feedforward

compensators can be calculated. Based on this FRF,

the compensators in eq. (9) are determined so as to

minimize the cost function J

()

*1 1

() () ,,1,2

ij ij k ij ij

JWqWqi

λω

−−

⎡⎤

=−

⎢⎥

⎣⎦

∑

(18)

where

lm k

()

is the frequency weighting and

()

−

is the estimated compensator obtained in

the first step and

()

−

is the compensator to be

determined. To avoid unstable compensator,

()Wq

−

can have the form of FIR(finite impulse

response) filter.

A DISTURBANCE COMPENSATION CONTROL FOR AN ACTIVE MAGNETIC BEARING SYSTEM BY A

MULTIPLE FXLMS ALGORITHM

267

4 EXPERIMENTS

To verify the effectiveness of the proposed control

scheme, experiments were conducted using the test

apparatus shown in Fig. 2. All control algorithms

were implemented on a digital computer equipped

with a DSP(TI-DS-1104)) board. Throughout the

experiments, the sampling frequency was kept at

2000Hz.

A pole placement feedback (FB) control was

designed to have a closed-loop system with a

damping ratio of

8.0=

and natural frequency of

in consideration of the spectral

characteristics of the base motion. The vehicle

motion is characterized by a band-limited random

process of bandwidth 15Hz-60Hz.

To evaluate the convergence of the estimated

compensator parameters and the corresponding

disturbance rejection performance, a sequence of

simple harmonic of frequency 30Hz was delivered to

the shakers. The resultant base motion kept the

relation

( ) 1.023 ( )

jDj

Figs. 5 and 6 show the estimated compensator

parameters of

and the corresponding air-gap

responses, respectively. We confirmed that all

estimated parameters converged to their final values

after 50 s. These figures reveal that the air-gap

responses were consequently reduced, as the

estimated parameters converged to their final values.

The aforementioned convergence property and the

disturbance rejection performance exhibit the

feasibility of the proposed compensation control by

means of the MFXLMS algorithm.

As explained in the above, at least, one more set

of compensator parameters is necessary to determine

the unique compensator polynomials which cancel

the disturbance responses perfectly at

The MFXLMS algorithm was applied to obtain

another set of compensator parameters under the

different base motion profile kept the relation

( ) 1.465 ( )

jeDj

Hz=

. Similar

convergence and disturbance rejection properties to

Figs. 6 and 7 were confirmed.

From the two sets of the parameters obtained, the

FRF of the disturbance neutralizing compensator at

Hz=

was determined. The disturbance rejection

performance of this compensator was evaluated

under the base motion yielding the relation

()0.69 ()

jeD

−

= ,30

Hz=

Fig. 7 shows the air-gap responses of the FB-

control by itself and the FB with the compensation

control. Fig. 7 reveals that the compensation control

can almost neutralize any base motion responses of

frequency 30Hz. Surprisingly, it was found that the

control effort is reduced when the compensation was

employed. The air-gap responses that remained after

employing the compensation came mainly from the

inability of the shakers to produce a pure sinusoidal

tone of motion.

Repeating the experiment, while changing the

harmonic base motion frequency, sets of disturbance

neutralizing compensator parameters for each

frequency were obtained. The FRF

calculated

from the estimated parameters is shown as an

example in Fig. 8. Based on the FRF in Fig. 8, the

best-fit compensator was determined to be the third-

order polynomials.

0 5 10 15 20 25 30

-5

-4

-3

-2

-1

Figure 5: Estimated coefficients of

)(

−

02468101214

-100

-50

100

f = 30 Hz

Time [sec]

02468101214

-200

-150

-100

-50

f = 30 Hz

Air gap of y

[µm]

Air gap of y

[µm]

Time [sec]

Figure 6: Air-gap responses during estimation by

MFXLMS algorithm

Figure 7: Compensated air gap responses

To investigate the efficiency of the designed

compensator, a comparison was made between the

air-gap response with the compensation and without

the compensation. During the control experiments, a

sequence of band-limited random signals of

bandwidth 15-60Hz was delivered to the shaker and

the resultant base motion resembled that of the real

vehicle.

As shown in Fig. 9, the air-gap responses were

greatly reduced by applying the feedforward

112

111

Updated parameters W

111

and W

112

Time [s]

0.0 0.5 1.0 1.5 2.0

-100

-50

W/ Conpensation

W/O Conpensation

Air Gap y

[µm]

Time [sec]

0.0 0.5 1.0 1.5 2.0

-200

-150

-100

-50

W/ Conpensation

W/O Conpensation

Air Gap y

[µm]

Time [sec]

ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

268

compensation. For y

the standard deviations of the

air-gap with compensation and without

compensation were calculated to be

53.14=

and

43.1

, respectively. For y

the standard deviations

of the air-gap with compensation and without

compensation were calculated to be

13.13=

and

08.1

, respectively. The control voltages were

slightly reduced after employing compensation.

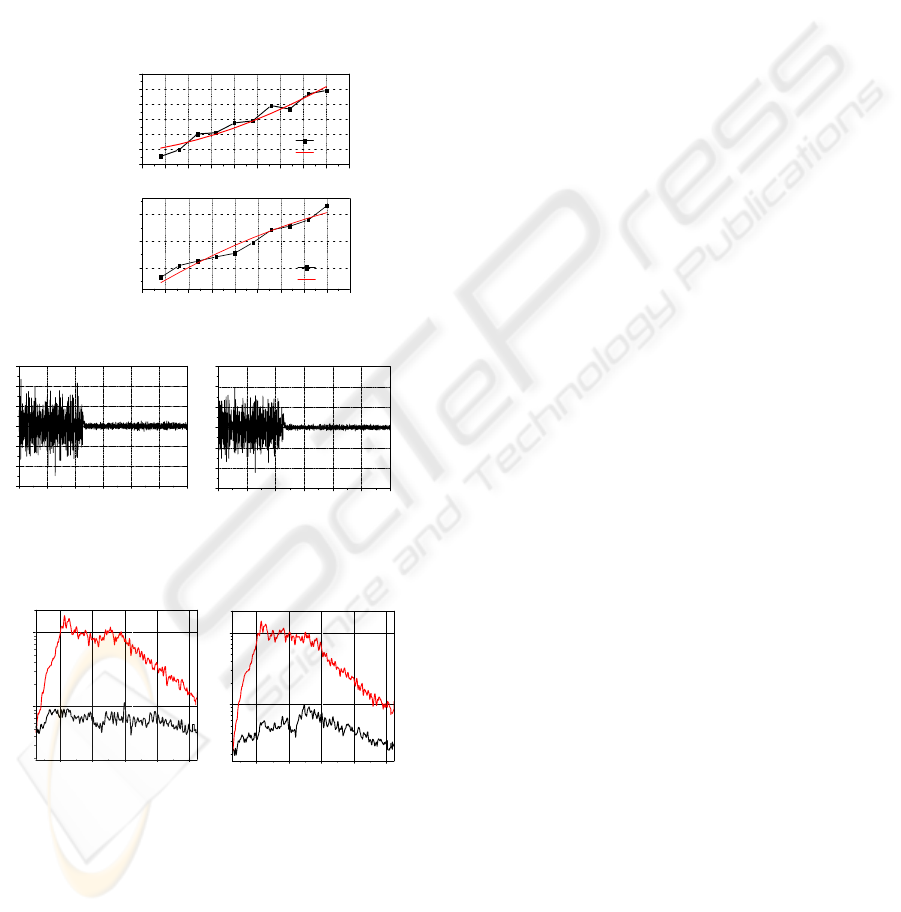
Figure 10 shows the spectra of the air-gap responses

in Fig. 9. The disturbance attenuation ratio is

approximately–20db within the frequency band of

the base motion.

Figure 8: Measured and fitted FRF of

Figure 9: Air-gap responses w/ and w/o compensation

20 40 60 80 100

-3

-2

Compensated

Uncompensated

Spectrum of y

Frequency [Hz]

20 40 60 80 100

-3

-2

Uncompensated

Compensated

Spectrum of y

Frequency [Hz]

Figure 10: Spectra of air-gap with and without

compensation

5 CONCLUSION

In this work, an experimental feedforward

compensator design technique, developed from an

adaptive estimation by means of the Multiple

Filtered-x least mean square (MFXLMS) algorithm

has been proposed. The feasibility of the proposed

technique has been verified by an experimental

study, by using a 2-DOF active magnetic bearing

system subject to base motion. The experimental

results showed that the standard deviation of the

compensated response was reduced to less than 10%

of that by feedback control alone.

ACKNOWLEDGEMENT

This work was supported by grant no.( R01-2003-

000-10857-0) from the Basic Research Program of

the Korea Science & Engineering Foundation.

10 15 20 25 30 35 40 45 50 55

-160

-150

-140

measured

fitted

Phase angle [degree]

Frequency [Hz]

10 15 20 25 30 35 40 45 50 55

0.45

0.50

0.55

0.60

0.65

0.70

0.75

measured

fitted

Magnitude

Frequency [Hz]

REFERENCES

Brunet, M., 1998. Practical Applications of Active

Magnetic Bearing to the Industrial World. 1’st

International Symposium on Magnetic Bearing. Zurich,

pp.225-244.

Cole, M. O. T., Keogh, P. S. and Burrows, C. R. , 1998.

Control and Non-linear Compensation of a

Rotor/Magnetic Bearing System Subject to base

Motion. 6th Int. Symposium on Magnetic Bearings.

Cambridge, MA, pp.618-627.

3456789

-60

-40

-20

Air gap y

[µm]

W/ compensation

W/O compensation

Time [s]

3456789

-60

-40

-20

Air gap y

[µm]

W/ compensation

W/O compensation

Time [s]

Jinzenji, A., Sasamoto, T., Aikawa, K., Yoshida, S. and

Aruga, K., 2001. Acceleration feedforward control

Against Rotational Disturbance in hard Disk Drives.

IEEE Trans. On Magnetics. Vol.37, No.2, pp.888-893,.

Kasada, M.E., Clements, J., Wicks, A. L., Hall, C. D., and

Kirk, R. G., 2000, Effect of sinusoidal base motion on

a magnetic bearing, Proc. IEEE International

Conference on Control Applications, pp.144-149.

Kuo, S. M. and Morgan, D. R., 1996. Active Noise Control

Systems. A Wiley-Interscience Publication, John Wiley

Sons, Inc.

Suzuki, Y., 1998. Acceleration Feedforward Control for

Active Magnetic Bearing Excited by Ground Motion.

IEEE Proc. Control Theory Appl. Vol.145, pp. 113-118.

Wang, A.K. and Ren, W., 1999, Convergence analysis of

the multiple-variable filtered-x LMS algorithm with

application to active noise control, IEEE Trans. On

Signal Processing, Vol.47, No.4, pp.1166-1169.

White, M. T. and Tomizuka, M., 1997. Increased

Disturbance Rejection in Magnetic Disk Drives by

Acceleration Feedforward Control and Parameter

Adaptation. Control Engineering Practice. vol.5, no.6.,

pp.741-751.

Widrow, B. and Stearns, S. D., 1985. Adaptive Signal

Processing. Prentice Hall. Englewood Cliffs, NJ.

A DISTURBANCE COMPENSATION CONTROL FOR AN ACTIVE MAGNETIC BEARING SYSTEM BY A

MULTIPLE FXLMS ALGORITHM

269