MOBILE ROBOT LOCALIZATION USING LINEAR SYSTEM

MODEL

Xu Zezhong

a,b

, Liu Jilin

a,Department of Information Science and Electronic Engineering,Zhejiang University, 310027, Hangzhou, China

b, Department of Computer Science and Engineering,Hangzhou Institute of Electronic Engineering, Hangzhou, China

Keywords: Mobile robot localization, Nonlinear state estimation, Extended Kalman filter, Linearization error.

Abstract: Localization is a fundamental problem for mobile robot autonomous navigation. EKF is an efficient tool for

position estimation, but it suffers from linearization errors due to linear approximation of nonlinear system

equations. In this paper we describe a position estimation method for mobile robot. Process and

measurement equations are linear by appropriately constructing the state vector and system models. The

position of mobile robot is estimated recursively based on optimal KF. It avoids linear approximation of

nonlinear system equations and is free of linearization error. All these techniques have been implemented on

our mobile robot ATRVII equipped with 2D laser rangefinder SICK.

1 INTRODUCTION

The mobile robot localization problem, especially

for pose tracking, is one fundamental problem in

mobile robotics. Dead reckoning technique is a

solution to estimate the position of mobile robot.

However, due to the uncertainties on odometer

modeling errors and occasional slipping errors, it

generally suffers from cumulative errors that

increase without bounds (Borenstein et al. 1995). In

order to overcome this disadvantage, probabilistic

localization method (Olson 2000; Thrun 2000) is

proposed by taking into account various

uncertainties on system state and sensor

measurement. In this way, the mobile robot

localization problem can be described as state

filtering or state estimation problem.

The optimal minimum mean square error

(MMSE) estimation is conditional expectation

conditioned on all prior observations. If system

equations are linear, the optimal state estimation

solution is the Kalman filter (KF) algorithm

(Kalman 1960). Unfortunately, system equations are

generally nonlinear in mobile robotics. System state

estimation requires a complete description of the

conditional probability density with unbounded

number of parameters. To estimate position of robot,

various suboptimal solutions for nonlinear

estimation problem have been proposed based on

different approximation techniques.

There are three types of approximation

techniques. The first is to approximate probability

distribution over state space. Grid-based Markov

Localization (Fox et al. 1998) is a discrete

approximation of probability density distribution

over all possible position and Monte Carlo

Localization (Fox et al. 1999) approximates the

posterior probability distribution over the state space

with a set of particles. The second is to approximate

nonlinear system equation with linear function.

Extended Kalman filter (EKF) (Kalman and Bucy

1961) and various variants apply the optimal

Kalman filter to deal with nonlinear estimation

problems by replacing nonlinear equations with

linear approximation. The third is to compute

conditional expectation with efficient numerical

approximation method. Gaussian filter (Ito et al.

2000) and Gaussian sum filter (Alspach 1972) resort

to numerical integration techniques to compute

conditional mean and conditional covariance.

The Kalman filter has brought revolutionary

improvement in stochastic estimation problem since

its introduction in 1960. The linear KF was

developed to provide optimal state estimation of

linear system with noisy measurement. The EKF

works by approximating the nonlinear process and

measurement equations about the current state

estimation. Classical EKF is a first order

approximation filter. It approximates nonlinear

function with first order Taylor series expansion

evaluated at current state estimation. However, EKF

243

Zezhong X. and Jilin L. (2004).

MOBILE ROBOT LOCALIZATION USING LINEAR SYSTEM MODEL.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 243-248

DOI: 10.5220/0001136202430248

 SciTePress

has two drawbacks. One is that this approximation is

not accurate if area around current estimation is very

nonlinear. Another is Jacobian matrix computation.

Some nonlinear functions may not be differentiable,

even if it is differential, computing the derivatives

may still be hard.

In order to improve the performance of state

estimation, various modified EKF methods are

proposed. The second-order filter (Nam et al. 1999)

is known to achieve better precision than the first-

order filter at the price of complex computation.

Higher order filter (Kelly 1994) is proposed by

taking into account higher order terms in the Taylor

series expansion, but the more complex

computations are involved. Iterated EKF (Bellaire et

al. 1995) is designed to improve the precision of

approximation by approximating measurement

equation about the corrected posterior estimation

instead of the predicted prior estimation. A range-

direction-cosine EKF (Mehra 1971) transforms

nonlinear measurement equation into linear function

by choosing a suitable coordinates system. A

modified EKF (Wall et al. 1997) algorithm offers

better performance by approximating nonlinear

equations about state vector computed from

deterministic equation rather than state vector

estimated from stochastic equation. Interlaced EKF

(Glielmo et al. 1999) partitions the state vector into

several parts. Each filter works independently and

considers the other parts of state vector as known

parameters. A modified EKF (Chui et al. 1990)

improves the filtering performance by modifying the

centre of Taylor series approximation. The linear

regression Kalman filter (Lefebvre et al. 2002)

approximates the process and measurement

functions by statistical linear regression of the

function with some sampling points. A typical

LRKF is unscented Kalman filter (UKF) (Julier et al.

1995; Wan et al. 2000). It approximates nonlinear

process and measurement function with sigma

points. A NMSKF (Lefebvre et al. 2002) linearize

process and measurement equations in a higher-

dimensional state space. It is applicable to state

estimation for static system and for a limited class of

dynamic systems.

In this paper, we apply KF to estimate

recursively the position of robot. The process and

measurement equation are linear by constructing

appropriately the system state and system models.

With linear system equations, the position estimation

of robot is optimal.

An outline of this paper is as follows. In Section

2 we describe the coordinate system. In Section 3 we

describe the system state space and system models.

Process equation and measurement equation are

defined. In Section 4 an efficient filter algorithm

with linear process equation and linear measurement

equation is described. Experimental results are

presented in Section 5. Finally we conclude in

Section 6.

2 COORDINATE SYSTEM

There are four coordinate systems. The first is world

coordinate system denoted with X

. The

second is odometer coordinate system denoted with

. The third is scanner coordinate system

denoted with X

. The fourth is the local

coordinate system of mobile robot, denoted with

. Robot local coordinate system has the

same orientation and origin as the odometer

coordinate system. Scanner coordinate system has

the same orientation as robot local coordinate

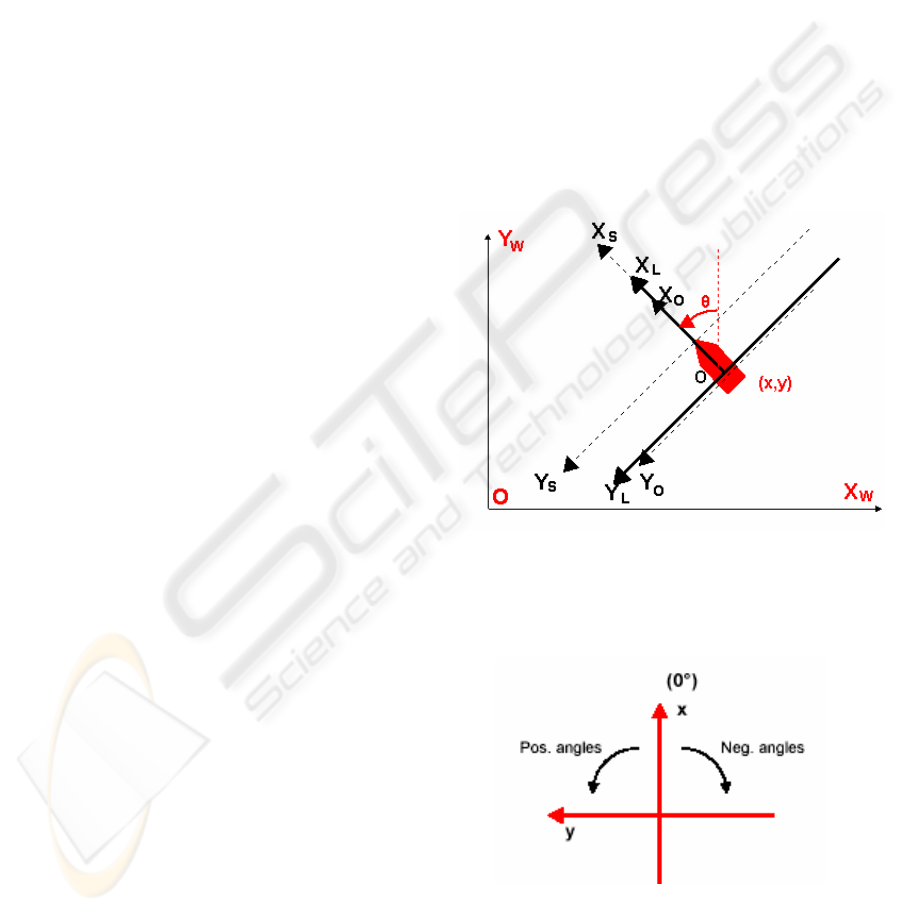
system. They are shown in Fig.1.

Robot local coordinate system, sensor coordinate

system and odometer coordinate system are defined

according to DIN70000. All angle are in the range of

–180

…180

. They are shown in Fig. 2.

In this paper, only world coordinate system and

robot local coordinate system are considered. All

values represented with scanner and odometer

Figure 1: coordinate system.

ure 2: DIN70000

ICINCO 2004 - ROBOTICS AND AUTOMATION

244

coordinate system are transformed into robot local

coordinate system.

3 STATE SPACE AND SYSTEM

MODEL

Mobile robot moves in an indoor environment.

Robot is equipped with an odometer and a laser

rangefinder. The data from the odometer is used to

predict the position of robot. Laser rangefinder scans

environment information and extracts natural

landmark, corner, to correct the predicted position of

robot. Data from sensor odometer and rangefinder

are all with uncertainty. The Kalman filter has

proven to be a valuable tool for mobile robot

position estimation given that the initial state and

covariance are known. The position of robot, [x, y,

θ]

, is considered as system state. Process equation

is based on odometer model and the world

coordinate of landmark is considered as observation

information. The position of robot is recursively

estimated as it evolves through time.

3.1 State space

We assume that environment is a 2D plane and

represent this 2D plane with a world coordinates

system X

. Another is robot’s local

coordinates system X

. The configuration of

robot is represented with a three-dimensional state

vector [x, y, θ]

. (x, y) represents the position of

robot. θ represents the orientation or heading of the

robot. It is defined in the counterclockwise. The

value of θ is from –π to π. It is shown in Fig.1.

The position prediction of robot is according to

the motion model. The observation prediction is

according to the observation model and the predicted

position of robot is corrected according to updated

rules.

3.2 Motion model

It is assumed that the robot moves along a circular

arc at each step. The position transition is based on

odometer information. Date from odometer is U

, γ

) at step k. D

is the distance traveled along

the arc and γ

is the change in motion direction. R

/γ

is the radius of arc. According to motion

model shown in Fig.3, the deterministic process

equation is:

3.3 Observation model

Laser rangefinder scans environmental information

and extracts landmark. A landmark is a typical

feature of environment. In this paper the corner is

considered as natural landmark. A range scan is

segmented and merged. The corner is extracted from

current laser scan and is represented with (x

, y

) in

local coordinates system. The corner is represented

with (x

, y

) in world coordinates system. We use

the position (x

, y

) of a corner as the observation

value. The position (x

, y

) of corner is computed in

local coordinates system. It is translated into world

coordinates system as observation prediction based

on current estimated position of robot. It is a two-

dimensional observation vector. According to

observation model shown in Fig.4, the deterministic

measurement equation is:

4 LOCALIZATION WITH KF

EKF approximates nonlinear system equations with

first-order terms of Taylor series and induces

linearization errors. If the initial position is assumed

as Gaussian distribution, the result position is not

Gaussian distribution after a nonlinear

transformation. So, it is incomplete that only

position expectation and position covariance are

recursively estimated. It is not an optimal estimation

solution for mobile robot localization with nonlinear

system equations.

()()()

kkk

γθθ

θγθ

−++=

sinsin

coscos

() ()

kLkLkW

yxyy

yxxx

θθ

sincos

cossin

−+=

−−=

Figure 3: Motion model.

MOBILE ROBOT LOCALIZATION USING LINEAR SYSTEM MODEL

245

We apply optimal linear Kalman filter to deal

with mobile robot localization by constructing

appropriately system state vector and system

models. In this way, the process equation and

measurement equation are linear. So, we estimate

the position of robot directly with a linear Kalman

filter. This estimation solution is optimal in MMSE

sense. State vector X

, observation vector Z

and

input vector U

are defined as:

We extend system state to four-dimensional

vector [x

, y

, s

, c

]

. (x

, y

) is the position of

robot. (s

, c

) is the sin and cosine of orientation θ of

robot. System state is estimated recursively

predicted and updated. The position (x

, y

, θ

) of

robot and its variance are computed from mean and

variance of system state [x

, y

, s

, c

]

. Observation

vector Z=[x

, y

]

is the position of corner in world

coordinates system. By replacing sin(θ

) and cos(θ

)

in system models with s

and c

, we get linear

process equation and linear measurement equation.

The process equation is:

Where ω

is noise vector representing

uncertainty on odometer modeling and slipping. Its

mean is zero and variance is Q.

The measurement equation is:

Where υ

is noise vector representing uncertainty

on sensor measurement. Its mean is zero and

variance is R.

Matrix F

only depends on the input vector and is

uncorrelated with current position estimation. Matrix

only depends on the position of landmark and is

uncorrelated with current position prediction. So,

process and measurement equations are linear. The

position of mobile robot is predicted and corrected

according to following update rules:

From step k to step k+1, system state mean and

covariance are predicted and corrected recursively.

The resulting position estimation of robot is an

optimal estimation. If the initial position of robot is

assumed as Gaussian distribution, the probability

distribution of position after each step is still

Gaussian. It is reasonable that only position mean

and variance are recursively computed.

5 EXPERIMENTAL RESULT

In this section, we demonstrate the experimental

result of proposed position estimation method. By

extending the state space of robot to four-

dimensional state vector, the system process and

measurement equations are linear. Localization

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

(

)

() ()

()

() ()

()

() ()

() ()()

()() ()

() ()

kkkk

scs

csc

UXfX

γγ

+∗=

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

−−

⎥

⎦

⎤

⎢

⎣

⎡

−

−++

−−+

cossin

sincos

cossin

sincos

110

101

(

)

sycxy

cysxx

XhZ

+∗=

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

−−

⎥

⎦

⎤

⎢

⎣

⎡

−+

−−

+++

111

1111

−

+++

∧

∗∗=

+∗∗=

∗∗−=

⎟

⎠

⎞

⎜

⎝

⎛

∗−+=

+∗∗=

∗=

kkk

kkkk

kkk

kkkk

SHPK

RHPHS

KSKPP

XHZKXX

QFPFP

XFX

Figure 4: Observation model.

ICINCO 2004 - ROBOTICS AND AUTOMATION

246

based on linear system model avoids linearization

error due to linear approximation of nonlinear

system equations.

In this section, we demonstrate the experimental

results of proposed position estimation method with

our mobile robot ATRVII. Fig. 5 is robot equipped

with laser range rangefinder. Robot moves around

our lab, scans landmark features and estimate its

position and heading.

Fig. 6 shows the estimated position errors with

one sigma confidence limit. Fig. 7 shows innovation

sequence and variance. Experimental results show

that the filter proposed here is consistent and

convergent.

With the same parameter, the position of robot is

estimated with classical EKF. Fig. 8 shows

difference of estimation results between KF and

EKF. Experimental results show that the Linear

filter gives more conservative estimation result than

nonlinear filter.

KF is an optimal state estimation for linear

system. Position estimation based on EKF induces

linearization error and brings additional uncertainty.

linearization error due to linear approximation of

nonlinear process equation affects mainly the long-

term position estimation. linearization error due to

linear approximation of nonlinear measurement

equation affects mainly the short-term position

estimation. By constructing appropriately state

vector and system models, we use optimal Kalman

filter for mobile robot position estimation. It is free

of linearization errors.

6 CONCLUSION

The extended Kalman filter has been widely used as

a position estimation method for mobile robot

localization and simultaneous localization and map

building (SLAM) problem. However, The classical

extended Kalman filter for this application suffers

from a fundamental flaw. Linear approximation of

nonlinear system equations with first-order Taylor

Figure 6: Estimated position error with KF.

Figure 7: Innovation and innovation variance

with KF.

Figure 5: Mobile robot.

Figure 8: Position estimation with KF and EKF.

solid line for KF and dashed line for EKF.

MOBILE ROBOT LOCALIZATION USING LINEAR SYSTEM MODEL

247

series induces linearization error. In this paper, a

position estimation method with linear process and

measurement equations is developed. Process and

measurement equations are linear by appropriately

constructing state vector and system models. With

linear process and measurement function, we apply

linear Kalman filter to estimate optimally the

position of robot. It avoids linear approximation of

nonlinear system equations and is free of

linearization error. The filter is consistent and

convergent. Comparing with EKF, it gives more

conservative estimation result.

REFERENCES

Alspach, D. and Sorenson, H. 1972. Nonlinear Bayesian

estimation using Gaussian sum approximations. IEEE

Transactions on Automatic Control, vol. AC-17, pp.

439-448.

Bellaire, R.L., Kamen E.W. and Zabin, S.M. 1995. A new

nonlinear iterated filter with applications to target

tracking. In SPIE Proceedings on Signal and Data

Processing of Small Targets, vol. 2561, pp. 240-251.

Borenstein, J. and Feng, L. 1995. Correction of Systematic

Odometer Errors in Mobile Robots. In Proceedings of

the 1995 International Conference on Intelligent

Robots and Systems (lROS'95), Pittsburgh,

Pennsylvania, pp. 569-574.

Chui, C.K., Chen, G. and Chui, H. 1990. Modified

extended Kalman filtering and parallel system

parameter identification, IEEE Transactions on

Automatic Control, 35 (1): 100-104.

Fox, D., Burgard, W., Thrun, S. and Cremers, A.B. 1998.

Position Estimation for Mobile Robots in Dynamic

Environments. AAAI/IAAI 1998: 983-988.

Fox, D., Burgard, W., Dellaert F. and Thrun, S. 1999.

Monte Carlo Localization: Efficient Position

Estimation for Mobile Robots. AAAI/IAAI 1999: 343-

349.

Glielmo, L., Setola R. and Vasca, F. 1999. An Interlaced

Extended Kalman Filter, IEEE Transactions on

Automatic Control, vol. 44, no. 8, pp. 1546-1549.

Ito, K. and Xiong, K. 2000. Gaussian Filters for Nonlinear

Filtering Problems. IEEE Transactions on Automatic

Control, 45(5): 910-927.

Julier, S., Uhlmann J. and Durrant-Whyte, H. 1995. A new

approach for filtering nonlinear systems. In

Proceedings of the American Control Conference,

pp.1628-1632.

Kalman, R.E. 1960. A New Approach to Linear Filtering

and Prediction Problems. Journal of Basic Engineering

Transactions of the ASME, pp.35-45.

Kalman, R.E. and Bucy, R. 1961. New results in linear

filtering and prediction theory. Journal of Basic

Engineering Transactions of the ASME, vol. 83, pp.

95-108.

Kelly, A.J. 1994. A 3D State Space Formulation of a

Navigation Kalman Filter for Autonomous Vehicles,

CMU Robotics Institute Technical Report CMU-RI-

TR-94-19.

Lefebvre, T., Bruyninckx, H. and De Schutter, J. 2002.

Comment on “A New Method for the Nonlinear

Transformation of Means and Covariances in Filters

and Estimators”. IEEE Transactions On Automatic

Control, Vol. 47, no. 8, pp.1406-1408.

Lefebvre, T., Bruyninckx, H. and De Schutter, J. 2003.

Non-linear Autonomous Compliant Motion with a

Non-minimal State Kalman Filter. In International

Conference on advanced Robotics, pp.136-141.

Mehra, R.K. 1971. A Comparison of Several Nonlinear

Filters for Reentry Vehicle Tracking. IEEE

Transactions on Automatic Control, AC-16(4): 307-

319.

Nam, K.H. and Tahk, M.J. 1999. A second-order

stochastic filter involving coordinate transformation.

IEEE Transactions on Automatic Control

, Vol. 44,

No.3, pp. 603-608.

Olson, C.F. 2000. Probabilistic self-localization for mobile

robots. IEEE Transactions on Robotics and

Automation, vol. 16(1), pp. 55-66.

Thrun, S. 2000. Probabilistic algorithms in robotics, AI

Magazine, 21(4): 93-109.

Wall, D.S. and Gaston, F.M.F. 1997. Modified extended

kalman filtering. In Proceedings of International

Conference on Digital Signal Processing, pp.703-706.

Wan, E.A. and van der Merwe, R. 2000. The unscented

Kalman filter for nonlinear estimation. In Proceedings

of Conf. Adaptive Systems for Signal Processing,

Communication and Control, Canada.

ICINCO 2004 - ROBOTICS AND AUTOMATION

248