SIMULTANEOUS LOCALIZATION AND MAPPING BASED ON

MULTI-RATE FUSION OF LASER AND ENCODERS

MEASUREMENTS

Leopoldo Armesto, Josep Tornero

Dept. of Systems Engineering and Control, Technical University of Valencia

Camino de Vera s/n, 46020, Spain

Keywords:

Multi-rate fusion, SLAM, Mobile robots, Kalman ﬁlter.

Abstract:

The SLAM problem in static environments with EKF is adapted for multi-rate sensor fusion of encoders and

laser rangers. In addition, the formulation is general and can be adapted for any multi-rate sensor fusion

application. The proposed algorithm, based on well-known techniques for feature extraction, data association

and map building, is validated with some experimental results. This algorithm should been seen as a part of a

complete autonomous robot navigation algorithm, also described in the paper.

1 INTRODUCTION

SLAM problem addresses the simultaneously locate

and build a map using a mobile robot with no previous

knowledge of robot initial localization and the map

(environment). A number of approaches have already

been proposed to solve the SLAM problem since the

seminal paper (Smith et al., 1988) was presented.

The most relevant of these are based on grid-based

methods (Thrun et al., 1998) and parametric methods

(Dissanayake et al., 2001), (Jensfelt and Christensen,

2001), (Castellanos et al., 2001).

Kalman ﬁlter approach of SLAM consists on join-

ing the robot state and the set of landmark parameters

of the environment. It is well known that landmark

covariance decreases monotonically. In fact, in the

limit, the determinant of the covariance matrix of a

map containing more than one landmark converges to

zero and is fully correlated (Dissanayake et al., 2001).

The main advantage of this approach is that KF gives

a robust, optimal recursive state estimation to fuse re-

dundant information from different sensors, assuming

Gaussian noise on the system and measurements.

Multi-rate fusion is used when sensors have differ-

ent sampling rates. In any complex application, it is

unrealistic to assume the same sampling period for all

system variables. In mobile robots, sensors such as

laser rangers, sonars, radars, encoders, GPS, vision

systems, etc., have different sampling rates.

In this paper, we present a realistic approach to

the SLAM problem, where sensor measurements are

treated as system outputs at their sampling rates. In

this approach data-missing problems are easily con-

sidered. In particular, we fuse encoder measurements

at fast sampling and laser ranger measurements at

slow sampling. The proposed multi-rate SLAM is

more appropriate for real-time control applications,

because it produces vehicle and map estimations at

the fast sampling rate of the control.

2 SLAM WITH MULTI-RATE

FUSION

2.1 Vehicle and Landmark Models

Let the robot pose be described by the following dis-

crete dynamic equation,

(k + 1) = f

(k)) + γ

(k), w(k))

with x

(k) = [x(k) y(k) θ(k) v(k) ω(k)]

the robot

state vector with Cartesian positions x(k) and y(k),

orientation θ(k), linear velocity v(k) and angular ve-

locity ω(k). The robot constant velocity model is,

(k)) =







x(k) + T v(k) cos(θ(k))

y(k) + T v(k) sin(θ(k))

θ(k) + T ω(k)

v(k)

ω(k)







where T is the sampling period.

435

Armesto L. and Tornero J. (2004).

SIMULTANEOUS LOCALIZATION AND MAPPING BASED ON MULTI-RATE FUSION OF LASER AND ENCODERS MEASUREMENTS.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 435-439

DOI: 10.5220/0001136804350439

 SciTePress

Figure 1: Vehicle and landmark variables deﬁnition

Inputs to the system are linear acceleration a(k)

and angular acceleration α(k) of the robot, which

are unknown and therefore treated as system noises

w(k) = [a(k) α(k)]

with Gaussian distribution

w(k) ∼ N(0, Q(k)). The noise mapping to robot

states is given by,

(k), w(k)) =







a(k) cos(θ(k))

a(k) sin(θ(k))

α(k)

T a(k)

T α(k)







Let M denote the map of the environment, which

is a set of segment lines m

. Each segment, m

described by a set of parameters: distance of a line

to the origin ρ

(k), orientation ϕ

(k), start point

s,i

) and end point (x

e,i

, y

e,i

), as shown in ﬁgure

1. The use of redundant information is due to the fact

that ρ

(k) and ϕ

(k) are used in the map state vector

m,i

(k) = [ρ

(k) ϕ

(k)]

, the start and end points

are used to predict only visible segment lines. Since

the landmarks are supposed to be stationary, their dy-

namic description is simply x

(k+1) = x

(k), with

(k) = [x

m,1

(k) . . . x

m,n

(k)]

In SLAM, the robot and the map states are treated

together x(k)=[x

(k) x

(k)]

, its covariance is,

P(k) =

(k) P

(k)

(k) P

(k)

The prediction of the state and its covariance is,

ˆx(k+1|k) =

(ˆx

(k))

ˆx

(k)

(k+1|k) =F

(k)P

(k)F

(k)+Γ

(k)Q(k)Γ

(k)

(k+1|k) =F

(k)P

(k)

(k+1|k) =P

(k)

where F

(k) and Γ

(k) are the Jacobians of

(k)) and γ

(k), w(k)), respectively.

2.2 Measurement Model

In our application, the robot is an industrial fork-

lift with tricycle conﬁguration. We have sensed the

two front wheels with incremental encoders, the rear

wheel with an absolute encoder and we have installed

laser rangers at the front and rear of the vehicle (Mora

et al., 2003). The measurement equations are particu-

larized for these sensors, however it is possible to ex-

tend the model to other sensors such as GPS, vision,

compass, sonar, etc.

Measurement equations of encoders are as follows:

inc

)+u

inc

v−lω

v+lω

inc

(1)

abs

=β = h

abs

)+u

abs

−Mω

abs

(2)

where u

inc

and u

abs

are measurement noises with co-

variances R

inc

and R

abs

, respectively. For simplicity

we suppress index k where no confusion can arise.

For each detected line, we the following sensor

model (Jensfelt and Christensen, 2001),

las

, x

m,i

) + u

las

= (3)

−

cos(ξ−ϕ

)

−θ

las

ρ,i

las

ϕ,i

where ξ = arctan(y, x) while u

las

is the measure-

ment noise with covariance R

las

Detected landmarks are those which successfully

pass the Data Association Test (DAT), described be-

low. When the DAT fails, the detected feature is in-

cluded in a temporary map M

, where the i-th ele-

ment x

tm,i

is deﬁned by the line parameters with re-

spect to the global frame. Until the feature is suf-

ﬁciently stable, it is not included in M. However,

DAT may fail despite the fact data belong to the same

feature. In that case, in order to avoid repeated land-

marks, a test between the map and the temporary map

is also performed. Only successfully associated ele-

ments are included as measurements,

m,i

)+u

ρ,i

ϕ,i

(4)

where u

is the noise with covariance R

The Jacobians of equations (1)-(4) are respectively

denoted as H

inc

(k), H

abs

(k), H

las

(k) and H

(k).

2.3 Multi-rate Fusion

Assume a general multi-rate sampling with peri-

ods associated to incremental encoders (T

inc

), ab-

solute encoder (T

abs

), laser measurements (T

las

)

and the measurements associated with the tempo-

rary map (T

). The base period is the great

common divisor of all sampling rates, T =

ICINCO 2004 - ROBOTICS AND AUTOMATION

436

gcd(T

inc

, T

abs

, T

las

, T

). We also deﬁne period-

icity ratios r

inc

= T

inc

/T , r

abs

= T

abs

/T , r

las

/T , r

/T .

Sensor measurements depend on functions δ

inc

(k),

abs

(k), δ

las

(k), δ

(k), indicating whether their re-

spective measurements are valid (δ(k) = 1) or not

(δ(k) =0). Thus, we can easily: discard erroneous in-

cremental encoder measurements if we detect wheel

slippage; not consider the absolute encoder measure-

ment when the vehicle is stopped, since its measure-

ment equation h

abs

(x(k)) is undetermined for v = 0;

not include features which do not pass the DAT.

Multi-rate fusion is performed by containing avail-

able measurements in rows on the output vector y(k),

inc

(k)⊆ y(k) iﬀ mod(k, r

inc

)= 0 and δ

inc

(k)= 1

abs

(k)⊆ y(k) iﬀ mod(k, r

abs

)= 0 and δ

abs

(k)= 1

las

(k)⊆ y(k) iﬀ mod(k, r

las

)= 0 and δ

las

(k)= 1

(k)⊆ y(k) iﬀ mod(k, r

)= 0 and δ

(k)= 1

Valid measurements are also combined by rows in

the Jacobian matrix H(k). Noise covariance matrix,

R(k), is a diagonal matrix of valid measurement co-

variances.

The state update is as usual in EKF:

S(k+1) = H(k+1)P(k+1|k)H

(k+1)+R(k+1)

K(k+1) = P(k+1|k)H

(k+1)S

−1

(k+1)

ˆx(k+1) = ˆx(k+1|k)+K(k+1)(y(k+1)−h(ˆx(k+1|k)))

P(k+1) = (I−K(k+1)H(k+1))P(k+1|k)

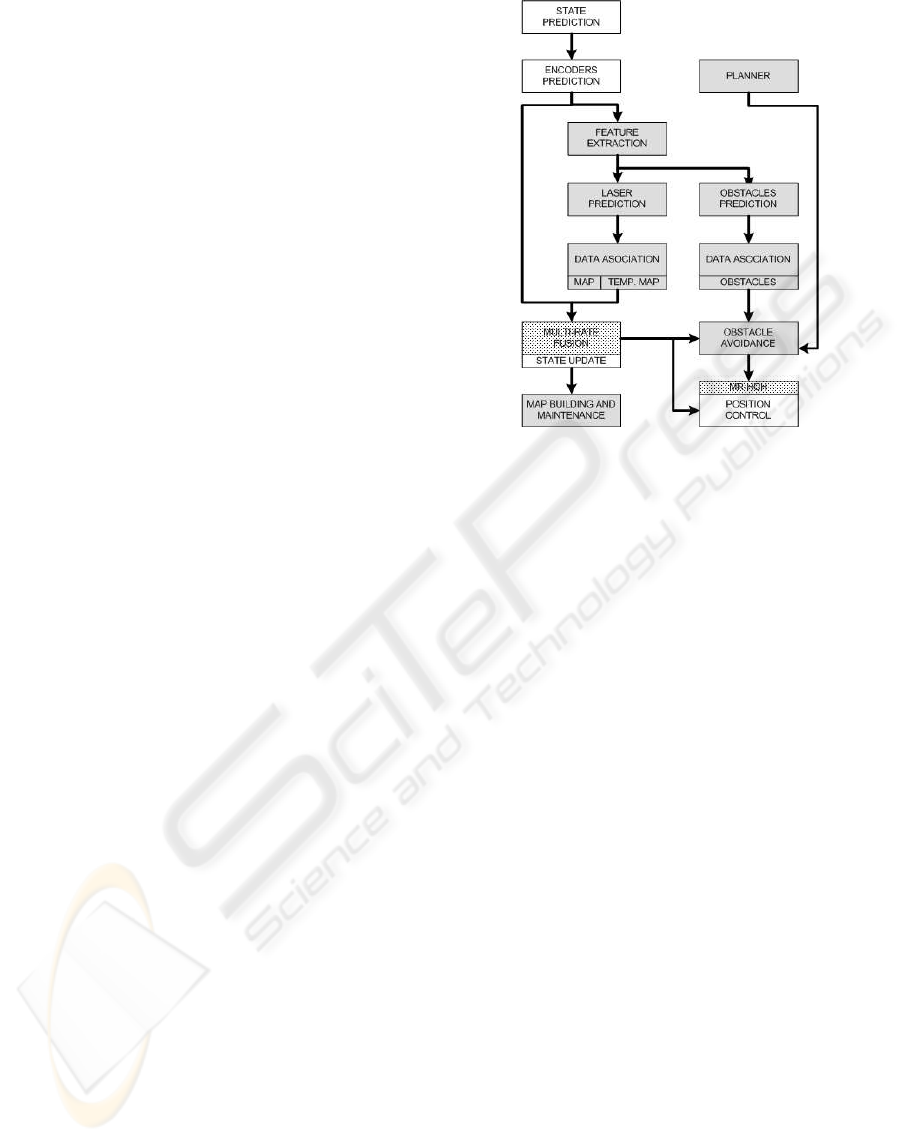
3 IMPLEMENTED ALGORITHM

The overall diagram can be seen in ﬁgure 2, where

white blocks are executed at a high sampling rate,

gray ones at a low sampling rate and dotted blocks act

as interfaces between high and low sampling rates.

Usually, object path planning and obstacle avoid-

ance algorithms require high computational power

and should be executed at lower sampling rates than

those required by the position controller. In this sense,

the block MR-HOH (multi-rate high order holds) is

used to extrapolate reference points to the control at

high sampling rate from points provided at a low sam-

pling rate (Armesto and Tornero, 2003).

3.1 Feature Extraction

For feature extraction, we have implemented the

RIEPFA (Recursive Iterative End Point Fit Algo-

rithm) (Duda and Hart, 1973). The algorithm per-

forms the segmentation of a laser scan providing

points belonging to the same line segment. Parame-

ters of segment lines are estimated with the Orthogo-

nal Least-Squares method. (Deriche et al., 1992) give

Figure 2: Bock diagram for SLAM with multi-rate fusion,

including obstacle avoidance and position control

the exact formulation for computing line parameter

covariances, assuming that data are affected by Carte-

sian and polar noise.

3.2 Data Association

The objective of data association is to associate mea-

surements to the features in the map. In this work,

data association is based on the Mahalanobis distance

in the innovation space (Bar-Shalom and Fortman,

1988). The innovation matrix of a feature i is given

by:

las

)

las

The innovation is z

las

= y

las

− h

las

, x

m,i

) and

the Mahalanobis distance (z

las

)

las

)

−1

las

≤ η,

where η = 9.0 represents 98.9% of a 2D Gaussian

curve. Additional gating conditions have been consid-

ered, such as the norm ||z

las

||, should be lower than

a threshold, z

norm

, and segments separated by more

than a distance, l

max

, are treated separately.

3.3 Map Building and Maintenance

In this section, we describe how a new feature m

N+1

is incorporated into the system vector state,

m,N+1

tm,i

, P

N+1N+1

tm,ii

where x

tm,i

is the feature in the temporary map M

once it has already been validated. The feature covari-

ance in the temporary map is assigned to the new fea-

ture covariance in the map. For simplicity, the cross-

SIMULTANEOUS LOCALIZATION AND MAPPING BASED ON MULTI-RATE FUSION OF LASER AND

ENCODERS MEASUREMENTS

437

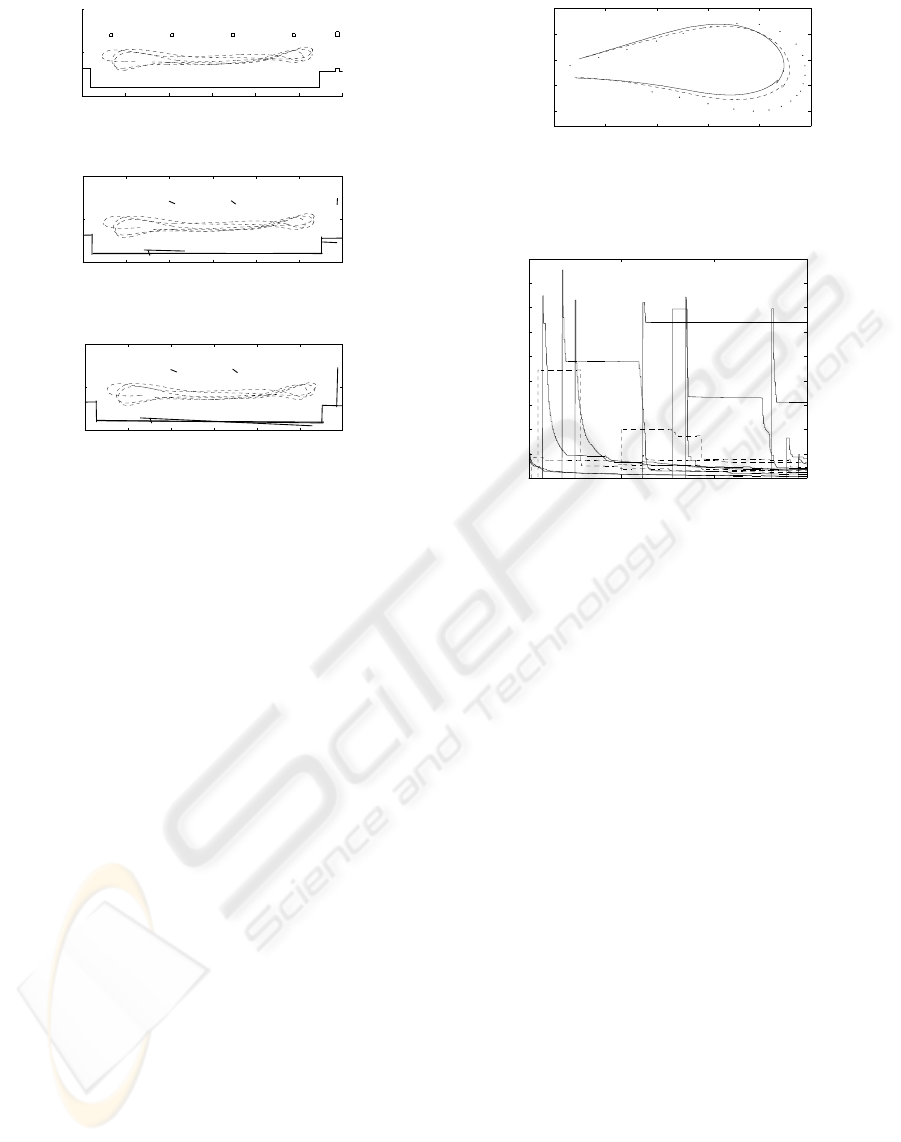
0 5 10 15 20 25 30

X [m.]

Y [m.]

(a) Ground-truth robot trace

0 5 10 15 20 25 30

X [m.]

Y [m.]

(b) SLAM with multi-rate EKF

0 5 10 15 20 25 30

X [m.]

Y [m.]

Figure 3: Robot trace estimation and map built with the

different Kalman ﬁlter approaches.

covariances of the new feature with the robot state and

the rest of the features is initialized to zero.

4 EXPERIMENTAL RESULTS

Data has been taken from a parking lot, where en-

coder measurements were sampled every 50ms and

the laser scans every 500ms for 150 sec. Ground-truth

estimation has been performed using a detailed park-

ing layout, see ﬁgure 3(a). In addition, the vehicle

trace and map estimation using the proposed multi-

rate ﬁlter is depicted in ﬁgure 3(b), where it can be

appreciated that the trace estimation is very similar to

ground-truth estimation and the estimated map con-

tains all the main features of the parking lot.

In order to compare the beneﬁts of using the multi-

rate ﬁlter, the single-rate estimation is also performed,

where all measurements were sampled at 500ms. Fig-

ure 4 shows the trace estimation of the three ﬁlters,

during the ﬁrst turn of the trajectory (time between

14.5-26.5sec.). It should be noted that, depending on

the tuning parameters, we have found many numeri-

cal cases where the multi-rate sampling stabilized the

estimation, which was not stable at single-rate.

Landmark standard deviation with the multi-rate

ﬁlter are shown in ﬁgure 5. Landmark covariance is

not represented until incorporated to the map.

21 22 23 24 25 26

3.5

4.5

5.5

X [m.]

Y [m.]

Figure 4: Trace comparison between ground-truth (solid

line), MR-EKF (dashed line) and SR-EKF (dotted line).

0 50 100 150

x 10

−3

Time [sec.]

Figure 5: Standard deviation of estimated landmarks (σ

Solid lines (walls) and dashed lines (columns).

5 CONCLUSIONS

In this paper, a multi-rate simultaneous localization

and mapping based on Extended Kalman ﬁlter has

been presented. Real-time control applications can

clearly beneﬁt from multi-rate SLAM algorithm, be-

cause vehicle and map estimation are computed at the

fast sampling rate of the vehicle control. The algo-

rithm is based on well-known techniques for feature

extraction, data association and map building. The

algorithm should be seen as part of a complete au-

tonomous robot navigation system.

Experimental results have shown that the estima-

tion is successfully performed, with the trace of the

robot and the map very close to the ground-truth es-

timation. In addition, MR-EKF performance is much

improved with respect to SR-EKF.

REFERENCES

Armesto, L. and Tornero, J. (2003). Trajectory extrapola-

tion using multi-rate high order holds. In Symp. on

Intelligent Components and Instruments for Control

Applications.

Bar-Shalom, Y. and Fortman, T. (1988). Tracking and Data

Association. Academic Press, New York.

Castellanos, J., Neira, J., and Tardos, J. (2001). Multisensor

ICINCO 2004 - ROBOTICS AND AUTOMATION

438

fusion for simultaneous localization and map building.

Trans. on Robotics and Automation, 17(6).

Deriche, R., Vaillant, R., and Faugeras, O. (1992). From

noise edges points to 3d reconstruction of a scene: A

robuts approach and its uncertainty analysis. In Ma-

chine Perception and Artiﬁcial Inteligence, volume 2,

pages 71–79. World Scientiﬁc.

Dissanayake, M., Newman, P., Clark, S., Durrant-Whyte,

H., and Csorba, M. (2001). A solution to the simul-

taneous localization and map building (SLAM) prob-

lem. IEEE Trans. Robot. Automation, 17(3):229–241.

Duda, R. and Hart, P. (1973). Classiﬁcation and Scene

Analysis. John Wiley and Sons, New York.

Jensfelt, P. and Christensen, H. (2001). Pose tracking using

laser scanning and minimalistic environmental mod-

els. Trans. Robotics and Automation, 17(2):138–147.

Mora, M., Suesta, V., Armesto, L., and Tornero, J. (2003).

Factory management and transport automation. In

IEEE Conference on Emerging Technologies and Fac-

tory Automation, volume 2, pages 508–515.

Smith, R., Self, M., and Cheeseman, P. (1988). A stochastic

map for uncertain spatial relationships. In Int. Symp.

in Robot. Res., pages 467–474.

Thrun, S., Fox, D., and Burgard, W. (1998). A probabilis-

tic approach to concurrent mapping and localization.

Mach. Learning Autonomous Robots, pages 29–53.

SIMULTANEOUS LOCALIZATION AND MAPPING BASED ON MULTI-RATE FUSION OF LASER AND

ENCODERS MEASUREMENTS

439