MODEL PREDICTIVE CONTROL FOR HYBRID SYSTEMS

UNDER A STATE PARTITION BASED MLD APPROACH

(SPMLD)

Jean Thomas, Didier Dumur

Supélec, F 91192 Gif sur Yvette cedex, France

Jean Buisson, Herve Guéguen

Supélec, F 35 511 Cesson-Sévigné cedex, France

Keywords: Hybrid dynamical systems, Mixed Logical Dynamical systems (MLD), Piecewise Affine systems (PWA),

Model Predictive Control (MPC)

Abstract This paper presents the State Partition based Mixed

Logical Dynamical (SPMLD) formalism as a new

modeling technique for a class of discrete-time hybrid systems, where the system is defined by different

modes with continuous and logical control inputs and state variables, each model subject to linear

constraints. The reformulation of the predictive strategy for hybrid systems under the SPMLD approach is

then developed. This technique enables to considerably reduce the computation time (with respect to the

classical MPC approaches for PWA and MLD models), as a positive feature for real time implementation.

This strategy is applied in simulation to the control of a three tanks benchmark.

1 INTRODUCTION

Hybrid systems become an attractive field of

research for engineers as it appears in many control

applications in industry. They include both continu-

ous and discrete variables, discrete variables coming

from parts described by logic such as for example

on/off switches or valves. Various approaches have

been proposed for modeling hybrid systems (Brani-

cky et al., 1998), like Automata, Petri nets, Linear

Complementary (LC), Piecewise Affine (PWA)

(Sontag, 1981), Mixed Logical Dynamical (MLD)

models (Bemporad, and Morari, 1999).

This paper examines a class of discrete-time

rid systems, which consists of several models

with different dynamics according to the feasible

state space partition. Each model is described with

continuous and logical states and control inputs.

Consequently, the dynamic of the system depends

on the model selected in relation to linear constraints

over the states and on the inputs values.

On the other hand, model predictive control

(MPC) appea

s to be an efficient strategy to control

hybrid systems. Considering the previous particular

class of hybrid systems, implementing MPC leads to

a problem including at each prediction step the states

and inputs vectors (both continuous and discrete

variables), the dynamic equation and linear

constraints, for which a quadratic cost function has

to be optimized. Two classical approaches exist for

solving this optimization problem.

First, all possible logical combinations can be

studie

at each prediction time, which leads solving

a great number of QPs. Each of these QPs is related

to a particular scenario of logical inputs and modes.

This is the PWA approach. The number of QPs can

be reduced by reachability considerations (Pena et

al., 2003).

The second moves the initial problem through

e MLD fo

rmalism to a single general model used

at each prediction step. This MLD formalism

introduces many auxiliary logical and continuous

variables and linear constraints. At each prediction

step, all the MLD model variables have to be solved

(even if some of them are not active). However, the

MLD transformation allows utilizing the Branch and

Bound (B&B) technique (Fletcher and Leyffer,

1995), reducing the number of QPs solved.

This paper develops a technique which aims at

ple

menting MPC strategy for the considered class

of hybrid systems, as a mixed solution of the two

classical structures presented before. It is based on a

Thomas J., Dumur D., Buisson J. and Guéguen H. (2004).

MODEL PREDICTIVE CONTROL FOR HYBRID SYSTEMS UNDER A STATE PARTITION BASED MLD APPROACH (SPMLD).

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 78-85

DOI: 10.5220/0001137000780085

 SciTePress

new modeling technique, called State Partition based

MLD approach (SPMLD) formalism, combining the

PWA and MLD models. The complexity of this

formalism is compared to that obtained with the

usual PWA and MLD forms, which can also model

this class of hybrid systems as well.

The paper is organized as follows. Section 2

presents a short description of the PWA and MLD

hybrid systems. General consideration about model

predictive control (MPC) and its classical

application to PWA and MLD systems are

summarized in Section 3. Section 4 develops the

State Partition based MLD approach (SPMLD) and

examines the application of MPC to hybrid systems

under this formalism. Section 5 gives an application

of this strategy to water level control of a three tanks

benchmark. Section 6 gives final conclusions.

2 HYBRID SYSTEMS MODELING

2.1 Mixed Logical Dynamical model

The MLD model appears as a suitable formalism for

various classes of hybrid systems, like linear hybrid

or constrained linear systems. It describes the sys-

tems by linear dynamic equations subject to linear

inequalities involving real and integer variables,

under the form (Bemporad and Morari, 1999)

(1)

54132

321

3211

ExEuEzEδE

zDδDuDCxy

zBδBuBAxx

++≤+

+++=

kkkk

kkkkk

where

{}

1,0×ℜ∈

⎟

⎠

⎞

⎜

⎝

⎛

x , ,

{}

1,0×ℜ∈

⎟

⎠

⎞

⎜

⎝

⎛

{}

1,0×ℜ∈

⎟

⎠

⎞

⎜

⎝

⎛

y , ,

{}

1,0∈δ

ℜ∈z

are respectively the vectors of continuous and binary

states of the system, of continuous and binary

(on/off) control inputs, of output signals, of auxiliary

binary and continuous variables.

Discrete/ Digital

Continuous dynamic

system

D/A

A/D

0 else

≤

bax

else

1 if

bxaz

Figure 1: MLD model structure

The auxiliary variables are introduced when

translating propositional logic into linear inequalities

as described in Figure 1. All matrices appearing in

(1) can be obtained through the specification

language HYSDEL (Hybrid System Description

Language), see (Torrisi et al., 2000).

2.2 Piecewise Affine model

Another framework for discrete time hybrid systems

is the PWA model (Sontag, 1981), defined as

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

++=

gxCy

fuBxAx

: , for: (2)

∈

⎥

⎦

⎤

⎢

⎣

⎡

where

{

}

is the polyhedral partition of the state

and input spaces (s being the number of subsystems

within the partition). Each

is given by

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

≤

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

(3)

where

kkk

denote the state, input and output

vector respectively at instant

. Each subsystem

defined by the 7-uple

yux ,,

k S

(

)

,,,,,,,

iiiiiii

qQgfCBA

(

)

si ,,2,1 L

∈

is a component of the PWA system

(2).

(

)

mnp

inpimninni

×××

ℜ∈ℜ∈ℜ∈ℜ∈ QCBA ,,,

and

are suitable constant vectors or

matrices, where

, , are respectively the

number of states, inputs, outputs, and

is the

number of hyperplanes defining the

i -polyhedral. In

this formalism, a logical control input is considered

by developing an affine model for each input value

(1/0), defining linear inequality constraints linking

the model with the relevant input value.

iii

qgf ,,

n m

It has been shown in (Bemporad et al., 2000),

that MLD and PWA models are equivalent, which

enables transformation from one model to the other.

A MLD model can be transferred to a PWA model

with the number of subsystems inside the polyhedral

partition equal to all possible combination of all the

integer variables of the MLD model (Bemporad et

al., 2000) (a technique for avoiding empty region is

presented in (Bemporad, 2003))

(4)

lll

rmn

= 2

3 MODEL PREDICTIVE CONTROL

Model predictive control (MPC) has proved to

efficiently control a wide range of applications in

industry, including systems with long delay times,

non-minimum phase, unstable, multivariable and

constrained systems.

The main idea of predictive control is the use of

a plant model to predict future outputs of the system.

Based on this prediction, at each sampling period, a

sequence of future control values is elaborated

MODEL PREDICTIVE CONTROL FOR HYBRID SYSTEMS UNDER A STATE PARTITION BASED MLD

APPROACH (SPMLD)

through an on-line optimization process, which

maximizes the tracking performance while satisfying

constraints. Only the first value of this optimal

sequence is applied to the plant according to the

‘receding’ horizon strategy (Dumur and Boucher,

1998).

Considering the particular class of hybrid

systems previously described, implementing MPC

leads to a problem including at each prediction step

the states vector, the inputs vector (both continuous

and discrete), the dynamic equation and linear

constraints, for which a quadratic cost function has

to be optimized. Two classical approaches exist for

solving this optimization problem, the Branch and

Bound technique that can be used with the MLD

formalism and the enumeration of all possible

logical system combinations at each prediction time

corresponding to all particular scenarios of logical

inputs and modes used with the PWA formalism.

3.1 Model predictive control for the

MLD systems

For a MLD system of the form (1), the following

model predictive control problem is considered. Let

be the current time,

the current state,

an equilibrium pair or a reference

trajectory value,

the final time, find

the sequence which

moves the state from

to and minimizes

k x

),(

Nk +

(

−+

Nkk

)

uuu L

),(min

yyxx

zzδδ

uxu

ekikekik

eikk

−+−+

+−+−+

+−=

+++

−

−+

∑

−+

(5)

subject to (1), where

is the prediction horizon,

are the auxiliary variables of the equilibrium

point or the reference trajectory value, calculated by

solving a MILP problem for the inequality equation

of (1).

denotes the predicted state vector at

time

, obtained by applying the input sequence

to model (1) starting from the current state

(same for the other input and output variables),

, , and

, for

δ z

k /+

ik +

1−+Nk

≥=

0>=

4,1for =i

5,3,2 =i

The optimization procedure of (5) leads to MIQP

problems with the following optimization vector

(6)

],,,

,,,,,,[

−+

−+−+

Nkk

NkkNkk

δδuuχ

The number of binary optimization variables is

(

)

rmNL

. In the worst case, the maximum

number of solved QP problems is

No of QPs

−

(7)

So the main drawback of this MLD formalism

remains the computational burden related to the

complexity of the derived Mixed Integer Quadratic

Programming (MIQPs) problems. Indeed MIQPs

problems are classified as NP-complete, so that in

the worst case, the optimization time grows expo-

nentially with the problem size, even if branch and

bounds methods (B&B) may reduce this solution

time (Fletcher and Leyffer, 1995).

3.2 Model Predictive control for the

PWA systems

Considering the PWA system under the form (2),

assuming that the current state

is known the

model predictive control requires solving at each

time step (Pena et al., 2003).

maxmin

:s.t.

),(min

uuu

wyxu

≤≤

−=

−

−+

∑

−+

ikii

ikkikiik

(8)

where

is the prediction horizon,

ik+

is the

output reference, and

denotes the predicted

output vector at time

N w

k /+

, obtained by applying the

input sequence

to the

system starting from the current state

iiii

are

the elements of

weighting diagonal matrices.

()

−+

Nkk

uu L

x rq ,

RQ,

In order to solve this equation the model applied

at each instant has to be determined and all potential

sequences of subsystems

have to be examined, where

is one sub-region

among the s subsystems at prediction time

for

{}

,,,

−++

Nkkk

IIII L

1,,2,1

−

Ni L

. As for each model the value of the

logical variable is fixed, the MPC problem is solved

by a QP for each potential sequence. As the current

state

is known, the starting region according to

the state partition is identified. But the initial sub-

region related to the current input control is not

known as it appears in the domain definition (3).

Similarly, the next steps subsystems are also

unknown, depending on the applied control

sequence. In general, all potential sequences of

subsystems

have to be examined, which increases

the computation burden. If no constraints are

considered, the number of possible sequences for a

prediction horizon

is , where

is the

number of all possible sub-regions at instant

1−N

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

according to the input space partition. In order to

solve the MPC problem of (8), the number of

quadratic programming problems to be solved is

No QPs

(9)

1−

4 MPC FOR STATE PARTITION

BASED MLD (SPMLD)

FORMALISM

4.1 The SPMLD formalism

The SPMLD model is a mixed approach where in

each region of the feasible space a simple MLD

model is developed. Starting from the MLD model,

the auxiliary binary variables are divided into two

groups

. Where is

chosen in order to include the

[

δδδ =

]

T r

{}

1,0

∈δ

variables that are

not directly depending on the state variables (the

inequalities that define

variables are not

depending on

x ), and depending on .

This partition will be further justified. The SPMLD

model is then developed by giving

δ a constant

value: for each possible combination of

δ a sub-

region is defined with the corresponding

constraints as in (3). As some logical combinations

may not be feasible, the number of sub-regions of

the polyhedral partition is

{}

1,0

∈δ

)(

zxfz

,,,, EDCBA

,, EDC

qQ ,

(10)

s ≤

Consequently, this model requires a smaller number

of sub-regions than the classical PWA model for the

same modeled system. Each sub-region has its own

dynamic described in the same way as (1) but with a

simpler MLD model that represents the system

behavior in this sub-region and includes only the

active variables in this sub-region. This partition

always implies a reduction in the size of

and/or

. For example, some control variables may not be

active in sub-regions and the auxiliary continuous

variables

depending on the

δ variables may

disappear or become fixed as

is fixed where:

(11)

⎩

⎨

⎧

=→=

1 if)(

0 if

Consequently, simplified sub-regions models can be

derived, an example of this simplification is given in

the application section.

The system is thus globally modeled as

(12)

54132

321

3211

ExEuEzEδE

zDδDuDxCy

zBδBuBxAx

++≤+

+++=

iiiii

513131

−−−

are the matrices of the i

MLD model defining the dynamics into that sub-

region.

constraints has to be included in (12). qQ ,

4.2 Reformulation of the MPC solution

At this stage, the MPC technique developed for the

PWA formalism must be rewritten to fit the new

SPMLD model. Consider the initial subsystem

(13)

zDδDuDxCy

zBδBuBxAx

321

+++=

with

δEExEzEuE

431

−+≤+−

Where

will now denote for simplification

purposes the

matrix of model i at instant (the

same notations are used for

kkkk

513131

−−−

For a given sequence over the prediction horizon

i.e. for

{

}

,,,

−++

Nkkk

IIII L , the system is

recursively defined as follows

zGδPuHxFy

zGδPuHxFx

yyyky

xxxkx

+++=

(14)

Where

[

]

21 Nkkk +++

= xxxx L

[

]

[

]

−+−+

NkkNkk

yyyuuu LL

[

]

[

]

−+−+

NkkNkk

δδδzzz LL

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−+−+

−+

kNkNk

kNk

AAC

⎥

⎦

⎤

⎢

⎣

⎡

−+++−++−+

NkkkNkkkNk

kkk

BBAABAA

BBA

LLL

MOMM

⎥

⎦

⎤

⎢

⎣

⎡

−+++−++−+

NkkkNkkkNk

kkk

BBAABAA

BBA

LLL

MOMM

⎥

⎦

⎤

⎢

⎣

⎡

−+++−++−+

NkkkNkkkNk

kkk

BBAABAA

BBA

LLL

MOMM

⎥

⎦

⎤

⎢

⎣

⎡

−+++−+−++−+−+

221

121

NkkkNkNkkkNkNk

kkk

DBAACBAAC

DBC

LLL

MOMM

⎥

⎦

⎤

⎢

⎣

⎡

−+++−+−++−+−+

221

121

NkkkNkNkkkNkNk

kkk

DBAACBAAC

DBC

LLL

MOMM

MODEL PREDICTIVE CONTROL FOR HYBRID SYSTEMS UNDER A STATE PARTITION BASED MLD

APPROACH (SPMLD)

⎥

⎦

⎤

⎢

⎣

⎡

−+++−+−++−+−+

221

121

NkkkNkNkkkNkNk

kkk

DBAACBAAC

DBC

LLL

MOMM

Then the MPC optimization problem (8) leads to the

following cost function

[]

ooo

HδzuJ +

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

= 2

(15)

where

⎥

⎦

⎤

⎢

⎣

⎡

yyy

PQPGQPHQP

PQGGQGHQG

PQHGQHRHQH

⎥

⎦

⎤

⎢

⎣

⎡

−

PQwPQFx

GQwGQFx

HQwHQFx

]2[ wQwxFQwxFQFxg

+−=

[]

(

)

[]

()

0,diag

QQQ

RRR

This technique allows choosing different weighting

factors for each sub-region according to its priority.

The constraints over the state and input domains

for each sub-region are included in the inequality

equation of the MLD model of that sub-region using

the HYSDEL program. The MPC optimization

problem (15) is solved subject to the constraints

[]

MMM ≤

⎥

⎦

⎤

⎢

⎣

⎡

231

(16)

where

⎥

⎦

⎤

⎢

⎣

⎡

−+−+−+

kNkNk

ExAAE

ExAE

ExE

⎥

⎦

⎤

⎢

⎣

⎡

−−−

−−

−

−+++−+−++−+−+

221

121

NkkkNkNkkkNkNk

kkk

EBAAEBAAE

EBE

LLL

OMM

⎥

⎦

⎤

⎢

⎣

⎡

−−

−

−+−+−++−+−+

121

NkNkNkkkNkNk

kkk

EBEBAAE

EBE

OMM

⎥

⎦

⎤

⎢

⎣

⎡

−−

−

−+−+−++−+−+

121

NkNkNkkkNkNk

kkk

EBEBAAE

EBE

OMM

The number of binary optimization variables, with

known and constant, is given by the relation

(17)

{

sjrmL

,,2,1,

L∈+=

∑

−

}

rm ,

Where

are the number of modeled logical

control and

elements respectively in the j

sub-

region at prediction time

Therefore, if the sequence

is fixed, the

problem can be solved minimizing (15) subject to

the constraints of (16). But, as only

is known

(where

is considered as known, and

depends on ), all possible sequences as in

Figure 2 have to be solved. So the number of

possible sequences is

. The optimal solution is

provided by the resolution of these

MIQPs. In

order to find the solution more quickly, these

problems are not solved independently and the

optimal value of the criterion provided by the solved

MIQP is used to bind the result of the others. It can

then be used by the B&B algorithm to cut branches.

)(kx

)(

kδ

)(kx

1−N

[

]

,*,*

1 2 s 1 2 s 1 2 s

[]

,*,

1+kk

[]

++ kkk

III

Figure 2: State transition graph of the MPC optimization

problem for a system under the SPMLD form (

N )

4.3 Compared computational burden

The global complexity of the MPC resolution with

systems under the SPMLD form is reduced. First the

related number of subsystems

is smaller than that

with the classical PWA model. Then, the B&B

technique considerably decreases the number of

solved QPs. The index sequence

imposes the

successive values of

δ over the prediction horizon

and then the succession of region on the state space

partition the state has to reach. This leads to non

feasible solutions in many sub-problems, effectively

reducing the number of solved QPs according to the

B&B technique. This is why we partition

δ vector.

First, the SPMLD technique is faster than the

classical MLD because for a known sequence of

index

, only simple B&B trees with only

optimization variables have to be solved;

i.e. smaller number of optimization binary variables

L (17), and simpler MLD models as previously

explained. Moreover, as explained, the optimization

algorithm just has to look for the control sequence

that could force the system to follow the index

)1(

−Nr

zδu ,,

and optimize the cost function with respect to all the

associated constraints. In many root nodes at level F

(Figure 3), this leads to non-feasible solution (more

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

frequent than in classical MLD approach), due to

non feasible sequence whatever the value of the

control inputs are, thus that MIQP will then quickly

be eliminated. Furthermore, if there is a solution for

a B&B tree at level F, it is considered as an upper

bound for the global optimized solution for all the

following B&B trees, which reduces the number of

solved QPs according to B&B technique.

)(k

)1(

−

[]

)1()1()(

111

−

+ Nkkk δδδ L

Figure 3: B&B trees for optimization with SPMLD

Then, the SPMLD technique is obviously faster than

the classical PWA technique. First the initial index

is completely known as the space partition only

depends on and not on (as in the PWA

model where

possible subsystems at instant

have to be examined). In addition, SPMLD models

use the B&B technique, which considerably reduces

the number of solved QPs while in classical PWA

systems all the QPs must be solved.

)(kx

4.4 Further improvements of the

optimization time

Two different techniques can be considered to

reduce the computation load for real time

applications. The first one introduces the control

horizon

, which reduces the number of unknown

future control values, i.e.

is constant for

. This decreases the number of binary optimi-

zation variables (17) a

)( ik +u

Ni ≥

nd the optimization time

(18)

{}

sjrmL

,,2,1,

L∈+=

∑∑

−

The second one, called the reach set, aims at

determining the set of possible regions that can be

reached from the actual region in next few sampling

times (Kerrigan, 2000). That is, all sequences that

cannot be obtained are not considered.

5 APPLICATION

5.1 Description of the benchmark

The proposed control strategy is applied on the three

tanks benchmark used in (Bemporad

et al., 1999).

The simplified physical description of the three

tanks system proposed by COSY as a standard

benchmark for control and fault detection problems

is presented in Figure 4 (Dolanc

et al., 1997).

Figure 4: COSY three tanks benchmark system

The system consists of three tanks, filled by two

independent pumps acting on tanks 1 and 2,

continuously manipulated from 0 up to a maximum

flow

and respectively. Four switching

valves

and

V control the flow

between the tanks, those valves are assumed to be

either completely opened or closed (

respectively). The

V manual valve controls the

nominal outflow of the middle tank. It is assumed in

further simulations that the

V and

V valves are

always closed and

V is open. The liquid levels to

be controlled are denoted

h ,

and

for each

tank respectively. The conservation of mass in the

tanks provides the following differential equations

V V V

0or 1=

h h

)

23232231313113

(

)

23232232

(

)

13131131

(

−+++=

−−=

(19)

where the

Qs denote the flows and A is the cross-

sectional area of each of the tanks. A MLD model is

derived as developed in (Bemporad et al., 1999),

introducing the following variables

(20)

231321030201

[

030201

[

23132121

[

321

[

z z z z z zz

δ δδ

V V V V QQ

h hh

where

[

]

[

]

()

2,1 )()(

2,1 )()()(

3,2,1 )()()(

3,2,1 )(1)(

333

030

=−=

=≥↔=

ihthVtz

itztzVtz

ihthttz

ihtht

iii

viii

vii

5.2 Application of MPC for the

SPMLD formalism

In this system, δδ

since the three introduced

auxiliary binary variables depend on the states, thus

and the number of sub-systems is

(21)

MODEL PREDICTIVE CONTROL FOR HYBRID SYSTEMS UNDER A STATE PARTITION BASED MLD

APPROACH (SPMLD)

Inside each sub-region, a simple MLD model is

developed, that takes into account only the system

dynamics in this sub-region. In some sub-regions a

reduction in the size of

u and appears; for

example in the sub-region where

clearly appears that the two valves

V and

V of the

input vector are not in progress, as the liquid level in

this region is always less than the valves level.

Consequently, the continuous auxiliary variables

3,2,1

and

{}

2,1=i

corresponding to the flows

that pass through the upper pipes are useless. It

results from this a simple model with:

[]

000'

=δ

{}

z z

(22)

2313

[

231321

[,']

321

[

z z

V V QQ h hh

Let us consider now the following specification:

starting from zero levels (the three tanks being

completely empty), the objective of the control

strategy is to reach the liquid levels

m 5.0

h ,

and . The MPC technique for

a SPMLD model has been implemented in

simulation to reach the level specification with

. The results are presented on Figure 5 for the

tanks levels and on Figure 6 for the control signals.

m 5.0

=h m 1.0

2=N

10 20 30

0.2

0.4

0.6

0 10 20 30

0.2

0.4

0.6

0.8

0 10 20 30

0.05

0.1

0.15

0.2

0 10 20 30

0.2

0.4

0.6

0.8

Level of the frist tank

Level of the third tank

Level of the second tank

The level of three tanks

Sampling instants

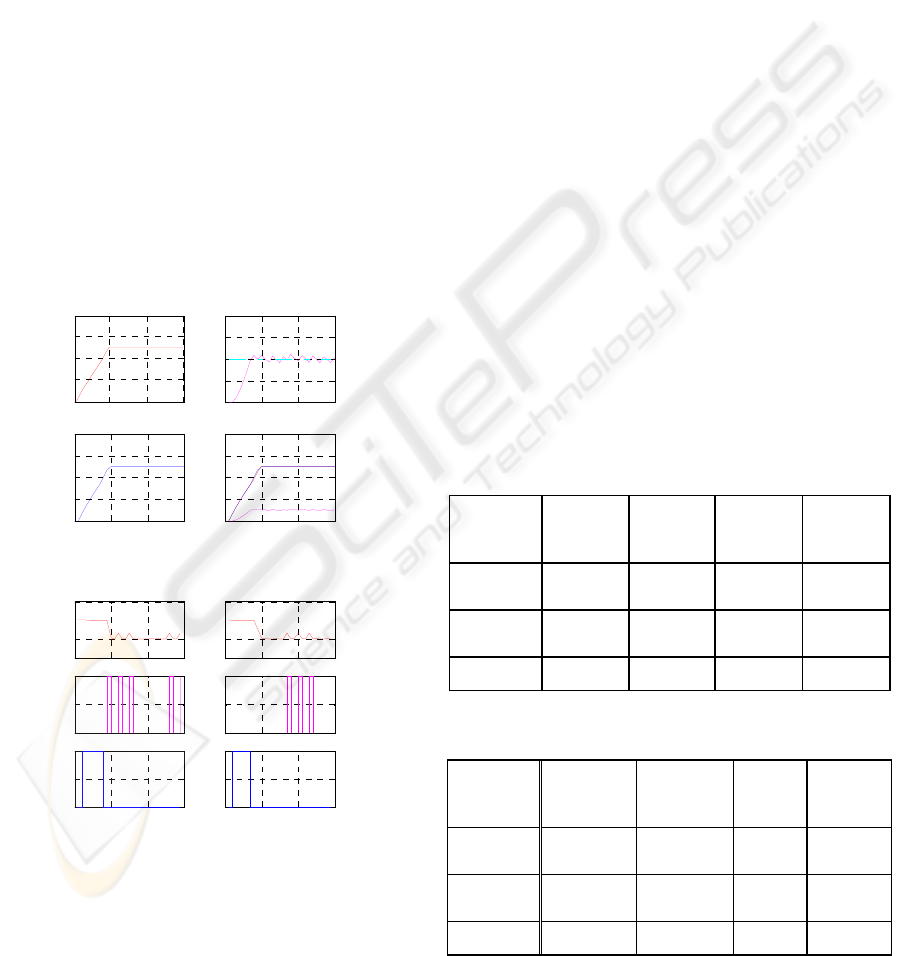
Figure 5: Water levels in the three tanks

0 10 20 30

x 10

-4

The flow (m

/5)

0 10 20 30

x 10

-4

0 10 20 30

0.5

The valve position

1 (open) - 0 (close)

0 10 20 30

0.5

0 10 20 30

0.5

0 10 20 30

0.5

Input Q1

Input Q2

V1 V2

V13

V23

Sampling instants

Figure 6: Controlled variables

The level of the third tank oscillates around 0.1 as

does not correspond to an equilibrium

point. Consequently, the system opens and closes the

two valves

V and

V to maintain the level in the

third tank around the desired level of 0.1m.

1.0

5.3 Comparison of the approaches

As a comparison purpose between the SPMLD

model, the classical MLD model and the classical

PWA model strategies, the same previous level

specification has been considered with

. The

MLD model described in (Bemporad et al., 1999)

has been used for the three tanks modeled by (20);

this MLD model transfers to a PWA model with

2=N

128

s subsystems (with 28 empty regions). The

classical PWA model has not been developed as it

needs 100 sub-models and is in fact not required to

compare complexity. For that comparison, looking

at the number of QPs that have to be solved during

optimization is sufficient.

Table 1 illustrates for

the total time

required to reach the specification level, the total

number of QPs solved, and the maximum time and

maximum QPs to find the optimized solution at each

iteration. It can be seen that the difference between

the SPMLD technique and the other classical

techniques is quite large, the SPMLD model

allowing real time implementation and avoiding

exponential explosion of the algorithm (the sampling

time of the three tanks benchmark is 10 s.). All data

given above were obtained using the MIQP Matlab

code (Bemporad and Mignone, 2000), on a 1.8 MHz

PC with 256 Mo of ram. Same comparisons are

presented with

2=N

N in table 2.

Table 1: Comparison of performances obtained with the

SPMLD model, the classical MLD model and the classical

PWA model for 2

N .

Approach

No of

QPs

solved

Max.

No. QPs

/ step

Total

time

Max.

time /

step

Classical

PWA

8 800 1 600 * *

Classical

MLD

11 130 2 089 822.97 s 138.97 s

SPMLD 832 218 15.28 s 3.90 s

Table 2: Comparison of performances obtained with the

SPMLD, MLD and PWA models for

3=N

Approach

No of QPs

solved

Max. No.

QPs / step

Total

time

Max.

time /

step

Classical

PWA

880 000 160 000 * *

Classical

MLD

25 606 6 867

5243.6

1 147.80

SPMLD 3 738 1 054 137.54 s 37.65 s

This table shows that no real time implementation is

possible with

N for the SPMLD form, although

the maximum time per iteration is much smaller in

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

this case. But it must be noticed that the results in

table 1 and 2 for the SPMLD model are achieved

without applying techniques described in section

4.4. For example using a prediction horizon

and a control horizon

N leads to the following

results enabling real time implementation

No QPs solved = 1224, Max. No QPs/step = 326

Total optimization time = 29.24 s., Max. time/step = 7.92 s.

The technique of MPC for SPMLD systems has

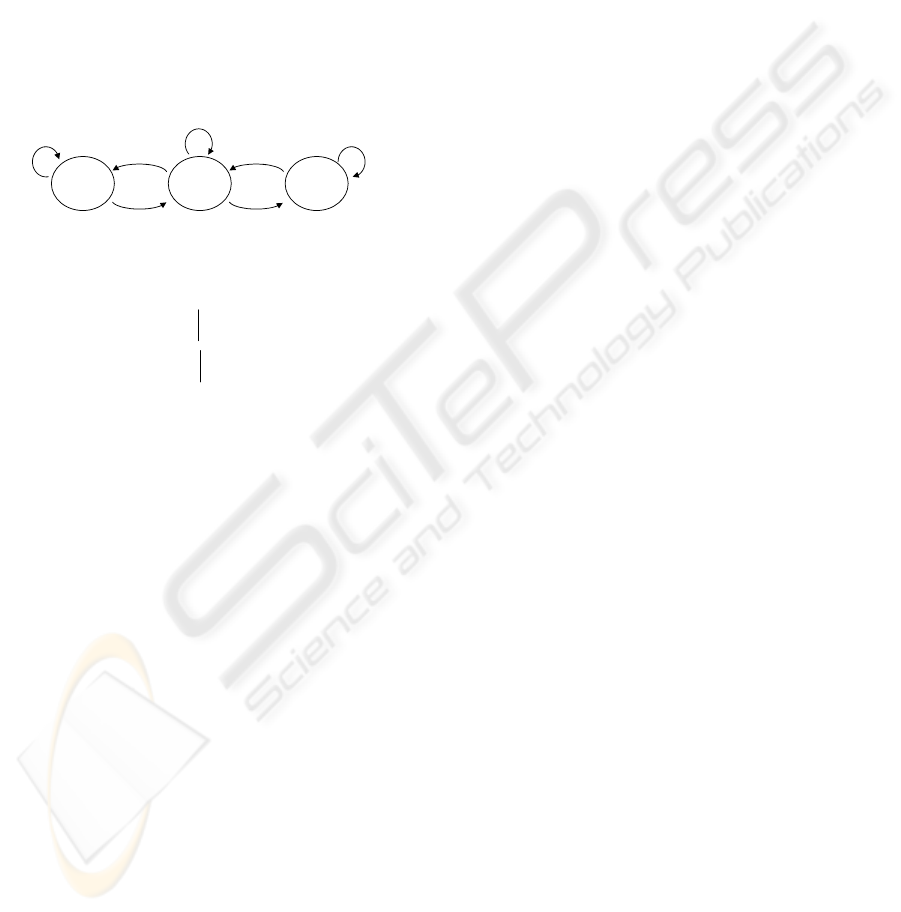
been examined also with a simple automata, where

automata of Figure 7 have been added to

V and

valves of the three tanks benchmark. We assumed

for a simplification purpose that

i.e. the

level in the third tank is always behind the h

level.

open

Wait

open

a b

close a

Figure 7: added Automata to the three tanks benchmark.

The automata of Figure 7 can be presented as follows

closeWait

bVbwaitV

aVawaitV

openopen

)&()&(

(23)

The SPMLD technique succeeds to reduce the total

optimization time to arrive to the specifications,

from 5691.4 s for the classical MLD technique to a

173.5 s, solving 3990 QPs instead of 60468 QPs

where for each sequence I,

variables as well as

the logical control variables that control the

automata are known.

6 CONCLUSION

This paper presents the SPMLD formalism. It is

developed by partitioning the feasible region

according to the auxiliary binary elements

of the

MLD model that depends on the state variables. A

reformulation of the MPC strategy for this

formalism has been presented. It is shown that the

SPMLD model successfully improves the

computational problem of the mixed Logical

Dynamical (MLD) model and Piecewise Affine

(PWA) model. Moreover, the partition into several

sub-regions enables to define particular weighting

factors according to the priority of each region.

Future work may consider examining

variables

that depends on the control inputs, by partitioning

the feasible region according to those variables also

instead of leaving them free included in the

optimization vector.

REFERENCES

Bemporad, A., 2003. “A Recursive Algorithm for

Converting Mixed Logical Dynamical Systems into an

Equivalent Piecewise Affine Form”, IEEE Trans.

Autom. Contr.

Bemporad, A., Ferrari-Trecate G., and Morari M., 2000.

Observability and controllability of piecewise affine

and hybrid systems. IEEE Trans. Automatic Control,

45(10):1864–1876.

Bemporad, A., and Mignone, D., 2000.: Miqp.m: A

Matlab function for solving mixed integer quadratic

programs. Technical Report.

Bemporad, A., Mignone, D. and Morari, M., 1999.

Moving horizon estimation for hybrid systems and

fault detection. In Proceedings of the American

Control Conference, San Diego.

Bemporad, A. and Morari, M., march 1999. Control of

systems integrating logical, dynamics, and constraints.

Automatica, 35(3):407-427.

Branicky, M.S., Borkar, V.S. and Mitter, S.K., January

1998. A unified framework for hybrid control: model

and optimal control theory. IEEE Transaction. on

Automatic. Control, 43(1): 31-45.

Dolanc, G., Juricic D., Rakar A., Petrovcic J. and Vrancic,

D., 1998. Three-tank Benchmark Test. Technical

Report Copernicus Project Report CT94-02337.

Dumur, D. and Boucher, P.,1998. A Review Introduction

to Linear GPC and Applications. Journal A, 39(4),

pp. 21-35.

Fletcher, R. and Leyffer, S., 1995. Numerical experience

with lower bounds for MIQP branch and bound.

Technical report, Dept. of Mathematics, University of

Dundee, Scotland.

Kerrigan, E., 2000. Robust Constraint Satisfaction:

Invariant sets and predictive control. PhD thesis

University of Cambridge.

Pena, M.., Camacho, E. F. and Pinon, S., 2003. Hybrid

systems for solving model predictive control of

piecewise affine system. IFAC conference, Hybrid

system analysis and design Saint Malo, France.

Sontag, E.D., April 1981: Nonlinear regulation: the

piecewise linear approach. IEEE Transaction. on

Automatic. Control, 26(2):346-358.

Torrisi, F., Bemporad, A. and Mignone, D., 2000. Hysdel

– a tool for generating hybrid models. Technical

report, AUT00-03, Automatic control laboratory, ETH

Zuerich.

MODEL PREDICTIVE CONTROL FOR HYBRID SYSTEMS UNDER A STATE PARTITION BASED MLD

APPROACH (SPMLD)