INTERACTIVE SOFTWARE FOR SYMBOLIC MODELING OF

PHYSICAL SYSTEMS USING GRAPHS

André Laurindo Maitelli

DCA – LECA – UFRN, CEP 59072–970, Natal/RN, Brazil

Gilbert Azevedo da Silva

GEINF – CEFET/RN, CEP 59015–000, Natal/RN, Brazil

Keywords: CAD/CAM, Control Education, System Modeling, Graph, Symbolic Transfer Function, Mason´s Rule.

Abstract: This paper presents a computational environment for teaching of control systems: Modsym. The software

implements a graphical interface for physical systems modeling using graphs and calculates systems transfer

functions in symbolic form. ModSym generalizes elements and dynamics variables of some physical

systems based on the energy concept. This approach allows to represent and to connect elements of different

systems in a linear graph. An algorithm implemented in the software, also presented in this paper, obtain a

signal flow graph for the system linear graph which makes possible to use the Mason’s rule in calculating of

the system transfer function.

1 INTRODUCTION

Control Engineering studies the physical systems

dynamics. The most important activities of this

engineering are modeling, analysis, simulation,

design, implementation and verification of physical

systems, (Kroumov and Inoue, 2001). The modeling

activity is an especially important step of the system

dynamics study. In this step, a mathematical model

for the system is proposed. The other activities are

realized based on this model. So, it is important to

define a model that represents the system dynamics.

The modeling activity demands a great effort of

control students. In modeling of a system, they have

to study the dynamics of each system element and to

analyze all connections between them. Due to this

hard task, a lot of control students have difficulties

in formulating and solving the system equations that

result from modeling process. So, computational

tools are frequently used as an aid to the educational

process of control courses. The information and

communication technologies have been widely

discussed in Pedagogy, (Quartiero, 1999), and in

Control Engineering, (Dorf and Bishop, 1999). A

great number of educators are also evaluating the

future directions in control education in face of the

new technologies related to this area, (Heck 1999).

However, despite the progress in computational

science, most of computers software related to

control system area is poor in the educational

process. An analysis of some available tools has

shown that these ones present a not suitable man-

machine interface. In general, they are based on

command interaction, which makes the work tedious

and difficulties the learning process, (Kroumov and

Inoue, 2001).

In this reality, this paper presents ModSym, a

computational tool for symbolic modeling of

physical systems. The software allows to model

systems of several physical domains using liner

graphs. The software aid the educational process in

control area and its purpose is to calculate system

transfer functions in symbolic form.

In modeling of physical systems, ModSym

implements an interactive and easy-to-use graphical

interface that allows connecting elements like

sources, dissipaters, stores, transformers and energy

couplers. When connections are done, the software

allows the students to calculate, step by step, the

system transfer function (STF). An important step of

this process is the generation of a signal-flow graph

(SFG) for the system. In particular, the algorithm

that makes this task is also a contribution of this

paper.

488

Laurindo Maitelli A. and Azevedo da Silva G. (2004).

INTERACTIVE SOFTWARE FOR SYMBOLIC MODELING OF PHYSICAL SYSTEMS USING GRAPHS.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 488-491

DOI: 10.5220/0001138404880491

 SciTePress

2 SYSTEM MODELING

2.1 Generalized Variables

The idea of systems as energy handling devices is

essential to modeling process using linear graphs,

(Wellstead, 1979). The energy concept implicates in

defining two generalized variables: effort and flow,

whose purpose is identify the similarities that exist

over some physical systems. The effort variable

represents a physical variable that is measured

across two distinct points of the system and the flow

variable is measured through only one system point.

The physical elements are thought of as energy

manipulators, which interact with inputs and outputs

via “energy ports”. The energetic interactions that

occur through these ports determinate just how and

in what sense energy are transmitted inside the

system. The elements are so classified in according

to number of energy ports and energy process. One-

port basic elements can be classified as sources:

effort sources (E) and flow sources (F); stores: effort

stores (ES) and flow stores (FS); and dissipaters

(ED). Two-port elements can be classified as

transformers, gyrators and couplers. Table 1 presents

generalized variables and elements for mechanical,

electrical and fluid systems.

Table 1: Generalized Variables and System Elements

System Mechanical Fluid Electrical

Effort

Velocity

v / w

Pressure

Voltage

Flow

Force/Torque

F / T

Flow

Current

Spring

Fluid Inductor

Inductor

Mass / Inertia

M / J

F. Capacitor

Capacitor

Damper

Fluid Resistor

Resistor

2.2 Linear Graphs

The Network Method is one way to systemize

physical system modeling, (Wellstead, 1979). This

method uses generalized variables and system

elements to represent a system as an oriented graph

usually known as linear graph. The graph nodes

represent points of common effort and the edges

represent the system elements.

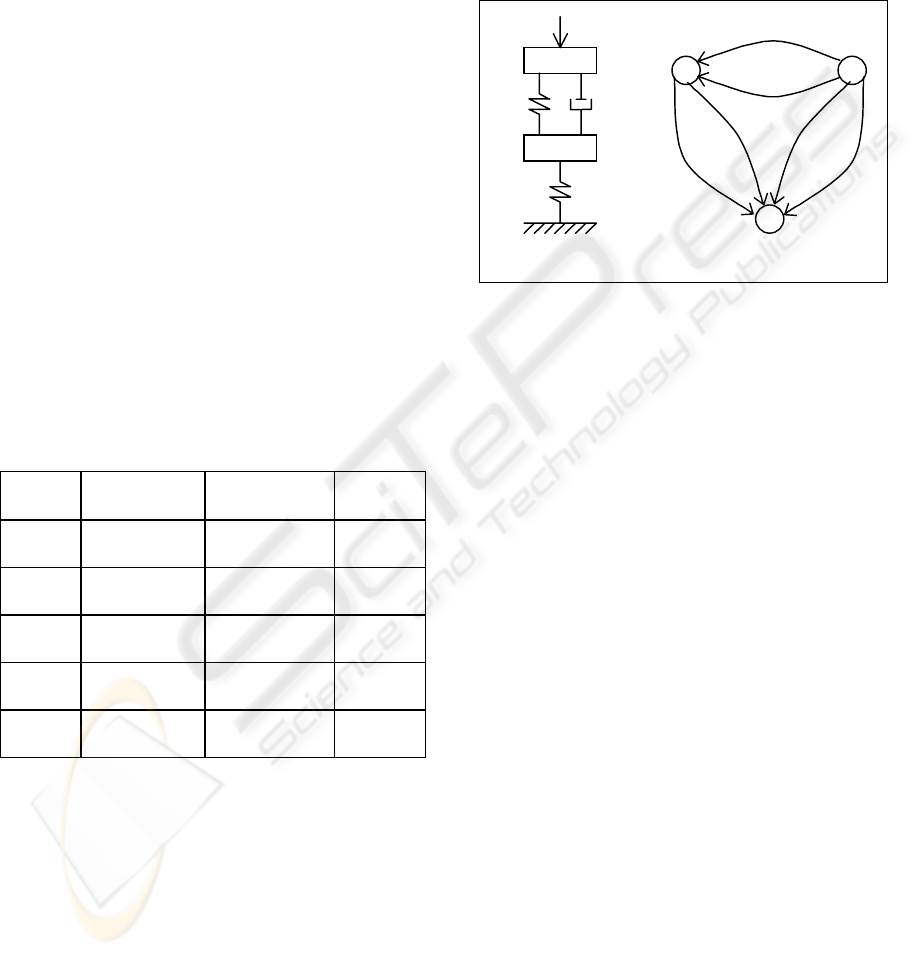
Figure 1a shows a simplified, quarter-body car

suspension. The suspension is modeled as a mass M

representing the mass of the wheel and other

components located between the leaf spring and the

road. This mass is coupled to the road through

spring K

that represents tire elasticity. The mass M

contains the car frame, car body and all components

within the body. It is connected to M

through spring

and damper B

that represent the leaf spring and

shock absorber of the suspension, (Durfee et al.,

1991).

(a) (b)

-1

Figure 1: Car Suspension Example

Figure 1b contains the linear graph for the

example. The reference and masses define the points

of common velocities that are indicated by the nodes

1 to 3. The passive elements - masses, springs and

damper - and the active element that indicates the

force F are represented by edges. All edges have a

gain given by constitutive property of the element

that describe its physical characteristics.

The constitutive properties and inter-connective

constraints on system elements can be used to obtain

a mathematical model for the system. With them,

ModSym generate a SFG for the physical system and

uses this new graph to calculate the system transfer

function using Mason’s rule (Mason, 1956).

3 MODSYM

The current version of ModSym implements two

graphical interfaces for physical system modeling:

one for linear graphs and other for signal-flow

graphs. A third interface with graphical components

will be present in a new version. This interface shall

allow users to model physical systems connecting

graphical components that represent electrical,

mechanical, fluid, thermal and magnetic elements.

3.1 Linear Graph Interface

The linear graph interface, shown in figure 2, allow

to model systems with nine types of graphical

components: 1 − node or vertex (V): linear graph

INTERACTIVE SOFTWARE FOR SYMBOLIC MODELING OF PHYSICAL SYSTEMS USING GRAPHS

489

node that represent common effort points;

2 − impedance (Z): passive one-port element that

represents energy stores and dissipaters; 3 − effort

source (E): energy source with a defined effort;

4 − controlled effort source (Ec): energy source with

effort controlled by a system variable; 5 − flow

source (F): energy source with a defined flow;

6 − controlled flow source (Fc): energy source with

flow controlled by a system variable;

7 − transformer (T): two-port element that act like

ideal transformer; 8 − gyrator (G): two-port element

that act like ideal gyrator and 9 − generic two-port

element (2).

The components palette shown at ModSym main

window aid users to select and add elements at the

system. Properties windows shown beside the graph

are used to define names, gains and elements

connections.

For calculating the system transfer function

(STF), the users have to select the its input and

output variables. Input variables must be a system

excitation and output variables can be the effort or

flow variable in any system element. The figure 3

shows a transfer function for the car suspension

example. The input and output variables were the

force F applied to the system and the velocity of the

mass M

, respectively.

Figure 3: STF for Car Suspension Example

3.2 Signal-Flow Graph Interface

The software interface for system modeling with

SFG is very similar to the interface previously

shown. It allows to model systems with two types of

graphical components: 1 − variables (V): graph

nodes that represent the signal-flow variables and

2 − transmittances (T): Graph edges that represent

the relations between those variables.

The SFG interface works in the same way of the

linear graph one.

3.3 Algorithm: Linear Graph to SFG

The algorithm linear graph to signal-flow graph

implemented at ModSym systematizes the generation

of SFG of physical systems. The aim is to use

computational algorithms, like Mason’s rule, to

obtain systems transfer functions in symbolic form.

The first algorithm step is the determination of

signal-flow graph variables. These variables are

given by effort and flow variables at all physical

system elements. So, each physical element

contributes with two SFG variables: the effort at the

element and the flow through it.

In the next step, the constitutive proprieties and

and inter-connective constraints of the system linear

graph are used to generate a equation system in

symbolic form. This system gives the relation

between the physical system excitations and the

generalized variables of the system elements.

Finally, a deep search algorithm is used to find

functions that associate each equation system

variable with the another variables. These functions

are used to determinate the SFG transmitances.

Figure 2: Linear Graph Interface

ICINCO 2004 - ROBOTICS AND AUTOMATION

490

4 EXAMPLE

4.1 Field Controlled DC Motor

Figure 4 shows a model for a field controlled DC

motor, (Dorf and Bishop, 1995). The motor converts

direct current electrical energy into rotational

mechanical energy, which is applied to a load.

J, B

Figure 4: Field Controlled DC Motor

Figure 5 shows the linear graph for DC motor.

An effort source represents the voltage source.

Generalized impedances represent the load and

electrical resistance and inductance. A controlled

flow source with gain K

proportional to field

current I

represents the motor.

Figure 5: Linear Graph for DC Motor

The SFG generated by algorithm is shown in

figure 6.

Figure 6: SFG for DC Motor

5 CONCLUSIONS

The software ModSym, presented in this paper, is a

very interesting tool for education in control and

related areas. The software can be used to solve

practical problems and to aid students in learning of

control theory.

In laboratories, the software is powerful in

physical system modeling and can aid students to

project systems and to obtain mathematical models.

The calculus of systems transfer functions that is

essential to several systems manipulations as

simulations and optimizations can be done with

precision and quickness.

In education process, the software can be used in

several courses like control, physics, mechanical an

electrical systems. The graphical resources of the

software that allow to model systems using linear

and signal-flow graphs can be used to produce high

quality educational texts. Moreover, the software

can be used to study a wide range of control systems

that aren’t available in laboratories.

REFERENCES

Dorf, R.C. and R.H. Bishop. 1995. Modern Control

Systems Addison-Wesley, MA, USA.

Dorf, R.C. & R.H. Bishop. 1999. “Teaching Modern

Control System Design”.

Proc. of the 38th IEEE

Conference on Decision and Control, Vol. 1 , pp. 364

–369.

Durfee, W.K., M.B. Wall, D. Rowell & F.K. Abbott.

1991. “Interactive Software for Dynamic System

Modeling Using Linear Graphs”.

IEEE Control

Systems Magazine

, Vol. 11(4), pp. 60-66.

Heck, B.S. 1999. “Future Directions in Control

Education”.

IEEE Control Systems Magazine, Vol.

19(5), pp. 16-17.

Kroumov, V. & H. Inoue. 2001. “Enhancing Education in

Automatic Control via Interactive Learning Tools”.

Proc. of the 40th SICE Annual Conference, pp. 220-

225.

Mason, S.J. 1956. “Feedback Theory – Further Properties

of Signal-Flow Graphs”.

Proc. IRE, Vol. 44, pp. 920-

926.

Quartiero, E.M. 1999. “As Tecnologias da Informação e

Comunicação e a Educação”.

Revista Brasileira de

Informática na Educação, Nº. 4, pp. 69-74.

Wellstead, P.E. 1979.

Introduction to Physical System

Modelling. Academic Press, London.

INTERACTIVE SOFTWARE FOR SYMBOLIC MODELING OF PHYSICAL SYSTEMS USING GRAPHS

491