SCALED GRADIENT DESCENT LEARNING RATE
Reinforcement learning with light-seeking robot
Kary Främling
Helsinki University of Technology, P.O. Box 5400, FI-02015 HUT, Finland.
Keywords: Linear function approximation, Gradient descent, Learning rate, Reinforcement learning, Light-seeking
robot
Abstract: Adaptive behaviour through machine learning is challenging in many real-world applications such as
robotics. This is because learning has to be rapid enough to be performed in real time and to avoid damage
to the robot. Models using linear function approximation are interesting in such tasks because they offer
rapid learning and have small memory and processing requirements. Adalines are a simple model for
gradient descent learning with linear function approximation. However, the performance of gradient descent
learning even with a linear model greatly depends on identifying a good value for the learning rate to use. In
this paper it is shown that the learning rate should be scaled as a function of the current input values. A
scaled learning rate makes it possible to avoid weight oscillations without slowing down learning. The
advantages of using the scaled learning rate are illustrated using a robot that learns to navigate towards a
light source. This light-seeking robot performs a Reinforcement Learning task, where the robot collects
training samples by exploring the environment, i.e. taking actions and learning from their result by a trial-
and-error procedure.
1 INTRODUCTION
The use of machine learning in real-world control
applications is challenging. Real-world tasks, such
as those using real robots, involve noise coming
from sensors, non-deterministic actions and
uncontrollable changes in the environment. In
robotics, experiments are also longer than simulated
ones, so learning must be relatively rapid and
possible to perform without causing damage to the
robot. Only information that is available from robot
sensors can be used for learning. This means that the
learning methods have to be able to handle partially
missing information and sensor noise, which may be
difficult to take into account in simulated
environments.
Artificial neural networks (ANN) are a well-
known technique
for machine learning in noisy
environments. In real robotics applications,
however, ANN learning may become too slow to be
practical, especially if the robot has to explore the
environment and collect training samples by itself.
Learning by autonomous exploration of the
environment by a learning agent is often performed
using reinforcement learning (RL) methods.
Due to these requirements, one-layer linear
fu
nction approximation ANNs (often called Adalines
(Widrow & Hoff, 1960)) are an interesting
alternative. Their training is much faster than for
non-linear ANNs and their convergence properties
are also better. Finally, they have small memory-
and computing power requirements.
However, when Adaline inputs come from
sens
ors that give values of different magnitude, it
becomes difficult to determine what learning rate to
use in order to avoid weight oscillation.
Furthermore, as shown in the experiments section of
this paper, using a fixed learning rate may be
problematic also because the optimal learning rate
changes depending on the state of the agent and the
environment. This is why the use of a scaled
learning rate is proposed, where the learning rate
value is modified according to Adaline input values.
The scaled learning rate makes learning steps of
similar magnitude independently of the input values.
It is also significantly easier to determine a suitable
value for the scaled learning rate than it is for a fixed
learning rate.
After this introduction, Section 2 gives
back
ground information about gradient descent
learning and RL. Section 3 defines the scaled
3
Främling K. (2004).
SCALED GRADIENT DESCENT LEARNING RATE - Reinforcement learning with light-seeking robot.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 3-11
DOI: 10.5220/0001138600030011
Copyright
c
 SciTePress

learning rate, followed by experimental results in
Section 4. Related work is treated in Section 5,
followed by conclusions.
2 GRADIENT DESCENT
REINFORCEMENT LEARNING
In gradient descent learning, the free parameters of a
model are gradually modified so that the difference
between the output given by a model and the
corresponding “correct” or target value becomes as
small as possible for all training samples available.
In such supervised learning, each training sample
consists of input values and the corresponding target
values. Real-world training samples typically
involve noise, which means that it is not possible to
obtain a model that would give the exact target value
for all training samples. The goal of learning is
rather to minimize a statistical error measure, e.g.
the Root Mean Square Error (RMSE)
()
∑
=
−=
M
k
k
j
k
j
at
M
RMSE
1
2
1
(1)
where M is the number of training examples, t
k
j
is the target value for output j and training sample k
and a
k
j
is the model output for output j and training
sample k. In RL tasks, each output a
j
typically
corresponds to one possible action.
RL differs from supervised learning at least in
the following ways:
• The agent has to collect the training samples by
exploring the environment, which forces it to
keep a balance between exploring the
environment for new training samples and
exploiting what it has learned from the existing
ones (the exploration/exploitation trade-off). In
supervised learning, all training samples are
usually pre-collected into a training set, so
learning can be performed off-line.
• Target values are only available for the used
actions. In supervised learning, target values are
typically provided for all actions.
• The target value is not always available directly;
it may be available only after the agent has
performed several actions. Then we speak about
a delayed reward learning task.
RL methods usually model the environment as a
Markov Decision Process (MDP), where every state
of the environment needs to be uniquely identifiable.
This is why the model used for RL learning is often
a simple “lookup-table”, where each environment
state corresponds to one row (or column) in the table
and the columns (or rows) correspond to possible
actions. The values of the table express how “good”
each action is in the given state.
Lookup-tables are not suitable for tasks
involving sensorial noise or other reasons for the
agent not being able to uniquely identify the current
state of the environment (such tasks are called
hidden state tasks). This is one of the reasons for
using state generalization techniques instead of
lookup-tables. Generalisation in RL is based on the
assumption that an action that is good in some state
is probably good also in “similar” states. Various
classification techniques have been used for
identifying similar states. Some kind of ANN is
typically used for the generalisation. ANNs can
handle any state descriptions, not only discrete ones.
Therefore they are well adapted for problems
involving continuous-valued state variables and
noise, which is usually the case in robotics
applications.
2.1 Gradient descent learning with
Adalines
The simplest ANN is the linear Adaline (Widrow &
Hoff, 1960), where neurons calculate their output
value as a weighted sum of their input values
∑
=
=
N
i
jiij
wssa
1
,
)(
(2)
where w
i,j
is the weight of neuron j associated
with the neuron’s input i, a
j
(s) is the output value of
neuron j, s
i
is the value of input i and N is the
number of inputs. They are trained using the
Widrow-Hoff training rule (Widrow & Hoff, 1960)
ijjji
new
ji
satww )(
,,
−+= α
(3)
where
α is a learning rate. The Widrow-Hoff
learning rule is obtained by inserting equation (2)
into the RMSE expression and taking the partial
derivative against s
i
. It can easily be shown that
there is only one optimal solution for the error as a
function of the Adaline weights. Therefore gradient
descent is guaranteed to converge if the learning rate
is selected sufficiently small.
When the back propagation rule for gradient
descent in multi-layer ANNs was developed
(Rumelhart et al., 1988), it became possible to learn
non-linear function approximations and
classifications. Unfortunately, learning non-linear
functions by gradient descent tends to be slow and to
converge to locally optimal solutions.
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
4

2.2 Reinforcement learning
RL methods often assume that the environment can
be modelled as a MDP. A (finite) MDP is a tuple
M=(S,A,T,R), where: S is a finite set of states; A =
{a
1
, …, a
k
} is a set of k ≥ 2 actions; T = [P
sa
(·) | s ∈
S, a ∈ A} are the next-state transition probabilities,
with P
sa
(s’) giving the probability of transitioning to
state s’ upon taking action a in state s; and R
specifies the reward values given in different states s
∈ S. RL methods are based on the notion of value
functions. Value functions are either state-values
(i.e. value of a state) or action-values (i.e. value of
taking an action in a given state). The value of a
state s ∈ S can be defined formally as
()
⎭
⎬
⎫
⎩
⎨
⎧
==
∑
∞
=
++
0
1
k
tkt
k
ssrEsV γ
π
π
(4)
where V
π
(s) is the state value that corresponds to
the expected return when starting in s and following
policy
π thereafter. The factor r
t+k+1
is the reward
obtained when arriving into states s
t+1
, s
t+2
etc. γ
k
is a
discounting factor that determines to what degree
future rewards affect the value of state s.
Action value functions are usually denoted
Q(s,a), where a ∈ A. In control applications, the goal
of RL is to learn an action-value function that allows
the agent to use a policy that is as close to optimal as
possible. However, since the action-values are
initially unknown, the agent first has to explore the
environment in order to learn it.
2.2.1 Exploring the environment for
training samples
Although convergence is guaranteed for Widrow-
Hoff learning in Adalines, in RL tasks convergence
of gradient descent cannot always be guaranteed
even for Adalines (Boyan & Moore, 1995). This is
because the agent itself has to explore the
environment and collect training samples by
exploring the environment. If the action selection
policy
π does not make the agent collect relevant
and representative training samples, then learning
may fail to converge to a good solution. Therefore,
the action selection policy must provide sufficient
exploration of the environment to ensure that “good”
training samples are collected. At the same time, the
goal of training is to improve the performance of the
agent, i.e. the action selection policy so that the
learned model can be exploited.
Balancing the exploration/exploitation trade-off
is one of the most difficult problems in RL for
control (Thrun, 1992). A random search policy
achieves maximal exploration, while a greedy policy
gives maximal exploitation by always taking the
action that has the highest action value. A commonly
used method for balancing exploration and
exploitation is to use
ε -greedy exploration
1
, where
the greedy action is selected with probability (1-
ε )
and an arbitrary action is selected with probability
ε
using a uniform probability distribution. This
method is an undirected exploration method in the
sense that it does not use any task-specific
information. Another undirected exploration method
selects actions according to Boltzmann-distributed
probabilities
∑
=
k
ki
ii
j
TasQ
TasQ
a
)/),(exp(
)/),(exp(
)(Prob
(5)
where T (called temperature) adjusts the
randomness of action selection. The main difference
between this method and
ε -greedy exploration is that
non-greedy actions are selected with a probability
that is proportional to their current value estimate,
while
ε -greedy exploration selects non-greedy
actions randomly.
Directed exploration uses task-specific
knowledge for guiding exploration. Many such
methods guide the exploration so that the entire state
space would be explored in order to learn the value
function as well as possible. In real-world tasks
exhaustive exploration may be impossible or
dangerous. However, a technique called optimistic
initial values offers a possibility of encouraging
exploration of previously un-encountered states
mainly in the beginning of exploration. It can be
implemented by using initial value function
estimates that are bigger than the expected ones.
This gives the effect that unused actions have bigger
action value estimates than used ones, so unused
actions tend to be selected rather than already used
actions. When all actions have been used a sufficient
number of times, the true value function overrides
the initial value function estimates. In this paper,
ε -
greedy exploration is used for exploration. The
effect of using optimistic initial values on learning is
also studied.
2.2.2 Delayed reward
When reward is not immediate for every state
transition, rewards somehow need to be propagated
“backwards” through the state history. Temporal
Difference (TD) methods (Sutton, 1988) are
currently the most used RL methods for handling
delayed reward. TD methods update the value of a
state not only based on immediate reward, but also
1
Thrun (1992) calls this semi-uniform
distributed exploration
SCALED GRADIENT DESCENT LEARNING RATE - Reinforcement learning with light-seeking robot
5

based on the discounted value of the next state of the
agent. Therefore TD methods update the value
function on every state transition, not only after
transitions that result in direct reward. When reward
has been “temporally back propagated” a sufficient
number of times, these discounted reward values can
be used as target values for gradient descent learning
(Barto, Sutton & Watkins, 1990). Such gradient
descent learning allows using almost any ANN as
the model for RL, but unfortunately the MDP
assumption underlying TD methods often gives
convergence problems.
Delayed reward tasks are out of the scope of this
paper, which is the reason why such tasks are not
analysed more deeply here. Good overviews on
delayed reward are (Kaelbling, Littman & Moore,
1996) and (Sutton & Barto, 1998). The main goal of
this paper is to show how scaling the Adaline
learning rate improves learning, which is illustrated
using an immediate reward RL task.
3 SCALED LEARNING RATE
In methods based on gradient descent, the learning
rate has a great influence on the learning speed and
on if learning succeeds at all. In this section it is
shown why the learning rate should be scaled as a
function of the input values of Adaline-type ANNs.
Scaling the learning rate of other ANNs is also
discussed.
3.1 Adaline learning rate
If we combine equations (2) and (3), we obtain the
following expression for the new output value after
updating Adaline weights using the Widrow-Hoff
learning rule:
()
∑
∑∑
∑
∑
=
==
=
=
−+
=−+
=−+
==
N
i
jjij
N
i
N
i
jjijii
N
i
ijjjii
N
i
new
jii
new
j
atsa
atsws
satws
wssa
1
2
11
2
,
1
,
1
,
)(
)(
)(
)(
α
α
α
(6)
where a
new
j
(s) is the new output value for output j
after the weight update when the input values s are
presented again. If the learning rate is set to
α = 1,
then a
new
j
(s) would be exactly equal to t
j
if the
expression
∑
=
−
N
i
jji
ats
1
2
)(
(7)
is multiplied by
∑
=
N
i
i
s
1
2
1
(8)
Then, by continuing from equation (6):
jjjj
N
i
i
N
i
jjij
new
j
tata
satsa
sa
=−+
=−+
=
∑∑
==
)(
)(
)(
1
2
1
2
α
α
(9)
when setting
α = 1. Multiplying (7) by (8) scales
the weight modification in such a way that the new
output value will approach the target value with the
ratio given by the learning rate, independently of the
input values s. In the rest of the paper, the term
scaled learning rate (slr) will be used for denoting a
learning rate that is multiplied by expression (8).
If the value of the (un-scaled) learning rate is
greater than the value given by expression (8), then
weights are modified so that the new output value
will be on the “opposite side” of the target value in
the gradient direction. Such overshooting easily
leads to uncontrolled weight modifications, where
weight values tend to oscillate towards infinity. This
kind of weight oscillations usually makes learning
fail completely.
The squared sum of input values in expression
(8) cannot be allowed to be zero. This can only
happen if all input values s
i
are zero. However, the
bias term used in most Adaline implementations
avoids this. A bias term is a supplementary input
with constant value one, by which expression (2) can
represent any linear function, no matter what is the
input space dimensionality. Most multi-layer ANNs
implicitly also avoid situations where all Adaline
input values would be zero at the same time. This is
studied more in detail in the following section.
3.2 Non-linear, multi-layer ANNs
In ANNs, neurons are usually organized into layers,
where the output values of neurons in a layer are
independent of each other and can therefore be
calculated simultaneously. Figure 1 shows a feed-
forward ANN with one input and one output (there
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
6

may be an arbitrary number of both). ANN input
values are distributed as input values to the hidden
neurons of the hidden layer. Hidden neurons usually
have a non-linear output function with values limited
to the range [0, 1]. Some non-linear output functions
have values limited to the range [-1, 1].
t
o
s
Figure 1: Three-layer feed-forward ANN with sigmoid
outputs in hidden layer and linear output layer.
A commonly used output function for hidden
neurons is the sigmoid function
A
e
Afo
−
+
==
1
1
)(
(10)
where o is the output value and A is the weighted
sum of the inputs (2). The output neurons of the
output layer may be linear or non-linear. If they are
linear, they are usually Adalines.
Learning in multi-layer ANNs can be performed
in many ways. For ANNs like the one in Figure 1, a
gradient descent method called back-propagation is
the most used one (Rumelhart et al., 1988). For such
learning, two questions arise:
• Is it possible to use a scaled learning rate also
for non-linear neurons?
• If the output layer (or some other layer) is an
Adaline, is it then useful to use the scaled
learning rate?
The answer to the first question is probably “no”.
The reason for this is that functions like the sigmoid
function (10) do not allow arbitrary output values.
Therefore, if the target value is outside the range of
possible output values, then it is not possible to find
weights that would modify the output value so that it
would become exactly equal to the target value.
Instead, the learning rate of non-linear neurons is
usually dynamically adapted depending on an
estimation of the steepness of the gradient over
several training steps (Haykin, 1999).
The answer to the second question is ”maybe”. If
Adaline inputs are limited to the range [0, 1], then
the squared sum in (8) remains limited. Still, in the
beginning of training, hidden neuron outputs are
generally very small. Then a scaled learning rate
might accelerate output layer learning, while
slowing down when hidden neurons become more
activated. This could be an interesting direction of
future research to investigate.
4 EXPERIMENTAL RESULTS
Experiments were performed using a robot built with
the Lego Mindstorms Robotics Invention System
(RIS). The RIS offers a cheap, standard and simple
platform for performing real-world tests. In addition
to Lego building blocks, it includes two electrical
motors; two touch sensors and one light sensor. The
main block contains a small computer (RCX) with
connectors for motors and sensors. Among others,
the Java programming language can be used for
programming the RCX.
Figure 2: Lego Mindstorms robot. Light sensor is at the
top in the front, directed forwards. One touch sensor is
installed at the front and another at the rear.
The robot had one motor on each side; touch sensors
in the front and in the back and a light sensor
directed straight forward mounted in the front
(Figure 2). Robots usually have more than one light
sensor, which were simulated by turning the robot
around and getting light readings from three
different directions. One light reading was from the
direction straight forward and the two others about
15 degrees left/right, obtained by letting one motor
go forward and the other motor backward for 250
milliseconds and then inversing the operation. The
light sensor reading from the forward direction after
performing an action is directly used as the reward
value, thus avoiding hand tuning of the reward
function.
Five actions are used, which consist in doing one
of the following motor commands for 450
milliseconds: 1) both motors forward, 2/3) one
forward, other stopped, 4/5) one forward, other
backward. Going straight forward means advancing
about 5 cm, actions 2/3 going forward about 2 cm
SCALED GRADIENT DESCENT LEARNING RATE - Reinforcement learning with light-seeking robot
7

and turning about 15 degrees and actions 4/5 turning
about 40 degrees without advancing.
The robot starts about 110 centimetres from the
lamp, initially directed straight towards it. Reaching
a light value of 80 out of 100 signifies that the goal
is reached, which means one to fifteen centimetres
from the lamp depending on the approach direction
and sensor noise. In order to reach the goal light
value, the robot has to be very precisely directed
straight towards the lamp. The lamp is on the floor
level and gives a directed light in a half-sphere in
front of it. If the robot hits an obstacle or drives
behind the lamp, then it is manually put back to the
start position and direction. The test room is an
office room with noise due to floor reflections, walls
and shelves with different colours etc. The robot
itself is also a source of noise due to imprecise
motor movements, battery charge etc. However, the
light sensor is clearly the biggest source of noise as
shown in Figure 3, where light sensor samples are
indicated for two different levels of luminosity.
15
17
19
21
23
25
27
1 9
17 25 33 41 49 57 65 73 81 89 97
105 113 121 129 137 14
5
sample index
light sensor value
0
5
10
15
20
25
30
35
40
45
18 19 20 21 22 23 24 25 26
light sensor value
number of samples
50
52
54
56
58
60
62
64
66
1 9
17 25 33 41 49 57 65 73 81 89 97
105 113 121 129 137 145
sample index
light sensor value
0
5
10
15
20
25
30
35
52 53 54 55 56 57 58 59 60 61 62 63 64 6
5
light sensor value
number of samples
Figure 3: 150 light samples for two different light
conditions, taken with 500 millisecond intervals. Average
values are 22.5 and 60.0. Raw values are shown to the left,
value distribution to the right.
Table 1: Hand-coded weights. One row per action, one
column per state variable (light sensor reading).
Action
Left Middle Right
Forward 0.1 0.8 0.1
Left/forward 0.6 0.3 0.1
Right/forward 0.1 0.3 0.6
Left 0.6 0.2 0.2
Right 0.2 0.2 0.6
When using an ANN there is one output per action,
where the output value corresponds to the action-
value estimate of the corresponding action. With
five actions and three state variables, a 5x3 weight
matrix can represent the weights (no bias input used
here). A “hand-coded agent” with pre-defined
weights (Table 1) was used in order to prove that an
Adaline linear function approximator can solve the
control task and as a reference for judging how good
the performance is for learning agents. These
weights were determined based on the principle that
if the light value is greatest in the middle, then make
the forward-going action have the biggest output
value. In the same way, if the light value is greater to
the left, then favour some left-turning action and
vice versa for the right side. The hand-coded agent
reached the goal after a 30-episode average of about
17 steps.
Learning agents used the same Adaline
architecture as the hand-coded agent. Weights are
modified by the Widrow-Hoff training rule (3). All
agents used
ε -greedy exploration with ε = 0.2, which
seemed to be the best value after experimentation.
Tests were performed both with weights initialised
to small random values in the range [0, 0.1) and with
weights having optimistic initial values in the range
[0, 1). Such weights are optimistic because their
expected sum per action neuron is 1.5, while weight
values after training should converge to values
whose sum is close to one. This is because state
variable values and reward values are all light sensor
readings, so the estimated reward value should be
close to at least one of the state variable values. If
the RL is successful, then the estimated reward
should even be a little bit bigger since the goal by
definition of RL is to make the agent move towards
states giving higher reward.
An un-scaled learning rate value of 0.0001 was
used after a lot of experimentation. This value is a
compromise. Far from the lamp, light sensor values
are about 10, so expression (8) gives the value 1/(10
2
+ 10
2
+ 10
2
) = 0,00333…. Close to the lamp, light
sensor values approach 80, so the corresponding
value would be 0.00005. According to expression
(8), the un-scaled learning rate value 0.0001
corresponds to light sensor values around 58, which
is already close to the lamp. Therefore, excessive
weight modifications probably occur close to the
lamp, but then the number of steps remaining to
reach the goal is usually so small that weights do not
have the time to oscillate.
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
8

0
10
20
30
40
50
60
70
80
90
12345678910
episode number
number of steps
lr=0.0001
slr=0.8
Figure 4: Comparison between static (lr) and scaled (slr)
learning rate. Averages for 10 runs.
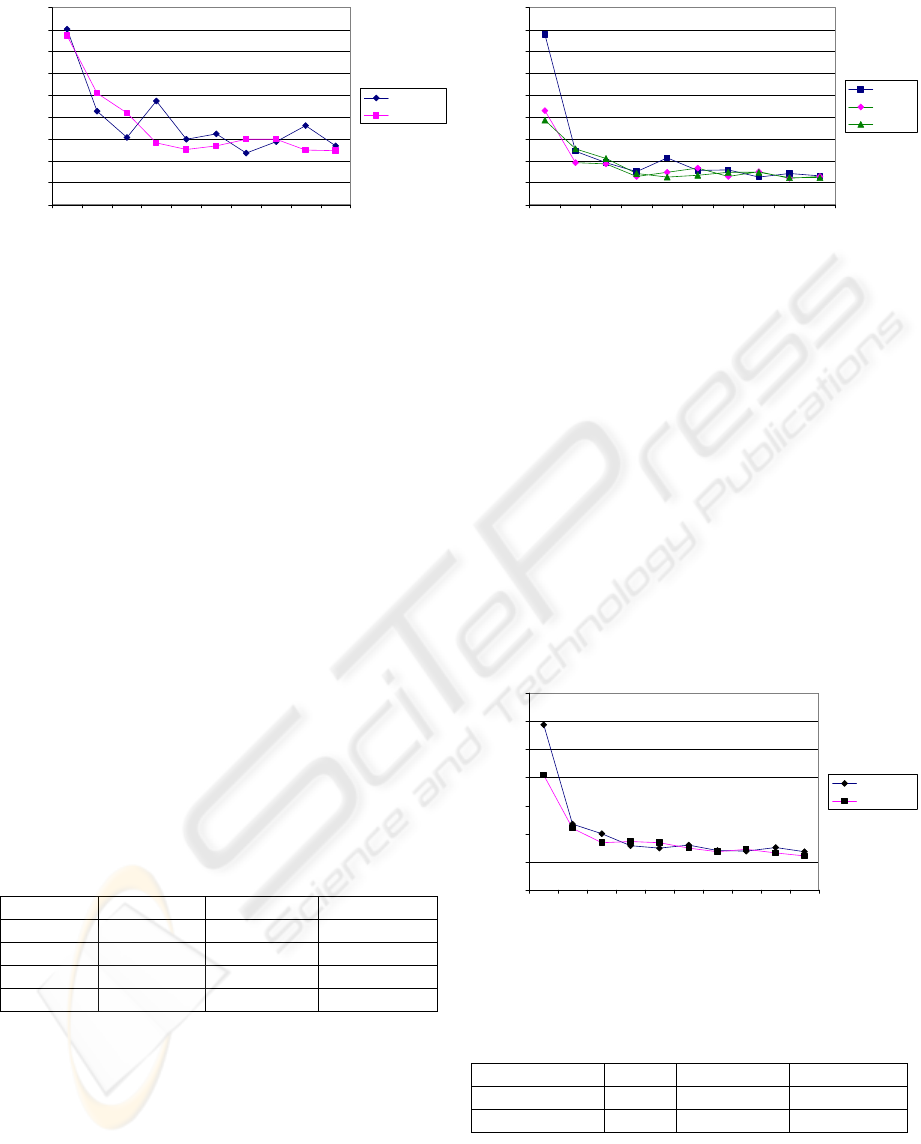
Figure 4 compares the performance of an agent
using the un-scaled learning rate 0.0001 and an
agent using slr = 0.8. With this scaled learning rate,
the first episode is slightly faster. Convergence is
also much smoother with the scaled learning rate
than with the un-scaled learning rate. The statistics
shown in Table 2 further emphasize the advantage of
using a scaled learning rate. The total number of
steps is slightly smaller, but the average length of
the last five episodes is clearly lower for the agents
using the scaled learning rate. This is most probably
because the un-scaled learning rate sometimes
causes excessive weight modifications that prevent
the agent from converging to optimal weights.
The number of manual resets is a further
indication of excessive weight modifications. One
bad light sensor reading may be sufficient to make
the robot get stuck into using the same action for
several steps. If that action happens to be going
straight forward, then the robot usually hits a wall
after a few steps. Reducing the value of the un-
scaled learning rate could reduce this phenomenon,
but it would also make learning slower.
Table 2: Statistics for agents using different learning rates.
Averages for 10 runs.
Agent Total Aver. 5 last Man. resets
lr=0.0001 378 29.5 30
slr=0.2 458 28.6 18
slr=0.5 355 27.7 10
slr=0.8 359 27.1 10
Figure 5 compares the performance of agents using
different values for the scaled learning rate. All
graphs are smooth and converge nearly as rapidly.
This result shows that the scaled learning rate is
tolerant to different values. The meaning of the
scaled learning rate is also easy to understand (i.e.
“percentage of modification of output value towards
target value”), so determining a good value for the
scaled learning rate is easier than for the un-scaled
learning rate.
0
20
40
60
80
100
120
140
160
180
12345678910
episode number
number of steps
slr=0.2
slr=0.5
slr=0.8
Figure 5: Results for different values of scaled learning
rate. Averages for 10 runs.
Figure 6 and Table 3 compare the performance of
agents whose weights are initialised with random
values from the range [0, 0.1) and agents whose
weights are initialised with optimistic initial values,
i.e. random values from the range [0, 1). Using
optimistic initial values clearly gives faster initial
exploration. The number of manual resets with
optimistic initial values is also lower for agents
using slr = 0.5 and slr = 0.8, but instead it is higher
for lr = 0.0001 and slr = 0.2.
Finally, when setting
ε = 0 after 10 episodes, i.e.
always taking the greedy action, the trained agents
had identical performance as the hand-coded agent.
However, one should remember that learning agents
could also adapt to changes in the environment or
differences in sensor sensibility, for instance.
0
20
40
60
80
100
120
140
12345678910
episode number
number of steps
init[0, 0.1)
init[0, 1)
Figure 6: Results for different initial weights. Averages for
20 runs.
Table 3: Statistics for different initial weights. Averages
for 20 runs.
Initial weights Total Aver. 5 last Man. resets
[0, 0.1) 411 29.1 33
[0, 1) 364 27.3 35
SCALED GRADIENT DESCENT LEARNING RATE - Reinforcement learning with light-seeking robot
9

5 RELATED WORK
The amount of literature on gradient descent
learning is abundant. One of the most recent and
exhaustive sources on the subject is (Haykin, 1999).
Adjusting the Adaline learning rate has been studied
previously at least by Luo (1991), who shows that
the Adaline learning rate should be reduced during
learning in order to avoid “cyclically jumping
around” the optimal solution. References in (Luo,
1991) also offer a good overview of research
concerning the gradient descent learning rate.
However, to the author’s knowledge, the concept of
scaled learning rate introduced in this paper is new.
RL has been used in many robotic tasks, but
most of them have been performed in simulated
environments. Only few results have been reported
on the use of RL on real robots. The experimental
setting used here resembles behavior learning
performed by Lin (1991) and Mahadevan & Connell
(1992). Behavioral tasks treated by them include
wall following, going through a door, docking into a
charger (guided by light sensors), finding boxes,
pushing boxes and getting un-wedged from stalled
states. Some of these behaviors are more challenging
than the light-seeking behavior used in this paper,
but the simple linear Adaline model used here for
state generalization greatly simplifies the learning
task compared to previous work. An example of
non-RL work on light-seeking robots is Lebeltel et
al. (2004).
6 CONCLUSIONS
One of the most important advantages of the scaled
learning rate presented in this paper is that it is easy
to understand the signification of the values used for
it. Evidence is also shown that the scaled learning
rate improves learning because it makes the network
output values approach the corresponding target
values with a similar amount independently of the
input values. Experimental results with a real-world
light-seeking robot illustrate the improvement in
learning results by using the scaled learning rate.
It seems rather surprising that a scaled learning
rate has not been used yet, according to the author’s
best knowledge. One explanation might be that in
supervised learning tasks, the training samples are
usually available beforehand, which makes it
possible to normalize them into suitable values. In
real-world RL tasks, with constraints on learning
time and the availability of training samples, this
may not be possible. Using multi-layer non-linear
ANNs also might reduce the utility of scaling the
learning rate, as explained in section 3.2.
In addition to the scaled learning rate, the RL
exploration/exploitation trade-off is also addressed
in the paper. The exploration policy used determines
the quality of collected training samples and
therefore greatly affects learning speed and the
quality of learned solutions. Empirical results are
shown mainly on the advantages of using optimistic
initial values for the network weights when possible.
Future work includes improving exploration
policies and handling delayed reward. Obtaining
further results on the use of the scaled learning rate
for other than RL tasks would also be useful.
ACKNOWLEDGEMENTS
I would like to thank Brian Bagnall for writing the
article “Building a Light-Seeking Robot with Q-
Learning“, published on-line on April 19 , 2002. It
gave me the idea to use the Lego Mindstorms kit and
his source code was of valuable help.
th
REFERENCES
Barto, A.G., Sutton, R.S., Watkins C.J.C.H. (1990).
Learning and Sequential Decision Making. In M.
Gabriel and J. Moore (eds.), Learning and
computational neuroscience : foundations of adaptive
networks. M.I.T. Press.
Boyan, J. A., Moore, A. W. (1995). Generalization in
Reinforcement Learning: Safely Approximating the
Value Function. In Tesauro, G., Touretzky, D., Leen,
T. (eds.), NIPS'1994 proc., Vol. 7. MIT Press, 369-
376.
Haykin, S. (1999). Neural Networks - a comprehensive
foundation. Prentice-Hall, New Jersey, USA.
Kaelbling, L.P., Littman, M.L., Moore, A.W. (1996).
Reinforcement Learning: A Survey. Journal of
Artificial Intelligence Research, Vol. 4, 237-285.
Lebeltel, O., Bessière, P., Diard, J., Mazer, E. (2004).
Bayesian Robot Programming. Autonomous Robots,
Vol. 16, 49-79.
Lin, L.-J. (1991). Programming robots using
reinforcement learning and teaching. In Proc. of the
Ninth National Conference on Artificial Intelligence
(AAAI), 781-786.
Luo, Z. (1991). On the convergence of the LMS algorithm
with adaptive learning rate for linear feedforward
networks. Neural Computation, Vol. 3, 226-245.
Mahadevan, S., Connell, J. (1992). Automatic
Programming of Behavior-based Robots using
Reinforcement Learning. Artificial Intelligence, Vol.
55, Nos. 2-3, 311-365.
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
10

Rumelhart, D. E., McClelland, J. L. et al. (1988). Parallel
Distributed Processing Vol. 1. MIT Press,
Massachusetts.
Sutton, R. S. (1988). Learning to predict by the method of
temporal differences. Machine Learning, Vol. 3, 9-44.
Sutton, R.S., Barto, A.G. (1998). Reinforcement Learning.
MIT Press, Cambridge, MA.
Thrun, S.B. (1992). The role of exploration in learning
control. In DA White & DA Sofge, (eds.), Handbook
of Intelligent Control: Neural, Fuzzy and Adaptive
Approaches. Van Nostrand Reinhold, New York.
Widrow, B., Hoff, M.E. (1960). Adaptive switching
circuits. 1960 WESCON Convention record Part IV,
Institute of Radio Engineers, New York, 96-104.
SCALED GRADIENT DESCENT LEARNING RATE - Reinforcement learning with light-seeking robot
11