
POSITION AND ORIENTATION CONTROL OF A TWO-WHEELED
DIFFERENTIALLY DRIVEN NONHOLONOMIC MOBILE ROBOT
Frederico C. Vieira Adelardo A. D. Medeiros Pablo J. Alsina Ant
ˆ
onio P. Ara
´
ujo Jr.
Federal University of Rio Grande do Norte – Departament of Computer Engineering and Automation
UFRN-CT-DCA – Campus Universit
´
ario – 59072-970 Natal RN Brazil
Keywords:
Nonholonomic robots, robot control, stabilization control, linear modeling of robots.
Abstract:
This paper addresses the dynamic stabilization problem of a two-wheeled differentially driven nonholonomic
mobile robot. The proposed strategy is based on changing the robot control variables from x, y and θ to
s and θ, where s represents the robot linear displacement. Using this model, the nonholonomic constraints
disappear and we show how the linear control theory can be used to design the robot controllers. This control
strategy only needs the robot localization (x, y, θ), not requiring any velocity measurement or estimation. The
complete derivation of the control strategy and some simulated results are presented.
1 INTRODUCTION
There are many feedback controllers proposed in the
literature (Aicardi et al., 1995; d’Andrea Novel et al.,
1995; Lizarralde, 1998; Samson, 1993; Tanner and
Kyriakopoulos, 2002; Yang and Kim, 1999) for non-
holonomic wheeled mobile robots. Most of these
strategies only deal with the problem of kinematic
compensation (Aicardi et al., 1995; d’Andrea Novel
et al., 1995; Samson, 1993). Pure kinematic con-
trollers lie on the simplification that the generated
control signal is instantaneously applied to the robot
actuators, not taking into account the dynamic effects.
Recently, some control strategies have been pro-
posed to deal with dynamic compensation of mobile
robots (Lages and Hemerly, 2000; Lizarralde, 1998;
Tanner and Kyriakopoulos, 2002). Most of them are
derived via Lyapunov techniques and do not present
a correspondence between the controller parameters
and the robot dynamic behavior. Many of the dy-
namic control laws also requires the measurement of
the robot velocities, not always accurate or available.
The control strategy proposed on this paper ad-
dresses the dynamic compensation of mobile robots
and only requires information about the robot local-
ization. The problem classification is presented on
section 2 and the kinematic and dynamic model of
the considered robot, on section 3. The control sys-
tem design is presented on section 4 and some results
and final considerations, on sections 5 and 6.
2 PROBLEM CLASSIFICATION
There are two main problems in mobile robots con-
trol: the trajectory tracking problem and the stabilisa-
tion problem.
The stabilisation problem states that the robot must
reach a desired configuration (x
d
, y
d
and θ
d
) start-
ing from a given initial configuration (x
0
, y
0
and θ
0
)
(Luca et al., 1998). This control problem is also
known as a parking problem. There are several feed-
back controllers proposed in the literature for the sta-
bilisation problem (Aicardi et al., 1995; Lizarralde,
1998; Tanner and Kyriakopoulos, 2002), some of
them with the previously presented limitations.
In the trajectory tracking problem, the robot must
reach and follow a trajectory in the Cartesian space
starting from a given initial configuration (Luca et al.,
1998). There are several feedback controllers pro-
posed in the literature that address only the trajectory
tracking problem (Oliveira and Lages, 2001; Samson,
1993; Yang and Kim, 1999).
The trajectory tracking problem is simpler than the
stabilisation problem because there is no need to con-
trol the robot orientation: it is automatically compen-
sated as the robot follows the trajectory, provided that
the specified trajectory respects the non-holonomic
constraints of the robot. As the control strategy pre-
sented in this paper is concerned with the stabilisation
problem, it can also be applied to the trajectory track-
ing problem.
256
Vieira F., Medeiros A., Alsina P. and Araújo Jr. A. (2004).
POSITION AND ORIENTATION CONTROL OF A TWO-WHEELED DIFFERENTIALLY DRIVEN NONHOLONOMIC MOBILE ROBOT.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 256-262
DOI: 10.5220/0001138702560262
Copyright
c
SciTePress
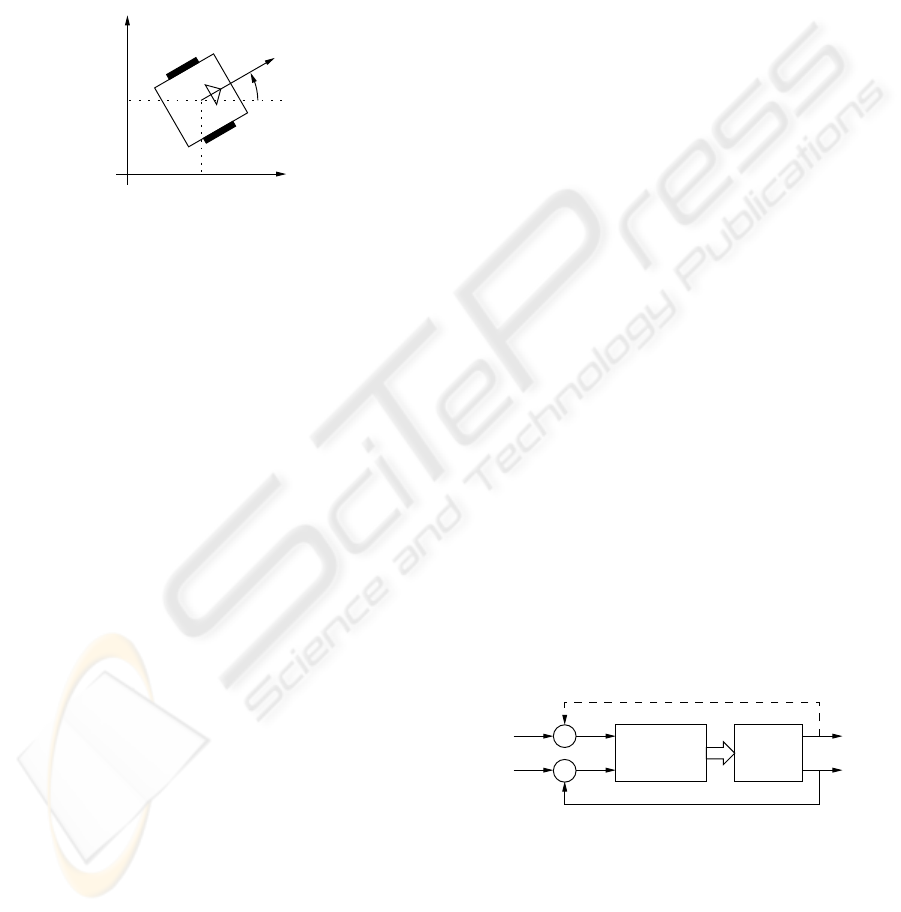
3 MODELLING
A schematic diagram of the considered robot is pre-
sented on figure 1. The robot configuration is repre-
sented by its position on the Cartesian space (x and y,
that is the position of the robot-body center with re-
lation to a referential frame fixed on the workspace),
and by its orientation θ (angle between the robot ori-
entation vector and the reference axis – X, fixed on
the workspace).
v
x
y
θ,ω
Figure 1: Schematic diagram of a two-wheeled nonholo-
nomic robot.
The kinematic model represents the movements
constraints of the robot body. For the considered
robot, the kinematic model is given by equation 1.
˙
q =
˙x
˙y
˙
θ
=
"
cos(θ) 0
sin(θ) 0
0 1
#
·
·
v
ω
¸
= G(θ)·v (1)
The vector q = [
x y θ
]
T
represents the linear
and angular positions and the vector v = [
v ω
]
T
represents the linear and angular velocities. The main
feature of this model for wheeled mobile robots is
the presence of nonholonomic constraints, due to the
rolling without slipping condition between the wheels
and the ground. The nonholonomic constraints im-
pose that the system generalized velocities ( ˙x, ˙y and
˙
θ) cannot assume independent values. It can be ob-
served that the kinematic model in equation 1 does
not include the dynamic effects of the robot body and
actuators.
The dynamic model is derived from the actua-
tors dynamics and the robot dynamics parameters,
like mass, inertia momentum and friction coefficients.
The final dynamic model for a robot with two DC
motors directly connected to the wheels (Yamamoto
et al., 2003) is given by equation 2:
Ku = M ˙v + Bv (2)
The vector u = [
u
l
u
r
]
T
represents the input sig-
nals, usually currents or tensions applied to the left
and right electrical motors of the robot. K is a gain
matrix that transforms the input signals u into forces
to be generated by the robot wheels. M is the gener-
alized inertia matrix and B is the generalized viscous
friction matrix.
The model in equation 2 is a multi-variable lin-
ear system and a simple control law for the dynamic
stabilisation problem could be designed. However,
two drawbacks can be highlighted: the measurement
of the state variables (v and ω) is usually inaccurate
or unavailable, and velocities references are not well
suited for the mobile robot stabilisation control prob-
lem, where the references are usually coordinates on
the Cartesian space and an orientation angle.
Models in equations 1 and 2 can be rearranged into
a single state space representation, by defining the
matrices
˜
A = −M
−1
B and
˜
B = M
−1
K
·
˙
v
˙
q
¸
=
˜
A
.
.
. 0
. . . . . . . . .
G(θ)
.
.
. 0
·
v
q
¸
+
˜
B
. .
0
u (3)
The outputs in equation 3 are x, y and θ. Although
this model allows the use of Cartesian coordinates and
orientation angles as references to the mobile robot,
it is a multi-variable non-linear model and the devel-
opment of control laws based on such model is not
trivial.
In order to reduce the model complexity, one could
rewrite it in terms of the robot linear and angular dis-
placement, s and θ, so that ˙s = v and
˙
θ = ω. Defining
a vector p = [
s θ
]
T
:
·
˙
v
˙
p
¸
=
˜
A
.
.
. 0
. . . . . .
I
.
.
. 0
·
v
p
¸
+
˜
B
. .
0
u (4)
The model in equation 4 is linear, with outputs s
and θ. One could easily design a control system based
on the block diagram on figure 2, if s and θ are mea-
surable and s
ref
and θ
ref
are defined. This controller
can be based on any of the classic design techniques
for linear systems where the controller receives the er-
ror signal and generates the input to the plant (a PID,
for example).
Controller Robot
+
+
−
−
us
ref
θ
ref
e
s
e
θ
s
θ
Figure 2: Control system block diagram.
As the design of such a controller is simple, this
model has been used for the control system design,
despite of two problems that still hold: the linear dis-
placement s along a trajectory is practically unmea-
surable and s
ref
is meaningless. However, these prob-
lems can be contoured, as will be shown on the next
section.
POSITION AND ORIENTATION CONTROL OF A TWO-WHEELED DIFFERENTIALLY DRIVEN
NONHOLONOMIC MOBILE ROBOT
257

4 CONTROL SYSTEM DESIGN
The robot stabilisation problem can be divided into
two different control problems: robot positioning
control and robot orientating control. The robot po-
sitioning control must assure the achievement of a de-
sired position (x
ref
, y
ref
), regardless of the robot ori-
entation. The robot orientating control must assure
the achievement of the desired position and orienta-
tion (x
d
, y
d
, θ
d
).
4.1 Robot positioning control
Figure 3 illustrates the positioning problem, where ∆l
is the distance between the robot and the desired ref-
erence (x
ref
, y
ref
) in the Cartesian space. The robot
positioning control problem will be solved if we as-
sure ∆l → 0. This is not trivial since the l variable do
not appear in the model of equation 4.
θ
φ
∆φ
(x
ref
, y
ref
)
R
∆λ
∆l
(x, y)
Figure 3: Robot positioning problem
To overcome this problem, we can define two new
variables, ∆λ and φ. ∆λ is the distance to R, the
nearest point from the desired reference that lies on
the robot orientation line; φ is the angle of the vector
that binds the robot position to the desired reference.
We can also define ∆φ as the difference between the
φ angle and the robot orientation: ∆φ = φ − θ.
We can now easily conclude that:
∆l =
∆λ
cos(∆φ)
(5)
So, if ∆λ → 0 and ∆φ → 0 then ∆l → 0. That is,
if we design a control system that assures the ∆λ and
∆φ convergence to zero
1
, then the desired reference,
x
ref
and y
ref
, is achieved. Thus, the robot positioning
control problem can be solved by applying any con-
trol strategy that assures such convergence.
1
It is not even necessary to assure the convergence
of ∆φ to zero: the convergence to any ∆φ value where
cos(∆φ) 6= 0 will be acceptable.
The block diagram in figure 2 suggests that the sys-
tem can be controlled using linear and angular ref-
erences, s
ref
and θ
ref
, respectively. We will generate
these references in order to ensure the converge of ∆λ
and ∆φ to zero, as required by equation 5. In other
words, we want e
s
= ∆λ and e
θ
= ∆φ. Thus, if the
controller assures the errors convergence to zero, the
robot positioning control problem is solved.
To make e
θ
= ∆φ, we just need to define θ
ref
= φ,
so e
θ
= θ
ref
− θ = φ − θ = ∆φ. For this, we make:
θ
ref
= tan
−1
µ
y
ref
− y
x
ref
− x
¶
= tan
−1
µ
∆y
ref
∆x
ref
¶
(6)
To calculate e
s
is generally not very simple, be-
cause the s output signal cannot be measured and we
cannot easily calculate a suitable value for s
ref
. But
if we define the R point in figure 3 as the reference
point for the s controller, only in this case it is true
that e
s
= s
ref
− s = ∆λ. So:
e
s
= ∆λ = ∆l · cos(∆φ) = (7)
p
(∆x
ref
)
2
+ (∆y
ref
)
2
· cos
·
tan
−1
µ
∆y
ref
∆x
ref
¶
− θ
¸
The complete robot positioning controller, based
on the diagram of figure 2 and the equations 6 and 7, is
presented on figure 4. It can be used as a stand-alone
robot control system if the problem is just to drive to
robot to a given position (x
ref
, y
ref
), regardless of the
final robot orientation.
+
−
+
−
+
−
Positioning control system
Controller Robot
u
θ
ref
e
θ
y
y
ref
x
ref
e
s
e
s
, θ
ref
Calcul of
θ
x
Figure 4: Robot positioning controller
4.1.1 Practical aspects
The Brockett’s theorem (Brockett, 1983; Stern, 2002)
proved that no continuous control law can completely
stabilize a system with the non-holonomic restriction
as in equation 1. The best any such control law can
do is to drive the system to a region delimited by a
circle of radius as small as posible around the desired
final position. This restriction naturally appears in the
control law proposed in this article: it is impossible to
calculate the angular reference θ
ref
in equation 6 when
the robot reaches the position reference (x
ref
, y
ref
). To
ICINCO 2004 - ROBOTICS AND AUTOMATION
258
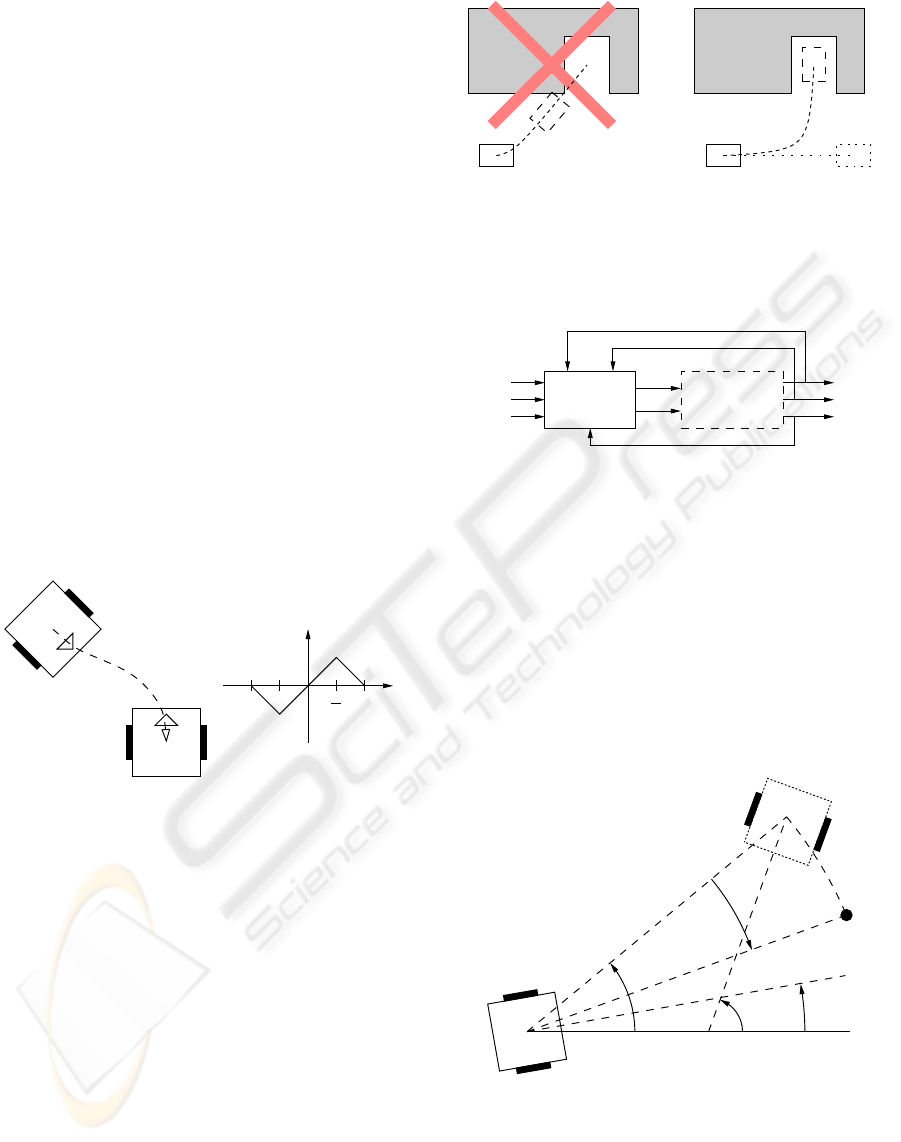
deal with this limitation, we define, based on the pre-
cision of the position measurement sensors, an ac-
ceptable distance error (²). When the robot enters this
circular region (∆l < ²), the angular error e
θ
and the
linear error e
s
are assumed to be zero.
The angular error e
θ
should be normalized to the
interval −π/2 ≤ e
θ
≤ π/2. When the robot is near
the sign change border (e
θ
≈ ±π/2), it is sometimes
better to slightly exceed the ±π/2 limit to maintain
the sign of the angular error the same of the previ-
ous iteration. This avoids unnecessary changes in the
direction of the angular movement.
Only allowing values between −π/2 and π/2 for
the angular error does not favor forward movements,
as illustrated by the first trajectory in figure 5. But if
the robot cannot move as better in the backward di-
rection as in the forward one, the second trajectory in
figure 5 would be preferable in some situations. To
obtain this behavior, the angular error e
θ
should be
restricted to the interval −π ≤ e
θ
≤ π. The ±π lim-
its for the angular error can only be applied when the
robot is far enough from the desired reference point.
If they are applied when the robot is near the final po-
sition, small overshots can make the robot indefinitely
turn around the reference point.
π
2
Figure 5: Forward and backward movements
4.2 Robot orientating control
The main idea behind the proposed orientating con-
trol strategy is that when we want to move to a final
position with a fixed orientation, it is not usually a
good idea to go straight to this position, as illustrated
by figure 6. Generally, we drive as if we wanted to
go to another place until a moment where, if we go
straight to the final position, we will reach it with the
desired orientation.
In order to attend the robot orientating control
problem, an external loop with a moving reference
scheme has been designed. The external loop gener-
ates Cartesian references, x
ref
and y
ref
, for the internal
loop (the positioning control scheme), such that the
robot reaches the desired position (x
d
and y
d
) with the
desired orientation (θ
d
). This approach is illustrated
Figure 6: The orientating control idea
on figure 7: the positioning controller block can be
the one presented on figure 4 or any other one.
Positioning
controller
reference
Moving
generator
y
θ
y
ref
x
ref
x
d
y
d
θ
d
x
Figure 7: Dynamic stabilisation controller
The strategy to calculate the internal reference is
presented on figure 8. The reference (x
ref
, y
ref
) is cal-
culated by rotating the vector of length ∆d pointing
from the robot position to the desired position by an
angle of γ. Practical aspects of calculating γ will be
discussed latter, but it is essentially equal to the dif-
ference between the desired final orientation (θ
d
) and
the angle to move to the desired position (β):
γ = β − θ
d
(8)
(x, y)
(x
d
, y
d
)
θθ
d
(x
ref
, y
ref
)
∆d
γ
β
∆d
Figure 8: Robot orientating problem
If β and θ
d
coincide, γ = 0 and the robot goes
straight to the final position (x
ref
, y
ref
) = (x
d
, y
d
). If
not, as long as the robot tries to move to the internal
reference (x
ref
, y
ref
), the difference between θ
d
and β
raises, γ decreases and (x
ref
, y
ref
) tends to (x
d
, y
d
).
POSITION AND ORIENTATION CONTROL OF A TWO-WHEELED DIFFERENTIALLY DRIVEN
NONHOLONOMIC MOBILE ROBOT
259
The moving reference scheme is so driven by the
following equations:
x
ref
= x + ∆d · cos (β − γ)
y
ref
= y + ∆d · sin (β − γ)
(9)
where x and y are the robot Cartesian coordinates, θ
d
is the desired orientation, and ∆d and β are presented
on figure 8:
∆d =
p
(x
d
− x)
2
+ (y
d
− y)
2
=
p
(∆x
d
)
2
+ (∆y
d
)
2
β = tan
−1
µ
y
d
− y
x
d
− x
¶
= tan
−1
µ
∆y
d
∆x
d
¶
(10)
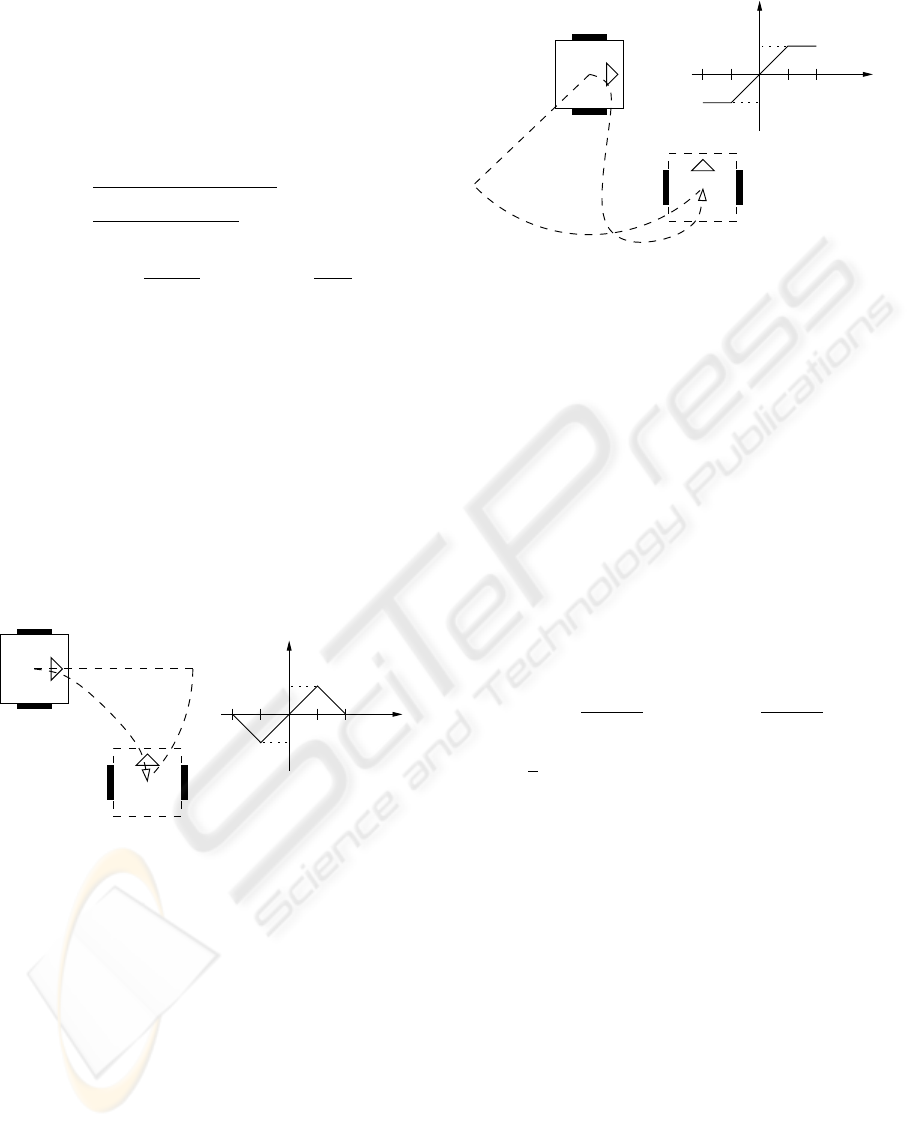
4.2.1 Practical aspects
The γ angle in equation 8 should be restrained to the
interval −π/2 ≤ γ ≤ π/2. The specific way to do
this restriction depends on the robot capabilities.
If the robot can move as well in one direction as in
the order, it is irrelevant if the robot reaches the de-
sired orientation with or without a rotation of π. In
the example of figure 9, we want a final orientation
θ
d
= π/2, but the robot finished the mouvement with
an orientation of θ
d
= −π/2. This behavior (bidi-
rectional orientation) is achieved by normalizing the
γ angle, as illustrated by the graphic in figure 9.
θ
d
= π/2
x
ref
, y
ref
β = −π/4
γ = π/4
π
π/2
γ
−π/2
−π
β − θ
d
Figure 9: Bidirectional orientation
Sometimes a non-inversed final orientation is re-
quired. In this case (unidirectional orientation), the γ
angle should be saturated (and not normalized), as il-
lustrated by the graphic in figure 10. This orientating
control strategy should be combined with a position
control strategies that favors forward mouvements, as
described in section 4.1.1. The limitation of this kind
of position control (see 4.1.1) imposes that the unidi-
recional orientating control strategy can only be ap-
plied when the robot is far enough from the desired
reference point.
4.3 The linear controller
The controller appearing on figures 2 and 4 can be
designed using any of the classical control techniques
γ = −π/2
β = −π/4
x
ref
, y
ref
π
π/2
γ
−π/2
β − θ
d
−π
θ
d
= π/2
Figure 10: Unidirectional orientation
that can be used with a linear multi-variable system
described by the model in equation 4. We will ex-
emplify with a simple controller based on decoupled
PIDs, but in no way it should be assumed that the con-
trol strategy presented on sections 4.1 and 4.2 must
necessarily be used with a PID-based controller.
If the robot is symmetrical and driven by two iden-
tical DC motors, the K, M and B matrices in equa-
tion 2 have the following properties (Yamamoto et al.,
2003):
K =
·
α α
β −β
¸
M, B are diagonals
We can define two new input signals, v
s
and v
θ
and
a new input vector w = [
v
s
v
θ
]
T
such that:
v
s
=
u
l
+ u
r
2
v
θ
=
u
l
− u
r
2
w =
1
2
·
1 1
1 −1
¸
u ⇒ u =
·
1 1
1 −1
¸
w (11)
If we introduce the new w input vector in equa-
tion 4 and calcute the transfer model equivalent to the
space stade equation, we obtain a decoupled system:
·
S(s)
Θ(s)
¸
=
·
G
s
(s) 0
0 G
θ
(s)
¸
·
·
V
s
(s)
V
θ
(s)
¸
(12)
Using equation 12, it is very simple to design two
independent PID controllers for s and θ, based on the
desired linear and angular behavior. The output of
these controllers are the virtual input signals v
s
and
v
θ
: to calculate the real input signals u
l
and u
r
, we
use equation 11.
5 RESULTS
Simulated results of the proposed strategy are pre-
sented on this section. A simple PD controller has
been implemented as the positioning controller. The
ICINCO 2004 - ROBOTICS AND AUTOMATION
260
robot dynamic model has been derived via experimen-
tal identification of a real mobile robot (Guerra et al.,
2004).
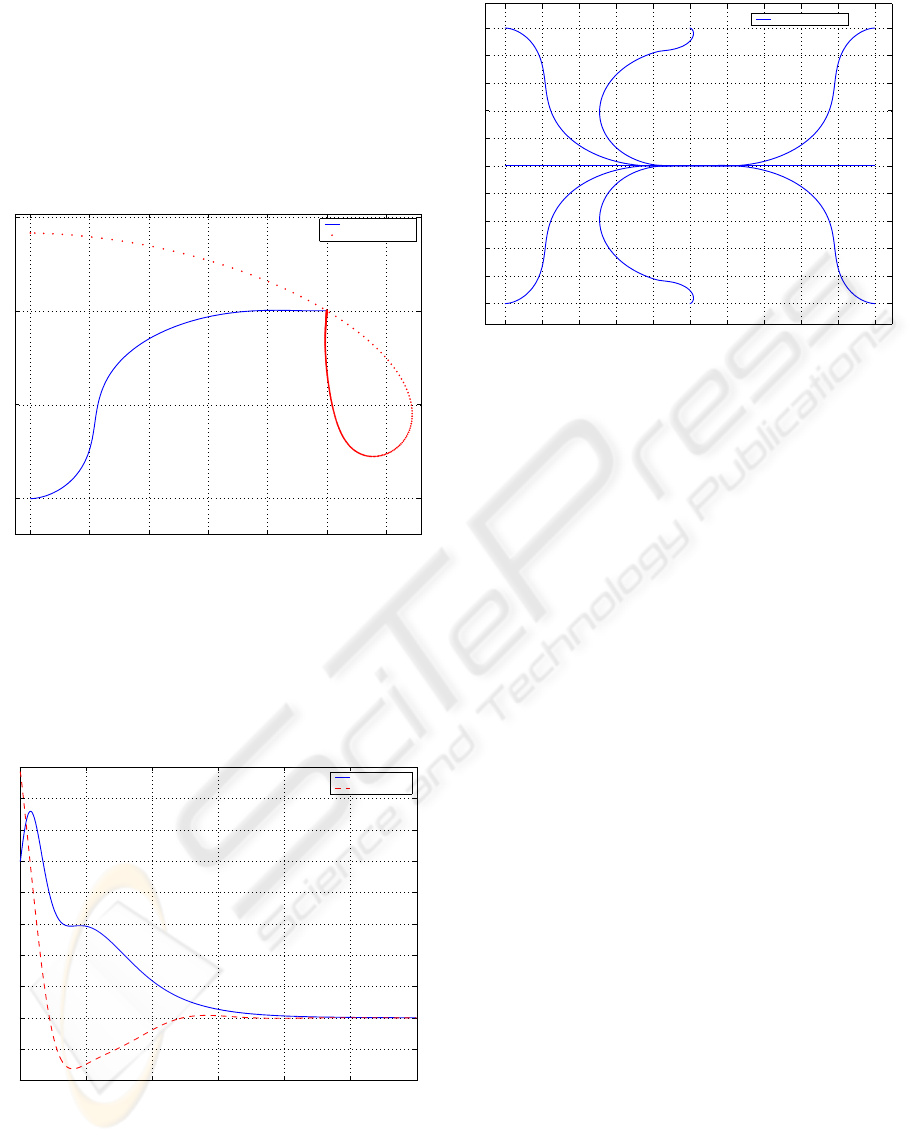
On figure 11 a simulation for the robot stabilisation
control problem is shown, where the initial conditions
are x = 0, y = 0 and θ = 0, and the desired config-
uration is x
d
= 1, y
d
= 1 and θ
d
= 0. The moving
reference scheme can also be observed on figure 11.
0 0.2 0.4 0.6 0.8 1 1.2
0
0.5
1
1.5
Robot Trajectory
Reference
Figure 11: Mobile robot stabilisation.
Figure 12 shows the linear and angular errors con-
vergence to zero, thus, assuring the achievement of
the control objective. It must be noticed that the con-
troller performance can be improved through the PD
gains adjustment.
0 5 10 15 20 25 30
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
time (seconds)
Linear Error
Angular Error
Figure 12: Linear and angular errors for the robot stabilisa-
tion simulation.
On figure 13 a set of simulations with the same final
configuration (x = 0, y = 0 and θ = 0) and different
initial conditions is presented.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Robot Trajectory
Figure 13: Simulation for different initial conditions.
6 CONCLUSIONS
This paper introduces a new approach to the stabil-
isation problem of two-wheeled nonholonomic mo-
bile robots, considering the robot dynamic. The im-
plementation of the proposed control strategy is very
simple and the simulations have shown very satisfac-
tory results.
Since the proposed control strategy can be imple-
mented with linear controllers, the system perfor-
mance adjustment is simpler and very meaningful (for
example, the adjustment of PID controller gains). We
can also use a classical technique to identify in real-
time the model of the system (Guerra et al., 2004) and
adopt an adaptive controller.
The proposed control strategy does not require any
information about the robot body velocities. The only
information needed is the robot Cartesian coordinates
and its orientation. Such information can be obtained
via any kind of absolute positioning system.
Future works will consider the proof for the pro-
posed moving reference control scheme.
REFERENCES
Aicardi, M., Casalino, G., Bicchi, A., and Balestrino, A.
(1995). Closed loop steering of unicycle-like vehi-
cles via lyapunov techniques. IEEE Transactions on
Robotics and Automation, 2(1).
Brockett, R. W. (1983). Asymptotic stability and feedback
stabilization. In Brockett, R. W., Millman, R. S., and
Sussmann, H. J., editors, Diferential Geometric Con-
trol Theory. Birkh
¨
auser, Boston, USA.
d’Andrea Novel, B., Bastin, G., and Campion, G. (1995).
Control of nonholonomic wheeled mobile robots by
state feedback linearization. Int. Journal of Robotics
Research, 14(6):543–559.
POSITION AND ORIENTATION CONTROL OF A TWO-WHEELED DIFFERENTIALLY DRIVEN
NONHOLONOMIC MOBILE ROBOT
261

Guerra, P. N., Alsina, P. J., Medeiros, A. A. D., and
Ara
´
ujo Jr., A. P. (2004). Linear modelling and iden-
tification of a mobile robot with differential drive. In
ICINCO – International Conference on Informatics in
Control, Automation and Robotics, Set
´
ubal, Portugal.
Lages, W. F. and Hemerly, E. M. (2000). Controle de
rob
ˆ
os m
´
oveis utilizando transformac¸
˜
ao descont
´
ınua
e linearizac¸
˜
ao adaptativa. In CBA - Congresso
Brasileiro de Autom
´
atica, Florian
´
opolis, SC, Brasil.
Lizarralde, F. C. (1998). Stabilization of Affine Nonlinear
Control Systems by a Newton Type Method. PhD the-
sis, Universidade Federal do Rio de Janeiro, COPPE,
Rio de Janeiro, RJ, Brasil.
Luca, A., Oriolo, G., Samson, C., and Laumond, J. P.
(1998). Robot Motion Planning and Control, chapter
Feedback Control of a Nonholomic Car-like Robot.
Lectures Notes in Control and Information Sciences.
Springer.
Oliveira, V. M. d. and Lages, W. F. (2001). Controle em
malha fechada de rob
ˆ
os m
´
oveis utilizando redes neu-
rais e transformac¸
˜
ao descontnua. In SBAI - Simp
´
osio
Brasileiro de Automac¸
˜
ao Inteligente, Canela, RS,
Brasil.
Samson, C. (1993). Time-varying feedback stabilization
of car-like wheeled mobile robots. Int. Journal of
Robotics Research, 12(1).
Stern, R. J. (2002). Brockett’s stabilization condition under
state constraints. Systems and Control Letters, 47(4).
Tanner, H. G. and Kyriakopoulos, K. J. (2002). Discon-
tinous backstepping for stabilization of nonholomic
mobile robots. In ICRA - IEEE International Confer-
ence on Robotics and Automation, Washington, DC,
USA.
Yamamoto, M. M., Pedrosa, D. P. F., and Medeiros, A.
A. D. (2003). Um simulador din
ˆ
amico para mini-
rob
ˆ
os m
´
oveis com modelagem de colises. In SBAI -
Simp
´
osio Brasileiro de Automac¸
˜
ao Inteligente, Bauru,
SP, Brazil.
Yang, J. M. and Kim, J. H. (1999). Sliding mode motion
control of nonholonomic mobile robots. IEEE Control
Systems Magazine.
ICINCO 2004 - ROBOTICS AND AUTOMATION
262
