
AUTOMATIC ANALYSIS AND VERIFICATION OF MSC-
SPECIFIED TELECOMMUNICATION SYSTEM
Lyudmila Matvyeyeva
Institute of Cybernetics, NAS of Ukraine, Pr. Glushkowa, 40, Kiev-03187, Ukraine
Sergiy Kryvyy
Institute of Cybernetics, NAS of Ukraine, Pr. Glushkowa, 40, Kiev-03187, Ukraine
Mariya Lopatina
Institute of Cybernetics, NAS of Ukraine, Pr. Glushkowa, 40, Kiev-03187, Ukraine
Keywords: Formal methods
, Petri nets, Linear algebra, MSC, Telecommunication system, verification
Abstract: Last 20 years formal methods are being used widely to specify formally, analyze, verify and test software
and hardware systems, particularly, telecommunication protocols. The paper presents automated verification
system based on Petri nets formal modelling technique and linear algebra methods for automatic proving
structural and some dynamic properties. Application of the system is considered on the telecom example.
1 INTRODUCTION
The Formal Methods are a set of methods and tools
based on mathematical modeling and formal logic
that are used to specify and verify requirements and
architecture of hardware or software systems.
Growing complexity of software and hardware
systems intensify popularity of the formal methods,
which supplement inductive methods, such as
testing, increasing product quality to the level
usually not reachable with the help of testing only
(Miller, 1995). In this respect it is very important to
automate processes of formal specification and
verification to the maximum. The development-
engineers and testers (verifiers) utilize different
language means in their work that usually leads to
the different interpretation of the same functionality,
to uncertainty, and even to inconsistencies or
incompleteness of the requirements. The way out of
this situation is the development of automatic
interfaces between languages of development-
engineers and testers.
2 VERIFICATION SYSTEM
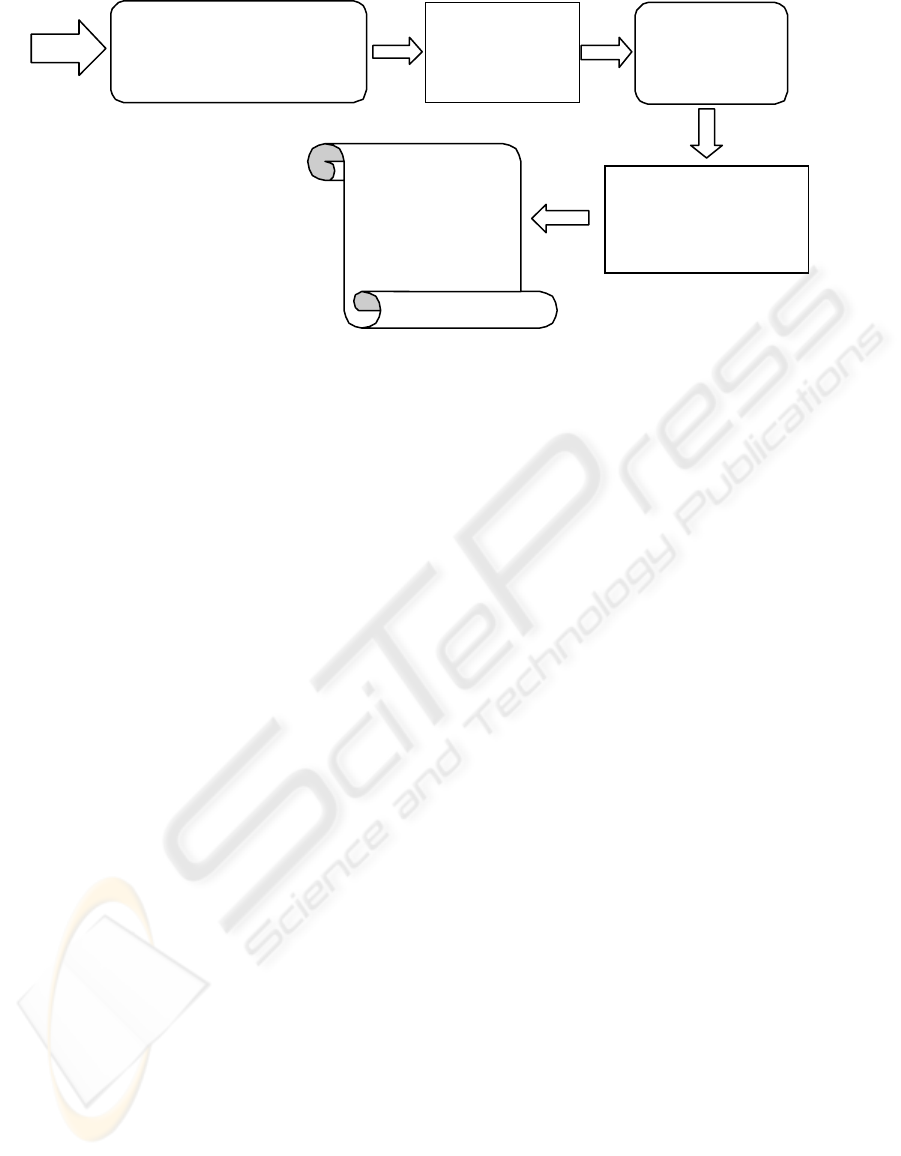
Let’s consider the automated verification system
(see Figure 1) developed to analyse software or
hardware systems specified in MSC language (ITU-
TS, 2000). The system conforms to the following
requirements: verification process is fully automatic;
the language of the output verdict is MSC as well.
As a formal model the system utilizes ordinary
Petri net (PN) because of their profound support for
analysis of many properties and problems associated
with concurrent systems – the most difficult in
manual testing.
Given work uses the algorithm of translation
MSC diagrams into Petri net (PN) developed by the
authors of this paper. The algorithm works over
selected subset of basic MSC elements. The
description of the translation algorithm with the
proof, and the example are presented in (Kryvyy,
2003). The proof of the algorithm correctness is
based on the use of process algebra ACP (Bergstra,
1984). We would like to underline here that the most
significant feature of the given algorithm is the way
of handling of MSC’s conditions, since the literature
402
Matvyeyeva L., Kryvyy S. and Lopatina M. (2004).
AUTOMATIC ANALYSIS AND VERIFICATION OF MSC-SPECIFIED TELECOMMUNICATION SYSTEM.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics , pages 402-405
DOI: 10.5220/0001138804020405
Copyright
c
SciTePress
indicates this problem in the translation process as
the most difficult (Mauw, 1995).
Resulted PN is analysed automatically to verify
the properties of the system using linear algebra.
Systems of linear equations over the set of natural
numbers are resolved using TSS method (Kryvyy,
2002) developed by one of the authors of this paper,
and which shows very high performance on large-
scale systems comparatively to the existing methods.
Given work is based on well-known definitions
of PNs theory, and classical definitions of Incidence
Matrix, State Equation and PN Invariants (Murata,
1989).
3 TELECOM EXAMPLE
Let’s consider the example of translation and
analysis of the real telephone system with basic
services traditionally called Plain Old Telephony
Service, POTS. The formal model of POTS is
presented as ordinary PN. One of the advantages of
building a formal model is to ensure the design is
correct and meets certain requirements. A correct
design of POTS at least has the following required
properties: must be a limitation on connection
channels resource usage; the telephone network
restores to its initial state after a talk of two
subscribers; the subscribers can call each other
indefinite number of times irrespectively given
network configuration; the telephone network can’t
get in deadlock state.
The set of MSC-diagrams presented in the
Figure 2 describes the work of POTS. Note that
MSC-diagrams Nº3, 4 and 8 on the Figure 2 shall be
repeated symmetrically relative to m
th
/n
th
instances.
m
th
(n
th
) instance corresponds to m
th
(n
th
) subscriber.
Let’s apply to the given set of MSCs the
algorithm of automatic translation (refer to section
2), and simplify obtained PN using net reduction
(Murata, 1989). The resulting ordinary PN is
illustrated in the Figure 3. The initial PN marking is
M
0
=(1,0,0,0,0,0,0,1,0,0,k), where k is the number of
connection channels. The 11-th place models pair
connections of the all network subscribers, and
corresponds to connection channels resource. So, we
have built the formal model aimed at analysis and
verification of the real system. In the given PN,
transitions are respectively interpreted as events of
data message transitions in the MSCs (Figure 2) in
the following way: t1=offhook(m), t2=dial_n,
t3=onhook(m), t4=busy, t5=onhook(m),
t6=ring(m,n), t7=offhook(n), t8=onhook(n),
t9=onhook(m), t10=onhook(m), t11=offhook(n),
t12=onhook(n); where offhook(m) means that the
m
th
subscriber hang off the phone,
onhook(n)/onhook(m) means that the n
th
/m
th
subscriber hang on the phone, ring(m,n) means that
m
th
is calling n
th
. The PN’s places in the Figure 3 are
named respectively as conditions of the given
MSCs: P1=“m free”, P2=“m busy”, P3=”dial state”,
P4=”NW_dial”, P5=”busy state”, P6=”ringing
state”, P7=”connected”, P8 =”n free”, P9=”n busy”,
P10=”dial state”, P11=”NW_free”.
To verify the correctness of the given model for
POTS with respect to the above properties it’s
necessary to calculate the PN’s S- and T-invariants.
The following invariants of the PN are obtained
automatically using TSS method (Kryvyy, 2002):
S-invariants — s
1
=(0,1,1,0,0,0,0,0,0,0,0),
s
2
=(0,0,0,0,0,1,0,1,0,0,0), s
3
=(1,0,0,1,1,1,1,0,0,0,0),
s
4
=(0,1,0,1,1,0,1,0,1,1,0), s
5
=(1,0,1,0,0,0,0,0,0,0,1,),
s
6
=(0,0,0,0,0,0,0,1,1,1,1), s
7
=(1,0,0,1,1,0,1,0,1,1,1);
T-invariants — t
1
=(1,0,1,0,0,0,0,0,0,0,0,0),
t
2
=(0,0,0,0,0,0,0,0,0,0,1,1), t
3
=(1,1,0,1,1,0,0,0,0,0,0,0),
t
4
=(1,1,0,0,0,1,0,0,0,1,0,0), t
5
=(0,1,0,0,0,1,1,1,0,0,0,0),
t
6
=(1,1,0,0,0,1,1,0,1,0,0,1).
Automatic analysis of invariants of the PN
proves the following properties of this model.
Boundedness: The given PN is structurally
A u tom a tic
tran slationofMSCs
intoPetriNet
Automaticanalysisof
th eformalmodel
PetriNetwhi c h
representtheformal
modelofthesy ste m
Theset ofMSCs
whi chdesc ribes
th esy st em
Ve rdictofthe
sy stem’sanalysis
(e rr orsan d
problemsofthe
sy stemrepresented
in MSC la ng uag e )
Fi
g
ure1
Figure 1
AUTOMATIC ANALYSIS AND VERIFICATION OF MSC-SPECIFIED TELECOMMUNICATION SYSTEM
403

bounded. Indeed, all PN’s places are covered by
non-zero coordinates from the set of S-invariants.
Physical interpretation of this property means that
there is a limitation on resource usage.
Repetitiveness, Consistency, and L3-liveness.
Since there exist a live initial marking
0
for this
PN, and all transitions are covered by non-zero
coordinates from the set of T-invariants the PN is
repetitive, and L3-live
. Physical interpretation of this
properties means that POTS will never be
deadlocked and any connection of two subscribers
can be performed as many times as needed. The PN
is consistent because any marking M is reachable
from itself. This means that the system always
returns into its initial state.
So far, conducted analysis shows that the formal
model has the required properties of the real system
and the given set of MSC diagrams correctly
describes POTS model.
The reference table, which is built during the
translation in order to preserve the correspondence
between system’s descriptions in MSC language and
Figure 2: MSC
- diagrams representing all possible POTS protocols
ICINCO 2004 - ROBOTICS AND AUTOMATION
404

Petri net representation, allows to present detected
problems and errors in MSC diagrams format in
output verdict.
4 CONCLUSION
To conclude, let’s underline, that the main properties
of the developed technological process are the
following: firstly, the process is completely
automated, and, secondly, the input language and the
language of output verdict represent the operating
language of the development-engineers, namely,
MSC, and so far do not require specific
mathematical background.
The further investigation will be directed at
extension to the whole MSC language and building
automated translators from SDL, UML and other
languages. The long term goal of this investigation is
building of the unified technological line partially or
fully automated, which will allow in its frames to
design, analyze, verify and test the wide class of the
properties of the systems under development.
REFERENCES
ITU-TS, 2000. Recommendation Z.120: Message
Sequence Chart (MSC). ITU-TS, Geneva.
Miller S.P., Srivas M., 1995. Formal Verification of the
AAMP5 Microprocessor – A Case Study in the
Industrial Use of Formal Methods. In Proceedings of
the 1995 Workshop on Industrial-Strength Formal
Specification Techniques (WIFT’95), IEEE Computer
Society, Orlando, Florida, USA, April 5-8.
Kryvyy S., Matvyeyeva L., Lopatina M., 2003. Automatic
Transformation of MSC Diagrams into Petri Nets. In
Proceedings of SCI’2003, Orlando, USA, 29-31 July,
vol. 5, pp. 140-146
Kryvyy S. , 2002. A Criteria of compatibility systems of
linear diophantine constraints. LNCS 2328, Springer
Verlag, pp. 264-271.
Murata T., 1989. Petri Nets: Properties, Analysis and
Applications. In Proceedings of the IEEE, vol.77, 4,
pp. 541-580.
Kluge O., Padberg J., Ehrig H., 2001. Modeling Train
Control Systems: From Message Sequence Charts to
Petri Nets, Technische Universität Berlin. Retrieved
on April 20, 2001 from http://cs.tu-
berlin.de/SPP/index.html.
McMillan K. L., 1992. Using Unfolding to Avoid the State
Explosion Problem in the Verification of
Asynchronous Circuits. In Proc. 4th Workshop on
Computer Aided Verification, LNCS 663, pp. 164-174.
Mauw S., Reniers M.A., 1995. Thoughts on the meaning
of conditions. Experts meeting SG10, St.Petersburg
TD9016, ITU-TS.
Bergstra J.A., Klop J.W., 1984. Process Algebra for
Synchronous Communication, Inf.&Control 60,
pp.109-137.
Figure 3: The PN corresponding to the set of MSC
-
diagrams in the Figure 2
AUTOMATIC ANALYSIS AND VERIFICATION OF MSC-SPECIFIED TELECOMMUNICATION SYSTEM
405
