SOLVING THE LONGEST WORD-CHAIN PROBLEM
Nobuo Inui, Yuji Shinano, Yuusuke Kounoike, Yoshiyuki Kotani
Tokyo University of Agriculture and Technology
Keywords: The Longest Distance Problem, Word–Chain Game, Integer Programming, Heuristic Search, Linear
Programming, Branch-and-Bound Method, Optimal Solution, Local-Maximum Solution
Abstract: The SHIRITORI game is a traditional Japanese word-chain game. This paper describes the definition of the
longest SHIRITORI problem (a kind of the longest distance problem) as a problem of graph and the solution
based on the integer problem (IP). This formulation requires the exponential order variables from the problem
size. Against this issue, we propose a solution based on the LP-based branch-and-bound method, which solves
the relaxation problems repeatedly. This method is able to calculate the longest SHIRITORI sequences for
130 thousand words dictionary within a second. In this paper, we compare the performances for the
heuristic-local search and investigate the results for several conditions to explore the longest SHIRITORI
problem.
1 INTRODUCTION
The SHIRITORI game (Word-Chain game) is a
traditional Japanese game using words (usually basic
nouns). There are many local rules for this game, but
the basic rule is simple as below:
SHIRITORI rule
N-players sit in a circle. The first player
prese
nts a word. A player of his turn also shows a
word such that its first character is same as the last
character of a word presented by the previous
player. While a game, any words are prohibited to
be shown twice. And the last character “N” is also
prohibited because any words cannot start with this
in Japanese. A player is a loser when he cannot say
any words.
An example of a SHIRITORI sequence is like
bel
ow.
RINGO
(apple) Æ GORIRA(gorilla) Æ
RA
PPA (trumpet) Æ PAIPU(pipe) Æ …
The SHIRITORI provides a way of child
education. The instance
research was appeared to
develop the association ability (Kanasugi, 1996). In
this research, any words could be accepted to present,
if these words presented were related to the previous
words. From a view of computer games, a research
(Ito, 2002) showed a perfect solution under a model
of the two-players, perfect information game. At that
point, the model of N-players game was hard to solve
under the limitation of time. This research, however,
showed the small-SHIRITORI results (limitations of
words and characters appeared in his experiment).
The problem of handling several thousand words or
an N-players game could not be computed under his
proposal.
When we consider the SHIRITORI as an
educat
ional game, many works would be devoted to
the long-continuation of a game. It is possible to
draw many words from human-players if a computer
makes a good plan for human to think of his words.
As a result, a system can develop the human-ability
of a way of thinking. A system (Kanasugu, 1996)
fails to do this, because a computer proposes words
randomly. We, as a basic research, propose a method
of solving the longest SHIRITORI problem. We
expect that our method provides useful information
for child education systems and general N-players
SHIRITORI game. The problem is defined as below:
The longest SHIRITORI problem
The longest SHIRITORI problem is a problem of
fi
nding a longest SHIRITORI sequence from
headwords in a pre-defined dictionary (we use a
term ‘word’ as a headword in this paper).
The longest SHIRITORI problem described in the
n
ext section is modelled under the directed graph in
214
Inui N., Shinano Y., Kounoike Y. and Kotani Y. (2004).
SOLVING THE LONGEST WORD-CHAIN PROBLEM.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 214-221
DOI: 10.5220/0001138902140221
Copyright
c
 SciTePress

this paper. It is known that a longest distance
algorithm for Directed Acyclic graphs (DAG) shows
the
performance for the number of
vertices N and arcs M. Though, for Directed Cyclic
graphs (DCG), it is known that Liao-Wong algorithm
or Bellman-Ford algorithm show reasonable
performances, these are only applied to DCG with
negative cycles. We cannot apply these algorithms
for the longest SHIRITORI problem, since
word-chain sequences as a graph contain positive
cycles.
)( MNO +
Solving the longest SHIRITORI problem by a
brute-force search algorithm requires dealing with
O(N) average arcs and O(MN
2
) depths of tree. Here,
“N” is the number of vertices and “M” is the
maximum number of arcs between two vertices (Ito,
2002). This means that we cannot actually solve the
longest SHIRITORI problem by brute-force methods.
Instead of using brute-force methods, we divide the
longest SHIRITORI problem into two problems:
determining the number of arcs of the longest
SHIRITORI route and making a SHIRITORI
sequences. The first problem is solved under a
framework of the integer programming in this paper.
2 MODELING OF THE LONGEST
SHIRITORI PROBLEM
The SHIRITORI described in the section 1 is
modelled under the graph theory. A basic idea is
coming from a model where vertices and arcs are
corresponding to characters and words, respectively.
“
V
” is a set of vertices corresponding to characters
which are the first or the last characters of words. We
denote
as , these numbers are
corresponding to the characters. In this case, ‘n’
characters are used. “
V
},,2,1{ nV "=
A
” is a set of arcs defined as
nn1211
.
ij
means a set of
words where the beginning character is
i
and the
terminating character is
. So we define a graph
for expressing the transition graph for SHIRITORI as
. Fig.1 shows an example of this graph.
From the SHIRITORI rule, each arc is followed at
once or none.
BBBA = ∪∪∪ "
B
j
G
),( AVG =
We introduce a super-source
s
and a super-sink
t
for the beginning vertex and the terminating
vertex, respectively. These vertices are added to the
initial transition graph G like this way: The
super-source has arcs for all other vertices and all
vertices have arcs for the super-sink. By the two
super vertices, we can find a longest SHIRITORI
sequence without trying all combinations of vertices
as the beginning and terminating vertices.
t
Though
is a basic idea, we do not need to
consider words themselves. For example, we can
select an arbitrary word, ‘AKAI’ or ‘ATAI’, while
moving from ‘A’ to ‘I’. So we only consider the
number of arcs between two vertices in the graph G.
We define
G
||
ijij
Bf
=
as the number of arcs
between two vertices such that the beginning
character is and the terminating character is .
i
j
A
I
U
SA
AKAI
A
TAI
I
KUSA
SASA
Figure 1: Transition Graph G for SHIRITORI.
From the graph G like Fig.1, we can find many
SHIRITORI sequences like ‘AÆIÆU’,
‘UÆSAÆSA’ and so on. A SHIRITORI sequence
can be viewed as a semi-Eulerian subgraph on the
graph G. The longest SHIRITORI problem is
equivalent to the largest semi-Eulerian subgraph
problem. Generally, finding the largest semi-Eulerian
subgraph is equivalent to finding the maximum
Hamiltonian path. This means that the longest
SHIRITORI problem is a NP-complete problem
(Nakayama, 1995, Lai, 2001, Skina, 1990).
When the longest SHIRITORI problem is treated
as a search problem, a brute-force search method
enumerates SHIRITORI sequences. In this case, the
depth of the enumeration tree is
, where
is the number of vertices and
)(
2
MNO
N
M
is the
maximum number of arcs between two vertices (Ito,
2002). This depth means that the brute-force search
algorithm cannot find the optimal solution within
reasonable time.
In this paper, we handle two sub-problems for the
longest SHIRITORI problem. The first problem is to
make a semi-Eulerian subgraph from a graph G. The
second problem is to constitute an actual SHIRITORI
sequence on the semi-Eulerian subgraph. We start to
solve the first problem using the integer
programming.
3 SOLVING THE LONGEST
SHIRITORI PROBLEM
In many researches, parallel algorithms are focused
on calculating the longest distance problem (Gu,
SOLVING THE LONGEST WORD-CHAIN PROBLEM
215

1996). There is the previous research on the longest
distance problem using Integer Programming
(Fischetti, 2002). We use the same way to describe
the longest SHIRITORI problem. We denote the
number of words
ij
on a SHIRITORI sequence
which first character and last character is
and ,
respectively, and
ij
means the number of words in
a word-dictionary. Obviously, the upper bound of
ij
is given by
ij
.The next two conditions are for
the semi-Eulerian graph of directed graphs.
x
i
j
f
x f
1) A graph is a connected graph.
2) In-degree and out-degree at every vertex but two
are same. A vertex with one more out-degree
becomes a beginning one and another vertex
with one more in-degree becomes a terminating
one (in our model, these vertices are
and ).
s
t
We formulate these conditions as an integer
programming problem (P), but the condition 1)
requires exponential order variables and constraints
in this problem formulation.
Instead of solving the integer programming
problem (P), we use the LP-based branch-and-bound
method. Our proposed method solves the problem
like: the first, solve the longest SHIRITORI problem
under the condition 2) that is formulated as the
problem (RP
0
). If the condition 1) is not satisfied in
the solution of (RP
0
), add conditions to satisfy the
condition 1). The detail about LP-based
branch-and-bound method is described later.
There are two states below after finding the solution
of (RP
0
).
a) The graph of the solution of (RP
0
) is a connected
graph. In this case, the solution is also optimal
for problem (P).
b) If the graph is disconnected, every connected
component of the solution of (RP
0
) is a
semi-Eulerian graph or Eulerian graph, then two
cases below is possible:
i) The Eulerian path from s to t in the
connected component gives an optimal
solution of problem (P).
kg
ky
tVjsVix
Vix
Vjx
VjVifx
Sfxfg
Sxg
Sgyx
y
x
Vjxx
x
xz
k
k
ij
it
sj
ijij
Sj
Si
Sj
Si
kijij
Sj
Si
ijk
k
Sj
Si
ijk
kkk
StsVj
Ski
ij
k
k
Vi
it
Vi
ji
Vi
ij
Vi
is
sVitVj
ij
k
k
k
k
k
k
k
k
k
tsV
∀∈
∀∈
∪∈∀∪∈∀∈
∈∀≤≤
∈∀≤≤
∈∀∈∀≤≤
∀≤+
∀≥+
∀−≥
=−
=
∈∀=−
=
=
∑∑∑
∑
∑
∑
∑
∑∑
∑
∑∑
∈
∈
∈
∈
∈
∈
∈
∈
∪∈
∈
−
=
∈
∈∈
∈
∪∈∪∈
∪
},1,0{
},1,0{
}{},{,
,10
,10
,,0
,
,1
,
1)1(
1
0
1
:toSubject
Maximize(P)
\},{
22
1
}{}{
0
},{
Z
ii) The path does not give an optimal solution
of problem (P).
}{},{,
,10
,10
,,0
1
0
1
:toSubject
Maximize)(RP
}{}{
0
0
tVjsVix
Vix
Vjx
VjVifx
x
Vjxx
x
xz
ij
it
sj
ijij
Vi
it
Vi
ji
Vi
ij
Vi
is
sVitVj
ij
∪∈∀∪∈∀∈
∈∀≤≤
∈∀≤≤
∈∀∈∀≤≤
=
∈∀=−
=
=
∑
∑∑
∑
∑
∑
∈
∈∈
∈
∪∈∪∈
Z
The connectivity of graph is easy to check
within
. We now denote the number of arcs in
the Eulerian path in the graph of solution of (RP
)(
2
nO
0
) as
N
0
. For the case ii), in order to find the alternative of
the solution, a new problem (RP
1
) is generated by
adding a constraint such that there is at least an arc
from the Eulerian path (including super vertices,
and ) to the outside. Let the objective value of
(RP
s
t
1
) be N
1
. If N
1
<N
0
, then the solution of (RP
0
) is
optimal for problem (P). The algorithm of finding the
optimal solution is illustrated in Fig. 2. We call this
procedure the LP-based branch-and-bound method.
A state b) corresponds to a branch operation. The
branch operation continues until the connected graph
is obtained or no solution is found in LP solver.
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
216

Figure 2: LP-Based Branch-and-Bound Method.
In the solution of RP
k
, means a set of vertices
on a Eulerian path from s to t.
*
means the all
vertices except
*
k
. So the conditions adding to past
solutions mean that there is at least an arc from
vertices on the semi-Eulerian graph to the outside
vertices. Two cases, i) and ii), partition the problem
into two. We can find the problem when IP solver
stops whether the graph of the solution is connected
or the solver cannot find the optimal solution because
of the severe conditions added.
*
k
V
\
k
VV
V
Note that the solution of (RP
0
) is always integer
solution, because the coefficient matrix of constraints
of (RP
0
) is a totally unimodular matrix. However,
(RP
k
) is not.
4 CONSTITUTION OF SHIRITORI
SEQUENCE
After executing the method described in section 3, the
number of words between vertices is available. The
number of words of a longest SHIRITORI sequence
is already founded until this point. In addition, we
constitute the concrete word sequence from the
transition graph. Generally, a transition graph
includes numerous sequences. But we would like to
line words up in a sequence. The algorithm for
extracting an Eulerian path is below and Fig.3 shows
an example of the process.
Solution:Connected?
Optimal Solution
Legth:Sub-Eulerian
Path: N1
Alternative Longest
Path: N2
YES
NO
The longest path, N1 or
N2, is op timal.
Solution:Connected?
S
KA
NA
A
SO
t
a) Example of Eulerian Transition Graph
KA NA NA
SO
NA
A
SO KA
NA
SO
b) Ring(L)
S
KA NA
A
SO
t
c) Route (R)
S
KA NA
A SO
t
KA
NA KA
SO
NA A
SO
NA
NA
SO
d) SHIRITORI
}{},{,
,10
,10
,,0
1,,1,0,1
1
0
1
:toSubject
Maximize)(RP
*
*
\
}{}{
0
k
tVjsVix
Vix
Vjx
VjVifx
klx
x
Vjxx
x
xz
ij
it
sj
ijij
VVj
Vi
ij
Vi
it
Vi
ji
Vi
ij
Vi
is
sVitVj
ij
l
l
∪∈∀∪∈∀∈
∈∀≤≤
∈∀≤≤
∈∀∈∀≤≤
−=≥
=
∈∀=−
=
=
∑
∑
∑∑
∑
∑∑
∈
∈
∈
∈∈
∈
∪∈∪∈
Z
"
Figure 3: Making SHIRITORI sequence.
T: a transition graph of the longest SHIRITORI
L: loop sequences
R: SHIRITORI sequence
1) All Loop are extracted from T, and put them to L.
2) A sequence, not including loops, is remained in
T, and put it to R. In this time, T becomes 0.
3) Insert an arbitrary loop in the L which starts a
vertex in R.
4) Repeat 3) while L is not 0.
As described in the experiment section, there are
many largest semi-Eulerian subgraphs from a word
dictionary and many SHIRITORI sequences for a
semi-Eulerian subgraph. Since what kind of sequence
is better depends on the application used, we do not
deal with the quality of SHIRITORI sequences in this
paper.
SOLVING THE LONGEST WORD-CHAIN PROBLEM
217

5 LOCAL SEARCH METHOD
In this paper, we compare the IP-based method with
the local-search method. Usually, a top-down
brute-force search method, where a SHIRITORI
sequence is created from the first character to the last
one, is not suitable for the longest SHIRITORI
problem, because the depth of search tree is too deep
to try alternatives. Instead of such a brute-force
search method, we use the local search method. The
local search method is previously applied to puzzles
like N-queen (Sosic, 1990). Fundamentally, two
component from different sources are exchanged like
genetic cross-over operation. Of course, there is a risk
to fall the solution into the local optimal solution. The
local optimal solution is a solution that there are not
any improved solutions around it. To avoid getting
local optimal solutions, we use a TABU search
technique which controls the next candidate of
exchainging by the history. The TABU search avoid
exchainging the same items repeatedly. An example
of exchainging routes are shown in Fig.4 and we
Figure 4: Example of L
describe the algorithm below:
ocal Search.
T: a initia
h
from i to j
st item is throwed.
1)
rom the shortest path from i to j
3) est path from i to j
on U. In this case, (i,j) is a member of TA. Find
4)
this case, (i,j) is not a member of TA.
5)
6 EXPERIMENTS
od for the longest
SHIRITORI problem using actual words in
memory
IP solver: GNU GLPK(ver. 4.2)
Dictionary
Dictionary)(Niimura, 1992). Three kinds of datasets
consonants as the beginning characters,
tal
Dataset
re omitted. The total
In Ta omitted after
ivided by 2 for each arc. The result shows that the
rat
l transition graph
U: a Eulerian transition grap
U(i,j) : the value of the matrix
TA: a tabu list. In case that the
queue overflows, the most pa
U=0, U(s,t)=1
2) Find a path P1 f
on U. In this case, (i,j) is not a member of TA.
Find a longer path P2 than P1 from i to j on T. If
P2 exists, exchange P1 on U and P2 on T and
push (i,j) to TA and goto 2).
Find a path P1 from the short
the longer path P2 than P1 from i to j on T. If P2
exists, exchange P1 on U and P2 on T and goto
2).
Find a path P1 from the shortest path from i to j
on U. In
Find a path P2 as same length as P1 from i to j on
T. If P2 exists, exchange P1 on U and P2 on T
and push (i,j) to TA and goto 2).
Output U.
We experiment our meth
dictionary and virtual small words. All experiments
are done under the environment as below:
PC: Xeon Dual Processor 2.8GHz, 2GB
OS: cygwin (ver. 2.218)under WINDOWS XP
Compiler: GNU GCC(ver. 3.2)
6.1 Experiment for Word
KA
A
SO
a) Current Situation
DU
A
KA
SHIRITORI seq.
Not used
SHIRITORI seq.
KA
A SO
b) Next Situation
A
KA
SHIRITORI seq.
Not used
SHIRITORI seq.
DU
First, we use actual words in KOUJIEN (Japanese
below are used in this experiment. The experimental
results for these three datasets are shown in Table.1, 2
and 3. In all cases, the number of vertices is 70.
Dataset 1: All words except word with voice
like, DA,DI, ZO, and so on. The to
number of words is 137,335.
2: All nouns are used. The total number of
words is 192,687.
Dataset 3: All nouns are used. But the same
transcribed words a
number of words is 154,150.
ble.1, 2 and 3, fractions are
d
io of longest SHIRITORI sequences is not constant.
It is because the number of arcs between vertices is
not distributed uniformly. From our commonsense,
the number of words deeply affects the length of
SHIRITORI sequences. From our experimental
results, when the number of words is large, the ratios
between the number of words and the length of the
longest SHIRITORI sequences appear to be
approximately constant. However, when the number
of words is small, the ratios are not constant. This is
considered because of the connectivity of vertices.
The difference between the numbers of arcs affects
the length of the longest SHIRITORI sequences. In
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
218

the previous research, the length of Eulerian
sequences is estimated to be 2/3 (Li, 2004) for
undirected graph. The length of the longest
SHIRITORI sequences seems to be shorter than
undirected graphs.
Table 1: Result (Dataset 1)
Num. of
Word(N)
Length of
SH
Ratio Num. of
es IP
Time
(sec)
IRITORI(L)
(L/N) tim
137,335 56,519 41% 1 0.53
68,417 27,718 41% 1 0.49
33,497 13,339 40% 1 0.47
16,079 6,183 38% 1 0.39
7,406 3,654 36% 1 0.30
3,219 1,016 32% 1 0.20
1,265 303 24% 1 0.16
444 70 16% 1 0.13
124 15 12% 1 0.11
Table 2: Result (Dataset 2)
Num. of
Word(N)
Length of
SHIRITORI(L)
Ratio
(L/N)
Num. of
times IP
Time
(sec)
192,687 86,788 45% 2 1.36
95,225 42,236 44% 1 1.20
46,596 20,077 43% 1 1.02
22,351 9,115 41% 3 0.84
10,361 3,792 37% 1 0.50
4,535 1,372 30% 1 0.27
1,853 401 22% 1 0.17
697 91 13% 1 0.12
231 18 8% 1 0.11
Table 3: Result (Dataset 3)
Num. of
Word(N)
Length of
SHIRITORI(L)
Ratio
(L/N)
Num. of
times IP
Time
(sec)
154,150 75,777 50% 1 1.30
75,984 36,759 48% 1 1.16
36,979 17,340 47% 1 0.97
17,543 7,769 44% 1 0.70
7,987 3,199 40% 1 0.47
3,396 1,130 34% 1 0.25
1,290 292 23% 1 0.14
446 62 14% 1 0.12
123 12 10% 1 0.09
In our experiments, IP solver was activated once in
almost cases. Even if the solver is called twice or
more, the CPU execution time is short. This is mainly
because of the performance of GNU GLPK. The
reason why the number of times IP is called is almost
1 seems that the longest SHIRITORI consisting of
loops includes vertices which are shared in other
loops. In other word, it is difficult to make isolated
loops from initial transition graphs made from an
actual dictionary.
Figure 5: Performance of Local Search.
Fig.5 shows the performance of the local search
described in the section 5. From this, we could find
the optimal solution for the dataset 1 but not for the
dataset 2. Our local search method cannot judge
whether the final solution is optimal or not. This
result shows that the performance of the local search
is deeply dependent on datasets. However, since the
optimal solution can be found in a dataset, the longest
SHIRITORI problem seems not to be difficult.
Table 4: R nd Ending
Character (Dataset 1)
Length
of
SHIRIT
ORI
Kinds of
pairs of
beg. and
end char.
Kinds
of beg.
Kinds
of end.
Example.
esult of Specific Beginning a
56,519 51 3 17 A.GU, HA,GO
56,518 197 13 26 MO.BE.FU.GE
56,517 389 29 35 MU.ZA,MA.BI
56,516 424 37 53 RO.BI,RI.ZA
56,515 449 38 65 RO.DE,WA.KU
56,514 504 38 53 WA.RE,YO.NO
56,513 395 35 44 WA.TA,MA.O
56,512 194 25 35 RI.SE,MU.HI
56,511 52 9 17 RO.HO,I.HA
56,510 5 1 5 RY.A,RU.HE
Table 4 shows the lengths of the longest SHIRITORI
sequences for the specific beginning and terminating
characters about the dataset 1. The length of these
longest SHIRITORI sequences becomes over 56,510
or 0. Here, when the beginning character is the same
as the terminating character (loop), the longest
SHIRITORI sequence become the closed longest
Eulerian circuit and the length is 56,514 in this case.
This result shows loops are mainly composed of the
longest SHIRITORI sequences. The difference
between the lengths of longest SHIRITORI
sequences comes from the points entering or getting
out of the loops.
0
10000
20000
30000
40000
50000
60000
0 100 200 300 400
Time (Sec.)
Length of SIRITO R
I
Dataset 1
Dataset 2
SOLVING THE LONGEST WORD-CHAIN PROBLEM
219

6.2 Comprehensive trials for the small
longest SHIRITORI problem
In the previous section, the experimental results show
that the branch-and-bound procedure was not
activated in almost cases. This means that it is enough
to solve the longest SHIRITORI problem by using
the relaxation problem which is not concerned of the
connectivity of graph. In this section, we investigate
the nature of the longest SHIRITORI problem by the
small size of comprehensive transition graphs. Table
5 shows the result of this. The size is the number of
vertices and the transition graphs satisfy the
following conditions. These conditions exclude the
redundancies of transition matrix.
The table 5 shows the number of times IP solver is
called, which means the depth of the
branch-and-bound method. From this table, we can
find the difficulty of the longest SHIRITORI problem.
The relaxation problem which describes node
conditions is enough to solve the longest SHIRITORI
problem in almost transition graphs. As, however, the
number of vertices increases, the number of times IP
solver is called also tends to increase. By contrast,
when the number of times is small, the improved
results, compared with the early results, can be
obtained. In addition to this, after IP is called many
times, the IP cannot find t solutions because of the
severe conditi om this result,
IP is not called many times against the size of
transition matrix.
Table 5: The number of Times IP solver is called
The Number of Times
he
ons of the connectivity. Fr
Size of
Problem
1 2 3
4 6
3 8 0 0 0 0
4 291 0 0 0 0
5 29,869 4
0
0 0
4
0
6 11,338,759 5903
0
3315
0
20
558
0
4
Upper line: the number of improved solution by
branch-and-bound.
Lower line: the number of solution where conditions
become severe.
Figure 6: Improved Solution by Branch-and-Bound.
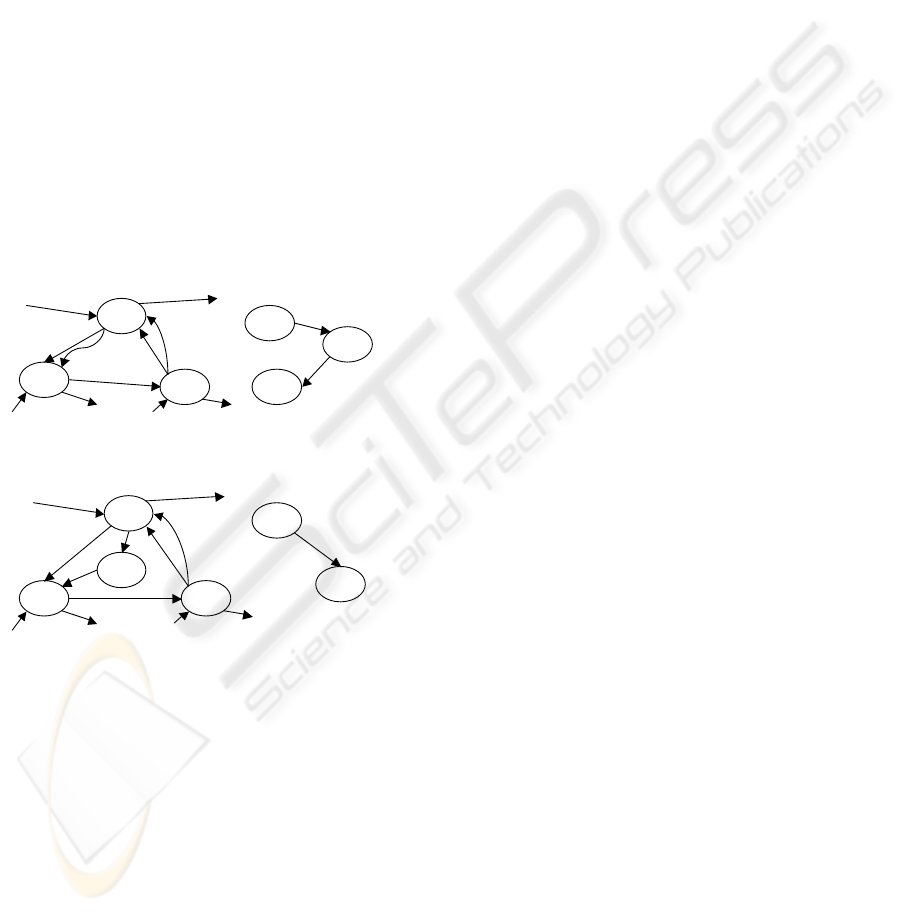
Fig.6 shows an example of the transition graphs
obtained as the longest SHIRITORI sequences. Two
separated graphs are obtained at the first solution. By
adding a constraint, the optimal solution is found. In
this case, the length of the longest SHIRITORI
sequence is improved from 10 to 12. Apparently, the
number of words of the first solution gives the upper
bound of the number of words of the longest
SHIRITORI sequence. Though the number of words
is the same between two transition graphs in this
example, it is possible to decrease the number of
words after the branch-and-bound method is applied.
At the problem (RP
0
), we can always get the
integer solution from any transition matrix. But by
adding constraints about connectivity in (RP
k
), it is
not guaranteed to get integer solutions. In our system,
GNUS GLPK is running on as the integer problem
mode after the linear problem mode. We checked the
number of transition graphs which output non-integer
solutions after the linear programming mode. There
are no transition graphs which output the non-integer
solutions! This might mean another index showing
the easiness of the longest SHIRITORI problem.
When we consider the another problem like the
longest SHIRITORI word sequence problem,
calculating the longest character length of
SHIRITORI sequence, the branch-and-bound method
would work more to find solutions.
.
}1,0{
1111
112/1
2/
1
12/1
2/
11
charactersotherto
characterfirstthefrompathaleastatisThere
ff
ff
ff
f
n
i
n
ij
ij
n
i
i
j
ij
n
i
n
nj
ij
n
i
n
j
ij
n
ni
n
j
ij
n
i
n
j
ij
ij
∑∑∑∑
∑∑∑∑
∑∑∑∑
=+===
=+===
+====
<
<
<
=
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
a) Initial Transition
b) First Solution
c) Improved Solution
ICINCO 2004 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
220

7 CONCLUSIONS
, we try to solve the more difficult
r
I
N-playe
PPENDIX
An example of the longest SHIRITORI sequence of
the dataset 1
1:ABEMARIA,ANMONIA,ANPEA,ANPURIFAIA
5:ANFEA,ANPAIA,ANTIOKIA,ANDARUSIA,
9:ANDAWEA,ANTAKIA
….
56511:YOUSUMONO,NOAZAMI,MIATUME,
56514:MEISIIRE,REIIKI,
56516:KIETUKU,KUIRA,RAIHARU,RUMONDO
REFERENCES
Abe, K., Araya, S., 1986. Train Traffic Simulation Using
the Longest Path Method. T.of IPSJ, Vol.27, No.1,
pp.103-111.
Gu, Q-P., Takaoka, T., 1996. A Parallel Algorith for the
Longest Paths Problem on Acyclic Graphs with Integer
Arc Length. T.of IPSJ,Vol.37, No.9,pp.1631-1636.
Fischetti, M., Salazar-Gonzalez, J-J., Toth, P., 2002. The
Genralized Traveling Salesman Problem and
Orienteering Problems in The Generalized Traveling
Salesman Problem and its Variations. Kluwer
Academic Publisher.
Ito, T., Tanaka, T., Hu, H., Takeuchi, M., 2002. An
Analysis of Word Chain Games. J.of IPSJ, Vol.43
No.10
Kanasugi, T., Matsuzawa, K., Kasahara K., 1996.
Applications of ABOUT Reasoning to Solving
Wordplays. TR.of IEICE, NLC96-31, pp.1-8.
Lai, H-J., 2001. Eulerian Subgraphs Containing given
Edges, Discrete Mathematics, 230, pp.63-69.
Li, Dengxin, Li, Deying, Mao, J., 2004. On Maximum
number of Edges in a spanning Eulerian Subgraph,
Discrete Mathematics, 274, pp.299-302.
Nakayama, S., Masuyama, S., 1995. A Parallel Algorithm
for Solving the Longest Path Problem in Outerplannar
Graphs, IEICE Transaction D-I, Vol.J78-D-I, No.6,
pp.563-568.
Niimura, I. (eds), 1992. Koujien Ver.4, Iwanami
Sosic, R., Gu, J., 1990. A Polynomial Time Algorithm to
the N-Queen Problem. SIGART, 1, pp.7-11
Skina, S., 1990. Eulerian Cycles. In Implementing Discrete
Mathematics: Combinatorics and Graph Theory with
Mathematica. Addison-Wesley.
This paper describes the definition of the longest
SHIRITORI problem and the solution using the
integer programming and the LP-based
branch-and-bound method. The length of the longest
SHIRITORI problem becomes over 40 percents for
words in the Japanese dictionary. This result surprises
us very much, because usual human SHIRITORI
sequences end up to several tens of words.
As future works
problem like the longest SIRITORO word problem
described in the previous section shortly and the
applications of the longest SHIRITORI problem. Fo
examples, by applying the longest SHIRITORI
problem, the system makes the game time long. It is
possible to keep up human interest against the game
by this. For another application, our method is useful
for the complete analysis of N-players SHIRITOR
game. As, actually, we can find the longest or the
shortest SHIRITORI word sequences in which n-th
player is defeated by adding the several conditions.
This would be useful for finding the solution of
rs SHIRITORI game.
ACKNOWLEDGEMENT
A part of this research is supported by Japan society
for the promotion of sciences, the grant-in-aid (No.
15300269).
A
SOLVING THE LONGEST WORD-CHAIN PROBLEM
221