
MORPHOLOGICAL CHOICE OF PLANAR MECHANISMS IN
ROBOTICS
Peter Mitrouchev
Integrated Design Centre, "Sols, Solids, Structures - 3S" Laboratory, UMR 5521, Domaine Universitaire, B.P. n° 53,
38041 GRENOBLE Cedex 9, France
Keywords: Robot design, architecture, plan mechanisms, morphology
Abstract: In this paper a morphological confined choice for kinematic mechanisms in robotics is presented. It is based
on symmetries of structures. Pairs of groups of mutually symmetrical mechanisms are detected. Thus, the
number of possible configurations is confined by eliminating the symmetrical ones. Different cases of
symmetries have been studied. Expressions for the calculation of the number of frames and end-effectors
are presented. It enables the reduction of the number of structures by avoiding those that are isomorphic.
Following this, examples for applications for various kinematic structures are presented, enabling the field
of research to be restricted to the possible solutions.
1 INTRODUCTION
The choice of a kinematic mechanism applied in
robotics is conditioned by the number of degrees of
freedom of the task to be carried out by the robot.
The task itself imposes a kinematic chain compatible
with its number of degrees of freedom. The
kinematic chain thus imposed will be compatible
with the task if it possesses a number and type of
links and joints as those defined by the mobility and
connection laws of Mechanism and Machine Theory
(MMT). MMT supplies lists of possible
mechanisms. As there may be a large number of
these mechanisms, it is usually difficult to make a
choice amongst the available structures in the initial
design phase of the robot chain. In fact taking into
account the symmetries it can be noticed that there
are a significant number of isomorphic structures as
far as the position of the frame and of the end-
effector of the robot
. MMT contributed greatly to
planar and spatial mechanism synthesis with
different degrees of freedom ( Hervè, 1982).
The morphological (topological) synthesis of
kinematic chains has, for a long time, been the
subject of many papers. There are different methods
for the kinematic synthesis of planar chains with
simple revolute joints, with different degrees of
mobility and different numbers of links and joints.
These methods which enabled the lists of chains,
called A
i
lists, to be obtained are: intuition and
inspection (Crossley, 1964), graph theory
(Dobrjanskyi 1967, Woo 1967). Others consist of
transformation of binary chains (Mruthyunjaya
1984a, Mruthyunjaya 1984b) the concept of Assur
groups (Manulescu, 1987), or Franke's notation
(Davies 1966, Crossley 1966). New methods based
on genetic algorithms or neuronal networks are also
used (Chedmail 1995, Yannou 1997). These A
i
lists
are subdivided into many sub-lists, called B
i
, taking
into account the position of the frame and of the
end-effector of the robot.
The problem is how to choose amongst the
possible structures provided by MMT as far as the
position of the frame and the end-effector. The
objective is to find planar mechanisms with revolute
joints that provide guidance of a moving frame e.g.
the end-effector of an industrial robot, relative to a
base frame with a given degree of freedom. The aim
of this paper is to present a new method enabling the
reduction of the number of kinematic structures
provided by the MMT which are suitable for
robotics applications. It is based on the exploitation
of symmetries of the mechanisms. The sub-lists B
i
are then studied in order to extract the minimum
number of possible structures for the initial design of
kinematic chains of industrial robots, the two criteria
being the position of the frame and of the end-
effector of the robot.
193
Mitrouchev P. (2004).
MORPHOLOGICAL CHOICE OF PLANAR MECHANISMS IN ROBOTICS.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 193-200
DOI: 10.5220/0001139801930200
Copyright
c
SciTePress
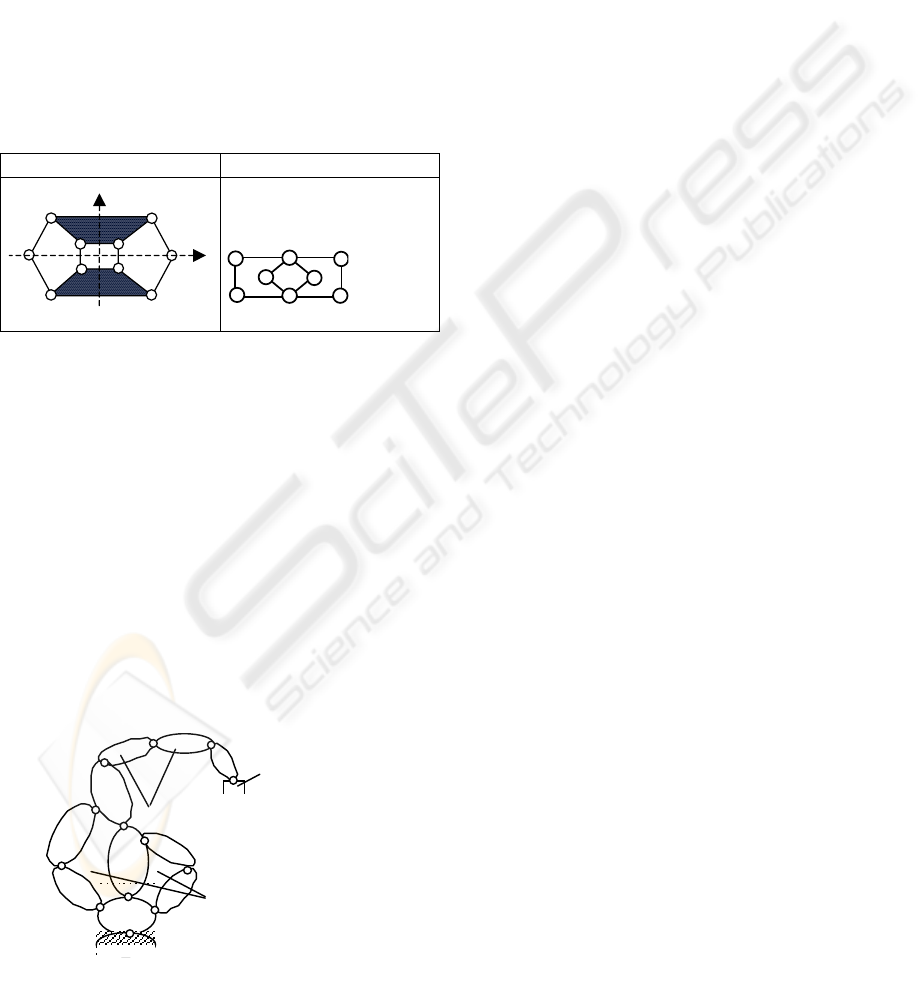
2 NOTIONS AND RESTRICTIONS
MMT proposes various ways of representing
kinematic structures. The most common, the
kinematic graph, consists in conserving a shape for
the links in order to better appraise the topology of
the structure. Nevertheless this presentation is
difficult to manage. Any kinematic structure may by
transformed into Crossley's inverse graph (Crossley,
1964) replacing every link (binary, ternary…) by a
point. The joints themselves are represented by a
line linking the points concerned. We note that the
kinematic graph expresses geometrical dimensions.
Obviously the inverse graph does not. But this letter
expresses better the symmetries of the structures if
there are any.
kinematic graph inverse graph
Figure 1: Representation of a structure by kinematic and
Crossley's inverse graph.
A robot being a complex mechanical system (MS)
characterised by a very important interaction
between its links, we define its architecture by
(Mitrouchev 1999): the main structure, which
generates the main motion of the robot and upon
which, stands the rest of the MS, the regional
structure, consisting of the arm and the forearm of
the robot (mechanical arm) and the local structure
usually consisting of three axes concurrent at one
point, and representing the wrist of the robot.
It is noted at this stage that the structure presented
by one or other ways (kinematic or inverse graph)
only presents the main structure of the robot (cf. fig.
2).
Let us consider a mechanism with M degree of
mobility, N links of any type, joined to each other by
C
simple revolute joints. In this paper only
mechanisms having main planar structures with
simple revolute joints usually applied in robotic
design will be studied. We note that the objective is
not to find among the mechanisms available a
particular one that fits well to a given task, but to
reduce the number of possible structures, the two
criteria being the position of the frame and the end-
effector of the robot.
3 MECHANISM DESIGN
MMT, being a part of the technological sciences, is
at the base of mechanism design in robotics. The
question is: amongst the available kinematic
structures supplied by MMT, how many of these are
suitable for application in kinematic chain design in
robotics? In order to reply to the above question it is
interesting to answer the following questions: why
and how?
Why ? Obviously it is not possible to dimension a
mechanism without being familiar with its topology.
The topological choice is normally made before the
dimensioning phase. It is this stage that presents the
most difficult problem in mechanism synthesis. It is
currently impossible to place the dimensioning
equations on the same level as the choice of
topology, because this choice is not governed by
equations i.e. assigning design variables for this or
that topology, except for: degree of mobility M,
number of links N and number of joints C (e.g. M=2,
N=7 and C=8).
How? Let us consider a list of mechanisms
provided by MMT and defined by the three
following parameters : number of links, number of
joints and number of degree of freedom. As we said,
we call this list A
i
list. We define also the B
i
list,
issued from an A
i
list taking into account the
position of the frame and of the end-effector. The
problem is to decide which structures may be
removed from the A
i
list, without restricting the
choice of available structures taking into account the
position of the frame and of the end-effector.
Let us consider an A
i
list of P topologies Topo i
extracted from a complete list of mechanisms with
respect to some parameters (e.g. mechanisms with
two degrees of mobility M=2, seven links N=7 and
eight joints C=8). Firstly from this list, B
i
sub-lists
are extracted with respect to criterion 1 "fixing a
frame" or "frame choice". Then each topology Topo
i gives several possibilities for attaching an end-
effector (pincers, paint gun, welding electrode). This
b
a
main structure
regional structure
local structure
frame
Fi
g
ure 2: To
p
olo
g
ical structure of a robot.
ICINCO 2004 - ROBOTICS AND AUTOMATION
194

is the second criterion "fixing an end-effector" or
"end-effector choice" with regard to the choice of
the frame used in the elaboration of the confined B
i
lists. For example, the B
i
list of fig. 3 below,
contains N.(N-1)=7.6 = 42 possible solutions but it
is noted that some of them appear twice: solutions 1
and 6, 2 and 5, 4 and 3 for the first possibility to fix
a frame. For the other possibilities it is reasonable to
suppose that there will be other dual (isomorphic)
solutions.
key: black element – frame;
- end -effector
Figure 3: Elaboration of the B
i
list.
4 PROPOSED METHOD
We indicate by:
- N
sc
number of the links of a sub-chain,
- n
c
the number of links cut by an axis of
symmetry coincident with their axis of symmetry,
- n
nc
the number of links not cut by an axis of
symmetry or cut, but not along their axis of
symmetry,
- n
a
the number of links cut solely by the axis of
symmetry a (cf. fig. 4 and figures below), or the
number of links containing the centre of symmetry
in the case of a central symmetry,
- n
b
the number of links cut solely by the axis of
symmetry b,
-n
ab
the number of links cut both by the axes of
symmetry a and b,
- s the number of symmetries .
In order to present the method, various cases will
be demonstrated with respect to their type and to
their number of symmetries.
4.1 Different cases of symmetries
4.1.1 No symmetry
The simplest case is the one without any symmetry
(fig. 4a.). In this case there are N possibilities to fix
the frame. Thus Fc
= N. Concerning the position of
the end-effector there are (N-1) possibilities to attach
it for each position of the frame. Thus to each frame
choice belong (N-1) end-effector choices.
a)
b)
Figure 4: Structures without and with symmetries.
The structure of fig. 4a. above has the peculiarity of
having no symmetry, then:
NFc
=
(1)
and
)1(
−
=
NNEc (2)
4.1.2 Only one symmetry
We define the axis of geometrical symmetry in the
kinematic graph like the axis of topological
symmetry in the inverse graph. If a link is cut by an
axis of symmetry in the kinematic graph, the same
link is cut by the same axis (called axis of
topological symmetry) in the inverse graph.
Many mechanisms, like the structure in fig. 4b.,
have one axis of symmetry noted “a”. There are two
sub-chains 1276, 2348 and each of them has a
symmetry of links 1 and 7 for the furst sub-chain
1276 and 3 and 8 for the second one (2348). As
regards the position (choice) of the frame Fc,
symmetry dictates that the case where the frame is
on link 1 is the same as the cases when it is on 3, 7
or 8. It is the same for the links 6 and 4. Therefore
an inventory of two possibilities (solutions) are
taken to which must be added the two possibilities:
links 2 and 5. The latter two have the particularity of
being cut by the axis of symmetry. The first two
possibilities correspond to ((N-n
c
)/2)-1 solutions,
consequently for Fc we have:
1
3
4
6
5
7
8
2
a
Ai List
..
..
..
..
..
..
Bi List (42 solutions)
…
etc………………etc……………… etc…………
9
8
7
1
3
4
5
1
6
2
Topo i (M=2, N=7, C=8)
axis of symm.
MORPHOLOGICAL CHOICE OF PLANAR MECHANISMS IN ROBOTICS
195

2
c
nN
Fc
+
=
(3)
Concerning the number of possibilities for the
attachment of an end-effector Ec, as a function of
the frame position:
- in the case where the frame is not situated
symmetrically, the number of possibilities for the
attachment of an end-effector is (N-1),
- in the case where the frame is placed
symmetrically, the same problem as the one treated
previously is found; that is to say the positions 1,3,7
and 8 are identical, as are 6 and 4. Consequently
there are (N-n
c
)/2+(n
c
-1) possibilities for Ec.
It should be noted that the number of cases when
the frame is placed symmetrically corresponds to the
number of the links cut by the axis of symmetry.
Thus for Ec we have:
()
⎟
⎠
⎞
⎜
⎝
⎛
−+
+−
−
=
2
2
1
2
c
nN
c
nN
c
nN
Ec
(4)
4.1.3 Two symmetries
Two cases are to be considered for the two
symmetries.
4.1.3.1 None of the links are cut by an axis of
symmetry
The structure in fig. 5a below has two axes of
symmetry but they do not cut each other in a link.
As regards the choice of frame Fc:
- in the case of a link that is not cut, each link is
found four times by the system of symmetries, for
example links 2-1-4-5,
Figure 5: Structures with two symmetry.
- in the case of a link, which is cut, each link is
found twice, for example 7-8, 3-6, thus:
4224
c
nN
b
n
a
n
nc
n
Fc
+
=++=
(5)
Then, as regards choice Ec, working in
discriminately with symmetry a or b, requires two
identical methods (reflections):
- in the case where the frame is not situated
symmetrically, the number of possibilities to attach
the end-effector is (N-1), so there are n
nc
/4 cases
thus described,
- in the case where the frame is placed
symmetrically with respect to symmetry a, the
number of possible solutions for the attachment of
an end-effector is (N-n
a
)/2+n
a
-1, so there are n
a
/2
cases thus described.
Finally, after simplification, for Ec we have:
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−+
+
+
−+
+−
−
=
2
2
2
2
2
2
)1(
4
b
nN
b
n
a
nN
a
n
N
c
nN
Ec
(6)
4.1.3.2 Links are cut by two axes of
symmetry
The structure of fig. 5.b has two axes of symmetry
that cross on a link. To fix the frame the same
reasoning as in the previous case can be adapted,
taking care to add the links cut by a and b
symmetries which are counted neither in n
a
nor in n
b
,
consequently:
4
2
ab
n
c
nN
Fc
++
=
(7)
It is the same process concerning the position of the
end-effector:
+
+−+
+−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
2
2
2
)1(
4
ab
n
a
nN
a
n
N
c
nN
Ec
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−+++
+
+−+
+
4
43
2
2
2
ab
n
b
n
a
nN
ab
n
ab
n
b
nN
b
n
(8)
4.1.4 Central symmetry
This is the case for the structure below. To fix the
frame, the difference between two cases must be
made:
5
2
3
7
6
4
1
b
a
2
1
6
3
4
5
8
7
a
b
ICINCO 2004 - ROBOTICS AND AUTOMATION
196
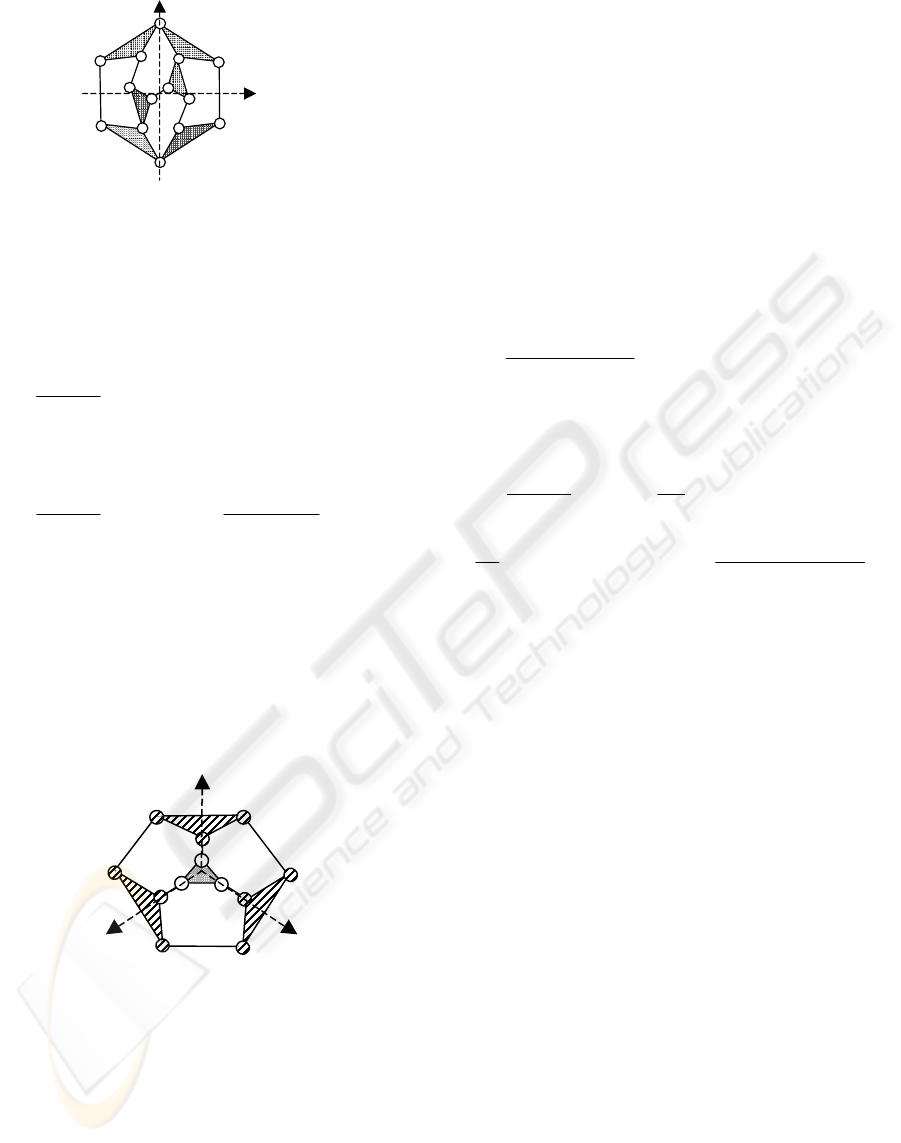
a
b
Figure 6: Structure with central symmetry.
- the centre of symmetry belongs to n
c
links, so there
are (N-n
c
)/2+n
c
possibilities,
- the centre of symmetry does not belong to a link,
so there are N/2 possibilities.
Finally for Fc we have:
2
c
nN
Fc
+
= (9)
As regards the Ec choice we have:
⎟
⎠
⎞
⎜
⎝
⎛
−+
+−
−
=
2
2
)1(
2
c
nN
c
nN
c
nN
Ec (10)
We can note that the equations (9) and (10) are the
same as the equations (3) and (4).
4.1.5 Three or more symmetries
Only one case of three symmetries is present in the
mechanisms studied (cf. fig 7.). This is the number
60 mechanism of the A
i
list of mechanisms, with
M=3, N=10 and C=12.
6
5
4
3
2
1
Figure 7: Structures with three symmetries.
In this particular case there are three symmetrical
sub-chains (1,2,3,4,5,6) with s=3. As regards the
position of the frame Fc (frame choice), we can note
that each sub-chain contains two symmetrical triples
of links (1,3,5 and 2,4,6) which correspond to (N
sc
/s)
solutions. Consequently for Fc we have: Fc=
(N
sc
/s)=2.
In order to fix the end-effector, for a given
position of the frame, there are (N
sc
-1)-n
sc
solutions.
Consequently for the Fc positions of the frame we
have : E
c
=F
c
[(N-1)- n
sc
]=12 positions of the end-
effector.
5 GENERAL CASE
It is possible to bring together most of the equations
above in one equation as regards Fc and Ec. It is
only necessary to add the variable s indicating the
number of symmetries. As a result it is relatively
easy for the choice of the frame to present only one
formula for the cases studied above.
1
2
2
−
++
=
s
ab
n
c
nN
Fc
, s = 1,2 (11)
For the choice Ec:
()
++−++−
−
=
ab
n
a
nN
s
a
n
N
s
c
nN
Ec 2
2
)1(
2
()
⎟
⎠
⎞
⎜
⎝
⎛
−++
++−++
s
ab
n
b
n
a
nN
ab
n
ab
n
b
nN
s
b
n
2
2
2
s = 1, 2 (12)
Only one case is different, this is the case without
symmetry (s = 0) because the equations (11) and
(12) have no mathematical significance. Thus it is
found that the two equations as far as the cases
without symmetries are mainly the equations (1)
and (2).
6 EXAMPLES FOR
APPLICATIONS
In order to illustrate the expressions thus presented,
they are applied for some structures with different
degrees of mobility. As has already been said, the
proposed help does not allow the optimum solution
to be found, but reduces the field of research for this
solution. This is what will be shown by the
following examples applied to descriptions of the
main structures of industrial robots.
MORPHOLOGICAL CHOICE OF PLANAR MECHANISMS IN ROBOTICS
197
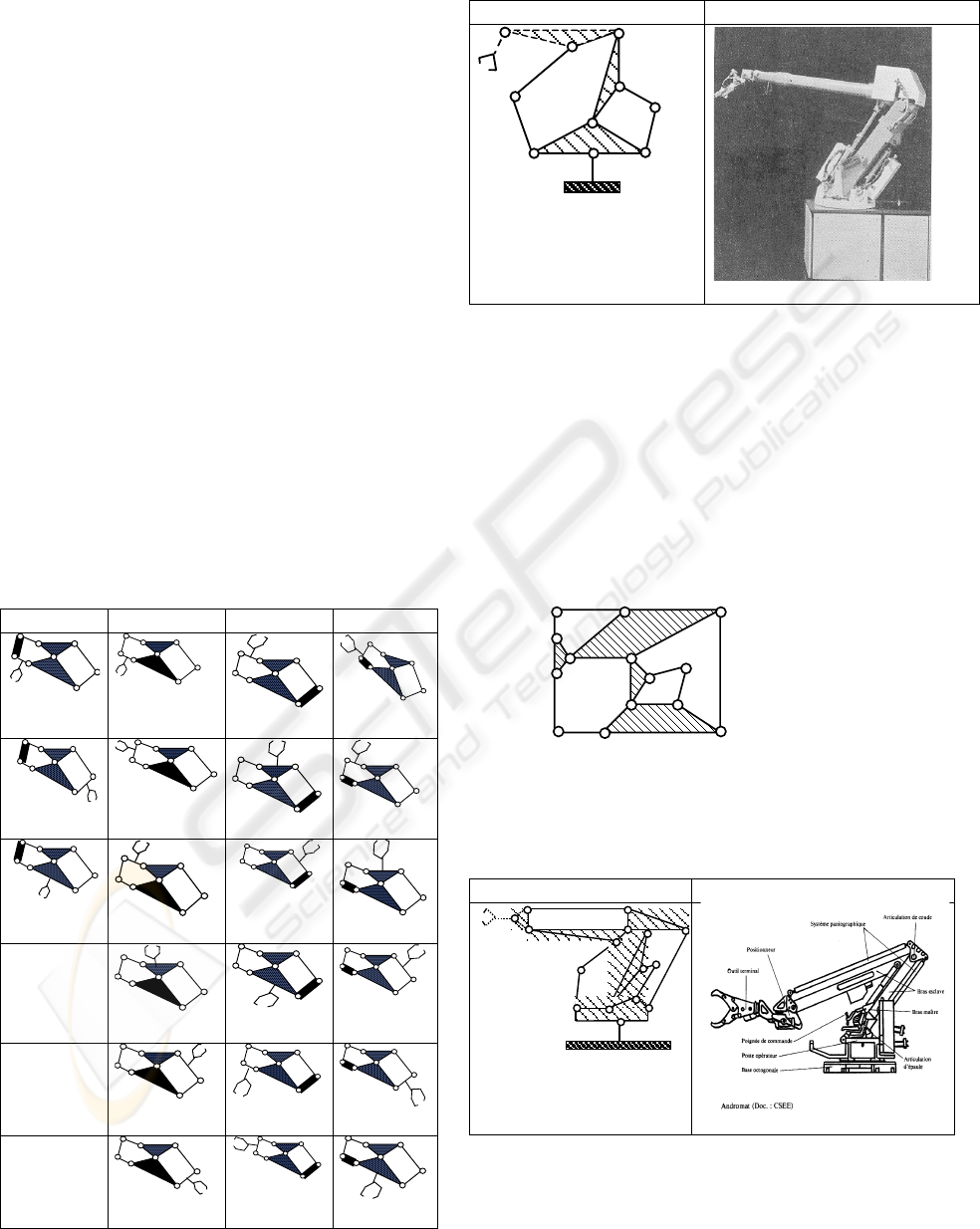
6.1 Structures with two degrees of
mobility, seven links and eight
joints
Let us consider the structure below found on an A
i
list provided by MMT with M=2, N=7 and C=8. The
B
i
list contains N(N-1) = 7.6 = 42 solutions (cf. fig.
3). Firstly the description file N=7, s=1, n
a
=1, n
b
=0,
n
ab
=0, n
c
=1 is established. The created program
computes the the Fc and Ec variables. When there is
a central symmetry and not an axial one, this is
noted as a note in the respective line of the tables.
The confined B
i
list contains Ec=21 solutions, where
the four possibilities for Fc are distinguished (cf.
Table 1)
Amongst the twenty one possibilities, solution
number B23 from the table below was chosen by a
robot manufacturer in order to design the main
structure of the AKR-3000 robot presented in fig. 8
(Ferreti, 1981). In this case the frame was
transformed in to a quaternary link and the binary
link, where the end-effector was attached, in to a
ternary one.
Table 1: Confined Bi list of structures with two degrees
of mobility, seven links and eight joints
List B1 List B2 List B3 List B4
B11
B21
B31
B41
B12
B22
B32
B42
B13
B23
B33
B43
B24
B34
B44
B25
B35
B45
B26
B36
B46
topological structure AKR-3000 robot
Figure 8: AKR-3000 robot.
6.2 Structures with two degrees of
mobility, eleven links and
fourteen joints
The kinematic graph for a structure from an A
i
list
created by MMT (M=2, N=11, C=14) is presented
below (description file N=11, s=0, n
a
=0, n
b
=0,
n
ab
=0). The Excel table gives the following results:
Fc=11 and Ec=110.
Amongst the one hundred and ten available
structures, a robot manufacturer has applied one
solution in order to design the main structure of the
Andromat robot presented below.
topological structure Andromat robot
Figure 9: Topological structure of Andromat robot.
ICINCO 2004 - ROBOTICS AND AUTOMATION
198
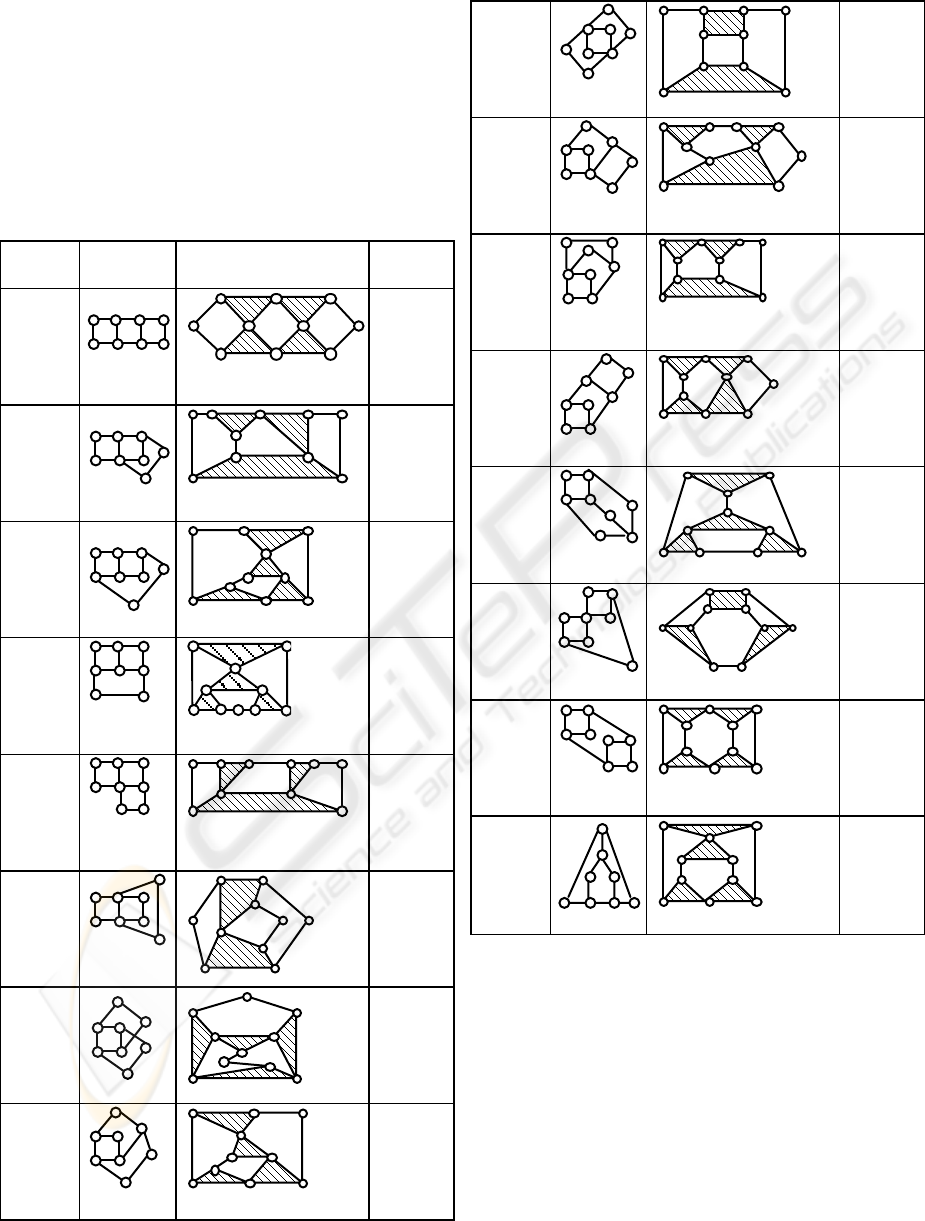
6.3 Structures with one degree of
mobility, eight links and ten joints
The table below groups the A
i
list of the sixteen
kinematic structures with one degree of mobility
represented by their kinematic and inverse graphs
and their description files.
Table 2: A
i
list of structures with one degree of mobility,
eight links and ten joints.
notat. inverse
graph
kinematic graph descrip.
file
G1-8
1
N=8,
s=2,
n
a
=0,
n
b
=0,
n
ab
=0
G1-8
2
N=8,
s=0,
n
a
=0,
n
b
=0,
n
ab
=0
G1-8
3
N=8,
s=0,
n
a
=0,
n
b
=0,
n
ab
=0
G1-8
4
N=8,
s=1,
n
a
=2,
n
b
=0,
n
ab
=0
G1-8
5
N=8,
s=1,
n
a
=2,
n
b
=0,
n
ab
=0
G1-8
6
N=8,
s=1,
n
a
=0,
n
b
=0,
n
ab
=0
G1-8
7
N=8,
s=1,
n
a
=4,
n
b
=0,
n
ab
=0
G1-8
8
N=8,
s=0,
n
a
=0,
n
b
=0,
n
ab
=0
G1-8
9
N=8,
s=2,
n
a
=2,
n
b
=2,
n
ab
=0
G1-8
10
N=8,
s=0,
n
a
=0,
n
b
=0,
n
ab
=0
G1-8
11
N=8,
s=0,
n
a
=0
n
b
=0,
n
ab
=0
G1-8
12
N=8,
s=1,
n
a
=2,
n
b
=0,
n
ab
=0
G1-8
13
N=8,
s=1,
n
a
=2,
n
b
=0,
n
ab
=0
G1-8
14
N=8,
s=1,
n
a
=2,
n
b
=0,
n
ab
=0
G1-8
15
N=8,
s=2,
n
a
=4,
n
b
=0,
n
ab
=0
G1-8
16
N=8,
s=1,
n
a
=2,
n
b
=0,
n
ab
=0
The possible choices for the frame and the end-
effector obtained by the proposed method are
presented in table 3.
6.4 Other examples
An application under Silicon Graphics /UNIX has
been created based on the method presented.
Enabling the restriction of the number of structures
it is applied to other structures as examples with:
- one degree of mobility, ten links and thirteen
joints,
MORPHOLOGICAL CHOICE OF PLANAR MECHANISMS IN ROBOTICS
199
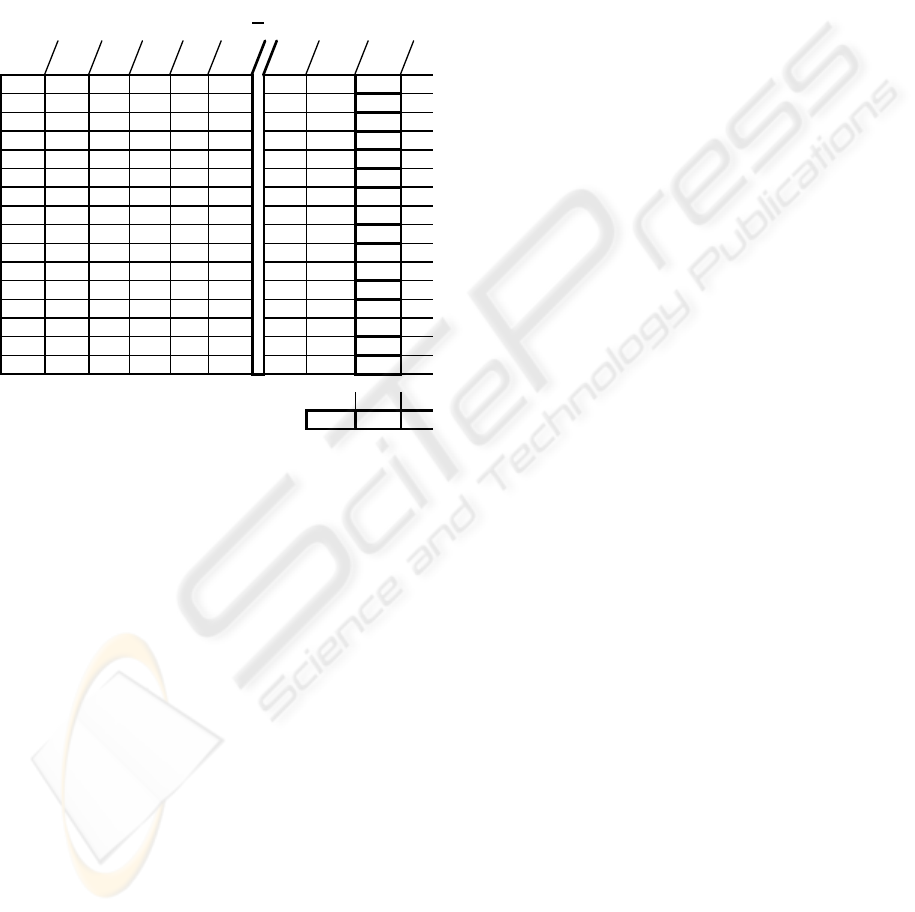
- two degrees of mobility, nine links and eleven
joints ,
- three degrees of mobility, ten links and twelve
joints.
In the majority of cases the kinematic structure
has axial symmetry. This symmetry is not mentioned
in the tables presented. However, the central
symmetry (not as much presented in the structures)
is mentioned, as previously stated in paragraph 6.1.
Table 3: Frame and the end-effector choices.
Structures with one degree of mobility, eight links and ten joints
n°
N
s
n
s
c
N
s
c
n
s
p
n
c
F
c
E
c
182242 0 214
280000 0 856
380000 0 856
481240 2 529
581240 2 529
681002 0 321
781250 4 210
880000 0 856
982250 4 315
10 8 0 0 0 0 0 8 56
11 8 0 0 0 0 0 8 56
12 8 1 0 0 0 2 5 29
13 8 1 2 5 0 2 6 34
14 8 1 2 4 2 2 4 16
15 8 2 2 4 2 4 3 17
16 8 1 2 5 0 2 5 29
tota l tota l
83 518
7 SUMMARY
The method presented in this paper enables the
morphological restriction for planar kinematic
mechanisms in robotics by avoiding those that are
isomorphic. It is based on the exploitation of
symmetries. The different cases of symmetry studied
provide expressions allowing the number of possible
structures to be calculated as regards the position of
the frame and of the end-effector. The proposed
expressions are then applied to different examples.
The results of this study may be useful to robot-
designers enabling them to limit the field of research
to the possible solutions.
REFERENCES
Chedmail, P., Ramstein E., 1995. Synthèse des
mécanismes et algorithmes génétiques, Journée
PRIMECA, Toulouse, pp.7-14.
Crossley, F. R. E., 1964. A cotribution to Grubler's theory
in the number synthesis of plane mechanisms, ASME,
Journal of Engineering for Industry, pp.1-8.
Crossley, F. E., 1966. On an unpublished work of alt, Jour.
Mechanisms,
1, pp.165-170.
Davies, T., Crossley F.E., 1966. Structural analysis of plan
linkages by Franke’s condensed notation, Jour.
Mechanisms,
1, pp.171-183, Pergamon Press.
Dobrjanskyi, L., Freudenstein, F., 1967. Some application
of graph theory to the structural analysis of
mechanisms, Journal of Engineering for Industry,
pp.153-158.
Ferreti, M., 1981. Panorama de 150 manipulateurs et
robots industriels, Le Nouvel Automatisme, n°
26,
Novembre-Décembre 1981, pp.56-77.
Hervè, L.M., 1982. Intrinsic formulation of problems of
geometry and kinematics of mechanisms, Mech. and
Mach. Theory,
17, N° 3 , pp.179-184.
Hwang, W-M., Hwang, Y-W., 1992. Computer-aided
structural synthesis of plan kinematic chains with
simple joints, Mech. Mach. Theory,
27, n°2, pp.189-
199.
Manolescu, N. et al., 1987. Structural and Kinematic
Synthesis of Planar Kinematic Chain (PKC) and
Mechanisms (PM) with Variable Structure During the
Work, Proc. of the 7-th World Congress, The Theory
of Mechines and Mechanisms,
1, 17-22 September
1987, Sevilla, Spain, pp. 45-48.
Mitrouchev P., André P. , 1999. Méthode de génération et
description de mécanismes cinématiques plans en
robotique. Journal Européen des Systèmes
Automatisés, ISSN : 0296-1598, (vol. 33, n°3) - avril
1999, pp. 285-304.
Mruthyunjaya, T.S., 1984a. A computerized methodology
for structural synthesis of kinematic chains : Part 1-
Formulation, Mech. Mach. Theory,
19, No.6, pp. 487-
495.
Mruthyunjaya, T.S., 1984b. A computerized methodology
for structural synthesis of kinematic chains : Part 2-
Application to several fully or partially known cases,
Mech. Mach. Theory,
19, No.6, pp. 497-505.
Woo, L. S., 1967. Type synthesis of plan linkages, Journal
of Engineering for Industry, February 1967, pp.159-
172.
Yannou B.,Vasiliu, A., 1997. Synhèse dimensionnelle de
mécanismes générateurs de trajectoires par réseaux de
neurones, 5
-ème
Colloque PRIMECA, La Plagne,
1997, pp.315-323.
ICINCO 2004 - ROBOTICS AND AUTOMATION
200
