
A FUZZY INTEGRATED APPROACH TO IMPEDANCE CONTROL
OF ROBOT MANIPULATORS
S.J.C. Marques
Polytechnic Institute of Lisbon, Instituto Superior de Engenharia de Lisboa
Department of Mechanical Engineering, Avenida Conselheiro Em
´
ıdio Navarro, 1900 Lisboa, Portugal
L.F. Baptista, J.M.G. S
´
a da Costa
Technical University of Lisbon, Instituto Superior T
´
ecnico
Department of Mechanical Engineering, GCAR/IDMEC, Avenida Rovisco Pais, 1049-001 Lisboa Codex, Portugal
Keywords:
Fuzzy adaptive control, fuzzy sliding mode control, force control, robot manipulators.
Abstract:
This paper presents an integrated fuzzy approach to recover the performance in impedance control, reducing
the errors in position and force, considering uncertainties in the parameters of the manipulator model and
contact surface model. This integrated strategy considers a fuzzy adaptive compensator in the outer control
loop that adjusts the manipulator tip position to compensate for uncertainties present in the environment. In the
inner loop, a fuzzy sliding mode-based impedance controller compensates for uncertainties in the manipulator
model, based on an inverse dynamics control law. The system error, defines the sliding surfaces of the fuzzy
sliding controller as the difference between the desired and the actual impedances. In order to evaluate the
force/position tracking performance and to validate the proposed control structure, simulations results are
presented with a three-degree-of freedom (3-DOF) PUMA robot.
1 INTRODUCTION
The development of robot manipulator applications
in industry to tasks that involve interaction between
the en-effector and the environment, requires the de-
velopment of more sophisticated force control strate-
gies. Classical force control schemes like hybrid
control (Mason, 1981) or impedance control (Hogan,
1985) are the theoretically foundation of force con-
trol strategies. However, they are not sufficient to
bring robots executing tasks with interaction with a
contact surface, like grinding, deburring and polish-
ing. This lack in performance is due to variable pay-
loads, torque disturbances, parameter variations, un-
modeled robot dynamics and uncertainties in the envi-
ronment parameters. Several approaches to deal with
those uncertainties have been proposed, like classi-
cal adaptive control (Colbaugh et al., 1993), robust
control (Liu and Goldenberg, 1991) and fuzzy adap-
tive control (Hsu and Fu, 1996), among others. A
great research activity in force control has been regis-
tered in the last decade, however, only a few of these
schemes have been implemented in experimental or
industrial robots (Hsu and Fu, 2000; Baptista et al.,
2001). Therefore, more sophisticated control struc-
tures are required to cope with the overall uncertain-
ties in the force control problem.
In this paper, an integrated approach of fuzzy ro-
bust impedance and adaptive control is proposed. In
this approach, an implicit force control formulation is
used to compensate for uncertainties in the manipula-
tor parameters and the contact surface model. The
fuzzy adaptive controller corrects the reference po-
sition to a fuzzy robust impedance controller in the
inner control loop. This controller includes a fuzzy
sliding mode term, where a new sliding surface is de-
fined, based on the impedance error. In the proposed
approach, the impedance controller design is equiva-
lent to the sliding mode controller design.
The outline of the paper is as follows: section 2
presents a brief description of the manipulator dy-
namics in the constrained coordinate frame. Section 3
presents the overall force control structure and a brief
description of the two control schemes. Simulation
results are presented in Section 4, and finally in Sec-
tion 5 some conclusions are drawn.
2 ROBOT DYNAMICS AND
ENVIRONMENT
Let’s consider an n−link rigid-joint robot manip-
ulator constrained by contact with the environment.
201
Marques S., Baptista L. and Sá da Costa J. (2004).
A FUZZY INTEGRATED APPROACH TO IMPEDANCE CONTROL OF ROBOT MANIPULATORS.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 201-206
DOI: 10.5220/0001139902010206
Copyright
c
SciTePress
The complete dynamic model in cartesian space is de-
scribed by:
H
x
(x)¨x + h
x
(x, ˙x)=u − f
e
(1)
The vectors x, u and f
e
∈
n
(n×1) represent the
end-effector position in the suitable reference coor-
dinate frame, the force control signal, and the force
exerted by the manipulator on the environment, re-
spectively. The term h
x
is given by C
x
(x, ˙x) ˙x +
g
x
(x)+d
x
( ˙x), where C
x
(x, ˙x), g
x
(x) and d
x
( ˙x)
are the Coriolis matrix, gravity and friction vectors,
respectively. Generally, a task frame attached to the
constrained surface is selected, when the robot ma-
nipulator tip moves in a force control task, so as to
easily describe the desired position x
d
and force f
d
trajectories. The internal joint coordinates q, ˙q and ¨q
must be transformed in external cartesian ones x, ˙x
and ¨x, by means of the forward kinematics, where x
is the position of the tip manipulator in the task frame
coordinates. Regarding the external forces, let’s de-
compose the force vector f
e
, given by the force sen-
sor in all of its components and already transformed
in the task frame: a normal component f
n
in the per-
pendicular direction to the surface environment and
a tangential component f
t
, in the velocity tip manip-
ulator direction. Let’s also assume that the friction
coefficient µ between the manipulator tip and the en-
vironment is known. Thus, it is possible to calcu-
late exactly the perpendicular direction
n to the envi-
ronment surface, implicitly given by the force sensor.
Thus, without lost of generality, only three elements
in force and position, f
e
and x, defined in its com-
ponents as f
e
=[f
n
,f
t
, 0]
T
and x =[x
1
,x
2
,x
3
]
T
,
respectively, are going to be considered. The force
control is exerted along the first component and the
position control is done on the other two components.
In what concerns the environment characteristics, sev-
eral models have been proposed, based on elementary
mechanic components (spring, dump and mass), with
one or two degree of freedom (Epping and Seering,
1987). In this article, the environment is modelled as
a spring mechanical element with stiffness coefficient
k
e
.
3 THE OVERALL CONTROL
STRUCTURE
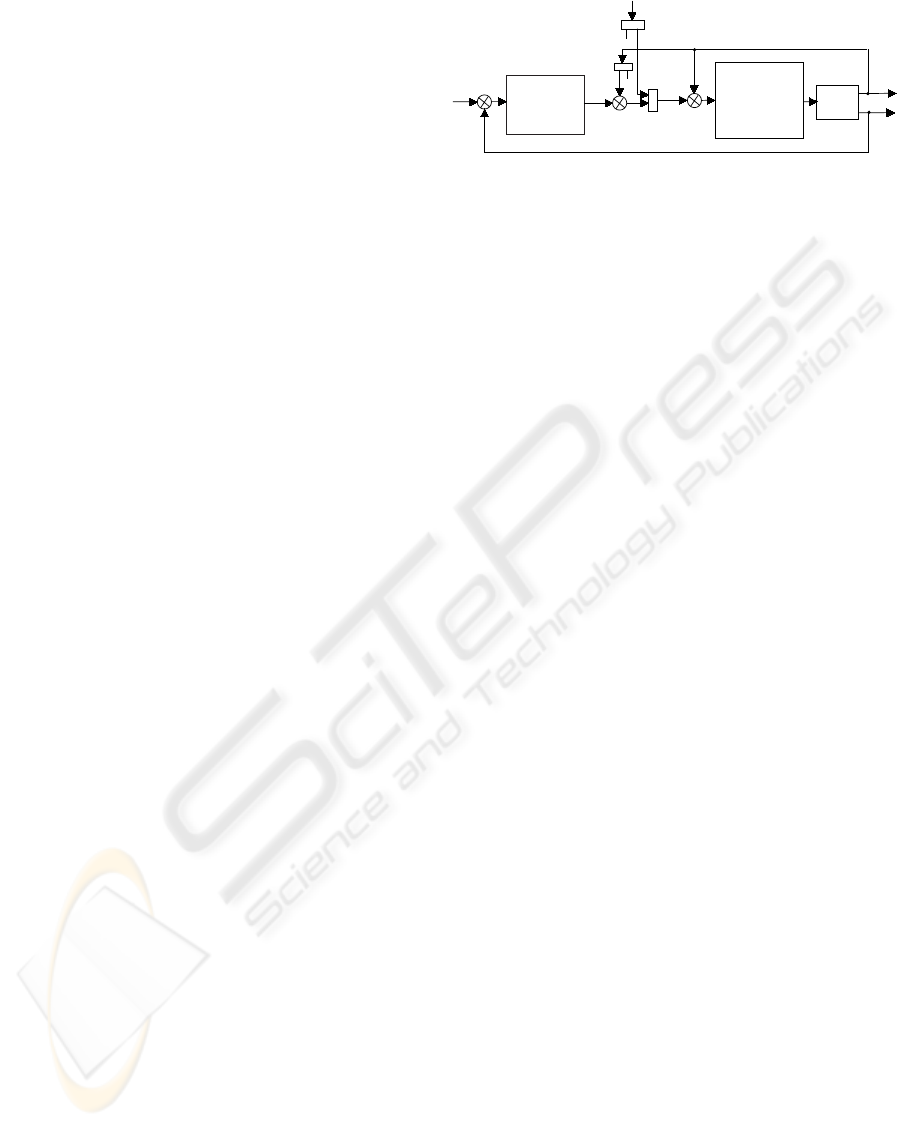
The proposed control structure can be defined as
a position based explicit force control, such that in
the inner loop a position based controller is feeded, in
part, with position errors by a controller in the exter-
nal loop (Fig. 1).
In the external loop, the controller is of fuzzy adap-
tive type, which transforms the force error in a po-
sition adjustment. The main objective of the fuzzy
Fuzzy
Adaptive
Controller
Fuzzy Sliding
Mode-Based
Impedance
Controller
Robot
d
d
f
f
e
e
f
f
d
d
x
x
1
1
d
d
x
x
c
c
x
x
x
x
Figure 1: Block diagram of the overall control structure.
adaptive controller is to compensate environment un-
certainties, like stiffness and geometric location. As
referred above, the fuzzy adaptive controller feeds in
part the inner position controller, because it corrects
only the manipulator tip position x
1
in the perpen-
dicular direction to the contact surface, based on the
force error e
f
. Moreover, the inner position controller
will compensate for uncertainties in the manipulator
dynamic model. The inner position controller, is a
fuzzy sliding mode-based impedance algorithm, with
an inverse dynamics control law. As the dynamic
model of the manipulator is not exactly known, an
impedance error will appear. This impedance error
defines a sliding surface, which, when the system is
in sliding mode, after it has reached the surface, the
state trajectory continues to be on it.
3.1 Fuzzy sliding mode-based
impedance controller
Let’s consider the following impedance control law:
σ = M
d
(¨x
d
− ¨x)+B
d
( ˙x
d
− ˙x)+
K
d
(x
d
− x) − f
e
, (2)
where M
d
, B
d
and K
d
are the inertial, damping and
stiffness positive definite matrices, respectively, and
x
d
is the desired position. The second term in (2) van-
ishes when no uncertainties are present in the manip-
ulator dynamic model. When uncertainties are con-
sidered, the second member in (2) assumes a value
with some norm different from zero. As σ = 0 does
not represent a manifold in the state space (x, ˙x), in-
tegrating σ a sliding surface s = 0, can be defined as
(Lu and Goldenberg, 1995):
s = ˙x − ˙x
d
+ M
d
−1
B
d
(x − x
d
)+M
d
−1
t
0
f
e
dτ
+M
d
−1
K
d
t
0
(x − x
d
)dτ (3)
When the system is in sliding mode, after it has
reached the surface, the state trajectory continues to
be on the sliding surface (s = 0) so that (
˙
s = 0)
and σ = −M
d
˙
s = 0 is obtained. This indicates that
ICINCO 2004 - ROBOTICS AND AUTOMATION
202
the impedance controller design is equivalent to de-
sign a sliding mode controller which guarantees that
the state trajectory reaches the sliding surface and re-
mains on it, thereafter. The norm of σ is used to repre-
sent the deviation of the system state from the sliding
surface. This deviation reflects the impedance control
error.
Let’s consider also an inverse dynamics control law,
based on the robot nominal dynamics:
u =
H
x
(x)¨x
s
+
h
x
(x, ˙x, ˙x
s
)+f
e
− K
fz
, (4)
where
h
x
(x, ˙x, ˙x
s
)=
C
x
(x, ˙x) ˙x
s
+
g
x
(x)+
d
x
( ˙x) (5)
The velocity ˙x
s
in (4) and (5), is defined as:
˙x
s
= ˙x
d
− M
d
−1
B
d
(x − x
d
) − M
d
−1
t
0
f
e
dτ
−M
d
−1
K
d
t
0
(x − x
d
)dτ (6)
From (3) and (6) the relation ˙x
s
= ˙x−s holds, which
means that when the state trajectory is on the sliding
surface, the actual velocity ˙x follows ˙x
s
exactly. The
term K
fz
is given by:
K
fz
= K
v
× u
fz
, (7)
where K
v
is a diagonal matrix of control gains based
on the upper bounds of the uncertainties in the dy-
namic model and u
fz
is a fuzzy system (Lu and
Goldenberg, 1995). This fuzzy system is a counter-
part of the Sliding Mode Controller with Boundary
Layer (SMC-BL). In the boundary layer (BL), near
the sliding line s =0, the control input dynamics
is smoothed, avoiding the chattering effects, ensur-
ing that the error states remain within the layer. In-
side this BL, a null control signal along the switching
line is verified, and increases the absolute value of the
control signal, as the error states are far away from the
switching line. A fuzzy system with a diagonal form
rule base considering the error and its derivative as in-
puts, has a similar behavior to the above prescribed in
(Palm et al., 1997). However, this rule base can be
reformulated as one input one output, with the input
variable s inside the BL and the output variable u,
accordingly Table 1 and regarding the following rule:
R
1
: IF
s is Negative High
THEN
u must be Negative High
This rule base reduces the number of fuzzy rule con-
trol and can assume a more general behavior than the
SMC-BL. In the SMC-BL with boundary layer thick-
ness φ, the control signal u is basically given by:
u = k × sat(
s
φ
) (8)
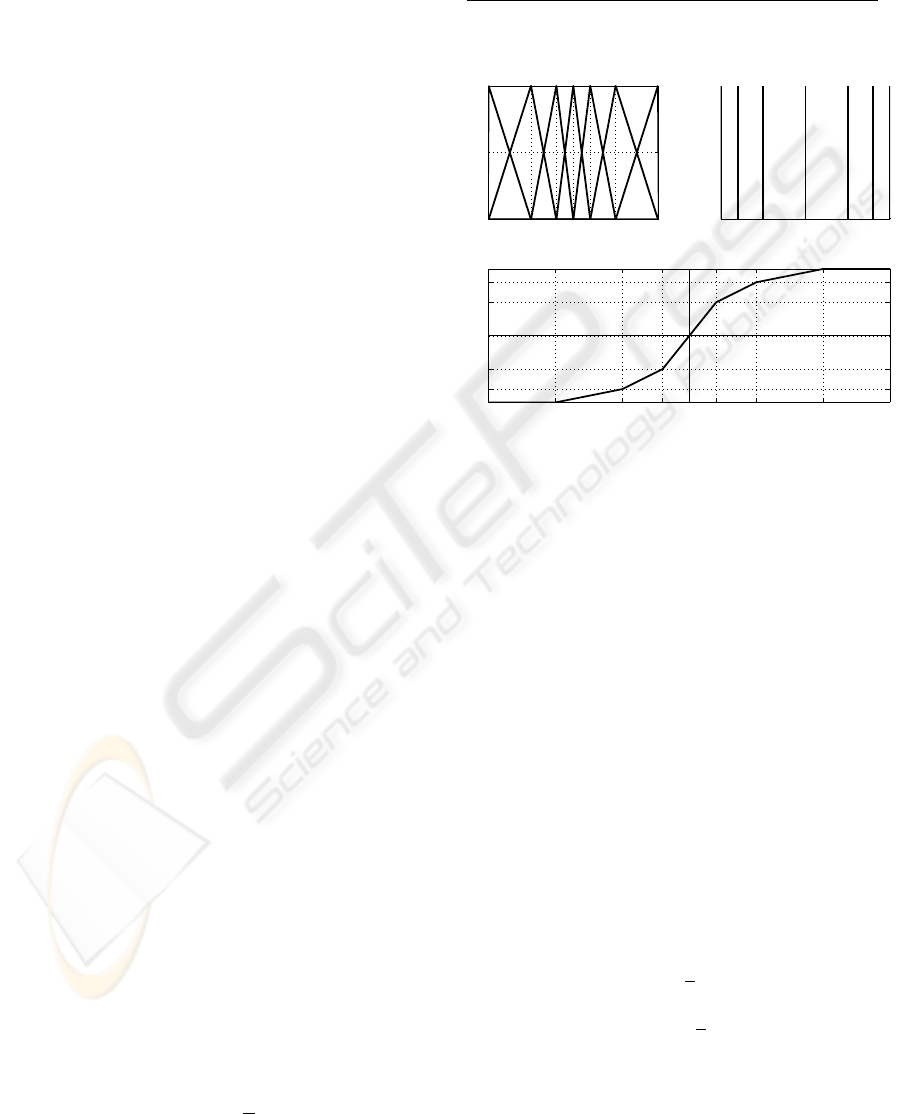
Table 1: Reformulated rule base of a fuzzy slid-
ing mode controller with input
s and output
u. (P-
Positive, N-Negative, ZE-Zero, L-Low, M-Medium
and H-High)
s NH NM NL ZE PL PM PH
u NH NM NL ZE PL PM PH
−1 −0.5−0.2 0 0.2 0.5 1
0
0.5
1
Input MFs
−1−0.8−0.5 0 0.5 0.8 1
0
0.5
1
Output MFs
−1 −0.5 −0.2 0 0.2 0.5 1
−1
−0.8
−0.5
0
0.5
0.8
1
Fuzzy System Output
s
N
u
N
Figure 2: Input and output membership functions and out-
put of the fuzzy system.
This control assumes a linear transfer characteristic
inside the BL. In the FSMC reformulated in that way,
using for instance triangular membership functions
with fuzzy partition leads to stretching the centers
of the input variable towards the origin and expand-
ing the centers of the output variable towards the ex-
tremes. The resulting output of the fuzzy system is
a transfer characteristic with different slopes, which
is greater then 1 near the origin and decreases to-
wards the extremes, where it is less than 1. This is
shown in Fig. 2, where the input and output are nor-
malized into the interval [−1, 1] and different φ
i
such
that
φ
i
= φ, that defines the tracking quality. The
resulting transfer characteristic achieved by this way
must be chosen if for small errors the system is sup-
posed to be more sensitive to disturbances and fast
responses where the error states are near the origin.
As the input of the reformulated FSMC is the variable
s, inside the BL with thickness φ, this can be imple-
mented with the input sat(
s
φ
), which results in the
normalized interval [−1, 1] by self. This is the same
as the input variable s with
1
φ
as the scaling factor
of the input variable considering the same normalized
interval. The output of the fuzzy system is inside the
interval [−1, 1], which will be scaled by the elements
of the matrix K
v
given in (7).
A FUZZY INTEGRATED APPROACH TO IMPEDANCE CONTROL OF ROBOT MANIPULATORS
203
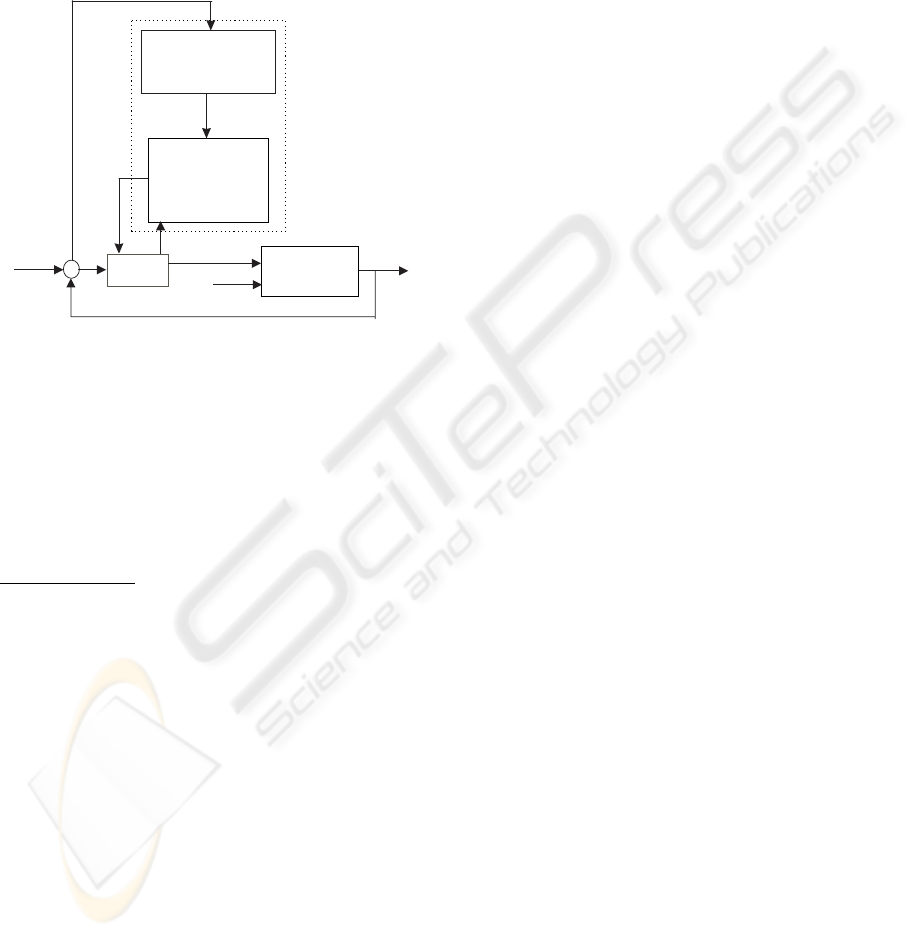
3.2 Fuzzy adaptive controller
The overall fuzzy adaptive control scheme (FAC) pre-
sented in this paper, based on the Fuzzy Model Refer-
ence Learning Controller (Layne and Passino, 1996),
is shown in Fig. 3.
Fuzzy Inverse
Model
Knowledge
Base
Modifier
FLC
Robot +
Controller
xD
d
x
n
f
d
f
p
Learning
Mechanism
Figure 3: Fuzzy adaptive control scheme (FAC).
The FAC is mainly based on the Fuzzy Logic Con-
troller (FLC), and the learning mechanism. The FLC
is adapted in the membership functions of its conse-
quents by the learning mechanism. The FLC inputs
are the force error e
f
(kT)=f
d
(kT) − f
n
(kT) and
its finite difference ∆
e
f
(kT)=e
f
(kT)−e
f
(kT −T )
or the trapezoidal area of the force error δe
f
(kT)=
e
f
(kT )+e
f
(kT −T )
2
T . The learning mechanism is com-
posed by the fuzzy inverse model and the knowledge-
base modifier. The fuzzy inverse model attempts to
characterize approximately the representation of the
inverse dynamics of the environment. This is called
by fuzzy inverse model that maps the error in the out-
put variables and possibly other parameters such as
the functions of the error and the process operating
conditions, to the necessary changes in the input pro-
cess (Layne and Passino, 1996). The fuzzy inverse
model is designed to adjust the manipulator tip po-
sition in the perpendicular direction to the environ-
ment surface to compel the force f
n
(kT) exerted on
it, to be as close as possible to f
d
(kT). The knowl-
edge base modifier performs the function of modi-
fying the fuzzy controller, in order to improve the
robot’s performance. Based on the necessary changes
given by the output of the fuzzy inverse model p(kT),
the knowledge base modifier changes the member-
ship functions of the FLC consequents, only for those
whose activation level δ
ij
are greater than zero at the
instant (kT − T ). All others remain unchanged. This
can be formulated as:
C
ij
(kT)=C
ij
(kT − T )+p(kT)
if δ
ij
(kT − T ) > 0; (9)
and
C
ij
(kT)=C
ij
(kT − T )
if δ
ij
(kT − T )=0 (10)
As shown in (Layne and Passino, 1996), the FAC out-
put that would have been desired, is expressed by:
∆x
∗
(kT − T )=∆x(kT − T )+p(kT) (11)
In the inner position control loop, the FSMC fol-
lows the reference or commanded positions and ve-
locities, given by the path planning algorithm in the
position controlled directions. In the force controlled
direction, those commanded position and velocity are
given by the FAC algorithm. In the last controlled
direction, representing the position and velocity as a
two component vector x
c
=[x
c
˙x
c
]
T
, the element x
c
is given by:
x
c
= x + u
FAC
, (12)
where x is the actual tip position manipulator and
u
FAC
is the FAC output. In order to compute the slid-
ing variable along this direction, the vector [e
x
˙e
x
]
T
is given by:
[e
x
˙e
x
]
T
= x − x
c
= −[u
FAC
˙u
FAC
]
T
(13)
4 SIMULATION RESULTS
The overall force/position control structure de-
scribed in Section 3 is now applied, by simulation,
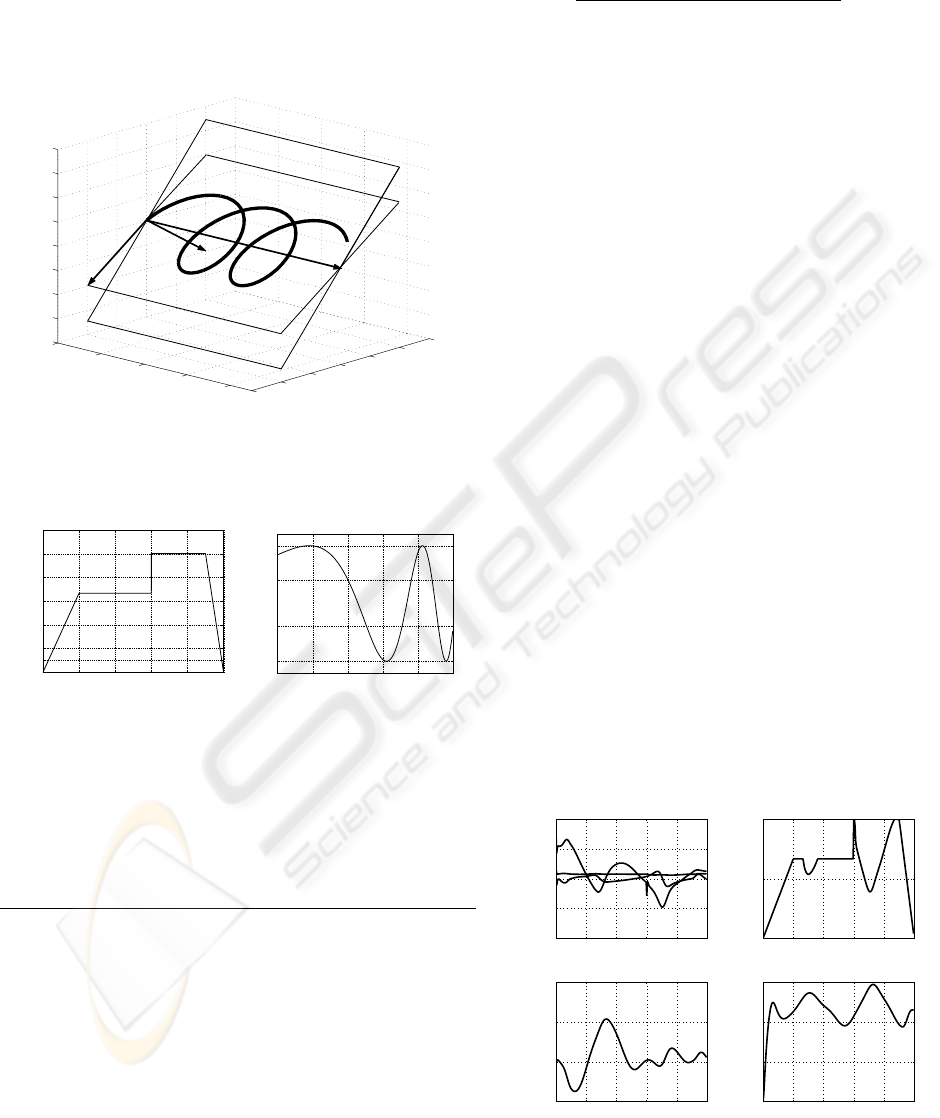
to a 3-DOF PUMA 560 robot model, that executes a
trajectory along a flat surface, as shown in Figure 4.
To simulate uncertainties in the environment geome-
try, a mismatch of about 15
◦
between the planned and
the actual plane is imposed. The simulation environ-
ment incorporates the model of the robot, as described
in (Corke, 1996), including the nonlinear arm dynam-
ics and joint friction, providing the basis for a real-
istic evaluation of the controller performance. The
control scheme applied to the robot dynamic model
used in this study, was implemented in the MAT-
LAB/SIMULINK environment, using the Runge-
Kutta fourth order integration method. The control
laws applied to the manipulator model where imple-
mented with a sampling frequency of 1 kHz. The in-
verse dynamics control law of the manipulator only
consider the diagonal terms of the inertial matrix and
the gravitational terms, as shown in Eq. (14):
τ
1
τ
2
τ
3
=
H
1,1
00
0
H
2,2
0
00
H
3,3
+
g
1
g
2
g
3
(14)
ICINCO 2004 - ROBOTICS AND AUTOMATION
204
For robustness analysis, the inertial parameters, like
link masses and moments of inertia are disturbed be-
tween 10% and 30% from its nominal value. The de-
sired force path is represented in Fig. 5(a) and the
stiffness coefficient of the environment varies along
time, accordingly Fig. 5(b).
0
0.1
0.2
0.3
0.4
0.5
0.6
−0.2
0
0.2
0.4
0.6
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
X
y
x
z
Y
Z
α
p
Φ
Φ
r
Figure 4: Trajectory of the 3-DOF PUMA manipulator.
0 1 2 3 4 5
1
2
4
6
8
10
Force profile
s
N
(a)
0 1 2 3 4 5
0.75
0.9
1.1
1.25
x 10
4
s
N/m
(b)
Figure 5: a) Desired force profile. b) Environment stiffness.
Table 2: Rule base of the fuzzy inverse model.
e
f
\
∆e
f
NH NM NL Z PL PM PH
PH Z Z PL PL PM PH PH
PM NL Z PL PL PM PM PH
PL NM NL Z PL PL PH PH
Z NH NM NL Z PL PM PH
NL NH NM NL NL Z PL PM
NM NH NM NM NL NL Z PL
NH NH NH NM NL NL Z Z
It is assumed that the manipulator is already in
contact with the surface and the end-effector al-
ways maintains contact with the environment dur-
ing the execution of the task. The impedance
matrices have the following values: M
d
=
Table 3: Rule base of the FLC.
e
f
\
∆e
f
NZP
P C
11
C
12
C
13
Z C
21
C
22
C
23
N C
31
C
32
C
33
diag(5, 5, 5), B
d
= diag(316, 141, 141) and
K
d
= diag(5000, 1000, 1000). The boundary
layer thickness for the three subsystems at the
fuzzy sliding mode controller was setting as Φ =
diag(0.05, 0.05, 0.05) and the matrix K
v
in (7) is
K
v
= diag(50, 20, 20) for the three orthogonal di-
rections. Also, the transfer characteristic inside the
boundary layer as presented in Fig. 2 is used, which
reveal an increasing velocity response. The rule base
of the fuzzy inverse model is presented on Table 2 and
the rule base of the FLC has nine rules, accordingly
to Table 3. The centers C
ij
are adapted by the learn-
ing mechanism. It is also assumed that the inputs to
the fuzzy inverse model and to the FLC algorithm are
the same: the force error e
f
and its difference ∆e
f
.
The scaling factors to the fuzzy inverse model are
[8 6; 0.25] and [6 6; 0.0005] for the FLC. All the fuzzy
systems are Takagi-Sugeno type (Palm et al., 1997),
with a fuzzy partition at the antecedents, trapezoidal
shape and singletons C
ij
at the consequents. The sim-
ulation results can be observed in Figs. 6, 7 and 8. In
Fig. 6 joint torques, tip position and force errors are
presented without compensation. It can be observed
that the performance is greatly reduced. In Fig. 7 both
fuzzy adaptive and fuzzy sliding controllers compen-
sate for the uncertainties, recovering the performance
of the impedance control. In Fig. 8 the adjustment ac-
tivity of the FLC consequents, done by the learning
mechanism in order to compensate for uncertainties
in the environment, is shown.
0 1 2 3 4 5
−0.01
0
0.01
0.02
error pos. acc. y
m
0 1 2 3 4 5
0
5
10
force error
N
0 1 2 3 4 5
−40
−20
0
20
40
Torque
τ
1
τ
2
τ
3
N.m
0 1 2 3 4 5
0
0.01
0.02
0.03
error pos. acc. z
m
Figure 6: Simulation results without compensation.
A FUZZY INTEGRATED APPROACH TO IMPEDANCE CONTROL OF ROBOT MANIPULATORS
205

0 1 2 3 4 5
−2
−1
0
1
2
x 10
−3
error pos. acc. y
m
0 1 2 3 4 5
−2
0
2
4
force error
N
0 1 2 3 4 5
−40
−20
0
20
40
Torque
τ
1
τ
2
τ
3
N.m
0 1 2 3 4 5
−5
0
5
x 10
−4
error pos. acc. z
m
Figure 7: Simulation results with compensation of
uncertainties in environment and robot dynamic model.
1 3 5
−1
0
1
C
11
1 3 5
−0.5
0
0.5
1
C
12
1 3 5
0
0.5
1
C
13
1 3 5
−1
−0.5
C
21
1 3 5
−0.5
0
0.5
1
C
22
1 3 5
0.4
0.6
0.8
1
C
23
1 3 5
−1
−0.5
0
0.5
C
31
1 3 5
−1
0
1
C
32
1 3 5
0.4
0.6
0.8
1
C
33
Figure 8: The adaptation of the consequents of the FLC
membership functions.
5 CONCLUSIONS
In this article, an integration of fuzzy adaptive and
fuzzy robust force/position control to compensate for
overall uncertainties, considering an impedance con-
trol formulation, is presented. The tip position ad-
justed by the fuzzy adaptive controller in the perpen-
dicular direction to the surface, to compensate for un-
certainties in the environment is feeded to an inner
position controller. This controller is a fuzzy slid-
ing mode-based impedance control that compensate
for uncertainties in the manipulator dynamic model.
The adjustment in position done by the fuzzy adap-
tive controller, based on the force error and the ef-
fort done by the fuzzy sliding mode-based impedance
controller in the inner loop, recovers the impedance
control performance and reduces the errors in position
and force. This control structure also exhibits a good
performance considering nonrigid materials with un-
certainties.
Future work will concentrate on the implementation
of this control structure on a industrial PUMA 562
robot.
ACKNOWLEDGEMENTS
This research was partially supported by program
POCTI, FCT, Minist
´
erio da Ci
ˆ
encia e do Ensino Su-
perior, Portugal
REFERENCES
Baptista, L., Sousa, J., and S
´
a da Costa, J. G. (2001). Fuzzy
predictive algorithms applied to real-time force con-
trol. Control Engineering Practice, 9(4):411–423.
Colbaugh, R., Seraji, H., and Glass, K. (1993). Direct adap-
tive impedance control of robot manipulators. Journal
of Robotic Systems, 10:217–242.
Corke, P. (1996). A robotics toolbox for MATLAB. IEEE
Robotics and Automation Magazine, 3(1):24–32.
Epping, S. D. and Seering, W. P. (1987). Introduction to
dynamic models for robot force control. IEEE Control
Systems Magazine, pages 48–51.
Hogan, N. (1985). Impedance control: an approach to ma-
nipulation: Part I-II-III. Journal of Dynamic Systems,
Measurement, and Control, 107:1–24.
Hsu, F.-Y. and Fu, L.-C. (1996). Adaptive fuzzy hybrid
force/position control for robot manipulators follow-
ing contours of an uncertain object. Proc. IEEE Inter-
national Conference on Robotics and Automation.
Hsu, F.-Y. and Fu, L.-C. (2000). Intelligent robot debur-
ring using adaptive fuzzy hybrid position/force con-
trol. IEEE Transactions on Robotics and Automation,
16(4):325–335.
Layne, J. and Passino, K. M. (1996). Fuzzy model reference
learning control. Journal of Intelligent and Fuzzy Sys-
tems, 4:33–47.
Liu, G. J. and Goldenberg, A. A. (1991). Robust hybrid
impedance control of robot manipulators. Proc. IEEE
International Conference on Robotics and Automa-
tion.
Lu, Z. and Goldenberg, A. A. (1995). Robust impedance
control and force regulation: Theory and experi-
ments. International Journal of Robotics Research,
14-3:225–254.
Mason, M. (1981). Compliance and force control for com-
puter controlled manipulators. IEEE Transactions on
Systems, Man and Cybernetics, 11(6):418–432.
Palm, R., Driankov, D., and Hans, H. (1997). Model Based
Fuzzy Control. Springer-Verlag, Berlin Heidellberg.
ICINCO 2004 - ROBOTICS AND AUTOMATION
206
