A PRO-ACTIVE RESOLVER MODEL TO COPE WITH

PARAMETER VARIABILITY IN THE

MANUFACTURING CHAIN

João Figueiredo

Universidade de Évora,R. Romão Ramalho, 59, 7000 Évora, Portugal

José Sá da Costa

Instituto Superior Técnico, Av. Rovisco Pais, 1049-001 Lisboa, Portugal

Keywords: Modeling, Simulation, Instrumentation

, Rotation Sensors, Synchros, Resolvers

Abstract: In this paper a linearized model for Pancake resolvers is developed with the aim of compensating deviations

on manufacturin

g inputs through computed corrections on the production controllable variables, mainly

winding parameters. This model follows a two-step strategy where at the first step an accurate model

computes the resolver nominal conditions and at a second step a linearized model based on production

controllable variables computes the corrections on these controllable variables in order to compensate small

deviations on the nominal conditions due to processes variability in the manufacturing. This model had been

simulated and experimentally tested in a Siemens resolver manufacturing plant. The tests done proved the

efficiency of the developed model and its usefulness in stabilizing the product specifications in a dynamic

environment with high variability of manufacturing processes.

1 INTRODUCTION

Resolvers are nowadays widely spread in Industrial

Applications (Logé, 1992). These electromagnetical

devices which were, in the past, largely used in

military applications, namely to control the position

stability of heavy guns, are presently very common

in industrial areas as a servomotor component

(Golker, 1981). Servomotors are today widely

spread in robotics, rotary machinery, aeronautics…

This continuing demand on resolvers pushes the

researc

h on new materials, new designs supported

by theoretical work. Continuing research on old

products is managed by the market. Similar research

is done also on other old electromagnetical devices

which improvements are demanded by the market

(Ostolaza, 2002; Chang, 2003; Lin 2003).

The main factors that promote the widespread of

he Resolvers as angular sensors in despite of

optoelectronics-encoders are its robustness and

stable accuracy in non-friendly environments such

as mechanical vibrations and shocks, environments

with dust, oil, radiations and very high stability in a

wide range of temperatures (-50º C to +150º C) and

rotational velocities (1000 to 10000 turns/min.).

The main disadvantages of resolvers in relation

to opt

oelectronic encoders are: the necessity of an

AC-power source and the delivery of an analog

output signal where the today’s processing devices

are mainly digital. However, the daily advances in

the signal processing technology allows more and

more speedy and cost efficient solutions to convert

analog to digital signals.

The main functional characteristics of resolvers

are: the angula

r error, the output voltage

(transformation ratio –ü), the phase shift and the

input current. All these important factors specified

by customers/ applications - usually referred as

Customer characteristics - are strongly influenced by

constructive factors such as: magnetic properties of

stators and rotors, winding geometries,

manufacturing tolerances of mechanical parts. As

the assembly factors change continuously in a

manufacturing plant (new material charge, different

thermal treatment of magnetic metals…) it means

that small adjustments at the windings parameters

have to be made in order to compensate the existing

Figueiredo J. and Sá da Costa J. (2004).

A PRO-ACTIVE RESOLVER MODEL TO COPE WITH PARAMETER VARIABILITY IN THE MANUFACTURING CHAIN.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 38-45

DOI: 10.5220/0001140000380045

 SciTePress

variability in the manufacturing process allowed by

its tolerance chain.

Facing this situation it is clear that the existence

of a mathematical model at the resolver

manufacturer that allows him to compensate the

variability of its processes by computing the

corrections at the windings parameters in order to

keep the customer specifications on target, saves

him, yearly, a big amount of money by drastically

reducing the number of trials needed, with different

windings, until the customer characteristics are met

again.

In this paper an inovative linearized

mathematical model for Pancake-Resolvers (fig. 1)

is developed in a way that it fits the needs of a

resolver manufacturer to stabilize its product

specifications in an environment with high

variability of manufacturing processes.

2 PANCAKE-RESOLVER MODEL

2.1 Description

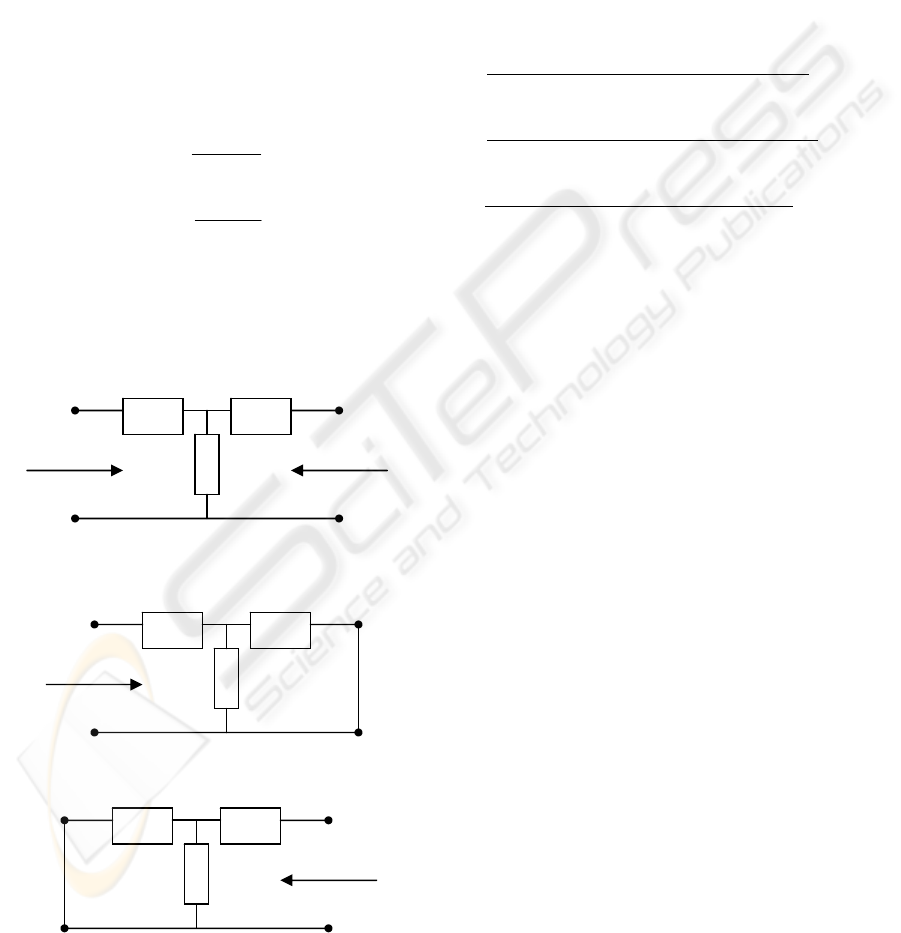
The Pancake resolver is today the most common

resolver design for industry and aeronautics (fig. 1).

The Pancake resolver carries the current into the

rotor through a transformer that is located at the

stator edge. The advantage of such design, over the

traditional resolver with collector system, is the

absence of the relative movement between

mechanical parts which causes wear, vibrations and

sound.

Fig. 1 presented the two above mentioned

designs.

Independently of how the energy is brought into

the resolver rotor, the function of a resolver can be

briefly illustrated in figure 2.

Resolver function schematics

Resolver input and output voltages

Figure 2: Resolver schematics and function

With an appropriate composition of the output

voltages, the angular position of the rotor referred to

the stator position can be obtained [2] as:

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

S1S3

S2S4

α cosU

αsin U

tgα

(1)

Where:

ü = transformation ratio;

α = relative angle rotor to stator;

= input voltage.

S1S3

cos

S2S4

sin

Roto

Stato

Pancake resolver

Traditional resolver with collector

Figure 1: Traditional and Pancake resolvers

A PRO-ACTIVE RESOLVER MODEL TO COPE WITH PARAMETER VARIABILITY IN THE MANUFACTURING

CHAIN

2.2 Mathematical Model

The common used mathematical model for a

resolver is shown in fig. 3, and it is the typical model

for a transformer.

This model is suitable to supply the usual

customer demanded electrical characteristics of the

resolver, namely the Rotor and Stator Impedances

(open and short circuited).

According the below schematics, using the

traditional circuit analysis methods, the following

equations are obtained:

; (2)

31ro

ZZZ +=

; (3)

32so

ZZZ +=

1rs

; (4)

2ss

; (5)

Where:

Zro = Rotor Impedance with Stator open

Zso = Stator Impedance with Rotor open

Zrs = Rotor Impedance with Stator shorted

Zss = Stator Impedance with Rotor shorted

Rotor Impedance with Stator open (Zro) and

Stator Impedance with Rotor open (Zso)

Rotor Impedance with Stator shorted (Zrs)

Stator Impedance with Rotor shorted (Zss)

Figure 3: Common used resolver models

This model although useful for computing the

main electrical characteristics for customer needs is

from less use for the sensors manufacturer. Actually

this model doesn’t copy with anyone of the directly

controllable variables in a resolver manufacture.

The new model proposed in this paper is

appropriate for resolver manufacturers because it

deals explicitly with the actually controllable

variables in a resolver production plant (mainly

winding parameters).

The main variables that influence directly the

customer specific electrical characteristics can be

divided into 3 groups:

Group 1: Material related variables: magnetic

permeability of the rotor, the stator, the rotor-

-transformer, the stator-transformer.

Group 2: Geometry related variables: stator

dimensional tolerances, rotor dimensional

tolerances, rotor/stator air-gap, transformer air-gap.

Group 3: windings related variables: windings

distribution around the rotor and the stator, number

of stator-windings, stator-windings wire diameter,

number of rotor-windings, rotor-windings wire

diameter, number of stator/transformer-windings,

stator/transformer-windings wire diameter, number

of rotor/transformer-windings, rotor/transformer-

windings wire diameter.

From this 3 groups of variables, the resolver

manufacturer can only influence on a feasible way

the 3

variables Group, since the other groups are

usually fixed for the sensor manufacturer as he buys

the materials and parts from external suppliers. Even

if the resolver manufacturer is vertically integrated,

producing also its parts, what is very unusual, the

parts production pace and environment is completely

apart from the resolver assembly line, this implies

that, for having its parts, the assembly line has to

deal always with stock management (the assembly

line can never control the groups 1 and 2 related

variables).

In such a scenario a useful resolver mathematical

model for a resolver manufacturer must deal

explicitly with the Group 3 Variables.

In Figueiredo, 2004, an explicit mathematical

model for Pancake resolvers was proposed. This

model although very accurate has its major

application on the design of new products. For

manufacturing purposes where the main needs are

the compensation of the processes variability that

affect the product characteristics and increase the

scrap, that model has less application. In fact, those

model variables cannot be directly used by the

resolver manufacturer, as they account for the

standard physical effects of an electromagnetic

device (transformer ohmic resistances, indutances,

electromagnetic losses in windings and metal…).

These standard electromagnetic variables are very

Roto

Stato

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

useful for design purposes but they are not suitable

for the resolver steady production as here the

controllable variables are only the winding

parameters (number of windings and wire

diameters).

The model developed in this paper follows a

two-step strategy where at first an accurate model

defines the resolver nominal conditions and at a

second step an additional linearized model (with

production controllable variables) compensates the

product for small changes on the manufacturing

processes.

Analogous to the mathematical methodology of

function expansion into a Taylor series, here also the

strategy adopted is to consider the model developed

by Figueiredo (Figueiredo, 2004) to compute the

system nominal values – f(x0) – and additionally a

linearized model dependent on production

controllable variables which computes the function

increments. These increments are able to cancel the

deviations on the standard parameters due to the

variability of the production processes in a resolver

manufacturer. The incremental model that is

developed in this paper is an innovative approach

based on experimental parameter identification.

2.2.1 Model for nominal conditions – [f(x

)]

Analysing the Pancake resolver functionally we can

split this device into two transformers associated in

series. The first one, the transformer which carries

on the energy into the rotor, which output voltage is

independent from the rotor position related to the

stator, and the resolver function itself that can be

modeled as a transformer which output voltage is

dependent on the rotor to stator position (see fig 4).

Figure 4: Pancake resolver schematics

The explicit mathematical model, proposed by

Figueiredo (Figueiredo, 2004), for the main

customer electrical characteristics: Output voltage

for each stator winding (Ucos, Usin) and Input

current (I), is shown in the eqs. 6 and 7.

This model proved to be very accurate in the

simulation of pancake resolvers (Figueiredo, 2004).

S1S3

&&&&

(6)

(7)

where:

= transformation ratio from Transformer

= transformation ratio from Sensor

(

)

hTDFehTTFe3

SLRLRA

′′

()

[

]

′

+++=

′′

hTTFeD1σT2σhDT1σT1

σT11

SLRLLLaRbLaSLA

(

)

[

′

D1T2hTTFehDT1σT1

RRLRLbRcL

(

)

][

++++

′

′′

cRdLSLLLRR

T1σT1

D1σT2σhTTFeDFe

(

)

]

dRSRRLRR

T1D1T2hTTFeDFe

′

d cSbSaSA

+++=

(

)

D1σT2σhThD

LLLLa

′′

′

(

)

(

)

[

]

′

′′

D1σT2σTFeD1T2hThD

LLRRRLLb

(

)

hDhTDFehDhTTFeD1σT2σhTDFe

LLRLLRLLLR

′

′′

(

)

′

hDTFeDFehTTFeDFeD1T2TFehD

LRRLRRRRRLc

(

)

(

)

[

]

D1σT2σTFeD1T2hTDFe

LLRRRL

′′

′

(

)

D1T2TFeDFe

RRRRd

′

where:

= primary winding resistance -Transformer

R’

= secondary winding resistance - Transformer

TFe

= magnetic metal resistance - Transformer

σT1

= primary winding leakage inductance - Transformer

σ’T2

= secondary winding leakage inductance -

Transformer

= common flux inductance – Transformer

= primary winding resistance -Sensor

R’

= secondary winding resistance - Sensor

DFe

= magnetic metal resistance - Sensor

σD1

= primary winding leakage inductance - Sensor

σ’D2

= secondary winding leakage inductance - Sensor

= common flux inductance – Sensor

A PRO-ACTIVE RESOLVER MODEL TO COPE WITH PARAMETER VARIABILITY IN THE MANUFACTURING

CHAIN

The above model will be taken to compute the

resolver nominal design variables (the standards for

all product variables - f(x0) - ). To compute the

influences on the resolver main functional

characteristics: output voltage (Ucos, Usin) and

input current (I) caused by small changes due to

production processes variability, a differential

model, that copies with the marginal changes on the

controllable variables, is developed, in this paper, on

sec. 2.2.2.

2.2.2 Incremental Model – [(∂f/∂x

)

(∆x

)]

Having a general function f in R

[f(x

,…,x

)] this

function can be linearized around the point

,…,x

) by cutting its Taylor’s series

development after the 1

order partial derivatives:

()(

n02010n21

x,...,x,xfx,...,x,xf

)

() ()

n0n

101

−

∂

++−

∂

+ K

(8)

This approach is used to compute the influences

on the resolver main functional characteristics:

output voltage (Ucos, Usin) and input current (I)

caused by small changes on the controllable

variables.

The production controllable variables for an

usual resolver manufacturer are essentially the

windings parameters.

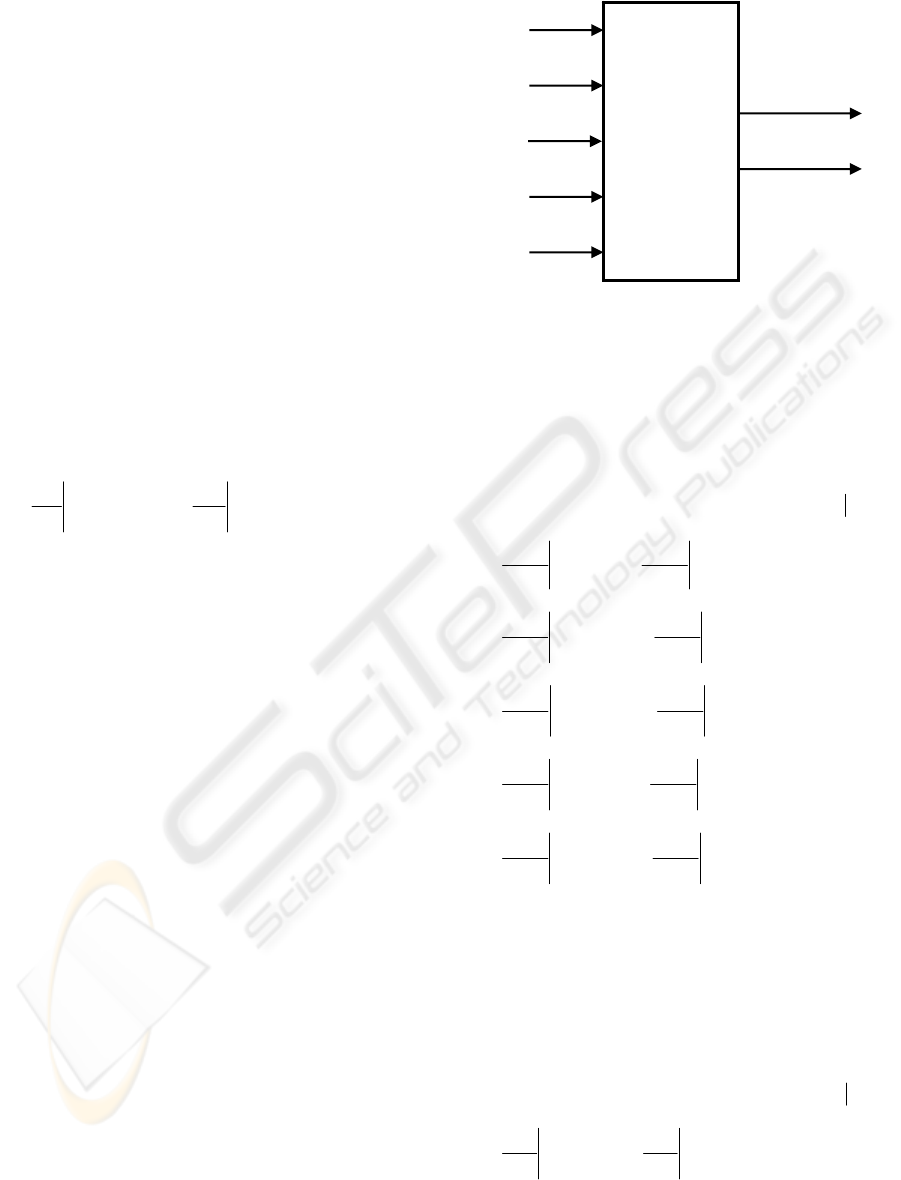
In Fig. 5 the resolver controllable model for a

standard manufacturer is shown, where the

considered variables account for:

= resolver input voltage;

F = input frequency;

= number of windings of the stator transformer;

= number of windings of the rotor transformer;

= number of windings of the stator sensor;

= number of windings of the rotor sensor;

= winding wire diameter of the stator transformer;

= winding wire diameter of the rotor transformer;

= winding wire diameter of the stator sensor;

= winding wire diameter of the rotor sensor;

U, F

, φ

cos

, U

sin

Resolver

Model

, φ

Figure 5: Resolver complete controllable Model

The differential model for the resolver output

voltage (U

cos

) that copies with the marginal changes

on the manufacturer controllable variables is:

(

)

rsssrtstrsssrtstcos

,,,,n,n,n,n F, U,U

(

)

rs0ss0rt0st0rs0ss0rt0st000cos

,,,,n,n,n,n ,F,UU

φφφφ

() ()

+−

∂

+−

∂

cos

() ()

+−

∂

+−

∂

rt0rt

cos

st0st

cos

() ()

+−

∂

+−

∂

rs0rs

cos

ss0ss

cos

() ()

+−

∂

+−

∂

rt0rt

cos

st0st

cos

φφ

() ()

rs0rs

cos

ss0ss

cos

φφ

−

∂

+−

∂

(9)

Using the same approach, the influences on the

input current (I) caused by small changes in the

controllable variables can be computed as:

(

)

rsssrtstrsssrtst

,,,,n,n,n,n F, U,I

(

)

rs0ss0rt0st0rs0ss0rt0st000

,,,,n,n,n,n ,F ,UI

φφφφ

()()

+−

∂

+−

∂

rt0rt

st0st

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

()()

+−

∂

+−

∂

()()

+−

∂

+−

∂

rs0rs

ss0ss

()()

+−

∂

+−

∂

rt0rt

st0st

φφ

()()

rs0rs

ss0ss

φφ

−

∂

+−

∂

(10)

The several partial diferencial functions stated

on both models (eqs. 9 and 10) have been

experimentally evaluated, with a set of measuring

points, which were fitted by 2

order polynomials.

This method proved to be very suitable for this

purpose (Cruz, 1997).

3 SIMULATION AND

EXPERIMENTAL RESULTS

3.1 Simulation Results

The nominal model shown in 2.2.1 was numerically

evaluated with the software Matlab (Mathworks) for

different resolver winding designs. All the winding

designs were configured for the Siemens 1-speed

resolver H2109 which has the following main

characteristics:

U = 5V;

Freq. = 4kHz

max

. = 50 mA

The parameters referred on the nominal model

(eqs. 6 and 7) were experimentally evaluated

following the methodology proposed by Figueiredo

(Figueiredo, 2004). Applying this methodology for

each one of the possible combinations of the 10

controllable variables, it resulted on 10 different sets

of parameters needed. These results account only for

a single change in each one of the 10 controllable

variables. Actually the experiments have been

repeated, at least, for 5 different values for each

variable, also it resulted finally on a total of 50 sets

of parameters evaluated.

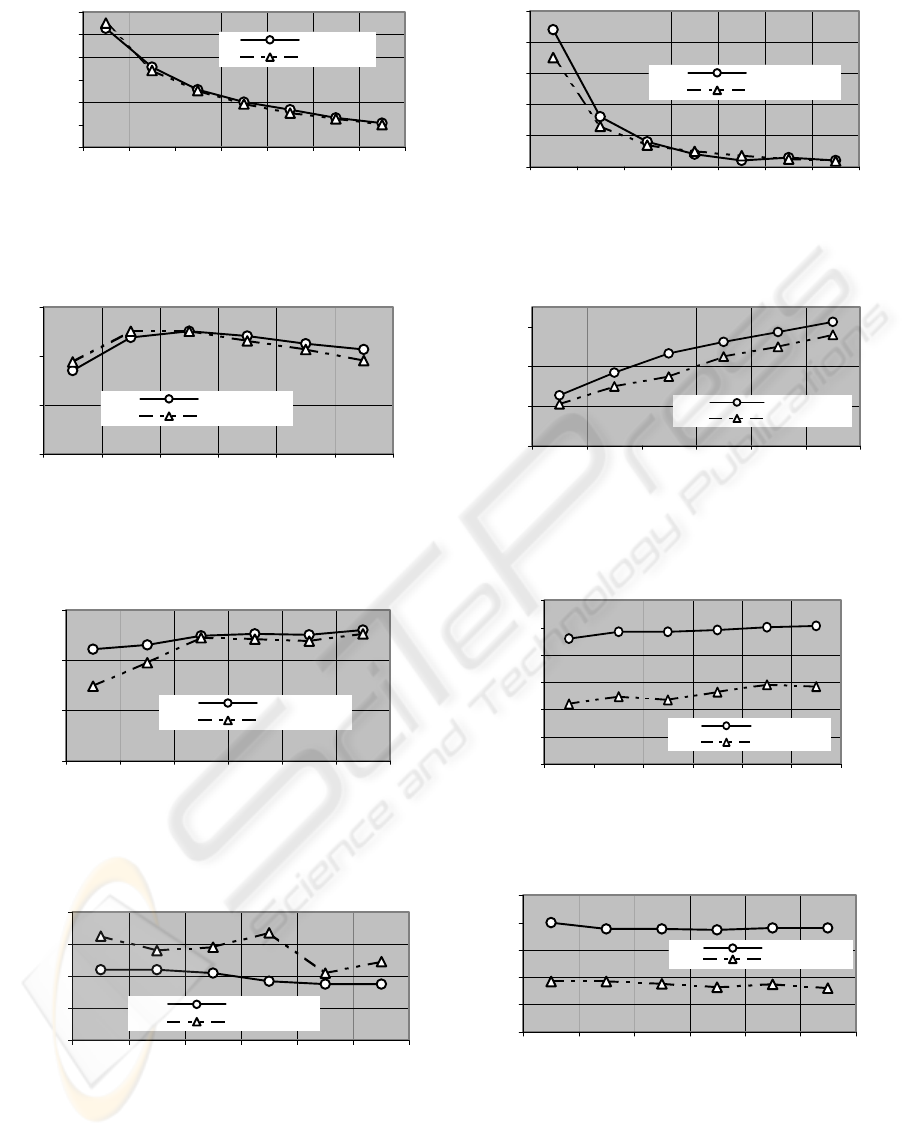
The simulated values for both customer main

specifications: U

cos

and I (according eqs. 6 and 7) are

shown in figs. 6 to 13.

These figures show the model ability to deliver

very good results when compared with the

experimental measurements for a broad

configuration of windings.

The results shown here were selected from a

huge quantity of computed data according to the

following main criterion: - selection from the 8

defined controllable variables (number of windings

and wire diameters) those that are, from

manufacturer side, easier to change, and that

produce effectiver results on the customer main

specifications (U

cos

and I).

Concerning the Output voltage (U

cos

) as it

depends on the rotor relative position to the stator,

the values shown, concern the zero electrical angle

where the stator and rotor are align at the null value.

This relative position rotor to stator is referred as

cos(0)

According the above criterion the following

studies are presented in the below figures:

cos(0)

); U

cos(0)

); U

cos(0)

(φ

); U

cos(0)

(φ

); I

(0)

);

(0)

); I

(0)

(φ

); I

(0)

(φ

3.2 Experimental Results

The experimental results have been taken from the

Siemens 1-speed Resolver H2109 which electrical

main specifications had already been shown in 3.1.

As it had been also related in 3.1, in order to

evaluate the model parameters, a huge amount of

measurements had been carried on.

The experimental results shown here correspond

to the simulated values shown in figs. 6 to 13. The

plotting of the experimental results side by side with

the simulated ones displays clearly the quality of the

model developed in this paper.

The knowledge of the experimental curves that

reflect the sensitivity of the resolver to each one of

the production controlable variables proved to be a

strong valuable tool to the manufacturer. Actually

this knowledge allows the manufacturer to react to

product deviations due to unknown changes in the

production processes.

The production variables, selected by the

manufacturer, to serve as the most suitable ones to

react quickly to undesirable changes in the assembly

processes have been already referred in 3.1. These

variables are: n

, n

, φ

and φ

A PRO-ACTIVE RESOLVER MODEL TO COPE WITH PARAMETER VARIABILITY IN THE MANUFACTURING

CHAIN

50 100 150 200 250 300 350

N. of windings Transformer-Stator

Output Voltage (Ucos) [V]

experimental

simulation

Figure 6: Output VoltageU

cos(0)

) vs number of windings of

the stator transformer (n

)

100 200 300 400 500 600

N. of windings Transformer-Rotor

Output Voltage (Ucos) [V]

experimental

sim ulation

Figure 7: Output Voltage (U

cos(0)

) vs number of windings

of the rotor transformer (n

)

1,5

2,5

0,06 0,08 0,10 0,12 0,14 0,16

Wire diameter Sensor-Rotor

Output Voltage (Ucos) [V]

experimental

sim ulation

Figure 8: Output Voltage (U

cos(0)

) vs winding wire

diameter of the rotor sensor (

)

2,5

2,6

2,7

2,8

2,9

0,06 0,08 0,10 0,12 0,14 0,16

Wire diameter Sensor-Stator

Output Voltage (Ucos) [V]

experimental

sim ulation

Figure 9: Output Voltage (U

cos(0)

) vs winding wire

diameter of the stator sensor (

)

100

150

200

250

50 100 150 200 250 300 350

N. of windings Transformer-Stator

Input Current (I) [mA]

experimental

sim ulation

Figure 10: Input Current (I

(0)

) vs number of windings of

the stator transformer (n

)

100 200 300 400 500 600

N. of windings Transformer-Rotor

Input Current (I) [mA]

experimental

simul ation

Figure 11: Input Current (I

(0)

) vs number of windings of

the rotor transformer (n

)

0,06 0,08 0,10 0,12 0,14 0,16

Wire diameter Sensor-Rotor [mm]

Input Current (I) [mA]

experim ental

sim ulation

Figure 12: Input Current (I

(0)

) vs winding wire diameter of

the rotor sensor (

)

0,06 0,08 0,10 0,12 0,14 0,16

Wire diameter Sensor-Stator [mm]

Input Current (I) [mA]

experimental

sim ul a tion

Figure 13: Input Current (I

(0)

) vs winding wire diameter of

the stator sensor (

)

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

4 CONCLUSIONS

From a practical point of view the results from this

research proved to be very valuable for the Siemens

resolver manufacturer. In fact the knowledge of the

experimental curves that reflect the sensitivity of the

resolver to each one of the production controllable

variables proved to be a strong valuable tool to the

manufacturer. Actually this knowledge allows the

manufacturer to react quickly to product deviations

due to unknown changes in the production

processes.

From a scientific point of view the accuracy of

the combined model strategy (nominal and

incremental models) delivers results with an average

error, in the worst case, of 22%.

This error is still substantial and it denotes that

there are some physical effects that should be better

accounted on the nominal model, specially when it

concerns the wire diameters. The incremental model

must remain as it was presented, as long as the

winding parameters remain the only controllable

variables for the resolver manufacturer.

ACKNOWLEDGMENTS

All the laboratorial work presented in this paper was

supported by means of manufacturing machinery,

test equipment and resolver products by Siemens SA

– plant Évora. This research was led according to an

existing cooperation program established between

University Evora and Siemens SA – plant Évora.

REFERENCES

Chang, Y. (2003). Buffered DDA command generation in

a CNC

. Control Engineering Practice 11 (2003) pp.

797-804

Cruz, A. (1997).

Modelling an analog rotation sensor. – in

portuguese version – P.G. Study. U. Evora, Phys. Dept

Figueiredo, J., Sá da Costa, J. (2004). Analog Rotation

Sensors: An Industrial Approach for Modeling and

Simulation

. Proc. Controlo 2004 - 6

Conf. on

Automatic Control, Faro

Golker, W., H. Tamm, S. Smith (1981).

Ein Messgetriebe

fuer den Airbus A310: Position Pick-off Unit

. Siemens

Components 19 (1981) Heft 4, pp. 125-128

Lin, T., Pan, Y., Hsieh, C. (2003).

Precision-Limit

positioning of direct drive systems with the existence

of friction

. Control Engineering Practice 11 (2003) pp.

133-244

Logé, H. (1992). Hohlwellendrehmelder: neue

Komponenten der Servotechnik

. Siemens Components

30 (1992) Heft 2, pp. 57-60

Ostolaza, J., Zubia, I., Tapia, G., Tapia, A., Sanz, M.

(2002).

An Alternative Approach for the control of

DC-DC Converters

. Proc. 10

IEEE Med. Conf. On

Control and Automation, 2002, IST, Lisboa.

A PRO-ACTIVE RESOLVER MODEL TO COPE WITH PARAMETER VARIABILITY IN THE MANUFACTURING

CHAIN