MULTILEVEL DARWINIST BRAIN IN ROBOTS

Initial Implementation

Franciso Bellas

Grupo de Sistemas Autónomos, Universidade da Coruña, Mendizábal S/N, Ferrol, A Coruña

Richard J. Duro

Grupo de Sistemas Autónomos, Universidade da Coruña, Mendizábal S/N, Ferrol, A Coruña

Keywords: Cognitive Mechanism, Evolutionary Computation, Neural Networks

Abstract: In this paper we present a Cognitive Mechanism called MDB (Multilevel Darwinist Brain) based on Darwinist

theories and its initial application to autonomous learning by robotic systems. The mechanism has been designed

to permit an agent to adapt to its environment and motivations in an autonomous way. The general structure of the

MDB is particularized into a two level architecture: reasoning and interaction. This structure corresponds to a

generic cognitive model where world, internal and satisfaction models are used to select strategies that fulfil the

motivation of the agent. The main idea behind the proposal is that all of the components of the mechanism are

obtained and modified through interaction with the environment in real time by means of on line Darwinist

processes, allowing for a natural learning curve. The mechanism is able to provide solutions based on experience

or original solutions to new situations. The knowledge used by the agent is acquired automatically and not

imposed by the designer. Here we discuss the basic operation of the mechanism and demonstrate it through a real

example in which a hexapod robot is taught to walk efficiently and to reach an objective in its surroundings.

1 INTRODUCTION

From a practical point of view, a Cognitive Mechanism

permits an artificial agent to autonomously control its

actuators using the sensorial information it has in order

to achieve a given objective or complete a task. After

revisiting the different tendencies found in the literature

of the last twenty years, we have extracted four basic

features that different authors propose as necessary for a

viable complete cognitive mechanism:

• The use of explicit models of the environment and

of the agent itself in order to be able to carry out complex

tasks requiring reasoning (deliberative capabilities).

• The system should display reactive capabilities in

order to provide quick response in real problems.

• The minimization of the influence of the designer

using techniques that permit an automatic design process

(such as evolution).

• The system should be adaptive in order to apply

the Cognitive Mechanism in dynamic environments.

Traditional deliberative systems were usually based

on symbol manipulation (Newell and Simon, 1976), and

classified as Symbolic Artificial Intelligence. Some

examples of Cognitive Mechanisms using this approach

could be (Bratman, Israel and Pollack, 1988) and (Agre

and Chapman, 1987). There are several studies, for

example (Chapman, 1987), concluding that the

complexity of a symbol based system necessary to solve

a high level reasoning problem make this approach

practical only for domain limited tasks. Furthermore, in

classical deliberative systems the intervention of the

designer is crucial, and the resulting mechanisms present

a low level of adaptability.

Most reactive solutions have been mainly variations

of the general concepts proposed in the Subsumption

Architecture (Brooks, 1986) designed by Brooks, where

simple behavior modules compete for the control of the

agent. These systems are characterized by a quick

response in real tasks due to their simplicity, but they

present limitations when applied to high level reasoning

problems because of the lack of reflexive elements. In

addition, the participation the designer is high because

the simple modules must be designed “by hand”. As

relevant examples of these systems we could cite

(Kaelbling, 1987) and (Maes, 1991).

In order to make the design process easier and to

minimize the tweaking by the designer, some authors

have applied different techniques that permit obtaining

Bellas F. and Duro R. (2004).

MULTILEVEL DARWINIST BRAIN IN ROBOTS - Initial Implementation .

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 25-32

DOI: 10.5220/0001140700250032

 SciTePress

the cognitive architectures (or some parts of them)

automatically. For instance, evolutionary algorithms

have been applied in different systems providing

adequate solutions in an autonomous way (Floreano and

Mondada, 1996).

In addition to these four features (deliberative,

reactive, automatic design and adaptive) we impose as

the main requirement to the mechanism that the

acquisition of knowledge be automatic, this is, the

designers should not impose their knowledge on the

system. A Cognitive Mechanism, in our opinion, is a

framework that allows the system to acquire knowledge

from its environment and itself and provides a way of

using it in the generation of actions that lead the agent to

fulfil its motivations and not the knowledge itself

whether in the form of a function relating perceptions

and actions or any other format.

In the quest for a way to fulfil all the aforementioned

requirements, especially the last one, we have resorted to

bio-psychological theories within the field of cognitive

science that relate the brain and its operation through a

Darwinist process. These theories are:

• The Theory of Evolutionary Learning Circuits

(TELC) (Conrad, 1974, 1976).

• The Theory of Selective Stabilization of Synapses

(TSSS) (Changeux et al., 1973) (Changeux & Danchin,

1976).

• The Theory of Selective Stabilization of Pre-

Representations (TSSP) (Changeux et al., 1984).

• The Theory of Neuronal Group Selection (TNGS)

or “Neural Darwinism” (Edelman, 1987).

Each theory has its own features, which can be

studied in the references, but they all lead to the same

concept of cognitive structure based on the fact that the

brain adapts its neural connections in real time through

evolutionary or selectionist processes. This idea of

Darwinism in the acquisition of knowledge is the basis

for the development of the practical Cognitive

Mechanism we propose here. In the following sections

we will explain how this idea can be implemented in a

working structure starting from the formal definition of a

cognitive model and how it leads to the successful

interaction of real robotic agents with their world during

their lifetime

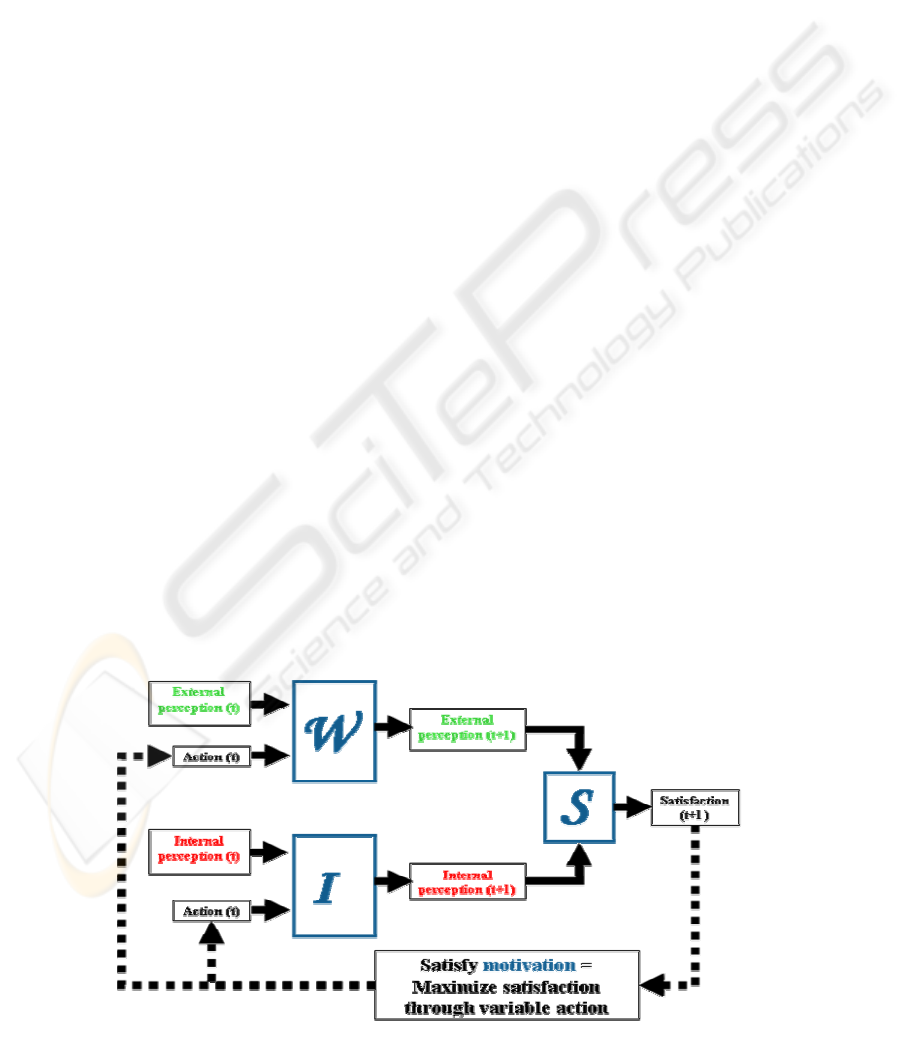
2 COGNITIVE MODEL

One classical way of formalizing the operation of a

general cognitive model from a utilitarian point of view

starts from the premise that to carry out any task, a

motivation (defined as the need or desire that makes an

agent act) must exist that guides the behaviour as a

function of its degree of satisfaction. The tools the agent

can use to modify the level of satisfaction of its

motivation are perceptions through sensors and actions

through actuators, thus we consider that the external

perception e(t) of an agent is made up of the sensorial

information it is capable of acquiring through its sensors

from the environment in which it operates. The external

perception depends on the last action performed by the

agent A(t) and on the sensorial perception it had of the

external world in the previous time instant e(t-1) through

a function W corresponding to the environment or to a

mathematical model of it:

e(t) = W [e(t-1), A(t)]

The internal perception i(t) of an agent is made up of

the sensorial information provided by its internal sensors

(for example, a hunger sensor). The internal perception

can be written in terms of the last action performed by

the agent A(t) and on the sensorial perception it had from

the internal sensors in the previous time instant i(t-1)

through a function I corresponding to the internal

environment itself or to a mathematical model of it:

i(t) = I [i(t-1), A(t)]

We define the global perception G(t) of the agent as a

function that is made up of the external perception e(t)

Figure 1: Functional diagram representing a general cognitive model

ICINCO 2004 - ROBOTICS AND AUTOMATION

and the internal perception i(t).

The satisfaction s(t) represents the degree of

fulfilment of the motivation and depends on the global

perception through a function S. Thus, generalizing:

s(t) = S [G(t)] = S [e(t), i(t)]=

= S [W [e(t-1), A(t)], I [i(t-1), A(t)]]

The Cognitive Mechanism must lead to the

satisfaction of the motivation, which, without any loss of

generality, may be expressed as the maximization of the

satisfaction. Thus:

max{s(t}) =

max {S [W [e(t-1), A(t)], I [i(t-1), A(t)]]}

To resolve this maximization problem, the only

parameter the agent can modify is the action it performs,

as the external and internal perceptions cannot be

manipulated (unless we change the environment or the

agent in order to facilitate the behaviour which is a topic

that is beyond the scope of this paper). That is, the

cognitive mechanism must explore the possible action

space in order to maximize the resulting satisfaction.

In a Cognitive Mechanism, the exploration of

actions must be carried out internally so W, I and S are

mathematical functions that must be somehow obtained.

These functions correspond to what are traditionally

called:

• World model (W): function that relates the external

perception before and after applying an action.

• Internal model (I): function that relates the internal

perception before and after applying an action.

• Satisfaction model (S): function that provides de

predicted satisfaction from the predicted external and

internal perceptions provided by the world and internal

models.

In Figure 1 we display a functional diagram

representing the cognitive model, and we can see that

there are two processes that must take place in a real non

preconditioned operating mechanism: models W, I and S

must be obtained as the agent interacts with the world,

and for every interaction of the world, the best possible

action must be selected through some sort of

optimization using the models available at that time.

When trying to implement this cognitive model

computationally, in addition to these basic elements

(perceptions, actions, motivations and models) we need

to include a new one: the action-perception pair. It is just

a collection of values from the interaction with the

environment after applying an action, that is, data from

the real world, and could be represented as follows:

As we can see, an action-perception pair is made up

of the sensorial data and the satisfaction related to the

application of an action and it is used as a pattern to

obtain the models in real time.

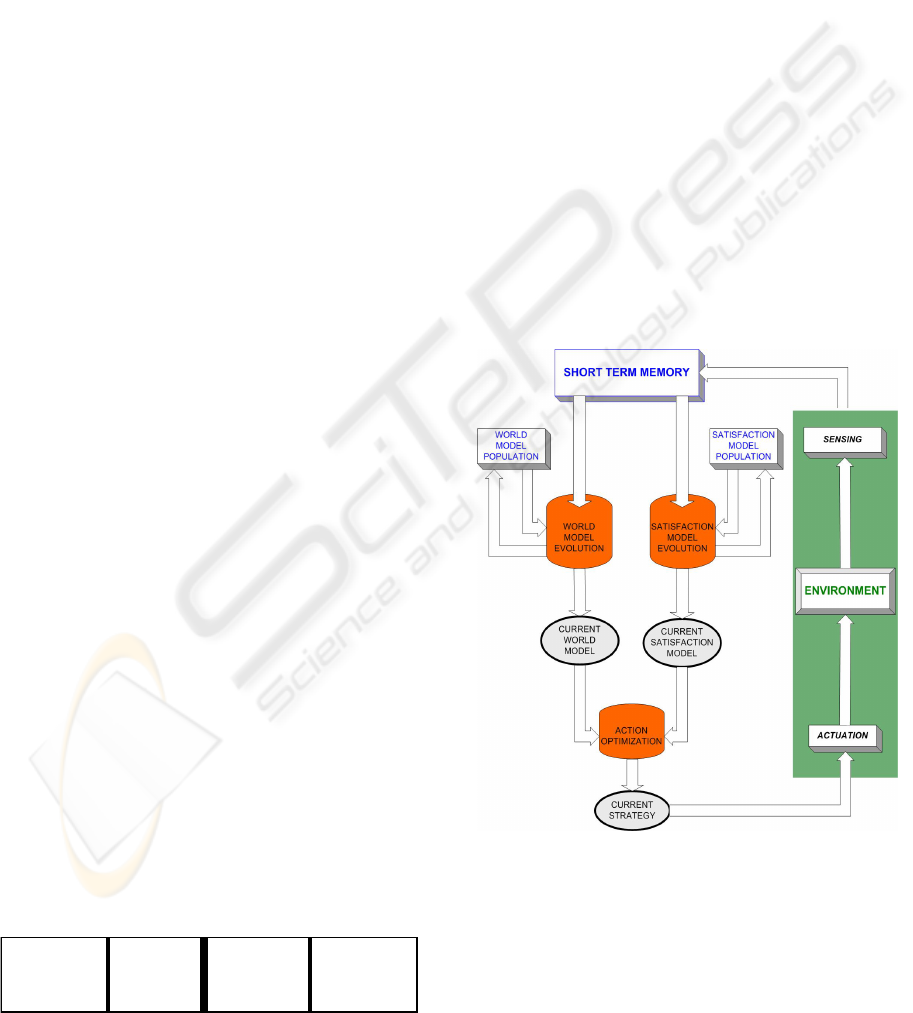
3 CONSTRUCTING THE MDB

As we have mentioned in the previous section, the

actions that must be applied in the environment are

selected internally by the agent and the internal operation

is made up of three main elements: a memory that stores

the action-perception pairs, a stage to improve the

models according to the real information available and

finally a stage to select the action to be applied.

Using this scheme we have constructed a new

Cognitive Mechanism called MDB (Multilevel

Darwinist Brain). The main difference of the MDB with

respect to other model based cognitive mechanisms is

the way the models are obtained and the actions planned

from them. Its functional structure is shown in Figure 2.

The final objective of the mechanism is to provide the

action the agent must apply in the environment to fulfil

its motivation. The main operation can be summarized

by considering that the selected action (represented by

the Current strategy block) is applied to the Environment

through the actuators (Actuation block) obtaining new

Sensing values. These acting and sensing values provide

a new action-perception pair that is stored in the Action-

Perception Memory. Then, the Model Search/evolution

Sensorial

Data

(t)

Action

Applied

(t)

Sensorial

Data

(t+1)

Satisfaction

(t+1)

Figure 2: Block diagram of the MDB including

evolutionary learning elements.

MULTILEVEL DARWINIST BRAIN IN ROBOTS - Initial Implementation

processes start (for world, internal and satisfaction

models) trying to find functions that generalize the real

samples (action-perception pairs) stored in the Action-

Perception Pair Memory. The best models in a given

instant of time are taken as Current World Model and

Current Satisfaction Model and are used in the process of

Optimizing the Action. After this process finishes, the

best action obtained is applied again to the Environment

through the actuators obtaining new Sensing values.

These five steps constitute the basic operation cycle

of the MDB, and we will call it an iteration of the

mechanism. As more iterations take place, the MDB

acquires more information from the real environment

(new action-perception pairs) so the models obtained

become more accurate and, consequently, the action

chosen using these models is more appropriate.

There are two main processes that must be solved in

MDB: the search for the best world and satisfaction

models predicting the contents of the action-perception

pair memory and the optimization of the action trying to

maximize the satisfaction using the previously obtained

models. In the way these processes are carried out lies

the main difference of the MDB with respect to other

cognitive mechanisms.

3.1 On line creation of Models

In this context, a model is just a non linear function

defined in an n-dimensional space that approximates and

tries to predict real characteristics. Taking this into

account, possible mathematical representations for the

models are polynomial functions, simple rules, fuzzy

logic rules, neural networks, etc. Whatever the

representation, techniques for obtaining these functions

must be found considering that we have samples (action-

perception pairs) of the function to model, these samples

are known in real time and we want to obtain the most

general model possible, not a model for a given set of

samples present in a particular instant.

Taking these three points into account, the model

search process in the MDB is not an optimization

process but a learning process. As commented in (Yao,

96), learning is different from optimization because we

seek the best generalization, which is different from

minimizing an error function. Consequently, the search

techniques must allow for gradual application as the

information is known progressively and in real time. In

addition, they must support a learning process through

input/output pairs (action/consequence samples) using an

error function.

To satisfy these requirements we have selected

Artificial Neural Networks as the mathematical

representation for the models and Evolutionary

Algorithms as the most appropriate search technique.

This combination presents all the required features for

the automatic acquisition of knowledge (the models)

based on the Darwinist theories.

After applying an action in the environment and

obtaining new sensing values, the search for the models

are now evolutionary processes, one for the world

models and another for the satisfaction models. The use

of evolutionary techniques permits a gradual learning

process by controlling the number of generations of

evolution for a given content of the action-perception

pair memory. This way, if evolutions last just for a few

generations (usually from 2 to 4) per iteration, we are

achieving a gradual learning of all the individuals. In

order to obtain a general model, the populations of the

evolutionary algorithms are maintained between

iterations (new entries in the action-perception memory)

of the MDB. Furthermore, the evolutionary algorithms

permit a learning process through input/output pairs

using as fitness function an error function between the

predicted values provided by the models and the

expected values for each action-perception pair.

Strongly related to this process is the management of

the action-perception pair memory, because the quality

of the learning process depends on the data stored in this

memory and the way it changes. The data that must be

managed (samples of the real world) and stored in this

memory is acquired in real time as the system interacts

with the environment. From this point forward, this

memory will be called Short Term Memory (STM). It is

not practical or even useful, if we want an adaptive

system, to store in the STM all the samples acquired in

agent’s lifetime. We need to develop a replacement

strategy for this memory that permits storing the most

relevant samples for the best possible modelling.

3.2 Managing the STM

The replacement process in the Short Term Memory

depends on the way we compare the elements stored, in

this case, samples of a function. Whenever we have a

new sample we must decide if it is stored replacing one

that was previously stored in the STM. To compare

samples we must label them taking into account that we

hope to store the most relevant information to model. We

have designed a replacement strategy that labels the

samples using four basic features:

1. The point in time a sample is stored (T): this

parameter favours the elimination of the oldest samples,

maximizing the learning of the most current information

acquired.

2. The distance between samples (D): measured as

the Euclidean distance between the action-perception

pair vectors, this parameter favours the storage of

samples from all over the feature space in order to

achieve a general modelling. A min-max strategy is

used, this is, each sample is assigned a label D

corresponding to the minimum of the distances (d

) to the

ICINCO 2004 - ROBOTICS AND AUTOMATION

remaining samples. The samples that maximize the D for

the STM are stored.

3. The complexity of a sample to be learned (C): this

parameter favours the storage of the hardest samples to

be learned. To calculate it, we use the error provided by

the current model (m) when predicting a sample j (X

,…, X

, Y

,…,Y

), that corresponds to a previously

stored model with n inputs and k outputs.

4. The relevance of a sample (R): this parameter

favours the storage of the most particular and relevant

samples, those that escape from generality, that is, those

that, even though they may be learnt by the models very

well, initially presented large errors. It is a fundamental

term when working with real environments where

functions are not smooth. To calculate it, we use the

error provided by the current model when predicting a

new sample n (X

,…, X

, Y

…,Y

). Consequently, it is

an initial error value and it doesn’t change while the

sample is in the STM:

Thus, each sample is stored in the STM has a label

(L) that is calculated every iteration as a linear

combination of these four basic terms:

where the constants K

control the relevance of each

term. This way, the main feature of the replacement

strategy presented is its dynamism and depending on the

value of the constants K

we can generate different

storage policies. For example, if we prefer to store the

newest samples without generalization considerations,

we can use K

= 1 and K

= K

= 0 which is a FIFO

replacement strategy. This modification of the

parameters can be carried out automatically by the MDB

as a function of perception or strategy.

3.3 Action Search

An action is a command to the actuators of the agent and

its representation depends on the particular agent. The

search for the best action in the MDB is not a learning

process because we are looking for the best possible

action for a given set of conditions. That is, we must

obtain the action whose predicted consequences given by

the world and internal models result in the best predicted

satisfaction. Consequently, for the actions, we must solve

a simple optimization problem in which any

optimization technique is valid. In our case, and for

homogeneity, we have used evolution.

It is important to note that the MDB always has

current world, internal and satisfaction models and a

current strategy available for the agent to make use of.

This implies that in its interaction with the world it does

not require waiting for the mechanism in order to act.

This provides the capability of real time interaction.

Obviously, the quality of these models and actions will

depend on how many action perception pairs the agent

has gone through in its life and how much “thinking”

time it has had to transform these data into information

in the form of useful models.

We have not imposed any restriction on the type of

evolutionary technique that can be applied: genetic

algorithms, evolution strategies, genetic programming or

macroevolutionary algorithms are suitable for the

process of learning the models.

In the next section, we present two simple

application examples to show the basic operation of the

MDB and its capabilities for the automatic acquisition of

knowledge that permits an agent to learn autonomously

from its interaction with the environment. To do this, we

have applied the MDB in a real hexapod robot trying to

perform a simple task.

4 MDB IN A REAL ROBOT

The left image of Figure 3 displays the Hermes II

hexapod robot used in this example. It is a robust robot

provided with six legs with two degrees of freedom and

six infrared sensors, each one placed on the top of each

leg, two whiskers, inclinometers and six force sensors.

The MDB mechanism was applied to a simulated model

(right image in Figure 3) of the Hermes II robot created

using the DADS 3-D mechanical simulator and then

transferred to the real robot

4.1 Learning to walk

In the first part of the example, we want the Hermes II

robot to learn to walk. We can describe the motion of

each leg through 3 parameters (for the swing and lift

motion): the initial phase, which establishes the starting

point of the leg motion, the frequency, which increases

or decreases the speed of the movement and the sweep

amplitude. In this case, all of the parameters are fixed

except the initial phase of the swing motion for each leg.

The different combinations of phases lead to different

gaits, some useful, some useless and some even

completely impractical. We want the mechanism to

RKCKDKTK=L

rcdt

⋅+⋅

Figure 3: The left image shows the Hermes II

robot and the right one shows the model used in

simulation.

MULTILEVEL DARWINIST BRAIN IN ROBOTS - Initial Implementation

allow the robot to develop an efficient gait so that it can

fulfil its motivations.

The robot starts from point (0,0) in each iteration and

an object (a block) is placed one meter away from it. The

mechanism selects the gait that must be applied and the

robot uses it during a fixed time (13 seconds in

simulation, 24 seconds in the real robot). Through its

infrared sensors using a time integration virtual sensor

presented in (Bellas et al., 2000), the robot always has an

indication (in general noisy) of the distance to the block.

These values are used as the input sensed values to the

world model.

The motivation of this behaviour for the agent is to

maximize the detection in the two front infrared sensors

(which corresponds to a minimization of the distance)

because we want it to reach the block frontally and using

a stable gait.

This way, we have a world model with 7 inputs, the

distance to the block provided by the virtual sensor and

the 6 input phases applied to the legs. The output from

the world model is the predicted distance to the block.

We have implemented the world models using

artificial neural networks (multilayer perceptrons). The

networks consisted of two 4 neuron hidden layers. In

Figure 4 we show the evolution of the mean squared

error between the distance predicted by the world model

and the real one. As we can see, the error becomes very

small about iteration 180 but it oscillates. This is because

a world model that is evolved for a given set of contents

in the short-term memory, could be less adequate for

another set. In this example, the short-term memory

contains 40 action-perception pairs and it works as a

FIFO memory, so the replacement strategy is purely

temporal in this first case.

For the evolution of the world models we have used

a simple genetic algorithm with 700 individuals, 57

genes (corresponding to the weights and bias of the 7-4-

4-1 neural network), 60% crossover and 2% mutation.

The satisfaction is directly the predicted distance to the

block. Thus the Hermes robot must select a gait in order

to minimize this distance. In this example, we will not

use an explicit satisfaction model.

For the optimization of the actions, we have also

used a genetic algorithm with 120 individuals, 6 genes

(direct encoding of the input phases), 60% crossover and

6% mutation.

In order to test how good a gait is, we define the

efficiency of a gait as the normalized distance in the

direction of the objective covered by the robot in a fixed

simulation time, weighted by the distance that its

trajectory is separated from a straight line. That is, we

consider that a gait is better if the robot goes straight to

the block without any lateral deviation. We must point

out that this measure is never used in the cognitive

mechanism; it is just a way of presenting results in

papers.

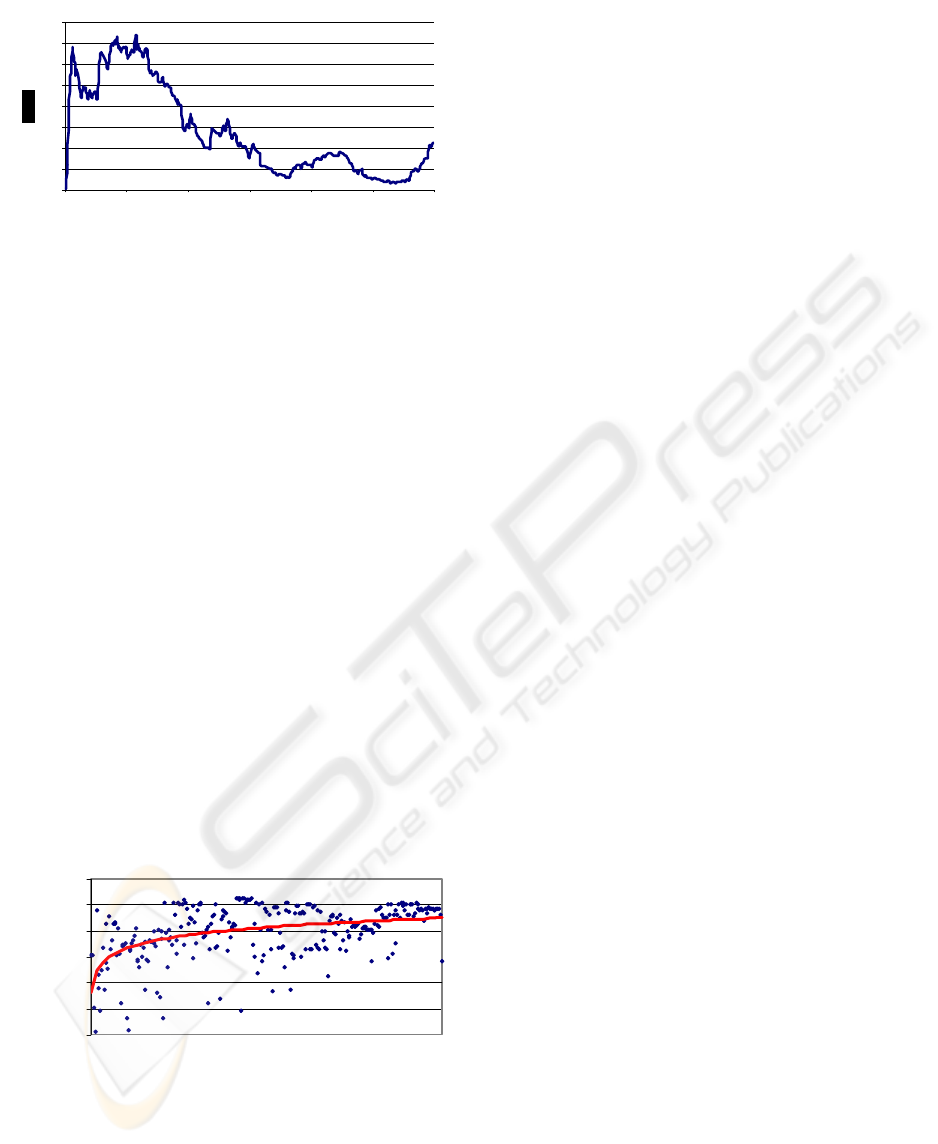
In Figure 5 we display the behavior of this efficiency

throughout the robot’s life. It can be observed that the

curve tends to 1 as expected. Initially, the gaits are poor

and the robot moves in irregular trajectories. This is

reflected in the efficiency graph by the large variations in

the efficiency from one instant to the next. Sometimes,

by chance it reaches the block, others it ends up very far

away from it. Note that whatever the result of the action,

it does produce a real action perception pair, which is

useful data in order to improve the models. As the

interaction progresses, the robot learns to reach the block

without any deviation in a consistent manner, and the

efficiency tends to one.

In the three graphs of Figure 6, we represent the

temporal occurrence of the end of the swing motion for

each leg. The top graph corresponds to iteration 6 and we

can see that the swings are completely out of phase. The

resulting gait is not appropriate for walking in a straight

line and the robot turns, leading to a low efficiency

value. The middle graph corresponds to iteration 87

where the resulting gait is more efficient than before

according to the level of error for that iteration (see

Figure 4). Finally, the bottom figure shows the

combination of phases corresponding to iteration 300. As

0,2

0,4

0,6

0,8

1, 2

1, 4

1, 6

0 50 100 150 200 250 300

It eration

Figure 4: Evolution of the mean squared error between

the output of the world model (distance to the object) and

the real distance.

-0,6

-0,3

0,0

0,3

0,6

0,9

1,2

1 41 81 121 161 201 241

Iteration

Efficiency

Figure 5: Efficiency of the gaits applied by the robot. As

time progresses it tends to one, this is, the robot moves

straight to the block without any lateral deviation.

ICINCO 2004 - ROBOTICS AND AUTOMATION

we can see, the initial phases are equal in groups of three

and the resulting gait is quite good. In fact, this

combination of phases leads to a very common and

efficient gait called tripod gait, where three legs move in

phase and the other three legs in counter-phase resulting

in a very fast and stable straight line motion.

We must point out that this gait was developed by

the robot itself, we just built the world for the robot to

learn and provided a motivation to reach an objective as

efficiently as possible.

4.2 Learning to turn

At this point, the Hermes II robot has learnt to walk, and

now we want it to learn to turn using the combination of

initial phases obtained (tripod gait). The main objective

of this second part of the example is to use an explicit

satisfaction model.

We place an object (a block) in a semicircunference

in front of the robot at a random distance between 50 and

100 cm, and the mechanism must select the best

combination of amplitudes in the swing motion in order

to reach it. The rest of the parameters in the gait are

fixed. If the robot reaches the block (distance of less than

20 cm) or if it loses it (distance larger than 100 cm) we

move it to a new position in the semicircunference. This

way, we develop a teaching method as we would do

with children: we present an objective and we reward the

good actions.

The world model has three inputs, the distance and

angle of the robot with respect to the block (provided by

the virtual sensor applied before) and the amplitude of

turn. The outputs are the predicted distance and angle.

These two magnitudes are the inputs to the satisfaction

model, which has just one output, the predicted

satisfaction. The motivation of the behavior is again the

maximization of the infrared sensing in the two front

sensors. Consequently, the robot must reach the block

(minimizing distance) with low deviation (minimizing

angle).

The models are represented by multilayer

perceptrons with two 4 neuron hidden layers for the

world models and two 3 neuron hidden layers for the

satisfaction models. The population in the genetic

algorithms was 600 individuals for the world models and

300 for the satisfaction models. In Figure 7 we have

represented the number of iterations between two

consecutive captures of the object. We can see clearly

how in the first stages of the behavior, there exists a big

delay from one capture to the next because the models

are poor and, as a consequence, the selected actions are

not successful. But the tendency changes about iteration

200 and the number of iterations between two

consecutive captures decreases to one.

In the top image of Figure 8 we display the path

followed by the real robot with the strategies applied in

iterations 53, 54, 55 and 56. As indicated in Figure 7,

these iterations correspond to the first stages of the

mechanism where the number of iterations required to

reach the object is large. In fact, the block remains in the

same position during the application of these four

strategies and the robot never turns towards it.

In the bottom image of Figure 8 we display the path

followed in iterations 421, 422, 423, 424. The robot

reaches the block in iterations 422, 423 and 424 and we

move it. The strategies are now very successful.

0 20 40 60 80 100 120 140

Capture

Iterations between captures

Iteration 60

Iterations 422, 423,

Figure 7: Iterations between two consecutive captures of

the object.

Figure 6: End of the swing motion for each leg in time.

Iteration 87

Iteration 300

0 5 10 15 20

Time (s)

Maximum am plitude

Front Left

Cente

Right

Rea

Left

Front Right

Cente

Left

Rear Right

Iteration 6

0 5 10 15 20

Time (s)

Maxim um amplitude

Front Left

Cente

Right

Rea

Left

Front Right

Cente

Left

Rear Right

0 5 10 15 20

Time (s)

Maxim um amplitude

Front Left

Cente

Right

Rea

Left

Front Right

Cente

Left

Rear Right

MULTILEVEL DARWINIST BRAIN IN ROBOTS - Initial Implementation

5 CONCLUSIONS

We have presented a Cognitive Mechanism for robots

(the Multilevel Darwinist Brain) that applies Darwinist

concepts like evolutionary learning to the autonomous

acquisition of knowledge by agents.

A classical utilitarian cognitive model including

motivations to guide the behaviors is particularized to

this Darwinist approach. There are evolutionary

optimization processes that must be continuously solved

in the MDB to internally decide the appropriate actions

and evolutionary search processes to obtain the models

where the actions are tested, following a deliberative

approach.

The mechanism was tested using a hexapod robot

which was trying to learn to walk and to reach an

objective. The results obtained are very promising, as the

robot was able to autonomously generate a tripod gait

and modulate the amplitudes of the legs in order to turn

to reach an objective through continuous interaction with

the environment using its own sensors and a very simple

motivation. This is very important because the

mechanism permits the robot to find the best solution

according to the limitations of its environment and its

sensorial and actuation apparatus allowing it to adapt and

survive in this particular world. One of the main features

of this type of mechanisms is that if the world changes,

the robot will adapt smoothly.

ACKNOWLEDGEMENTS

This work was partially funded by the Xunta de Galicia

(proyect PGIDIT02PXIB10501PR), the MCYT of Spain

(proyect VEM2003-20088-C04-01), and NATO

(PST.CLG.978744).

REFERENCES

Agre, P. E., Chapman, D. 1987. Pengi: An implementation of a

theory of activity. American Association for Artificial

Intelligence. pp 268-272

Bellas F., Becerra J.A., Santos J. and Duro R.J., 2000. Applying

Synaptic Delays for Virtual Sensing and Actuation in

Mobile Robots. Proc IJCNN 2000. pp 6144-6153

Beer R., Quinn R., Chiel H., Ritzmann R. 1997. Biologically

Inspired Approaches to Robotics. Communications of the

ACM, V.40 N. 3, pp 30-38

Bratman, M., Israel, D., Pollack, M., 1988. Plans and Resource-

bounded Practical Reasoning. Computational Intelligence,

4. pp 349-355.

Brooks, R., 1986. A Robust Layered Control System for a

Mobile Robot. IEEE J. Robotics and Automation RA-2 (1).

pp 14-23

Changeux, J., Courrege, P., Danchin, A., 1973. A Theory of the

Epigenesis of Neural Networks by Selective Stabilization

of Synapses, Proc.Nat. Acad. Sci. USA 70, pp 2974-2978

Changeux, J., Danchin, A., 1976. Selective Stabilization of

Developing Synapsis as a Mechanism for the Specification

of Neural Networks. Nature 264. pp 705-712.

Changeux, J., Heidmann, T., Patte, P., 1984 Learning by

Selection. Springer-Verlag

Chapman, D., 1987. Planning for conjunctive goals, Artificial

Intelligence, 32, pp 333-378

Conrad, M, 1974. Evolutionary Learning Circuits. Theor. Biol.

46, pp 167-188

Conrad, M., 1976. Complementary Molecular Models of

Learning and Memory. BioSystems 8, pp 119-138

Edelman, G., 1987. Neural Darwinism. The Theory of

Neuronal Group Selection. Basic Books

Floreano, D., Mondada, F., 1996. Evolution of Homing

Navigation in a Real Mobile Robot. IEEE Trans. on Sys.

Man and Cybernetics Part B, 26(3), pp 396-407.

Kaelbling L., 1986. An Architecture for Intelligent Reactive

Systems. Reasoning about Actions and Plans. Proceedings

for the 1986 Workshop. pp 395-410

Maes, P., 1991. The Agent Network Architecture (ANA)"

SIGART Bulletin, 2(4), pp 115-120.

Yao, X., Liu, Y., Darwen, P., 1996. How to make best use of

evolutionary learning. Complex Systems: From Local

Interactions to Global Phenomena, pp 229-242.

Figure 8: The top image shows the path followed by

the Hermes II robot in the first iterations. The bottom

image shows the path when the behavior is successful.

Iteration 53

Iteration 54

Iteration 55

Iteration 56

Iteration 421

Iteration 422

Iteration 423

Iteration 424

ICINCO 2004 - ROBOTICS AND AUTOMATION