
ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS
Filipe Morais and J. M. Sá da Costa
Instituto Superior Técnico, Technical University of Lisbon,
Dept. of Mechanical Engineering / GCAR - IDMEC
Av. Rovisco Pais, 1049-001Lisboa, Portugal
Keywords: Active noise control, feedforward control, filtered-reference LMS, modified filtered-reference
LMS, filtered-u, frequency domain filtered-reference LMS.
Abstract: In this paper existing classical and advanced techniques of active acoustic noise cancellation (ANC) in ducts
are collected and compared. The laboratory plant used in experience showed a linear behaviour and so the
advanced techniques were not used. Due to delay on the plant, the feedback classical techniques could not
be applied. The best results were obtained with the modified filtered-reference LMS (MFX-LMS) and
filtered-u techniques. A very important conclusion is that the quadratic normalisation is needed to maintain
the algorithms always stable. In this paper 18dB of attenuation of white noise and 35 dB of attenuation of
tonal noise were achieved. Thus, ANC can be applied in a real situation resulting in important noise
attenuations.
1 INTRODUCTION
Acoustic noise is since a long time considered as
pollution due to the diverse problems that it causes in
the human being, both physical, as for instance
deafness, and psychological. As a consequence,
competent authorities tend to enforce restrictive laws
on the allowed sound levels, and it is thus necessary
to look for solutions leading to its fulfilment. On the
other hand, acoustic noise is a cause of lack of
productivity. By these reasons, there is a pressing
need to solve the problem of acoustic noise.
In practice passive solutions for the cancellation
of acoustic noise can be found by simple use of
absorption and reflection phenomena. However, they
are of little use for frequencies below 1000Hz. In
these other cases acoustic noise cancellation (ANC)
based on the principle of interference, should be
used.
The idea of the ANC is 70 years old. One of the
first references remounts to 1934 when P. Lueg
patented some ideas on the subject (Elliot, 2001 and
Tokhi et al., 1992). Lueg addressed ANC in ducts
and in the three-dimensional space. For ducts, Lueg
considered a microphone that captured the acoustic
noise. The signal from the microphone would pass
through the controller and feed the loudspeaker as
shown in fig. 1. The controller would result in
acoustic waves emitted by the loudspeaker with the
same amplitude of the acoustic noise but in phase
opposition, so that the two waves would cancel each
other (interference principle). This configuration is
nowadays the most used in ANC applications in
ducts.
Controller
Loudspeaker
Figure 1: Single-channel feedforward control in a duct.
The purpose of using ANC in ducts is to cancel
the plane waves that are propagated in the duct due to
fans, like in an air conditioner installation. The ANC
mostly used techniques were developed to control
stochastic disturbances, because acoustic noise can
be considered as a disturbance with significant
spectral richness. Furthermore, techniques for
stochastic disturbances can be applied in
deterministic disturbances but the inverse is not
feasible. ANC techniques for stochastic disturbances
can be divided into two main groups: classical or
advanced. Those of the first group are based on plant
linearity, and consequent validity of the superposition
principle (Ogata, 1997).
Linear techniques can also be applied to
nonlinear systems, but they usually have bad
performance. Advanced techniques were developed
214
Morais F. and Sá da Costa J. (2004).
ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS.
In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 214-221
DOI: 10.5220/0001141102140221
Copyright
c
SciTePress
to nonlinear plants, although they can be applied to
linear systems with good performance. However,
they are also more complex and demand more
computational power than the classic ones. For that
reason advanced techniques are not preferred instead
of classic ones when linear plants are concerned.
Both classic and advanced techniques can be
divided according to the type of control: feedforward
or feedback. In the feedforward control information
is collected in advance about the disturbance and so
the controller can act in anticipation; while the
feedback control has no information in advance
about the disturbance and thus the controller reacts to
the disturbance. The feedback control is useful when
the acoustic noise is created by several different
sources, or by distributed sources, or when it is not
practical or possible to get information in advance
concerning all the noise sources. However, this is not
the case of ducts because the noise source is well
defined and acoustic waves are plane and travel in a
single direction.
In this paper existing feedforward techniques for
ANC in ducts are compared to assess the
performance of these techniques in a real situation.
In ducts it is possible to have only plane acoustic
waves, rending ANC much simpler since some
acoustic effects are not to be found, as for instance
the diffraction of acoustic waves. In this work the
range of frequencies to be deal with ANC is limited
to the interval [200 Hz; 1000 Hz] since ANC is not
effective for frequencies above 1000 Hz and the
actual set-up used does not allow to go below 200
Hz.
Digital Controller
+
-
+
s(n)
+
x(n)
+
G (z)
G (z)
G (z)
+
W(z)
u(n)
e(n)
d(n)
f(n)
s
f
f
Figure 2: Block diagram of feedforward control.
2 FEEDFORWARD CONTROL
The general block diagram of the feedforward
control of acoustic plane waves in a duct is found in
fig. 2. The signal x(n) is the reference signal
measured by the reference microphone, d(n) is the
primary noise signal passed through the primary
path, e(n) is the error signal given by the error
microphone, and G
s
(z) is the secondary path between
the secondary source and the error sensor. It is
assumed that the controller is digitally implemented
and made up by a direct filter W(z) and a feedback
filter Ĝ
f
(z). The feedback filter consists of an
estimation of the natural feedback path of the system
G
f
(z), i.e., reproduces the influence of the secondary
source to the reference sensor. When Ĝ
f
(z) = G
f
(z),
the two feedback loops cancel each other and the
signal that feeds the controller is equal to x(n). In this
situation the control is purely feedforward. In the
situation in which the estimate of G
f
(z) is not perfect,
a residue appears from the cancellation of two loops.
If Ĝ
f
(z) is a good estimate of the path G
f
(z), the
residue has a small value and will not affect the
performance of the control. If the estimate of G
f
(z) is
poor, this can influence the performance of the
control, that may become unstable.
In this situation it
might be necessary to use feedback control
techniques to improve the performance or to stabilize
the control (Elliot, 2001).
Assuming that the two feedback loops cancel
each other completely and that the plants are linear
and time invariant (LTI), so that the filter W(z) and
the discrete transfer function G
s
(z) can be
interchanged, the error signal e(n) comes
, (1)
T
() () () () ()
T
en dn n dn n=+ =+wr r w
where w is a vector with the coefficients of the filter
and r(n) the vector with the last samples of the
iltered reference signal r(n) given by: f
, (2)
∑
−
=
−=
1
0
)()(
I
i
i
inxgnr
where the g
i
are the I coefficients of the discrete
transfer function G
s
(z), assuming that has a FIR
structure.
2.1 Filtered-reference LMS (FX-LMS)
Algorithm
This algorithm is based on the steepest descent
algorithm, which is mostly used for adapting FIR
controllers (Elliot, 2001). The expression for
adapting the coefficients of controller W(z) of fig. 2 is
iven by: g
(1) ()
J
nn
µ
∂
+= −
∂
ww
w
(3)
where J is a quadratic index of performance, equal to
the error signal squared e
2
(n), and ∂·/∂w is the
radient: g
[
2()()
J
]
E
nen
∂
=
∂
r
w
(4)
For this algorithm a simpler version than the one
given by eq. (4) is used, since the expected value of
the product is not reckoned, but only the current
alue of the gradient. Thus, v
ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS
215

2
() ()
2() 2()()
en en
en en n
∂∂
==
∂∂
r
ww
(5)
The expression for adapting the coefficients of the
controller is given by:
ˆ
(1) () ()(nnne)n
α
+= −wwr
(6)
where
α
= 2
µ
is the convergence coefficient and
is the estimate of the filtered reference signal,
obtained with the estimate of the G
ˆ
()rn
s
(z) model. The
algorithm is called filtered-reference LMS because
the filtered reference signal is used to adapt the
coefficients. The block diagram of the algorithm is in
iven in fig. 3. g
u(n)
xG (z)
s
e(n)
+
r(n)
G (z)
s
w(n)
+
x(n)
d(n)
Figure 3: Block diagram for FX-LMS algorithm.
If the reference signal x(n) were used instead of the
filtered reference r(n) to adapt the coefficients, the
adaptation would be wrong because there is a time
shift between the signal x(n) and the error signal
e(n). This is a consequence of the existence of a time
delay in G
s
(z). This algorithm is rather simple to
implement and is numerically stable, being therefore
frequently used (Elliot, 2001).
2.2 Normalized filtered-reference LMS
algorithm (NFX-LMS)
In the previous approach the adaptation of the
coefficients of the controller W(z) is directly
proportional to the coefficient of convergence
α
and
the vector r(n). Sometimes, when r(n) has large
values, the FX-LMS algorithm has a problem of
amplification of the gradient noise (Haykin, 2002).
The coefficients of the vector r(n) are normalized in
order to solve this problem. Haykin (2002) suggests
dividing the coefficients by the Euclidean norm of
vector r(n). The expression for adapting the
coefficients becomes:
2
(1) () ()()
()
nn ne
n
n
α
δ
+= −
+
ww r
r
%
(7)
where
δ
it is a very small and positive number. This
term allows preventing numerical difficulties when
r(n) is small because the Euclidean norm takes small
values. Elliot (2001) suggests another solution where
the coefficients of vector r(n) are divided by the
inner product of vector r(n), r
T
r. Whatever the
option is, algorithm NFX-LMS presents the
following advantages over algorithm FX-LMS: faster
convergence rate and sometimes better performance
of the obtained controller; the algorithm is more
stable when there is a change of the spectral richness
of the reference signal x(n). This normalization of the
filtered reference signal can be applied to other
algorithms.
2.3 Leaky LMS algorithm
For this algorithm another index of quadratic
performance is used:
(8)
2
2
()JEen
β
⎡⎤
=+
⎣⎦
ww
T
nen
where
β
is a positive constant. This performance
index weighs both the average of the error signal e(n)
squared as well as the sum of the squares of the
coefficients of the controller. This performance index
prevents the coefficients of the controller from taking
large values that can render the algorithm unstable
when both the amplitude of the reference signal, x(n),
and its spectral components undergo variations
Elliot, 2001). The adaptation becomes: (
ˆ
( 1) (1 ) () ()()nn
α
βα
+
=− −wwr
. (9)
Eq. (9) is different for the FX-LMS algorithm
because of term (1-
αβ
), which is called leakage
factor. This term must take values between 0 and 1
and is normally 1. When it takes another value the
error signal e(n) is not zero and the value of
coefficients decreases with each iteration. Adding the
term (1-
αβ
) to the coefficients adapting equation
allows the increasing of the robustness of the
algorithm. On the other hand the term (1-
αβ
)
reduces the noise attenuation that can be reached.
Thus, the choice of the value for beta must take into
account the robustness of the algorithm and the
reduction of the attenuation. In most applications, the
use of a small value of beta allows a sufficient
increase of robustness and the attenuation of the
acoustic noise suffers little (Elliot, 2001). The
modification introduced in the FX-LMS algorithm
can also be implemented in the other algorithms.
2.4 Modified filtered-reference LMS
algorithm (MFX-LMS)
The FX-LMS algorithm requires a rather slow
adaptation compared with the plant dynamics so that
the error may be given by eq. (1). This is because
adapting the coefficients is somehow a nonlinearity
which influence depends on the speed of adaptation
(Elliot, 2001). Thus, to make this influence negligible
the adaptation of the coefficients must be very slow
when compared with the dynamics of the plant. This
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
216

should be regarded as a disadvantage. The
arrangement shown in fig. 4 allows overcoming this
limitation. In this scheme, the estimated filtered
reference signal,
, in the adaptation path of the
controller is common to the adaptive filter and to the
adaptation, and has no time shift in relation to the
modified error, e’
ˆ
()rn
m
(n).
-
+
+
+
w(n)
x
r(n)
G (z)
u(n)
G (z)
+
G (z)w(n)
+
e(n)
x(n)
Controller
Adaptive
filter
s
s
s
e' (n)
m
d(n)
Figure 4: Block diagram for MFX-LMS algorithm.
F
or this algorithm the adaptation is given by:
ˆ
(1) () ()(
m
nnne
)
n
α
+= −wwr
(10)
w
here e
m
(n) is the modified error, given by:
. (11)
11
00
ˆ
ˆ
() () () ( )
IJ
mij
ij
en dn wngxni j
−−
==
=+ −−
∑∑
The modified error can be seen as a prediction of the
error for the case where the coefficients of the
controller do not change at each instant. The MFX-
LMS algorithm usually presents convergence rates
larger than those of the FX-LMS algorithm (Elliot,
2001). This is because the adaptive filter and the
plant estimate were interchanged and thus the delay
between the exit of the controller and the error signal
was eliminated. For this reason it is no longer
necessary to consider the delay in the restriction of
the convergence coefficient, and larger steps may be
used with the MFX-LMS algorithm. However the
MFX-LMS algorithm has the disadvantage of
requiring more computational means.
2.5 Frequency domain filtered-reference
LMS algorithm (FX-LMS Freq)
For the FX-LMS algorithm the estimate of the
gradient of eq. (5) was used to adapt the coefficients
of the controller. The estimate of the gradient will be
assumed to be given by the average of the product
r(n)e(n) during N instants. Thus, the adaptation is
given by:
1
( ) ( ) () ()
nN
ln
nN n lel
N
α
+−
=
+= +
∑
ww r
(12)
In this case, the adaptation is carried only after N
time samples. The use of the average of the product
r(n)e(n) during N instants can be considered as a
more precise estimate of the gradient than the use of
the product r(n)e(n) for each time sample. In practice
adaptation with eq. (12) has a convergence rate very
similar to the FX-LMS algorithm, since though the
adaptation for eq. (12) has a lower frequency, the
value of the update of the coefficients is larger
(Elliot, 2001). The summation in eq. (12) can be
thought of as an estimate of the crossed correlation
between the filtered reference r(n) and the error
signal e(n). The estimate must be reckoned from i =
0 up to I-1, where I is the number of coefficients of
the adaptive filter. For long filters the reckoning of
the estimate can be inefficient in the time domain,
requiring a large computational effort. For large
values of I it is more efficient to calculate the cross
correlation in the frequency domain. If discrete
Fourier transform (DFT) with 2N points for the
signals e(n) and r(n) are considered, an estimate of
the cross spectral density can be calculated through:
(13)
*
ˆ
() () ()
re
Sk RkEk=
where k is the index of discrete frequency and *
means the complex conjugate. Some care must be
taken to prevent the effect of circular convolution.
Thus, before reckoning the DFT of the error signal,
e(n), with 2N points, in the block with 2N points of
the error signal the first N points must be zero. This
will eliminate the non-causal part of the cross
correlation (Elliot, 2001). The expression that gives
he adaptation of the coefficients is: t
{
}
*
(1) () ()()
mm
m m IFFT R k E k
α
+
+= −ww
(14)
where { }
+
means the causal part of the cross
correlation, IFFT is the inverse fast Fourier transform
and
α
is the convergence coefficient. R
m
(k) is directly
obtained multiplying the DFT of the reference signal
X(k) by the frequency response estimate of the
system. This algorithm is called fast LMS. Fig. 5
shows the block diagram of this algorithm.
The advantage of the fast LMS algorithm over
the FX-LMS is that it requires few computations.
Assuming that the implementation of the DFT
requires
2
2log2
N
N
multiplications, the FX-LMS
algorithm requires 2N
2
calculations per iteration
hile fast LMS needsw
2
(16 6 log 2 )
N
N
+
.
ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS
217
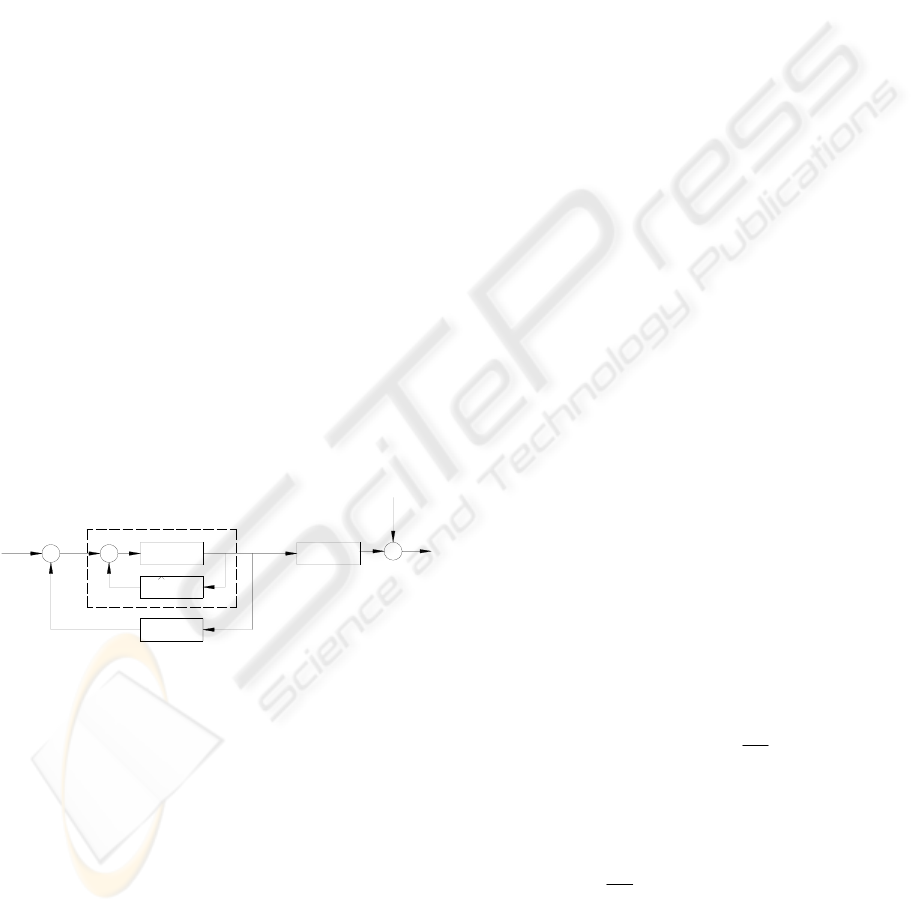
s
W(z) G (z)
e(n)
d(n)
+
+
E(k)
H
R (k)
R(k)
X(k)
x(n)
^
G(k)
Conjugate
Get
first N
points
α
IFFT
FFT
xx
e0
Insert Zero
Block
FFT
Concatenate
two blocs
Figure 5: Block diagram for FX-LMS Freq algorithm.
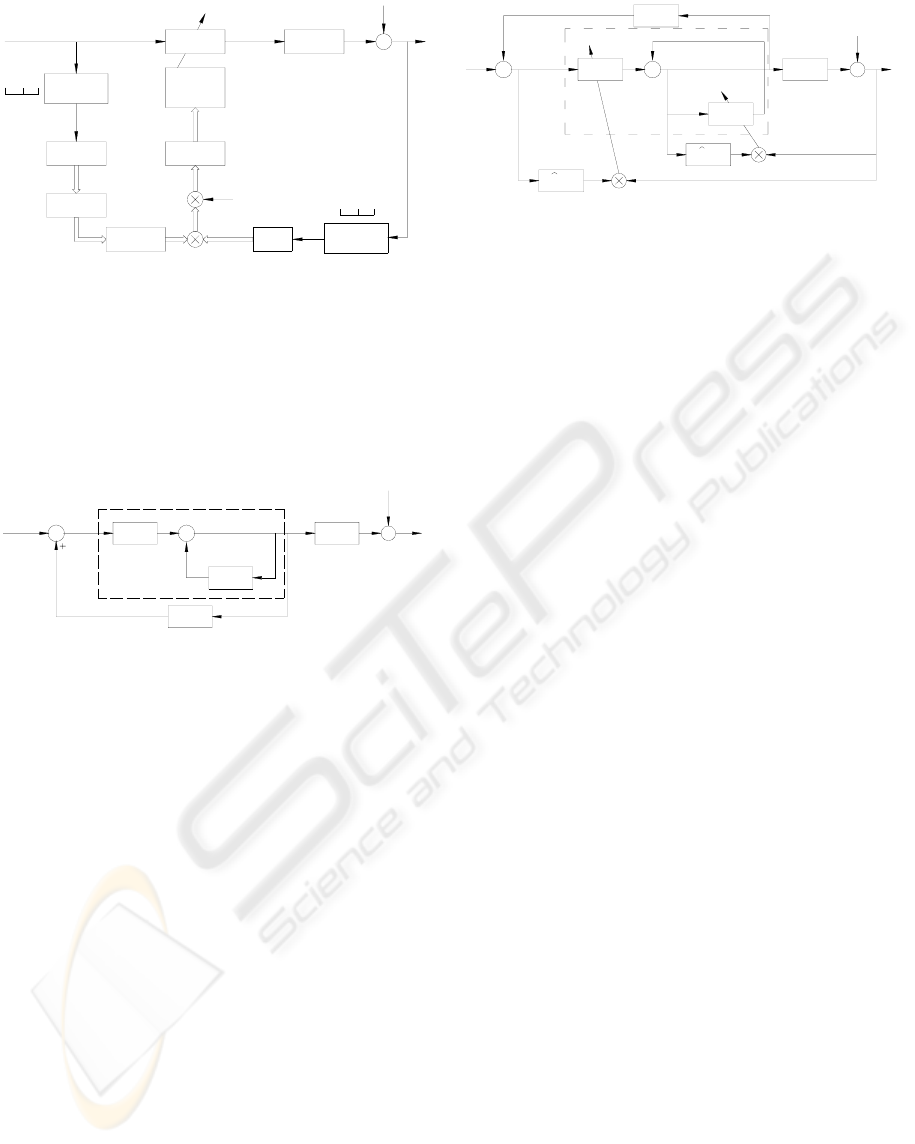
2.6 Filtered-u Algorithm
Up to now Finite Impulse Response (FIR) filters
have been considered to build the controllers.
However, Infinite Impulse Response (IIR) filters can
be used as well. In this case, the equivalent to fig.2
for IIR controllers is shown in fig. 6.
t(n)
H(z)
+
1-A(z)
B(z)
u(n)
f
s
G (z)
G (z)
e(n)
d(n)
s(n)
x(n)
+
+
+
+
Figure 6: Block diagram for IIR controller.
Compared with the block diagram of fig. 2 for the
FIR controllers, we can notice that this does not
possess a specific feedback to cancel the natural
feedback path of the system. In this case the
recursive characteristic of IIR controllers is assumed
to deal with the feedback path problem. However,
practice shows that if this estimation is included
numerical stability is guaranteed and the
performance is improved.
The filtered-u algorithm uses IIR filter as
controller. It is based on the recursive LMS (RLMS)
algorithm (see Elliot (2001) or Haykin (2002)). Fig.
7 shows the block diagram of the filtered-u
algorithm. The adaptation of the coefficients a
j
and b
i
is given by:
11
(1) () ()(nnen)n
γ
α
+= −aa t
)n
(15)
22
(1) () ()(nnen
γ
α
+= −bb r
(16)
where
α
1
,
α
2
are the convergence coefficients, t(n)
and r(n) are respectively the filtered output and the
filtered reference, and
γ
1
and
γ
2
are the forgetting
factors.
H(z)
u(n)
f
i
j
G (z)
G (z)
a (n)
b (n)
G'(z)
G'(z)
e(n)
d(n)
t(n)
r(n)
s(n)
x(n)
+
+
+
+
+
+
s
Figure 7: Block diagram for filtered-u algorithm.
The use of different convergence coefficients may be
shown in practice to allow for higher convergence
rates and the use of leakage factors slightly under 1
allows for a greater robustness of the algorithm
(Elliot, 2001). The plants modified response, G'(z), is
equal to G
s
(z). For that purpose, the coefficients of
the controller H(z) are assumed to be very slowly
adapted in comparison to the dynamics of the system
of the system G
s
(z). The same had already been
assumed for the adaptation of the FIR controller, but
for the adaptation of the IIR controller this is even
more necessary since the controller is recursive. One
of the interesting characteristics of the filtered-u
algorithm is that it presents a self-stabilising
behaviour that is also to be found in RLMS
algorithms (Elliot, 2001). During the adaptation of
the controller, if a pole leaves the unit-radius circle,
the natural evolution of filtered-u algorithm brings it
back inside. Although some researchers have
addressed this behaviour, still it was not possible to
discover the mechanism that results in this self-
stabilising property (Elliot, 2001). The self-
stabilising behaviour is found in many practical
applications, and that is why the filtered-u algorithm
is the most used in active cancellation of noise
applications (Elliot, 2001).
3 EXPERIMENTAL SET-UP
The experimental set-up used is shown in Fig. 8. A
PVC pipe with 0.125 m of diameter and 3 m of
length was used for simulating the cylindrical duct.
Given the diameter of the duct, the cut-on frequency,
which is the frequency above which waves may no
longer be considered plane, is 1360 Hz. To simulate
the acoustic noise to cancel a conventional
loudspeaker was placed in one of the ends of the
duct. At 1.25 m away from this end two loudspeakers
are placed to act as source of acoustics waves for
noise cancellation. For the detection of acoustic noise
a microphone, placed 0.08 m away from the primary
noise source, is used. The error microphone is placed
t the opposite end of the primary noise source. a
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
218

Windows - Matlab
xPC Target
NI-DAQ 6024E
A/D
20dB0dB
Amp.
212
1
D/A
Fc = 1050Hz
Low-Pass Filter
Pre-Amp
Slave Computer
Master Computer
Reference
Mic.
Source
Cancellation
Error
Mic.
Noise
Source
Figure 8: Block diagram of experimental setup.
Besides the duct, loudspeakers and microphones,
the experimental set-up consists of: four low-pass
filters that allow filtering the signals to remove the
effects of aliasing and zero-order-hold; an amplifier
that allows amplifying the signals that feed the
loudspeakers; pre-amplifiers for the microphones;
and two computers, one the slave act has a digital
controller and the other the master is used for data
analysis. The slave computer is a Pentium III
733MHz with 512MB of RAM memory, running on
xPC Target, having a data acquisition board NI-DAQ
6024E. Algorithms have been implemented as S-
Functions in the Matlab/Simulink environment.
Due to hardware restrictions on the cancellation
source this set-up cannot generate relevant signals
for frequencies below 200 Hz. Therefore, the
frequency range where acoustic noise cancellation is
intended is restricted to the frequency bandwidth of
[200 Hz - 1000 Hz].
4 IDENTIFICATION
The models used are discrete in time since the
implementation of the controller is made using a
digital computer. Therefore, the simulations will be
based on discrete models. This requires the models to
include the devices associated with the discretisation
and restoration of the signals, A/D and D/A
conversions, anti-aliasing and reconstruction filters,
and the dynamic of the microphones, loudspeakers
and amplifiers associated to the experimental set-up.
Assuming that the behaviour of these devices is
linear, then each one can be represented by a discrete
ransference function. The necessary models are: t
G
s
(z) - secondary acoustic path: includes computer -
secondary source - error microphone - computer;
G
f
(z) - acoustic feedback path: includes computer-
secondary source - reference microphone-computer.
Models have been obtained for the sampling
frequency of 2500 Hz (sampling time 0.4ms) because
that allows the Nyquist frequency of 1250Hz, to be
slightly larger than the superior limit of the frequency
range to cancel, 1000 Hz. FIR and ARX models have
been obtained. Variance account for (VAF) criterion
and root mean square (RMS) have been used for
models validation. Table 1 shows the results obtained
in these identifications.
Table 1: Order, VAF and RMS of the obtained models.
Order
FIR ARX
VAF (%) RMS (V)
Model
I n
a
n
b
FIR ARX FIR ARX
G
s
(z) 500 150 150 99.96 99.94 0.0193 0.0195
G
F
(z) 450 150 150 99.60 99.57 0.0363 0.0373
As shown above the obtained models have
excellent performances. This shows the plant to have
a linear behaviour being unnecessary to appeal to
ANC advanced techniques.
5 EXPERIMENTAL RESULTS
The previously mentioned algorithms have been
implemented and test for different noise conditions in
the duct. However, before presenting the results it
must be point out that the use of the normalisation of
the filtered reference signal was very important.
Experiences have shown that the normalised LMS
technique has a significant influence in the behaviour
of the algorithms. In fig. 9 the evolution of the
attenuation is shown for the FX-LMS algorithm
when the variance of white noise changed, for the
following cases: the filtered reference signal was not
normalized, was normalised using the Euclidean
norm, and was normalised using quadratic
normalization. The behaviour of the other algorithms
is similar. In the figures that follow, attenuation is
iven by the expression g
2
10
2
() 10log
Ee
Attenuation dB
Ed
⎛
⎡⎤
⎣⎦
⎜
=
⎜⎟
⎡⎤
⎣⎦
⎝⎠
⎞
⎟
(18)
where e is the error signal, d the disturbance and E[ ]
is the expected value operator. In this case the
expected value is given by the average of last 50
samples.
ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS
219

0 50 100 150 200
-25
-20
-15
-10
-5
0
5
10
15
Tim e (s)
Attenuation (dB)
Without normal.
Quadratic norm
Euclidean norm
Figure 9: Evolution of attenuation for the FX-LMS
algorithm.
As can be observed the normalization of the
filtered reference signal allows obtaining higher
attenuations. The quadratic norm is the only one that
ensures the stability of the algorithms when the
spectral power changes. If this were not the case
different adaptation steps would have to be used to
keep the algorithms stable.
For the comparison of the algorithms two types
of disturbances had been considered: white noise and
pure tones. The frequency range of the white noise is
[200 Hz; 1000 Hz], for the reason explained before.
Tones under 200 Hz have also not been used.
Parameters in the algorithms were chosen based
upon other experiences that had shown the influence
of parameters in algorithms performance. These
alues are: v
• FX-LMS: w = 200,
µ
= 0.10;
• MFX-LMS: w = 400,
µ
= 0.1;
• Filtered-u: n
a
= 150, n
b
= 100,
µ
a
= 0.01,
µ
b
= 0.025;
• FX-LMS Freq: w = 256,
µ
= 0.16.
Common to all the algorithms are the leakage factor,
equal to one, and the normalization method, which
was the quadratic norm.
Results are shown in fig. 10-13 for different
types of noise to be cancelled, and Table 2 that
indicates the computational burden for the white
oise case. n
• White noise
0 50 100 150 200 250 300
-20
-18
-16
-14
-12
-10
-8
-6
-4
-2
0
Time (s)
Attenuation (dB)
FX-LMS
Mod FX-LMS
Filtered-U
FX-LMS Freq
Figure 10: Evolution of attenuation for white noise.
Table 2: Execution time of each iteration for the white
noise case.
Algorithm
FX-
LMS
MFX-
LMS
Filtered
-u
FX-LMS
Freq
Average time (ms) 0.044 0.067 0.081 0.027
Maximum time (ms) 0.047 0.081 0.089 0.065
• Pure tones: 320 Hz + 640 Hz + 960Hz.
All pure tones have the same spectral power. The
adaptation steps of FX-LMS and FX-LMS Freq
algorithms had to be reduced so that they would
remain stable. Steps used were
µ
= 0,03 for the FX-
LMS and
µ
= 0,06 for the FX-LMS Freq.
0 5 10 15 20 25 30
-40
-35
-30
-25
-20
-15
-10
-5
0
Time (s)
Attenuation (dB)
FX-LMS
MFX-LMS
Filtered-u
FX-LMS Freq
Figure 21: Evolution of attenuation for pure tones.
The two previous figures show that the MFX-
LMS algorithm obtains a larger attenuation sooner
but the filtered-u algorithm obtains slightly larger
attenuations. These two algorithms get the best
performances of the four. Worst of them all is the
FX-LMS Freq, even though it presents the most
reduced average time for executing each iteration.
This shows how efficient algorithms are in the
frequency domain. However, the execution time of
each iteration is not important in this case since all
times are clearly under the sampling time of 0.4ms.
ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
220

This is because of the high computational power of
the slave computer.
Robustness to the variations of the model of the
eedback path f
An important question is the robustness to the
degradation of the model of the acoustic feedback
path G
f
(z), since when this model becomes poor the
simplification assumed on point 2.1 (that the model
cancels the feedback path exactly) is no longer
verified. If the residual of the cancellation is large,
the performance of the algorithms based on scheme
of Fig. 2 will degrade and may even be unstable.
The filtered-u algorithm can deal with the
feedback path problem. However, using the model of
Fig. 6, this algorithm has revealed to be unstable on
start. To solve this problem the adaptation steps had
to be reduced, and thus, have a slower evolution of
attenuation. Using the scheme of fig. 2 with filtered-
u algorithm has proved to be more robust and have a
faster and more regular evolution of attenuation.
That is why two experiences have been carried
out in which the performance of estimated model of
G
f
(z) was reduced. In the two following figures the
results for the MFX-LMS algorithms and filtered-u
algorithms are shown. Only those are shown because
they are the ones with better performances, as was
seen above. Parameters used in the algorithms are
those given above.
Figures 12 and 13 show that the filtered-u
algorithm is more robust to variations of the
estimated model of G
f
(z) model even though it leads
to more irregular evolutions. This shows that the
filtered-u algorithm is the one that should be applied
in practice since it has a performance identical to the
MFX-LMS but is more robust to modelling errors.
0 50 100 150 200 250 300
-20
-18
-16
-14
-12
-10
-8
-6
-4
-2
0
Time (s)
Attenuation (dB)
VAF = 99.6%
VAF = 99.0%
VAF = 95.0%
VAF = 90.0%
Figure 12: Evolution of attenuation for MFX-LMS
algorithm for different estimated models of G
f
(z).
0 50 100 150 200 250 300
-20
-18
-16
-14
-12
-10
-8
-6
-4
-2
0
Time (s)
Attenuation (dB)
VAF = 99.6%
VAF = 99.0%
VAF = 95.0%
VAF = 90.0%
Figure 13: Evolution of attenuation for filtered-u algorithm
for different estimated models of G
f
(z).
6 CONCLUSIONS
This paper evaluates the use of feedforward ANC to
cancel noise in ducts. The FX-LMS, NFX-LMS, Leaky
LMS, MFX-LMS, FX-LMS Freq and the Filtered-u
algorithms have been considered. The best
performance was achieved with the filtered-u
algorithm. Active cancellation of acoustic noise was
seen to be possible in practice since attenuations
obtained were about 18 dB for white noise and 35 dB
for pure tones. Moreover, algorithms were seen to be
robust when models degrade.
In what concerns the algorithms it was shown
that the normalization of the filtered reference signal
is of extreme importance allowing to ensure the
stability of the algorithms as well as better
attenuations. However this happens only for the
quadratic norm.
REFERENCES
Elliot, S. J., 2001. Signal Processing for Active
Control. Academic Press, London.
Haykin, Simon, 2002. Adaptive Filter Theory.
Prentice Hall, New Jersey, 4
th
edition.
Ogata, Katsuhiko, 1997. Modern Control
Engineering. Prentice Hall, New Jersey, 3
rd
edition.
Oppenheim, Alan V., Schafer, Ronald W. and Buck,
John R., 1999. Discrete-time Signal Processing.
Prentice Hall, New Jersey, 2
nd
edition.
Tokhi, M. and Leitch, R. R., 1992. Active Noise
Control. Oxford University Press, New York.
ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS
221
